Let ${\mathcal {A}}$ be a unital ${\mathbb {F}}$-algebra and let ${\mathcal {S}}$ be a generating set of ${\mathcal {A}}$. The length of ${\mathcal {S}}$ is the smallest number k such that ${\mathcal {A}}$ equals the ${\mathbb {F}}$-linear span of all products of length at most k of elements from ${\mathcal {S}}$. The length of ${\mathcal {A}}$, denoted by $l({\mathcal {A}})$, is defined to be the maximal length of its generating sets. We show that $l({\mathcal {A}})$ does not exceed the maximum of $\dim {\mathcal {A}} / 2$ and $m({\mathcal {A}})-1$, where $m({\mathcal {A}})$ is the largest degree of the minimal polynomial among all elements of the algebra ${\mathcal {A}}$. As an application, we show that for arbitrary odd n, the length of the group algebra of the dihedral group of order $2n$ equals n.

We use deformations and mutations of scattering diagrams to show that a scattering diagram with initial functions $f_1=(1+tx)^\mu $ and $f_2=(1+ty)^\nu $ has a dense region. This answers a question asked by Gross and Pandharipande [‘Quivers, curves, and the tropical vertex’, Port. Math. 67(2) (2010), 211–259] which had been proved only for the case $\mu =\nu $.

Our work owes its origin to a recent note of Ram Murty [‘Irrationality of zeros of the digamma function’, Number Theory in Memory of Eduard Wirsing (eds. H. Maier, R. Steuding and J. Steuding) (Springer, Cham, 2023), 237–243], in which he proves that all the zeros of the digamma function are irrational with at most one possible exception. We extend this investigation to higher-order polygamma functions.

Let $g(x)=x^3+ax^2+bx+c$ and $f(x)=g(x^3)$ be irreducible polynomials with rational coefficients, and let $ {\mathrm{Gal}}(f)$ be the Galois group of $f(x)$ over $\mathbb {Q}$. We show $ {\mathrm{Gal}}(f)$ is one of 11 possible transitive subgroups of $S_9$, defined up to conjugacy; we use $ {\mathrm{Disc}}(f)$, $ {\mathrm{Disc}}(g)$ and two additional low-degree resolvent polynomials to identify $ {\mathrm{Gal}}(f)$. We further show how our method can be used for determining one-parameter families for a given group. Also included is a related algorithm that, given a field $L/\mathbb {Q}$, determines when L can be defined by an irreducible polynomial of the form $g(x^3)$ and constructs such a polynomial when it exists.

We show that March’s criterion for the existence of a bounded nonconstant harmonic function on a weak model (that is, $\mathbb {R}^n$ with a rotationally symmetric metric) is also a necessary and sufficient condition for the solvability of the Dirichlet problem at infinity on a family of metrics that generalise metrics with rotational symmetry on $\mathbb {R}^n$. When the Dirichlet problem at infinity is not solvable, we prove some quantitative estimates on how fast a nonconstant harmonic function must grow.

H. H. Chan, K. S. Chua and P. Solé [‘Quadratic iterations to $\pi $ associated to elliptic functions to the cubic and septic base’, Trans. Amer. Math. Soc. 355(4) (2002), 1505–1520] found that, for each positive integer d, there are theta series 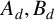$A_d, B_d$ and $C_d$ of weight one that satisfy the Pythagoras-like relationship 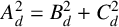$A_d^2=B_d^2+C_d^2$. In this article, we show that there are two collections of theta series 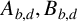$A_{b,d}, B_{b,d}$ and 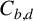$C_{b,d}$ of weight one that satisfy 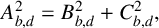$A_{b,d}^2=B_{b,d}^2+C_{b,d}^2,$ where b and d are certain integers.

We consider conjugacy classes in a locally compact group G that support finite G-invariant measures. If G is a property (M) extension of an abelian group, in particular, if G is a metabelian group, then any such conjugacy class is relatively compact. As an application, centralisers of lattices in such groups have bounded conjugacy classes. We use the same techniques to obtain results in the case of totally disconnected, locally compact groups.

In 2003, Ozsváth, Szabó and Rasmussen introduced the $\tau $ invariant for knots, and in 2011, Sarkar [‘Grid diagrams and the Ozsváth–Szabó tau-invariant’, Math. Res. Lett. 18(6) (2011), 1239–1257] published a computational shortcut for the $\tau $ invariant of knots that can be represented by diagonal grid diagrams. Previously, the only knots known to have diagonal grid diagram representations were torus knots. We prove that all such knots are positive knots and we produce an example of a knot with a diagonal grid diagram representation which is not a torus knot.

We show that for any set D of at least two digits in a given base b, almost all even integers taking digits only in D when written in base b satisfy the Goldbach conjecture. More formally, if $\mathcal {A}$ is the set of numbers whose digits base b are exclusively from D, almost all elements of $\mathcal {A}$ satisfy the Goldbach conjecture. Moreover, the number of even integers in $\mathcal {A}$ which are less than X and not representable as the sum of two primes is less than $|\mathcal {A}\cap \{1,\ldots ,X\}|^{1-\delta }$.

Let E be an elliptic curve defined over $\mathbb {Q}$ with good ordinary reduction at a prime $p\geq 5$ and let F be an imaginary quadratic field. Under appropriate assumptions, we show that the Pontryagin dual of the fine Mordell–Weil group of E over the $\mathbb {Z}_{p}^2$-extension of F is pseudo-null as a module over the Iwasawa algebra of the group $\mathbb {Z}_{p}^2$.

We compute primes $p \equiv 5 \bmod 8$ up to $10^{11}$ for which the Pellian equation $x^2-py^2=-4$ has no solutions in odd integers; these are the members of sequence A130229 in the Online Encyclopedia of Integer Sequences. We find that the number of such primes $p\leqslant x$ is well approximated by

$$ \begin{align*}\frac{1}{12}\pi(x) - 0.037\int_2^x \frac{dt}{t^{1/6}\log t},\end{align*} $$

where $\pi (x)$ is the usual prime counting function. The second term shows a surprising bias away from membership of this sequence.

Let $\{\omega _n\}_{n\geq 1}$ be a sequence of independent and identically distributed random variables on a probability space $(\Omega , \mathcal {F}, \mathbb {P})$, each uniformly distributed on the unit circle $\mathbb {T}$, and let $\ell _n=cn^{-\tau }$ for some $c>0$ and $0<\tau <1$. Let $I_{n}=(\omega _n,\omega _n+\ell _n)$ be the random interval with left endpoint $\omega _n$ and length $\ell _n$. We study the asymptotic property of the covering time $N_n(x)=\sharp \{1\leq k\leq n: x\in I_k\}$ for each $x\in \mathbb {T}$. We prove the quenched central limit theorem for the covering time, that is, $\mathbb {P}$-almost surely,

$$ \begin{align*}\frac{N_n(x)-\mathbb{E}_{\mathbb{P}}(N_n(x))}{\sqrt{\sum_{k=1}^n \ell_k(1-\ell_k)}}\end{align*} $$

converges in law to the standard normal distribution.

Given a unital $C^*$-algebra and a faithful trace, we prove that the topology on the associated density space induced by the $C^*$-norm is finer than the Bures metric topology. We also provide an example when this containment is strict. Next, we provide a metric on the density space induced by a quantum metric in the sense of Rieffel and prove that the induced topology is the same as the topology induced by the Bures metric and $C^*$-norm when the $C^*$-algebra is assumed to be finite dimensional. Finally, we provide an example where the Bures metric and induced quantum metric are not metric equivalent. Thus, we provide a bridge between these aspects of quantum information theory and noncommutative metric geometry.

Let X be a smooth projective variety defined over a number field K. We give an upper bound for the generalised greatest common divisor of a point $x\in X$ with respect to an irreducible subvariety $Y\subseteq X$ also defined over K. To prove the result, we establish a rather uniform Riemann–Roch-type inequality.

For an integer $k \geq 2$, let $P_{n}^{(k)}$ be the k-generalised Pell sequence, which starts with $0, \ldots ,0,1$ (k terms), and each term thereafter is given by the recurrence $P_{n}^{(k)} = 2 P_{n-1}^{(k)} +P_{n-2}^{(k)} +\cdots +P_{n-k}^{(k)}$. We search for perfect powers, which are sums or differences of two k-generalised Pell numbers.

We consider the relationship between the Mahler measure $M(f)$ of a polynomial f and its separation $\operatorname {sep}(f)$. Mahler [‘An inequality for the discriminant of a polynomial’, Michigan Math. J. 11 (1964), 257–262] proved that if $f(x) \in \mathbb {Z}[x]$ is separable of degree n, then $\operatorname {sep}(f) \gg _n M(f)^{-(n-1)}$. This spurred further investigations into the implicit constant involved in that relationship and led to questions about the optimal exponent on $M(f)$. However, there has been relatively little study concerning upper bounds on $\operatorname {sep}(f)$ in terms of $M(f)$. We prove that if $f(x) \in \mathbb {C}[x]$ has degree n, then $\operatorname {sep}(f) \ll n^{-1/2}M(f)^{1/(n-1)}$. Moreover, this bound is sharp up to the implied constant factor. We further investigate the constant factor under various additional assumptions on $f(x)$; for example, if it has only real roots.

Consider a possibly unsaturated Fell bundle $\mathcal {A}\to G$ over a locally compact, possibly non-Hausdorff, groupoid G. We list four notions of continuity of representations of $\mathit {C_c}(G;\mathcal {A})$ on a Hilbert space and prove their equivalence. This allows us to define the full $\mathit {C}^*$-algebra of the Fell bundle in different ways.