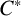1. Introduction and background
The Bures metric, which was introduced by Bures in [Reference Bures2], is a vital tool in quantum information theory (for example, the Bures metric is the quantum version of the Hellinger distance; see [Reference Hayashi6, Section 3.1.2]). Recently, the Bures metric has been adapted to von Neumann algebras and
![]() $C^*$
-algebras by Farenick and Rahaman [Reference Farenick and Rahaman4]. The quantum metric, which was introduced by Rieffel in [Reference Rieffel11], allows one to prove powerful results about convergence of quantum spaces including those arising from high energy physics (see [Reference Reiffel10], where Rieffel proved that matrix algebras converge to the sphere and continuity of quantum tori) and many more continuity results related to the
$C^*$
-algebras by Farenick and Rahaman [Reference Farenick and Rahaman4]. The quantum metric, which was introduced by Rieffel in [Reference Rieffel11], allows one to prove powerful results about convergence of quantum spaces including those arising from high energy physics (see [Reference Reiffel10], where Rieffel proved that matrix algebras converge to the sphere and continuity of quantum tori) and many more continuity results related to the
![]() $C^*$
-algebraic structure and noncommutative geometric structure (see [Reference Aguilar and Yu1, Reference Farsi, Latrémolière and Packer5, Reference Kaad and Kyed7–Reference Latrémolière and Packer9]). This paper brings these two important metrics together in a natural way to make comparisons between their topological and geometric properties in the hope of introducing these methods of measurement to the other field.
$C^*$
-algebraic structure and noncommutative geometric structure (see [Reference Aguilar and Yu1, Reference Farsi, Latrémolière and Packer5, Reference Kaad and Kyed7–Reference Latrémolière and Packer9]). This paper brings these two important metrics together in a natural way to make comparisons between their topological and geometric properties in the hope of introducing these methods of measurement to the other field.
In Section 2, we provide comparisons of the topological structure of the Bures metric and a third metric, the one induced by the
![]() $C^*$
-norm on the density space. The purpose of bringing this third metric into the picture is not just to provide another interesting comparison, but also to provide a method of comparing the Bures metric and the quantum metric. In Section 3, we show how one can place a metric on the density space using quantum metrics, and then show that this induced quantum metric is topologically equivalent to the Bures metric. Our approach uses the results in Section 2. Finally, in Section 4, we provide a case when the Bures metric and induced quantum metric are not metric equivalent, which is of interest since contractivity of quantum channels is a main aspect of quantum information theory [Reference Farenick and Rahaman4]. The quantum metric approach offers a truly new avenue to study contractivity of quantum channels and fixed points while still agreeing with the Bures metric topology. For the remainder of this section, we provide some necessary background for the rest of the paper.
$C^*$
-norm on the density space. The purpose of bringing this third metric into the picture is not just to provide another interesting comparison, but also to provide a method of comparing the Bures metric and the quantum metric. In Section 3, we show how one can place a metric on the density space using quantum metrics, and then show that this induced quantum metric is topologically equivalent to the Bures metric. Our approach uses the results in Section 2. Finally, in Section 4, we provide a case when the Bures metric and induced quantum metric are not metric equivalent, which is of interest since contractivity of quantum channels is a main aspect of quantum information theory [Reference Farenick and Rahaman4]. The quantum metric approach offers a truly new avenue to study contractivity of quantum channels and fixed points while still agreeing with the Bures metric topology. For the remainder of this section, we provide some necessary background for the rest of the paper.
Convention 1.1. Given a unital
![]() $C^*$
-algebra
$C^*$
-algebra
![]() ${\mathcal {A}}$
, we denote its unit by
${\mathcal {A}}$
, we denote its unit by
![]() $1_{\mathcal {A}}$
, its norm by
$1_{\mathcal {A}}$
, its norm by
![]() $\|\cdot \|_{\mathcal {A}}$
, its self-adjoint elements by
$\|\cdot \|_{\mathcal {A}}$
, its self-adjoint elements by
![]() $\mbox {sa}({\mathcal {A}})$
and positive elements by
$\mbox {sa}({\mathcal {A}})$
and positive elements by
![]() ${\mathcal {A}}_+$
. We denote its state space by
${\mathcal {A}}_+$
. We denote its state space by
![]() $S({\mathcal {A}})$
. We also denote the metric induced by
$S({\mathcal {A}})$
. We also denote the metric induced by
![]() $\|\cdot \|_{\mathcal {A}}$
by
$\|\cdot \|_{\mathcal {A}}$
by
![]() $d_{\mathcal {A}}.$
$d_{\mathcal {A}}.$
However, given a compact Hausdorff space X, we denote the
![]() $C^*$
-norm on
$C^*$
-norm on
![]() $C(X)$
by
$C(X)$
by
![]() $\|\cdot \|_X$
and the unit (the constant
$\|\cdot \|_X$
and the unit (the constant
![]() $1$
function) by
$1$
function) by ![]() .
.
Definition 1.2 [Reference Rieffel11].
Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra. If
$C^*$
-algebra. If
![]() $L:{\mathcal {A}} \rightarrow [0,\infty ]$
is a seminorm on
$L:{\mathcal {A}} \rightarrow [0,\infty ]$
is a seminorm on
![]() ${\mathcal {A}}$
such that:
${\mathcal {A}}$
such that:
-
(1)
 $\mbox {dom}(L)=\{a \in {\mathcal {A}} : L(a)< \infty \}$
is dense in
$\mbox {dom}(L)=\{a \in {\mathcal {A}} : L(a)< \infty \}$
is dense in
 ${\mathcal {A}}$
;
${\mathcal {A}}$
; -
(2)
 $L(a)=0$
if and only if
$L(a)=0$
if and only if
 $a \in {\mathbb {C}}1_{\mathcal {A}}$
;
$a \in {\mathbb {C}}1_{\mathcal {A}}$
; -
(3)
 $L(a)=L(a^*)$
for every
$L(a)=L(a^*)$
for every
 $a \in {\mathcal {A}}$
; and
$a \in {\mathcal {A}}$
; and -
(4) the Monge–Kantorovich metric, defined for any two states
 $\varphi , \psi \in S({\mathcal {A}})$
by metrises the weak* topology on
$\varphi , \psi \in S({\mathcal {A}})$
by metrises the weak* topology on $$ \begin{align*}\mbox{mk}_L(\varphi, \psi)=\textrm{sup} \{ |\varphi(a)- \psi(a)| : a \in {\mathcal{A}}, L(a) \leqslant 1\}, \end{align*} $$
$$ \begin{align*}\mbox{mk}_L(\varphi, \psi)=\textrm{sup} \{ |\varphi(a)- \psi(a)| : a \in {\mathcal{A}}, L(a) \leqslant 1\}, \end{align*} $$
 $S({\mathcal {A}}),$
$S({\mathcal {A}}),$
then
![]() $({\mathcal {A}}, L)$
is a compact quantum metric space, and we call L an L-seminorm.
$({\mathcal {A}}, L)$
is a compact quantum metric space, and we call L an L-seminorm.
Theorem-Definition 1.3 [Reference Farenick and Rahaman4, Theorem 2.6].
Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra. Let
$C^*$
-algebra. Let
![]() $\tau $
be a faithful trace. Define the density space with respect to
$\tau $
be a faithful trace. Define the density space with respect to
![]() $\tau $
to be
$\tau $
to be
Define the Bures metric with respect to
![]() $\tau $
for every
$\tau $
for every
![]() $x,y \in D_\tau ({\mathcal {A}})$
by
$x,y \in D_\tau ({\mathcal {A}})$
by
Here, by a faithful trace, we mean a positive linear functional (not necessarily of norm one) such that, for every
![]() $a,b \in {\mathcal {A}}$
, we have
$a,b \in {\mathcal {A}}$
, we have
![]() $\tau (ab)=\tau (ba)$
and
$\tau (ab)=\tau (ba)$
and
![]() $\tau (a^*a)=0$
implies that
$\tau (a^*a)=0$
implies that
![]() $a=0$
. We call the statement above a ‘Theorem-Definition’ since the proof that the Bures metric is indeed a metric in this general setting of unital
$a=0$
. We call the statement above a ‘Theorem-Definition’ since the proof that the Bures metric is indeed a metric in this general setting of unital
![]() $C^*$
-algebras equipped with a faithful trace is a nontrivial result of [Reference Farenick and Rahaman4].
$C^*$
-algebras equipped with a faithful trace is a nontrivial result of [Reference Farenick and Rahaman4].
We also formally state what we mean by topological equivalence and metric equivalence so that there is no confusion.
Definition 1.4. Let X be a nonempty set and let d and
![]() $d'$
be two metrics on X.
$d'$
be two metrics on X.
-
(1) We say that d and
 $d'$
are topologically equivalent if they induce the same topologies.
$d'$
are topologically equivalent if they induce the same topologies. -
(2) We say that d and
 $d'$
are metric equivalent if there exist
$d'$
are metric equivalent if there exist
 $\alpha ,\beta>0$
such that or, equivalently,
$\alpha ,\beta>0$
such that or, equivalently, $$ \begin{align*} \alpha d(x,y) \leqslant d'(x,y) \leqslant \beta d(x,y) \quad\mbox{for every } x,y \in X, \end{align*} $$
$$ \begin{align*} \alpha d(x,y) \leqslant d'(x,y) \leqslant \beta d(x,y) \quad\mbox{for every } x,y \in X, \end{align*} $$
 $$ \begin{align*} \alpha \leqslant \frac{d'(x,y)}{d(x,y)} \leqslant\beta \quad\mbox{for every } x,y \in X \mbox{ such that } x \neq y. \end{align*} $$
$$ \begin{align*} \alpha \leqslant \frac{d'(x,y)}{d(x,y)} \leqslant\beta \quad\mbox{for every } x,y \in X \mbox{ such that } x \neq y. \end{align*} $$
2. Comparison of the
 $C^*$
-metric and Bures metric topologies
$C^*$
-metric and Bures metric topologies
In this section, we show that the
![]() $C^*$
-metric topology is finer than the topology induced by the Bures metric. We also show that this containment can be strict by providing an explicit example in the
$C^*$
-metric topology is finer than the topology induced by the Bures metric. We also show that this containment can be strict by providing an explicit example in the
![]() $C^*$
-algebra of complex-valued continuous functions on
$C^*$
-algebra of complex-valued continuous functions on
![]() $[0,1]$
with the trace given by Lebesgue integration. First, we prove two lemmas that are likely to be well known, but we provide their proofs for convenience.
$[0,1]$
with the trace given by Lebesgue integration. First, we prove two lemmas that are likely to be well known, but we provide their proofs for convenience.
Lemma 2.1. Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra. Let
$C^*$
-algebra. Let
![]() $(x_n)_{n \in {\mathbb {N}}}$
be a sequence in
$(x_n)_{n \in {\mathbb {N}}}$
be a sequence in
![]() ${\mathcal {A}}_+$
that converges in the
${\mathcal {A}}_+$
that converges in the
![]() $C^*$
-norm to
$C^*$
-norm to
![]() $x \in {\mathcal {A}}_+$
. Let
$x \in {\mathcal {A}}_+$
. Let
![]() $r \geqslant 0$
be such that, for any
$r \geqslant 0$
be such that, for any
![]() $n \in {\mathbb {N}}$
,
$n \in {\mathbb {N}}$
,
![]() $\| x_n \|_{\mathcal {A}}, \| x \|_{\mathcal {A}} \leqslant r$
. If
$\| x_n \|_{\mathcal {A}}, \| x \|_{\mathcal {A}} \leqslant r$
. If
![]() $f:[0,r] \rightarrow \mathbb {R}$
is continuous, then
$f:[0,r] \rightarrow \mathbb {R}$
is continuous, then
![]() $(f(x_n))_{n \in {\mathbb {N}}}$
converges to
$(f(x_n))_{n \in {\mathbb {N}}}$
converges to
![]() $f(x)$
in the
$f(x)$
in the
![]() $C^*$
-norm.
$C^*$
-norm.
Proof. By the Weierstrass approximation theorem, there exist polynomials
![]() $(p_n)_{n \in {\mathbb {N}}}$
that converge uniformly to f on
$(p_n)_{n \in {\mathbb {N}}}$
that converge uniformly to f on
![]() $[0, r]$
.
$[0, r]$
.
Let
![]() $\varepsilon> 0$
. By uniform convergence of
$\varepsilon> 0$
. By uniform convergence of
![]() $(p_n)_{n \in {\mathbb {N}}}$
to f, there exists
$(p_n)_{n \in {\mathbb {N}}}$
to f, there exists
![]() $N \in {\mathbb {N}}$
such that, for any
$N \in {\mathbb {N}}$
such that, for any
![]() $n \geqslant N$
, we have
$n \geqslant N$
, we have
![]() $\|p_n - f\|_{[0,r]} < {\varepsilon }/{3}$
, and, in particular,
$\|p_n - f\|_{[0,r]} < {\varepsilon }/{3}$
, and, in particular,
![]() $\|p_N - f\|_{[0,r]} < {\varepsilon }/{3}$
. Since
$\|p_N - f\|_{[0,r]} < {\varepsilon }/{3}$
. Since
![]() $p_N$
is a polynomial, there exists
$p_N$
is a polynomial, there exists
![]() $N^{\prime } \geqslant N$
such that, for any
$N^{\prime } \geqslant N$
such that, for any
![]() $n \geqslant N^{\prime }$
,
$n \geqslant N^{\prime }$
,
Let
![]() $n \geqslant N'$
. By functional calculus,
$n \geqslant N'$
. By functional calculus,
since
![]() $\sigma (x_n) \subseteq [0,r]$
. Similarly,
$\sigma (x_n) \subseteq [0,r]$
. Similarly,
since
![]() $\sigma (x)\subseteq [0,r]$
. By the triangle inequality for the norm,
$\sigma (x)\subseteq [0,r]$
. By the triangle inequality for the norm,
 $$ \begin{align*} \|f(x_n) - f(x)\|_{\mathcal{A}} & \leqslant \|f(x_n) - p_N(x_n)\|_{\mathcal{A}} + \|p_N(x_n) - p(x)\|_{\mathcal{A}} + \|p_N(x) - f(x)\|_{\mathcal{A}} \\ & < \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} = \varepsilon. \end{align*} $$
$$ \begin{align*} \|f(x_n) - f(x)\|_{\mathcal{A}} & \leqslant \|f(x_n) - p_N(x_n)\|_{\mathcal{A}} + \|p_N(x_n) - p(x)\|_{\mathcal{A}} + \|p_N(x) - f(x)\|_{\mathcal{A}} \\ & < \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} = \varepsilon. \end{align*} $$
Thus, for any
![]() $\varepsilon> 0$
, we can find
$\varepsilon> 0$
, we can find
![]() $N^{\prime }$
such that
$N^{\prime }$
such that
![]() $\|f(x_n) - f(x)\|_{\mathcal {A}} \leqslant \varepsilon $
for any
$\|f(x_n) - f(x)\|_{\mathcal {A}} \leqslant \varepsilon $
for any
![]() $n \geqslant N^{\prime }$
. Thus,
$n \geqslant N^{\prime }$
. Thus,
![]() $(f(x_n))_{n \in {\mathbb {N}}}$
converges to
$(f(x_n))_{n \in {\mathbb {N}}}$
converges to
![]() $f(x)$
in the
$f(x)$
in the
![]() $C^*$
-norm.
$C^*$
-norm.
Lemma 2.2. Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra. If
$C^*$
-algebra. If
![]() $(x_n)_{n \in {\mathbb {N}}}$
is a sequence in
$(x_n)_{n \in {\mathbb {N}}}$
is a sequence in
![]() ${\mathcal {A}}$
that converges in the
${\mathcal {A}}$
that converges in the
![]() $C^*$
-norm to some
$C^*$
-norm to some
![]() $x \in {\mathcal {A}}$
, then
$x \in {\mathcal {A}}$
, then
![]() $(|x_n|)_{n \in {\mathbb {N}}}$
converges in the
$(|x_n|)_{n \in {\mathbb {N}}}$
converges in the
![]() $C^*$
-norm to
$C^*$
-norm to
![]() $|x|$
.
$|x|$
.
Proof. Note that
![]() $|x| = \sqrt {x^* x}$
and
$|x| = \sqrt {x^* x}$
and
![]() $|x_n| = \sqrt {x_n^* x_n}$
for every
$|x_n| = \sqrt {x_n^* x_n}$
for every
![]() $n \in {\mathbb {N}}$
. For any
$n \in {\mathbb {N}}$
. For any
![]() $n \in {\mathbb {N}}$
, let
$n \in {\mathbb {N}}$
, let
![]() $a_n = x_n^* x_n$
and
$a_n = x_n^* x_n$
and
![]() $a = x^* x$
. Since multiplication and the adjoint are continuous in the
$a = x^* x$
. Since multiplication and the adjoint are continuous in the
![]() $C^*$
-norm,
$C^*$
-norm,
![]() $(a_n)_{n \in {\mathbb {N}}}$
converges to a in the
$(a_n)_{n \in {\mathbb {N}}}$
converges to a in the
![]() $C^*$
-norm. For any
$C^*$
-norm. For any
![]() $n \in {\mathbb {N}}$
,
$n \in {\mathbb {N}}$
,
![]() $|x| = \sqrt {a}$
and
$|x| = \sqrt {a}$
and
![]() $|x_n| = \sqrt {a_n}$
. Therefore, by Lemma 2.1 and continuity of the square root, we know that
$|x_n| = \sqrt {a_n}$
. Therefore, by Lemma 2.1 and continuity of the square root, we know that
![]() $(|x_n|)_{n \in {\mathbb {N}}}$
converges to
$(|x_n|)_{n \in {\mathbb {N}}}$
converges to
![]() $|x|$
in the
$|x|$
in the
![]() $C^*$
-norm.
$C^*$
-norm.
We now prove our main theorem that allows us to compare the
![]() $C^*$
-metric topology and the Bures metric topology.
$C^*$
-metric topology and the Bures metric topology.
Theorem 2.3. Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\tau $
be a faithful trace. Let
$\tau $
be a faithful trace. Let
![]() $(x_n)_{n \in {\mathbb {N}}}$
be a sequence in
$(x_n)_{n \in {\mathbb {N}}}$
be a sequence in
![]() $D_{\tau }({\mathcal {A}})$
and let
$D_{\tau }({\mathcal {A}})$
and let
![]() $x \in D_{\tau }({\mathcal {A}})$
. If
$x \in D_{\tau }({\mathcal {A}})$
. If
![]() $(x_n)_{n \in {\mathbb {N}}}$
converges to x in the
$(x_n)_{n \in {\mathbb {N}}}$
converges to x in the
![]() $C^*$
-norm, then
$C^*$
-norm, then
![]() $(x_n)_{n \in {\mathbb {N}}}$
converges to x with respect to the Bures metric
$(x_n)_{n \in {\mathbb {N}}}$
converges to x with respect to the Bures metric
![]() $d_{B}^{\tau }$
.
$d_{B}^{\tau }$
.
Proof. If
![]() $(x_n)_{n \in {\mathbb {N}}}$
converges to x in the
$(x_n)_{n \in {\mathbb {N}}}$
converges to x in the
![]() $C^*$
-norm, then, since
$C^*$
-norm, then, since
![]() $g(x) = \sqrt {x}$
is continuous,
$g(x) = \sqrt {x}$
is continuous,
![]() $(\sqrt {x_n})_{n \in {\mathbb {N}}}$
converges to
$(\sqrt {x_n})_{n \in {\mathbb {N}}}$
converges to
![]() $\sqrt {x}$
in the
$\sqrt {x}$
in the
![]() $C^*$
-norm by Lemma 2.1.
$C^*$
-norm by Lemma 2.1.
Since x is positive and fixed,
![]() $(\sqrt {x_n}\cdot \sqrt {x})_{n \in {\mathbb {N}}}$
converges to
$(\sqrt {x_n}\cdot \sqrt {x})_{n \in {\mathbb {N}}}$
converges to
![]() $\sqrt {x} \cdot \sqrt {x}$
in the
$\sqrt {x} \cdot \sqrt {x}$
in the
![]() $C^*$
-norm. By definition,
$C^*$
-norm. By definition,
![]() $\sqrt {x} \cdot \sqrt {x} = x$
, so
$\sqrt {x} \cdot \sqrt {x} = x$
, so
![]() $(\sqrt {x_n}\cdot \sqrt {x})_{n \in {\mathbb {N}}}$
converges in the
$(\sqrt {x_n}\cdot \sqrt {x})_{n \in {\mathbb {N}}}$
converges in the
![]() $C^*$
-norm to x. By Lemma 2.2, this implies that
$C^*$
-norm to x. By Lemma 2.2, this implies that
![]() $(|\sqrt {x_n}\cdot \sqrt {x}|)_{n \in {\mathbb {N}}}$
converges in the
$(|\sqrt {x_n}\cdot \sqrt {x}|)_{n \in {\mathbb {N}}}$
converges in the
![]() $C^*$
-norm to
$C^*$
-norm to
![]() $|x|=x$
.
$|x|=x$
.
Since
![]() $\tau $
is
$\tau $
is
![]() $C^*$
-norm continuous,
$C^*$
-norm continuous,
![]() $(|\sqrt {x_n}\cdot \sqrt {x}|)_{n \in {\mathbb {N}}}$
converging to x in the
$(|\sqrt {x_n}\cdot \sqrt {x}|)_{n \in {\mathbb {N}}}$
converging to x in the
![]() $C^*$
-norm implies that
$C^*$
-norm implies that
![]() $(\tau (|\sqrt {x_n}\cdot \sqrt {x}|))_{n \in {\mathbb {N}}}$
converges to
$(\tau (|\sqrt {x_n}\cdot \sqrt {x}|))_{n \in {\mathbb {N}}}$
converges to
![]() $\tau (x)$
. Since
$\tau (x)$
. Since
![]() $x \in D_{\tau }(A)$
, we have
$x \in D_{\tau }(A)$
, we have
![]() $\tau (x) = 1$
. Hence,
$\tau (x) = 1$
. Hence,
![]() $(\tau (|\sqrt {x_n}\cdot \sqrt {x}|))_{n \in {\mathbb {N}}}$
converges to
$(\tau (|\sqrt {x_n}\cdot \sqrt {x}|))_{n \in {\mathbb {N}}}$
converges to
![]() $1$
.
$1$
.
Consider
Since
![]() $(\tau (|\sqrt {x_n}\cdot \sqrt {x}|))_{n \in {\mathbb {N}}}$
converges to
$(\tau (|\sqrt {x_n}\cdot \sqrt {x}|))_{n \in {\mathbb {N}}}$
converges to
![]() $1$
, it follows that
$1$
, it follows that
![]() $(d_{B}^{\tau }(x_n,x))_{n \in {\mathbb {N}}} $
converges to
$(d_{B}^{\tau }(x_n,x))_{n \in {\mathbb {N}}} $
converges to
![]() $\sqrt {1-1} = 0$
. Hence,
$\sqrt {1-1} = 0$
. Hence,
![]() $(x_n)_{n \in {\mathbb {N}}}$
converges to x with respect to the Bures metric
$(x_n)_{n \in {\mathbb {N}}}$
converges to x with respect to the Bures metric
![]() $d_{B}^{\tau }$
.
$d_{B}^{\tau }$
.
Corollary 2.4. Let
![]() ${\mathcal {A}}$
be a unital C*-algebra and let
${\mathcal {A}}$
be a unital C*-algebra and let
![]() $\tau $
be a faithful trace. Then the topology induced by
$\tau $
be a faithful trace. Then the topology induced by
![]() $d_{\mathcal {A}}$
is finer than the topology induced by
$d_{\mathcal {A}}$
is finer than the topology induced by
![]() $d_B^\tau $
.
$d_B^\tau $
.
This raises the question of whether these topologies are the same in general. The answer is no, and the rest of this section is devoted to providing an example on which these topologies disagree.
Consider,
![]() $C([0,1])$
, the
$C([0,1])$
, the
![]() $C^*$
-algebra of continuous complex-valued functions on
$C^*$
-algebra of continuous complex-valued functions on
![]() $[0,1]$
. The map
$[0,1]$
. The map
 $$ \begin{align*} \rho: f \in C([0,1]) \longmapsto \int_0^1 f(x) \, dx, \end{align*} $$
$$ \begin{align*} \rho: f \in C([0,1]) \longmapsto \int_0^1 f(x) \, dx, \end{align*} $$
where
![]() $\int _0^1 \cdot \, dx$
is the standard Lebesgue integral, is a faithful trace on
$\int _0^1 \cdot \, dx$
is the standard Lebesgue integral, is a faithful trace on
![]() $C([0,1])$
.
$C([0,1])$
.
Proposition 2.5. The topology induced by the metric
![]() $d_{C([0,1])}$
induced by the
$d_{C([0,1])}$
induced by the
![]() $C^*$
-norm on the density space
$C^*$
-norm on the density space
![]() $D_\rho (C([0,1]))$
is strictly finer than the topology induced by the Bures metric
$D_\rho (C([0,1]))$
is strictly finer than the topology induced by the Bures metric
![]() $d_B^\rho .$
$d_B^\rho .$
Proof. The fact that the topology induced by
![]() $d_{C([0,1])}$
is finer is provided by Corollary 2.4. Thus, it remains to show that the topologies are not equal. To accomplish this, we find a sequence in
$d_{C([0,1])}$
is finer is provided by Corollary 2.4. Thus, it remains to show that the topologies are not equal. To accomplish this, we find a sequence in
![]() $D_\rho (C([0,1]))$
that converges with respect to
$D_\rho (C([0,1]))$
that converges with respect to
![]() $d_B^\rho $
, but does not converge uniformly (that is, with respect to
$d_B^\rho $
, but does not converge uniformly (that is, with respect to
![]() $d_{C([0,1])}$
).
$d_{C([0,1])}$
).
Let
![]() $n \in {\mathbb {N}}$
. Consider
$n \in {\mathbb {N}}$
. Consider
 $$ \begin{align} f_{n}(x)= \begin{cases} 2nx & \text{if } x \in [0, {1}/{2n}],\\ 1 & \text{if } x \in ({1}/{2n}, 1-{1}/{2n}),\\ 2nx-2n+2 & \text{if } x \in [1-{1}/{2n}, 1], \end{cases} \end{align} $$
$$ \begin{align} f_{n}(x)= \begin{cases} 2nx & \text{if } x \in [0, {1}/{2n}],\\ 1 & \text{if } x \in ({1}/{2n}, 1-{1}/{2n}),\\ 2nx-2n+2 & \text{if } x \in [1-{1}/{2n}, 1], \end{cases} \end{align} $$
defined for all
![]() $x \in [0,1]$
(see Figure 1). Note that
$x \in [0,1]$
(see Figure 1). Note that
![]() $f_n \in C([0,1]).$
Define
$f_n \in C([0,1]).$
Define
![]() $f:[0,1]\rightarrow {\mathbb {R}}$
by
$f:[0,1]\rightarrow {\mathbb {R}}$
by
![]() $f(x)=1$
for all
$f(x)=1$
for all
![]() $x \in [0,1].$
Note that
$x \in [0,1].$
Note that
![]() $f \in D_\rho (C([0,1])).$
$f \in D_\rho (C([0,1])).$

Figure 1
![]() $f_1,f_2,f_3$
given by the formula (2.1). (Plotted in GeoGebra).
$f_1,f_2,f_3$
given by the formula (2.1). (Plotted in GeoGebra).
Next, we check that
![]() $f_n\in D_\rho (C([0,1])$
for every
$f_n\in D_\rho (C([0,1])$
for every
![]() $n \in {\mathbb {N}}$
. Let
$n \in {\mathbb {N}}$
. Let
![]() $n\in {\mathbb {N}}$
. First,
$n\in {\mathbb {N}}$
. First,
![]() $f_n\geqslant 0$
by construction. Second,
$f_n\geqslant 0$
by construction. Second,
 $$ \begin{align*} \rho(f_n) = \int_{0}^{1} f_n(x) \,dx & = \int_{0}^{{1}/{2n}} 2nx \,dx + \int_{{1}/{2n}}^{1 - {1}/{2n}} 1 \,dx + \int_{1 - {1}/{2n}}^{1} (2nx-2n+2) \,dx \\ &= [nx^2]_0^{{1}/{2n}} + [x]_{{1}/{2n}}^{1 - {1}/{2n}} + [nx^2-2nx+2x]_{1 - {1}/{2n}}^{1} \\ &= \frac{1}{4n} + 1 - \frac{1}{n} + \frac{3}{4n} = 1. \end{align*} $$
$$ \begin{align*} \rho(f_n) = \int_{0}^{1} f_n(x) \,dx & = \int_{0}^{{1}/{2n}} 2nx \,dx + \int_{{1}/{2n}}^{1 - {1}/{2n}} 1 \,dx + \int_{1 - {1}/{2n}}^{1} (2nx-2n+2) \,dx \\ &= [nx^2]_0^{{1}/{2n}} + [x]_{{1}/{2n}}^{1 - {1}/{2n}} + [nx^2-2nx+2x]_{1 - {1}/{2n}}^{1} \\ &= \frac{1}{4n} + 1 - \frac{1}{n} + \frac{3}{4n} = 1. \end{align*} $$
Hence,
![]() $f_n \in D_\rho (C([0,1])).$
$f_n \in D_\rho (C([0,1])).$
We now prove that the sequence of functions
![]() $(f_n)_{n\in {\mathbb {N}}}$
converges to the function
$(f_n)_{n\in {\mathbb {N}}}$
converges to the function
![]() $f $
in the Bures metric,
$f $
in the Bures metric,
![]() $d_B^\rho $
, but fails to converge to f uniformly.
$d_B^\rho $
, but fails to converge to f uniformly.
Let
![]() $n \in {\mathbb {N}}.$
Then
$n \in {\mathbb {N}}.$
Then
 $$ \begin{align*} \rho(\sqrt{f_n}\sqrt{f}) &= \int_{0}^{{1}/{2n}} (\sqrt{2nx}\cdot 1) \,dx + \int_{{1}/{2n}}^{1 - {1}/{2n}} (\sqrt{1}\cdot 1) \,dx \\ &\quad + \int_{1 - {1}/{2n}}^{1} (\sqrt{2nx-2n+2}\cdot 1) \,dx \\ &= \int_{0}^{{1}/{2n}} \sqrt{2nx} \,dx + \int_{{1}/{2n}}^{1 - {1}/{2n}} 1 \,dx + \int_{1 - {1}/{2n}}^{1} \sqrt{2nx-2n+2} \,dx \\ &= \sqrt{2n} \cdot \bigg[\frac{2}{3} x^{{3}/{2}}\bigg]_0^{{1}/{2n}} + [x]_{{1}/{2n}}^{1 - {1}/{2n}} + \sqrt{2} \cdot \bigg[\frac{2}{3n} \cdot (nx-n+1)^{{3}/{2}}\bigg]_{1 - {1}/{2n}}^{1} \\ &= \frac{1}{3n} + 1 - \frac{1}{n} + \frac{2\sqrt{2}}{3n} - \frac{1}{3n} = 1 - \frac{3-2\sqrt{2}}{3n}. \end{align*} $$
$$ \begin{align*} \rho(\sqrt{f_n}\sqrt{f}) &= \int_{0}^{{1}/{2n}} (\sqrt{2nx}\cdot 1) \,dx + \int_{{1}/{2n}}^{1 - {1}/{2n}} (\sqrt{1}\cdot 1) \,dx \\ &\quad + \int_{1 - {1}/{2n}}^{1} (\sqrt{2nx-2n+2}\cdot 1) \,dx \\ &= \int_{0}^{{1}/{2n}} \sqrt{2nx} \,dx + \int_{{1}/{2n}}^{1 - {1}/{2n}} 1 \,dx + \int_{1 - {1}/{2n}}^{1} \sqrt{2nx-2n+2} \,dx \\ &= \sqrt{2n} \cdot \bigg[\frac{2}{3} x^{{3}/{2}}\bigg]_0^{{1}/{2n}} + [x]_{{1}/{2n}}^{1 - {1}/{2n}} + \sqrt{2} \cdot \bigg[\frac{2}{3n} \cdot (nx-n+1)^{{3}/{2}}\bigg]_{1 - {1}/{2n}}^{1} \\ &= \frac{1}{3n} + 1 - \frac{1}{n} + \frac{2\sqrt{2}}{3n} - \frac{1}{3n} = 1 - \frac{3-2\sqrt{2}}{3n}. \end{align*} $$
Therefore,
 $$ \begin{align*}d_{B}^{\rho}(f_n,f) = \sqrt{1 - \rho(\sqrt{f_n}\sqrt{f})} = \sqrt{1 - \bigg(1 - \frac{3-2\sqrt{2}}{3n}\bigg)} = \sqrt{\frac{3-2\sqrt{2}}{3n}}\end{align*} $$
$$ \begin{align*}d_{B}^{\rho}(f_n,f) = \sqrt{1 - \rho(\sqrt{f_n}\sqrt{f})} = \sqrt{1 - \bigg(1 - \frac{3-2\sqrt{2}}{3n}\bigg)} = \sqrt{\frac{3-2\sqrt{2}}{3n}}\end{align*} $$
and
![]() $\lim _{n \to \infty }d_{B}^{\rho }(f_n,f) =0$
. Therefore, we have shown that
$\lim _{n \to \infty }d_{B}^{\rho }(f_n,f) =0$
. Therefore, we have shown that
![]() $(f_n)_{n \in {\mathbb {N}}}$
converges to
$(f_n)_{n \in {\mathbb {N}}}$
converges to
![]() $f $
in the
$f $
in the
![]() $\rho $
-Bures metric.
$\rho $
-Bures metric.
Finally, suppose, by way of contradiction, that
![]() $(f_n)_{n\in {\mathbb {N}}}$
converges uniformly to
$(f_n)_{n\in {\mathbb {N}}}$
converges uniformly to
![]() $f $
. Then, for any
$f $
. Then, for any
![]() $\delta> 0$
, there exists
$\delta> 0$
, there exists
![]() $M \in {\mathbb {N}}$
such that, for any
$M \in {\mathbb {N}}$
such that, for any
![]() $n> M$
and any
$n> M$
and any
![]() $x \in [0,1]$
, we have
$x \in [0,1]$
, we have
![]() $|f_n(x) - f| < \delta $
. Therefore, for some
$|f_n(x) - f| < \delta $
. Therefore, for some
![]() $\delta _0 \in (0,1)$
, there exists
$\delta _0 \in (0,1)$
, there exists
![]() $M_0 \in {\mathbb {N}}$
such that, for any
$M_0 \in {\mathbb {N}}$
such that, for any
![]() $n> M_0$
and any
$n> M_0$
and any
![]() $x \in [0,1]$
, we have
$x \in [0,1]$
, we have
![]() $|f_n(x) - f| < \delta _0$
. However, let
$|f_n(x) - f| < \delta _0$
. However, let
![]() $x = 1$
. Then
$x = 1$
. Then
![]() $|f_n(1) - f(1)| = |2 - 1| = 1> \delta _0$
, which is a contradiction. Hence, our assumption is false.
$|f_n(1) - f(1)| = |2 - 1| = 1> \delta _0$
, which is a contradiction. Hence, our assumption is false.
3. Topological equivalence of Bures
 $C^*$
- and quantum metrics for finite-dimensional
$C^*$
- and quantum metrics for finite-dimensional
 $C^*$
-algebras
$C^*$
-algebras
Although we just saw an example where the
![]() $C^*$
-metric topology and Bures metric topology do not agree on the density space, in this section, we will see that if the
$C^*$
-metric topology and Bures metric topology do not agree on the density space, in this section, we will see that if the
![]() $C^*$
-algebra is assumed to be finite dimensional, then these topologies agree. Moreover, we will also show that in the finite-dimensional case, the Bures metric agrees with a metric on the density space induced by the quantum metric, which thus brings these two important metrics together. Some of the results in this section are similar to some of those of [Reference Farenick and Rahaman4] or can be obtained from finite-dimensionality arguments without much further effort. We include the results and proofs of this section to create a bridge between the previous section and the next, while also introducing the third metric that we study in this article.
$C^*$
-algebra is assumed to be finite dimensional, then these topologies agree. Moreover, we will also show that in the finite-dimensional case, the Bures metric agrees with a metric on the density space induced by the quantum metric, which thus brings these two important metrics together. Some of the results in this section are similar to some of those of [Reference Farenick and Rahaman4] or can be obtained from finite-dimensionality arguments without much further effort. We include the results and proofs of this section to create a bridge between the previous section and the next, while also introducing the third metric that we study in this article.
We first show how one can induce a metric on the density space using a quantum metric in a natural way. Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra. Let
$C^*$
-algebra. Let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. For each
${\mathcal {A}}$
. For each
![]() $a \in D_\tau ({\mathcal {A}})$
, define
$a \in D_\tau ({\mathcal {A}})$
, define
The next result might be well known, but we provide a proof here for convenience.
Proposition 3.1. Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. The map
${\mathcal {A}}$
. The map
is well defined and injective.
Proof. For
![]() $a\in {\mathcal {A}}_+$
, there exists
$a\in {\mathcal {A}}_+$
, there exists
![]() $b\in {\mathcal {A}}$
such that
$b\in {\mathcal {A}}$
such that
![]() $a=b^*b$
by [Reference Davidson3, Lemma I.4.3]. Let
$a=b^*b$
by [Reference Davidson3, Lemma I.4.3]. Let
![]() $c\in {\mathcal {A}}$
. Since
$c\in {\mathcal {A}}$
. Since
![]() $\tau $
is a trace,
$\tau $
is a trace,
Thus,
![]() $\varphi $
is a positive linear functional, and, in particular,
$\varphi $
is a positive linear functional, and, in particular,
![]() $\varphi _a^\tau (1_{\mathcal {A}})=\|\varphi _a^\tau \|_{\mathrm {op}}$
by [Reference Davidson3, Lemma I.9.5]. Since
$\varphi _a^\tau (1_{\mathcal {A}})=\|\varphi _a^\tau \|_{\mathrm {op}}$
by [Reference Davidson3, Lemma I.9.5]. Since
![]() $a \in D_\tau ({\mathcal {A}})$
,
$a \in D_\tau ({\mathcal {A}})$
,
Thus,
![]() $\varphi _a^\tau $
is a state, and therefore,
$\varphi _a^\tau $
is a state, and therefore,
![]() $\Phi _\tau $
is well defined.
$\Phi _\tau $
is well defined.
Next, let
![]() $a,a'\in {\mathcal {A}}_+$
such that
$a,a'\in {\mathcal {A}}_+$
such that
![]() $\Phi _\tau (a)=\Phi _\tau (a')$
. Hence,
$\Phi _\tau (a)=\Phi _\tau (a')$
. Hence,
![]() $\varphi _a^\tau ((a-a')^*)=\varphi ^\tau _{a'}((a-a')^*)$
. Thus,
$\varphi _a^\tau ((a-a')^*)=\varphi ^\tau _{a'}((a-a')^*)$
. Thus,
![]() $\tau (a(a-a')^*)=\tau (a'(a-a')^*)$
and so
$\tau (a(a-a')^*)=\tau (a'(a-a')^*)$
and so
![]() $\tau ((a-a')(a-a')^*)=0$
. Therefore,
$\tau ((a-a')(a-a')^*)=0$
. Therefore,
![]() $a-a'=0$
as
$a-a'=0$
as
![]() $\tau $
is faithful, that is,
$\tau $
is faithful, that is,
![]() $a=a'.$
Thus,
$a=a'.$
Thus,
![]() $\Phi _\tau $
is injective.
$\Phi _\tau $
is injective.
This allows us to define a new metric on
![]() $D_\tau ({\mathcal {A}}).$
$D_\tau ({\mathcal {A}}).$
Definition 3.2. Let
![]() $({\mathcal {A}}, L)$
be a compact quantum metric space. Let
$({\mathcal {A}}, L)$
be a compact quantum metric space. Let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. For every
${\mathcal {A}}$
. For every
![]() $x,y \in D_\tau ({\mathcal {A}})$
, define
$x,y \in D_\tau ({\mathcal {A}})$
, define
which defines a metric on
![]() $D_\tau ({\mathcal {A}})$
since
$D_\tau ({\mathcal {A}})$
since
![]() $\Phi _\tau $
is well defined and injective. We will still call
$\Phi _\tau $
is well defined and injective. We will still call
![]() $d_L^\tau $
a quantum metric.
$d_L^\tau $
a quantum metric.
Before moving on to the finite-dimensional setting, we prove that the topology generated by the
![]() $C^*$
-norm is always finer than the topology induced by a quantum metric.
$C^*$
-norm is always finer than the topology induced by a quantum metric.
Proposition 3.3. Let
![]() $({\mathcal {A}}, L)$
be a compact quantum metric space and let
$({\mathcal {A}}, L)$
be a compact quantum metric space and let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. Then, on
${\mathcal {A}}$
. Then, on
![]() $D_\tau ({\mathcal {A}})$
, the topology induced by
$D_\tau ({\mathcal {A}})$
, the topology induced by
![]() $d_{\mathcal {A}}$
is finer than the topology induced by
$d_{\mathcal {A}}$
is finer than the topology induced by
![]() $d_L^\tau $
.
$d_L^\tau $
.
Proof. Let
![]() $(a_n)_{n \in {\mathbb {N}}}$
be a sequence in
$(a_n)_{n \in {\mathbb {N}}}$
be a sequence in
![]() $D_\tau ({\mathcal {A}})$
that converges to
$D_\tau ({\mathcal {A}})$
that converges to
![]() $a\in D_\tau ({\mathcal {A}})$
with respect to
$a\in D_\tau ({\mathcal {A}})$
with respect to
![]() $d_{\mathcal {A}}$
. Then, for each
$d_{\mathcal {A}}$
. Then, for each
![]() $b \in {\mathcal {A}}$
,
$b \in {\mathcal {A}}$
,
since multiplication is continuous and
![]() $\tau $
is continuous. Since convergence in
$\tau $
is continuous. Since convergence in
![]() $\mathrm {mk}_L$
is equivalent to weak* convergence by definition, the proof is complete.
$\mathrm {mk}_L$
is equivalent to weak* convergence by definition, the proof is complete.
For the remainder of this section,
![]() ${\mathcal {A}}$
will be a finite-dimensional
${\mathcal {A}}$
will be a finite-dimensional
![]() $C^*$
-algebra. We will now prove that the
$C^*$
-algebra. We will now prove that the
![]() $C^*$
-metric topology and quantum metric topology are the same. First, we establish that
$C^*$
-metric topology and quantum metric topology are the same. First, we establish that
![]() $(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is a compact metric space.
$(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is a compact metric space.
Proposition 3.4. If
![]() ${\mathcal {A}}$
is a finite-dimensional
${\mathcal {A}}$
is a finite-dimensional
![]() $C^*$
-algebra, then
$C^*$
-algebra, then
![]() $(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is a compact metric space.
$(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is a compact metric space.
Proof. We only need to show that
![]() $D_\tau ({\mathcal {A}})$
is closed and bounded with respect to the
$D_\tau ({\mathcal {A}})$
is closed and bounded with respect to the
![]() $C^*$
-norm. First, it is closed since
$C^*$
-norm. First, it is closed since
![]() $\tau $
is continuous with respect to the
$\tau $
is continuous with respect to the
![]() $C^*$
-norm.
$C^*$
-norm.
Since
![]() ${\mathcal {A}}$
is finite dimensional, the norms
${\mathcal {A}}$
is finite dimensional, the norms
![]() $\|\cdot \|_{\mathcal {A}}$
and
$\|\cdot \|_{\mathcal {A}}$
and
![]() $\|\cdot \|_\tau $
are equivalent, where
$\|\cdot \|_\tau $
are equivalent, where
![]() $\|a\|_\tau =\sqrt {\tau (a^*a)}$
for
$\|a\|_\tau =\sqrt {\tau (a^*a)}$
for
![]() $ a\in {\mathcal {A}}$
. Now, let
$ a\in {\mathcal {A}}$
. Now, let
![]() $a \in D_\tau ({\mathcal {A}})$
and let
$a \in D_\tau ({\mathcal {A}})$
and let
![]() $\sqrt {a}$
denote its unique positive square root. By the
$\sqrt {a}$
denote its unique positive square root. By the
![]() $C^*$
-identity,
$C^*$
-identity,
 $$ \begin{align*} \sqrt{\|a\|_{\mathcal{A}}} = \sqrt{\|(\sqrt{a})^*\sqrt{a}\|_{\mathcal{A}}} & =\|\sqrt{a}\|_{\mathcal{A}} \\ &\leqslant \alpha \|\sqrt{a}\|_\tau =\alpha\sqrt{\tau((\sqrt{a})^*\sqrt{a})}=\alpha\sqrt{\tau(a)}=\alpha, \end{align*} $$
$$ \begin{align*} \sqrt{\|a\|_{\mathcal{A}}} = \sqrt{\|(\sqrt{a})^*\sqrt{a}\|_{\mathcal{A}}} & =\|\sqrt{a}\|_{\mathcal{A}} \\ &\leqslant \alpha \|\sqrt{a}\|_\tau =\alpha\sqrt{\tau((\sqrt{a})^*\sqrt{a})}=\alpha\sqrt{\tau(a)}=\alpha, \end{align*} $$
since
![]() $\tau (a)=1$
. So
$\tau (a)=1$
. So
![]() $\|a\|_{\mathcal {A}}\leqslant \alpha ^2$
. Hence,
$\|a\|_{\mathcal {A}}\leqslant \alpha ^2$
. Hence,
![]() $D_\tau ({\mathcal {A}})$
is bounded and thus is compact by the Heine–Borel theorem.
$D_\tau ({\mathcal {A}})$
is bounded and thus is compact by the Heine–Borel theorem.
Theorem 3.5. Let
![]() $({\mathcal {A}}, L)$
be a compact quantum metric space and let
$({\mathcal {A}}, L)$
be a compact quantum metric space and let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. If
${\mathcal {A}}$
. If
![]() ${\mathcal {A}}$
is finite dimensional, then
${\mathcal {A}}$
is finite dimensional, then
![]() $d_L^\tau $
and
$d_L^\tau $
and
![]() $d_{\mathcal {A}}$
are topologically equivalent.
$d_{\mathcal {A}}$
are topologically equivalent.
Proof. The proof that
![]() $\Phi _\tau $
is continuous from
$\Phi _\tau $
is continuous from
![]() $(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
to
$(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
to
![]() $(D_\tau ({\mathcal {A}}),d^\tau _L )$
is the same as the proof of Proposition 3.3. Since
$(D_\tau ({\mathcal {A}}),d^\tau _L )$
is the same as the proof of Proposition 3.3. Since
![]() $(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is compact by Proposition 3.4,
$(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is compact by Proposition 3.4,
![]() $\Phi _\tau $
is a homeomorphism onto its image with respect to the weak* topology on
$\Phi _\tau $
is a homeomorphism onto its image with respect to the weak* topology on
![]() $S({\mathcal {A}})$
.
$S({\mathcal {A}})$
.
Since convergence in
![]() $\mathrm {mk}_L$
is equivalent to weak* convergence by definition,
$\mathrm {mk}_L$
is equivalent to weak* convergence by definition,
![]() $ d_{\mathcal {A}} $
and
$ d_{\mathcal {A}} $
and
![]() $ d^\tau _L $
are topologically equivalent.
$ d^\tau _L $
are topologically equivalent.
Now, we establish the topological equivalence of the
![]() $C^*$
-metric and Bures metric.
$C^*$
-metric and Bures metric.
Theorem 3.6. Let
![]() ${\mathcal {A}}$
be a unital
${\mathcal {A}}$
be a unital
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. If
${\mathcal {A}}$
. If
![]() ${\mathcal {A}}$
is finite dimensional, then the
${\mathcal {A}}$
is finite dimensional, then the
![]() $C^*$
-metric
$C^*$
-metric
![]() $d_{\mathcal {A}}$
and the Bures metric
$d_{\mathcal {A}}$
and the Bures metric
![]() $d_B^\tau $
are topologically equivalent.
$d_B^\tau $
are topologically equivalent.
Proof. Consider
By Theorem 2.3, convergence in
![]() $d_{\mathcal {A}}$
implies convergence in
$d_{\mathcal {A}}$
implies convergence in
![]() $d^\tau _B$
. Hence,
$d^\tau _B$
. Hence,
![]() $ \mathrm {id}_{D_\tau ({\mathcal {A}})}$
is continuous, and since
$ \mathrm {id}_{D_\tau ({\mathcal {A}})}$
is continuous, and since
![]() $(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is compact,
$(D_\tau ({\mathcal {A}}), d_{\mathcal {A}})$
is compact,
![]() $ \mathrm {id}_{D_\tau ({\mathcal {A}})}$
is a homeomorphism. Hence,
$ \mathrm {id}_{D_\tau ({\mathcal {A}})}$
is a homeomorphism. Hence,
![]() $d_{\mathcal {A}}$
and
$d_{\mathcal {A}}$
and
![]() $d_B^\tau $
are topologically equivalent.
$d_B^\tau $
are topologically equivalent.
We conclude this section with the topological equivalence of the Bures metric and quantum metric.
Corollary 3.7. Let
![]() $({\mathcal {A}},L)$
be a compact quantum metric space and let
$({\mathcal {A}},L)$
be a compact quantum metric space and let
![]() $\tau $
be a faithful trace on
$\tau $
be a faithful trace on
![]() ${\mathcal {A}}$
. If
${\mathcal {A}}$
. If
![]() ${\mathcal {A}}$
is finite dimensional, then the Bures metric
${\mathcal {A}}$
is finite dimensional, then the Bures metric
![]() $d_B^\tau $
and quantum metric
$d_B^\tau $
and quantum metric
![]() $d_L^\tau $
are topologically equivalent.
$d_L^\tau $
are topologically equivalent.
4. Metric inequivalence for
 ${\mathbb {C}}^2$
${\mathbb {C}}^2$
In this last section, we see that, although the Bures metric and quantum metric are topologically equivalent for finite-dimensional
![]() $C^*$
-algebras, there exist finite-dimensional
$C^*$
-algebras, there exist finite-dimensional
![]() $C^*$
-algebras for which they are not equivalent as metric spaces. Our approach also proves that the Bures metric and
$C^*$
-algebras for which they are not equivalent as metric spaces. Our approach also proves that the Bures metric and
![]() $C^*$
-norm are not metrically equivalent since we find a quantum metric that, in fact, agrees with the metric on the density space induced by the
$C^*$
-norm are not metrically equivalent since we find a quantum metric that, in fact, agrees with the metric on the density space induced by the
![]() $C^*$
-norm.
$C^*$
-norm.
Consider the unital
![]() $C^*$
-algebra
$C^*$
-algebra
![]() ${\mathbb {C}}^2$
. For every
${\mathbb {C}}^2$
. For every
![]() $x=(x_1,x_2)\in {\mathbb {C}}^2$
, define
$x=(x_1,x_2)\in {\mathbb {C}}^2$
, define
Then
![]() $L^B$
is an L-seminorm since
$L^B$
is an L-seminorm since
![]() ${\mathbb {C}}^2$
is finite dimensional and by [Reference Rieffel11, Proposition 1.6]. So
${\mathbb {C}}^2$
is finite dimensional and by [Reference Rieffel11, Proposition 1.6]. So
![]() $\mathrm {mk}_{L^B}$
is a quantum metric.
$\mathrm {mk}_{L^B}$
is a quantum metric.
Consider the faithful trace
![]() $\tau $
on
$\tau $
on
![]() ${\mathbb {C}}^2$
defined by
${\mathbb {C}}^2$
defined by
The Bures metric is given explicitly by the trace, but as the quantum metric is defined by way of a supremum, we first find a formula to explicitly calculate the quantum metric in this case. This recovers the
![]() $C^*$
-metric.
$C^*$
-metric.
Theorem 4.1. With the setting as above, for every
![]() $x,y \in D_\tau ({\mathbb {C}}^2)$
,
$x,y \in D_\tau ({\mathbb {C}}^2)$
,
Proof. First, let
![]() $x \in D_\tau ({\mathbb {C}}^2)$
and let
$x \in D_\tau ({\mathbb {C}}^2)$
and let
![]() $x'\in {\mathbb {C}}^2$
. Then
$x'\in {\mathbb {C}}^2$
. Then
Now, assume that
![]() $y \in D_\tau ({\mathbb {C}}^2)$
. Since
$y \in D_\tau ({\mathbb {C}}^2)$
. Since
![]() $\tau (x)=1=\tau (y)$
, we have
$\tau (x)=1=\tau (y)$
, we have
![]() $x_1+x_2=1=y_1+y_2$
and so
$x_1+x_2=1=y_1+y_2$
and so
![]() $x_1-y_1=y_2-x_2$
. Hence, if
$x_1-y_1=y_2-x_2$
. Hence, if
![]() $L^B(x')\leqslant 1$
,
$L^B(x')\leqslant 1$
,
 $$ \begin{align*} |\varphi^\tau_x(x')-\varphi^\tau_y(x')|& =|x_1x_1'+x_2x_2'-y_1x_1'-y_2x_2'|\\ & = |(x_1-y_1)x_1'+(x_2-y_2)x_2'|\\ &= |(x_1-y_1)x_1'-(y_2-x_2)x_2'|\\ & =|(x_1-y_1)x_1'-(x_1-y_1)x_2'|\\ & = |(x_1-y_1)(x_1'-x_2')|\\ & =|x_1-y_1|\cdot |x_1'-x_2'|\\ & \leqslant |x_1-y_1|. \end{align*} $$
$$ \begin{align*} |\varphi^\tau_x(x')-\varphi^\tau_y(x')|& =|x_1x_1'+x_2x_2'-y_1x_1'-y_2x_2'|\\ & = |(x_1-y_1)x_1'+(x_2-y_2)x_2'|\\ &= |(x_1-y_1)x_1'-(y_2-x_2)x_2'|\\ & =|(x_1-y_1)x_1'-(x_1-y_1)x_2'|\\ & = |(x_1-y_1)(x_1'-x_2')|\\ & =|x_1-y_1|\cdot |x_1'-x_2'|\\ & \leqslant |x_1-y_1|. \end{align*} $$
Now, consider
![]() $x'=(1,0)$
. Then
$x'=(1,0)$
. Then
Thus,
We also note that
as desired.
Theorem 4.2. Let
![]() $d=d_{L^B}^\tau $
, the Bures metric, or
$d=d_{L^B}^\tau $
, the Bures metric, or
![]() $d=d_{\mathcal {A}}$
. With the setting as above, the quantum metric
$d=d_{\mathcal {A}}$
. With the setting as above, the quantum metric
![]() $d_{L^B}^\tau $
and d are topologically equivalent but not metric equivalent.
$d_{L^B}^\tau $
and d are topologically equivalent but not metric equivalent.
Proof. Corollary 3.7 provides topological equivalence.
Consider
![]() $x=(1,0)\in D_\tau ({\mathbb {C}}^2)$
. Let
$x=(1,0)\in D_\tau ({\mathbb {C}}^2)$
. Let
![]() $y=(y_1,y_2)\in D_\tau ({\mathbb {C}}^2)$
. By Theorem 4.1,
$y=(y_1,y_2)\in D_\tau ({\mathbb {C}}^2)$
. By Theorem 4.1,
Also,
Now, consider the ratio
 $$ \begin{align*}\frac{d_B^\tau(x,y)}{d_{L^B}^\tau(x,y)}=\frac{\sqrt{1-\sqrt{y_1}}}{|1-y_1|}.\end{align*} $$
$$ \begin{align*}\frac{d_B^\tau(x,y)}{d_{L^B}^\tau(x,y)}=\frac{\sqrt{1-\sqrt{y_1}}}{|1-y_1|}.\end{align*} $$
We have
![]() $\lim _{y_1\to 1^-}\sqrt {1-\sqrt {y_1}}=0$
and
$\lim _{y_1\to 1^-}\sqrt {1-\sqrt {y_1}}=0$
and
![]() $\lim _{y_1\to 1^-}1-y_1=0$
. Further,
$\lim _{y_1\to 1^-}1-y_1=0$
. Further,
 $$ \begin{align*}\frac{d}{dy_1}\Big(\sqrt{1-\sqrt{y_1}}\Big)=\frac{-1}{4\sqrt{y_1}\sqrt{1-\sqrt{y_1}}}, \quad \frac{d}{dy_1}(1-y_1)=-1\end{align*} $$
$$ \begin{align*}\frac{d}{dy_1}\Big(\sqrt{1-\sqrt{y_1}}\Big)=\frac{-1}{4\sqrt{y_1}\sqrt{1-\sqrt{y_1}}}, \quad \frac{d}{dy_1}(1-y_1)=-1\end{align*} $$
and
 $$ \begin{align*} \lim_{y_1\to1^-} \frac{\frac{-1}{4\sqrt{y_1}\sqrt{1-\sqrt{y_1}}}}{-1}=\lim_{y_1\to1^-}\frac{1}{4\sqrt{y_1}\sqrt{1-\sqrt{y_1}}}=\infty. \end{align*} $$
$$ \begin{align*} \lim_{y_1\to1^-} \frac{\frac{-1}{4\sqrt{y_1}\sqrt{1-\sqrt{y_1}}}}{-1}=\lim_{y_1\to1^-}\frac{1}{4\sqrt{y_1}\sqrt{1-\sqrt{y_1}}}=\infty. \end{align*} $$
Thus, by L’Hopital’s rule,
 $$ \begin{align*} \lim_{y_1\to 1^-}\frac{d_B^\tau(x,y)}{d_{L^B}^\tau(x,y)}=\infty. \end{align*} $$
$$ \begin{align*} \lim_{y_1\to 1^-}\frac{d_B^\tau(x,y)}{d_{L^B}^\tau(x,y)}=\infty. \end{align*} $$
Hence, the set
 $$ \begin{align*} \bigg\{ \frac{d_B^\tau(x,y)}{d_{L^B}^\tau(x,y)}: x,y \in D_\tau({\mathbb{C}}^2), x \neq y\bigg\} \end{align*} $$
$$ \begin{align*} \bigg\{ \frac{d_B^\tau(x,y)}{d_{L^B}^\tau(x,y)}: x,y \in D_\tau({\mathbb{C}}^2), x \neq y\bigg\} \end{align*} $$
is unbounded, and so the metrics
![]() $d_B^\tau $
and
$d_B^\tau $
and
![]() $ d_{L^B}^\tau $
are not metric equivalent.
$ d_{L^B}^\tau $
are not metric equivalent.
Acknowledgement
The third author would like to thank Erik Bédos for helpful discussions.