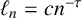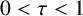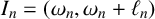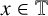1 Introduction
Let
![]() $\mathbb {T}=\mathbb {R}/\mathbb {Z}$
be the unit circle and let
$\mathbb {T}=\mathbb {R}/\mathbb {Z}$
be the unit circle and let
![]() $\{\ell _n\}_{n\geq 1}$
be a sequence of real numbers decreasing to zero with
$\{\ell _n\}_{n\geq 1}$
be a sequence of real numbers decreasing to zero with
![]() $0<\ell _n<1$
and
$0<\ell _n<1$
and
![]() $\sum _{n=1}^{\infty }\ell _n=\infty $
. Let
$\sum _{n=1}^{\infty }\ell _n=\infty $
. Let
![]() $\{\omega _n\}_{n\geq 1}$
be a sequence of independent and identically distributed random variables, each uniformly distributed on
$\{\omega _n\}_{n\geq 1}$
be a sequence of independent and identically distributed random variables, each uniformly distributed on
![]() $\mathbb {T}$
. Let
$\mathbb {T}$
. Let
![]() $I_{n}=(\omega _n,\omega _n+\ell _n)$
be the random interval with left endpoint
$I_{n}=(\omega _n,\omega _n+\ell _n)$
be the random interval with left endpoint
![]() $\omega _n$
and length
$\omega _n$
and length
![]() $\ell _n$
. Throughout this paper,
$\ell _n$
. Throughout this paper,
![]() $(\Omega , \mathcal {F}, \mathbb {P})$
denotes the underlying probability space,
$(\Omega , \mathcal {F}, \mathbb {P})$
denotes the underlying probability space,
![]() $\lambda $
stands for the Lebesgue measure on
$\lambda $
stands for the Lebesgue measure on
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\mathbb {P}\times \lambda $
stands for the product probability measure on the product space
$\mathbb {P}\times \lambda $
stands for the product probability measure on the product space
![]() $\Omega \times \mathbb {T}$
. By abuse of notation, sometimes we may write
$\Omega \times \mathbb {T}$
. By abuse of notation, sometimes we may write
![]() $I_n=I_n(\omega )$
with
$I_n=I_n(\omega )$
with
![]() $\omega \in \Omega $
to indicate the dependence of
$\omega \in \Omega $
to indicate the dependence of
![]() $I_n$
on the underlying probability space
$I_n$
on the underlying probability space
![]() $(\Omega , \mathcal {F}, \mathbb {P})$
.
$(\Omega , \mathcal {F}, \mathbb {P})$
.
The limsup set
![]() $E=\limsup _{n\rightarrow \infty }I_n$
is usually called the random covering set, which consists of all points in
$E=\limsup _{n\rightarrow \infty }I_n$
is usually called the random covering set, which consists of all points in
![]() $\mathbb {T}$
that are covered by random intervals
$\mathbb {T}$
that are covered by random intervals
![]() $\{I_n\}_{n\geq 1}$
infinitely many times. The Dvoretzky covering problem [Reference Dvoretzky5] aims to find necessary and sufficient conditions on
$\{I_n\}_{n\geq 1}$
infinitely many times. The Dvoretzky covering problem [Reference Dvoretzky5] aims to find necessary and sufficient conditions on
![]() $\ell _n$
for
$\ell _n$
for
![]() $E=\mathbb {T}$
almost surely. After a series of contributions by Kahane et al., Shepp [Reference Shepp21] solved this problem by showing that
$E=\mathbb {T}$
almost surely. After a series of contributions by Kahane et al., Shepp [Reference Shepp21] solved this problem by showing that
![]() $E=\mathbb {T}$
almost surely if and only if
$E=\mathbb {T}$
almost surely if and only if
 $$ \begin{align} \sum_{n=1}^{\infty}\frac{1}{n^{2}}\exp(\ell_{1}+\ell_{2}+\cdots+\ell_{n})=\infty. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}\frac{1}{n^{2}}\exp(\ell_{1}+\ell_{2}+\cdots+\ell_{n})=\infty. \end{align} $$
(See [Reference Fan7, Reference Kahane17] for more background and [Reference Ekström and Persson6, Reference Fan and Karagulyan10–Reference Järvenpää, Järvenpää, Koivusalo, Li, Suomala and Xiao16, Reference Seuret20] for various dimension results related to this problem.)
If Shepp’s condition (1.1) is satisfied, Carleson asked for a description of the infinite set of intervals covering a given point. Fan [Reference Fan7] advanced two ways to resolve this problem. One way is to introduce, for any
![]() $x\in \mathbb {T}$
and any
$x\in \mathbb {T}$
and any
![]() $n\geq 1$
, the covering time of the point x up to time n, which is defined by
$n\geq 1$
, the covering time of the point x up to time n, which is defined by
 $$ \begin{align*}N_n(x)=\sharp\{k:1\leq k\leq n, x\in I_k\}=\sum_{k=1}^n\mathbf{1}_{I_k}(x).\end{align*} $$
$$ \begin{align*}N_n(x)=\sharp\{k:1\leq k\leq n, x\in I_k\}=\sum_{k=1}^n\mathbf{1}_{I_k}(x).\end{align*} $$
Here
![]() $\mathbf {1}_{I_{k}}(x)$
denotes the indicator function of the random interval
$\mathbf {1}_{I_{k}}(x)$
denotes the indicator function of the random interval
![]() $I_{k}$
. The second method was fully developed in [Reference Fan and Kahane9] and the multifractal analysis of the asymptotic behaviours of
$I_{k}$
. The second method was fully developed in [Reference Fan and Kahane9] and the multifractal analysis of the asymptotic behaviours of
![]() $N_n(x)$
was first studied in [Reference Fan8] and refined in [Reference Barral and Fan4].
$N_n(x)$
was first studied in [Reference Fan8] and refined in [Reference Barral and Fan4].
When
![]() $\sum _{n=1}^{\infty } \ell _n=\infty $
, it was pointed out in [Reference Barral and Fan4] that
$\sum _{n=1}^{\infty } \ell _n=\infty $
, it was pointed out in [Reference Barral and Fan4] that
![]() $\mathbb {P}$
-almost surely,
$\mathbb {P}$
-almost surely,
giving a quantitative description of the infinite covering time. This may be viewed as a quenched self-normalised law of large numbers, that is, the self-normalised law of large numbers holds
![]() $\mathbb {P}$
-almost surely. The terminology ‘quenched’ is motivated by the theory of random walks in a random environment and
$\mathbb {P}$
-almost surely. The terminology ‘quenched’ is motivated by the theory of random walks in a random environment and
![]() $\Omega $
is the space of ‘environment parameters’.
$\Omega $
is the space of ‘environment parameters’.
Write
 $$ \begin{align*} Y_n:=\frac{N_n(x)-\mathbb{E}_{\mathbb{P}}(N_n(x))}{V_n} =\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\ell_{k})}{V_n}. \end{align*} $$
$$ \begin{align*} Y_n:=\frac{N_n(x)-\mathbb{E}_{\mathbb{P}}(N_n(x))}{V_n} =\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\ell_{k})}{V_n}. \end{align*} $$
The variance of
![]() $N_n(x)$
is
$N_n(x)$
is
 $$ \begin{align*}V_n^2=\sum_{k=1}^n \ell_k(1-\ell_k),\end{align*} $$
$$ \begin{align*}V_n^2=\sum_{k=1}^n \ell_k(1-\ell_k),\end{align*} $$
which satisfies
![]() $\lim _{n\rightarrow \infty }L_n/V_n^2=1$
. We prove that the self-normalised quantity
$\lim _{n\rightarrow \infty }L_n/V_n^2=1$
. We prove that the self-normalised quantity
![]() $Y_n$
satisfies a quenched central limit theorem. (See [Reference Abdelkader and Aimino1–Reference Ayyer, Liverani and Stenlund3, Reference Kifer18] for a quenched central limit theorem and other quenched limit theorems for random dynamical systems.) We state our main theorem as follows.
$Y_n$
satisfies a quenched central limit theorem. (See [Reference Abdelkader and Aimino1–Reference Ayyer, Liverani and Stenlund3, Reference Kifer18] for a quenched central limit theorem and other quenched limit theorems for random dynamical systems.) We state our main theorem as follows.
Theorem 1.1. Let
![]() $\ell _{n}=c n^{-\tau }$
with
$\ell _{n}=c n^{-\tau }$
with
![]() $c>0$
and
$c>0$
and
![]() $0<\tau < 1$
. Then
$0<\tau < 1$
. Then
![]() $\mathbb {P}$
-almost surely,
$\mathbb {P}$
-almost surely,
![]() $Y_{n}$
converges in law to the standard normal distribution.
$Y_{n}$
converges in law to the standard normal distribution.
Theorem 1.1 will be derived from the next proposition. We remark that, by our assumption on
![]() $\ell _n$
, we have
$\ell _n$
, we have
![]() $L_n\sim V_n^2 \sim {c}n^{1-\tau }/{(1-\tau )}$
. Here and throughout the paper, we employ the Vinogradov and Bachmann–Landau notation: for a function f and a positive-valued function g, we write
$L_n\sim V_n^2 \sim {c}n^{1-\tau }/{(1-\tau )}$
. Here and throughout the paper, we employ the Vinogradov and Bachmann–Landau notation: for a function f and a positive-valued function g, we write
![]() $f\sim g$
if f is equal to g asymptotically,
$f\sim g$
if f is equal to g asymptotically,
![]() $f\ll g$
or
$f\ll g$
or
![]() $f=O(g)$
if there exists a constant C such that
$f=O(g)$
if there exists a constant C such that
![]() $|f|\leq C g$
pointwise, and
$|f|\leq C g$
pointwise, and
![]() $f\asymp g$
if
$f\asymp g$
if
![]() $f\ll g$
and
$f\ll g$
and
![]() $g\ll f$
simultaneously. For
$g\ll f$
simultaneously. For
![]() $x, y\in \mathbb {T}$
, we define
$x, y\in \mathbb {T}$
, we define
 $$ \begin{align*}Z_n:=\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))}{V_n}.\end{align*} $$
$$ \begin{align*}Z_n:=\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))}{V_n}.\end{align*} $$
Proposition 1.2. Let
![]() $\ell _n$
be as in Theorem 1.1 and let
$\ell _n$
be as in Theorem 1.1 and let
![]() $Y_n, Z_n, V_n$
be defined as above. Assume that there exists a constant
$Y_n, Z_n, V_n$
be defined as above. Assume that there exists a constant
![]() $\sigma $
with
$\sigma $
with
![]() $\sigma>\min \{{(1-\tau )}/{2}, {\tau }/{2}\}$
such that, for all
$\sigma>\min \{{(1-\tau )}/{2}, {\tau }/{2}\}$
such that, for all
![]() $t\in \mathbb {R}$
and
$t\in \mathbb {R}$
and
![]() $n\geq 1$
with
$n\geq 1$
with
![]() $|t/V_n|$
arbitrarily small:
$|t/V_n|$
arbitrarily small:
-
(1)
 $|\mathbb {E}_{\mathbb {P}\times \lambda }(e^{it Y_{n}})-e^{-t^{2}/2}|\ll |t|^{3}e^{-t^{2}/3}n^{-\sigma };$
$|\mathbb {E}_{\mathbb {P}\times \lambda }(e^{it Y_{n}})-e^{-t^{2}/2}|\ll |t|^{3}e^{-t^{2}/3}n^{-\sigma };$
-
(2)
 $|\mathbb {E}_{\mathbb {P}\times \lambda \times \lambda }(e^{it Z_{n}})-e^{-t^{2}}|\ll (1+|t|^3) n^{-\sigma }$
; and
$|\mathbb {E}_{\mathbb {P}\times \lambda \times \lambda }(e^{it Z_{n}})-e^{-t^{2}}|\ll (1+|t|^3) n^{-\sigma }$
; and -
(3) for
 $\epsilon>0$
and n sufficiently large,
$\epsilon>0$
and n sufficiently large,
 $\mathbb {P}\times \lambda (|Y_{n}|\geq \varepsilon )\leq 2e^{-\varepsilon ^{2}/4}.$
$\mathbb {P}\times \lambda (|Y_{n}|\geq \varepsilon )\leq 2e^{-\varepsilon ^{2}/4}.$
Then
![]() $\mathbb {P}$
-almost surely,
$\mathbb {P}$
-almost surely,
![]() $Y_n$
converges in law to the standard normal distribution.
$Y_n$
converges in law to the standard normal distribution.
Our method was inspired by [Reference Ayyer, Liverani and Stenlund3], which established a quenched central limit theorem for a smooth observable of random sequences of iterated linear hyperbolic maps on the torus. In contrast to the quenched limit theorems in [Reference Abdelkader and Aimino1–Reference Ayyer, Liverani and Stenlund3, Reference Kifer18], the sequence of random variables we consider is not stationary, which causes additional difficulties.
2 Preliminaries
In this section, we collect some preliminary results. In the first two lemmas,
![]() $\{\widetilde {X}_{n}\}_{n\geq 1}$
is assumed to be a sequence of independent random variables on a probability space
$\{\widetilde {X}_{n}\}_{n\geq 1}$
is assumed to be a sequence of independent random variables on a probability space
![]() $(\widetilde {\Omega }, \widetilde {\mathcal {F}}, \widetilde {\mathbb {P}})$
with
$(\widetilde {\Omega }, \widetilde {\mathcal {F}}, \widetilde {\mathbb {P}})$
with
![]() $\mathbb {E}_{\widetilde {\mathbb {P}}}(\widetilde {X}_{n})=0$
. For any
$\mathbb {E}_{\widetilde {\mathbb {P}}}(\widetilde {X}_{n})=0$
. For any
![]() $n\geq 1$
, write
$n\geq 1$
, write
![]() $\widetilde {\sigma }_n^2=\mathbb {E}_{\widetilde {\mathbb {P}}}(\widetilde {X}_{n}^{2}), \widetilde {V}_{n}^2=\sum _{i=1}^{n}\widetilde {\sigma }_i^2$
and
$\widetilde {\sigma }_n^2=\mathbb {E}_{\widetilde {\mathbb {P}}}(\widetilde {X}_{n}^{2}), \widetilde {V}_{n}^2=\sum _{i=1}^{n}\widetilde {\sigma }_i^2$
and
![]() $\widetilde {B}_{n}=\widetilde {V}_{n}^{-3}\sum _{i=1}^{n}\mathbb {E}_{\widetilde {\mathbb {P}}}(|\widetilde {X}_{i}|^{3})$
.
$\widetilde {B}_{n}=\widetilde {V}_{n}^{-3}\sum _{i=1}^{n}\mathbb {E}_{\widetilde {\mathbb {P}}}(|\widetilde {X}_{i}|^{3})$
.
Lemma 2.1 [Reference Petrov19, Lemma 5.1].
Let
![]() $\{\widetilde {X}_{n}\}_{n\geq 1}, \widetilde {V}_{n}, \widetilde {B}_n$
be defined as above and satisfying
$\{\widetilde {X}_{n}\}_{n\geq 1}, \widetilde {V}_{n}, \widetilde {B}_n$
be defined as above and satisfying
![]() $\mathbb {E}_{\widetilde {\mathbb {P}}}(|\widetilde {X}_{n}|^{3})<\infty $
for each
$\mathbb {E}_{\widetilde {\mathbb {P}}}(|\widetilde {X}_{n}|^{3})<\infty $
for each
![]() $n\geq 1$
. Write
$n\geq 1$
. Write
![]() $\widetilde {Y}_n=\widetilde {V}_{n}^{-1}\sum _{i=1}^{n}\widetilde {X}_{i}$
. Then
$\widetilde {Y}_n=\widetilde {V}_{n}^{-1}\sum _{i=1}^{n}\widetilde {X}_{i}$
. Then
 $$ \begin{align*}|\mathbb{E}_{\widetilde{\mathbb{P}}}(e^{it\widetilde{Y}_n})-e^{-t^{2}/2}|\leq 16 \widetilde{B}_{n}|t|^{3}e^{-t^{2}/3} \quad\mbox{for } |t|\leq\frac{1}{4\widetilde{B}_{n}}. \end{align*} $$
$$ \begin{align*}|\mathbb{E}_{\widetilde{\mathbb{P}}}(e^{it\widetilde{Y}_n})-e^{-t^{2}/2}|\leq 16 \widetilde{B}_{n}|t|^{3}e^{-t^{2}/3} \quad\mbox{for } |t|\leq\frac{1}{4\widetilde{B}_{n}}. \end{align*} $$
Lemma 2.2 (Bernstein inequality, [Reference Petrov19, Theorem 2.8]).
Let
![]() $\{\widetilde {X}_{n}\}_{n\geq 1}, \widetilde {\sigma }_{n}, \widetilde {V}_n$
be defined as above and satisfying
$\{\widetilde {X}_{n}\}_{n\geq 1}, \widetilde {\sigma }_{n}, \widetilde {V}_n$
be defined as above and satisfying
![]() $\widetilde {\sigma }_n^2<\infty $
for each
$\widetilde {\sigma }_n^2<\infty $
for each
![]() $n\geq 1$
. Suppose that there exists a constant
$n\geq 1$
. Suppose that there exists a constant
![]() $H>0$
such that
$H>0$
such that
![]() $|\mathbb {E}_{\widetilde {\mathbb {P}}}(\widetilde {X}_n^m)|\leq \tfrac 12m!\widetilde {\sigma }_n^2H^{m-1}$
for all
$|\mathbb {E}_{\widetilde {\mathbb {P}}}(\widetilde {X}_n^m)|\leq \tfrac 12m!\widetilde {\sigma }_n^2H^{m-1}$
for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $m\geq 2$
. Then
$m\geq 2$
. Then
 $$ \begin{align*}\widetilde{\mathbb{P}}\bigg(\bigg\{\bigg|\!\sum_{i=1}^n \widetilde{X}_i\bigg|\geq a\bigg\}\bigg)\leq 2\exp\bigg[\frac{-a^2}{2(\widetilde{V}_n^2+H a)}\bigg].\end{align*} $$
$$ \begin{align*}\widetilde{\mathbb{P}}\bigg(\bigg\{\bigg|\!\sum_{i=1}^n \widetilde{X}_i\bigg|\geq a\bigg\}\bigg)\leq 2\exp\bigg[\frac{-a^2}{2(\widetilde{V}_n^2+H a)}\bigg].\end{align*} $$
In the next two lemmas,
![]() $(\Omega , \mathcal {F}, \mathbb {P})$
denotes the underlying probability space,
$(\Omega , \mathcal {F}, \mathbb {P})$
denotes the underlying probability space,
![]() $\lambda $
denotes the Lebesgue measure on the unit circle
$\lambda $
denotes the Lebesgue measure on the unit circle
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $I_{n}=(\omega _n,\omega _n+\ell _n)$
is the random interval with left endpoint
$I_{n}=(\omega _n,\omega _n+\ell _n)$
is the random interval with left endpoint
![]() $\omega _n$
and length
$\omega _n$
and length
![]() $\ell _n$
. For a measurable function f on
$\ell _n$
. For a measurable function f on
![]() $\Omega \times \mathbb {T}$
, the next lemma allows us to estimate
$\Omega \times \mathbb {T}$
, the next lemma allows us to estimate
![]() $\mathbb {P}(\{\mathbb {E}_{\lambda }(f)\geq a\})$
by virtue of
$\mathbb {P}(\{\mathbb {E}_{\lambda }(f)\geq a\})$
by virtue of
![]() $\mathbb {P}\times \lambda (\{f\geq b\})$
, which is easier to treat via Markov’s inequality and Fubini’s theorem.
$\mathbb {P}\times \lambda (\{f\geq b\})$
, which is easier to treat via Markov’s inequality and Fubini’s theorem.
Lemma 2.3 [Reference Ayyer, Liverani and Stenlund3, Section 5].
Let
![]() $M>0$
and let
$M>0$
and let
![]() $f=f(\omega , x)$
be a measurable function on
$f=f(\omega , x)$
be a measurable function on
![]() $\Omega \times \mathbb {T}$
with
$\Omega \times \mathbb {T}$
with
![]() $0\leq f\leq M$
. Then, for any
$0\leq f\leq M$
. Then, for any
![]() $\alpha>0$
,
$\alpha>0$
,
Proof. Note that
![]() $\mathbb {P}\times \lambda (\{f\geq \alpha \})= \mathbb {E}_{\mathbb {P}\times \lambda }(\mathbf {1}_{\{f\geq \alpha \}}) \geq \mathbb {E}_{\mathbb {P}}(\mathbb {E}_{\lambda }(\mathbf {1}_{\{f\geq \alpha \}})\cdot \mathbf {1}_{\{\mathbb {E}_{\lambda }(f)\geq 2\alpha \}})$
. Since
$\mathbb {P}\times \lambda (\{f\geq \alpha \})= \mathbb {E}_{\mathbb {P}\times \lambda }(\mathbf {1}_{\{f\geq \alpha \}}) \geq \mathbb {E}_{\mathbb {P}}(\mathbb {E}_{\lambda }(\mathbf {1}_{\{f\geq \alpha \}})\cdot \mathbf {1}_{\{\mathbb {E}_{\lambda }(f)\geq 2\alpha \}})$
. Since
![]() $M\cdot \mathbb {E}_{\lambda }(\mathbf {1}_{\{f\geq \alpha \}})+\alpha \geq \mathbb {E}_{\lambda }(f)$
, the bound
$M\cdot \mathbb {E}_{\lambda }(\mathbf {1}_{\{f\geq \alpha \}})+\alpha \geq \mathbb {E}_{\lambda }(f)$
, the bound
![]() $\mathbb {E}_{\lambda }(f)\geq 2\alpha $
implies that
$\mathbb {E}_{\lambda }(f)\geq 2\alpha $
implies that
![]() $\mathbb {E}_{\lambda }(\mathbf {1}_{\{f\geq \alpha \}})\geq \alpha /M$
. Thus, by Fubini’s theorem and Markov’s inequality,
$\mathbb {E}_{\lambda }(\mathbf {1}_{\{f\geq \alpha \}})\geq \alpha /M$
. Thus, by Fubini’s theorem and Markov’s inequality,
Lemma 2.4. For any fixed
![]() $x, y\in \mathbb {T}$
and any integers
$x, y\in \mathbb {T}$
and any integers
![]() $k, m\geq 1$
,
$k, m\geq 1$
,
and
 $$ \begin{align} \mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))^m) = \begin{cases} 0 & m \ \text{is odd},\\ 2 \min\{\ell_k, |x-y|\} & m \ \text{is even}. \end{cases} \end{align} $$
$$ \begin{align} \mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))^m) = \begin{cases} 0 & m \ \text{is odd},\\ 2 \min\{\ell_k, |x-y|\} & m \ \text{is even}. \end{cases} \end{align} $$
Proof. By the binomial formula,
 $$ \begin{align*} \mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\ell_k)^m) & = \mathbb{E}_{\mathbb{P}}\bigg(\sum_{j=0}^{m-1}(-1)^j C_{m}^{j}\mathbf{1}_{I_{k}}(x)\cdot\ell_k^j+(-1)^m\ell_k^m\bigg) \\ & = \ell_k(1-\ell_k)^m+ (-1)^m\ell_k^m (1-\ell_k). \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\ell_k)^m) & = \mathbb{E}_{\mathbb{P}}\bigg(\sum_{j=0}^{m-1}(-1)^j C_{m}^{j}\mathbf{1}_{I_{k}}(x)\cdot\ell_k^j+(-1)^m\ell_k^m\bigg) \\ & = \ell_k(1-\ell_k)^m+ (-1)^m\ell_k^m (1-\ell_k). \end{align*} $$
Notice that
![]() $|\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)|$
takes only 0 and 1 as values. For fixed
$|\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)|$
takes only 0 and 1 as values. For fixed
![]() $x, y\in \mathbb {T}$
, the function
$x, y\in \mathbb {T}$
, the function
![]() $|\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)|$
as a function of
$|\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)|$
as a function of
![]() $\omega $
is the indicator function of the event that
$\omega $
is the indicator function of the event that
![]() $\omega $
belongs to one of the two intervals
$\omega $
belongs to one of the two intervals
![]() $(x-\ell _k, x)$
and
$(x-\ell _k, x)$
and
![]() $(y-\ell _k, y)$
but not the other, that is, to the symmetric difference of the two intervals. There are two cases: when
$(y-\ell _k, y)$
but not the other, that is, to the symmetric difference of the two intervals. There are two cases: when
![]() $|x-y|>\ell _k$
, the two intervals are disjoint and the event has probability
$|x-y|>\ell _k$
, the two intervals are disjoint and the event has probability
![]() $2\ell _k$
; when
$2\ell _k$
; when
![]() $|x-y|\leq \ell _k$
, the symmetric difference is the union of two disjoint intervals of length
$|x-y|\leq \ell _k$
, the symmetric difference is the union of two disjoint intervals of length
![]() $|x-y|$
and the event has probability
$|x-y|$
and the event has probability
![]() $2|x-y|$
. Then (2.2) follows immediately.
$2|x-y|$
. Then (2.2) follows immediately.
If m is even, as we just proved,
If m is odd, by the fact that
![]() $\mathbb {E}_{\mathbb {P}}(\mathbf {1}_{I_{k}}(x)\cdot \mathbf {1}_{I_{k}}(y))=\max \{\ell _k-|x-y|, 0\}$
and the binomial formula,
$\mathbb {E}_{\mathbb {P}}(\mathbf {1}_{I_{k}}(x)\cdot \mathbf {1}_{I_{k}}(y))=\max \{\ell _k-|x-y|, 0\}$
and the binomial formula,
 $$ \begin{align*} \mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))^m) & = \mathbb{E}_{\mathbb{P}}\bigg(\mathbf{1}_{I_{k}}(x)+\sum_{j=1}^{m-1}(-1)^j C_{m}^{j}\mathbf{1}_{I_{k}}(x)\cdot \mathbf{1}_{I_{k}}(y)- \mathbf{1}_{I_{k}}(y)\bigg) \\ & = \ell_k+ \max\{\ell_k-|x-y|, 0\}\sum_{j=1}^{m-1}(-1)^j C_{m}^{j} -\ell_k=0. \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))^m) & = \mathbb{E}_{\mathbb{P}}\bigg(\mathbf{1}_{I_{k}}(x)+\sum_{j=1}^{m-1}(-1)^j C_{m}^{j}\mathbf{1}_{I_{k}}(x)\cdot \mathbf{1}_{I_{k}}(y)- \mathbf{1}_{I_{k}}(y)\bigg) \\ & = \ell_k+ \max\{\ell_k-|x-y|, 0\}\sum_{j=1}^{m-1}(-1)^j C_{m}^{j} -\ell_k=0. \end{align*} $$
For the last equality, we have used
![]() $\sum _{j=0}^{m}(-1)^j C_{m}^{j}=(1-1)^m=0$
.
$\sum _{j=0}^{m}(-1)^j C_{m}^{j}=(1-1)^m=0$
.
3 Proof of Proposition 1.2
Recall that
 $$ \begin{align*} Y_n=\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-l_{k})}{V_n}\quad\text{and}\quad Z_n=\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))}{V_n}, \end{align*} $$
$$ \begin{align*} Y_n=\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-l_{k})}{V_n}\quad\text{and}\quad Z_n=\frac{\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))}{V_n}, \end{align*} $$
where
![]() $x, y\in \mathbb {T}$
. By Lévy’s continuity theorem, we need to prove that,
$x, y\in \mathbb {T}$
. By Lévy’s continuity theorem, we need to prove that,
![]() $\mathbb {P}$
-almost surely,
$\mathbb {P}$
-almost surely,
![]() $\mathbb {E}_{\lambda }(e^{itY_{n}})\rightarrow e^{-t^{2}/2}$
for all
$\mathbb {E}_{\lambda }(e^{itY_{n}})\rightarrow e^{-t^{2}/2}$
for all
![]() $t\in \mathbb {R}$
. For simplicity, let
$t\in \mathbb {R}$
. For simplicity, let
Since
![]() $\mathbb {R}$
can be covered by countably many compact sets, it suffices to prove that
$\mathbb {R}$
can be covered by countably many compact sets, it suffices to prove that
where
![]() $T>0$
is a fixed integer. This is implied by
$T>0$
is a fixed integer. This is implied by
We start by estimating the second moment
![]() $\mathbb {E}_{\mathbb {P}}(|\xi _n^2(t)-e^{-t^{2}/2}|^{2})$
. First, we can write
$\mathbb {E}_{\mathbb {P}}(|\xi _n^2(t)-e^{-t^{2}/2}|^{2})$
. First, we can write
Note that
![]() $|\xi _n|^2=\mathbb {E}_{\lambda \times \lambda }(e^{itZ_{n}})$
by Fubini’s theorem. Hence, taking expectations with respect to
$|\xi _n|^2=\mathbb {E}_{\lambda \times \lambda }(e^{itZ_{n}})$
by Fubini’s theorem. Hence, taking expectations with respect to
![]() $\mathbb {P}$
leads to
$\mathbb {P}$
leads to
We apply hypotheses (1) and (2) of the theorem to compute an
![]() $L^2$
estimate of the random variable
$L^2$
estimate of the random variable
![]() $\xi _n(t)-e^{-t^{2}/2}$
, which gives
$\xi _n(t)-e^{-t^{2}/2}$
, which gives
By Chebyshev’s inequality and (3.1), for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Now we choose b with
![]() $\max \{{(\tau +1)}/{2}, 1-{\tau }/{2}\}<b<1$
. We divide the interval of integers
$\max \{{(\tau +1)}/{2}, 1-{\tau }/{2}\}<b<1$
. We divide the interval of integers
![]() $[2^k, 2^{k+1})$
into
$[2^k, 2^{k+1})$
into
![]() $2^{(1-b)k}$
intervals of length
$2^{(1-b)k}$
intervals of length
![]() $2^{bk}$
, denoted by
$2^{bk}$
, denoted by
![]() $\{I_{k, p}\}_{p=1}^{2^{(1-b)k}}$
, and we divide the interval of real numbers
$\{I_{k, p}\}_{p=1}^{2^{(1-b)k}}$
, and we divide the interval of real numbers
![]() $[-T, T]$
into
$[-T, T]$
into
![]() $2Tk$
intervals of length
$2Tk$
intervals of length
![]() $k^{-1}$
, denoted by
$k^{-1}$
, denoted by
![]() $\{J_{k, q}\}_{q=1}^{2Tk}$
. In this way,
$\{J_{k, q}\}_{q=1}^{2Tk}$
. In this way,
 $$ \begin{align*}\{(n, t)\in\mathbb{N}\times\mathbb{R}: \;2^{k}\leq n< 2^{k+1}, \;t\in [-T, T]\}\subset \bigcup_{p, q} I_{k, p}\times J_{k, q},\end{align*} $$
$$ \begin{align*}\{(n, t)\in\mathbb{N}\times\mathbb{R}: \;2^{k}\leq n< 2^{k+1}, \;t\in [-T, T]\}\subset \bigcup_{p, q} I_{k, p}\times J_{k, q},\end{align*} $$
so that
In each ‘rectangle’
![]() $I_{k, p}\times J_{k, q}$
, we choose a point
$I_{k, p}\times J_{k, q}$
, we choose a point
![]() $(n_{k, p}, t_{k, q})$
and we compare the maximum on this ‘rectangle’ with the value at the point
$(n_{k, p}, t_{k, q})$
and we compare the maximum on this ‘rectangle’ with the value at the point
![]() $(n_{k, p}, t_{k, q})$
. For
$(n_{k, p}, t_{k, q})$
. For
![]() $(n, t)\in I_{k, p}\times J_{k, q}$
,
$(n, t)\in I_{k, p}\times J_{k, q}$
,
 $$ \begin{align*} |\xi_n(t)-e^{-t^{2}/2}|&\leq |\xi_n(t)-\xi_{n_{k, p}}(t)| + |\xi_{n_{k, p}}(t)-\xi_{n_{k, p}}(t_{k, q})|\\ &\quad+|\xi_{n_{k, p}}(t_{k, q})-e^{-t_{k, q}^{2}/2}| + |e^{-t_{k, q}^{2}/2}-e^{-t^{2}/2}|. \end{align*} $$
$$ \begin{align*} |\xi_n(t)-e^{-t^{2}/2}|&\leq |\xi_n(t)-\xi_{n_{k, p}}(t)| + |\xi_{n_{k, p}}(t)-\xi_{n_{k, p}}(t_{k, q})|\\ &\quad+|\xi_{n_{k, p}}(t_{k, q})-e^{-t_{k, q}^{2}/2}| + |e^{-t_{k, q}^{2}/2}-e^{-t^{2}/2}|. \end{align*} $$
The third term on the right-hand side of the above inequality does not depend on t but only on
![]() $t_{k, q}$
. By using the inequality
$t_{k, q}$
. By using the inequality
![]() $|e^{ia}-e^{ib}|\leq |a-b|$
, the first, second and fourth terms can be estimated by
$|e^{ia}-e^{ib}|\leq |a-b|$
, the first, second and fourth terms can be estimated by
and
The fourth term tends to zero. So we only need to prove that,
![]() $\mathbb {P}$
-almost surely,
$\mathbb {P}$
-almost surely,
and
To prove (3.3)–(3.5), we bound the tail probability of certain events and then apply the Borel–Cantelli lemma. Let
![]() $\epsilon>0$
be arbitrarily small. First,
$\epsilon>0$
be arbitrarily small. First,
 $$ \begin{align} & \mathbb{P}(\sup_{p, q}\max_{n\in I_{k, p}}\max_{t\in J_{k, q}} \mathbb{E}_{\lambda}(|e^{itY_{n}}-e^{itY_{n_{k, p}}}|)\geq 2\epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\mathbb{P}(\max_{n\in I_{k, p}}\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n}}-e^{itY_{n_{k, p}}}|)\geq 2\epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 2 \epsilon^{-1}\mathbb{P}\times\lambda(\{\max_{n\in I_{k, p}}\max_{t\in J_{k, q}}|e^{itY_{n}}-e^{itY_{n_{k, p}}}|\geq\epsilon\}) \notag \quad (\text{by Lemma } 2.3)\\ & \leq \kern-1pt \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} \kern-3pt 2\epsilon^{-1} \mathbb{P}\times\lambda\bigg(\bigg\{\max_{n\in I_{k, p}}\max_{t\in J_{k, q}}|Y_n-Y_{n_{k, p}}|\geq\frac{\epsilon}{T}\bigg\}\bigg) \quad (\text{since} \;|e^{ia}-e^{ib}|\leq |a-b|) \notag\\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\sum_{n\in I_{k, p}} 2\epsilon^{-1} \mathbb{P}\times\lambda\bigg(\bigg\{|Y_n-Y_{n_{k, p}}|\geq\frac{\epsilon}{T}\bigg\}\bigg). \end{align} $$
$$ \begin{align} & \mathbb{P}(\sup_{p, q}\max_{n\in I_{k, p}}\max_{t\in J_{k, q}} \mathbb{E}_{\lambda}(|e^{itY_{n}}-e^{itY_{n_{k, p}}}|)\geq 2\epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\mathbb{P}(\max_{n\in I_{k, p}}\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n}}-e^{itY_{n_{k, p}}}|)\geq 2\epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 2 \epsilon^{-1}\mathbb{P}\times\lambda(\{\max_{n\in I_{k, p}}\max_{t\in J_{k, q}}|e^{itY_{n}}-e^{itY_{n_{k, p}}}|\geq\epsilon\}) \notag \quad (\text{by Lemma } 2.3)\\ & \leq \kern-1pt \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} \kern-3pt 2\epsilon^{-1} \mathbb{P}\times\lambda\bigg(\bigg\{\max_{n\in I_{k, p}}\max_{t\in J_{k, q}}|Y_n-Y_{n_{k, p}}|\geq\frac{\epsilon}{T}\bigg\}\bigg) \quad (\text{since} \;|e^{ia}-e^{ib}|\leq |a-b|) \notag\\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\sum_{n\in I_{k, p}} 2\epsilon^{-1} \mathbb{P}\times\lambda\bigg(\bigg\{|Y_n-Y_{n_{k, p}}|\geq\frac{\epsilon}{T}\bigg\}\bigg). \end{align} $$
Note that
![]() $Y_n-Y_{n_{k, p}}$
is a weighted sum of
$Y_n-Y_{n_{k, p}}$
is a weighted sum of
![]() $\mathbf {1}_{I_{k}}-\ell _{k}$
and that the probability law of
$\mathbf {1}_{I_{k}}-\ell _{k}$
and that the probability law of
![]() $\mathbf {1}_{I_{k}}-\ell _{k}$
is independent of x, so
$\mathbf {1}_{I_{k}}-\ell _{k}$
is independent of x, so
Write
![]() $S_n=\sum _{k=1}^{n}(\mathbf {1}_{I_{k}}-\ell _{k})$
and assume that
$S_n=\sum _{k=1}^{n}(\mathbf {1}_{I_{k}}-\ell _{k})$
and assume that
![]() $n> n_{k, p}$
(the case
$n> n_{k, p}$
(the case
![]() $n<n_{k, p}$
is the same). Since
$n<n_{k, p}$
is the same). Since
![]() $Y_n-Y_{n_{k, p}}=(V_n^{-1}-V_{n_{k, p}}^{-1})S_n-V_{n_{k, p}}^{-1}(S_n-S_{n_{k, p}}) = a_n S_n+b_n(S_n-S_{n_{k, p}})$
, say,
$Y_n-Y_{n_{k, p}}=(V_n^{-1}-V_{n_{k, p}}^{-1})S_n-V_{n_{k, p}}^{-1}(S_n-S_{n_{k, p}}) = a_n S_n+b_n(S_n-S_{n_{k, p}})$
, say,
By (2.1), the hypotheses of Lemma 2.2 are satisfied for the sequence
![]() $\{\mathbf {1}_{I_{n}}-\ell _{n}\}_{n\geq 1}$
with the constant
$\{\mathbf {1}_{I_{n}}-\ell _{n}\}_{n\geq 1}$
with the constant
![]() $H=1$
. Now apply Lemma 2.2 twice to
$H=1$
. Now apply Lemma 2.2 twice to
![]() $S_n$
and
$S_n$
and
![]() $S_n-S_{n_{k, p}}$
, which are both sums of independent random variables under the probability
$S_n-S_{n_{k, p}}$
, which are both sums of independent random variables under the probability
![]() $\mathbb {P}$
. This gives
$\mathbb {P}$
. This gives
 $$ \begin{align} \mathbb{P}\bigg(\bigg\{|S_n|\geq\frac{\epsilon}{2T|a_n|}\bigg\}\bigg)\leq 2\exp\bigg[\frac{-\epsilon^2}{8T^2a_n^2 V_n^2+4T|a_n|\epsilon}\bigg] \end{align} $$
$$ \begin{align} \mathbb{P}\bigg(\bigg\{|S_n|\geq\frac{\epsilon}{2T|a_n|}\bigg\}\bigg)\leq 2\exp\bigg[\frac{-\epsilon^2}{8T^2a_n^2 V_n^2+4T|a_n|\epsilon}\bigg] \end{align} $$
and
 $$ \begin{align} \mathbb{P}\bigg(\bigg\{|S_n-S_{n_{k, p}}|\geq\frac{\epsilon}{2T|b_n|}\bigg\}\bigg)\leq 2\exp\bigg[\frac{-\epsilon^2}{8T^2 b_n^2 (V_n^2-V_{n_{k, p}}^2)+4T\epsilon |b_n|}\bigg]. \end{align} $$
$$ \begin{align} \mathbb{P}\bigg(\bigg\{|S_n-S_{n_{k, p}}|\geq\frac{\epsilon}{2T|b_n|}\bigg\}\bigg)\leq 2\exp\bigg[\frac{-\epsilon^2}{8T^2 b_n^2 (V_n^2-V_{n_{k, p}}^2)+4T\epsilon |b_n|}\bigg]. \end{align} $$
Since
![]() $2^k\leq n < 2^{k+1}$
,
$2^k\leq n < 2^{k+1}$
,
![]() $|n-n_{k, p}|\leq 2^{bk}$
and
$|n-n_{k, p}|\leq 2^{bk}$
and
![]() $V_n^2\sim {c}n^{1-\tau }/{(1-\tau )}$
, by the mean value theorem,
$V_n^2\sim {c}n^{1-\tau }/{(1-\tau )}$
, by the mean value theorem,
 $$ \begin{align} |V_n^2-V_{n_{k, p}}^2|=\sum_{k=n_1+1}^n ck^{-\tau}\ll |n^{1-\tau}-n_1^{1-\tau}|\ll 2^{(b-\tau)k}. \end{align} $$
$$ \begin{align} |V_n^2-V_{n_{k, p}}^2|=\sum_{k=n_1+1}^n ck^{-\tau}\ll |n^{1-\tau}-n_1^{1-\tau}|\ll 2^{(b-\tau)k}. \end{align} $$
Recall that
![]() $a_n=V_n^{-1}-V_{n_{k, p}}^{-1}$
,
$a_n=V_n^{-1}-V_{n_{k, p}}^{-1}$
,
![]() $b_n=V_{n_{k, p}}^{-1}$
and
$b_n=V_{n_{k, p}}^{-1}$
and
![]() $\max \{{(\tau +1)}/{2}, 1-{\tau }/{2}\}< b <1$
. Combining (3.7)–(3.11),
$\max \{{(\tau +1)}/{2}, 1-{\tau }/{2}\}< b <1$
. Combining (3.7)–(3.11),
 $$ \begin{align} \mathbb{P}\times\lambda\bigg(\bigg\{|Y_n-Y_{n_{k, p}}|\geq\frac{\epsilon}{T}\bigg\}\bigg)\ll \exp\bigg[\frac{-\varepsilon^2 2^{(1-b)) k}}{8T^2}\bigg]. \end{align} $$
$$ \begin{align} \mathbb{P}\times\lambda\bigg(\bigg\{|Y_n-Y_{n_{k, p}}|\geq\frac{\epsilon}{T}\bigg\}\bigg)\ll \exp\bigg[\frac{-\varepsilon^2 2^{(1-b)) k}}{8T^2}\bigg]. \end{align} $$
Substituting (3.12) into (3.6) yields
 $$ \begin{align*} \mathbb{P}(\sup_{p, q}\max_{n\in I_{k, p}}\max_{t\in J_{k, q}} \mathbb{E}_{\lambda}(|e^{itY_{n}}-e^{itY_{n_{k, p}}}|)\geq 2\epsilon)\ll Tk2^{k}\exp\bigg[\frac{-\varepsilon^2 2^{(1-b)) k}}{8T^2}\bigg]. \end{align*} $$
$$ \begin{align*} \mathbb{P}(\sup_{p, q}\max_{n\in I_{k, p}}\max_{t\in J_{k, q}} \mathbb{E}_{\lambda}(|e^{itY_{n}}-e^{itY_{n_{k, p}}}|)\geq 2\epsilon)\ll Tk2^{k}\exp\bigg[\frac{-\varepsilon^2 2^{(1-b)) k}}{8T^2}\bigg]. \end{align*} $$
Since the sum over k of the terms on the right-hand side of the last inequality is finite, by the convergence part of the Borel–Cantelli lemma, the events
happen only finitely many times with probability one. Since
![]() $\epsilon>0$
is arbitrarily small, this shows that (3.3) holds
$\epsilon>0$
is arbitrarily small, this shows that (3.3) holds
![]() $\mathbb {P}$
-almost surely.
$\mathbb {P}$
-almost surely.
Second, for the proof of (3.4), observe that
 $$ \begin{align} &\;\mathbb{P}(\max_{1\leq p\leq 2^{(1-b)k}}\max_{1\leq q\leq 2Tk}|\xi_{n_{k, p}}(t_{k, q})-e^{-t_{k, q}^{2}/2}|\geq \epsilon)\notag\\ &\quad \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\mathbb{P}(|\xi_{n_{k, p}}(t_{k, q})-e^{-t_{k, q}^{2}/2}|\geq \epsilon)\notag \\ &\quad \ll \varepsilon^{-2}(1+|T|^3)Tk 2^{(1-b-\sigma)k} \quad (\text{using } (3.2), n_{k, p}<2^{k+1}\;\text{and}\;|t_{k, q}|\leq T). \end{align} $$
$$ \begin{align} &\;\mathbb{P}(\max_{1\leq p\leq 2^{(1-b)k}}\max_{1\leq q\leq 2Tk}|\xi_{n_{k, p}}(t_{k, q})-e^{-t_{k, q}^{2}/2}|\geq \epsilon)\notag\\ &\quad \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\mathbb{P}(|\xi_{n_{k, p}}(t_{k, q})-e^{-t_{k, q}^{2}/2}|\geq \epsilon)\notag \\ &\quad \ll \varepsilon^{-2}(1+|T|^3)Tk 2^{(1-b-\sigma)k} \quad (\text{using } (3.2), n_{k, p}<2^{k+1}\;\text{and}\;|t_{k, q}|\leq T). \end{align} $$
By the choice of b, we have
![]() $\sigma>1-b$
, so the sum over k of the terms in (3.13) is finite. Applying Borel–Cantelli again gives the
$\sigma>1-b$
, so the sum over k of the terms in (3.13) is finite. Applying Borel–Cantelli again gives the
![]() $\mathbb {P}$
-almost sure convergence of (3.4).
$\mathbb {P}$
-almost sure convergence of (3.4).
Third, for the proof of (3.5),
 $$ \begin{align*} & \mathbb{P}(\sup_{p, q}\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n_{k, p}}}-e^{it_{k, q}Y_{n_{k, p}}}|)\geq 2 \epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\mathbb{P}(\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n_{k, p}}}-e^{it_{k, q}Y_{n_{k, p}}}|)\geq 2\epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 2 \epsilon^{-1}\mathbb{P}\times\lambda(\{\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n_{k, p}}}-e^{it_{k, q}Y_{n_{k, p}}}|)\geq \epsilon\}) \notag \quad (\text{by Lemma } 2.3)\\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 2\epsilon^{-1} \mathbb{P}\times\lambda(\{|Y_{n_{k, p}}|\geq k \epsilon\}) \quad(\text{since} \;|e^{ia}-e^{ib}|\leq |a-b|) \notag\\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 4\epsilon^{-1} e^{-{k^2\epsilon^2}/{4}}\leq 8\epsilon^{-1} Tk 2^{(1-b)k} e^{-{k^2\epsilon^2}/{4}} \quad (\text{by Hypothesis (3)}). \end{align*} $$
$$ \begin{align*} & \mathbb{P}(\sup_{p, q}\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n_{k, p}}}-e^{it_{k, q}Y_{n_{k, p}}}|)\geq 2 \epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk}\mathbb{P}(\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n_{k, p}}}-e^{it_{k, q}Y_{n_{k, p}}}|)\geq 2\epsilon) \notag \\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 2 \epsilon^{-1}\mathbb{P}\times\lambda(\{\max_{t\in J_{k, q}}\mathbb{E}_{\lambda}(|e^{itY_{n_{k, p}}}-e^{it_{k, q}Y_{n_{k, p}}}|)\geq \epsilon\}) \notag \quad (\text{by Lemma } 2.3)\\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 2\epsilon^{-1} \mathbb{P}\times\lambda(\{|Y_{n_{k, p}}|\geq k \epsilon\}) \quad(\text{since} \;|e^{ia}-e^{ib}|\leq |a-b|) \notag\\ & \leq \sum_{1\leq p\leq 2^{(1-b)k}}\sum_{1\leq q\leq 2Tk} 4\epsilon^{-1} e^{-{k^2\epsilon^2}/{4}}\leq 8\epsilon^{-1} Tk 2^{(1-b)k} e^{-{k^2\epsilon^2}/{4}} \quad (\text{by Hypothesis (3)}). \end{align*} $$
Since the sum over k of the terms in the last inequality is finite, the Borel–Cantelli lemma implies the
![]() $\mathbb {P}$
-almost sure convergence of (3.5). This completes the proof.
$\mathbb {P}$
-almost sure convergence of (3.5). This completes the proof.
4 Proof of Theorem 1.1 modulo Proposition 1.2
We only need to verify hypotheses (1)–(3) in Proposition 1.2.
Hypothesis (1). For fixed
![]() $x\in \mathbb {T}$
and each
$x\in \mathbb {T}$
and each
![]() $k\geq 1$
, the three moments of
$k\geq 1$
, the three moments of
![]() $\{\mathbf {1}_{I_{k}}(x)-\ell _{k}\}_{k\geq 1}$
are trivially computed: that is,
$\{\mathbf {1}_{I_{k}}(x)-\ell _{k}\}_{k\geq 1}$
are trivially computed: that is,
and
As
![]() $x(1-x)\leq 1/4$
for
$x(1-x)\leq 1/4$
for
![]() $1\leq x\leq 1$
, it follows that
$1\leq x\leq 1$
, it follows that
 $$ \begin{align*}\frac{1}{2V_n}\leq B_{n}:=V_{n}^{-3}\sum_{k=1}^{n}\mathbb{E}_{\mathbb{P}}(|\mathbf{1}_{I_{k}}(x)-\ell_k|^{3})\leq\frac{1}{V_n}.\end{align*} $$
$$ \begin{align*}\frac{1}{2V_n}\leq B_{n}:=V_{n}^{-3}\sum_{k=1}^{n}\mathbb{E}_{\mathbb{P}}(|\mathbf{1}_{I_{k}}(x)-\ell_k|^{3})\leq\frac{1}{V_n}.\end{align*} $$
By Lemma 2.1, for any
![]() $|t|\leq V_n/4$
,
$|t|\leq V_n/4$
,
 $$ \begin{align} |\mathbb{E}_{\mathbb{P}}(e^{it Y_{n}})-e^{-t^{2}/2}|\leq \frac{16|t|^{3}e^{-t^{2}/3}}{V_n}. \end{align} $$
$$ \begin{align} |\mathbb{E}_{\mathbb{P}}(e^{it Y_{n}})-e^{-t^{2}/2}|\leq \frac{16|t|^{3}e^{-t^{2}/3}}{V_n}. \end{align} $$
Since (4.1) holds uniformly for any fixed
![]() $x\in \mathbb {T}$
, we can integrate both sides with respect to x. Hypothesis (1) then follows by Fubini’s theorem and the fact
$x\in \mathbb {T}$
, we can integrate both sides with respect to x. Hypothesis (1) then follows by Fubini’s theorem and the fact
![]() $V_n\asymp n^{(1-\tau )/2}$
.
$V_n\asymp n^{(1-\tau )/2}$
.
Hypothesis (2). We also appeal to Lemma 2.1, but, in this case, for the sequence of random variables
![]() $\{\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)\}_{k\geq 1}$
for any fixed
$\{\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)\}_{k\geq 1}$
for any fixed
![]() $x, y\in \mathbb {T}$
. By Lemma 2.4, for any
$x, y\in \mathbb {T}$
. By Lemma 2.4, for any
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
![]() $\mathbb {E}_{\mathbb {P}}(\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y))=0$
and
$\mathbb {E}_{\mathbb {P}}(\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y))=0$
and
Since
![]() $\ell _k=c k^{-\tau }$
is strictly decreasing, there exists
$\ell _k=c k^{-\tau }$
is strictly decreasing, there exists
![]() $k_0=\lfloor c^{1/\tau }|x-y|^{-1/\tau }\rfloor +1$
such that
$k_0=\lfloor c^{1/\tau }|x-y|^{-1/\tau }\rfloor +1$
such that
![]() $\ell _k<|x-y|$
if and only if
$\ell _k<|x-y|$
if and only if
![]() $k> k_0$
. We denote
$k> k_0$
. We denote
 $$ \begin{align*}\widetilde{V}_n^2:=\sum_{i=1}^{n}\mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))^{2})=\sum_{i=1}^{k_0}2|x-y|+\sum_{k=k_0+1}^n 2\ell_k\end{align*} $$
$$ \begin{align*}\widetilde{V}_n^2:=\sum_{i=1}^{n}\mathbb{E}_{\mathbb{P}}((\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y))^{2})=\sum_{i=1}^{k_0}2|x-y|+\sum_{k=k_0+1}^n 2\ell_k\end{align*} $$
and
 $$ \begin{align*}\widetilde{B}_{n}=\widetilde{V}_{n}^{-3}\sum_{k=1}^{n}\mathbb{E}_{\mathbb{P}}(|\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)|^{3})=\widetilde{V}_n^{-1}, \quad \widetilde{Z}_n=\widetilde{V}_n^{-1}\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)).\end{align*} $$
$$ \begin{align*}\widetilde{B}_{n}=\widetilde{V}_{n}^{-3}\sum_{k=1}^{n}\mathbb{E}_{\mathbb{P}}(|\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)|^{3})=\widetilde{V}_n^{-1}, \quad \widetilde{Z}_n=\widetilde{V}_n^{-1}\sum_{k=1}^{n}(\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)).\end{align*} $$
By Lemma 2.1, for all
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
![]() $|t|\leq {1}/{4\sqrt {2}\widetilde {B}_{n}}$
,
$|t|\leq {1}/{4\sqrt {2}\widetilde {B}_{n}}$
,
In addition, the inequality
![]() $|e^{ia}-e^{ib}|\leq |a-b|$
implies that
$|e^{ia}-e^{ib}|\leq |a-b|$
implies that
 $$ \begin{align} |\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-\mathbb{E}_{\mathbb{P}}(e^{i\sqrt{2}t\widetilde{Z}_n})| \leq |t|\cdot|1/V_n-\sqrt{2}/\widetilde{V}_n|\cdot\mathbb{E}_{\mathbb{P}}\bigg(\bigg|\!\sum_{i=1}^n\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)\bigg|\bigg). \end{align} $$
$$ \begin{align} |\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-\mathbb{E}_{\mathbb{P}}(e^{i\sqrt{2}t\widetilde{Z}_n})| \leq |t|\cdot|1/V_n-\sqrt{2}/\widetilde{V}_n|\cdot\mathbb{E}_{\mathbb{P}}\bigg(\bigg|\!\sum_{i=1}^n\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)\bigg|\bigg). \end{align} $$
Now we estimate the right-hand sides of (4.2) and (4.3). For any sufficiently large n, if
![]() $x, y\in \mathbb {T}$
satisfies
$x, y\in \mathbb {T}$
satisfies
![]() $|x-y|>n^{-\tau /2}$
, then
$|x-y|>n^{-\tau /2}$
, then
 $$ \begin{align} \widetilde{V}_n^2=\sum_{k=1}^{k_0}2|x-y|+\sum_{k=k_0+1}^n 2\ell_k=2 k_0 |x-y|+\sum_{k=k_0+1}^n 2 ck^{-\tau}\asymp |x-y|^{1-1/\tau}+n^{1-\tau}\asymp n^{1-\tau}. \end{align} $$
$$ \begin{align} \widetilde{V}_n^2=\sum_{k=1}^{k_0}2|x-y|+\sum_{k=k_0+1}^n 2\ell_k=2 k_0 |x-y|+\sum_{k=k_0+1}^n 2 ck^{-\tau}\asymp |x-y|^{1-1/\tau}+n^{1-\tau}\asymp n^{1-\tau}. \end{align} $$
Since
![]() $V_n^2\sim {c}n^{1-\tau }/{(1-\tau )}$
,
$V_n^2\sim {c}n^{1-\tau }/{(1-\tau )}$
,
 $$ \begin{align} |1/V_n-\sqrt{2}/\widetilde{V}_n| \ll n^{-3(1-\tau)/2} \bigg|\!\sum_{i=1}^{i_0}\ell_k-\sum_{i=1}^n \ell_k^2-\sum_{i=1}^{i_0}|x-y|\bigg|\ll n^{-(1+\tau)/2}+n^{-(1-\tau)}. \end{align} $$
$$ \begin{align} |1/V_n-\sqrt{2}/\widetilde{V}_n| \ll n^{-3(1-\tau)/2} \bigg|\!\sum_{i=1}^{i_0}\ell_k-\sum_{i=1}^n \ell_k^2-\sum_{i=1}^{i_0}|x-y|\bigg|\ll n^{-(1+\tau)/2}+n^{-(1-\tau)}. \end{align} $$
In addition, by (2.3), for any fixed
![]() $x, y\in \mathbb {T}$
,
$x, y\in \mathbb {T}$
,
where
![]() $H=1$
and
$H=1$
and
![]() $\widetilde {\sigma }_k^2=\mathbb {E}_{\mathbb {P}}((\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y))^2)$
. Write
$\widetilde {\sigma }_k^2=\mathbb {E}_{\mathbb {P}}((\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y))^2)$
. Write
![]() $T_n=\sum _{i=1}^n (\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y))$
, where
$T_n=\sum _{i=1}^n (\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y))$
, where
![]() $x, y$
satisfy
$x, y$
satisfy
![]() $|x-y|> n^{-\tau /2}$
. Since
$|x-y|> n^{-\tau /2}$
. Since
![]() $|\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)|\leq 2$
, applying Lemma 2.2 to the sequence
$|\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)|\leq 2$
, applying Lemma 2.2 to the sequence
![]() $\{\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)\}_{k\geq 1}$
with
$\{\mathbf {1}_{I_{k}}(x)-\mathbf {1}_{I_{k}}(y)\}_{k\geq 1}$
with
![]() $a=\widetilde {V}_n^{1+\eta }$
gives
$a=\widetilde {V}_n^{1+\eta }$
gives
 $$ \begin{align*} \mathbb{E}_{\mathbb{P}}\bigg(\bigg|\!\sum_{i=1}^n\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)\bigg|\bigg) & = \mathbb{E}_{\mathbb{P}}(|T_n|\cdot\mathbf{1}_{\{|T_n|\geq a\}})+\mathbb{E}_{\mathbb{P}}(|T_n|\cdot\mathbf{1}_{\{|T_n|< a\}}) \\ & \leq 2n\mathbb{P}(\{|T_n|\geq a\}) + a \leq 4n\exp\bigg(\frac{-\widetilde{V}_n^{2\eta}}{4}\bigg)+\widetilde{V}_n^{1+\eta}, \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\mathbb{P}}\bigg(\bigg|\!\sum_{i=1}^n\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)\bigg|\bigg) & = \mathbb{E}_{\mathbb{P}}(|T_n|\cdot\mathbf{1}_{\{|T_n|\geq a\}})+\mathbb{E}_{\mathbb{P}}(|T_n|\cdot\mathbf{1}_{\{|T_n|< a\}}) \\ & \leq 2n\mathbb{P}(\{|T_n|\geq a\}) + a \leq 4n\exp\bigg(\frac{-\widetilde{V}_n^{2\eta}}{4}\bigg)+\widetilde{V}_n^{1+\eta}, \end{align*} $$
where
![]() $\eta>0$
is a constant arbitrarily close to 0. Combining this with (4.4) yields
$\eta>0$
is a constant arbitrarily close to 0. Combining this with (4.4) yields
 $$ \begin{align} \mathbb{E}_{\mathbb{P}}\bigg(\bigg|\!\sum_{i=1}^n\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)\bigg|\bigg) \ll n e^{-n^{\eta (1-\tau)}/4} + n^{(1+\eta)(1-\tau)/2}. \end{align} $$
$$ \begin{align} \mathbb{E}_{\mathbb{P}}\bigg(\bigg|\!\sum_{i=1}^n\mathbf{1}_{I_{k}}(x)-\mathbf{1}_{I_{k}}(y)\bigg|\bigg) \ll n e^{-n^{\eta (1-\tau)}/4} + n^{(1+\eta)(1-\tau)/2}. \end{align} $$
Substituting (4.5) and (4.6) into (4.3), we obtain
Combining (4.2), (4.4) and (4.7), we see that, for any
![]() $x, y\in \mathbb {T}$
with
$x, y\in \mathbb {T}$
with
![]() $|x-y|> n^{-\tau /2}$
,
$|x-y|> n^{-\tau /2}$
,
 $$ \begin{align*} |\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}| & \leq |\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-\mathbb{E}_{\mathbb{P}}(e^{i\sqrt{2}t\widetilde{Z}_n})|+ |\mathbb{E}_{\mathbb{P}}(e^{i\sqrt{2}t\widetilde{Z}_n})-e^{-t^2}|\nonumber\\ & \ll |t|(n^{-\tau+\eta} + n^{-(1-\tau)/2+\eta}) + |t|^3 n^{-(1-\tau)/2} \end{align*} $$
$$ \begin{align*} |\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}| & \leq |\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-\mathbb{E}_{\mathbb{P}}(e^{i\sqrt{2}t\widetilde{Z}_n})|+ |\mathbb{E}_{\mathbb{P}}(e^{i\sqrt{2}t\widetilde{Z}_n})-e^{-t^2}|\nonumber\\ & \ll |t|(n^{-\tau+\eta} + n^{-(1-\tau)/2+\eta}) + |t|^3 n^{-(1-\tau)/2} \end{align*} $$
holds for all
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
![]() $|t|\leq {\widetilde {V}_{n}}/{4\sqrt {2}}$
. Therefore, by Fubini’s theorem,
$|t|\leq {\widetilde {V}_{n}}/{4\sqrt {2}}$
. Therefore, by Fubini’s theorem,
 $$ \begin{align*} &|\mathbb{E}_{\mathbb{P}\times\lambda\times\lambda}(e^{it Z_{n}})-e^{-t^{2}}| \leq \mathbb{E}_{\lambda\times\lambda}(|\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}|)\nonumber\\ &\quad \leq \mathbb{E}_{\lambda\times\lambda}(|\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}|\cdot\mathbf{1}_{\{|x-y|\leq n^{-\tau/2}\}})+\mathbb{E}_{\lambda\times\lambda}(|\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}|\cdot\mathbf{1}_{\{|x-y|>n^{-\tau/2}\}})\nonumber\\ &\quad \ll n^{-\tau/2} + |t|(n^{-\tau+\eta} + n^{-(1-\tau)/2+\eta}) + |t|^3 n^{-(1-\tau)/2} \ll (1+|t|^3) n^{-\sigma}, \end{align*} $$
$$ \begin{align*} &|\mathbb{E}_{\mathbb{P}\times\lambda\times\lambda}(e^{it Z_{n}})-e^{-t^{2}}| \leq \mathbb{E}_{\lambda\times\lambda}(|\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}|)\nonumber\\ &\quad \leq \mathbb{E}_{\lambda\times\lambda}(|\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}|\cdot\mathbf{1}_{\{|x-y|\leq n^{-\tau/2}\}})+\mathbb{E}_{\lambda\times\lambda}(|\mathbb{E}_{\mathbb{P}}(e^{i t Z_n})-e^{-t^2}|\cdot\mathbf{1}_{\{|x-y|>n^{-\tau/2}\}})\nonumber\\ &\quad \ll n^{-\tau/2} + |t|(n^{-\tau+\eta} + n^{-(1-\tau)/2+\eta}) + |t|^3 n^{-(1-\tau)/2} \ll (1+|t|^3) n^{-\sigma}, \end{align*} $$
where
![]() $\sigma $
is a constant satisfying
$\sigma $
is a constant satisfying
![]() $\sigma>\min \{{(1-\tau )}/{2}, {\tau }/{2}\}$
.
$\sigma>\min \{{(1-\tau )}/{2}, {\tau }/{2}\}$
.
Hypothesis (3). We first appeal to Lemma 2.2 for the sequence of random variables
![]() $\{\mathbf {1}_{I_{k}}(x)-\ell _{k}\}_{k\geq 1}$
for any fixed
$\{\mathbf {1}_{I_{k}}(x)-\ell _{k}\}_{k\geq 1}$
for any fixed
![]() $x\in \mathbb {T}$
. From the discussion in Section 3,
$x\in \mathbb {T}$
. From the discussion in Section 3,
with
![]() $H=1$
and
$H=1$
and
![]() $\sigma _k^2=\mathbb {E}_{\mathbb {P}}((\mathbf {1}_{I_{k}}(x)-\ell _{k})^2$
. Moreover,
$\sigma _k^2=\mathbb {E}_{\mathbb {P}}((\mathbf {1}_{I_{k}}(x)-\ell _{k})^2$
. Moreover,
![]() $V_n^2=\sum _{k=1}^n \ell _k(1-\ell _k)$
. Applying Lemma 2.2 to
$V_n^2=\sum _{k=1}^n \ell _k(1-\ell _k)$
. Applying Lemma 2.2 to
![]() $\{\mathbf {1}_{I_{k}}(x)-\ell _{k}\}_{k\geq 1}$
and
$\{\mathbf {1}_{I_{k}}(x)-\ell _{k}\}_{k\geq 1}$
and
![]() $a=\varepsilon V_n$
gives
$a=\varepsilon V_n$
gives
 $$ \begin{align*}\mathbb{P}(|Y_{n}|\geq\varepsilon)=\mathbb{P}\bigg(\bigg|\!\sum_{k=1}^n \mathbf{1}_{I_{k}}(x)-\ell_{k}\bigg|\geq \varepsilon V_n\bigg)\leq 2\exp\bigg[\frac{-\varepsilon^2 V_n^2}{2(V_n^2+\epsilon V_n)}\bigg] \leq 2\exp\bigg[\frac{-\varepsilon^2}{4}\bigg],\end{align*} $$
$$ \begin{align*}\mathbb{P}(|Y_{n}|\geq\varepsilon)=\mathbb{P}\bigg(\bigg|\!\sum_{k=1}^n \mathbf{1}_{I_{k}}(x)-\ell_{k}\bigg|\geq \varepsilon V_n\bigg)\leq 2\exp\bigg[\frac{-\varepsilon^2 V_n^2}{2(V_n^2+\epsilon V_n)}\bigg] \leq 2\exp\bigg[\frac{-\varepsilon^2}{4}\bigg],\end{align*} $$
where the last inequality is due to the fact that
![]() $\epsilon V_n<V_n^2$
for n large enough. The inequality in Hypothesis (3) follows from Fubini’s theorem.
$\epsilon V_n<V_n^2$
for n large enough. The inequality in Hypothesis (3) follows from Fubini’s theorem.
Acknowledgement
The authors express their gratitude to the anonymous referee for many helpful suggestions which greatly improved the paper, and clarified the proofs.