Hostname: page-component-6dbcb7884d-fw45b Total loading time: 0 Render date: 2025-02-13T14:55:29.907Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ANALOGUE OF AN IDENTITY OF JACOBI

Part of: Other special functions Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 February 2025

HENG HUAT CHAN Open the ORCID record for HENG HUAT CHAN [Opens in a new window] ,
SONG HENG CHAN Open the ORCID record for SONG HENG CHAN [Opens in a new window]  and
PATRICK SOLÉ Open the ORCID record for PATRICK SOLÉ [Opens in a new window]
HENG HUAT CHAN
Affiliation:
Mathematics Research Center, Shandong University, No. 1 Building, 5 Hongjialou Road, Jinan 250100, P.R. China e-mail: chanhh6789@sdu.edu.cn
SONG HENG CHAN*
Affiliation:
Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University, 21 Nanyang link, Singapore 637371, Republic of Singapore
PATRICK SOLÉ
Affiliation:
I2M (CNRS, University of Aix-Marseille), 163 Av. de Luminy, 13 009 Marseilles, France e-mail: sole@enst.fr
*
e-mail: ChanSH@ntu.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

H. H. Chan, K. S. Chua and P. Solé [‘Quadratic iterations to $\pi $ associated to elliptic functions to the cubic and septic base’, Trans. Amer. Math. Soc. 355(4) (2002), 1505–1520] found that, for each positive integer d, there are theta series 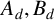$A_d, B_d$ and $C_d$ of weight one that satisfy the Pythagoras-like relationship 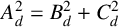$A_d^2=B_d^2+C_d^2$. In this article, we show that there are two collections of theta series 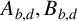$A_{b,d}, B_{b,d}$ and 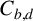$C_{b,d}$ of weight one that satisfy 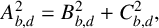$A_{b,d}^2=B_{b,d}^2+C_{b,d}^2,$ where b and d are certain integers.

Keywords

Jacobi identityRamanujan elliptic functions

MSC classification

Primary: 33C05: Classical hypergeometric functions, $_2F_1$
Secondary: 33E05: Elliptic functions and integrals 11F03: Modular and automorphic functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author is partially supported by the Ministry of Education, Singapore, Academic Research Fund, Tier 1 (RG15/23).

References

Berndt, B. C., Chan, H. H. and Liaw, W.-C., ‘On Ramanujan’s quartic theory of elliptic functions’, J. Number Theory 88(1) (2001), 129–156.CrossRefGoogle Scholar
Borwein, J. M. and Borwein, P. B., $\pi$ and the AGM: A Study in Analytic Number Theory and Computational Complexity (Wiley, Chichester, 1987).Google Scholar
Borwein, J. M. and Borwein, P. B., ‘A cubic counterpart of Jacobi’s identity and the AGM’, Trans. Amer. Math. Soc. 323(2) (1991), 691–701.Google Scholar
Chan, H. H., Theta Functions, Elliptic Functions and $\pi$ (De Gruyter, Berlin–Boston, 2020).CrossRefGoogle Scholar
Chan, H. H., Chua, K. S. and Solé, P., ‘Quadratic iterations to $\pi$ associated to elliptic functions to the cubic and septic base’, Trans. Amer. Math. Soc. 355(4) (2002), 1505–1520.CrossRefGoogle Scholar
Chan, H. H., Chua, K. S. and Solé, P., ‘Seven modular lattices and a septic base Jacobi identity’, J. Number Theory 99(2) (2003), 361–372.CrossRefGoogle Scholar
Chua, K. S. and Solé, P., ‘Jacobi identities, modular lattices, and modular towers’, European J. Combin. 25(4) (2004), 495–503.CrossRefGoogle Scholar
Solé, P. and Loyer, P., ‘ ${U}_n$ lattices, construction $B$ , and AGM iterations’, European J. Combin. 19(2) (1998), 227–236.CrossRefGoogle Scholar