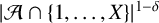1 Introduction
The Goldbach conjecture states that for all sufficiently large even n there exist primes
![]() $p_1$
,
$p_1$
,
![]() $p_2$
such that
$p_2$
such that
In this paper, we study how many exceptions to the Goldbach conjecture can have restricted digits. Given a base b and a set of digits
![]() $D\subseteq \{0,1,2,\ldots ,b-1\}$
with
$D\subseteq \{0,1,2,\ldots ,b-1\}$
with
![]() $|D|> 2$
we define
$|D|> 2$
we define
![]() $\mathcal {A}_k$
to be the set of k-digit numbers whose base-b representations only contain elements of D. More formally,
$\mathcal {A}_k$
to be the set of k-digit numbers whose base-b representations only contain elements of D. More formally,
![]() $\mathcal {A}_k$
is the set of numbers of the form
$\mathcal {A}_k$
is the set of numbers of the form
 $$ \begin{align*}\sum_{i=0}^k a_i b^i\end{align*} $$
$$ \begin{align*}\sum_{i=0}^k a_i b^i\end{align*} $$
with
![]() $a_i\in D$
. We call sets
$a_i\in D$
. We call sets
![]() $\mathcal {A}_k$
of this form, with general k and D, digitally restricted sets, and similarly we call their elements digitally restricted numbers. Let
$\mathcal {A}_k$
of this form, with general k and D, digitally restricted sets, and similarly we call their elements digitally restricted numbers. Let
![]() $\mathcal {A}$
be the union over k of
$\mathcal {A}$
be the union over k of
![]() $\mathcal {A}_k$
, that is, the set of digitally restricted integers with any number of digits. Let E be the set of even n which are not the sum of two primes and let
$\mathcal {A}_k$
, that is, the set of digitally restricted integers with any number of digits. Let E be the set of even n which are not the sum of two primes and let
![]() $E(X)=E\cap \{1,\ldots ,X\}$
.
$E(X)=E\cap \{1,\ldots ,X\}$
.
Theorem 1.1. There exists some
![]() $\delta =\delta (D,b)$
such that
$\delta =\delta (D,b)$
such that
![]() $|E(X)\cap \mathcal {A}| \ll |\mathcal {A}(X)|^{1-\delta }$
.
$|E(X)\cap \mathcal {A}| \ll |\mathcal {A}(X)|^{1-\delta }$
.
To see the relevance of this result, we look at historical results on the Goldbach conjecture. First conjectured by Goldbach in 1742, little progress occurred until the work of Vinogradov [Reference Vinogradov13] in 1937, who showed that all sufficiently large odd numbers are the sum of three primes. Heilbronn [Reference Heilbronn4] noted in his review that one could use the same method to prove that almost all even numbers are the sum of two primes, and within a year Estermann [Reference Estermann3], van der Corput [Reference van der Corput11] and Chudakov [Reference Chudakov2] all independently did so. Although van der Corput’s paper appears in the 1936 edition of Acta Arithmetica, it was submitted in 1937, after Vinogradov’s work. The initial bound of
![]() $|E(X)| \ll X(\log X)^{-c}$
has since been improved, most notably by Montgomery and Vaughan in [Reference Montgomery and Vaughan8] to
$|E(X)| \ll X(\log X)^{-c}$
has since been improved, most notably by Montgomery and Vaughan in [Reference Montgomery and Vaughan8] to
![]() $|E(X)|\ll X^{1-\delta }$
for some
$|E(X)|\ll X^{1-\delta }$
for some
![]() $\delta>0$
, and the current best
$\delta>0$
, and the current best
![]() $\delta $
which can be found in the literature is
$\delta $
which can be found in the literature is
![]() $\delta =0.28$
by Pintz in [Reference Pintz10].
$\delta =0.28$
by Pintz in [Reference Pintz10].
Another motivation for our result is previous study of how many exceptions lie in other specific thin sets. This was first studied by Perelli in [Reference Perelli9], who showed that for any polynomial
![]() $\phi $
of degree k with integer coefficients the values of
$\phi $
of degree k with integer coefficients the values of
![]() $2\phi (n)$
obey the Goldbach conjecture for all but
$2\phi (n)$
obey the Goldbach conjecture for all but
![]() $N(\log N)^{-A}$
many
$N(\log N)^{-A}$
many
![]() $n<N$
. This estimate was improved by Brüdern et al. in [Reference Brüdern, Kawada and Wooley1] who lowered the bound on the exceptions to
$n<N$
. This estimate was improved by Brüdern et al. in [Reference Brüdern, Kawada and Wooley1] who lowered the bound on the exceptions to
![]() $N^{1-c/k}$
for some positive absolute constant c. When bounding the number of exceptions in a thin set, it is important to check that the thin set is thinner than the potential set of exceptions, or the result will trivially follow without looking at any specifics of the thin set. In the case of values of a polynomial we can see that provided the polynomial is not linear it may have at most
$N^{1-c/k}$
for some positive absolute constant c. When bounding the number of exceptions in a thin set, it is important to check that the thin set is thinner than the potential set of exceptions, or the result will trivially follow without looking at any specifics of the thin set. In the case of values of a polynomial we can see that provided the polynomial is not linear it may have at most
![]() $cX^{1/2}$
many values less than X, which is considerably fewer than
$cX^{1/2}$
many values less than X, which is considerably fewer than
![]() $X^{0.72}$
many values in the thin set. When considering digitally restricted sets, we first note that by counting strings of length k in an alphabet with
$X^{0.72}$
many values in the thin set. When considering digitally restricted sets, we first note that by counting strings of length k in an alphabet with
![]() $|D|$
letters,
$|D|$
letters,
and hence
When
![]() $|D|<b^{0.72}$
, there are thus significantly fewer than
$|D|<b^{0.72}$
, there are thus significantly fewer than
![]() $X^{0.72}$
numbers with restricted digits less than X, and Theorem 1.1 is nontrivial.
$X^{0.72}$
numbers with restricted digits less than X, and Theorem 1.1 is nontrivial.
Also motivating our result is work studying the set
![]() $\mathcal {A}$
. The analytic structure of
$\mathcal {A}$
. The analytic structure of
![]() $\mathcal {A}$
has led to many results. Particularly notable results include those of Maynard [Reference Maynard7] who proved that
$\mathcal {A}$
has led to many results. Particularly notable results include those of Maynard [Reference Maynard7] who proved that
![]() $\mathcal {A}$
has infinitely many primes provided that the digit set D omits sufficiently few digits, and Mauduit and Rivat [Reference Mauduit and Rivat6] who proved that sums of digits of primes are well distributed in residue classes.
$\mathcal {A}$
has infinitely many primes provided that the digit set D omits sufficiently few digits, and Mauduit and Rivat [Reference Mauduit and Rivat6] who proved that sums of digits of primes are well distributed in residue classes.
2 Preliminaries
We first introduce notation. As is common in analytic number theory, let
![]() $e(\alpha ):=e^{2\pi i\alpha }$
and let the symbol
$e(\alpha ):=e^{2\pi i\alpha }$
and let the symbol
![]() $f(x)\ll g(x)$
mean that there exists a positive constant c such that
$f(x)\ll g(x)$
mean that there exists a positive constant c such that
![]() $|f(x)|\leq cg(x)$
after restricting to an appropriate domain. Whenever we use the letter
$|f(x)|\leq cg(x)$
after restricting to an appropriate domain. Whenever we use the letter
![]() $\varepsilon $
, we mean that the statement is true for every
$\varepsilon $
, we mean that the statement is true for every
![]() $\varepsilon>0$
. Throughout this paper, the letter p always denotes primes. Take k, the number of digits, to be sufficiently large, and let
$\varepsilon>0$
. Throughout this paper, the letter p always denotes primes. Take k, the number of digits, to be sufficiently large, and let
![]() $X=b^k$
, so that
$X=b^k$
, so that
![]() $\mathcal {A}_k$
has only values less than X.
$\mathcal {A}_k$
has only values less than X.
When discussing digitally restricted sets we need to deal with the technicality of leading zeros. We want to study all digitally restricted numbers less than X, of any number of digits, but when
![]() $0\not \in D$
we see that
$0\not \in D$
we see that
![]() $\mathcal {A}_k$
only contains numbers with precisely k digits and when
$\mathcal {A}_k$
only contains numbers with precisely k digits and when
![]() $j< k$
we have
$j< k$
we have
![]() $\mathcal {A}_j\cap \mathcal {A}_{k}=\emptyset $
, in contrast to the case where
$\mathcal {A}_j\cap \mathcal {A}_{k}=\emptyset $
, in contrast to the case where
![]() $0\in D$
, in which a j-digit number is also a k-digit number with
$0\in D$
, in which a j-digit number is also a k-digit number with
![]() $k-j$
leading zeros and
$k-j$
leading zeros and
![]() $\mathcal {A}_j\subset \mathcal {A}_k$
. When
$\mathcal {A}_j\subset \mathcal {A}_k$
. When
![]() $0\in D$
we may show that
$0\in D$
we may show that
![]() $|\mathcal {A}_k\cap E(X)|$
is small to obtain the desired result, but when
$|\mathcal {A}_k\cap E(X)|$
is small to obtain the desired result, but when
![]() $0\not \in D$
we note that
$0\not \in D$
we note that
![]() $|\mathcal {A}\cap E(X)| = \sum _{j\leq k}|\mathcal {A}_k\cap E(X)|$
, so proving the result for
$|\mathcal {A}\cap E(X)| = \sum _{j\leq k}|\mathcal {A}_k\cap E(X)|$
, so proving the result for
![]() $\mathcal {A}_k$
will prove it for
$\mathcal {A}_k$
will prove it for
![]() $\mathcal {A}(X)$
in either case, and we will henceforth deal only with
$\mathcal {A}(X)$
in either case, and we will henceforth deal only with
![]() $\mathcal {A}_k$
.
$\mathcal {A}_k$
.
Now we define the generating function for
![]() $\mathcal {A}_k$
to be
$\mathcal {A}_k$
to be
The generating function for primes on the other hand will require a parameter. Let
![]() $\delta _0$
be a sufficiently small constant, which may depend on b, to be chosen later. We define
$\delta _0$
be a sufficiently small constant, which may depend on b, to be chosen later. We define
 $$ \begin{align*}S(\alpha) := \sum_{X^{6\delta_0}<p<X} e(p\alpha)\log p.\end{align*} $$
$$ \begin{align*}S(\alpha) := \sum_{X^{6\delta_0}<p<X} e(p\alpha)\log p.\end{align*} $$
For any
![]() ${\mathfrak B}\subset [0,1]$
and any even
${\mathfrak B}\subset [0,1]$
and any even
![]() $n<X$
, we define
$n<X$
, we define
By orthogonality,
![]() $r(n,[0,1])$
counts solutions to
$r(n,[0,1])$
counts solutions to
![]() $p_1+p_2=n$
with weight
$p_1+p_2=n$
with weight
![]() $\log p_1\log p_2$
. To evaluate this integral we apply the Hardy–Littlewood circle method. Define the major arcs to be
$\log p_1\log p_2$
. To evaluate this integral we apply the Hardy–Littlewood circle method. Define the major arcs to be
 $$ \begin{align} \mathfrak{M}_{\delta_0} := \bigcup_{0<q<X} \{\alpha\in [0,1]:\|q\alpha\|<X^{6\delta_0-1}\} \end{align} $$
$$ \begin{align} \mathfrak{M}_{\delta_0} := \bigcup_{0<q<X} \{\alpha\in [0,1]:\|q\alpha\|<X^{6\delta_0-1}\} \end{align} $$
and the minor arcs to be
In Section 3 we establish Lemmas 3.1 and 3.2, the facts about
![]() $f(\alpha )$
and
$f(\alpha )$
and
![]() $\mathcal {A}_k$
which we will use in the proof. In Section 4 we combine Section 3 with commonly known facts about S to prove Theorem 1.1.
$\mathcal {A}_k$
which we will use in the proof. In Section 4 we combine Section 3 with commonly known facts about S to prove Theorem 1.1.
3 Properties of digital restrictions
In this section we prove the properties of digitally restricted sets which we will need to show Theorem 1.1. The two results we need are Lemma 3.1, a mean value estimate, and Lemma 3.2, a bound on how many elements of
![]() $\mathcal {A}_k$
can be multiples of a given large value.
$\mathcal {A}_k$
can be multiples of a given large value.
Lemma 3.1. For all
![]() $\delta>0$
, there exists a
$\delta>0$
, there exists a
![]() $t_0=t_0(b,\delta )$
such that whenever
$t_0=t_0(b,\delta )$
such that whenever
![]() $t\geq t_0$
,
$t\geq t_0$
,
 $$ \begin{align*}\int_0^1 |f(\alpha)|^t\,d \alpha \ll |\mathcal{A}_k|^tX^{\delta-1}.\end{align*} $$
$$ \begin{align*}\int_0^1 |f(\alpha)|^t\,d \alpha \ll |\mathcal{A}_k|^tX^{\delta-1}.\end{align*} $$
Proof. We prove the bound by exploiting the independence of digits of values in
![]() $\mathcal {A}_k$
. By treating each digit as its own variable, the number of variables goes to infinity while the number of values any variable can take remains constant.
$\mathcal {A}_k$
. By treating each digit as its own variable, the number of variables goes to infinity while the number of values any variable can take remains constant.
Note that by orthogonality, if
![]() $t=2s$
is an even integer, the integral counts solutions to the equation
$t=2s$
is an even integer, the integral counts solutions to the equation
 $$ \begin{align*} \sum_{i=1}^{s}(x_i-y_i)=0 \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{s}(x_i-y_i)=0 \end{align*} $$
with
![]() $x_i,y_i\in \mathcal {A}_k$
. We now interpret each
$x_i,y_i\in \mathcal {A}_k$
. We now interpret each
![]() $x_i$
and
$x_i$
and
![]() $y_i$
as a linear combination of k variables, each corresponding to a digital place. Let
$y_i$
as a linear combination of k variables, each corresponding to a digital place. Let
 $$ \begin{align*}x_i = \sum_{j=0}^{k-1} x_{i,j}b^j\end{align*} $$
$$ \begin{align*}x_i = \sum_{j=0}^{k-1} x_{i,j}b^j\end{align*} $$
and the same for
![]() $y_i$
. We are now counting solutions to
$y_i$
. We are now counting solutions to
 $$ \begin{align} \sum_{j=0}^k b^j\sum_{i=1}^{s}(x_{i,j}-y_{i,j})=0 \end{align} $$
$$ \begin{align} \sum_{j=0}^k b^j\sum_{i=1}^{s}(x_{i,j}-y_{i,j})=0 \end{align} $$
with
![]() $x_{i,j},y_{i,j}\in D$
.
$x_{i,j},y_{i,j}\in D$
.
First, if every allowed digit shares a common factor then we know that every
![]() $x_{i,j}$
and
$x_{i,j}$
and
![]() $y_{i,j}$
will share that common factor, permitting us to divide everything by that common factor. Thus, we may assume that the allowed digits do not share a common factor. To count solutions to (3.1) we investigate what addition looks like in base b, and in particular we look at each digital place. Let
$y_{i,j}$
will share that common factor, permitting us to divide everything by that common factor. Thus, we may assume that the allowed digits do not share a common factor. To count solutions to (3.1) we investigate what addition looks like in base b, and in particular we look at each digital place. Let
 $$ \begin{align*}\sigma_{j} : = \sum_{i=1}^s (x_{i,j}-y_{i,j})\end{align*} $$
$$ \begin{align*}\sigma_{j} : = \sum_{i=1}^s (x_{i,j}-y_{i,j})\end{align*} $$
and
 $$ \begin{align*}\tau_{j} := \sum_{l<j}b^l\sigma_{l}.\end{align*} $$
$$ \begin{align*}\tau_{j} := \sum_{l<j}b^l\sigma_{l}.\end{align*} $$
Now, we note that for (3.1) to hold, we require that it holds modulo b, and thus
![]() $\sigma _0\equiv 0\,\mod b$
, or to be precise, the 1s digits must add up to 0 mod b. Further, we know that (3.1) holds mod
$\sigma _0\equiv 0\,\mod b$
, or to be precise, the 1s digits must add up to 0 mod b. Further, we know that (3.1) holds mod
![]() $b^j$
for any j, meaning that
$b^j$
for any j, meaning that
![]() $\tau _{j} \equiv -b^j \sigma _{j}\,\mod b^{j+1}$
. After we have chosen the digits up to j we will thus require that
$\tau _{j} \equiv -b^j \sigma _{j}\,\mod b^{j+1}$
. After we have chosen the digits up to j we will thus require that
![]() $\sigma _{j} \equiv n$
mod b for some fixed n which is determined by the digits up to j.
$\sigma _{j} \equiv n$
mod b for some fixed n which is determined by the digits up to j.
No matter what the digits in the other places are, we will thus have at most
choices for how to assign the jth digits. By orthogonality, we can count these using the function
 $$ \begin{align*} u(n,b,D):=\frac{1}{b}\sum_{0\leq a<b} \bigg(\bigg|\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)\bigg|^{2s}e\bigg(-\frac{na}{b}\bigg)\bigg). \end{align*} $$
$$ \begin{align*} u(n,b,D):=\frac{1}{b}\sum_{0\leq a<b} \bigg(\bigg|\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)\bigg|^{2s}e\bigg(-\frac{na}{b}\bigg)\bigg). \end{align*} $$
Noting that this does not depend on j, we thus have an upper bound on the number of solutions to (3.1) which is the product of the upper bounds on the sums of each digit, which is bounded by the maximum of
![]() $u(n,b,D)^k$
over all possible n. Finally, noting that by the lack of a common factor of acceptable digits, for all nonzero a,
$u(n,b,D)^k$
over all possible n. Finally, noting that by the lack of a common factor of acceptable digits, for all nonzero a,
 $$ \begin{align*}\bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg|<|D|.\end{align*} $$
$$ \begin{align*}\bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg|<|D|.\end{align*} $$
Dividing both sides by
![]() $|D|$
and noting that there are finitely many nonzero a then yields
$|D|$
and noting that there are finitely many nonzero a then yields
 $$ \begin{align}\max_{0<a<b}\frac{1}{D} \bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg| <1.\end{align} $$
$$ \begin{align}\max_{0<a<b}\frac{1}{D} \bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg| <1.\end{align} $$
We now choose s to be at least
 $$ \begin{align*}\frac{\log(\delta/a)}{\log\big({\max_{0<a<b}\tfrac{1}{D}|{\sum_{d\in D}e\big(\tfrac{da}{b}\big)}|}\big)}.\end{align*} $$
$$ \begin{align*}\frac{\log(\delta/a)}{\log\big({\max_{0<a<b}\tfrac{1}{D}|{\sum_{d\in D}e\big(\tfrac{da}{b}\big)}|}\big)}.\end{align*} $$
By (3.2), this must be a finite constant depending only on b, D and
![]() $\delta $
, which makes it a valid choice of s. Summing over all values of a then yields
$\delta $
, which makes it a valid choice of s. Summing over all values of a then yields
 $$ \begin{align*}\sum_{0\leq a<b} \bigg({\frac{1}{D}\bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg|}^{2s}\bigg)<1+\delta.\end{align*} $$
$$ \begin{align*}\sum_{0\leq a<b} \bigg({\frac{1}{D}\bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg|}^{2s}\bigg)<1+\delta.\end{align*} $$
Rearranging this and noting that since
![]() $|D|\geq 2$
, we have
$|D|\geq 2$
, we have
![]() $|D|^{\delta }>1+\delta $
, we can see that
$|D|^{\delta }>1+\delta $
, we can see that
 $$ \begin{align*}u(b;D)=\frac{1}{b}\sum_{0\leq a<b}\bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg|^{2s} \leq \frac{(1+\delta_s)}{b}|D|^{2s}\leq \frac{1}{b}|D|^{2s+\delta}.\end{align*} $$
$$ \begin{align*}u(b;D)=\frac{1}{b}\sum_{0\leq a<b}\bigg|{\sum_{d\in D}e\bigg(\frac{da}{b}\bigg)}\bigg|^{2s} \leq \frac{(1+\delta_s)}{b}|D|^{2s}\leq \frac{1}{b}|D|^{2s+\delta}.\end{align*} $$
Taking the product across all digital places now yields the desired result.
Lemma 3.2. For any m, we have
Proof. Note that for every integer
![]() $n\in \mathcal {A}_k$
which is a multiple of m, we may change the last
$n\in \mathcal {A}_k$
which is a multiple of m, we may change the last
![]() $\lfloor {\log (m/2)}/{\log b}\rfloor $
many digits and obtain
$\lfloor {\log (m/2)}/{\log b}\rfloor $
many digits and obtain
![]() $|D|^{\lfloor {\log (m/2)}/{\log b}\rfloor } \geq b^{-1}(m/2)^{{\log |D|}/{\log b}}$
many other values in
$|D|^{\lfloor {\log (m/2)}/{\log b}\rfloor } \geq b^{-1}(m/2)^{{\log |D|}/{\log b}}$
many other values in
![]() $\mathcal {A}_k$
which are less than
$\mathcal {A}_k$
which are less than
![]() $m/2$
away from n. Since any integer may be less than
$m/2$
away from n. Since any integer may be less than
![]() $m/2$
from at most one multiple of m, this provides a map from values in
$m/2$
from at most one multiple of m, this provides a map from values in
![]() $\mathcal {A}_k$
which are multiples of m to disjoint sets of at least
$\mathcal {A}_k$
which are multiples of m to disjoint sets of at least
![]() $b^{-1}(m/2)^{{\log |D|}/{\log b}}$
many integers in
$b^{-1}(m/2)^{{\log |D|}/{\log b}}$
many integers in
![]() $\mathcal {A}_k$
which are not multiples of m. Taking the disjoint union of all these sets, along with the associated multiples of m, returns a subset of
$\mathcal {A}_k$
which are not multiples of m. Taking the disjoint union of all these sets, along with the associated multiples of m, returns a subset of
![]() $\mathcal {A}_k$
, and hence the sum of the cardinalities must be at most
$\mathcal {A}_k$
, and hence the sum of the cardinalities must be at most
![]() $|\mathcal {A}_k|$
. More formally, we see that
$|\mathcal {A}_k|$
. More formally, we see that
 $$ \begin{align*}\sum\limits_{\substack{n\in\mathcal{A}_k\\ m|n}}1+b^{-1}(m/2)^{{\log|D|}/{\log b}} \leq |\mathcal{A}_k|.\end{align*} $$
$$ \begin{align*}\sum\limits_{\substack{n\in\mathcal{A}_k\\ m|n}}1+b^{-1}(m/2)^{{\log|D|}/{\log b}} \leq |\mathcal{A}_k|.\end{align*} $$
and hence, dividing by the term being summed, we see that
 $$ \begin{align*}\sum\limits_{\substack{n\in\mathcal{A}_k\\ m|n}} 1 \leq \frac{b|\mathcal{A}_k|}{b^{-1}+(m/2)^{\log|D|/\!\log b}},\end{align*} $$
$$ \begin{align*}\sum\limits_{\substack{n\in\mathcal{A}_k\\ m|n}} 1 \leq \frac{b|\mathcal{A}_k|}{b^{-1}+(m/2)^{\log|D|/\!\log b}},\end{align*} $$
which is the desired result.
Remark 3.3. The above lemma also holds, with the same proof, if we count any particular residue class modulo m. In particular, it is not unique to 0.
Since the expected number of multiples of m lying in
![]() $\mathcal {A}_k$
would be
$\mathcal {A}_k$
would be
![]() $|\mathcal {A}_k|/m$
, it is natural to ask whether we can obtain this or possibly
$|\mathcal {A}_k|/m$
, it is natural to ask whether we can obtain this or possibly
![]() $|\mathcal {A}_k|/m^c$
for some absolute c which does not depend on b and
$|\mathcal {A}_k|/m^c$
for some absolute c which does not depend on b and
![]() $|D|$
. Unfortunately, this is ruled out by those m which are multiples of powers of b. Taking
$|D|$
. Unfortunately, this is ruled out by those m which are multiples of powers of b. Taking
![]() $m=b^j$
, we see that
$m=b^j$
, we see that
![]() $n\in \mathcal {A}_k$
being a multiple of m is equivalent to the last j digits being 0, and that when 0 is an allowed digit there will be
$n\in \mathcal {A}_k$
being a multiple of m is equivalent to the last j digits being 0, and that when 0 is an allowed digit there will be
![]() $N/N^{j/k}=N/m^{\log |D|/\!\log b}$
of these. For values m which are coprime to b, a significant amount of research has been done (see, for example, [Reference Konyagin5]), but this only applies to small values of m and not the large values we will need, about which few positive results are known. Konyagin [Reference Konyagin5] showed that we cannot hope for too much, as there exist relatively small coprime moduli, of the order of
$N/N^{j/k}=N/m^{\log |D|/\!\log b}$
of these. For values m which are coprime to b, a significant amount of research has been done (see, for example, [Reference Konyagin5]), but this only applies to small values of m and not the large values we will need, about which few positive results are known. Konyagin [Reference Konyagin5] showed that we cannot hope for too much, as there exist relatively small coprime moduli, of the order of
![]() $\exp (c\log X/\!\log \log X)$
, in which
$\exp (c\log X/\!\log \log X)$
, in which
![]() $\mathcal {A}$
is not evenly distributed between residue classes. Despite not being evenly distributed, it is still expected that
$\mathcal {A}$
is not evenly distributed between residue classes. Despite not being evenly distributed, it is still expected that
![]() $\mathcal {A}$
is not too badly distributed. In particular, Konyagin conjectured that
$\mathcal {A}$
is not too badly distributed. In particular, Konyagin conjectured that
![]() $\mathcal {A}(X)$
meets every residue class modulo m whenever
$\mathcal {A}(X)$
meets every residue class modulo m whenever
![]() $(m,b)=1$
and
$(m,b)=1$
and
![]() $m<X^c$
for some constant
$m<X^c$
for some constant
![]() $c=c(b)$
.
$c=c(b)$
.
4 Exceptional sets in Goldbach’s conjecture
In this section, following [Reference Brüdern, Kawada and Wooley1], we use what we have proven about numbers with restricted digits to prove Theorem 1.1. We now study
![]() $r(n,{\mathfrak B})$
as we defined it in Section 2. In particular, we study
$r(n,{\mathfrak B})$
as we defined it in Section 2. In particular, we study
![]() $r(n,\mathfrak {M})$
and
$r(n,\mathfrak {M})$
and
![]() $r(n,\mathfrak {m})$
as defined in (2.1) and (2.2), respectively. Our goal will be to show, for almost all n in
$r(n,\mathfrak {m})$
as defined in (2.1) and (2.2), respectively. Our goal will be to show, for almost all n in
![]() $\mathcal {A}_k$
, that
$\mathcal {A}_k$
, that
![]() $r(n,\mathfrak {m})\ll X^{1-\delta _1}$
and
$r(n,\mathfrak {m})\ll X^{1-\delta _1}$
and
![]() $r(n,\mathfrak {M})\gg X^{1-\delta _2}$
with
$r(n,\mathfrak {M})\gg X^{1-\delta _2}$
with
![]() $\delta _1<\delta _2$
. First, we handle the minor arcs.
$\delta _1<\delta _2$
. First, we handle the minor arcs.
Lemma 4.1. There exists
![]() $\delta _1=\delta _1(b,D)>0$
such that for all sufficiently large X, there exists a set
$\delta _1=\delta _1(b,D)>0$
such that for all sufficiently large X, there exists a set
![]() $B\subset \mathcal {A}_k$
with
$B\subset \mathcal {A}_k$
with
![]() $|B|\ll |\mathcal {A}_k|X^{-\delta _1}$
, and for all even n in
$|B|\ll |\mathcal {A}_k|X^{-\delta _1}$
, and for all even n in
![]() $\mathcal {A}_k\setminus B$
we have
$\mathcal {A}_k\setminus B$
we have
Proof. By symmetry of
![]() $\mathfrak {m}$
, we see that
$\mathfrak {m}$
, we see that
![]() $r(n,\mathfrak {m})$
is real. Set
$r(n,\mathfrak {m})$
is real. Set
Now, we let
 $$ \begin{align*}K(\alpha):= \sum\limits_{\substack{0<n<X\\n\in\mathcal{A}}} \eta(n)e(-n\alpha)\end{align*} $$
$$ \begin{align*}K(\alpha):= \sum\limits_{\substack{0<n<X\\n\in\mathcal{A}}} \eta(n)e(-n\alpha)\end{align*} $$
and rewrite the expression we are trying to bound as
 $$ \begin{align*}\sum_{n\in \mathcal{A}_k} |r(n,\mathfrak{m})| = \int_{\mathfrak{m}} S(\alpha)^2 K(-\alpha)\,d \alpha.\end{align*} $$
$$ \begin{align*}\sum_{n\in \mathcal{A}_k} |r(n,\mathfrak{m})| = \int_{\mathfrak{m}} S(\alpha)^2 K(-\alpha)\,d \alpha.\end{align*} $$
From Hölder’s inequality, this is at most
 $$ \begin{align*} \bigg(\sup_{\alpha\in\mathfrak{m}}|S(\alpha)|\bigg)^{2/t}\bigg(\int_0^1|S(\alpha)|^2\,d \alpha\bigg)^{1-1/t}\bigg(\int_0^1|K(-\alpha)|^t\,d \alpha\bigg)^{1/t}, \end{align*} $$
$$ \begin{align*} \bigg(\sup_{\alpha\in\mathfrak{m}}|S(\alpha)|\bigg)^{2/t}\bigg(\int_0^1|S(\alpha)|^2\,d \alpha\bigg)^{1-1/t}\bigg(\int_0^1|K(-\alpha)|^t\,d \alpha\bigg)^{1/t}, \end{align*} $$
and we can now estimate each term individually.
First, by [Reference Vaughan12],
By applying orthogonality, we trivially have
 $$ \begin{align*}\int_0^1 |S(\alpha)|^2\,d \alpha \ll \sum_{P<p<X}(\log p)^2 \ll X\log X.\end{align*} $$
$$ \begin{align*}\int_0^1 |S(\alpha)|^2\,d \alpha \ll \sum_{P<p<X}(\log p)^2 \ll X\log X.\end{align*} $$
Now we estimate the contribution of K. Observe that for integer values of t, the mean value
![]() $\int _0^1 |K(\alpha )|^{2t}\,d \alpha $
counts solutions with
$\int _0^1 |K(\alpha )|^{2t}\,d \alpha $
counts solutions with
![]() $x_i,y_i\in \mathcal {A}_k$
to the additive equation
$x_i,y_i\in \mathcal {A}_k$
to the additive equation
with each solution being weighted with
![]() $\pm 1$
. Thus, it is clearly less than or equal to the unweighted version, namely
$\pm 1$
. Thus, it is clearly less than or equal to the unweighted version, namely
![]() $\int _0^1 |f(\alpha )|^{2t}\,d \alpha $
, which when we take t sufficiently large is itself
$\int _0^1 |f(\alpha )|^{2t}\,d \alpha $
, which when we take t sufficiently large is itself
![]() $O(|\mathcal {A}_k|^{2t}X^{\delta _0-1})$
by Lemma 3.1.
$O(|\mathcal {A}_k|^{2t}X^{\delta _0-1})$
by Lemma 3.1.
Thus, in total,
 $$ \begin{align*} \int_0^1S(\alpha)^2K(-\alpha)\,d \alpha &\ll |\mathcal{A}_k|X^{1-1/t+(2-6\delta_0)/t+(-1+\delta)/t}(\log X)^{8/t+1-1/t}\\ &=|\mathcal{A}_k|X^{1-5\delta_0/t}(\log X)^{1+7/t} \end{align*} $$
$$ \begin{align*} \int_0^1S(\alpha)^2K(-\alpha)\,d \alpha &\ll |\mathcal{A}_k|X^{1-1/t+(2-6\delta_0)/t+(-1+\delta)/t}(\log X)^{8/t+1-1/t}\\ &=|\mathcal{A}_k|X^{1-5\delta_0/t}(\log X)^{1+7/t} \end{align*} $$
implying that
 $$ \begin{align*}\sum\limits_{\substack{n<X\\n\in\mathcal{A}}}|r(n,\mathfrak{m})|\ll NX^{1-2\delta_2}\end{align*} $$
$$ \begin{align*}\sum\limits_{\substack{n<X\\n\in\mathcal{A}}}|r(n,\mathfrak{m})|\ll NX^{1-2\delta_2}\end{align*} $$
for some
![]() $\delta _2>0$
. Now using the trivial bound, that
$\delta _2>0$
. Now using the trivial bound, that
 $$ \begin{align*}|\{n\in\mathcal{A}_k:|r(n,\mathfrak{m})|>X^{1-\delta_1}\}|\leq X^{\delta_1-1}\sum_{n\in |\mathcal{A}_k|}|r(n,\mathfrak{m})|,\end{align*} $$
$$ \begin{align*}|\{n\in\mathcal{A}_k:|r(n,\mathfrak{m})|>X^{1-\delta_1}\}|\leq X^{\delta_1-1}\sum_{n\in |\mathcal{A}_k|}|r(n,\mathfrak{m})|,\end{align*} $$
we obtain the desired result. We note that we just bounded the number of values in
![]() $\mathcal {A}$
with a large minor arc, and the number of even values in
$\mathcal {A}$
with a large minor arc, and the number of even values in
![]() $\mathcal {A}$
with a large minor arc is clearly even less.
$\mathcal {A}$
with a large minor arc is clearly even less.
Next we deal with the major arcs.
Lemma 4.2. Given Y such that
![]() $1\leq Y\leq |\mathcal {A}_k|^{\delta _0}$
, we have
$1\leq Y\leq |\mathcal {A}_k|^{\delta _0}$
, we have
for all even
![]() $n\in \mathcal {A}_k(X)$
except for at most
$n\in \mathcal {A}_k(X)$
except for at most
![]() $O(|\mathcal {A}_k|^{1+\varepsilon }Y^{-(\log |D|)/\!\log b})$
many n.
$O(|\mathcal {A}_k|^{1+\varepsilon }Y^{-(\log |D|)/\!\log b})$
many n.
Proof. This follows immediately from the proof of Lemma 2 in [Reference Brüdern, Kawada and Wooley1]. Note that the only step in the proof which depends on the set being counted occurs in the display following (18) of the latter paper, where numbers n such that
![]() $(n,\tilde {r})>Y$
were discarded. We replace that with
$(n,\tilde {r})>Y$
were discarded. We replace that with
 $$ \begin{align*}\sum\limits_{\substack{d|\tilde{r}\\ d>Y}}\sum\limits_{\substack{n\in \mathcal{A}_k\\ D|n}} 1\ll \sum\limits_{\substack{d|\tilde{r}\\ d>Y}} (|\mathcal{A}_k|/d^{\log|D|/\!\log b}) \ll |\mathcal{A}_k|^{1+\varepsilon}Y^{-\log|D|/\!\log b}.\end{align*} $$
$$ \begin{align*}\sum\limits_{\substack{d|\tilde{r}\\ d>Y}}\sum\limits_{\substack{n\in \mathcal{A}_k\\ D|n}} 1\ll \sum\limits_{\substack{d|\tilde{r}\\ d>Y}} (|\mathcal{A}_k|/d^{\log|D|/\!\log b}) \ll |\mathcal{A}_k|^{1+\varepsilon}Y^{-\log|D|/\!\log b}.\end{align*} $$
If we discard
![]() $O(|\mathcal {A}_k|^{1+\varepsilon }Y^{-\log |D|/\!\log b})$
many numbers, the rest of the proof follows.
$O(|\mathcal {A}_k|^{1+\varepsilon }Y^{-\log |D|/\!\log b})$
many numbers, the rest of the proof follows.
Now that we have both the major arcs and the minor arcs, we are equipped to prove Theorem 1.1. Taking Y to be less than
![]() $X^{\delta _1/3}$
, we see that there is some set B such that for all
$X^{\delta _1/3}$
, we see that there is some set B such that for all
![]() $n\in B$
, we have
$n\in B$
, we have
![]() $r(n,\mathfrak {m})=o(r(n,\mathfrak {M}))$
and
$r(n,\mathfrak {m})=o(r(n,\mathfrak {M}))$
and
Recalling that the number of solutions to (1.1) is
for all n other than those exceptions, shows that the Goldbach conjecture holds for all other values in
![]() $\mathcal {A}_k$
.
$\mathcal {A}_k$
.
Acknowledgements
The author would like to thank Trevor Wooley for considerable assistance on this paper. The author would also like to thank the anonymous referee for many helpful suggestions.