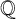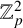1 Introduction
At the turn of the millennium, Coates and Sujatha [Reference Coates and Sujatha4] and, a little later, Wuthrich [Reference Wuthrich22] initiated a systematic study on the fine Selmer group of an elliptic curve E. The fine Selmer group is a subgroup of the classical p-primary Selmer group defined by stricter local conditions at primes above p. Analogous to the usual Selmer group, this fine Selmer group
$R(E/F)$
sits in the middle of the short exact sequence
where
$\mathcal {M}(E/F)$
and 
are the fine Mordell–Weil group and fine Tate–Shafarevich group, respectively (defined in the sense of Wuthrich [Reference Wuthrich23]), which can be thought as the ‘fine’ counterparts of the usual Mordell–Weil group and Tate–Shafarevich group.
In [Reference Coates and Sujatha4, Conjecture B], Coates and Sujatha proposed the following conjecture.
Conjecture 1.1 (Conjecture B).
Let E be an elliptic curve defined over a number field F. Suppose that
$F_\infty $
is a p-adic Lie extension of F for which
$\operatorname {\mathrm {Gal}}(F_\infty /F)$
has dimension
$\geq 2$
containing the cyclotomic
$\mathbb {Z}_{p}$
-extension
$F^{\mathrm {cyc}}$
. Then,
$R(A/F_\infty )^\vee $
is pseudo-null over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(F_\infty /F) ]]$
.
Here, a finitely generated
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(F_\infty /F) ]]$
-module M is said to be pseudo-null if
$$ \begin{align*}\operatorname{\mathrm{Ext}}^i_{\mathbb{Z}_{p}[[ \operatorname{\mathrm{Gal}}(F_\infty/F) ]]}(M, \mathbb{Z}_{p}[[ \operatorname{\mathrm{Gal}}(F_\infty/F) ]]) =0 \quad\text{for } i=0,1.\end{align*} $$
This conjecture remains wide open but we refer readers to [Reference Bhave2, Reference Jha7, Reference Lim11, Reference Lim12] for some discussion and numerical examples in support of the conjecture. The goal of this note is to provide further theoretical support for Conjecture B. We will prove the following result.
Theorem 1.2. Let E be an elliptic curve defined over
$\mathbb {Q}$
with good ordinary reduction at a prime
$p\geq 5$
, and let F be an imaginary quadratic field. Suppose that E has no complex multiplication and that the discriminant of F is coprime to the conductor of E. In the event that the root number
$\epsilon (E/F, 1)$
equals
$-1$
, assume further that p does not divide the class number of F. Suppose that
$\operatorname {\mathrm {Sel}}(E/F^{\mathrm {cyc}})$
is cofinitely generated over
$\mathbb {Z}_{p}$
. Then, the Pontryagin dual
$\mathcal {M}(E/F_\infty )^\vee $
of the fine Mordell–Weil group is a pseudo-null
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(F_\infty /F) ]]$
-module, where
$F_\infty $
is the
$\mathbb {Z}_{p}^2$
-extension of F.
As an application, we can prove the following result, where we note that every
$\mathbb {Z}_{p}$
-extension of F is necessarily contained in
$F_\infty $
.
Corollary 1.3. Retain the settings of Theorem 1.2. Then, for every
$\mathbb {Z}_{p}$
-extension
$L_\infty $
of F, the Pontryagin dual
$\mathcal {M}(E/L_\infty )^\vee $
is torsion over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(L_\infty /L) ]]$
.
It is conjectured that
$R(E/L_\infty )^\vee $
should always be torsion over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(L_\infty /L) ]]$
(see [Reference Lim13, Reference Perrin-Riou18, Reference Wuthrich21]). The above corollary thus constitutes partial evidence towards this conjecture. Furthermore, if one is willing to assume the finiteness of the fine Tate–Shafarevich group, we have the following observation.
Corollary 1.4. Retain the settings of Theorem 1.2. Suppose that
$L_\infty $
is a
$\mathbb {Z}_{p}$
-extension of F with the property that 
is finite for every finite extension L of F contained in
$L_\infty $
. Then,
$R(E/L_\infty )^\vee $
is torsion over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(L_\infty /L) ]]$
.
The proofs of the preceding theorem and corollaries will be given in Section 4.
2 Selmer group
We now introduce the Selmer group in a slightly more general context. As a start, we let F be an arbitrarily fixed number field and E an elliptic curve defined over F. Let S be a finite set of primes of F which contains all the primes above p, the infinite primes and the primes of bad reduction of E. We shall also write
$S_p$
for the set of primes of F above p. Denote by
$F_S$
the maximal algebraic extension of F which is unramified outside S. If
$\mathcal {L}$
is a (possibly infinite) extension of F contained in
$F_S$
and
$S'\subseteq S$
, we write
$S'(\mathcal {L})$
for the set of primes of
$\mathcal {L}$
above
$S'$
.
For each
$v\in S$
and a finite extension L of F, set
$$ \begin{align*} J_v(E/L) = \bigoplus_{w|v}H^1(L_w,E)_{p^\infty}.\end{align*} $$
If
$\mathcal {L}$
is an infinite extension of F contained in
$F_S$
, we define
$$ \begin{align*} J_v(E/\mathcal{L}) = \displaystyle \mathop{\varinjlim}\limits_L J_v(E/L),\end{align*} $$
where L runs through all finite extensions of F contained in
$\mathcal {L}$
.
The classical (p-primary) Selmer group of E over
$\mathcal {L}$
is defined by
$$ \begin{align*} \operatorname{\mathrm{Sel}}(E/\mathcal{L})=\ker\Big(H^1(G_S(\mathcal{L}), E_{p^{\infty}})\longrightarrow \bigoplus_{v\in S}J_v(E/\mathcal{L})\Big),\end{align*} $$
where we write
$G_S(\mathcal {L}) = \operatorname {\mathrm {Gal}}(F_S/\mathcal {L})$
. The Pontryagin dual of
$\operatorname {\mathrm {Sel}}(E/\mathcal {L})$
is then denoted by
$X(E/\mathcal {L})$
.
From now on, we will always assume that the elliptic curve E has good ordinary reduction at all primes of F above p. For each prime v of F above p, denote by
$\hat {E}_v$
and
$\tilde {E}_v$
the formal group of E at v and the reduced curve of E at v, respectively. Furthermore, we have a short exact sequence
$$ \begin{align*} 0\longrightarrow \hat{E}_{v, p^\infty}\longrightarrow E_{p^{\infty}}\longrightarrow \tilde{E}_{v,p^\infty}\longrightarrow 0 \end{align*} $$
of discrete
$\operatorname {\mathrm {Gal}}(\bar {F}_v/F_v)$
-modules. Since E is assumed to have good ordinary reduction, both
$\hat {E}_{v, p^\infty }$
and
$\tilde {E}_{v,p^\infty }$
are cofree
$\mathbb {Z}_{p}$
-modules of corank 1.
It is convenient to work with an equivalent description of the local terms
$J_v(E/\mathcal {L})$
, following an insight of Coates and Greenberg [Reference Coates and Greenberg3]. Let
$\mathcal {L}$
be an algebraic extension of F. For every non-Archimedean prime w of
$\mathcal {L}$
, write
$\mathcal {L}_w$
for the union of the completions at w of the finite extensions of F contained in
$\mathcal {L}$
. If w is a prime above p, we write
$E_w = E_v$
, where v is a prime of F below w. Finally, we shall always denote by
$F^{\mathrm {cyc}}$
the cyclotomic
$\mathbb {Z}_{p}$
-extension of F. With these in hand, we have the following lemma.
Lemma 2.1. Let
$\mathcal {L}$
be an algebraic extension of
$F^{\mathrm {cyc}}$
which is unramified outside a set of finite primes of F. Then, we have an isomorphism
$$ \begin{align*} J_v(E/\mathcal{L})\cong \begin{cases} \displaystyle \mathop{\varinjlim}\limits_{\mathcal{L}'}\bigoplus_{w|v}H^1(\mathcal{L}^{\prime}_w, \tilde{E}_{w,p^\infty}) & \text{if } v \text{ divides } p, \\[6pt] \displaystyle \mathop{\varinjlim}\limits_{\mathcal{L}'}\bigoplus_{w|v}H^1(\mathcal{L}^{\prime}_w, E_{p^{\infty}}) & \text{if } v \text{ does not divide } p,\end{cases} \end{align*} $$
where the direct limit is taken over all finite extensions
$\mathcal {L}'$
of
$F^{\mathrm {cyc}}$
contained in
$\mathcal {L}$
.
Proof. See [Reference Coates and Greenberg3, Propositions 4.1, 4.7 and 4.8] or [Reference Lim10, Lemma 4.1].
We now establish a control theorem for the Selmer group over a
$\mathbb {Z}_{p}^2$
-extension.
Proposition 2.2. Let E be an elliptic curve defined over F which has good ordinary reduction at each prime of F above p. Suppose that
$F_\infty $
is a
$\mathbb {Z}_{p}^2$
-extension of F which contains
$F^{\mathrm {cyc}}$
. Write
$H=\operatorname {\mathrm {Gal}}(F_\infty /F^{\mathrm {cyc}})$
. Then, the restriction map
$$ \begin{align*} \operatorname{\mathrm{Sel}}(E/F^{\mathrm{cyc}})\longrightarrow \operatorname{\mathrm{Sel}}(E/F_\infty)^H\end{align*} $$
has finite kernel and cokernel.
Proof. The proposition should definitely be well known. For the convenience of the readers, we shall supply an argument here. Consider the commutative diagram
with exact rows. Via the snake lemma, it suffices to show that
$\ker h$
,
$\ker g_v$
and
$\mathrm {coker}\, h$
are finite. To begin with, we show that h is surjective with a finite kernel. Indeed, since
$H\cong \mathbb {Z}_{p}$
, the restriction-inflation sequence tells us that the map h is surjective with kernel
$H^1(H, E(F_\infty )_{p^\infty })$
. However,
$$ \begin{align*} 0 = \operatorname{\mathrm{rank}}_{\mathbb{Z}_{p}[[ H ]]}\big( E(F_{\infty})_{p^\infty}\big)^\vee = \operatorname{\mathrm{rank}}_{\mathbb{Z}_{p}} \big((E(F_{\infty})_{p^\infty})^\vee\big)_H- \operatorname{\mathrm{rank}}_{\mathbb{Z}_{p}} \big((E(F_{\infty})_{p^\infty})^\vee\big)^H,\end{align*} $$
where the second equality follows from [Reference Neukirch, Schmidt and Wingberg17, Proposition 5.3.20]. Nevertheless, observe that
$$ \begin{align*}\big((E(F_{\infty})_{p^\infty})^\vee\big)_H = \big((E(F_{\infty})_{p^\infty})^H\big)^\vee = \big(E(F^{\mathrm{cyc}})_{p^\infty}\big)^\vee, \end{align*} $$
and the latter is finite by a theorem of Imai [Reference Imai6]. Hence,
$\big ((E(F_{\infty })_{p^\infty })^\vee \big )^H$
is also finite. However, this group is precisely
$H^1(H, E(F_\infty )_{p^\infty })^\vee $
, and so we have our claim.
It remains to show that
$g_v$
has finite kernel for every v. Again, by the restriction-inflation sequence, we have
$\ker g_v = \oplus _{w|v} H^1(H_w, D)$
, where here the sum runs over all the primes of
$F^{\mathrm {cyc}}$
above v,
$H_w$
is the decomposition group of w in H and D denotes either
$\tilde {E}_{v,p^\infty }$
or
$E_{p^{\infty }}$
according as to whether v divides p or not. In particular, if
$H_w=1$
, then
$H^1(H_w, D)=0$
. This is indeed the case when v does not divide p for a
$\mathbb {Z}_{p}^2$
-extension that is unramified outside p. It remains to consider primes w which divide p and for which
$H_w$
is nontrivial. Since
$H\cong \mathbb {Z}_{p}$
, it then follows that
$H_w\cong \mathbb {Z}_{p}$
. We may then apply the same argument as in the preceding paragraph to conclude that
$H^1(H_w, \tilde {E}_{v,p^\infty })$
is finite. The proof of the proposition is now complete.
The following is a corollary of the preceding proposition.
Corollary 2.3. Retain the setting as in Proposition 2.2. Then,
$\operatorname {\mathrm {Sel}}(E/F^{\mathrm {cyc}})$
is cofinitely generated over
$\mathbb {Z}_{p}$
if and only if
$\operatorname {\mathrm {Sel}}(E/F_\infty )$
is cofinitely generated over
$\mathbb {Z}_{p}[[ H ]]$
.
3 Mordell–Weil group over a
$\mathbb {Z}_{p}^2$
-extension
We continue to suppose that
$F_\infty $
is a
$\mathbb {Z}_{p}^2$
-extension of F which contains
$F^{\mathrm {cyc}}$
. Write
$H=\operatorname {\mathrm {Gal}}(F_\infty /F^{\mathrm {cyc}})$
and denote by
$H_n$
the unique subgroup of H with index
$p^n$
. The fixed field of
$H_n$
is in turn denoted by
$K_n$
. The following hypothesis will be in full force for the remainder of the section.
-
(Fg)
$\operatorname {\mathrm {Sel}}(E/F^{\mathrm {cyc}})$
is cofinitely generated over
$\mathbb {Z}_{p}$
.
Write
$\Lambda =\mathbb {Z}_{p}[[ H ]]$
. We shall identify this latter ring with the power series ring
$\mathbb {Z}_{p}[[ T ]]$
in one variable. By abuse of notation, we shall also write
$\Lambda $
for the ring
$\mathbb {Z}_{p}[[ T ]]$
. Denote by
$\Phi _n$
the
$p^n$
th-cyclotomic polynomial which is viewed as an element in
$\Lambda $
.
Proposition 3.1. Suppose that hypothesis
$\mathbf {(Fg)}$
is valid. Write
$\Lambda =\mathbb {Z}_{p}[[ H ]]$
.
-
(a) There is an injective
$\Lambda $
-homomorphism with a finite cokernel, where
$$ \begin{align*} \big(E(F_\infty)\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p}\big)^\vee \longrightarrow \Lambda^{\oplus r}\oplus \Big(\!\!\bigoplus_{n\geq 0}(\Lambda/\Phi_n)^{\oplus t_n}\Big)\end{align*} $$
$\{t_n\}$
is a sequence of nonnegative integers with
$t_n = 0$
for
$n\gg 0$
.
-
(b) Define
$$ \begin{align*} e_n = \begin{cases} \displaystyle\frac{\operatorname{\mathrm{rank}}_{\mathbb{Z}}E(K_n) - \operatorname{\mathrm{rank}}_{\mathbb{Z}}E(K_{n-1}) }{p^n-p^{n-1}} & \text{if } n\geq 1, \\[2pt] \operatorname{\mathrm{rank}}_{\mathbb{Z}}E(F^{\mathrm{cyc}}) & \text{if } n=0. \end{cases} \end{align*} $$
Then,
$$ \begin{align*} T_p\big(E(K_n)\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p} \big) \cong \bigoplus_{j=0}^n(\Lambda/\Phi_j)^{\oplus e_j}.\end{align*} $$
Proof. By hypothesis
$\mathbf {(Fg)}$
,
$\operatorname {\mathrm {Sel}}(E/K_n)$
is cofinitely generated over
$\mathbb {Z}_{p}$
for every n (for instance, see [Reference Hachimori and Matsuno5, Corollary 3.4]). Thus, it follows that
$E(K_n)\otimes \mathbb {Q}_{p}/\mathbb {Z}_{p}$
is also cofinitely generated over
$\mathbb {Z}_{p}$
for every n. In view of this observation, we may apply a similar argument to that of Lee in [Reference Lee8, Theorem 2.1.2] to obtain the conclusion of statement (a). Once, we have statement (a), statement (b) will follow by carrying out the argument in [Reference Lim15, Proposition 3.8].
4 Fine Selmer groups
Let L be a finite extension of F contained in
$F_S$
. Recall that the fine Selmer group of E over L is defined by
$$ \begin{align*} R(E/L) =\ker\Big(H^1(G_S(L),E_{p^{\infty}})\longrightarrow \bigoplus_{v\in S(L)} H^1(L_v, E_{p^{\infty}})\Big).\end{align*} $$
The fine Selmer group and the classical Selmer group are related by the following exact sequence.
Lemma 4.1. We have an exact sequence
$$ \begin{align*} 0\longrightarrow R(E/L) \longrightarrow \operatorname{\mathrm{Sel}}(E/L) \longrightarrow \bigoplus_{v\in S_p(L)}E(L_v)\otimes_{\mathbb{Z}_{p}}\mathbb{Q}_{p}/\mathbb{Z}_{p}.\end{align*} $$
In particular, the definition of the fine Selmer group does not depend on the choice of the set S.
Proof. See [Reference Lim and Murty16, Lemma 4.1] or [Reference Wuthrich23, Section 2].
Following Wuthrich [Reference Wuthrich23], the fine Mordell–Weil group
$\mathcal {M}(E/L)$
is defined by
$$ \begin{align*} \mathcal{M}(E/L) = \ker\Big(E(L)\otimes_{\mathbb{Z}_{p}}\mathbb{Q}_{p}/\mathbb{Z}_{p} \longrightarrow \bigoplus_{v\in S_p(L)} E(L_v)\otimes_{\mathbb{Z}_{p}}\mathbb{Q}_{p}/\mathbb{Z}_{p} \Big),\end{align*} $$
where
$S_p(L)$
denotes the set of primes of L above p. This fits into the commutative diagram
with exact rows, where the leftmost vertical map is induced by the middle vertical map. Following Wuthrich [Reference Wuthrich23], the fine Tate–Shafarevich group 
is given by
Since the middle vertical map in the above diagram is injective, so is the leftmost vertical map. Consequently, a snake lemma argument yields a short exact sequence
with 
injecting into 
, the p-primary part of the usual Tate– Shafarevich group.
We can now give the proof of our main theorem.
Proof of Theorem 1.2.
Set
$C_n$
and
$C_\infty $
to be the respective cokernels of
$\mathcal {M}(E/K_n)\longrightarrow E(K_n)\otimes \mathbb {Q}_{p}/\mathbb {Z}_{p}$
and
$\mathcal {M}(E/F_\infty )\longrightarrow E(F_\infty )\otimes \mathbb {Q}_{p}/\mathbb {Z}_{p}$
. From the argument in [Reference Van Order19, Proposition 3.14], we see that
$$ \begin{align} \operatorname{\mathrm{rank}}_{\mathbb{Z}_{p}[[ H ]]} \big(E(F_\infty)\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p}\big)^\vee= \begin{cases} 0 & \text{if } \epsilon(E/F,1)=+1; \\ 1 & \text{if } \epsilon(E/F,1)=-1. \end{cases} \end{align} $$
Plainly, if
$\epsilon (E/F,1)=+1$
, then
$\mathcal {M}(E/F_\infty )$
has trivial
$\mathbb {Z}_{p}[[ H ]]$
-corank, and so by a result of Venjakob [Reference Venjakob20] (or see [Reference Lim12, Lemma 5.1]),
$\mathcal {M}(E/F_\infty )^\vee $
is pseudo-null over
$\mathbb {Z}_{p}[[ G ]]$
.
Now suppose that we have
$\epsilon (E/F,1)=-1$
. In view of (4.1) and the tautological short exact sequence
$$ \begin{align*} 0 \longrightarrow \mathcal{M}(E/F_\infty)\longrightarrow E(F_\infty)\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p} \longrightarrow C_\infty \longrightarrow 0, \end{align*} $$
it therefore remains to show that
$\operatorname {\mathrm {rank}}_{\mathbb {Z}_{p}[[ H ]]} C_\infty>0$
.
Now, consider the commutative diagram
with exact rows. Since
$\ker \beta _n$
is contained in
$H^1(H_n, E(F_\infty )_{p^\infty })$
, it follows from the argument in Proposition 2.2 that the latter, and hence
$\ker \beta _n$
, is finite. Similarly, we see that
$\ker \gamma _n$
is finite. Consequently, the map
$C_n \longrightarrow (C_{\infty })^{H_n}$
also has a finite kernel.
We claim that
$\mathrm {corank}_{\mathbb {Z}_{p}} C_n \geq p^n-p^{n-1}$
for sufficiently large n. Suppose that this claim holds. Since we have seen above that the map
$C_n\longrightarrow (C_\infty )^H$
has finite kernel, it follows that
$\mathrm {corank}_{\mathbb {Z}_{p}}(C_\infty )^H\geq p^n-p^{n-1}$
. However, since
$$ \begin{align*} \mathrm{corank}_{\mathbb{Z}_{p}}(C_\infty)^H = \big(\mathrm{corank}_{\mathbb{Z}_{p}[[ H ]]} C_\infty \big)p^n +O(1), \end{align*} $$
we therefore have
$$ \begin{align*} \mathrm{corank}_{\mathbb{Z}_{p}[[ H ]]} C_\infty>0, \end{align*} $$
which is what we want to show.
It therefore remains to establish our claim. For this, we follow an idea of Lei [Reference Lei9]. Consider the natural map
$$ \begin{align*} f_n: E(K_n)\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p} \longrightarrow \bigoplus_{w\in S_p(K_n)} E(K_{n,w})\otimes_{\mathbb{Z}_{p}}\mathbb{Q}_{p}/\mathbb{Z}_{p}, \end{align*} $$
where
$\mathrm {im}~ f_n =C_n$
. Write
$F^{\mathrm {ac}}$
for the anticyclotomic
$\mathbb {Z}_{p}$
-extension of F, and
$L_n$
for the intermediate subextension of
$F^{\mathrm {ac}}/F$
with
$|L_n:F|=p^n$
. Since
$\epsilon (E/F,1)=-1$
,
$$ \begin{align*} \operatorname{\mathrm{rank}}_{\mathbb{Z}} E(L_n) = p^n +O(1) \end{align*} $$
by [Reference Bertolini1, Proposition 7.6]. As
$L_n\subseteq K_n$
, this in turn implies that
$e_n \geq 1$
for sufficiently large n, where
$e_n$
is defined as in Proposition 3.1. For each such n, choose an element
$x_n\in E(K_n)\setminus E(K_{n-1})$
which is of infinite order. Then, for a prime w of
$K_n$
above p, the image of
$x_n$
in
$E(K_{n,w})$
is still of infinite order and so cannot be divisible by an arbitrary power of p. Therefore, the image of
$x_n$
in
$E(K_{n,w})\otimes \mathbb {Q}_{p}/\mathbb {Z}_{p}$
is nontrivial.
As before, write
$\Phi _n$
for the
$p^n$
th-cyclotomic polynomial viewed as an element in
$\mathbb {Z}_{p}[[ H ]]$
. For brevity, we write
$$ \begin{align*} V_n =T_p\big(E(K_{n})\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p}\big)\otimes\mathbb{Q}_{p}. \end{align*} $$
Then, the map
$f_n$
induces the
$\mathbb {Q}_{p}[H/H_n]$
-homomorphism
$$ \begin{align*} V_n[\Phi_n] \hookrightarrow V_n \longrightarrow T_p\big(E(K_{n,w})\otimes\mathbb{Q}_{p}/\mathbb{Z}_{p}\big)\otimes\mathbb{Q}_{p}, \end{align*} $$
which is nonzero. Since
$\Phi _n$
is irreducible over
$\mathbb {Q}_{p}[T]$
, it follows that the image of this homomorphism contains at least a copy of
$\mathbb {Q}_{p}[T]/\Phi _n$
, and since
$\mathrm {dim}_{\mathbb {Q}_{p}}\big (\mathbb {Q}_{p}[T]/\Phi _n\big ) = p^n-p^{n-1}$
, this image has
$\mathbb {Q}_{p}$
-dimension at least
$p^n-p^{n-1}$
. Consequently, one has
$\mathrm {corank}_{\mathbb {Z}_{p}}(C_n) \geq p^n-p^{n-1}$
for sufficiently large n. This establishes our claim and completes the proof of the theorem.
We end the paper with the proofs of the two corollaries stated in the introductory section.
Proof of Corollary 1.3.
For each
$\mathbb {Z}_{p}$
-extension
$L_\infty $
of F, we write
$H_{L_\infty } = \operatorname {\mathrm {Gal}}(F_\infty /L_\infty )$
. Consider the commutative diagram
with exact rows. From the proof of [Reference Lim14, Proposition 3.8], we see that the kernel of
$\delta $
is cofinitely generated over
$\mathbb {Z}_{p}$
and hence so is the kernel of
$\alpha $
. However, combining Theorem 1.2 with [Reference Lim14, Lemma 2.1(ii)], we see that
$\mathcal {M}(E/F_\infty )^{H_{L_\infty }}$
is cotorsion over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(L_\infty /F) ]]$
. Therefore, it follows that
$\mathcal {M}(E/L_\infty )$
is cotorsion over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(L_\infty /F) ]]$
as required.
Proof of Corollary 1.4.
Under the finiteness of 
, it is shown in [Reference Lim13, Proposition 4.1] that 
is cotorsion over
$\mathbb {Z}_{p}[[ \operatorname {\mathrm {Gal}}(L_\infty /F) ]]$
. The conclusion therefore follows from this, Corollary 1.3 and the tautological short exact sequence
Acknowledgements
We would like to thank Jishnu Ray for his interest and comments on our paper. Some part of the research of this article took place when the first named author was visiting Harbin Engineering University and Harbin Institute of Technology, and he would like to acknowledge the hospitality and conducive working conditions provided by these institutes. The second named author would especially like to thank Chenyan Wu for her invaluable support and guidance during his visit to the University of Melbourne. The second named author is also grateful to the University of Melbourne for providing a stimulating research environment and the necessary resources, which greatly contributed to the completion of this work.
