Let G be a graph with m edges, minimum degree  $\delta $ and containing no cycle of length 4. Answering a question of Bollobás and Scott, Fan et al. [‘Bisections of graphs without short cycles’, Combinatorics, Probability and Computing 27(1) (2018), 44–59] showed that if (i) G is
$\delta $ and containing no cycle of length 4. Answering a question of Bollobás and Scott, Fan et al. [‘Bisections of graphs without short cycles’, Combinatorics, Probability and Computing 27(1) (2018), 44–59] showed that if (i) G is  $2$-connected, or (ii)
$2$-connected, or (ii)  $\delta \ge 3$, or (iii)
$\delta \ge 3$, or (iii) 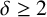 $\delta \ge 2$ and the girth of G is at least 5, then G admits a bisection such that
$\delta \ge 2$ and the girth of G is at least 5, then G admits a bisection such that  $\max \{e(V_1),e(V_2)\}\le (1/4+o(1))m$, where
$\max \{e(V_1),e(V_2)\}\le (1/4+o(1))m$, where  $e(V_i)$ denotes the number of edges of G with both ends in
$e(V_i)$ denotes the number of edges of G with both ends in  $V_i$. Let
$V_i$. Let  $s\ge 2$ be an integer. In this note, we prove that if
$s\ge 2$ be an integer. In this note, we prove that if  $\delta \ge 2s-1$ and G contains no
$\delta \ge 2s-1$ and G contains no  $K_{2,s}$ as a subgraph, then G admits a bisection such that
$K_{2,s}$ as a subgraph, then G admits a bisection such that  $\max \{e(V_1),e(V_2)\}\le (1/4+o(1))m$.
$\max \{e(V_1),e(V_2)\}\le (1/4+o(1))m$.
 ${PST}$-GROUPS
${PST}$-GROUPS