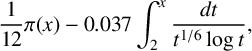1 Introduction
For a prime
$p \equiv 5 \bmod 8$
, consider the real quadratic field
$K={\mathbb {Q}}(\sqrt {p})$
, with ring of integers
${\mathcal O}_K = {\mathbb {Z}}[\tfrac 12(1 + \sqrt {p})]$
and fundamental unit
$\varepsilon _p = \tfrac 12(x_0 + y_0\sqrt {p})> 1$
. Then,
$(x_0, y_0)$
is a fundamental solution to the Pellian equation
$$ \begin{align} x^2 - py^2 = -4. \end{align} $$
The prime
$2$
is inert in
$K/{\mathbb {Q}}$
, and
$\varepsilon _p \equiv 1 \bmod 2{\mathcal O}_K$
if and only if (1.1) has no odd integer solutions. Primes
$p \equiv 5 \bmod 8$
satisfying the above equivalent conditions define sequence A130229 in [5]. They also appear in [Reference Breuer1, Reference Breuer2, Reference Xue, Yang and Yu7].
Since
$\varepsilon _p \bmod 2{\mathcal O}_K$
can take any of three nonzero values in
${\mathcal O}_K/2{\mathcal O}_K \cong {\mathbb {F}}_4$
, it is reasonable to expect roughly one third of all primes
$p\equiv 5 \bmod 8$
to be members of this sequence.
Define
$$ \begin{align*} \chi(p) := \left\{\begin{array}{ll} 1 & \text{if } p \equiv 5 \bmod 8 \text{ and } \varepsilon_p \equiv 1 \bmod 2{\mathcal O}_K, \\ -\frac{1}{2} & \text{if } p \equiv 5 \bmod 8 \text{ and } \varepsilon_p \not\equiv 1 \bmod 2{\mathcal O}_K, \\ 0 & \text{if } p \not\equiv 5 \bmod 8, \end{array} \right. \end{align*} $$
and define the modified counting function
$$ \begin{align*} \theta_\chi(x) := \sum_{p\leqslant x}\chi(p)\log p. \end{align*} $$
Then, the above heuristic leads us to expect
$\theta _\chi (x) = o(x)$
as
$x\rightarrow \infty $
.
In this note, we report on computations of
$\theta _\chi (x)$
for
$x\leqslant 10^{11}$
, which show a surprising bias away from the
$\varepsilon _p \equiv 1 \bmod 2{\mathcal O}_K$
case, hinted at in related computations reported in [Reference Breuer1, Section 4]. We thus pose a conjecture.
Conjecture 1.1. There exists a constant
$c \approx -0.066$
for which
$$ \begin{align*} \theta_\chi(x) \sim c x^{{5}/{6}} \end{align*} $$
as
$x \rightarrow \infty $
.
2 Results
We computed
$\varepsilon _p$
using the continued fraction method in [Reference Jacobson and Williams3, Section 3.3], with the modification that
$B_i$
and
$G_i$
are only computed modulo 2, since we only need to know the parity of
$\varepsilon _p$
. This significantly reduces the memory requirements of the calculation.
We implemented the algorithm to run on a GPU using the Python Numba library [Reference Lam, Pitrou, Seibert and Finkel4]. The final computation for all
$p < 10^{11}$
took approximately 17 hours on an entry-level gaming laptop with an Nvidia RTX 3050 GPU. The source code and data are available at https://github.com/florianbreuer/A130229.
Table 1 lists some values for the naive counting function
$$ \begin{align*} \pi_1(x) = \sum_{p\leqslant x, \; \chi(p)=1}1. \end{align*} $$
However, it is advantageous to study the ‘smoothed’ counting function
${\theta _\chi (x)=\sum _{p\leqslant x}\chi (p)\log p}$
. Figure 1 plots
$-\theta _\chi (x)$
for
$x\leqslant 10^{11}$
on logarithmic axes. The plot approximates a straight line with slope
$5/6$
. The least squares best fit of the form
$f(x) = cx^{5/6}$
is found to have
$c \approx -0.06626$
, computed using the find_fit method in SageMath v9.3 [6]. The error term
$\theta _\chi (x) - cx^{5/6}$
is shown in Figure 2. This provides evidence for Conjecture 1.1. Moreover, it appears likely that the error is of the order
$O(x^{{1}/{2}+\varepsilon })$
.
Table 1 Some values of the counting function
$\pi _1(x)$
for sequence A130229.
Figure 1 Log-log plot of
$-\theta _\chi (x)$
for
$x\leqslant 10^{11}$
.
Figure 2 Plot of the error term
$\theta _\chi (x) - cx^{5/6}$
for
$c\approx -0.06626$
.
From this, we may also deduce a good approximation for
$\pi _1(x)$
. Define
$$ \begin{align*} \pi_{-{1}/{2}}(x) = \sum_{p\leqslant x, \; \chi(p)=-{1}/{2}} 1 \quad\text{and}\quad \pi_\chi(x) = \sum_{p\leqslant x}\chi(p) = \pi_1(x) - \frac{1}{2}\pi_{-{1}/{2}}(x). \end{align*} $$
Then,
$\theta _\chi (x)\sim c x^{5/6} \approx c\cdot \tfrac 56\int _2^x t^{-1/6}\,dt$
suggests
$$ \begin{align*} \pi_\chi(x) \approx c\cdot\frac{5}{6}\int_2^x \frac{t^{-1/6}}{\log t}\,dt \sim c\,\frac{x^{5/6}}{\log x}. \end{align*} $$
Then, from
$\pi _1(x) + \pi _{-{1}/{2}}(x) \approx \tfrac 14\pi (x)$
, where
$\pi (x)$
is the usual prime counting function, we arrive at
$$ \begin{align*} \pi_1(x) \approx \frac{1}{12}\pi(x) + \frac{2}{3}\pi_\chi(x) \approx \frac{1}{12}\pi(x) + c\cdot\frac{5}{9}\int_2^x \frac{t^{-1/6}}{\log t}\,dt. \end{align*} $$
These approximations are compared with the computed values of
$\pi _1(x)$
in Table 1.
Acknowledgements
The first author would like to thank James Punch for useful discussions, Frank Calegari for suggesting that the correct exponent is likely to be
$5/6$
and GPT-4 for help with porting the algorithm to a GPU.
