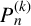1 Introduction
The Pell sequence
$\{P_n\}_{n\geq 0}$
is the binary recurrence sequence given by
$$ \begin{align*} P_{n+2} = 2P_{n+1} + P_{n} \quad\mathrm{for}\ n\geq 0, \end{align*} $$
with the initial terms
$P_{0} = 0$
and
$P_{1} = 1$
.
Let
$ k \geq 2 $
be an integer. We consider a generalisation of the Pell sequence known as the k-generalised Pell sequence:
$\{P_{n}^{(k)} \}_{n \geq -(k-2)}$
is given by the recurrence
$$ \begin{align*} P_{n}^{(k)} = 2 P_{n-1}^{(k)} +P_{n-2}^{(k)} +\cdots+P_{n-k}^{(k)} \quad\text{for all} \ n\geq 2, \end{align*} $$
with the initial terms
$P_{-(k-2)} ^{(k)} = P_{-(k-3)} ^{(k)} =\cdots = P_{0} ^{(k)} = 0 $
and
$P_{1} ^{(k)} = 1$
. We shall refer to
$P_{n}^{(k)}$
as the nth k-generalised Pell number. This generalisation is a family of sequences, with each new choice of k producing a unique sequence. For example, if
$k = 2$
, we get
$P_{n}^{(2)} = P_{n}$
, the nth Pell number.
There are several studies dealing with Diophantine equations involving perfect powers and Pell numbers. For instance, Pethö [Reference Pethö12] studied all perfect powers in the Pell sequence, where he showed that the only positive integer solutions
$(n, y,s)$
to
$$ \begin{align*} P_{n} = y^{s} \end{align*} $$
with
$s \geq 2$
are
$(n, y,s) = (1, 1,s)$
and
$(7, 13, 2)$
. Later, Aboudja et al. [Reference Aboudja, Hernane, Rihane and Togbé1] extended Pethö’s work by considering two Pell numbers and, for
$s \geq 2$
, studied the Diophantine equation
$$ \begin{align} P_{n} \pm P_{m} = y^{s}. \end{align} $$
In particular, they found all solutions of (1.1) in positive integers
$(n, m, y, s)$
under the assumption
$n \equiv m \pmod {2}$
. This problem is still unsolved for
$n \not \equiv m \pmod {2}$
. Recently, Şiar et al. [Reference Şiar, Keskin and Oztas14] investigated the Diophantine equation
$$ \begin{align} P_{n}^{(k)} = y^{m} \end{align} $$
in positive integers
$n, m$
with
$y, k \geq 2$
. They found that (1.2) has only one solution
$(n, m, k, y) = (7, 2, 2, 13)$
for
$2 \leq y \leq 1000$
.
Motivated by these results, we study the Diophantine equation
$$ \begin{align} P_{n}^{(k)} \pm P_{m}^{(k)} = y^{a} \end{align} $$
in positive integers
$n, m, k$
and a with
$y \geq 2$
,
$k \geq 3$
and
$1 \leq m \leq n$
. Our main result is as follows.
Theorem 1.1. All the solutions of the Diophantine equation (1.3) in positive integers with
$2 \leq y \leq 200$
and
$k \geq 3$
are given by
$$ \begin{align*} \begin{array}{llll} P_{2}^{(k)} + P_{2}^{(k)} = 2^{2} & \text{for all} \ k \geq 3, & P_{5}^{(k)} + P_{2}^{(k)} = 6^{2} & \text{for all} \ k \geq 3, \\[2pt] P_{3}^{(k)} - P_{1}^{(k)} = 2^{2} & \text{for all} \ k \geq 3, & P_{4}^{(k)} - P_{3}^{(k)} = 2^{3} & \text{for all} \ k \geq 3, \\[2pt] P_{5}^{(k)} - P_{2}^{(k)} = 2^{5} & \text{for all} \ k \geq 4, & P_{7}^{(k)} - P_{6}^{(k)} = 12^{2} & \text{for all} \ k \geq 6, \\[2pt] P_{8}^{(k)} - P_{5}^{(k)} = 24^{2} & \text{for all} \ k \geq 7, & P_{7}^{(3)} + P_{2}^{(3)} = 6^{3}, & P_{8}^{(4)} + P_{5}^{(4)} = 5^{4}, \\[2pt] P_{8}^{(4)} + P_{5}^{(4)} = 25^{2}, & P_{9}^{(6)} + P_{6}^{(6)} = 41^{2}, & P_{12}^{(7)} + P_{10}^{(7)} = 2^{15}, & P_{12}^{(7)} + P_{10}^{(7)} = 8^{5}, \\[2pt] P_{12}^{(7)} + P_{10}^{(7)} = 32^{3}, & P_{5}^{(3)} - P_{1}^{(3)} = 2^{5}, & P_{8}^{(3)} - P_{5}^{(3)} = 2^{9}, & P_{8}^{(3)} - P_{5}^{(3)} = 8^{3}, \\[2pt] P_{9}^{(4)} - P_{6}^{(4)} = 38^{2}, & P_{10}^{(4)} - P_{2}^{(4)} = 63^{2}, & P_{11}^{(6)} - P_{7}^{(6)} = 22^{3}. \end{array} \end{align*} $$
We briefly describe our method before going into more detail. We first obtain an upper bound for n and m in terms of k by applying Matveev’s result on linear forms in logarithms [Reference Matveev11]. When k is small, we may address our problem computationally by reducing the range of possible values using a result of Dujella and Pethö [Reference Dujella and Pethö8]. When k is large, the dominant root of the k-generalised Pell sequence is exponentially close to
$\phi ^2$
where
$\phi = {(1 + \sqrt {5})}/{2}$
(see [Reference Bravo and Herrera4, Lemma 2]), so we apply this estimate in our computations to complete the proof.
2 Auxiliary results
This section is devoted to gathering several definitions, notation, properties and results that will be used in the rest of this study.
2.1 Linear forms in logarithms
Let
$\gamma $
be an algebraic number of degree d with minimal primitive polynomial
$$ \begin{align*} f(Y):= b_0 Y^d+b_1 Y^{d-1}+ \cdots +b_d = b_0 \prod_{j=1}^{d}(Y- \gamma^{(j)}) \in \mathbb{Z}[Y], \end{align*} $$
where the
$b_{j}$
are relatively prime integers, with
$b_0>0$
, and the
$\gamma ^{(j)}$
are the conjugates of
$\gamma $
. Then, the logarithmic height of
$\gamma $
is given by
$$ \begin{align*} h(\gamma)=\frac{1}{d}\bigg(\log b_0+\sum_{j=1}^{d}\log(\max\{|\gamma^{(j)}|,1\})\bigg). \end{align*} $$
Theorem 2.1 (Matveev [Reference Matveev11]; see also [Reference Bugeaud, Mignotte and Siksek7, Theorem 9.4]).
Let
$\eta _1, \ldots , \eta _s$
be positive real algebraic numbers in a real algebraic number field
$\mathbb {L}$
of degree
$d_{\mathbb {L}}$
. Let
$a_1, \ldots , a_s$
be nonzero integers such that
$$ \begin{align*} \Lambda :=\eta_1^{a_1}\cdots\eta_s^{a_s}-1 \neq 0. \end{align*} $$
Then,
$$ \begin{align*} \log |\Lambda| \geq -1.4\cdot 30^{s+3}\cdot s^{4.5}\cdot d_{\mathbb{L}}^2(1+\log d_{\mathbb{L}})(1+\log D)\cdot B_1 \cdots B_s, \end{align*} $$
where
$$ \begin{align*} D\geq \max\{|a_1|,\ldots,|a_s|\} \end{align*} $$
and
$$ \begin{align*} B_j\geq \max\{d_{\mathbb{L}}h(\eta_j),|\!\log \eta_j|, 0.16\} \quad\text{for } j=1,\ldots,s. \end{align*} $$
2.2 The reduction method
Our next tool is a version of the reduction method of Baker and Davenport (see [Reference Baker and Davenport2]). Here, we use a slight variant of the version given by Dujella and Pethö (see [Reference Dujella and Pethö8]). For a real number x, we write
$||x||$
for the distance from x to the nearest integer.
Lemma 2.2. Let M be a positive integer,
$p/q$
be a convergent of the continued fraction of the irrational
$\tau $
such that
$q> 6M$
, and
$A, B, \mu $
be some real numbers with
$A>0$
and
$B>1$
. Furthermore, let
$$ \begin{align*}\epsilon:=||\mu q|| - M \cdot ||\tau q||. \end{align*} $$
If
$\epsilon>0$
, then there is no solution to the inequality
$$ \begin{align*} 0< |u \tau - v + \mu| <AB^{-w} \end{align*} $$
in positive integers u, v and w with
$$ \begin{align*} u \leq M \quad\text{and}\quad w \geq \frac{\log(Aq/\epsilon)}{\log B}. \end{align*} $$
2.3 Properties of the k-generalised Pell sequence
The characteristic polynomial of the k-generalised Pell sequence is
$$ \begin{align*} \Phi_{k}(x) = x^k - 2 x^{k-1} - x^{k-2} - \cdots - x -1. \end{align*} $$
This polynomial is irreducible over
$\mathbb {Q} [x]$
and it has one positive real root
$\gamma := \gamma (k)$
which is located between
$ \phi ^ 2(1 - \phi ^{-k})$
and
$\phi ^2$
and lies outside the unit circle (see [Reference Bravo, Herrera and Luca6]). The other roots all lie inside the unit circle. To simplify the notation, we will omit the dependence of
$\gamma $
on k whenever no confusion may arise.
For an integer
$k \geq 2$
, the Binet formula for
$P_{n}^{(k)}$
found in [Reference Bravo, Herrera and Luca6] is
$$ \begin{align} P_{n}^{(k)} = \displaystyle\sum_{i=1}^{k} g_{k} (\gamma_{i})\gamma_{i}^{n} , \end{align} $$
where the
$\gamma _{i}$
are the roots of the characteristic polynomial
$\Phi _{k}(x)$
and the function
$g_{k}$
is given by
$$ \begin{align*} g_{k}(z) := \frac{z-1}{(k+1)z^2 - 3kz + k -1}. \end{align*} $$
It is also shown in [Reference Bravo, Herrera and Luca6, Theorem 3.1] that the roots located inside the unit circle have minimal influence on (2.1), giving the approximation
$$ \begin{align} | P_{n}^{(k)} - g_{k} (\gamma) \gamma^{n} | < \tfrac{1}{2} \quad \text{for all} \ n \geq 2 - k. \end{align} $$
Furthermore, from [Reference Bravo, Herrera and Luca6, Theorem 3.1],
$$ \begin{align*} \gamma ^ {n-2} \leq P_{n} ^ {(k)} \leq \gamma ^ {n-1} \quad\text{for all } n \geq 1. \end{align*} $$
Lemma 2.3 [Reference Bravo and Herrera4, Lemma 1].
Let
$k \geq 2 $
be an integer. Then,
$$ \begin{align*} 0.276 < g_{k}(\gamma) < 0.5 \quad\mbox{and}\quad | g_{k}(\gamma_{i}) | < 1 \quad\mbox{for}\ 2 \leq i \leq k. \end{align*} $$
Furthermore, the logarithmic height of
$g_{k} (\gamma )$
satisfies
$$ \begin{align} h(g_{k}(\gamma)) < 4k\log \phi + k \log(k+1) \quad \text{for all} \ k \geq 2. \end{align} $$
Lemma 2.4 [Reference Bravo and Herrera3, Lemma 2.2]; see also [Reference Bravo and Herrera4, Lemma 2].
If
$k \geq 30$
and
$n \ge 1$
are integers such that
$n < \phi ^{k/2}$
, then
$$ \begin{align*} g_{k} (\gamma) \gamma^{n} = \frac{\phi^{2n}}{\phi + 2}(1 + \xi) \quad \text{where} \quad |\xi| < \frac{4}{\phi^{k/2}}. \end{align*} $$
2.4 Useful lemmas
We conclude this section by recalling two lemmas that we will need.
Lemma 2.5 [Reference Bravo, Herrera and Luca5, Lemma 8].
For any nonzero real number x:
-
(a)
$0 < x < |e^{x} - 1|$
; -
(b) if
$x < 0$
and
$|e^{x} - 1| < 1/2$
, then
$|x| < 2 |e^{x} - 1|$
.
Lemma 2.6 [Reference Sanchez and Luca13, Lemma 7].
If
$m \geq 1$
,
$S \geq (4m^{2})^{m}$
and
${x}/{(\log x)^{m}} < S$
, then
$x < 2^{m} S (\log S)^{m}$
.
3 Proof of Theorem 1.1
3.1 Preliminary considerations
We begin our analysis of (1.3) for
$1 \leq n \leq k+1$
. In this case, it is known that
$P_{n}^{(k)} = F_{2n-1}$
, and thus (1.3) becomes
$$ \begin{align*} F_{2n-1} \pm F_{2m-1} = y^{a}, \end{align*} $$
which has no solution for
$1 \leq m \leq n$
according to the results of [Reference Kebli, Kihel, Larone and Luca9] and [Reference Kihel and Larone10]. From now on, we assume that
$n \geq k+2$
and
$k \geq 3$
.
Let us now get an initial relation between a and n. Combining (1.3) with the fact
$\phi ^{2}(1 - \phi ^{-3}) < \gamma (k) < \phi ^{2} $
for all
$k \geq 3$
, we have
$$ \begin{align*} y^{a} \leq \gamma^{n-1} \pm \gamma^{m-1} < \phi^{2(n-1)} \pm \phi^{2(m-1)} = \phi^{2(n-1)} ( 1 \pm \phi^{2(m-n)} ) < 2 \cdot \phi^{2(n-1)}. \end{align*} $$
We deduce that
$$ \begin{align*} a < \bigg( \frac{\log 2}{\log y} \bigg) + 2(n - 1) \bigg( \frac{\log \phi}{\log y}\bigg), \end{align*} $$
which leads to
$$ \begin{align} a < 1.4 n - 0.4 < 1.4 n \quad \text{for} \ n \geq 5. \end{align} $$
3.2 Bounding n in terms of k
In this subsection, we will bound n in terms of k by proving the following lemma.
Lemma 3.1. If
$(n, m, k, y, a)$
is a solution of (1.3) with
$k \geq 3$
and
$n \geq m \geq 1$
, then
$$ \begin{align*} n < 9.67 \times 10^{29} k^{9} \log^{5} k. \end{align*} $$
Proof. By using (1.3), (2.2) and taking absolute values, we obtain
$$ \begin{align*} | y^{a} - g_{k}(\gamma) \gamma^{n} | < \tfrac{1}{2} \pm P_{m}^{(k)} \leq \tfrac{1}{2} + \gamma^{m-1}. \end{align*} $$
Dividing both sides of this inequality by
$g_{k}(\gamma ) \gamma ^{n}$
and using
$g_{k}(\gamma )> 0.276$
, we obtain
$$ \begin{align} | y^{a} \gamma^{-n} (g_{k}(\gamma))^{-1} - 1 | < \frac{1.82}{\gamma^{n}} + \frac{1.82}{\gamma^{n-m}} < \frac{3.64}{\gamma^{n-m}}. \end{align} $$
Let
$$ \begin{align} \Lambda_{1} := y^{a} \gamma^{-n} (g_{k}(\gamma))^{-1} - 1. \end{align} $$
From (3.2),
$$ \begin{align} |\Lambda_{1}| < 3.64 \cdot \gamma^{-(n-m)}. \end{align} $$
If
$\Lambda _{1} = 0$
, then
$g_{k}(\gamma ) = y^{a} \gamma ^{-n}$
, which implies that
$g_{k}(\gamma )$
is an algebraic integer, which is a contradiction. Hence,
$\Lambda _{1} \neq 0$
. To apply Theorem 2.1 to
$\Lambda _{1}$
given by (3.3), we take the parameters
$$ \begin{align*} \eta_{1} := y, \quad \eta_{2} := \gamma , \quad \eta_{3} := g_{k}(\gamma), \quad a_{1}:= a, \quad a_{2} := -n, \quad a_{3} := -1. \end{align*} $$
Note that the algebraic numbers
$\eta _{1}, \eta _{2}, \eta _{3}$
belong to the field
$\mathbb {L} := \mathbb {Q}(\gamma )$
, so we can take
$d_{\mathbb {L}} = [\mathbb {L}:\mathbb {Q}] \leq k$
. Since
$ h(\eta _{1}) = \log y $
, we find
$h(\eta _{2}) = (\log \gamma ) / k < (2 \log \phi ) /k$
and
$h(\eta _{3}) < 4k\log \phi + k \log (k+1) < 5k \log k$
for all
$k \geq 3$
. So it follows that
$B_{1} := k \log y$
,
$B_{2} := 2 \log \phi $
and
$B_{3} := 5k^{2} \log k$
. In addition, by (3.1), we can take
$D:= 1.4 n$
. Then, by Theorem 2.1,
$$ \begin{align} \log |\Lambda_{1}|> - 1.432 \times 10^{11} (k)^{2} (1+ \log k) (1 +\log 1.4 n) (k \log y) (2 \log \phi) (5k^{2} \log k). \end{align} $$
Combining the inequality (3.5) with (3.4) gives
$$ \begin{align*} ( n - m ) \log \gamma - \log 3.64 < 6.9 \times 10^{11} k^{5} (1 + \log 1.4 n) (1 + \log k) (\log y) (\log k). \end{align*} $$
Using the facts
$1+\log k < 2 \log k$
for all
$k \geq 3$
and
$1+ \log 1.4n < 1.9 \log n$
for all
$n \geq 5$
, we obtain
$$ \begin{align*} (n - m) \log \gamma < 2.64 \times 10^{12} k^{5} \log^{2} k \log n \log y. \end{align*} $$
Now from (1.3),
$$ \begin{align*} |y^{a} - g_{k}(\gamma) \gamma^{n} ( 1 \pm \gamma^{m-n}) | & \leq | P_{n}^{(k)} - g_{k}(\gamma) \gamma^{n} | \pm | P_{m}^{(k)} - g_{k}(\gamma) \gamma^{m} | \leq 1. \end{align*} $$
Dividing both sides of the above inequality by
$g_{k} (\gamma ) \gamma ^{n} ( 1 \pm \gamma ^{m-n} )$
yields
$$ \begin{align} |y^{a} \gamma^{-n} (g_{k}(\gamma) ( 1 \pm \gamma^{m-n}) )^{-1} - 1 | < \frac{1.82}{\gamma^{n}}, \end{align} $$
where
$$ \begin{align*} \Lambda_{2}:= y^{a} \gamma^{-n} (g_{k}(\gamma) ( 1 \pm \gamma^{m-n}))^{-1} - 1. \end{align*} $$
For the left-hand side, we apply Theorem 2.1 with the parameters
$$ \begin{align*} \eta_{1} := y, \quad \eta_{2} := \gamma , \quad \eta_{3} := (g_{k}(\gamma)) ( 1 \pm \gamma^{m-n}), \quad a_{1}:= a, \quad a_{2}:= -n, \quad a_{3}:= -1. \end{align*} $$
As before,
$\mathbb {L} := \mathbb {Q}(\gamma )$
contains
$\eta _{1}, \eta _{2}, \eta _{3}$
and has degree k. Here,
$\Lambda _{2} \neq 0$
. Indeed, if it were zero, we would get
$$ \begin{align*} y^{a} = g_{k}(\gamma) ( \gamma^{n-1} \pm \gamma^{m-1}). \end{align*} $$
Conjugating this relation by an automorphism
$\sigma $
of the Galois group of
$\Phi _{k}(x)$
over
$\mathbb {Q}$
such that
$\sigma (\gamma ) = \gamma ^{(i)}$
for some
$i> 1$
and then taking absolute values,
$$ \begin{align*} y^{a} = |g_{k}(\gamma^{(i)})| |{\gamma^{(i)}}^{n-1} \pm {\gamma^{(i)}}^{m-1}| < 2, \end{align*} $$
which is impossible. Hence,
$\Lambda _{2} \neq 0$
. Since
$h(\eta _{1}) = \log y $
and
$h(\eta _{2}) = (\log \gamma ) / k < (2 \log \phi ) /k$
, it follows that
$B_{1}:= k \log y$
and
$B_{2}:= 2 \log \phi $
. Therefore, by the estimate (2.3) and the properties of the logarithmic height, it follows that for all
$k \geq 3$
,
$$ \begin{align*} h(\eta_{3}) & < h( g_{k}(\gamma) ) + h (1 \pm \gamma^{m-n}) \\ & < 4k\log \phi + k \log(k+1) + |m-n| h (\gamma) + \log 2 \\ & < 5k \log k + (n-m) \log \gamma + \log 2 \\ & < 2.65 \times 10^{12} k^{5} (\log n) (\log y) (\log^{2} k). \end{align*} $$
Hence, we obtain
$B_{3} := 2.65 \times 10^{12} k^{6} (\log n) (\log y) (\log ^{2} k)$
. In addition, by (3.1), we can take
$D:= 1.4n$
. Then, by Theorem 2.1,
$$ \begin{align} -\log |\Lambda_{2}| < 3.66 \times 10^{23} k^{9} (1+ \log k) (1 +\log 1.4n) (\log^{2} k )(\log n) (\log^{2} y). \end{align} $$
Combining the inequality (3.7) with (3.6) gives
$$ \begin{align*} n \log \gamma - \log 1.82 < 3.66 \times 10^{23} k^{9} (1+ \log k) (1 +\log 1.4n) (\log^{2} k )(\log n) (\log^{2} y). \end{align*} $$
Using the facts
$1 + \log k < 2 \log k$
for all
$k \geq 3$
,
$1 + \log 1.4 n < 1.9 \log n$
for all
$n \geq 5$
and
$y \leq 200$
, it follows that
$$ \begin{align*} n < 5.9 \times 10^{25} k^{9} \log^{3} k \log^{2} n. \end{align*} $$
This leads to
$$ \begin{align} \frac{n}{\log^{2} n} < 5.9 \times 10^{25} k^{9} \log^{3} k. \end{align} $$
Thus, putting
$S := 5.9 \times 10^{25} k^{9} \log ^{3} k$
and using Lemma 2.6 in (3.8), and noting that
$59.33 + 9 \log k + 3 \log (\log k) < 64 \log k$
for all
$k \geq 3$
,
$$ \begin{align*} n & < 4(5.9 \times 10^{25} k^{9} \log^{3} k) (\log (5.9 \times 10^{25} k^{9} \log^{3} k))^{2} \\ & < (2.36 \times 10^{26} k^{9} \log^{3} k) (59.33 + 9 \log k + 3 \log (\log k))^{2} \\ & < 9.67 \times 10^{29} k^{9} \log^{5} k. \end{align*} $$
This completes the proof of Lemma 3.1.
3.3 The case when
$3 \leq k \leq 570$
In the previous section, we obtained a very large upper bound of n. We apply Lemma 2.2 to reduce the upper bound by means of the following lemma.
Lemma 3.2. If
$(n, m, k, y, a)$
is an integer solution of (1.3) with
$3 \leq k \leq 570$
and
$n \geq k+2$
, then
$n \leq 314$
.
Proof. To apply Lemma 2.2, we define
$$ \begin{align} \Gamma_{1} := a \log y - n \log \gamma - \log g_{k}(\gamma). \end{align} $$
Then,
$e^{\Gamma _{1}} - 1 := \Lambda _{1}$
, where
$\Lambda _{1}$
is defined by (3.3). Therefore, (3.4) implies that
$$ \begin{align} |e^{\Gamma_{1}} -1 | < \frac{3.64}{\gamma^{-(n-m)}}. \end{align} $$
Note that
$\Gamma _{1} \neq 0$
. Thus, we distinguish the following cases. If
$\Gamma _{1}> 0$
, then we can apply Lemma 2.5(a) to obtain
$$ \begin{align*} 0 < \Gamma_{1} < e^{\Gamma_{1}} - 1 < 3.64 \cdot \gamma^{-(n-m)}. \end{align*} $$
If
$\Gamma _{1} < 0$
, then from (3.10),
$|e^{\Gamma _{1}} - 1|< 1/2$
and therefore,
$e^{|\Gamma _{1}|} < 2$
. Thus, by Lemma 2.5(b),
$$ \begin{align*} 0 < |\Gamma_{1}| \leq e^{|\Gamma_{1}|} - 1 = e^{|\Gamma_{1}|}|e^{\Gamma_{1}} - 1 | < 7.28 \cdot \gamma^{-(n-m)}. \end{align*} $$
So in both cases,
$$ \begin{align} 0 < |\Gamma_{1}| < 7.28 \cdot \gamma^{-(n-m)}. \end{align} $$
Inserting (3.9) into (3.11) and dividing both sides by
$\log \gamma $
,
$$ \begin{align} \bigg| a \bigg( \frac{\log y}{\log \gamma}\bigg) - n + \frac{\log g_{k}(\gamma)}{\log \gamma}\bigg| < 10.51 \cdot \gamma^{-(n-m)}. \end{align} $$
With
$$ \begin{align*} \tau = \tau(k) := \frac{\log y}{\log \gamma}, \quad \mu = \mu(k):= \frac{\log g_{k}(\gamma)}{\log \gamma}, \quad A:= 10.51 \quad \text{and} \quad B:= \gamma, \end{align*} $$
the inequality (3.12) yields
$$ \begin{align*} 0 < |a \tau - n + \mu| < A \cdot B^{-(n-m)}. \end{align*} $$
Note that
$\tau $
is an irrational number. We take
$ M_{k} := \lfloor 9.67 \times 10^{29} k^{9} \log ^{5} k \rfloor $
which is an upper bound on n. Then, by Lemma 2.2, for each
$ k \in [3, 570]$
,
$$ \begin{align*} n - m < \frac{\log(Aq/\epsilon)}{\log B}, \end{align*} $$
where
$ q = q(k)> 6M_{k}$
is a denominator of a convergent of the continued fraction of
$\tau $
with
$ \epsilon = \epsilon (k):= \| \mu q \| - M_{k} \|\tau q\|> 0$
. A computer search with Mathematica found that for
$k \in [3, 530]$
, the maximum value of
$\log (Aq/\epsilon )/ \log B $
is
$< 233$
.
Assuming
$1 \leq n-m \leq 232$
, we consider
$$ \begin{align*} \Gamma_{2} := a \log y - n \log \gamma - \log \mu(k, n-m), \end{align*} $$
where
$\mu (k, n-m) := g_{k}(\gamma )(1 \pm \gamma ^{n-m})$
. Therefore, (3.6) can be written as
$$ \begin{align*} |e^{\Gamma_{2}} -1 | < \frac{1.82}{\gamma^{n}}. \end{align*} $$
In this case,
$\Gamma _{2} \neq 0$
. If
$\Gamma _{2}> 0$
, we apply Lemma 2.5(a) to obtain
$|\Gamma _{2}| < 1.82 \cdot \gamma ^{-n}$
. If
$\Gamma _{2} < 0$
, then
$|e^{\Gamma _{2}} - 1|< 1/2$
for all
$n \geq 2$
. Thus, by Lemma 2.5(b),
$|\Gamma _{2}| < 2 |e^{\Gamma _{1}} - 1| < 3.64 \cdot \gamma ^{-n}$
. In any case,
$$ \begin{align} 0 < |\Gamma_{2}| < 3.64 \cdot \gamma^{-n}. \end{align} $$
Replacing
$\Gamma _{2}$
in (3.13) by its formula and dividing through by
$\log \gamma $
yields
$$ \begin{align} 0 < |a \tau - n + \mu| < A \cdot B^{-n}, \end{align} $$
where
$$ \begin{align*} \tau = \tau(k) := \frac{\log y}{\log \gamma}, \quad \mu = \mu(k):= - \frac{\log \mu(k, n-m)}{\log \gamma}, \quad A:= 5.26 \quad \text{and} \quad B:= \gamma. \end{align*} $$
Here, we put
$ M_{k} := \lfloor 9.67 \times 10^{29} k^{9} \log ^{5} k \rfloor $
and as we explained before, we apply Lemma 2.2 to inequality (3.14) to obtain an upper bound on n. Indeed, with the help of Mathematica, we find that if
$k \in [3, 570]$
and
$n-m \in [1, 232]$
, then the maximum value of
$\log (Aq/ \epsilon ) / \log B$
is
$< 315$
.
3.4 The case when
$k> 570$
In this subsection, our goal is to prove the following lemma which shows that there are no solutions when
$k> 570$
and
$n \geq k+2$
.
Lemma 3.3. The Diophantine equation (1.3) has no solution for
$n \geq k+2$
and
$k> 570$
.
Proof. After Lemma 3.1, for
$k> 570$
,
$$ \begin{align*} n < 9.67 \times 10^{29} k^{9} \log^{5} k < \phi^{k / 2}. \end{align*} $$
It follows from (1.3) and (2.2) that
$$ \begin{align*} | y^{a} - g_{k}(\gamma) \gamma^{n} - g_{k}(\gamma) \gamma^{m} | = | P_{n}^{(k)} - g_{k}(\gamma) \gamma^{n} | \pm | P_{m}^{(k)} - g_{k}(\gamma) \gamma^{m} | < 1. \end{align*} $$
The above inequality together with Lemma 2.4 give
$$ \begin{align*} \bigg| y^{a} - \frac{\phi ^{2n}}{\phi + 2}(1+\xi) - \frac{\phi ^{2m}}{\phi + 2}(1+\xi) \bigg| < 1. \end{align*} $$
This implies that
$$ \begin{align*} \bigg| y^{a} - \frac{\phi ^{2n}}{\phi + 2} - \frac{\phi ^{2m}}{\phi + 2} \bigg| < 1 + \frac{\phi ^{2n}}{\phi + 2} \cdot \frac{4}{\phi^{k/2}} + \frac{\phi ^{2m}}{\phi + 2} \cdot \frac{4}{\phi^{k/2}}. \end{align*} $$
Dividing both sides of the above inequality by
${\phi ^{2n}}/{(\phi + 2)}$
,
$$ \begin{align} \bigg| \frac{y^{a} (\phi + 2)}{\phi ^{2n}} -1 - \phi^{2(m-n)} \bigg| < \frac{\phi + 2}{\phi^{2n}} + \frac{4}{\phi^{k/2}} + \frac{4 \cdot \phi^{2(m-n)}}{\phi^{k/2}}. \end{align} $$
Since
$n \geq k+2$
and
$n \geq m$
, (3.15) becomes
$$ \begin{align*} \bigg| 1 + \phi^{2(m-n)} - \frac{y^{a} (\phi + 2)}{\phi ^{2n}} \bigg| < \frac{11.618}{\phi^{k/2}}. \end{align*} $$
However, the above inequality is impossible for all
$y \in [2, 200]$
and
$k> 570$
.
3.5 The final computation
As a result of Lemmas 3.2 and 3.3, if
$(n, m, k, y, a)$
is a solution of the Diophantine equation (1.3), then
$$ \begin{align*} 3 \leq k \leq 570, \quad k + 2 \leq n \leq 314 \quad \text{and} \quad 1 \leq m \leq n. \end{align*} $$
We checked this range using Mathematica to conclude that all the solutions to the Diophantine equation (1.3) are listed in the statement of Theorem 1.1. This completes the proof of Theorem 1.1.
Acknowledgement
The author would like to thank the anonymous referee for useful comments.
