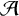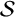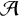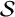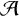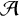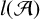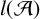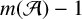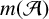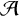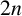1 Introduction
All algebras considered in this paper are associative finite-dimensional algebras with an identity over a field. First, we recall the notion of the length of an algebra
${\mathcal {A}}$
.
Let
${\mathcal {A}}$
be an algebra. Any product of a finite number of elements from a finite subset
${\mathcal {S}} \subset {\mathcal {A}}$
is called a word over the alphabet
${\mathcal {S}}$
. The length of a word equals the number of letters in this product that are different from
$1_{{\mathcal {A}}}$
. We consider
$1_{{\mathcal {A}}}$
to be the empty word of length 0.
If
${\mathcal {S}}$
is a generating system (or a generating set) of the algebra
${\mathcal {A}}$
, that is,
${\mathcal {A}}$
is the minimal subalgebra of
${\mathcal {A}}$
containing
${\mathcal {S}}$
, then any element of the algebra
${\mathcal {A}}$
can be expressed as a linear combination of words over
${\mathcal {S}}$
. The minimal k such that all elements of
${\mathcal {A}}$
can be expressed using words of length no more than k is called the length of the generating system
${\mathcal {S}}$
. The length of the algebra
${\mathcal {A}}$
is defined as the maximum length among its generating systems and will be denoted by
$l({\mathcal {A}})$
(see Definition 2.4). In defining the length of the algebra
${\mathcal {A}}$
, we consider the set of all generating systems for
${\mathcal {A}}$
. This explains the difficulty of calculating the length even for classical algebras. The main algebraic properties of the length function were studied by Markova in [Reference Markova8].
The general problem of calculating the length was first formulated by Paz in 1984 for the full matrix algebra
$M_n({\mathbb {F}})$
over a field in [Reference Paz11] and still remains open.
Conjecture 1.1 [Reference Paz11].
Let
${\mathbb {F}}$
be an arbitrary field. Then,
$l(M_n({\mathbb {F}}))=2n-2.$
A nontrivial upper bound on
$l({\mathcal {A}})$
in terms of
$\dim {\mathcal {A}}$
and
$m({\mathcal {A}})$
(the largest degree of the minimal polynomial among all elements of the algebra
${\mathcal {A}}$
) was obtained in [Reference Pappacena10] by Pappacena. We continue the study of upper bounds for the length in these terms.
The question of calculating the lengths of group algebras is of particular interest. Due to their matrix representations, solving this question is closely linked to solving Paz’s problem. For group algebras of small-order groups, it is possible to calculate the length precisely over arbitrary fields. For the permutation group
$S_3$
, Klein four-group
$K_4$
and quaternion group
$Q_8$
, the lengths were found by Guterman and Markova in [Reference Guterman and Markova2, Reference Guterman, Markova, Shum, Zelmanov, Kolesnikov and Wong3].
The joint works of the author with Guterman and Markova [Reference Guterman, Khrystik and Markova1, Reference Guterman, Markova and Khrystik4] were dedicated to the systematic study of the general problem of finding the lengths of group algebras of finite abelian groups. The works of Markova [Reference Markova9] and the author [Reference Khrystik5] continued the study of the lengths of group algebras of finite abelian groups in the modular case.
Studying all nonabelian groups appears to be too difficult due to the diversity of their structure. Therefore, it is proposed to study the length function separately for families of classical nonabelian groups. Thus, in the joint work of the author with Markova [Reference Khrystik and Markova7], the study of the lengths of group algebras of dihedral groups began, and the length was calculated in the semisimple case. This series of groups in the semisimple case is a natural next step after the abelian case. Indeed, for group algebras of abelian groups in the decomposition into a direct sum of matrix algebras, all terms are one-dimensional, whereas the sizes of the matrix algebras in the decomposition into a direct sum of group algebras of dihedral groups do not exceed 2. The work [Reference Khrystik and Markova6] continued the study of the lengths of group algebras of dihedral groups of order
$2^k$
and calculated their lengths in the modular case. Here, we consider the length of the group algebra of the dihedral group over an arbitrary field.
In Section 2, the main definitions and notation are introduced. In Section 4, the concept of bicirculant algebra is introduced and, in particular, its length is calculated. A bicirculant representation of the group algebra of the dihedral group is constructed. Using the bicirculant representation,
$l({\mathcal {A}})$
and
$m({\mathcal {A}})$
are estimated for the group algebra of the dihedral group.
2 Main definitions and notation
Denote by
$\langle S \rangle $
the linear span (the set of all finite linear combinations with coefficients from
${\mathbb {F}}$
) of a subset S of some vector space over
${\mathbb {F}}$
.
Let
$B=\{b_1,\ldots ,b_m\}$
be a nonempty finite set (alphabet). Finite sequences of letters from B are called words. Let
$B^*$
denote the set of all words in the alphabet B and
$F_B$
the free semigroup over the alphabet B, that is,
$B^*$
with the operation of concatenation.
Definition 2.1. The length of the word
$b_{i_1}\cdots b_{i_t}$
, where
$b_{i_j}\in B$
, is equal to t. We will consider
$1$
(the empty word) as a word from the elements B of length 0.
Let
$B^i$
denote the set of all words in the alphabet B of length no greater than
$i\, (i\geq 0)$
and
$B^{=i}$
denote the set of all words in the alphabet B of length equal to
$i\, (i\geq 1)$
.
Remark 2.2. Products of elements from the generating set
${\mathcal {S}}$
can be considered as images of elements of the free semigroup
$F_{{\mathcal {S}}}$
under the natural homomorphism. They can also be called words from the generators and we use the natural notation
${\mathcal {S}}^i$
and
${\mathcal {S}}^{=i}$
.
Denote by
${\mathcal {L}}_i({\mathcal {S}})$
the linear span of words from
${\mathcal {S}}^i$
. Note that
${\mathcal {L}}_0({\mathcal {S}})=\langle 1_{{\mathcal {A}}}\rangle ={\mathbb {F}}$
. Let
${\mathcal {L}}({\mathcal {S}})=\bigcup _{i=0}^\infty {\mathcal {L}}_i({\mathcal {S}})$
denote the linear span of all words in the alphabet
${\mathcal {S}}=\{a_1,\ldots , a_k\}$
.
Definition 2.3. The length of a generating system
${\mathcal {S}}$
of the algebra
${\mathcal {A}}$
is defined by
$l({\mathcal {S}})=\min \{k\in {\mathbb {Z}}_+: {\mathcal {L}}_k({\mathcal {S}})={\mathcal {A}}\}$
.
Definition 2.4. The length of an algebra
${\mathcal {A}}$
is
$l({\mathcal {A}})=\max \{l({\mathcal {S}}): {\mathcal {L}}({\mathcal {S}})={\mathcal {A}}\}$
.
Let
${\mathcal {A}}$
be an algebra,
$\tau \in {\mathcal {A}}$
. Denote the minimal polynomial of
$\tau $
by
$\mu _{\tau }(x)$
. We set
$m(\tau )=\deg \mu _{\tau }(x)$
and
$m({\mathcal {A}})=\max _{\tau \in {\mathcal {A}}} m(\tau )$
.
Denote by
${\mathbb {F}} G$
or
${\mathbb {F}}[G]$
the group algebra of the group G over the field
${\mathbb {F}}$
,
$E_{i,j}$
the matrix unit with
$i,j$
entry 1 and all other entries
$0$
,
$\mathcal D_n$
the dihedral group of order
$2n$
,
$S_n$
the symmetric group, and
$M_n({\mathbb {F}})$
the algebra of
$n \times n$
matrices over
${\mathcal {F}}$
.
A circulant matrix is a square matrix in which all rows are composed of the same elements and each row is rotated one element to the right relative to the preceding row. An anticirculant matrix is a square matrix in which all rows are composed of the same elements and each row is rotated one element to the left relative to the preceding row.
Definition 2.5. Let
$\mathcal {S}$
generate the algebra
$\mathcal {A}$
. Two words u and v of length i on the alphabet
$\mathcal {S}$
are equivalent if
$u-\alpha v\in {\mathcal {L}}_{i-1}({\mathcal {S}})$
for some nonzero
$\alpha \in {\mathbb {F}}$
. We will use the notation
$u\sim v$
in this case.
Definition 2.6. A word u of length i from the generators is reducible if
$u\in {\mathcal {L}}_{i-1}({\mathcal {S}})$
. Otherwise, we will call the word irreducible.
3 General bound on the length
3.1 Equivalence of words
Before proceeding to prove the main statement of the section, let us note some properties of the concept of word equivalence.
Lemma 3.1. Equivalence of words is an equivalence relation on the set of words.
Proof.
Reflexivity.
$u-\alpha u \in {\mathcal {L}}_{i-1}({\mathcal {S}})$
with
$\alpha =1.$
Symmetry. Let
$u-\alpha v \in {\mathcal {L}}_{i-1}({\mathcal {S}})$
. Multiplying the element
$u-\alpha v$
by
$-\alpha ^{-1}$
gives
$v-\alpha ^{-1} u \in {\mathcal {L}}_{i-1}({\mathcal {S}}).$
Transitivity. Let
$u-\alpha _1 v \in {\mathcal {L}}_{i-1}({\mathcal {S}})$
and
$v-\alpha _2 w \in {\mathcal {L}}_{i-1}({\mathcal {S}})$
. By adding the second element multiplied by
$\alpha _1$
to the first one, we obtain
$u-\alpha _1 \alpha _2 w \in {\mathcal {L}}_{i-1}({\mathcal {S}}).$
The proofs of the next two lemmas are straightforward.
Lemma 3.2. Let
$u \sim v$
. Then, u is reducible if and only if v is reducible.
Lemma 3.3. If the word u is irreducible, then any subword of u is irreducible.
Lemma 3.4. Let the word w of length i contain a subword u of length j and
$u \sim v$
. Then,
$w \sim w'$
, where
$w'$
is the word obtained from w by replacing the subword u with the subword v.
Proof. By the hypothesis,
$w=w_1uw_2$
for some words
$w_1$
,
$w_2$
and
$u-\alpha v \in {\mathcal {L}}_{j-1}({\mathcal {S}})$
. Multiplying the expression
$u-\alpha v$
on the left by
$w_1$
and on the right by
$w_2$
gives
${w-\alpha w' \in {\mathcal {L}}_{i-1}({\mathcal {S}}).}$
3.2 Estimating
$l({\mathcal {A}})$
using
$\dim {\mathcal {A}}$
and
$m({\mathcal {A}})$
Theorem 3.5. Let
${\mathcal {A}}$
be an associative finite-dimensional algebra with an identity. Then,
$$ \begin{align*}l({\mathcal{A}})\leq \max\bigg\{m({\mathcal{A}})-1,\frac{\dim{\mathcal{A}}}{2} \bigg\}.\end{align*} $$
Proof. Let
$l({\mathcal {A}})\geq m({\mathcal {A}})$
(otherwise there is nothing to prove). Let
${\mathcal {S}}$
be a generating set of length
$l({\mathcal {A}})$
of the algebra
${\mathcal {A}}$
(in the case of other generating sets, the length of the algebra will be no greater). We will prove that
$\dim {\mathcal {L}}_k({\mathcal {S}})-\dim {\mathcal {L}}_{k-1}({\mathcal {S}})\geq 2$
for all
$k\in [1,l({\mathcal {A}})-1]$
.
We will reason by contradiction. Suppose there exists
$k\in [1,l({\mathcal {A}})-1]$
such that
$\dim {\mathcal {L}}_k({\mathcal {S}})-\dim {\mathcal {L}}_{k-1}({\mathcal {S}})=1$
(this difference cannot be zero by the definition of the length of the algebra). Let
$a_1a_2\cdots a_{l({\mathcal {A}})}$
be an irreducible word of length
$l({\mathcal {A}})$
in the alphabet
${\mathcal {S}}$
(such a word exists by definition of the length of the algebra). We will break the reasoning into steps which lead to a contradiction.
First step. The word
$a_1a_2\cdots a_{l({\mathcal {A}})}$
is irreducible. Therefore, its subword
$a_1a_2\cdots a_k$
is irreducible by Lemma 3.3. By assumption,
$a_2a_3\cdots a_{k+1} \sim a_1a_2\cdots a_k$
(here we use the fact that k is no greater than
$l({\mathcal {A}})-1$
). Indeed, if this were not the case, we would get
$\dim {\mathcal {L}}_k({\mathcal {S}})-\dim {\mathcal {L}}_{k-1}({\mathcal {S}})\geq 2$
, since the dimension would increase by at least 2 due to these two words. Thus,
$a_1a_2\cdots a_{l({\mathcal {A}})} \sim a_2 a_3\cdots a_k a_{k+1} a_{k+1} a_{k+2} \cdots a_{l({\mathcal {A}})}$
by Lemma 3.4. Therefore, the word
$ a_2 a_3\cdots a_k a_{k+1} a_{k+1} a_{k+2} \cdots a_{l({\mathcal {A}})}$
is irreducible.
Second step. Now consider the irreducible word
$ a_2 a_3\cdots a_k a_{k+1} a_{k+1} a_{k+2} \cdots a_{l({\mathcal {A}})}$
of length
$l({\mathcal {A}})$
obtained in the previous step. By reasoning similarly (considering subwords of length k starting from the first and second letters), we will eliminate the letter
$a_2$
similarly to the way in which we eliminated the letter
$a_1$
in the first step. This shows that the word
$ a_3 a_4\cdots a_k a_{k+1} a_{k+1} a_{k+1} a_{k+2} \cdots a_{l({\mathcal {A}})}$
is irreducible.
After k steps of this reasoning, we obtain the irreducible word
$a_{k+1}\cdots a_{k+1} a_{k+2} \cdots a_{l({\mathcal {A}})}$
of length
$l({\mathcal {A}})$
. Now, we can proceed to the last step and obtain a contradiction.
$(k+1)$
st step. The word
$a_{k+1}^{k+1} a_{k+2} \cdots a_{l({\mathcal {A}})}$
is irreducible. Therefore, its subword
$a_{k+1}^{k}$
is irreducible. By assumption, all words of length k are expressed through the word
$a_{k+1}^{k}$
and words of shorter length. Thus,
$a_1a_2\cdots a_{l({\mathcal {A}})} \sim a_{k+1}^{l({\mathcal {A}})}$
. Therefore, the word
$a_{k+1}^{l({\mathcal {A}})}$
is irreducible and
$l({\mathcal {A}})< m({\mathcal {A}})$
, which is a contradiction.
We return to the proof of the main statement. Represent the dimension of the algebra in the form
$$ \begin{align*} \dim {\mathcal{A}} & =\dim{\mathcal{L}}_{l({\mathcal{A}})}({\mathcal{S}}) \\ & =(\dim{\mathcal{L}}_{l({\mathcal{A}})}({\mathcal{S}})-\dim{\mathcal{L}}_{l({\mathcal{A}})-1}({\mathcal{S}}))+(\dim{\mathcal{L}}_{l({\mathcal{A}})-1}({\mathcal{S}})-\dim{\mathcal{L}}_{l({\mathcal{A}})-2}({\mathcal{S}})) \\ &\quad +\cdots+(\dim{\mathcal{L}}_1({\mathcal{S}})-\dim{\mathcal{L}}_0({\mathcal{S}}))+\dim{\mathcal{L}}_0({\mathcal{S}}). \end{align*} $$
The first term of the sum is not less than 1, the last one equals 1 and all the others are not less than 2. Thus,
$\dim {\mathcal {A}} \geq 1+2(l({\mathcal {A}})-1)+1$
, that is,
$l({\mathcal {A}}) \leq {\dim {\mathcal {A}}}/{2}$
. Thus,
$l({\mathcal {A}})\leq \max \{m({\mathcal {A}})-1,{\dim {\mathcal {A}}}/{2}\}.$
3.3 Comparison with other estimates
To conclude this section, we will compare the bound in Theorem 3.5 with other similar bounds. The first comparison is with the bound in the joint work of the author with Markova.
Lemma 3.6 [Reference Khrystik and Markova6, Lemma 2.10].
Let
$\mathcal A$
be an
${\mathbb {F}}$
-algebra,
$\dim \mathcal A\leq m(\mathcal A)+4$
and
${m({\mathcal {A}}) \geq 3}$
. Then,
$l(\mathcal A) \leq m(\mathcal A)$
.
Since
$m({\mathcal {A}})-1$
is unequivocally less than
$m({\mathcal {A}})$
, we see that the new estimate will be worse than the estimate from Lemma 3.6 only if
${\dim {\mathcal {A}}}/{2} \geq m({\mathcal {A}})+1$
(that is, if
$\dim {\mathcal {A}} \geq 2m({\mathcal {A}})+2$
). Also, by the condition of Lemma 3.6,
$\dim \mathcal A\leq m(\mathcal A)+4$
. From the last two inequalities, it follows that
$m({\mathcal {A}}) \leq 2$
. However, in the condition of Lemma 3.6, it is also required that
$m({\mathcal {A}}) \geq 3$
. Therefore, the new bound is better in any case.
Next, we will compare Theorem 3.5 with the following estimate of Pappacena.
Theorem 3.7 [Reference Pappacena10, Theorem 3.1].
Let
${\mathcal {A}}$
be any algebra. Then,
$ l({\mathcal {A}})\kern1.4pt{<}\kern1.4pt f(\dim {\mathcal {A}},m({\mathcal {A}}))$
, where
$$ \begin{align*}f(d,m)=m\sqrt{\frac{2d}{m-1}+\frac{1}{4}}+\frac{m}{2}-2.\end{align*} $$
Since
$\dim {\mathcal {A}} \geq m({\mathcal {A}})-1$
, we have
$$ \begin{align*}m\sqrt{\dfrac{2d}{m-1}+\dfrac{1}{4}}+\dfrac{m}{2}-2 \geq m\sqrt{\dfrac{9}{4}}+\dfrac{m}{2}-2 = 2m-2.\end{align*} $$
Since
$m({\mathcal {A}})-1$
is less than
$2m({\mathcal {A}})-2$
, we see that the new estimate will be worse than Pappacena’s estimate only if
${\dim {\mathcal {A}}}/{2}> 2m({\mathcal {A}})-2$
(that is, if
$\dim {\mathcal {A}}> 4(m({\mathcal {A}})-1)$
). In particular, the new estimate is unequivocally better when considering group algebras of dihedral groups, which will be discussed in the next section. However, Theorem 3.5 may give a more accurate estimate than Theorem 3.7 even if
$\dim {\mathcal {A}} \leq 4(m({\mathcal {A}})-1)$
. Let us show that by the following example.
Example 3.8. Let
${\mathcal {A}} = M_3(\mathbb {F})$
. Then,
$\dim {\mathcal {A}} = 9$
,
$m({\mathcal {A}})=3$
. Theorem 3.7 gives an estimate
$l({\mathcal {A}}) \leq 8$
. Theorem 3.5 gives an estimate
$l({\mathcal {A}}) \leq 4$
, which corresponds to the value
$l(M_3(\mathbb {F}))$
in Paz’s conjecture.
4 Calculating
$l({\mathbb {F}}{\mathcal {D}}_n$
)
4.1 Bicirculant algebra
The circulant
$A_n=E_{n,1}+E_{1,2}+\cdots +E_{n-1,n}$
and the anticirculant
$B_n=E_{1,n}+\cdots +E_{n,1}$
are the
$n\times n$
matrices
$$ \begin{align*} A_n= \begin{pmatrix} 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 1 & 0 &\cdots & 0\\ 0 & 0 & 0 & 1 &\cdots & 0\\ \vdots& \vdots & \vdots &\vdots & \ddots & \vdots\\ 0 & 0 & 0 & 0 &\cdots & 1\\ 1 & 0 & 0 & 0 & \cdots & 0 \end{pmatrix} ,\quad B_n= \begin{pmatrix} 0 & 0 & 0 &\cdots & 0 & 1\\ 0 & 0 & 0 &\cdots & 1 & 0\\ \vdots& \vdots & \vdots & \cdots &\vdots & \vdots\\ 0 & 0 & 1 & \cdots & 0 & 0\\ 0 & 1 & 0 & \cdots & 0 & 0\\ 1 & 0 & 0 & \cdots & 0 & 0 \end{pmatrix}. \end{align*} $$
Definition 4.1. The bicirculant algebra of order n over the field
${\mathbb {F}}$
is the algebra generated by the circulant and the anticirculant, that is,
${\mathcal {C}}_n({\mathbb {F}})={\mathcal {L}}(\{A_n,B_n\})$
.
Let us study the structure of this algebra. The next lemma can be checked directly by multiplying matrices.
Lemma 4.2. We have
$A_n^n=E$
,
$B_n^2=E$
and
$A_nB_n=B_nA_n^{n-1}$
, where E is the identity matrix.
Lemma 4.3. We have
$\dim {\mathcal {C}}_n({\mathbb {F}})=\begin {cases} 2n-2\ \mbox {for even}\; n;\\ 2n-1 \ \mbox {for odd}\; n. \end {cases}$
Proof. From Lemma 4.2,
${\mathcal {C}}_n({\mathbb {F}})={\mathcal {C}}_n'({\mathbb {F}})+{\mathcal {C}}_n"({\mathbb {F}})$
, where
${\mathcal {C}}_n'({\mathbb {F}})=\langle E,A_n,A_n^2,\ldots , A_n^{n-1}\rangle $
and
${\mathcal {C}}_n"({\mathbb {F}})=\langle B_n,B_nA_n,B_nA_n^2,\ldots ,B_nA_n^{n-1}\rangle $
. Note that
${\mathcal {C}}_n'({\mathbb {F}})$
is nothing else but the space of circulants, and
${\mathcal {C}}_n"({\mathbb {F}})$
is the space of anticirculants, each of which has dimension n.
The basis of the intersection of the spaces
${\mathcal {C}}_n'({\mathbb {F}})$
and
${\mathcal {C}}_n"({\mathbb {F}})$
in the odd case is the matrix in which each element equals 1, and in the even case, the basis comprises the two matrices
$$ \begin{align*} \begin{pmatrix} 1 & 0 & 1 &\cdots & 0\\ 0 & 1 & 0 &\cdots & 1\\ 1 & 0 & 1 &\cdots & 0\\ \vdots& \vdots & \vdots &\cdots & \vdots\\ 1 & 0 & 1 &\cdots & 0\\ 0 & 1 & 0 &\cdots & 1 \end{pmatrix} \quad \mbox{and}\quad \begin{pmatrix} 0 & 1 & 0 &\cdots & 1\\ 1 & 0 & 1 &\cdots & 0\\ 0 & 1 & 0 &\cdots & 1\\ \vdots& \vdots & \vdots &\cdots & \vdots\\ 0 & 1 & 0 &\cdots & 1\\ 1 & 0 & 1 &\cdots & 0 \end{pmatrix}. \end{align*} $$
Thus, the statement of the lemma follows from the formula for the dimension of the sum of subspaces.
Theorem 4.4. We have
$l({\mathcal {C}}_n({\mathbb {F}}))=n-1.$
Proof. Let us first prove the lower bound
$l({\mathcal {C}}_n({\mathbb {F}}))\geq n-1.$
Consider a generating set
${\mathcal {S}}=\{u,v\}$
, where
$u=B_n, v=A_nB_n$
. This is indeed a generating set, as
${{\mathcal {C}}_n({\mathbb {F}})={\mathcal {L}}(\{A_n,B_n\})={\mathcal {L}}(\{vu,u\})\subseteq {\mathcal {L}}(\{u,v\})\ =\ {\mathcal {L}}(\{B_n,A_nB_n\})\subseteq {\mathcal {L}}(\{A_n,B_n\}) = {\mathcal {C}}_n({\mathbb {F}})}$
. At the same time,
$u^2=v^2=E$
, meaning that there are no more than two irreducible words of each length (of the form
$uvuv\dots $
and
$vuvu\dots $
). Thus,
$\dim {\mathcal {L}}_{n-2}({\mathcal {S}})= (\dim {\mathcal {L}}_{n-2}({\mathcal {S}})\ -\ \dim {\mathcal {L}}_{n-3}({\mathcal {S}}))\ +\ (\dim {\mathcal {L}}_{n-3}({\mathcal {S}})-\dim {\mathcal {L}}_{n-4}({\mathcal {S}}))+\cdots +(\dim {\mathcal {L}}_1({\mathcal {S}})-\dim {\mathcal {L}}_0({\mathcal {S}}))+\dim {\mathcal {L}}_0({\mathcal {S}})\leq 2(n-2)+1<\dim {\mathcal {C}}_n({\mathbb {F}})$
, from which it follows that the length of the algebra is at least
$n-1$
.
The upper bound
$l({\mathcal {C}}_n({\mathbb {F}}))\leq n-1$
follows from Theorem 3.5. Indeed, by the Cayley–Hamilton theorem,
$m({\mathcal {C}}_n({\mathbb {F}}))\leq n$
. By Lemma 4.3,
$\dim {\mathcal {C}}_n({\mathbb {F}})\leq 2n-1$
. Applying Theorem 3.5, we obtain the inequality
$l({\mathcal {C}}_n({\mathbb {F}})) \leq \max \{n-1,{(2n-1)}/{2}\}$
. This completes the proof.
4.2 Bicirculant representation of
${\mathbb {F}}{\mathcal {D}}_n$
Let us number the vertices of a regular n-gon. Let
$d\in {\mathcal {D}}_n$
map the vertex i to the vertex
$\sigma (i)$
for all i, where
$\sigma \in S_n$
. Then, we can consider a group homomorphism, defining its values on elements of
${\mathcal {D}}_n$
by the rule
$f(d)=\sigma $
, and then extend it to an algebra homomorphism
$f:{\mathbb {F}}{\mathcal {D}}_n\rightarrow {\mathbb {F}} S_n$
by linearity.
Let us now consider a group homomorphism
$g: S_n \rightarrow M_n(\{0,1\})$
, which maps a permutation from
$S_n$
into the corresponding permutation matrix. We extend it to an algebra homomorphism
$g: {\mathbb {F}} S_n \rightarrow M_n({\mathbb {F}})$
by linearity.
The composition
$g\circ f$
defines a linear representation of the algebra
${\mathbb {F}}{\mathcal {D}}_n$
which we call the bicirculant representation. Let us study some properties of this composition.
Lemma 4.5. We have
${\mathrm {Im}\,} g\circ f = {\mathcal {C}}_n({\mathbb {F}})$
.
Proof. Let a be the rotation by an angle
${2\pi }/{n}$
and b be the symmetry about the axis passing through the vertex
$[{n}/{2}]+1$
. Then,
${\mathbb {F}} {\mathcal {D}}_n=\langle e, a, a^2, \ldots , a^{n-1}, b, ba, \ldots , ba^{n-1} \rangle $
.
It is easy to see that
$g\circ f(a)=A_n$
,
$g\circ f(b)=B_n$
. Since
$g\circ f$
is a homomorphism,
$g\circ f(b^ia^j)=B_n^iA_n^j$
, from which the statement of the lemma follows.
Lemma 4.6. For odd n,
$\ker g\circ f = \langle e+a+\cdots +a^{n-1}-b-ba-\cdots -ba^{n-1} \rangle $
; for even n,
$\ker g\circ f = \langle e+a^2+\cdots +a^{n-2}-b-ba^2-\cdots -ba^{n-2}, a+a^3+\cdots +a^{n-1}-ba-ba^3-\cdots -ba^{n-1}\rangle $
.
4.3 Length of
${\mathbb {F}}{\mathcal {D}}_n$
First, let us present known results about the length of
${\mathbb {F}}{\mathcal {D}}_n$
.
Lemma 4.7 [Reference Khrystik and Markova7, Lemma 2.1].
Let
${\cal D}_{n}$
be the dihedral group of order
$2n$
,
$n\geq 3$
, and
${\mathbb {F}}$
be an arbitrary field. Then,
$l({\mathbb {F}}{\cal D}_{n})\geq n$
.
Theorem 4.8 [Reference Khrystik and Markova7, Theorem 1.15].
Let
${\mathbb {F}}$
be a field such that
${\mathrm {char}\,} {\mathbb {F}}$
does not divide
$2n$
. Then,
$l({\mathbb {F}} {\cal D}_n)=n$
for
$n\geq 3$
.
Theorem 4.9 [Reference Khrystik and Markova6, Theorem 4.10].
Let
${\mathrm {char}\,} {\mathbb {F}} = 2$
,
$k\geq 2$
. Then,
$l({\mathbb {F}}{\mathcal {D}}_{2^k})=2^k$
.
We will try to generalise the last two theorems to eliminate the condition on the field. In what follows, we assume that
$n\geq 3$
.
The proof of the following lemma uses the idea from the proof of [Reference Guterman and Markova2, Lemma 3.11].
Lemma 4.10. If
$\varphi :\cal A \rightarrow \cal B$
is a surjective homomorphism of algebras, then
$$ \begin{align*} l(\mathcal A) \leq l (\mathcal B)+\dim \mathcal A -\dim \cal B. \end{align*} $$
Proof. Consider an arbitrary generating set
${\mathcal {S}}=\{a_1,\ldots ,a_k\}$
of the algebra
${\mathcal {A}}$
.
Since the homomorphism
$\varphi $
is surjective, the set
${\mathcal {S}}_{\mathcal {B}}=\{c_1=\varphi (a_1),\ldots ,c_k=\varphi (a_k)\}$
is a generating set of the algebra
$\mathcal {B}$
. Therefore,
$\dim {\mathcal {L}}_{l(\mathcal {B})}({\mathcal {S}}_{{\mathcal {B}}})=\dim {\mathcal {B}}$
. However,
${\mathcal {L}}_{l({\mathcal {B}})}({\mathcal {S}}_{{\mathcal {B}}})={\mathcal {L}}_{l({\mathcal {B}})}(\varphi ({\mathcal {S}}))=\varphi ({\mathcal {L}}_{l({\mathcal {B}})}({\mathcal {S}}))$
. Therefore,
$\dim {\mathcal {L}}_{l({\mathcal {B}})}({\mathcal {S}})\geq \dim \varphi ({\mathcal {L}}_{l({\mathcal {B}})}({\mathcal {S}}))=\dim {\mathcal {L}}_{l({\mathcal {B}})}({\mathcal {S}}_{{\mathcal {B}}})=\dim {\mathcal {B}}$
.
Since the dimensions
${\mathcal {L}}_{i}({\mathcal {S}})$
must increase with i until stabilisation, we have
$\dim {\mathcal {L}}_{l({\mathcal {B}})+\dim {\mathcal {A}} - \dim {\mathcal {B}}}({\mathcal {S}})\geq \dim {\mathcal {B}} + (\dim {\mathcal {A}} - \dim {\mathcal {B}}) = \dim {\mathcal {A}}$
. At the same time, the minimal i such that
$\dim {\mathcal {L}}_{i}({\mathcal {S}}) = \dim {\mathcal {A}}$
, by definition, is
$l({\mathcal {S}})$
. Due to the arbitrariness of
${\mathcal {S}}$
, we obtain
$l(\mathcal A) \leq l (\mathcal B)+\dim \mathcal A -\dim \cal B$
.
Theorem 4.11. Let
${\cal D}_{n}$
be the dihedral group of order
$2n$
,
$n\geq 3$
, and
${\mathbb {F}}$
be an arbitrary field. Then:
-
(1)
$l({\mathbb {F}}{\cal D}_{n})=n$
for odd n; -
(2)
$n \leq l({\mathbb {F}}{\cal D}_{n}) \leq n+1$
for even n.
Proof. The lower bound is given by Lemma 4.7. Let us prove the upper bound.
From Theorem 4.4, it follows that
$l({\mathcal {C}}_n({\mathbb {F}}))=n-1$
. From Lemma 4.3, it follows that
$\dim {\mathcal {C}}_n({\mathbb {F}})=2n-1$
for odd n,
$\dim {\mathcal {C}}_n({\mathbb {F}})=2n-2$
for even n. Consider the homomorphism of algebras
$g \circ f : {\mathbb {F}} \mathcal {D}_n \rightarrow {\mathcal {C}}_n({\mathbb {F}})$
, described in Section 4.2. Since by Lemma 4.5 the homomorphism
$g \circ f$
is surjective, we can apply Lemma 4.10 and get the upper bound
$l({\mathbb {F}} \mathcal {D}_n) \leq l ({\mathcal {C}}_n({\mathbb {F}}))+\dim {\mathbb {F}} \mathcal {D}_n -\dim {\mathcal {C}}_n({\mathbb {F}})$
. Then, application of Theorem 4.4, Lemma 4.3 and the fact that
$\dim {\mathbb {F}} \mathcal {D}_n = 2n$
completes the proof.
Remark 4.12. We have shown that the only possible values of
$l({\mathbb {F}}{\cal D}_{n})$
are n and
$n+1$
. However, no examples of algebras with length
$n+1$
have been found (and are not expected given Theorem 4.8). The technique developed in this paper allows finding the exact value only for odd n, but the result is a noticeable advancement in the study of the lengths of group algebras of dihedral groups, demonstrating the usefulness of the bound proven in Theorem 3.5 and the bicirculant representation.
4.4 Bound for
$m({\mathbb {F}}{\cal D}_{n})$
Using the bicirculant representation, we get an estimate of
$m({\mathbb {F}}{\cal D}_{n})$
.
Theorem 4.13. Let
${\cal D}_{n}$
be the dihedral group of order
$2n$
,
$n\geq 3$
, and
${\mathbb {F}}$
be an arbitrary field. Then,
$$ \begin{align*}m({\mathbb{F}}{\cal D}_{n})\leq \begin{cases} n+1\ \mbox{for odd}\; n;\\ n+2 \ \mbox{for even}\; n. \end{cases}\end{align*} $$
Proof. Let
$\tau \in {\mathbb {F}}{\cal D}_{n}$
,
$g \circ f : {\mathbb {F}} \mathcal {D}_n \rightarrow {\mathcal {C}}_n({\mathbb {F}})$
be the homomorphism of algebras described in Section 4.2, using the rotation a by an angle
${2\pi }/{n}$
and the symmetry b.
Let
$g \circ f(\tau ) = T \in M_n({\mathbb {F}})$
. Then, by the Cayley–Hamilton theorem,
$m(T)=\deg \mu _T(x) \leq n$
. Since
$g \circ f(\mu _{T}(\tau ))=\mu _T(T)=0$
, we get
$\mu _{T}(\tau ) \in \ker g \circ f$
. Next, consider two cases separately.
Case 1: n is odd. From Lemma 4.6, it follows that
$\ker g \circ f$
is one-dimensional. However, the kernel of a homomorphism of algebras is an ideal, which means
$\mu _{T}(\tau )$
and
$\mu _{T}(\tau )\tau $
are linearly dependent. Thus,
$m({\mathbb {F}}{\cal D}_{n})\leq n+1$
.
Case 2: n is even. From Lemma 4.6, it follows that
$\ker g \circ f$
is two-dimensional. However, the kernel of a homomorphism of algebras is an ideal, which means
$\mu _{T}(\tau )$
,
$\mu _{T}(\tau )\tau $
and
$\mu _{T}(\tau )\tau ^2$
are linearly dependent. Thus,
$m({\mathbb {F}}{\cal D}_{n})\leq n+2$
.
Remark 4.14. The main conjecture regarding the lengths of group algebras in the case of dihedral groups is that
$l({\mathbb {F}}{\cal D}_{n})=n$
for all
$n\geq 3$
over an arbitrary field. Due to Theorem 3.5, to prove the conjecture, it is sufficient to obtain an estimate
$m({\mathbb {F}}{\cal D}_{n})\leq n+1$
. However, using an estimate from Theorem 4.13, we get the same result as presented in Theorem 4.11. Nevertheless, estimating
$m({\mathbb {F}}{\cal D}_{n})$
allows us to demonstrate another application of Theorem 3.5 and the bicirculant representation, and the study of numerical characteristics of algebras is of interest in itself.
