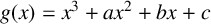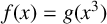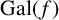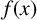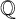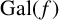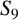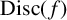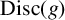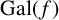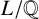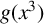1 Introduction
Let
![]() $\mathbb {Q}$
denote the rational numbers and consider an irreducible polynomial
$\mathbb {Q}$
denote the rational numbers and consider an irreducible polynomial
![]() $f(x)\in \mathbb {Q}[x]$
. An important problem in computational algebra is the determination of the Galois group,
$f(x)\in \mathbb {Q}[x]$
. An important problem in computational algebra is the determination of the Galois group,
![]() $ {\mathrm{Gal}}(f)$
, of
$ {\mathrm{Gal}}(f)$
, of
![]() $f(x)$
. Standard techniques for doing so involve forming and factoring resolvent polynomials, which are polynomials that define subfields of the splitting field of
$f(x)$
. Standard techniques for doing so involve forming and factoring resolvent polynomials, which are polynomials that define subfields of the splitting field of
![]() $f(x)$
(see [Reference Soicher14, Reference Stauduhar15]). In general, forming and factoring resolvent polynomials is a difficult task. However, in the special case where
$f(x)$
(see [Reference Soicher14, Reference Stauduhar15]). In general, forming and factoring resolvent polynomials is a difficult task. However, in the special case where
![]() $f(x)=g(x^k)$
for some integer
$f(x)=g(x^k)$
for some integer
![]() $k>1$
, it is often possible to compute the Galois group via more elementary methods. Previous results in this direction have produced elementary characterisations for
$k>1$
, it is often possible to compute the Galois group via more elementary methods. Previous results in this direction have produced elementary characterisations for
![]() $ {\mathrm{Gal}}(f)$
in the following cases:
$ {\mathrm{Gal}}(f)$
in the following cases:
-
•
 $k=2$
and
$k=2$
and
 $g(x) = x^2+ax+b$
(see [Reference Kappe and Warren13]);
$g(x) = x^2+ax+b$
(see [Reference Kappe and Warren13]); -
•
 $k=3$
and
$k=3$
and
 $g(x) = x^2+ax+b$
(see [Reference Awtrey, Beuerle and Griesbach1]);
$g(x) = x^2+ax+b$
(see [Reference Awtrey, Beuerle and Griesbach1]); -
•
 $k=4$
and
$k=4$
and
 $g(x) = x^2+ax+b$
(see [Reference Awtrey and Patane3]);
$g(x) = x^2+ax+b$
(see [Reference Awtrey and Patane3]); -
•
 $k=2$
and
$k=2$
and
 $g(x) = x^3+ax^2+bx+c$
(see [Reference Awtrey and Jakes2]).
$g(x) = x^3+ax^2+bx+c$
(see [Reference Awtrey and Jakes2]).
The purpose of this paper is to give a similar characterisation for the case
![]() $k=3$
and
$k=3$
and
![]() $g(x)=x^3+ax^2+bx+c$
. Such polynomials are of the form
$g(x)=x^3+ax^2+bx+c$
. Such polynomials are of the form
![]() $f(x) =x^9+ax^6+bx^3+c$
, and we call them power compositional nonic polynomials, in accordance with [Reference Harrington and Jones9]. Further, we give an algorithm to determine when an extension
$f(x) =x^9+ax^6+bx^3+c$
, and we call them power compositional nonic polynomials, in accordance with [Reference Harrington and Jones9]. Further, we give an algorithm to determine when an extension
![]() $L/\mathbb {Q}$
can be defined by a power compositional polynomial of the form
$L/\mathbb {Q}$
can be defined by a power compositional polynomial of the form
![]() $f(x)=g(x^3)$
. This is similar in spirit to what was done in [Reference Awtrey, Beuerle and Griesbach1], where the focus was on the special case where the degree of
$f(x)=g(x^3)$
. This is similar in spirit to what was done in [Reference Awtrey, Beuerle and Griesbach1], where the focus was on the special case where the degree of
![]() $g(x)$
was 2. An implementation of our algorithm is available at [Reference Awtrey, Patane and Toone4].
$g(x)$
was 2. An implementation of our algorithm is available at [Reference Awtrey, Patane and Toone4].
The remainder of the paper is organised as follows. In Section 2, we give a formula for discriminants of general power compositional polynomials of the form
![]() $f(x)=g(x^n)$
, where the degree of
$f(x)=g(x^n)$
, where the degree of
![]() $g(x)$
is m. In the subsequent sections, we restrict our attention to irreducible polynomials
$g(x)$
is m. In the subsequent sections, we restrict our attention to irreducible polynomials
![]() $f(x) = g(x^3)$
, where
$f(x) = g(x^3)$
, where
![]() $g(x)=x^3+ax^2+bx+c$
. In Section 3, we establish notation, and recall two basic results about Galois groups of cubic polynomials and the relationship between
$g(x)=x^3+ax^2+bx+c$
. In Section 3, we establish notation, and recall two basic results about Galois groups of cubic polynomials and the relationship between
![]() $ {\mathrm{Gal}}(f)$
and
$ {\mathrm{Gal}}(f)$
and
![]() $ {\mathrm{Disc}}(f)$
, the discriminant of
$ {\mathrm{Disc}}(f)$
, the discriminant of
![]() $f(x)$
. We end by establishing bounds on the degree of the splitting field of
$f(x)$
. We end by establishing bounds on the degree of the splitting field of
![]() $f(x)$
as well as the Galois group of the relative extension
$f(x)$
as well as the Galois group of the relative extension
![]() $L/K$
, where L and K are the fields defined by
$L/K$
, where L and K are the fields defined by
![]() $f(x)$
and
$f(x)$
and
![]() $g(x)$
, respectively. The purpose of Section 4 is to develop a list of possibilities for
$g(x)$
, respectively. The purpose of Section 4 is to develop a list of possibilities for
![]() $ {\mathrm{Gal}}(f)$
, defined up to conjugacy in
$ {\mathrm{Gal}}(f)$
, defined up to conjugacy in
![]() $S_9$
(the symmetric group of degree 9). The list includes 11 possible groups, and we show that each one is realised as a Galois group over
$S_9$
(the symmetric group of degree 9). The list includes 11 possible groups, and we show that each one is realised as a Galois group over
![]() $\mathbb {Q}$
of an irreducible power compositional nonic polynomial. In Section 5, we develop a characterisation of
$\mathbb {Q}$
of an irreducible power compositional nonic polynomial. In Section 5, we develop a characterisation of
![]() $ {\mathrm{Gal}}(f)$
that involves the squareness of
$ {\mathrm{Gal}}(f)$
that involves the squareness of
![]() $ {\mathrm{Disc}}(f)$
and
$ {\mathrm{Disc}}(f)$
and
![]() $ {\mathrm{Disc}}(g)$
as well as the factorisation pattern of a related degree 9 resolvent polynomial. These three pieces of information are enough to determine
$ {\mathrm{Disc}}(g)$
as well as the factorisation pattern of a related degree 9 resolvent polynomial. These three pieces of information are enough to determine
![]() $ {\mathrm{Gal}}(f)$
in 9 out of 11 cases. For the other two cases, we use a standard linear resolvent (following [Reference Soicher14]). This section culminates in our main result, Theorem 5.5. In the following section, we give several examples that illustrate the use of Theorem 5.5. Example 6.1 recovers the characterisation in [Reference Jones and Phillips11] that
$ {\mathrm{Gal}}(f)$
in 9 out of 11 cases. For the other two cases, we use a standard linear resolvent (following [Reference Soicher14]). This section culminates in our main result, Theorem 5.5. In the following section, we give several examples that illustrate the use of Theorem 5.5. Example 6.1 recovers the characterisation in [Reference Jones and Phillips11] that
![]() $ {\mathrm{Gal}}(x^9+9mx^6+192m^3)$
is isomorphic to the dihedral group of order 18 for all
$ {\mathrm{Gal}}(x^9+9mx^6+192m^3)$
is isomorphic to the dihedral group of order 18 for all
![]() $m\neq 0$
. In addition, Table 5 gives one-parameter families with a given Galois group, where the verification that each polynomial in a given family has the associated Galois group follows from Theorem 5.5; Examples 6.2 and 6.3 illustrate this. We end with Section 7, which is devoted to describing an algorithm that, given an extension
$m\neq 0$
. In addition, Table 5 gives one-parameter families with a given Galois group, where the verification that each polynomial in a given family has the associated Galois group follows from Theorem 5.5; Examples 6.2 and 6.3 illustrate this. We end with Section 7, which is devoted to describing an algorithm that, given an extension
![]() $L/\mathbb {Q}$
, constructs an irreducible power compositional polynomial of the form
$L/\mathbb {Q}$
, constructs an irreducible power compositional polynomial of the form
![]() $g(x^3)$
that defines L when such a polynomial exists; we make no restrictions on the degree of
$g(x^3)$
that defines L when such a polynomial exists; we make no restrictions on the degree of
![]() $g(x)$
.
$g(x)$
.
Note. While we are assuming all polynomials have rational coefficients, this is only for concreteness. Our proofs are valid for polynomials defined over any finite extension of
![]() $\mathbb {Q}$
that does not contain the cube roots of unity. With minor modifications, the results also apply more generally, including all fields of characteristic 0.
$\mathbb {Q}$
that does not contain the cube roots of unity. With minor modifications, the results also apply more generally, including all fields of characteristic 0.
2 Discriminants of power compositional polynomials
In this section, we give a formula for the discriminant of a polynomial of the form
![]() $g(x^n)$
that we will use later. We note that our result is a special case of [Reference Harrington and Jones10, Theorem 2.7], but our method of proof is different.
$g(x^n)$
that we will use later. We note that our result is a special case of [Reference Harrington and Jones10, Theorem 2.7], but our method of proof is different.
For complete generality, we let K be a field,
![]() $\overline {K}$
an algebraic closure of K,
$\overline {K}$
an algebraic closure of K,
![]() $f(x)\in K[x]$
a monic polynomial of degree n,
$f(x)\in K[x]$
a monic polynomial of degree n,
![]() $R_f$
the set of roots of
$R_f$
the set of roots of
![]() $f(x)$
in
$f(x)$
in
![]() $\overline {K}$
and
$\overline {K}$
and
![]() $f'(x)$
the derivative of
$f'(x)$
the derivative of
![]() $f(x)$
. Recall that the discriminant of
$f(x)$
. Recall that the discriminant of
![]() $f(x)$
, which we denote by
$f(x)$
, which we denote by
![]() $ {\mathrm{Disc}}(f)$
, can be computed as follows (see for example [Reference Cohen6, Section 3.3]):
$ {\mathrm{Disc}}(f)$
, can be computed as follows (see for example [Reference Cohen6, Section 3.3]):
 $$ \begin{align*} {\mathrm{Disc}}(f) = (-1)^{n(n-1)/2} \prod_{\rho\in R_f} f'(\rho). \end{align*} $$
$$ \begin{align*} {\mathrm{Disc}}(f) = (-1)^{n(n-1)/2} \prod_{\rho\in R_f} f'(\rho). \end{align*} $$
Lemma 2.1. Let K be a field and
![]() $f(x)\in K[x]$
a monic polynomial, where
$f(x)\in K[x]$
a monic polynomial, where
![]() $f(x) = g(x^n)$
and
$f(x) = g(x^n)$
and
![]() $g(x)\in K[x]$
is monic of degree m. Let
$g(x)\in K[x]$
is monic of degree m. Let
![]() $c = f(0)$
. Then,
$c = f(0)$
. Then,
Proof. Let
![]() $R_f$
and
$R_f$
and
![]() $R_g$
denote the roots of
$R_g$
denote the roots of
![]() $f(x)$
and
$f(x)$
and
![]() $g(x)$
in an algebraic closure
$g(x)$
in an algebraic closure
![]() $\overline {K}$
, respectively. Let
$\overline {K}$
, respectively. Let
![]() $\zeta \in \overline {K}$
be a primitive nth root of unity. Thus, there exist
$\zeta \in \overline {K}$
be a primitive nth root of unity. Thus, there exist
![]() $\rho _1,\ldots , \rho _m \in \overline {K}$
such that
$\rho _1,\ldots , \rho _m \in \overline {K}$
such that
![]() $R_f = \{ \rho _i\zeta ^j : 1\leq i\leq m, 0\leq j\leq n-1\}$
and
$R_f = \{ \rho _i\zeta ^j : 1\leq i\leq m, 0\leq j\leq n-1\}$
and
![]() $R_g = \{\rho _1^n, \ldots , \rho _m^n\}$
. We note that
$R_g = \{\rho _1^n, \ldots , \rho _m^n\}$
. We note that
 $$ \begin{align*} c = f(0) = (-1)^{nm} \prod_{\rho\in R_f} \rho.\end{align*} $$
$$ \begin{align*} c = f(0) = (-1)^{nm} \prod_{\rho\in R_f} \rho.\end{align*} $$
We define
![]() $d_f$
and
$d_f$
and
![]() $d_g$
by
$d_g$
by
 $$ \begin{align*} d_f = \prod_{\rho\in R_f} g'(\rho^n), \quad d_g = \prod_{\rho\in R_g} g'(\rho). \end{align*} $$
$$ \begin{align*} d_f = \prod_{\rho\in R_f} g'(\rho^n), \quad d_g = \prod_{\rho\in R_g} g'(\rho). \end{align*} $$
Since the map
![]() $R_f$
to
$R_f$
to
![]() $R_g$
defined by
$R_g$
defined by
![]() $x\mapsto x^n$
is n-to-one, we have
$x\mapsto x^n$
is n-to-one, we have
![]() $d_f = d_g^n$
. Further,
$d_f = d_g^n$
. Further,
 $$ \begin{align*} {\mathrm{Disc}}(g) = (-1)^{m(m-1)/2} \prod_{\rho\in R_g} g'(\rho) = (-1)^{m(m-1)/2} d_g. \end{align*} $$
$$ \begin{align*} {\mathrm{Disc}}(g) = (-1)^{m(m-1)/2} \prod_{\rho\in R_g} g'(\rho) = (-1)^{m(m-1)/2} d_g. \end{align*} $$
We can therefore conclude that
Using the chain rule, we see that
![]() $f'(x) = nx^{n-1}g'(x^n)$
. Therefore, the discriminant of
$f'(x) = nx^{n-1}g'(x^n)$
. Therefore, the discriminant of
![]() $f(x)$
is
$f(x)$
is
 $$ \begin{align*} {\mathrm{Disc}}(f) &= (-1)^{nm(nm-1)/2} \prod_{\rho\in R_f} f'(\rho) = (-1)^{nm(nm-1)/2} \prod_{\rho\in R_f} (n\cdot \rho^{n-1}\cdot g'(\rho^n)) \\ &= (-1)^{nm(nm-1)/2} \bigg(\prod_{\rho\in R_f} n \bigg) \bigg(\prod_{\rho\in R_f} \rho^{n-1} \bigg) \bigg(\prod_{\rho\in R_f} g'(\rho^n) \bigg) \\ &= (-1)^{nm(nm-1)/2} \cdot n^{nm} \cdot (-1)^{nm(n-1)}\cdot c^{n-1} \cdot d_f \\ &= (-1)^{nm(nm-2n-3)/2} \cdot n^{nm} \cdot c^{n-1} \cdot d_g^n \\ &= (-1)^{nm(n-1)(m+2)/2} \cdot n^{nm} \cdot c^{n-1} \cdot {\mathrm{Disc}}(g)^n.\\[-2.7pc] \end{align*} $$
$$ \begin{align*} {\mathrm{Disc}}(f) &= (-1)^{nm(nm-1)/2} \prod_{\rho\in R_f} f'(\rho) = (-1)^{nm(nm-1)/2} \prod_{\rho\in R_f} (n\cdot \rho^{n-1}\cdot g'(\rho^n)) \\ &= (-1)^{nm(nm-1)/2} \bigg(\prod_{\rho\in R_f} n \bigg) \bigg(\prod_{\rho\in R_f} \rho^{n-1} \bigg) \bigg(\prod_{\rho\in R_f} g'(\rho^n) \bigg) \\ &= (-1)^{nm(nm-1)/2} \cdot n^{nm} \cdot (-1)^{nm(n-1)}\cdot c^{n-1} \cdot d_f \\ &= (-1)^{nm(nm-2n-3)/2} \cdot n^{nm} \cdot c^{n-1} \cdot d_g^n \\ &= (-1)^{nm(n-1)(m+2)/2} \cdot n^{nm} \cdot c^{n-1} \cdot {\mathrm{Disc}}(g)^n.\\[-2.7pc] \end{align*} $$
3 Notation and preliminary results
For the rest of this paper, we fix the following notation:
-
•
 $f(x) = x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
, irreducible;
$f(x) = x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
, irreducible; -
•
 $g(x) = x^3+ax^2+bx+c$
;
$g(x) = x^3+ax^2+bx+c$
; -
•
 $\zeta $
a primitive cube root of unity (that is, a root of
$\zeta $
a primitive cube root of unity (that is, a root of
 $x^2+x+1$
);
$x^2+x+1$
); -
•
 $S_n$
the symmetric group of degree n;
$S_n$
the symmetric group of degree n; -
•
 $A_n$
the alternating group of degree n;
$A_n$
the alternating group of degree n; -
•
 $ {\mathrm{Gal}}(h)$
the Galois group of a polynomial
$ {\mathrm{Gal}}(h)$
the Galois group of a polynomial
 $h(x)$
, where the base field will be clear from context.
$h(x)$
, where the base field will be clear from context.
It follows that the complex roots of
![]() $f(x)$
are
$f(x)$
are
where
![]() $\alpha ^3, \beta ^3, \gamma ^3$
are the roots of
$\alpha ^3, \beta ^3, \gamma ^3$
are the roots of
![]() $g(x)$
. From Lemma 2.1,
$g(x)$
. From Lemma 2.1,
This leads to the following results.
Corollary 3.1. Suppose
![]() $f(x)=x^9+ax^6+bx^3+c$
is irreducible over
$f(x)=x^9+ax^6+bx^3+c$
is irreducible over
![]() $\mathbb {Q}$
. Then,
$\mathbb {Q}$
. Then,
![]() $ {\mathrm{Disc}}(f) \in \mathbb {Q}^2$
if and only if
$ {\mathrm{Disc}}(f) \in \mathbb {Q}^2$
if and only if
![]() $-3 {\mathrm{Disc}}(g) \in \mathbb {Q}^2$
.
$-3 {\mathrm{Disc}}(g) \in \mathbb {Q}^2$
.
We recall two facts about discriminants and Galois groups (see for example [Reference Dummit and Foote8, Section 14.6]).
-
(1) For any irreducible polynomial
 $\tilde {g}(x) \in \mathbb {Q}[x]$
of degree n,
$\tilde {g}(x) \in \mathbb {Q}[x]$
of degree n,
 $ {\mathrm{Gal}}(\tilde {g})$
is isomorphic to a subgroup of
$ {\mathrm{Gal}}(\tilde {g})$
is isomorphic to a subgroup of
 $A_n$
if and only if
$A_n$
if and only if
 $ {\mathrm{Disc}}(\tilde {g}) \in \mathbb {Q}^2$
.
$ {\mathrm{Disc}}(\tilde {g}) \in \mathbb {Q}^2$
. -
(2) If F is any field of characteristic 0 and
 $\tilde {g}(x) \in F[x]$
is irreducible of degree 3, then
$\tilde {g}(x) \in F[x]$
is irreducible of degree 3, then
 $ {\mathrm{Gal}}(\tilde {g})$
over F is isomorphic to
$ {\mathrm{Gal}}(\tilde {g})$
over F is isomorphic to
 $A_3$
(cyclic of order 3) if
$A_3$
(cyclic of order 3) if
 $ {\mathrm{Disc}}({\tilde {g}}) \in F^2$
and is isomorphic to
$ {\mathrm{Disc}}({\tilde {g}}) \in F^2$
and is isomorphic to
 $S_3$
if
$S_3$
if
 $ {\mathrm{Disc}}(\tilde {g}) \notin F^2$
.
$ {\mathrm{Disc}}(\tilde {g}) \notin F^2$
.
Combining item (2) above with Corollary 3.1 yields the following result.
Corollary 3.2. Suppose
![]() $f(x)=x^9+ax^6+bx^3+c$
is irreducible over
$f(x)=x^9+ax^6+bx^3+c$
is irreducible over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $g(x)=x^3+ax^2+bx+c$
. If
$g(x)=x^3+ax^2+bx+c$
. If
![]() $ {\mathrm{Gal}}(g)$
is cyclic of order 3 (that is,
$ {\mathrm{Gal}}(g)$
is cyclic of order 3 (that is,
![]() $A_3$
), then
$A_3$
), then
![]() $ {\mathrm{Disc}}(f) \notin \mathbb {Q}^2$
.
$ {\mathrm{Disc}}(f) \notin \mathbb {Q}^2$
.
Let L denote the splitting field of
![]() $f(x)$
over
$f(x)$
over
![]() $\mathbb {Q}$
. Thus,
$\mathbb {Q}$
. Thus,
![]() $L = \mathbb {Q}(\alpha ,\beta ,\gamma ,\zeta )$
. Since
$L = \mathbb {Q}(\alpha ,\beta ,\gamma ,\zeta )$
. Since
![]() ${[\mathbb {Q}(\alpha ) : \mathbb {Q}] = 9}$
and
${[\mathbb {Q}(\alpha ) : \mathbb {Q}] = 9}$
and
![]() $[\mathbb {Q}(\zeta ):\mathbb {Q}]=2$
, we see that
$[\mathbb {Q}(\zeta ):\mathbb {Q}]=2$
, we see that
![]() $[L:\mathbb {Q}]\geq 18$
. Let K denote the splitting field of
$[L:\mathbb {Q}]\geq 18$
. Let K denote the splitting field of
![]() $g(x)$
. Thus,
$g(x)$
. Thus,
![]() $K = \mathbb {Q}(\alpha ^3,\sqrt { {\mathrm{Disc}}(g)})$
, and we have
$K = \mathbb {Q}(\alpha ^3,\sqrt { {\mathrm{Disc}}(g)})$
, and we have
![]() $\beta ^3,\gamma ^3\in K$
as well. We note further that
$\beta ^3,\gamma ^3\in K$
as well. We note further that
![]() $[K:\mathbb {Q}]\leq 6$
and, therefore,
$[K:\mathbb {Q}]\leq 6$
and, therefore,
![]() $[K(\zeta ):\mathbb {Q}] \leq 12$
. It follows that for each
$[K(\zeta ):\mathbb {Q}] \leq 12$
. It follows that for each
![]() $\rho \in \{\alpha ,\beta ,\gamma \}$
, we have
$\rho \in \{\alpha ,\beta ,\gamma \}$
, we have
![]() $[K(\rho ,\zeta ): K(\zeta )] \leq 3$
. We have therefore established the following result.
$[K(\rho ,\zeta ): K(\zeta )] \leq 3$
. We have therefore established the following result.
Lemma 3.3. Suppose
![]() $f(x)=x^9+ax^6+bx^3+c$
is irreducible over
$f(x)=x^9+ax^6+bx^3+c$
is irreducible over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $L/\mathbb {Q}$
denote its splitting field. Then,
$L/\mathbb {Q}$
denote its splitting field. Then,
![]() $18 \leq [L:\mathbb {Q}] \leq 324$
.
$18 \leq [L:\mathbb {Q}] \leq 324$
.
We turn our attention to the relative extension
![]() $\mathbb {Q}(\alpha )/\mathbb {Q}(\alpha ^3)$
. Factoring
$\mathbb {Q}(\alpha )/\mathbb {Q}(\alpha ^3)$
. Factoring
![]() $f(x)$
over
$f(x)$
over
![]() $\mathbb {Q}(\alpha ^3)$
, we obtain the factorisation
$\mathbb {Q}(\alpha ^3)$
, we obtain the factorisation
which can be verified by expanding the factored expression and using the fact that
![]() $f(\alpha )=0$
so that
$f(\alpha )=0$
so that
![]() $c = -\alpha ^9-a\alpha ^6-b\alpha ^3$
. It follows that
$c = -\alpha ^9-a\alpha ^6-b\alpha ^3$
. It follows that
![]() $x^3-\alpha ^3$
is irreducible, for if it were not, then this would contradict the fact that
$x^3-\alpha ^3$
is irreducible, for if it were not, then this would contradict the fact that
![]() $[\mathbb {Q}(\alpha ):\mathbb {Q}] = 9$
, thereby contradicting the irreducibility of
$[\mathbb {Q}(\alpha ):\mathbb {Q}] = 9$
, thereby contradicting the irreducibility of
![]() $f(x)$
. It therefore also follows that
$f(x)$
. It therefore also follows that
![]() $x^3-\alpha ^3$
defines the relative extension
$x^3-\alpha ^3$
defines the relative extension
![]() $\mathbb {Q}(\alpha )/\mathbb {Q}(\alpha ^3)$
. The following result will be useful in the determination of
$\mathbb {Q}(\alpha )/\mathbb {Q}(\alpha ^3)$
. The following result will be useful in the determination of
![]() $ {\mathrm{Gal}}(f)$
.
$ {\mathrm{Gal}}(f)$
.
Lemma 3.4. Suppose
![]() $f(x)=x^9+ax^6+bx^3+c$
is irreducible over
$f(x)=x^9+ax^6+bx^3+c$
is irreducible over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $f(\alpha )=0$
. Then,
$f(\alpha )=0$
. Then,
![]() $ {\mathrm{Gal}}(x^3-\alpha ^3)$
over
$ {\mathrm{Gal}}(x^3-\alpha ^3)$
over
![]() $\mathbb {Q}(\alpha ^3)$
is isomorphic to
$\mathbb {Q}(\alpha ^3)$
is isomorphic to
![]() $S_3$
, the symmetric group of degree 3.
$S_3$
, the symmetric group of degree 3.
Proof. Let
![]() $\tilde {f} = x^3-\alpha ^3$
. Since
$\tilde {f} = x^3-\alpha ^3$
. Since
![]() $\tilde {f}$
is irreducible over
$\tilde {f}$
is irreducible over
![]() $\mathbb {Q}(\alpha ^3)$
, we have already mentioned that
$\mathbb {Q}(\alpha ^3)$
, we have already mentioned that
![]() $ {\mathrm{Gal}}(\tilde {f})$
is isomorphic to
$ {\mathrm{Gal}}(\tilde {f})$
is isomorphic to
![]() $S_3$
if and only if
$S_3$
if and only if
![]() $ {\mathrm{Disc}}(\tilde {f}) \notin \mathbb {Q}(\alpha ^3)^2$
. Since
$ {\mathrm{Disc}}(\tilde {f}) \notin \mathbb {Q}(\alpha ^3)^2$
. Since
![]() $ {{\mathrm{Disc}}(\tilde {f}) = -27\alpha ^6}$
, we have
$ {{\mathrm{Disc}}(\tilde {f}) = -27\alpha ^6}$
, we have
![]() $ {\mathrm{Disc}}(\tilde {f}) \notin \mathbb {Q}(\alpha ^3)^2$
since
$ {\mathrm{Disc}}(\tilde {f}) \notin \mathbb {Q}(\alpha ^3)^2$
since
![]() $-3\notin \mathbb {Q}(\alpha ^3)^2$
(since
$-3\notin \mathbb {Q}(\alpha ^3)^2$
(since
![]() $[\mathbb {Q}(\alpha ^3):\mathbb {Q}] = 3$
and therefore does not contain the quadratic extension
$[\mathbb {Q}(\alpha ^3):\mathbb {Q}] = 3$
and therefore does not contain the quadratic extension
![]() $\mathbb {Q}(\sqrt {-3})$
).
$\mathbb {Q}(\sqrt {-3})$
).
4 Possible Galois groups
Since
![]() $f(x)$
is irreducible of degree 9,
$f(x)$
is irreducible of degree 9,
![]() $\text {Gal}(f)$
can be realised as a transitive subgroup of
$\text {Gal}(f)$
can be realised as a transitive subgroup of
![]() $S_9$
, the symmetric group of degree 9; it is well defined up to conjugation as different orderings of the roots correspond to conjugate groups.
$S_9$
, the symmetric group of degree 9; it is well defined up to conjugation as different orderings of the roots correspond to conjugate groups.
There are 34 such transitive subgroups, and they can be accessed with GAP [16] or at the L-functions and Modular Forms Database [17]. We use the standard ‘T-number’ notation to identify transitive groups as given in [Reference Butler and McKay5]. For example, 9T1 represents cyclic groups of order 9 and 9T34 represents
![]() $S_9$
. See Table 1, which gives several pieces of information about representatives of conjugacy classes of transitive subgroups of
$S_9$
. See Table 1, which gives several pieces of information about representatives of conjugacy classes of transitive subgroups of
![]() $S_9$
.
$S_9$
.
Table 1 Transitive subgroups of
![]() $S_9$
by T-number, order, parity and subfield information, as defined in Section 4.
$S_9$
by T-number, order, parity and subfield information, as defined in Section 4.

Specifically, let G be a representative from one of these conjugacy classes. Then, the table gives the following information:
-
• the T-number of G;
-
• the order of G;
-
• the parity of G; the parity is
 $+1$
if
$+1$
if
 $G \leq A_9$
and
$G \leq A_9$
and
 $-1$
otherwise;
$-1$
otherwise; -
• the subfields of G.
The subfields of G are identified as follows. Let
![]() $G_1$
denote the stabiliser of 1 in G. For each subgroup H of G of index 3 containing
$G_1$
denote the stabiliser of 1 in G. For each subgroup H of G of index 3 containing
![]() $G_1$
up to conjugacy, we compute the action of G on the cosets
$G_1$
up to conjugacy, we compute the action of G on the cosets
![]() $G/H$
and the action of H on the cosets
$G/H$
and the action of H on the cosets
![]() $H/G_1$
, and we identify each action as a transitive subgroup of
$H/G_1$
, and we identify each action as a transitive subgroup of
![]() $S_3$
. We are justified in calling this list the ‘subfields’ of G for the following reason: if
$S_3$
. We are justified in calling this list the ‘subfields’ of G for the following reason: if
![]() $ {\mathrm{Gal}}(f)$
is isomorphic to G and
$ {\mathrm{Gal}}(f)$
is isomorphic to G and
![]() $f(\alpha )=0$
, then
$f(\alpha )=0$
, then
![]() $G_1$
corresponds to
$G_1$
corresponds to
![]() $\mathbb {Q}(\alpha )$
under the Galois correspondence and the nontrivial proper subfields
$\mathbb {Q}(\alpha )$
under the Galois correspondence and the nontrivial proper subfields
![]() $\mathbb {Q}(\alpha )$
correspond to the proper subgroups H properly containing
$\mathbb {Q}(\alpha )$
correspond to the proper subgroups H properly containing
![]() $G_1$
; conjugate subgroups correspond to isomorphic subfields. For each such subgroup H, let K denote its fixed field. Let the irreducible cubic polynomials
$G_1$
; conjugate subgroups correspond to isomorphic subfields. For each such subgroup H, let K denote its fixed field. Let the irreducible cubic polynomials
![]() $g(x)$
and
$g(x)$
and
![]() $\tilde {g}(x)$
define
$\tilde {g}(x)$
define
![]() $K/\mathbb {Q}$
and
$K/\mathbb {Q}$
and
![]() $\mathbb {Q}(\alpha )/K$
, respectively. Then, by the Galois correspondence,
$\mathbb {Q}(\alpha )/K$
, respectively. Then, by the Galois correspondence,
![]() $ {\mathrm{Gal}}(g)$
and
$ {\mathrm{Gal}}(g)$
and
![]() $ {\mathrm{Gal}}(\tilde {g})$
are isomorphic to the actions of G on
$ {\mathrm{Gal}}(\tilde {g})$
are isomorphic to the actions of G on
![]() $G/H$
and H on
$G/H$
and H on
![]() $H/G_1$
, respectively. Each entry in this column of the table is of the form
$H/G_1$
, respectively. Each entry in this column of the table is of the form
![]() $[i,j]$
, where
$[i,j]$
, where
![]() $ {\mathrm{Gal}}(g)$
is isomorphic to 3Ti and
$ {\mathrm{Gal}}(g)$
is isomorphic to 3Ti and
![]() $ {\mathrm{Gal}}(\tilde {g})$
is isomorphic to 3Tj; there is an entry for each such subgroup H (up to conjugacy). This is slightly more general than what is listed at [17], which only includes the transitive number for
$ {\mathrm{Gal}}(\tilde {g})$
is isomorphic to 3Tj; there is an entry for each such subgroup H (up to conjugacy). This is slightly more general than what is listed at [17], which only includes the transitive number for
![]() $ {\mathrm{Gal}}(g)$
for each subfield
$ {\mathrm{Gal}}(g)$
for each subfield
![]() $K/\mathbb {Q}$
.
$K/\mathbb {Q}$
.
Proposition 4.1. Suppose
![]() $f(x)=x^9+ax^6+bx^3+c$
is irreducible over
$f(x)=x^9+ax^6+bx^3+c$
is irreducible over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $g(x)=x^3+ax^2+bx+c$
. If
$g(x)=x^3+ax^2+bx+c$
. If
![]() $G = {\mathrm{Gal}}(f)$
, then G is isomorphic to 9Tj for some
$G = {\mathrm{Gal}}(f)$
, then G is isomorphic to 9Tj for some
![]() ${j\in \{3, 4, 5, 8, 10, 11, 13, 18, 21, 22, 24\}}$
.
${j\in \{3, 4, 5, 8, 10, 11, 13, 18, 21, 22, 24\}}$
.
Proof. We make use of Table 1. By Lemma 3.3, the order of G is bounded between 18 and 324. This rules out
![]() $j=1,2$
and all
$j=1,2$
and all
![]() $j>25$
. If
$j>25$
. If
![]() $f(\alpha )=0$
, then
$f(\alpha )=0$
, then
![]() $\mathbb {Q}(\alpha ^3)$
is a cubic subfield of
$\mathbb {Q}(\alpha ^3)$
is a cubic subfield of
![]() $\mathbb {Q}(\alpha )$
defined by
$\mathbb {Q}(\alpha )$
defined by
![]() $g(x)$
. Thus, we can use Lemma 3.4 to rule out
$g(x)$
. Thus, we can use Lemma 3.4 to rule out
![]() $j \in \{6,7,9,12,14,15,16,17,19,20,23\}$
since these groups do not have at least one entry of the form
$j \in \{6,7,9,12,14,15,16,17,19,20,23\}$
since these groups do not have at least one entry of the form
![]() $[1,2]$
or
$[1,2]$
or
![]() $[2,2]$
. To rule out 9T25, we note that its parity is
$[2,2]$
. To rule out 9T25, we note that its parity is
![]() $+1$
and its subfield entry is
$+1$
and its subfield entry is
![]() $[1,2]$
. This means
$[1,2]$
. This means
![]() $ {\mathrm{Disc}}(f) \in \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f) \in \mathbb {Q}^2$
and
![]() $ {\mathrm{Gal}}(g)$
is isomorphic to 3T1. However, this is a contradiction to Corollary 3.2.
$ {\mathrm{Gal}}(g)$
is isomorphic to 3T1. However, this is a contradiction to Corollary 3.2.
We note that if
![]() $ {\mathrm{Gal}}(f)$
is isomorphic to 9T4, then it is not clear immediately if
$ {\mathrm{Gal}}(f)$
is isomorphic to 9T4, then it is not clear immediately if
![]() $ {\mathrm{Gal}}(g)$
is isomorphic to 3T1 or 3T2. However, it follows from Lemma 3.4 that
$ {\mathrm{Gal}}(g)$
is isomorphic to 3T1 or 3T2. However, it follows from Lemma 3.4 that
![]() $ {\mathrm{Gal}}(g)$
must be 3T1. We formalise this in the following corollary.
$ {\mathrm{Gal}}(g)$
must be 3T1. We formalise this in the following corollary.
Corollary 4.2. Suppose
![]() $f(x)=x^9+ax^6+bx^3+c$
is irreducible over
$f(x)=x^9+ax^6+bx^3+c$
is irreducible over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $g(x)=x^3+ax^2+bx+c$
. If
$g(x)=x^3+ax^2+bx+c$
. If
![]() $ {\mathrm{Gal}}(f)$
is isomorphic to 9T4, then
$ {\mathrm{Gal}}(f)$
is isomorphic to 9T4, then
![]() $ {\mathrm{Gal}}(g)$
is isomorphic to 3T1.
$ {\mathrm{Gal}}(g)$
is isomorphic to 3T1.
We also note that each of the 11 groups appearing in Table 1 does indeed occur as a Galois group of some irreducible power compositional polynomial of degree 9 over
![]() $\mathbb {Q}$
; see Table 2 for one such polynomial per group. Also in the table, we give standard descriptive names, such as
$\mathbb {Q}$
; see Table 2 for one such polynomial per group. Also in the table, we give standard descriptive names, such as
![]() $C_n$
for the cyclic group of order n,
$C_n$
for the cyclic group of order n,
![]() $D_n$
for the dihedral group of order
$D_n$
for the dihedral group of order
![]() $2n$
and
$2n$
and
![]() $S_n$
for the symmetric group of degree n. We use
$S_n$
for the symmetric group of degree n. We use
![]() $\times $
for direct products and : for semidirect products (that are not direct products).
$\times $
for direct products and : for semidirect products (that are not direct products).
Table 2 Sample irreducible power compositional nonic polynomials with specified Galois group over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.

5 Determining
 $\text {Gal}(f)$
$\text {Gal}(f)$
In this section, we fix a generic ordering of the roots of
![]() $f(x)$
as defined in Table 3.
$f(x)$
as defined in Table 3.
As the roots of
![]() $g(x)$
are
$g(x)$
are
![]() $\{\alpha ^3,\beta ^3,\gamma ^3\}$
, we see that
$\{\alpha ^3,\beta ^3,\gamma ^3\}$
, we see that
![]() $\mathcal {B} = \{B_1,B_2,B_3\}$
forms a complete block system for
$\mathcal {B} = \{B_1,B_2,B_3\}$
forms a complete block system for
![]() $ {\mathrm{Gal}}(f)$
, where
$ {\mathrm{Gal}}(f)$
, where
![]() $B_1 = \{1,4,7\}$
,
$B_1 = \{1,4,7\}$
,
![]() $B_2 = \{2,5,8\}$
and
$B_2 = \{2,5,8\}$
and
![]() $B_3 = \{3,6,9\}$
. In other words, for each
$B_3 = \{3,6,9\}$
. In other words, for each
![]() $\sigma \in {\mathrm{Gal}}(f)$
, we have
$\sigma \in {\mathrm{Gal}}(f)$
, we have
![]() $\sigma (B_i) \in \mathcal {B}$
.
$\sigma (B_i) \in \mathcal {B}$
.
By reordering the roots within each block if necessary, it follows that
![]() $ {\mathrm{Gal}}(f)$
is a subgroup of the permutation group
$ {\mathrm{Gal}}(f)$
is a subgroup of the permutation group
![]() $G \simeq \text {9T24}$
, where
$G \simeq \text {9T24}$
, where
Consider the subgroup
![]() $H \simeq \text {9T8}$
of G, where
$H \simeq \text {9T8}$
of G, where
Consider also the multivariable function
![]() $T(x_1, \ldots , x_9) = (x_1+x_2+x_3)^3$
. Letting each
$T(x_1, \ldots , x_9) = (x_1+x_2+x_3)^3$
. Letting each
![]() $\sigma \in G$
act on T via subscripts, we see that the stabiliser of T inside G is H; this straightforward computation can be carried out with [16], for example.
$\sigma \in G$
act on T via subscripts, we see that the stabiliser of T inside G is H; this straightforward computation can be carried out with [16], for example.
Let
![]() $r(x)$
be the resolvent polynomial corresponding to G, H and T, according to [Reference Cohen6, Definition 6.3.2]. More concretely, we can specify the roots of
$r(x)$
be the resolvent polynomial corresponding to G, H and T, according to [Reference Cohen6, Definition 6.3.2]. More concretely, we can specify the roots of
![]() $r(x)$
in terms of the roots of
$r(x)$
in terms of the roots of
![]() $f(x)$
as follows. A group computation shows that a complete set of right coset representatives for
$f(x)$
as follows. A group computation shows that a complete set of right coset representatives for
![]() $G/H$
is:
$G/H$
is:
![]() $\text {Id}$
,
$\text {Id}$
,
![]() $(3,6,9)$
,
$(3,6,9)$
,
![]() $(3,9,6)$
,
$(3,9,6)$
,
![]() $(2,3,5,6,8,9)$
,
$(2,3,5,6,8,9)$
,
![]() $(2,5,8)(3,6,9)$
,
$(2,5,8)(3,6,9)$
,
![]() $(2,5,8)(3,9,6)$
,
$(2,5,8)(3,9,6)$
,
![]() $(2,3,8,9,5,6)$
,
$(2,3,8,9,5,6)$
,
![]() $(2,6)(3,8)(5,9)$
and
$(2,6)(3,8)(5,9)$
and
![]() $(2,8,5)(3,9,6)$
. Letting each of these coset representatives act on T via subscripts and then evaluating each image of T at the roots of
$(2,8,5)(3,9,6)$
. Letting each of these coset representatives act on T via subscripts and then evaluating each image of T at the roots of
![]() $f(x)$
as specified in Table 3, we see that the roots of
$f(x)$
as specified in Table 3, we see that the roots of
![]() $r(x)$
are of the form
$r(x)$
are of the form
![]() $(\alpha +\beta \zeta ^i+\gamma \zeta ^j)^3$
for
$(\alpha +\beta \zeta ^i+\gamma \zeta ^j)^3$
for
![]() $0 \leq i,j \leq 2$
. We can expand
$0 \leq i,j \leq 2$
. We can expand
![]() $r(x)$
and express its coefficients as elementary symmetric polynomials in the roots of
$r(x)$
and express its coefficients as elementary symmetric polynomials in the roots of
![]() $f(x)$
. Doing so leads us to the following definition.
$f(x)$
. Doing so leads us to the following definition.
Definition 5.1. Let
![]() $f(x) = x^9 +ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and let
$f(x) = x^9 +ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and let
![]() ${r(x) = x^9 + \sum _{i=0}^8 a_ix^i}$
, where
${r(x) = x^9 + \sum _{i=0}^8 a_ix^i}$
, where
 $$ \begin{align*} a_8 &= -9a;\\ a_7 &= 36a^2 - 81b;\\ a_6 &= -84a^3 + 486ab - 4293c;\\ a_5 &= 9(14a^4 - 135a^2b + 243b^2 + 189ac);\\ a_4 &= -9(14a^5 - 180a^3b + 729ab^2 - 1836a^2c + 4860bc);\\ a_3 &= -2673c(19a^3 - 81ab)(28a^6 - 405a^4b + 2187a^2b^2 - 6561b^3) + 61236c^2;\\ a_2 &= -9(4a^7 - 54a^5b + 243a^3b^2 + 108a^4c + 1458a^2bc - 6561b^2c + 13851ac^2);\\ a_1 &= 9(a^8 - 9a^6b + 432a^5c - 1701a^3bc + 7290a^2c^2 - 6561bc^2);\\ a_0 &= -(a^3 - 27c)^3. \end{align*} $$
$$ \begin{align*} a_8 &= -9a;\\ a_7 &= 36a^2 - 81b;\\ a_6 &= -84a^3 + 486ab - 4293c;\\ a_5 &= 9(14a^4 - 135a^2b + 243b^2 + 189ac);\\ a_4 &= -9(14a^5 - 180a^3b + 729ab^2 - 1836a^2c + 4860bc);\\ a_3 &= -2673c(19a^3 - 81ab)(28a^6 - 405a^4b + 2187a^2b^2 - 6561b^3) + 61236c^2;\\ a_2 &= -9(4a^7 - 54a^5b + 243a^3b^2 + 108a^4c + 1458a^2bc - 6561b^2c + 13851ac^2);\\ a_1 &= 9(a^8 - 9a^6b + 432a^5c - 1701a^3bc + 7290a^2c^2 - 6561bc^2);\\ a_0 &= -(a^3 - 27c)^3. \end{align*} $$
We have the following result about
![]() $r(x)$
.
$r(x)$
.
Proposition 5.2. Let
![]() $f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and define
$f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and define
![]() $r(x)$
as in Definition 5.1. Then:
$r(x)$
as in Definition 5.1. Then:
-
(1)
 $r(x)$
is separable;
$r(x)$
is separable; -
(2) the degrees of the irreducible factors of
 $r(x)$
are listed in Table 4, according to
$r(x)$
are listed in Table 4, according to
 $ {\mathrm{Gal}}(f)$
.
$ {\mathrm{Gal}}(f)$
.
Proof. Item (2) follows from item (1) and a group computation, since the degrees of the irreducible factors of
![]() $r(x)$
correspond to the orbit lengths of the action of
$r(x)$
correspond to the orbit lengths of the action of
![]() $ {\mathrm{Gal}}(f)$
on the cosets
$ {\mathrm{Gal}}(f)$
on the cosets
![]() $G/H$
; which in turn follows from a general result about irreducible factors of resolvent polynomials (see for example [Reference Cohen6, Theorem 6.3.3]).
$G/H$
; which in turn follows from a general result about irreducible factors of resolvent polynomials (see for example [Reference Cohen6, Theorem 6.3.3]).
Table 3 Generic ordering of the roots of
![]() $f(x) = x^9+ax^6+bx^3+c$
.
$f(x) = x^9+ax^6+bx^3+c$
.

Table 4 Possible Galois groups of
![]() $f(x) = g(x^3)$
, where
$f(x) = g(x^3)$
, where
![]() $g(x)=x^3+ax^2+bx+c$
. For each possible
$g(x)=x^3+ax^2+bx+c$
. For each possible
![]() $G = {\mathrm{Gal}}(f)$
, we include the T-number of G, the parity of G, the T-number of
$G = {\mathrm{Gal}}(f)$
, we include the T-number of G, the parity of G, the T-number of
![]() $ {\mathrm{Gal}}(g)$
, the degrees of the irreducible factors of
$ {\mathrm{Gal}}(g)$
, the degrees of the irreducible factors of
![]() $r(x)$
and the degrees of the irreducible factors of
$r(x)$
and the degrees of the irreducible factors of
![]() $s(x)$
when
$s(x)$
when
![]() $ {\mathrm{Gal}}(f)$
is either 9T10 or 9T21. The polynomials
$ {\mathrm{Gal}}(f)$
is either 9T10 or 9T21. The polynomials
![]() $r(x)$
and
$r(x)$
and
![]() $s(x)$
are given in Definitions 5.1 and 5.3, respectively.
$s(x)$
are given in Definitions 5.1 and 5.3, respectively.

To prove item (1), we verify that
![]() $(\alpha +\beta \zeta ^i+\gamma \zeta ^j)^3$
is not equal to
$(\alpha +\beta \zeta ^i+\gamma \zeta ^j)^3$
is not equal to
![]() $(\alpha +\beta \zeta ^k+\gamma \zeta ^l)^3$
except when
$(\alpha +\beta \zeta ^k+\gamma \zeta ^l)^3$
except when
![]() $(i,j)=(k,l)$
. This is equivalent to showing
$(i,j)=(k,l)$
. This is equivalent to showing
![]() $\beta \zeta ^i+\gamma \zeta ^j$
is not equal to
$\beta \zeta ^i+\gamma \zeta ^j$
is not equal to
![]() ${\beta \zeta ^k+\gamma \zeta ^l}$
for
${\beta \zeta ^k+\gamma \zeta ^l}$
for
![]() $(i,j)\neq (k,l)$
and
$(i,j)\neq (k,l)$
and
![]() $j,k,l\in \{0,1,2\}$
.
$j,k,l\in \{0,1,2\}$
.
If
![]() $i=k$
(and
$i=k$
(and
![]() $j\neq l)$
, then
$j\neq l)$
, then
![]() $\gamma =0$
; this contradicts the irreducibility of
$\gamma =0$
; this contradicts the irreducibility of
![]() $f(x)$
. We reach a similar contradiction if
$f(x)$
. We reach a similar contradiction if
![]() $j=l$
(and
$j=l$
(and
![]() $i\neq k$
). By dividing both expressions by
$i\neq k$
). By dividing both expressions by
![]() $\zeta ^i$
, we may also assume
$\zeta ^i$
, we may also assume
![]() $i=0$
. This leaves 12 cases to analyse; namely
$i=0$
. This leaves 12 cases to analyse; namely
![]() $j\in \{0,1,2\}$
,
$j\in \{0,1,2\}$
,
![]() $k\in \{1,2\}$
and
$k\in \{1,2\}$
and
![]() $l\in \{0,1,2\}\setminus \{j\}$
.
$l\in \{0,1,2\}\setminus \{j\}$
.
Suppose
![]() $(j,k,l) = (0,1,1)$
so that
$(j,k,l) = (0,1,1)$
so that
![]() $\beta +\gamma = \beta \zeta + \gamma \zeta $
. In this case,
$\beta +\gamma = \beta \zeta + \gamma \zeta $
. In this case,
![]() $\beta = -\gamma $
, which implies that
$\beta = -\gamma $
, which implies that
![]() $\beta ^3 = -\gamma ^3$
. This in turn implies
$\beta ^3 = -\gamma ^3$
. This in turn implies
![]() $-\alpha ^3 = a$
is a rational root of
$-\alpha ^3 = a$
is a rational root of
![]() $g(x)$
, indicating that
$g(x)$
, indicating that
![]() $g(x)$
is reducible, contradicting the irreducibility of
$g(x)$
is reducible, contradicting the irreducibility of
![]() $f(x)$
. Similar reasoning also applies to the cases
$f(x)$
. Similar reasoning also applies to the cases
![]() $(j,k,l) \in \{(0,2,2), (1,1,2), (1,2,0), (2,1,0), (2,2,1)\}$
.
$(j,k,l) \in \{(0,2,2), (1,1,2), (1,2,0), (2,1,0), (2,2,1)\}$
.
Suppose
![]() $(j,k,l) = (0,1,2)$
so that
$(j,k,l) = (0,1,2)$
so that
![]() $\beta +\gamma = \beta \zeta + \gamma \zeta ^2$
. Thus,
$\beta +\gamma = \beta \zeta + \gamma \zeta ^2$
. Thus,
![]() $\beta (1-\zeta ) = \gamma (\zeta ^2-1)$
. This implies
$\beta (1-\zeta ) = \gamma (\zeta ^2-1)$
. This implies
![]() $\beta = \gamma \zeta ^2$
, and thus
$\beta = \gamma \zeta ^2$
, and thus
![]() $f(x)$
is not separable and therefore reducible. Similar reasoning also applies to the cases
$f(x)$
is not separable and therefore reducible. Similar reasoning also applies to the cases
![]() $(j,k,l) \in \{(0,2,1), (1,1,0), (1,2,2), (2,1,1), (2,2,0)\}$
.
$(j,k,l) \in \{(0,2,1), (1,1,0), (1,2,2), (2,1,1), (2,2,0)\}$
.
An inspection of Table 4 shows that
![]() $ {\mathrm{Gal}}(f)$
is uniquely determined in all cases except for 9T10 versus 9T21 by considering: (1) whether
$ {\mathrm{Gal}}(f)$
is uniquely determined in all cases except for 9T10 versus 9T21 by considering: (1) whether
![]() $ {\mathrm{Disc}}(f)$
is a square in
$ {\mathrm{Disc}}(f)$
is a square in
![]() $\mathbb {Q}$
; (2) whether
$\mathbb {Q}$
; (2) whether
![]() $ {\mathrm{Disc}}(g)$
is a square in
$ {\mathrm{Disc}}(g)$
is a square in
![]() $\mathbb {Q}$
; and (3) the degrees of the irreducible factors of
$\mathbb {Q}$
; and (3) the degrees of the irreducible factors of
![]() $r(x)$
.
$r(x)$
.
To determine whether
![]() $ {\mathrm{Gal}}(f)$
is 9T10 or 9T21, we use another resolvent polynomial, which we define next.
$ {\mathrm{Gal}}(f)$
is 9T10 or 9T21, we use another resolvent polynomial, which we define next.
Definition 5.3. Let
![]() $f(x) = x^9 +ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and
$f(x) = x^9 +ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and
![]() $r(x)$
be as in Definition 5.1. Let
$r(x)$
be as in Definition 5.1. Let
![]() $s(x)$
be defined by
$s(x)$
be defined by
 $$ \begin{align*} s(x)^2=\frac{\text{Resultant}_y(r(y),r(x-y))}{2^9\cdot r(x/2)}. \end{align*} $$
$$ \begin{align*} s(x)^2=\frac{\text{Resultant}_y(r(y),r(x-y))}{2^9\cdot r(x/2)}. \end{align*} $$
Thus,
![]() $s(x)$
is the polynomial whose roots are sums of the form
$s(x)$
is the polynomial whose roots are sums of the form
![]() $\rho _i+\rho _j$
for
$\rho _i+\rho _j$
for
![]() $i<j$
, where
$i<j$
, where
![]() $\rho _1, \ldots , \rho _9$
are the roots of
$\rho _1, \ldots , \rho _9$
are the roots of
![]() $r(x)$
.
$r(x)$
.
We note that resultants can be computed via [Reference Cohen6, Algorithm 3.3.7]. The following result completes our classification.
Proposition 5.4. Let
![]() $f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible,
$f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible,
![]() $r(x)$
as defined in Definition 5.1 and assume
$r(x)$
as defined in Definition 5.1 and assume
![]() $ {\mathrm{Gal}}(f)$
is either 9T10 or 9T21. Let
$ {\mathrm{Gal}}(f)$
is either 9T10 or 9T21. Let
![]() $s(x)$
be defined as in Definition 5.3 and assume
$s(x)$
be defined as in Definition 5.3 and assume
![]() $s(x)$
is separable. If the degrees of the irreducible factors of
$s(x)$
is separable. If the degrees of the irreducible factors of
![]() $s(x)$
are:
$s(x)$
are:
-
(1)
 $[9,9,18]$
, then
$[9,9,18]$
, then
 $ {\mathrm{Gal}}(f)$
is 9T10;
$ {\mathrm{Gal}}(f)$
is 9T10; -
(2)
 $[9,27]$
, then
$[9,27]$
, then
 $ {\mathrm{Gal}}(f)$
is 9T21.
$ {\mathrm{Gal}}(f)$
is 9T21.
Proof. By Table 4, we see that
![]() $r(x)$
is irreducible of degree 9. Letting 9T10 act on the cosets of
$r(x)$
is irreducible of degree 9. Letting 9T10 act on the cosets of
![]() $G/H$
, where G and H are defined in (5.1) and (5.2), respectively, we see that:
$G/H$
, where G and H are defined in (5.1) and (5.2), respectively, we see that:
-
•
 $ {\mathrm{Gal}}(r)$
is 9T4 if
$ {\mathrm{Gal}}(r)$
is 9T4 if
 $ {\mathrm{Gal}}(f)$
is 9T10;
$ {\mathrm{Gal}}(f)$
is 9T10; -
•
 $ {\mathrm{Gal}}(r)$
is 9T12 if
$ {\mathrm{Gal}}(r)$
is 9T12 if
 $ {\mathrm{Gal}}(f)$
is 9T21.
$ {\mathrm{Gal}}(f)$
is 9T21.
It follows from [Reference Soicher14, Section 3.5] that
![]() $s(x)$
is the resolvent polynomial corresponding to the subgroup
$s(x)$
is the resolvent polynomial corresponding to the subgroup
![]() $\tilde {H} = \langle (1,2), (3,4), (3,4,5,6,7,8,9)\rangle $
of
$\tilde {H} = \langle (1,2), (3,4), (3,4,5,6,7,8,9)\rangle $
of
![]() $S_9$
that stabilises the multivariable function
$S_9$
that stabilises the multivariable function
![]() $x_1+x_2$
. We can assume
$x_1+x_2$
. We can assume
![]() $s(x)$
is separable by taking a Tschirnhaus transformation of
$s(x)$
is separable by taking a Tschirnhaus transformation of
![]() $r(x)$
if necessary and recomputing
$r(x)$
if necessary and recomputing
![]() $s(x)$
; see [Reference Cohen6, Algorithm 3.6.4]. Letting representatives for the conjugacy classes of 9T10 and 9T21 act on the cosets
$s(x)$
; see [Reference Cohen6, Algorithm 3.6.4]. Letting representatives for the conjugacy classes of 9T10 and 9T21 act on the cosets
![]() $S_9/\tilde {H}$
and extracting the orbit lengths of these actions proves the proposition.
$S_9/\tilde {H}$
and extracting the orbit lengths of these actions proves the proposition.
Using Table 4, we can summarise the characterisation of
![]() $ {\mathrm{Gal}}(f)$
as follows.
$ {\mathrm{Gal}}(f)$
as follows.
Theorem 5.5. Let
![]() $f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and let
$f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
be irreducible and let
![]() $g(x)=x^3+ax^2+bx+c$
. Let
$g(x)=x^3+ax^2+bx+c$
. Let
![]() $r(x)$
and
$r(x)$
and
![]() $s(x)$
be defined as in Definitions 5.1 and 5.3, respectively, and let R and S be the degrees of the irreducible factors of
$s(x)$
be defined as in Definitions 5.1 and 5.3, respectively, and let R and S be the degrees of the irreducible factors of
![]() $r(x)$
and
$r(x)$
and
![]() $s(x)$
, respectively.
$s(x)$
, respectively.
-
• If
 $R = [3,3,3]$
, then
$R = [3,3,3]$
, then
 $ {\mathrm{Gal}}(f)$
is 9T3
$ {\mathrm{Gal}}(f)$
is 9T3
 $\simeq D_9$
.
$\simeq D_9$
. -
• If
 $R = [1,1,1,6]$
, then
$R = [1,1,1,6]$
, then
 $ {\mathrm{Gal}}(f)$
is 9T5
$ {\mathrm{Gal}}(f)$
is 9T5
 $\simeq C_3:S_3$
.
$\simeq C_3:S_3$
. -
• If
 $R = [1,2,6]$
, then:
$R = [1,2,6]$
, then:-
– if
 $ {\mathrm{Disc}}(g)\in \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(g)\in \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T4
$ {\mathrm{Gal}}(f)$
is 9T4
 $\simeq C_3\times S_3$
;
$\simeq C_3\times S_3$
; -
– if
 $ {\mathrm{Disc}}(g)\notin \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(g)\notin \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T8
$ {\mathrm{Gal}}(f)$
is 9T8
 $\simeq S_3\times S_3$
.
$\simeq S_3\times S_3$
.
-
-
• If
 $R = [3,6]$
, then:
$R = [3,6]$
, then:-
– if
 $ {\mathrm{Disc}}(f)\in \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(f)\in \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T11
$ {\mathrm{Gal}}(f)$
is 9T11
 $\simeq C_9:C_6$
;
$\simeq C_9:C_6$
; -
– if
 $ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
 $ {\mathrm{Disc}}(g)\in \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(g)\in \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T13
$ {\mathrm{Gal}}(f)$
is 9T13
 $\simeq C_3^3:S_3$
;
$\simeq C_3^3:S_3$
; -
– if
 $ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
 $ {\mathrm{Disc}}(g)\notin \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(g)\notin \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T18
$ {\mathrm{Gal}}(f)$
is 9T18
 $\simeq C_3^3:D_6$
.
$\simeq C_3^3:D_6$
.
-
-
• If
 $r(x)$
is irreducible, then:
$r(x)$
is irreducible, then:-
– if
 $ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
 $ {\mathrm{Disc}}(g)\in \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(g)\in \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T22
$ {\mathrm{Gal}}(f)$
is 9T22
 $\simeq C_3^3:C_6$
;
$\simeq C_3^3:C_6$
; -
– if
 $ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f)\notin \mathbb {Q}^2$
and
 $ {\mathrm{Disc}}(g)\notin \mathbb {Q}^2$
, then
$ {\mathrm{Disc}}(g)\notin \mathbb {Q}^2$
, then
 $ {\mathrm{Gal}}(f)$
is 9T24
$ {\mathrm{Gal}}(f)$
is 9T24
 $\simeq C_3^3:D_6$
;
$\simeq C_3^3:D_6$
; -
– if
 $ {\mathrm{Disc}}(f)\in \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f)\in \mathbb {Q}^2$
and
 $S = [9,9,18]$
, then
$S = [9,9,18]$
, then
 $ {\mathrm{Gal}}(f)$
is 9T10
$ {\mathrm{Gal}}(f)$
is 9T10
 $\simeq C_9:C_6$
;
$\simeq C_9:C_6$
; -
– if
 $ {\mathrm{Disc}}(f)\in \mathbb {Q}^2$
and
$ {\mathrm{Disc}}(f)\in \mathbb {Q}^2$
and
 $S = [9,27]$
, then
$S = [9,27]$
, then
 $ {\mathrm{Gal}}(f)$
is 9T21
$ {\mathrm{Gal}}(f)$
is 9T21
 $\simeq C_3^3:S_3$
.
$\simeq C_3^3:S_3$
.
-
6 Examples
In this section, we give several examples that apply Theorem 5.5 to compute Galois groups of power compositional nonic polynomials. Our first example recovers [Reference Jones and Phillips11, Theorem 1.1].
Example 6.1. Let
![]() $f(x) = x^9 +9mx^6 +192m^3 \in \mathbb {Q}[x]$
,
$f(x) = x^9 +9mx^6 +192m^3 \in \mathbb {Q}[x]$
,
![]() $m\neq 0$
. Then,
$m\neq 0$
. Then,
![]() $ {\mathrm{Gal}}(f) = \text {9T3} \simeq ~D_9$
.
$ {\mathrm{Gal}}(f) = \text {9T3} \simeq ~D_9$
.
Proof. Factoring
![]() $r(x)$
gives three irreducible factors of degree 3:
$r(x)$
gives three irreducible factors of degree 3:
 $$ \begin{align*} &x^3 + 27mx^2 + 7047m^2x - 107811m^3, \\ &x^3 - 135mx^2 + 2187m^2x - 10125m^3, \\ &x^3 + 27mx^2 + 243m^2x + 81m^3. \end{align*} $$
$$ \begin{align*} &x^3 + 27mx^2 + 7047m^2x - 107811m^3, \\ &x^3 - 135mx^2 + 2187m^2x - 10125m^3, \\ &x^3 + 27mx^2 + 243m^2x + 81m^3. \end{align*} $$
By Theorem 5.5, this shows
![]() $ {\mathrm{Gal}}(f) = \text {9T3} \simeq D_9$
.
$ {\mathrm{Gal}}(f) = \text {9T3} \simeq D_9$
.
Table 5 gives one-parameter families of polynomials for each of the 11 possible Galois groups of
![]() $f(x)$
, assuming the resulting polynomial is irreducible when specialised at a particular rational value of the parameter. Here are two additional examples that illustrate the correctness of Table 5.
$f(x)$
, assuming the resulting polynomial is irreducible when specialised at a particular rational value of the parameter. Here are two additional examples that illustrate the correctness of Table 5.
Table 5 One parameter families of polynomials of the form
![]() $f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
with prescribed Galois group when
$f(x)=x^9+ax^6+bx^3+c \in \mathbb {Q}[x]$
with prescribed Galois group when
![]() $f(x)$
is irreducible.
$f(x)$
is irreducible.

Example 6.2. Let
![]() $f(x) = x^9 +3tx^6 - 4t^2x^3 + t^3\in \mathbb {Q}[x]$
. Then,
$f(x) = x^9 +3tx^6 - 4t^2x^3 + t^3\in \mathbb {Q}[x]$
. Then,
![]() $ {\mathrm{Gal}}(f) = \text {9T4} \simeq {C_3\times S_3}$
.
$ {\mathrm{Gal}}(f) = \text {9T4} \simeq {C_3\times S_3}$
.
Proof. Factoring
![]() $r(x)$
gives
$r(x)$
gives
Thus,
![]() $R = [1,2,6]$
. It follows from Theorem 5.5 that
$R = [1,2,6]$
. It follows from Theorem 5.5 that
![]() $ {\mathrm{Gal}}(f)$
is either 9T4 or 9T8. We have
$ {\mathrm{Gal}}(f)$
is either 9T4 or 9T8. We have
![]() $g(x) = x^3+3tx^2-4t^2x+t^3$
and
$g(x) = x^3+3tx^2-4t^2x+t^3$
and
![]() $ {\mathrm{Disc}}(g) = (7t^3)^2$
which is a square. Thus,
$ {\mathrm{Disc}}(g) = (7t^3)^2$
which is a square. Thus,
![]() $ {\mathrm{Gal}}(f) = \text {9T4} \simeq C_3\times S_3$
.
$ {\mathrm{Gal}}(f) = \text {9T4} \simeq C_3\times S_3$
.
Example 6.3. Let
![]() $f(x) = x^9 + 9tx^6 + 9t(2t+1)x^3 - t(t-1)^3\in \mathbb {Q}[x]$
. Then,
$f(x) = x^9 + 9tx^6 + 9t(2t+1)x^3 - t(t-1)^3\in \mathbb {Q}[x]$
. Then,
![]() $ {\mathrm{Gal}}(f) = \text {9T10} \simeq C_9 : C_6$
.
$ {\mathrm{Gal}}(f) = \text {9T10} \simeq C_9 : C_6$
.
Proof. Using Mathematica, we see that
![]() $r(x)$
is irreducible over
$r(x)$
is irreducible over
![]() $\mathbb {Q}(t)$
. Thus, we assume that
$\mathbb {Q}(t)$
. Thus, we assume that
![]() $t\in \mathbb {Q}$
is chosen so that
$t\in \mathbb {Q}$
is chosen so that
![]() $r(x)$
is irreducible. We also see that
$r(x)$
is irreducible. We also see that
which is a perfect square. By Theorem 5.5, we see that
![]() $ {\mathrm{Gal}}(f)$
is either 9T10 or 9T21. Forming
$ {\mathrm{Gal}}(f)$
is either 9T10 or 9T21. Forming
![]() $s(x)$
as given in Definition 5.3 and factoring it, we see it has three factors:
$s(x)$
as given in Definition 5.3 and factoring it, we see it has three factors:
 $$ \begin{align*} &x^9 - 162tx^8 + (8019t^2 + 729t)x^7 + \cdots; \\ &x^9 - 162tx^8 + (10206t^2 + 729t)x^7 + \cdots; \\ &x^{18} + 324tx^{17} + \cdots. \end{align*} $$
$$ \begin{align*} &x^9 - 162tx^8 + (8019t^2 + 729t)x^7 + \cdots; \\ &x^9 - 162tx^8 + (10206t^2 + 729t)x^7 + \cdots; \\ &x^{18} + 324tx^{17} + \cdots. \end{align*} $$
Assuming t is chosen so that
![]() $s(x)$
is separable, we see that
$s(x)$
is separable, we see that
![]() $S = [9,9,18]$
. Thus,
$S = [9,9,18]$
. Thus,
![]() $ {\mathrm{Gal}}(f) = \text {9T10} \simeq C_9:C_6$
.
$ {\mathrm{Gal}}(f) = \text {9T10} \simeq C_9:C_6$
.
7 Field extensions defined by polynomials of the form
 $g(x^3)$
$g(x^3)$
In this section, we are interested in determining when a field extension
![]() $L/\mathbb {Q}$
of degree n can be defined by an irreducible polynomial
$L/\mathbb {Q}$
of degree n can be defined by an irreducible polynomial
![]() $f(x)=g(x^3) \in \mathbb {Q}[x]$
. We make use of the following previous results.
$f(x)=g(x^3) \in \mathbb {Q}[x]$
. We make use of the following previous results.
Theorem 7.1 [Reference Awtrey, Beuerle and Griesbach1, Proposition 1.2].
Suppose
![]() $L/\mathbb {Q}$
is an extension of degree
$L/\mathbb {Q}$
is an extension of degree
![]() $mk$
. Then, L can be defined by an irreducible polynomial
$mk$
. Then, L can be defined by an irreducible polynomial
![]() $g(x^k)\in \mathbb {Q}[x]$
if and only if L has a subfield K of degree m such that
$g(x^k)\in \mathbb {Q}[x]$
if and only if L has a subfield K of degree m such that
![]() $L/K$
is defined by an irreducible polynomial
$L/K$
is defined by an irreducible polynomial
![]() $x^k-a\in K[x]$
.
$x^k-a\in K[x]$
.
Moreover, if
![]() $\tilde {g}(x)\in \mathbb {Q}[x]$
is irreducible of degree m defining K and
$\tilde {g}(x)\in \mathbb {Q}[x]$
is irreducible of degree m defining K and
![]() $h(x)=x^k-a\in K[x]$
is irreducible defining
$h(x)=x^k-a\in K[x]$
is irreducible defining
![]() $L/K$
, then
$L/K$
, then
![]() $f(x)=g(x^k)$
defines
$f(x)=g(x^k)$
defines
![]() $L/\mathbb {Q}$
, where
$L/\mathbb {Q}$
, where
We can guarantee that
![]() $f(x)$
is irreducible by replacing a by
$f(x)$
is irreducible by replacing a by
![]() $ab^k$
for some
$ab^k$
for some
![]() $b\in K$
, if necessary (see for example [Reference Dixon7, Appendix A]).
$b\in K$
, if necessary (see for example [Reference Dixon7, Appendix A]).
Theorem 7.2 [Reference Kang12, Theorem 1].
Let
![]() $K/\mathbb {Q}$
be a finite extension and let
$K/\mathbb {Q}$
be a finite extension and let
![]() $L/K$
be a cubic extension defined by the irreducible polynomial
$L/K$
be a cubic extension defined by the irreducible polynomial
![]() $h(x)=x^3+ax^2+bx+c$
. Then,
$h(x)=x^3+ax^2+bx+c$
. Then,
![]() $L/K$
is defined by a polynomial of the form
$L/K$
is defined by a polynomial of the form
![]() $x^3-d\in K[x]$
if and only if
$x^3-d\in K[x]$
if and only if
![]() $-3 {\mathrm{Disc}}(h) \in K^2$
.
$-3 {\mathrm{Disc}}(h) \in K^2$
.
Moreover, if
![]() $-3 {\mathrm{Disc}}(h)\in K^2$
, let
$-3 {\mathrm{Disc}}(h)\in K^2$
, let
![]() $u = 3a^2-9b$
,
$u = 3a^2-9b$
,
![]() $v=-2a^3+9ab-27c$
and e be a solution to
$v=-2a^3+9ab-27c$
and e be a solution to
![]() $u^2x^2-9vx+3u=0$
. Then,
$u^2x^2-9vx+3u=0$
. Then,
![]() $L/K$
is defined by
$L/K$
is defined by
![]() $x^3-u/(3e)$
.
$x^3-u/(3e)$
.
As a consequence of Theorems 7.1 and 7.2, the following algorithm is guaranteed to produce an irreducible power compositional polynomial
![]() $g(x^3)$
defining
$g(x^3)$
defining
![]() $L/\mathbb {Q}$
, when it exists.
$L/\mathbb {Q}$
, when it exists.
Algorithm 7.3. Suppose L = ℚ(α), where α is a root of the irreducible polynomial f(x) ∈ ℚ[x] of degree n = km.
-
(1) Determine irreducible polynomials g i (x) defining subfields K i of L of degree m. If no such polynomials exist, L does not have subfields of degree m. (Note: computing subfields is a built-in command in several computer algebra systems, such as Pari/GP [18].)
-
(2) Factor f(x) over each K i and extract an irreducible cubic polynomial h i (x) ∈ K i [x]. Discard polynomials where − 3Disc(h i ) ∉ K i 2, since in these cases, L/K i cannot be defined by a polynomial of the form x 3 − a ∈ K i [x].
-
(3) For each h i (x) that remains, use Theorem 7.2 to produce an irreducible polynomial
 $\tilde{h}_i(x)$
= x
3 − a
i
∈ K
i
[x] that defines L/K
i
.
$\tilde{h}_i(x)$
= x
3 − a
i
∈ K
i
[x] that defines L/K
i
. -
(4) For each
 $\tilde{h}(x)$
, compute f
i
(x) = Resultant
y
(
$\tilde{h}(x)$
, compute f
i
(x) = Resultant
y
(
 $\tilde{h}_i(x)$
, g
i
(y)) to produce power compositional polynomials. If none of the f
i
(x) are irreducible, choose an
$\tilde{h}_i(x)$
, g
i
(y)) to produce power compositional polynomials. If none of the f
i
(x) are irreducible, choose an
 $\tilde{h}_i(x)$
, perform a Tschirnhaus transformation as described in Theorem 7.1 and recompute f
i
(x).
$\tilde{h}_i(x)$
, perform a Tschirnhaus transformation as described in Theorem 7.1 and recompute f
i
(x).
We have implemented [18, Algorithm 7.3] and created a web-interface [Reference Awtrey, Patane and Toone4], where a user can enter a polynomial
![]() $f(x)\in \mathbb {Q}[x]$
. The website returns a power compositional
$f(x)\in \mathbb {Q}[x]$
. The website returns a power compositional
![]() $g(x^3)$
that defines an extension isomorphic to the extension defined by
$g(x^3)$
that defines an extension isomorphic to the extension defined by
![]() $f(x)$
, when such a power compositional polynomial exists.
$f(x)$
, when such a power compositional polynomial exists.
Example 7.4. To illustrate Algorithm 7.3, consider the irreducible polynomial in
![]() $\mathbb {Q}[x]$
:
$\mathbb {Q}[x]$
:
 $$ \begin{align*} f(x) = x^{18} &- 6x^{17} + 19x^{16} - 35x^{15} + 41x^{14} \\ &- 29x^{13} + 9x^{12} + 14x^{11} - 35x^{10} + 34x^9 - 9x^8 \\ & - 6x^7 + 4x^6 - 15x^5 + 12x^4 + 8x^3 - 6x^2 - x + 1. \end{align*} $$
$$ \begin{align*} f(x) = x^{18} &- 6x^{17} + 19x^{16} - 35x^{15} + 41x^{14} \\ &- 29x^{13} + 9x^{12} + 14x^{11} - 35x^{10} + 34x^9 - 9x^8 \\ & - 6x^7 + 4x^6 - 15x^5 + 12x^4 + 8x^3 - 6x^2 - x + 1. \end{align*} $$
Let
![]() $f(\alpha )=0$
and
$f(\alpha )=0$
and
![]() $L = \mathbb {Q}(\alpha )$
.
$L = \mathbb {Q}(\alpha )$
.
-
(1) Using [18], we see that the irreducible polynomial
 $g(x) = x^6 + 7x^5 + 18x^4 + 18x^3 + 2x^2 - 4x + 1$
defines a subfield K of L of degree 6.
$g(x) = x^6 + 7x^5 + 18x^4 + 18x^3 + 2x^2 - 4x + 1$
defines a subfield K of L of degree 6. -
(2) Let
 $g(\beta )=0$
. Factoring
$g(\beta )=0$
. Factoring
 $f(x)$
over K and extracting an irreducible cubic factor, we obtain the polynomial
$f(x)$
over K and extracting an irreducible cubic factor, we obtain the polynomial
 $h(x) = x^3+h_2x^2+h_1x-\beta $
, where
$h(x) = x^3+h_2x^2+h_1x-\beta $
, where  $$ \begin{align*} h_2 = \beta^5 + 6\beta^4 + 12\beta^3 + 8\beta^2 + \beta; \quad h_1 = -\beta^5 - 5\beta^4 - 7\beta^3 + 3\beta - 1. \end{align*} $$
$$ \begin{align*} h_2 = \beta^5 + 6\beta^4 + 12\beta^3 + 8\beta^2 + \beta; \quad h_1 = -\beta^5 - 5\beta^4 - 7\beta^3 + 3\beta - 1. \end{align*} $$
-
(3) Using Theorem 7.2, we obtain
 $$ \begin{align*} \tilde{h}(x) = x^3 + (-9\beta^5 - 42\beta^4 - 60\beta^3 - 12\beta^2 - 9\beta - 3)\in K[x], \end{align*} $$
$$ \begin{align*} \tilde{h}(x) = x^3 + (-9\beta^5 - 42\beta^4 - 60\beta^3 - 12\beta^2 - 9\beta - 3)\in K[x], \end{align*} $$
which is irreducible over K and also defines
 $L/K$
.
$L/K$
. -
(4) Computing
 $\text {Resultant}_\beta (\tilde {h}(x),g(\beta ))$
, we obtain
$\text {Resultant}_\beta (\tilde {h}(x),g(\beta ))$
, we obtain  $$ \begin{align*}x^{18} + 108x^{15} + 3834x^{12} + 43011x^9 - 107892x^6 - 2755620x^3 + 24111675, \end{align*} $$
$$ \begin{align*}x^{18} + 108x^{15} + 3834x^{12} + 43011x^9 - 107892x^6 - 2755620x^3 + 24111675, \end{align*} $$
which is a power compositional polynomial and irreducible over
 $\mathbb {Q}.$
$\mathbb {Q}.$
Acknowledgements
The authors are grateful for the referee’s close reading of the manuscript, and for the helpful suggestions which have increased accuracy and improved clarity throughout the paper.