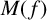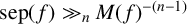1 Introduction
A well-studied subject in number theory is the distribution of roots of polynomials. This tradition includes, for example, Descartes’ rule of signs, the Gauss–Lucas theorem and the Schinzel–Zassenhaus conjecture. Here, we study the relationship between the separation of a polynomial (the minimal distance between its roots) and its Mahler measure. To be precise, we now define these terms.
Definition 1.1. Given a polynomial
$f(x) \in \mathbb {C}[x]$
with roots
$\alpha _1,\ldots ,\alpha _n \in \mathbb {C}$
, the separation of
$f(x)$
is the quantity
$$ \begin{align*}\operatorname{sep}(f) := \min_{\alpha_i \neq \alpha_j} |\alpha_i - \alpha_j|.\end{align*} $$
Since, for any nonzero
$b \in \mathbb {C}$
,
$\operatorname {sep}(f) = \operatorname {sep}(bf)$
, we assume in the remainder of the paper that all polynomials are monic. Our results can be easily adapted otherwise.
Definition 1.2. Given a monic polynomial
$f(x) \in \mathbb {C}[x]$
with roots
$\alpha _1,\ldots ,\alpha _n \in \mathbb {C}$
, the Mahler measure of
$f(x)$
is the quantity
$$ \begin{align*}M(f) :=\prod_{i=1}^n \max\{1,|\alpha_i|\}.\end{align*} $$
These two quantities are useful for rather different reasons. Knowledge about root separation is helpful for writing algorithms that compute the number of real roots of a polynomial (see Koiran [Reference Koiran13]), for bounding the number of solutions to Thue equations (see Grundman and Wisniewski [Reference Grundman and Wisniewski10]) and for deriving lower bounds on the absolute values of certain products of algebraic integers (see Albayrak et al. [Reference Albayrak, Ghosh, Knapp and Nguyen1]).
The Mahler measure is a versatile tool for measuring the complexity of a polynomial. On the one hand, the Mahler measure contains information about the roots of a polynomial via its definition. On the other hand, the Mahler measure contains information about the coefficients of the polynomial: for any polynomial
$f(x) \in \mathbb {C}[x]$
of degree n,
$M(f) \asymp _n H(f)$
, where
$H(f)$
is the maximum absolute value of its coefficients [Reference Bombieri and Gubler3, Lemma 1.6.7]. Additionally, the Mahler measure preserves algebraic information about polynomials since it is multiplicative. These facts together make the Mahler measure valuable for translating information about the roots of a polynomial into information about its coefficients, and vice versa. The Mahler measure is the main object in Lehmer’s conjecture (see [Reference Lehmer14]). Smyth’s excellent survey [Reference Smyth18] contains more information on the use and study of the Mahler measure.
In general, it is valuable to find effective lower bounds on polynomial root separation. After all, separation gives the minimum distance between distinct roots of a polynomial, so a lower bound on separation gives a lower bound on the distance between any two roots of that polynomial. Indeed, this is how separation is used in [Reference Albayrak, Ghosh, Knapp and Nguyen1, Reference Grundman and Wisniewski10, Reference Koiran13]. A foundational lower bound on separation is the following result of Mahler. It relies on the discriminant, defined for monic
$f(x) \in \mathbb {C}[x]$
with roots
$\alpha _1,\ldots ,\alpha _n$
to be
$$ \begin{align*}D(f) := \prod_{1 \leqslant i < j \leqslant n} (\alpha_i - \alpha_j)^2.\end{align*} $$
Theorem 1.3 (Mahler, [Reference Mahler15]).
Let
$f(x) \in \mathbb {C}[x]$
be separable of degree
$n \geqslant 2$
with discriminant
$D(f)$
. Then
$$ \begin{align*} \operatorname{sep}(f)> \frac{\sqrt{3|D(f)|}}{n^{(n+2)/2}M(f)^{n-1}}; \end{align*} $$
in particular, if
$f(x) \in \mathbb {Z}[x]$
, then
$$ \begin{align*} \operatorname{sep}(f)> \frac{\sqrt{3}}{n^{(n+2)/2}M(f)^{n-1}}. \end{align*} $$
This particular result has spurred much investigation, as it leaves many questions open. Is the exponent of
$n-1$
on
$M(f)$
optimal? This remains unknown, although Bugeaud and Dujella [Reference Bugeaud and Dujella5] show that the optimal exponent is at least
$(2n-1)/3$
for
$f \in \mathbb {Z}[x]$
, while Evertse [Reference Evertse9] considers other ways to improve the exponent. Is the separability hypothesis necessary? Rump removes the separability hypothesis in [Reference Rump17], and Dujella and Pejković improve his result in [Reference Dujella and Pejković8]. Can better results be obtained with additional hypotheses (for example, if
$f(x)$
is assumed to be irreducible and/or monic)? Many papers have looked at these kinds of questions, including [Reference Bugeaud and Dujella4, Reference Dujella and Pejković8, Reference Koiran13]. What if we look at distances between the absolute values of the roots, rather than distances between the roots themselves? Bugeaud, Dujella, Fang, Pejković and Salvy look at these questions in [Reference Bugeaud, Dujella, Fang, Pejković and Salvy6, Reference Bugeaud, Dujella, Pejković and Salvy7].
Although lower bounds on separation have been well studied, the authors are not aware of any attempt to provide upper bounds on separation. On the face of it, an upper bound on separation provides less intuitive information about a polynomial’s roots than does a lower bound. However, upper bounds on separation can provide us with useful information for Lehmer’s conjecture, which we will describe after our main theorem.
One can easily obtain a trivial upper bound on separation using the triangle inequality:
$\operatorname {sep}(f) = \min _{\alpha _i \neq \alpha _j} |\alpha _i - \alpha _j| \leqslant 2M(f).$
Combining Mahler’s inequality
$|D(f)| \leqslant n^nM(f)^{2n-2}$
[Reference Mahler15, Theorem 1] with the fact that
$\operatorname {sep}(f)^{n(n-1)} \leqslant |D(f)|$
when
$f(x)$
is separable gives the improved upper bound
$$ \begin{align*} \operatorname{sep}(f) \leqslant n^{1/(n-1)}M(f)^{2/n} \end{align*} $$
for separable polynomials
$f(x) \in \mathbb {C}[x]$
. However, numerical experiments conducted by the first author at the outset of this project in [Reference Knapp12] suggested that this upper bound is still suboptimal, and, indeed, we can prove the following result.
Theorem 1.4. Let
$f(x) \in \mathbb {C}[x]$
be monic and separable of degree
$n \geqslant 2$
. Then
$$ \begin{align*}\operatorname{sep}(f) \leqslant \min\bigg\{2,\frac{34}{\sqrt{n}}\bigg\}M(f)^{1/(n-1)}.\end{align*} $$
If, in addition,
$f(x) \in \mathbb {R}[x]$
and one of the roots of
$f(x)$
with minimum absolute value is not real (for example, if
$f(x) \in \mathbb {R}[x]$
has no real roots), then
$$ \begin{align*}\operatorname{sep}(f) \leqslant \min\bigg\{2,\frac{34}{\sqrt{n}}\bigg\} M(f)^{1/n}.\end{align*} $$
In both cases, the dependence of the bound on n is optimal, although the constant 34 could possibly be improved.
Our next result finds the optimal constant for certain values of the signature of
$f(x)$
. A polynomial
$f(x) \in \mathbb {R}[x]$
has signature
$(t,s)$
if it has t real roots and s pairs of complex conjugate roots.
Theorem 1.5. Suppose that
$f(x) \in \mathbb {R}[x]$
is monic and separable of degree
$n \geqslant 2$
and signature
$(t,s)$
, where
$s = 0$
,
$(t,s) = (1,1)$
or
$(t,s) = (0,2)$
. Then
$$ \begin{align*}\operatorname{sep}(f) \leqslant C_{t,s}M(f)^{1/(n - \delta)},\end{align*} $$
where
$\delta $
is
$1$
if
$t \neq 0$
and
$0$
otherwise, and
$C_{t,s}$
is defined in the following table.
$$ \begin{align*} \begin{array}{| c || c | c | c |}\hline (t,s) & (1,1) & (0,2) & (t,0)\\\hline C_{t,s} & \sqrt{3} & \sqrt{2} & (2e+o(1))/t\\\hline \end{array} \end{align*} $$
It is worth noting that each of our main theorems produces the same bounds on absolute separation, defined in [Reference Bugeaud, Dujella, Fang, Pejković and Salvy6] to be
$$ \begin{align*}\operatorname{abs\, sep}(f) = \min_{|\alpha_i| \neq |\alpha_j|} ||\alpha_i| - |\alpha_j||,\end{align*} $$
since we have
$\operatorname {abs\, sep}(f) \leqslant \operatorname {sep}(f)$
for all f.
With our main theorems described, we can detail the connection to Lehmer’s conjecture.
Conjecture 1.6 (Lehmer’s conjecture).
There exists an absolute constant
$\mu> 1$
so that, for every irreducible, noncyclotomic
$f(x) \in \mathbb {Z}[x]$
of degree at least two,
$M(f) \geqslant \mu $
.
Observe that Theorem 1.3 provides a lower bound on
$M(f)$
that is useful when
$\operatorname {sep}(f)$
is small: that is,
$$ \begin{align*}M(f) \geqslant \bigg(\frac{\sqrt{3}}{n^{(n+2)/2}\operatorname{sep}(f)}\bigg)^{1/(n-1)}.\end{align*} $$
On the other hand, Theorem 1.4 provides a lower bound on
$M(f)$
that is useful when
$\operatorname {sep}(f)$
is large: that is,
$$ \begin{align*}M(f) \geqslant \bigg(\frac{\operatorname{sep}(f)}{\min\{2,34/\sqrt{n}\}}\bigg)^{n-1}.\end{align*} $$
Hence, proving Lehmer’s conjecture reduces to the case where
$f(x)$
satisfies
$$ \begin{align*}\frac{\sqrt{3}}{n^{(n+2)/2}\mu^{n-1}} < \operatorname{sep}(f) < \min\bigg\{2,\frac{34}{\sqrt{n}}\bigg\}\mu^{1/(n-1)}.\end{align*} $$
2 The optimal upper bound up to constant factor
The main goal of this section is to prove Theorem 1.4.
Proof of Theorem 1.4.
Write
$f(x) = \prod _{i=1}^n (x - \alpha _i)$
, where
$|\alpha _1| \leqslant |\alpha _2| \leqslant \cdots \leqslant |\alpha _n|$
.
We first prove that
$\operatorname {sep}(f) \leqslant 2M(f)^{1/(n-1)}$
. Note that, for any
$j \geqslant 2$
, we have
$0 < |\alpha _j - \alpha _1| \leqslant 2|\alpha _j|$
. As a consequence,
$$ \begin{align*} \operatorname{sep}(f)^{n-1} \leqslant |\alpha_2 - \alpha_1||\alpha_3 - \alpha_1|\cdots|\alpha_n - \alpha_1| \leqslant \prod_{j = 2}^n 2|\alpha_j| \leqslant 2^{n-1}M(f), \end{align*} $$
and the claim follows.
Next, we show that if
$f(x) \in \mathbb {R}[x]$
and if there exists
$\alpha _j \notin \mathbb {R}$
with
$|\alpha _j| = |\alpha _1|$
, then, actually,
$\operatorname {sep}(f) \leqslant 2M(f)^{1/n}$
. The argument is very similar, except we may now assume that
$\alpha _1$
and
$\alpha _2$
are complex conjugates. In this case,
$$ \begin{align*} \operatorname{sep}(f)^n \leqslant |\alpha_2 - \alpha_1|^2|\alpha_3 - \alpha_1|\cdots|\alpha_n - \alpha_1| \leqslant \prod_{j=1}^n 2|\alpha_j| \leqslant 2^nM(f), \end{align*} $$
and the claim again follows.
Now we return to the situation where we only assume that
$f(x) \in \mathbb {C}[x]$
is separable of degree n, and we aim to show that
$$ \begin{align*}\operatorname{sep}(f) \leqslant \frac{34}{\sqrt{n}}\cdot M(f)^{1/(n-1)}.\end{align*} $$
Since
${34}/{\sqrt {n}} \geqslant 2$
for
$n \leqslant 289$
, we assume that
$n \geqslant 290$
in the following discussion.
Let
$r = \operatorname {sep}(f)/2$
and, for any
$R \geqslant 0$
, let
$$ \begin{align*}N(R) := \#\{i: |\alpha_i| < R, 1\leqslant i \leqslant n\}.\end{align*} $$
Additionally, for any
$z \in \mathbb {C}$
, let
$B_R(z)$
denote the open ball of radius R centred at z. We may safely assume that
$r \geqslant {1}/{\sqrt {n}}$
, as the theorem easily follows otherwise.
Next, observe that, for any
$i \neq j$
,
$B_r(\alpha _i)$
and
$B_r(\alpha _j)$
are disjoint. Additionally, for any
$R> 0$
,
$$ \begin{align*}B_{R+r}(0) \supsetneq \bigcup_{|\alpha_i| \leqslant R} B_r(\alpha_i).\end{align*} $$
As a consequence,
$$ \begin{align*}\pi(R+r)^2 = \operatorname{vol}(B_{R+r}(0))> \sum_{|\alpha_i| \leqslant R} \operatorname{vol}(B_r(\alpha_i)) = N(R)\cdot\pi r^2,\end{align*} $$
which implies that
$$ \begin{align} N(R) < \bigg(\frac{R}{r} + 1\bigg)^2. \end{align} $$
Now, for each positive integer
$j \leqslant \lceil \log _2(n)\rceil - 1 =: L$
(here, we use the assumption that
$n \geqslant 3$
to obtain
$L \geqslant 1$
), define
$R_j = r(\sqrt {n/2^j} - 1)$
. Note that
$R_j> 0$
for
$j \leqslant L$
. For each j, we aim to bound from below the number of roots
$\alpha _i$
that satisfy
$R_j < |\alpha _i|$
.
Observe that
$N(R_j) < n/2^j$
by (2.1), and hence, for each j with
$1 \leqslant j \leqslant L$
, there must be at least
$n(2^j - 1)/2^j$
roots
$\alpha _i$
that satisfy
$|\alpha _i| \geqslant R_j$
. Therefore,
$$ \begin{align} M(f) \geqslant \prod_{|\alpha_i| \geqslant R_L} |\alpha_i| & = (r\sqrt{n})^{n-N(R_L)} \prod_{|\alpha_i| \geqslant R_L} \frac{|\alpha_i|}{r\sqrt{n}}\nonumber\\ &\geqslant (r\sqrt{n})^{n-N(R_L)}\bigg(\frac{R_1}{r\sqrt{n}}\bigg)^{n/2}\bigg(\frac{R_2}{r\sqrt{n}}\bigg)^{n/4}\cdots \bigg(\frac{R_L}{r\sqrt{n}}\bigg)^{n/2^L}. \end{align} $$
The remainder of this proof will be dedicated to showing that
$$ \begin{align*}\bigg(\frac{R_1}{r\sqrt{n}}\bigg)^{n/2}\bigg(\frac{R_2}{r\sqrt{n}}\bigg)^{n/4}\cdots \bigg(\frac{R_L}{r\sqrt{n}}\bigg)^{n/2^L} \geqslant \frac{1}{4n^2\cdot16^n}.\end{align*} $$
First, note that, for any
$j \leqslant L$
,
$$ \begin{align*} \frac{R_j}{r\sqrt{n}} = 2^{-j/2} - n^{-1/2} = \frac{2^{-j} - n^{-1}}{2^{-j/2} + n^{-1/2}} = \frac{n - 2^j}{n\cdot2^j(2^{-j/2} + n^{-1/2})}. \end{align*} $$
Since
$j \leqslant L$
, we have
$n^{-1/2} \leqslant 2^{-j/2}$
, which implies that
$2^{-j/2} + n^{-1/2} \leqslant 2^{-j/2 + 1}$
. Hence,
$$ \begin{align*}\frac{R_j}{r\sqrt{n}} \geqslant \frac{n - 2^j}{n\cdot2^{j/2 + 1}}.\end{align*} $$
We now make slightly different estimates for
$j = L$
and for
$j < L$
. If
$j = L$
,
$$ \begin{align*}\frac{R_L}{r\sqrt{n}} \geqslant \frac{1}{n\cdot2^{L/2 + 1}}.\end{align*} $$
If
$j < L$
, we use the fact that
$2^L < n \leqslant 2^{L+1}$
to find that
$$ \begin{align*}\frac{R_j}{r\sqrt{n}} \geqslant \frac{n - 2^j}{n\cdot2^{j/2 + 1}} \geqslant \frac{2^L - 2^j}{2^{L + j/2 + 2}} = \frac{1 - 2^{j-L}}{2^{j/2 + 2}} \geqslant \frac{1}{2^{j/2 + 3}}.\end{align*} $$
Consequently,
$$ \begin{align*} \prod_{j=1}^L \bigg(\frac{R_j}{r\sqrt{n}}\bigg)^{n/2^j} &\geqslant \bigg[\bigg(\frac{1}{n\cdot2^{L/2+1}}\bigg)^{2^{-L}}\cdot\prod_{j=1}^{L-1}2^{(-j/2 - 3)/2^j}\bigg]^n\\ &= \bigg[\frac{1}{(2n)^{2^{-L}}} \cdot 2^{-\sum_{j=1}^L j/2^{j+1}} \cdot 8^{-\sum_{j=1}^{L-1} 2^{-j}}\bigg]^n\\ & \geqslant \bigg[\frac{1}{(2n)^{2^{-L}}} \cdot 2^{-\sum_{j\geqslant1} j/2^{j+1}} \cdot 8^{-\sum_{j\geqslant1} 2^{-j}}\bigg]^n. \end{align*} $$
The series in the above exponents converge, with
$\sum _{j \geqslant 1} 2^{-j} = 1$
and
$\sum _{j \geqslant 1} j \cdot 2^{-(j+1)} = 1$
. Hence, since
$n \leqslant 2^{L+1}$
,
$$ \begin{align*}\prod_{j=1}^L \bigg(\frac{R_j}{r\sqrt{n}}\bigg)^{n/2^j} \geqslant \frac{1}{(2n)^{n/2^L}}\cdot(2^{-1}\cdot 8^{-1})^n \geqslant \frac{1}{4n^2\cdot16^n}.\end{align*} $$
Finally, we can return to inequality (2.2) and we acquire
$$ \begin{align} M(f) \geqslant \frac{1}{4n^2\cdot16^n}\cdot(r\sqrt{n})^{n - N(R_L)}. \end{align} $$
Since
$N(R_L) < n/2^L \leqslant 2$
and since
$N(R_L)$
is an integer, we actually have
$N(R_L) \leqslant 1$
. Since we have assumed that
$r \geqslant 1/\sqrt {n}$
, inequality (2.3) implies that
$$ \begin{align*}M(f) \geqslant \frac{1}{4n^2\cdot16^n}\cdot(r\sqrt{n})^{n-1}\end{align*} $$
and we get
$$ \begin{align*}\operatorname{sep}(f) = 2r \leqslant \frac{2\cdot(4n^2)^{1/(n-1)}\cdot16^{1 + 1/(n-1)}}{\sqrt{n}}\cdot M(f)^{1/(n-1)} \leqslant \frac{34}{\sqrt{n}} \cdot M(f)^{1/(n-1)}, \end{align*} $$
where we use the fact that
$n \geqslant 290$
in the final inequality.
Note that the additional, stronger statement for
$f(x) \in \mathbb {R}[x]$
also follows. If
$f(x)$
has a nonreal root among its roots of minimum absolute value, then we cannot have
$N(R_L) = 1$
, so we must have
$N(R_L) = 0$
. Hence, inequality (2.3) implies that
$$ \begin{align*}M(f) \geqslant \frac{1}{4n^2}\bigg(\frac{r\sqrt{n}}{16}\bigg)^n,\end{align*} $$
and the theorem statement again follows.
We now demonstrate that both bounds are optimal except possibly for the constant 34. We do this by constructing a family of polynomials whose separation nearly attains the upper bound which we have now proved.
Before we do this, we note the following fact about the Gaussian integers. For
$r \geqslant 0$
, let
$G(r)$
denote the number of Gaussian integers
$a + bi$
for
$a,b \in \mathbb {Z}$
that satisfy
$|a + bi| \leqslant r$
. A well-known result of Gauss (see, for example, [Reference Berndt, Kim and Zaharescu2, page 101]) states that
$$ \begin{align*}\pi(r - \sqrt{2})^2 \leqslant G(r) \leqslant \pi (r + \sqrt{2})^2 \quad\mbox{for}\ r \geqslant \sqrt{2}.\end{align*} $$
Fix an integer
$n \geqslant 2$
and a real number
$t \geqslant 1$
. Set
$R = \sqrt {n/\pi } + \sqrt {2}$
, which implies that there are at least n Gaussian integers
$a + bi$
with
$|a + bi| \leqslant R$
. Select n distinct Gaussian integers
$\alpha _1,\ldots ,\alpha _n$
so that:
-
(1)
$\alpha _1 = 0$
; and -
(2)
$|\alpha _j| \leqslant R$
for
$1 \leqslant j \leqslant n$
.
Now define
$$ \begin{align*}f_t(x) = \prod_{j=1}^n (x - t\alpha_j).\end{align*} $$
For
$j \geqslant 2$
, we have
$|\alpha _j| \geqslant 1$
, which implies that
$$ \begin{align*}M(f_t) = \prod_{j=2}^n t|\alpha_j| \leqslant (tR)^{n-1} \leqslant (1.6\operatorname{sep}(f_t)\sqrt{n})^{n-1},\end{align*} $$
and that
$\operatorname {sep}(f_t) \geqslant M(f_t)^{1/(n-1)}/{1.6\sqrt {n}}.$
Hence, the first upper bound on separation in Theorem 1.4 has the best possible dependence on n.
For the remaining examples, we take
$R = \sqrt {(n+1)/\pi } + \sqrt {2}$
and we choose n distinct Gaussian integers
$\beta _1,\ldots ,\beta _n$
so that:
-
(1)
$0 < |\beta _j| \leqslant R$
for
$1 \leqslant j \leqslant n$
; -
(2) the set
$\{\beta _1,\ldots ,\beta _n\}$
is closed under complex conjugation; and -
(3) there exists
$\beta _j \notin \mathbb {R}$
so that
$|\beta _j| = \min _k|\beta _k|$
.
Observe that condition (1) together with the fact that the
$\beta _k$
are Gaussian integers implies that
$\min _k |\beta _k| \geqslant 1$
. For real
$t \geqslant 1$
, we define
$$ \begin{align*}g_t(x) = \prod_{j=1}^n (x - t\beta_j) \in \mathbb{R}[x]\end{align*} $$
and now we have
$$ \begin{align*}M(g_t) = \prod_{j=1}^n t|\beta_j| \leqslant (tR)^n \leqslant (1.7\sqrt{n}\operatorname{sep}(g_t))^n,\end{align*} $$
which implies that
$\operatorname {sep}(g_t) \geqslant M(g_t)^{1/n}/{1.7\sqrt {n}}$
. Hence, the second upper bound on separation in Theorem 1.4 has the best possible dependence on n.
We remark that the constant factors of 1.6 and 1.7 can be improved by replacing the square lattice of Gaussian integers with the hexagonal lattice, and with some extra work using partial summation to find a more efficient upper bound on
$M(f_t)$
and
$M(g_t)$
.
3 Improving the constant factor
Our main goal of this section is to prove Theorem 1.5, which we will do in stages.
Proposition 3.1. Let
$f(x) \in \mathbb {R}[x]$
be monic and separable with degree
$n \geqslant 4$
. Suppose, further, that all n of the roots of f are real. Then
$$ \begin{align*}\operatorname{sep}(f) \leqslant \frac{6.33}{n}\cdot M(f)^{1/(n-1)}.\end{align*} $$
Moreover, as
$n \to \infty $
,
$$ \begin{align} \operatorname{sep}(f) \leqslant \frac{2e+o(1)}{n}\cdot M(f)^{1/(n-1)}, \end{align} $$
and the constant
$2e$
is asymptotically sharp.
Proposition 3.2. Let
$f(x) \in \mathbb {R}[x]$
be monic and separable with degree three. If
$f(x)$
has exactly one real root, then
$$ \begin{align*}\operatorname{sep}(f) \leqslant \sqrt{3M(f)}.\end{align*} $$
Moreover, the constant
$\sqrt {3}$
is optimal.
Proposition 3.3. Let
$f(x) \in \mathbb {R}[x]$
be monic and separable with degree four. If
$f(x)$
has no real roots, then
$$ \begin{align*}\operatorname{sep}(f) \leqslant \sqrt{2} \cdot M(f)^{1/4}.\end{align*} $$
Moreover, the constant
$\sqrt {2}$
is optimal.
These propositions cover each of the cases stated in Theorem 1.5 except the case where the signature is
$(2,0)$
or
$(3,0)$
, when the result follows from Theorem 1.4.
We first prove a lemma on bounding binomial coefficients.
Lemma 3.4. For any positive integer
$n \geqslant 3$
,
$$ \begin{align*}\binom{n}{\lfloor n/2\rfloor} \leqslant \frac{2^{n+1}}{\sqrt{\pi(2n+1)}}.\end{align*} $$
Proof. It is known that, for any positive integer
$\ell $
,
$$ \begin{align*}\binom{2\ell}{\ell} \leqslant \frac{2^{2\ell}}{\sqrt{\pi (\ell+1/4)}}\end{align*} $$
(see, for example, [Reference Johnson11]). If n is even,
$$ \begin{align*}\binom{n}{\lfloor n/2\rfloor} \leqslant \frac{2^{n}}{\sqrt{\pi(n/2 + 1/4)}} = \frac{2^{n+1}}{\sqrt{\pi(2n + 1)}}.\end{align*} $$
If n is odd, say
$n = 2k + 1$
, then
$$ \begin{align*} \binom{n}{\lfloor n/2\rfloor} = \binom{2k + 1}{k} = \frac{2k + 1}{k + 1} \binom{2k}{k} \leqslant \frac{2k + 1}{k + 1}\cdot\frac{2^{2k}}{\sqrt{\pi(k+1/4)}} = \frac{n}{n + 1}\cdot\frac{2^{n+1}}{\sqrt{\pi (2n-1)}} \end{align*} $$
and one can now check that
${n}/{((n+1)\sqrt {2n-1})} \leqslant {1}/{\sqrt {2n + 1}}$
to complete the proof.
Proof of Proposition 3.1.
Denote the closest root of
$f(x)$
to 0 by
$\alpha $
and let
$r = \operatorname {sep}(f)$
. Suppose that there are s roots of
$f(x)$
which are less than
$\alpha $
and t roots of
$f(x)$
which are greater than
$\alpha $
. Define
$$ \begin{align*}g(x) = \prod_{i = 1}^t (x - \alpha - ri) \cdot (x - \alpha) \cdot \prod_{j = 1}^s (x - \alpha + rj)\end{align*} $$
and observe that
$M(f) \geqslant M(g)$
because the roots of g are no further from the origin than the corresponding roots of f. Furthermore,
$\operatorname {sep}(f) = r = \operatorname {sep}(g)$
, so it suffices to prove the proposition for
$g(x)$
.
We first consider the case where all roots of g have the same sign. In this case, we can assume that
$\alpha \geqslant 0$
without loss of generality. Then the roots of g are simply given by
$\alpha , \alpha +r, \ldots , \alpha +(n-1)r$
. Thus,
$$ \begin{align*}M(g)\geqslant \prod_{j=1}^{n-1} (\alpha+jr) \geqslant \prod_{j=1}^{n-1} (jr)=(n-1)!r^{n-1}.\end{align*} $$
It follows that
$$ \begin{align*}\operatorname{sep}(g)=r\leqslant \bigg(\frac{M(g)}{(n-1)!}\bigg)^{1/(n-1)}<\frac{e}{n} \cdot M(g)^{1/(n-1)}.\end{align*} $$
Next, we consider the case where not all roots of g have the same sign. Let
$\beta $
be the closest root of
$g(x)$
to the origin and write
$$ \begin{align*}g(x) = \prod_{i = 1}^T (x - \beta - ri) \cdot (x - \beta) \cdot \prod_{j = 1}^S (x - \beta + rj). \end{align*} $$
Since
$\beta $
is the closest root of
$g(x)$
to 0 and since
$g(x)$
has a root with the opposite sign to
$\beta $
, we find that
$|\beta | \leqslant r/2$
. We may also assume, without loss of generality, that
$\beta \leqslant 0$
(otherwise, we may apply the same proof to
$g(-x)$
). We now have
$$ \begin{align} M(g) \geqslant \prod_{i = 1}^{T} |\beta + ri| \cdot \prod_{j = 1}^{S} |\beta - rj| & \geqslant \prod_{i = 1}^{T} \bigg(ri - \frac{r}{2}\bigg) \cdot \prod_{j = 1}^{S} \bigg(rj + \frac{r}{2}\bigg) \notag \\ &= r^{n-1} \cdot \prod_{i = 1}^{T} \bigg(i - \frac{1}{2}\bigg) \cdot \prod_{j = 1}^{S} \bigg(j + \frac{1}{2}\bigg). \end{align} $$
Getting an understanding of the lower bound given in inequality (3.2) will require use of the gamma function. We use the fact that
$\Gamma (\tfrac 12) = \sqrt {\pi }$
together with the usual fact that
$\Gamma (z) = (z - 1)\Gamma (z-1)$
to note that
$$ \begin{align*}\prod_{i = 1}^T \bigg(i - \frac{1}{2}\bigg) = \frac{\Gamma(T + \frac{1}{2})}{\sqrt{\pi}}\quad \text{and}\quad \prod_{j = 1}^S \bigg(j + \frac{1}{2}\bigg) = \frac{2\Gamma(S + \frac{3}{2})}{\sqrt{\pi}}.\end{align*} $$
By Wendel’s inequality [Reference Wendel19], if m is a nonnegative integer, then
$$ \begin{align*} \Gamma\bigg(m+\frac{1}{2}\bigg)> \frac{m\Gamma(m)}{\sqrt{m+\frac{1}{2}}}=\frac{m!}{\sqrt{m+\frac{1}{2}}}. \end{align*} $$
Thus,
$$ \begin{align*} \prod_{i = 1}^{T} \bigg(i - \frac{1}{2}\bigg) = \frac{\Gamma(T + \frac{1}{2})}{\sqrt{\pi}}> \frac{T!}{\sqrt{\pi(T+\frac{1}{2})}}, \quad \prod_{j = 1}^{S} \bigg(j + \frac{1}{2}\bigg) = \frac{2\Gamma(S + \frac{3}{2})}{\sqrt{\pi}} > \frac{2(S +1)!}{\sqrt{\pi(S + \frac{3}{2})}}. \end{align*} $$
Now we have
$$ \begin{align} M(g) \geqslant r^{n-1} \cdot \frac{T!}{\sqrt{\pi(T+\frac{1}{2})}}\cdot \frac{2(S +1)!}{\sqrt{\pi(S + \frac{3}{2})}} \end{align} $$
from inequality (3.2) and we aim to estimate the right-hand side of this inequality from below in terms of n. We have the restrictions
$0 \leqslant S,T \leqslant n$
and
$S + T + 1 = n$
, so we can replace
$S + 1$
in equation (3.3) by
$n - T$
to find
$$ \begin{align} \frac{T!}{\sqrt{\pi(T+\frac{1}{2})}}\cdot \frac{2(S +1)!}{\sqrt{\pi(S + \frac{3}{2})}} &= \frac{T!}{\sqrt{\pi(T+\frac{1}{2})}}\cdot \frac{2(n-T )!}{\sqrt{\pi(n-T + \frac{1}{2})}} \notag\\ &= \frac{2n!}{\pi\binom{n}{T}\sqrt{(T + \frac{1}{2})(n - T + \frac{1}{2})}} \geqslant \frac{4n!}{\pi\binom{n}{\lfloor n/2 \rfloor} (n+1)}. \end{align} $$
Using Lemma 3.4 and Robbins’ bound
$n!>\sqrt {2\pi n} (n/e)^n e^{1/(12n+1)}$
[Reference Robbins16] gives
$$ \begin{align*} & \frac{T!}{\sqrt{\pi(T+\frac{1}{2})}}\cdot \frac{2(S +1)!}{\sqrt{\pi(S + \frac{3}{2})}} \geqslant \frac{4n!}{\pi\binom{n}{\lfloor n/2 \rfloor} (n+1)} \geqslant \frac{n!\cdot \sqrt{2n+1}}{\sqrt{\pi}2^{n-1} (n+1)}\\& \quad > \frac{\sqrt{2n}(n/e)^n e^{{1}/{(12n + 1)}}\sqrt{2n + 1}}{2^{n-1}(n + 1)} =\bigg(\frac{n}{2e}\bigg)^n \cdot \frac{2\sqrt{2n(2n+1)}e^{{1}/{(12n + 1)}}}{n+1} > 3.46\bigg(\frac{n}{2e}\bigg)^n \end{align*} $$
by the fact that
$n \geqslant 4$
.
Finally, we return to inequality (3.3) to find that that
$$ \begin{align*} M(g) &\geqslant 3.46\operatorname{sep}(g)^{n-1} \bigg(\frac{n}{2e}\bigg)^n, \end{align*} $$
and we can conclude that
$$ \begin{align*}\operatorname{sep}(g) \leqslant \bigg(\frac{M(g)}{3.46}\bigg)^{{1}/{(n-1)}} \bigg(\frac{2e}{n}\bigg)^{{n}/{(n-1)}} \leqslant \frac{2e(2e/3.46)^{1/3}}{n^{{n}/{(n-1)}}} M(g)^{{1}/{(n-1)}} \leqslant \frac{6.33}{n} M(g)^{{1}/{(n-1)}}.\end{align*} $$
Asymptotically, using Stirling’s approximation
$n! \sim \sqrt {2\pi n} (n/e)^n$
, we can combine inequality (3.3) and inequality (3.4) to deduce that
$$ \begin{align*} M(g) \geqslant \operatorname{sep}(g)^{n-1} \frac{4n!}{\pi\binom{n}{\lfloor n/2 \rfloor} (n+1)} \geqslant (4-o(1))\operatorname{sep}(g)^{n-1} \bigg(\frac{n}{2e}\bigg)^n, \end{align*} $$
as
$n \to \infty $
. It follows that
$\operatorname {sep}(g)\leqslant ({(2e+o(1))}/{n}) M(g)^{{1}/{(n-1)}}$
as
$n \to \infty $
.
Finally, we show that the constant
$2e$
is asymptotically sharp in inequality (3.1). Let
$r>1$
be fixed. For each integer
$n \geqslant 4$
, set
$f_n(x)=\prod _{j=-m}^{m} (x-jr)$
if
$n=2m+1$
is odd, and
$f_n(x)=\prod _{j=-m}^{m+1} (x-jr)$
if
$n=2m+2$
is even. Stirling’s approximation then yields
$\operatorname {sep}(f_n)=({(2e+o(1))}/{n}) M(f_n)^{{1}/{(n-1)}}$
as
$n \to \infty $
.
Next, we consider cubic polynomials that have only one real root.
Proof of Proposition 3.2.
Suppose that the real root of
$f(X)$
is
$\alpha $
; without loss of generality, we may assume that
$\alpha \geqslant 0$
. Let
$\beta $
denote the complex root of
$f(X)$
with positive imaginary part. Write
$\beta = x + iy$
for
$x,y \in \mathbb {R}$
.
We claim that we may assume that
$x \leqslant 0$
. If not, then set
$\beta ' = -x + iy$
and
$g(X) = (X - \alpha )(X - \beta ')(X - \overline {\beta '})$
. Since
$\operatorname {sep}(g) \geqslant \operatorname {sep}(f)$
and
$M(g) = M(f)$
, proving the proposition for
$g(X)$
will prove it for
$f(X)$
. Hence, we only need to prove the proposition under the assumption that
$x \leqslant 0$
.
Let
$R = |\beta |$
. Note that, if
$y \leqslant {\sqrt {3}R}/{2}$
, then
$$ \begin{align*}\operatorname{sep}(f) \leqslant |\beta - \overline{\beta}| = 2y \leqslant \sqrt{3}R \leqslant \sqrt{3}M(f)^{1/2}\end{align*} $$
and the proof is complete. Hence, for the rest of the proof, assume that
$y> {\sqrt {3}R}/{2}$
. In particular, this implies that
$y> -x\sqrt {3}$
.
Our next goal is to reduce to the case where
$\alpha $
is ‘small’. Let t be the unique value in
$\mathbb {R}$
for which the points
$t,\beta ,\overline {\beta }$
form an equilateral triangle. One can check that
$t = \sqrt {3}y + x$
. Note that
$t> -x\sqrt {3} + x = -x(\sqrt {3}-1) \geqslant 0$
. Now, if
$\alpha \geqslant t$
, set
$h(X) = (X - t)(X - \beta )(X - \overline {\beta })$
; we have
$\operatorname {sep}(f) = 2y = \operatorname {sep}(h)$
and
$M(f) \geqslant M(h)$
, so it suffices to prove the proposition for h. Hence, we may assume that
$0 \leqslant \alpha < t$
.
Note that
$M(f)=\max \{1, \alpha \} \cdot \max \{1, x^2+y^2\}$
and
$\operatorname {sep}(f)=|\alpha -\beta |=\sqrt {(\alpha -x)^2+y^2}$
. Our goal is to show that
$M(f)/\operatorname {sep}(f)^2 \geqslant \tfrac 13$
. We divide our proof into two cases.
Case 1:
$x^2 + y^2 \geqslant 1$
. Within this case, we have two subcases. First, assume that
$\alpha < 1$
. Then
$$ \begin{align*}\frac{M(f)}{\operatorname{sep}(f)^2} = \frac{x^2 + y^2}{(\alpha - x)^2 + y^2} \geqslant \frac{x^2 + y^2}{(1 - x)^2 + y^2}.\end{align*} $$
We aim to show that
$$ \begin{align*}\frac{x^2 + y^2}{(1 - x)^2 + y^2} \geqslant \frac{1}{3}\end{align*} $$
or, equivalently, that
$2(x^2 + y^2) \geqslant 1 - 2x.$
If
$-1/2 \leqslant x \leqslant 0$
, then this follows immediately from the fact that
$x^2 + y^2 \geqslant 1$
. If
$x < -1/2$
, then we can use the fact that
$y> -x\sqrt {3}$
to deduce that
$2(x^2 + y^2) \geqslant 8x^2> 1 - 2x.$
Next, assume that
$1 \leqslant \alpha \leqslant t$
. Then
$$ \begin{align*}\frac{M(f)}{\operatorname{sep}(f)^2} = \frac{\alpha(x^2 + y^2)}{(\alpha - x)^2 + y^2} = \frac{x^2 + y^2}{\alpha - 2x + \frac{x^2 + y^2}{\alpha}}.\end{align*} $$
Observe that the denominator, as a function of
$\alpha $
, will be maximized at either
$\alpha = 1$
or
$\alpha = t$
. In the case of
$\alpha = 1$
, we have already shown that
$$ \begin{align*}\frac{x^2 + y^2}{(1 - x)^2 + y^2} \geqslant \frac{1}{3}.\end{align*} $$
So it remains to check that
$$ \begin{align*}\frac{t(x^2 + y^2)}{(t-x)^2 + y^2} \geqslant \frac{1}{3}.\end{align*} $$
First, observe that, since
$t = x + y\sqrt {3}$
,
$$ \begin{align*}\frac{t(x^2 + y^2)}{(t-x)^2 + y^2} = \frac{t((t-y\sqrt{3})^2 + y^2)}{4y^2} = \frac{t^3 - 2\sqrt{3}t^2y+4ty^2}{4y^2}.\end{align*} $$
Next, observe that
$(t^3 - 2\sqrt {3}t^2y+4ty^2)/(4y^2)$
is a nondecreasing function of t since its partial derivative with respect to t is
$3(t - 2y/\sqrt {3})^2/(4y^2)$
. Note, additionally, that, since
$y \geqslant -x\sqrt {3}$
,
$$ \begin{align*}t = \sqrt{3}y + x \geqslant \bigg(\sqrt{3} - \frac{1}{\sqrt{3}}\bigg)y = \frac{2}{\sqrt{3}}y.\end{align*} $$
Since
$(t^3 - 2\sqrt {3}t^2y+4ty^2)/(4y^2)$
is nondecreasing in t and
$t \geqslant ({2}/{\sqrt {3}})y$
, we must have
$$ \begin{align*}\frac{t^3 - 2\sqrt{3}t^2y+4ty^2}{4y^2} \geqslant \frac{2}{3\sqrt{3}}y.\end{align*} $$
But the fact that
$x^2 + y^2 \geqslant 1$
together with the assumption that
$y \geqslant -x\sqrt {3}$
imply that
$y \geqslant \sqrt {3}/2$
, and hence we can finally conclude that
$$ \begin{align*}\frac{M(f)}{\operatorname{sep}(f)^2} = \frac{t(x^2 + y^2)}{(t-x)^2 + y^2} = \frac{t^3 - 2\sqrt{3}t^2y+4ty^2}{4y^2} \geqslant \frac{2}{3\sqrt{3}}y \geqslant \frac{1}{3}.\end{align*} $$
Case 2:
$x^2 + y^2 < 1$
. Now note that, since
$x^2 + y^2 < 1$
and
$y \geqslant -x\sqrt {3}$
, we must have
$x \geqslant -1/2$
. Again, we have two subcases. First, if
$\alpha < 1$
, then
$$ \begin{align*}\frac{M(f)}{\operatorname{sep}(f)^2} = \frac{1}{(\alpha - x)^2 + y^2} \geqslant \frac{1}{(1 - x)^2 + y^2} = \frac{1}{1 - 2x + x^2 + y^2} \geqslant \frac{1}{2 - 2x} \geqslant \frac{1}{3}\end{align*} $$
and the proof is complete.
Now assume that
$1 \leqslant \alpha \leqslant t$
. The fact that
$t \geqslant 1$
implies that
$y = (t-x)/\sqrt {3} \geqslant 1/\sqrt {3}$
. In this case,
$$ \begin{align*}\frac{M(f)}{\operatorname{sep}(f)^2} = \frac{\alpha}{(\alpha - x)^2 + y^2} = \frac{1}{\alpha - 2x + \frac{x^2 + y^2}{\alpha}},\end{align*} $$
which is again minimised when
$\alpha = 1$
or
$\alpha = t$
. We have already shown that
$$ \begin{align*}\frac{1}{(1 - x)^2 + y^2} \geqslant \frac{1}{3},\end{align*} $$
so it remains to show that
$$ \begin{align*} \frac{t}{4y^2}= \frac{t}{(t - x)^2 + y^2} \geqslant \frac{1}{3}.\end{align*} $$
If
$y \leqslant {\sqrt {3}}/{2}$
, then
${t}/{4y^2}\geqslant {t}/{3} \geqslant {1}/{3}$
. If
$y \geqslant \sqrt {3}/2$
, then we use the fact that
$x \geqslant -\sqrt {1-y^2}$
to get
$$ \begin{align*}\frac{t}{4y^2} = \frac{x + y\sqrt{3}}{4y^2} \geqslant \frac{y\sqrt{3}-\sqrt{1-y^2}}{4y^2}\geqslant \frac{1}{3}.\end{align*} $$
We can see that the constant
$\sqrt {3}$
is optimal for the polynomial
$f(x) = x^3 - 1$
.
Finally, we turn our attention to the case where
$f(x)$
is a quartic with no real roots.
Proof of Proposition 3.3.
Suppose that the roots of
$f(x)$
are
$\alpha ,\bar {\alpha },\beta ,\bar {\beta }$
where
${\mathrm {Im}}[\alpha ]$
,
${\mathrm {Im}}[\beta ]> 0$
and
$|\alpha | = r \leqslant |\beta | = R$
. Note that
$\operatorname {sep}(f) = \min \{2{\mathrm { Im}}[\alpha ],2{\mathrm {Im}}[\beta ], |\alpha - \beta |\}$
. We have the following two cases.
Case 1:
$2 r \leqslant R$
. In this case, we note that
$$ \begin{align*}\operatorname{sep}(f) \leqslant 2{\mathrm{Im}}[\alpha] \leqslant 2r\leqslant 2r^{1/2}\bigg(\frac{R}{2}\bigg)^{1/2} = \sqrt{2}r^{1/2}R^{1/2} \leqslant \sqrt{2}M(f)^{1/4}.\end{align*} $$
Case 2:
$r \leqslant R < 2r$
. In this case, we first observe that if
${\mathrm {Im}}[\alpha ] < \tfrac 12{\sqrt {2}}r^{1/2}R^{1/2}$
or if
${\mathrm {Im}}[\beta ] < \tfrac 12\sqrt {2}r^{1/2}R^{1/2}$
, then the proof is complete because
$$ \begin{align*}\operatorname{sep}(f) \leqslant \min\{2{\mathrm{Im}}[\alpha],2{\mathrm{Im}}[\beta]\} \leqslant \sqrt{2}r^{1/2}R^{1/2} \leqslant \sqrt{2}M(f)^{1/4}.\end{align*} $$
Hence,
$$ \begin{align*}\alpha \in \bigg\{z \in \mathbb{C} : |z| = r \text{ and } {\mathrm{Im}}[z] \geqslant \frac{\sqrt{2}}{2}r^{1/2}R^{1/2}\bigg\}=:S\end{align*} $$
and
$$ \begin{align*}\beta \in \bigg\{z \in \mathbb{C} : |z| = R \text{ and } {\mathrm{Im}}[z] \geqslant \frac{\sqrt{2}}{2}r^{1/2}R^{1/2}\bigg\}=:T.\end{align*} $$
As a result,
$$ \begin{align*} \operatorname{sep}(f) &\leqslant |\alpha - \beta| \leqslant \sup_{\substack{z_1 \in S\\z_2 \in T}} |z_1 - z_2|\\ &= \bigg|\bigg(\sqrt{r^2 - \frac{rR}{2}} + i\cdot \frac{\sqrt{2}}{2}r^{1/2}R^{1/2}\bigg) - \bigg(-\sqrt{R^2 - \frac{rR}{2}} + i\cdot \frac{\sqrt{2}}{2}r^{1/2}R^{1/2}\bigg)\bigg|\\ &= \sqrt{r^2 - \frac{rR}{2}} + \sqrt{R^2 - \frac{rR}{2}}. \end{align*} $$
We claim that
$$ \begin{align*}\sqrt{r^2 - \frac{rR}{2}} + \sqrt{R^2 - \frac{rR}{2}} \leqslant \sqrt{2}r^{1/2}R^{1/2}.\end{align*} $$
To see this, divide both sides of the inequality by
$r^{1/2}R^{1/2}$
to obtain the equivalent inequality
$$ \begin{align*}\sqrt{\frac{r}{R} - \frac{1}{2}} + \sqrt{\frac{R}{r} - \frac{1}{2}} \leqslant \sqrt{2}.\end{align*} $$
Observe that this new inequality depends only on the ratio
$x = {R}/{r}$
, which we have bounded by
$1 \leqslant x < 2.$
It is now a simple calculus problem to show that
$$ \begin{align*}\sqrt{\frac{1}{x} - \frac{1}{2}} + \sqrt{x - \frac{1}{2}} \leqslant \sqrt{2}\end{align*} $$
for
$1 \leqslant x < 2$
, and the proof that
$\operatorname {sep}(f) \leqslant \sqrt {2}M(f)^{1/4}$
is complete.
To see that the bound is sharp, consider the family of polynomials
$$ \begin{align*}f_t(x) = (x - t(1+i))(x - t(1-i))(x - t(-1+i))(x - t(-1-i))\end{align*} $$
for
$t \in \mathbb {R}$
with
$t \geqslant 1/\sqrt {2}$
. Every polynomial in this family has
$\operatorname {sep}(f_t) = \sqrt {2}M(f_t)^{1/4}.$
Acknowledgements
The first author would like to thank Chris Sinclair and Joe Webster for their helpful suggestions regarding the development of this project. The second author thanks Gabriel Currier and Kenneth Moore for helpful discussions. Both authors would like to thank Andrej Dujella and Tomislav Pejković for their comments on an early draft of this paper. The authors are also grateful to anonymous referees for their valuable comments and corrections.
