Hostname: page-component-6dbcb7884d-t8hx9 Total loading time: 0 Render date: 2025-02-13T18:17:28.262Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MARCH’S CRITERION FOR TRANSIENCE ON ROTATIONALLY SYMMETRIC MANIFOLDS

Part of: Global differential geometry Other generalizations

Published online by Cambridge University Press:  10 February 2025

JOHN E. BRAVO Open the ORCID record for JOHN E. BRAVO [Opens in a new window]  and
JEAN C. CORTISSOZ Open the ORCID record for JEAN C. CORTISSOZ [Opens in a new window]
JOHN E. BRAVO
Affiliation:
Department of Mathematics, Universidad de los Andes, Bogotá DC, Colombia e-mail: j.bravob@uniandes.edu.co
JEAN C. CORTISSOZ*
Affiliation:
Department of Mathematics, Universidad de los Andes, Bogotá DC, Colombia
*
e-mail: jcortiss@uniandes.edu.co
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that March’s criterion for the existence of a bounded nonconstant harmonic function on a weak model (that is, 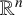$\mathbb {R}^n$ with a rotationally symmetric metric) is also a necessary and sufficient condition for the solvability of the Dirichlet problem at infinity on a family of metrics that generalise metrics with rotational symmetry on 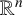$\mathbb {R}^n$. When the Dirichlet problem at infinity is not solvable, we prove some quantitative estimates on how fast a nonconstant harmonic function must grow.

Keywords

Dirichlet problem at infinitybounded harmonic functionsmodel Riemannian space

MSC classification

Primary: 31C12: Potential theory on Riemannian manifolds
Secondary: 31C05: Harmonic, subharmonic, superharmonic functions 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ancona, A., ‘Convexity at infinity and Brownian motion on manifolds with unbounded negative curvature’, Rev. Mat. Iberoam. 10(1) (1994), 189–220.CrossRefGoogle Scholar
Anderson, M., ‘The Dirichlet problem at infinity for manifolds of negative curvature’, J. Differential Geom. 18(4) (1983), 701–721.CrossRefGoogle Scholar
Anderson, M. and Schoen, R., ‘Positive harmonic functions on complete manifolds of negative curvature’, Ann. of Math. (2) 121(3) (1985), 429–461.CrossRefGoogle Scholar
Bravo, J. E. and Cortissoz, J. C., ‘On Liouville’s theorem’, Preprint, 2024, arXiv:2405.14443.Google Scholar
Choi, H., ‘An asymptotic Dirichlet problems for harmonic functions on Riemannian manifolds’, Trans. Amer. Math. Soc. 281(2) (1984), 691–716.CrossRefGoogle Scholar
Colding, T. and Minicozzi, W. III, ‘Harmonic functions with polynomial growth’, J. Differential Geom. 45 (1997), 1–77.Google Scholar
Cortissoz, J. C., ‘An observation on the Dirichlet problem at infinity in Riemannian cones’, Nagoya Math. J. 250 (2023), 352–364.CrossRefGoogle Scholar
Grigor’yan, A., ‘Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds’, Bull. Amer. Math. Soc. (N.S.) 36(2) (1999), 135–249.CrossRefGoogle Scholar
Hsu, E. P., Stochastic Analysis on Manifolds, Graduate Studies in Mathematics, 38 (American Mathematical Society, Providence, RI, 2002).CrossRefGoogle Scholar
March, P., ‘Brownian motion and harmonic functions on rotationally symmetric manifolds’, Ann. Probab. 14(3) (1986), 793–801.CrossRefGoogle Scholar
Milnor, J., ‘On deciding whether a surface is parabolic or hyperbolic’, Amer. Math. Monthly 84 (1977), 43–46.CrossRefGoogle Scholar
Neel, R., ‘Brownian motion and the Dirichlet problem at infinity on two-dimensional Cartan–Hadamard manifolds’, Potential Anal. 41, 443–462.CrossRefGoogle Scholar
Peetre, J., ‘Absolute convergence of eigenfunction expansions’, Math. Ann. 169 (1967), 307–314.CrossRefGoogle Scholar
Sullivan, D., ‘The Dirichlet problem at infinity for a negatively curved manifold’, J. Differential Geom. 18(4) (1983), 723–732.CrossRefGoogle Scholar