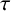1 Introduction
Knot Floer homology, abbreviated HFK, is a package of knot invariants defined in 2003 by Ozsváth, Szabó and Rasmussen. These invariants can be defined combinatorially using grid diagrams [Reference Manolescu, Ozsváth, Szabó and Thurston5]. The
$\tau $
invariant is an integer-valued knot invariant in the HFK package [Reference Ozsváth and Szabó7]. Although computations of
$\tau $
are generally very difficult, in 2011, Sarkar gave a computational shortcut for knots represented on diagonal grid diagrams [Reference Sarkar9]. As far as the authors are aware, the only use of this method to date was in the paper in which Sarkar presented it and used it to calculate the
$\tau $
invariants of torus knots (as well as giving a new proof of Kronheimer and Mrowka’s theorem regarding the unknotting numbers of torus knots). We ask which knots can be represented using diagonal grid diagrams, prove that for any knot K which can be represented on a diagonal grid diagram,
$\tau (K) \geq 0$
, and show that not all such knots are torus knots.
In Section 2, we give background information about grid diagrams and the
$\tau $
invariant, and describe the computational methods that led us towards our main results. In Section 3, we prove our main results about diagonal knots.
2 Preliminaries
We will use grid diagrams to represent knots. A grid diagram of size n has n rows and n columns. The rows are numbered bottom to top, while the columns are numbered left to right. In each row and column, there will be exactly one X-marking and one O-marking, meaning there are n X-markings and n O-markings in the grid diagram. To recover the knot given by a diagram, connect the Xs to the Os in each column, then connect the Os to the Xs in each row. At each crossing, the vertical strand passes over the horizontal strand. Figure 1 shows an example of a grid diagram, along with the knot diagram recovered from it.
2.1 The
$\tau $
invariant
The
$\tau $
invariant has some nice geometric properties, including the following bound on slice genus.
Theorem 2.1 [Reference Ozsváth and Szabó7].
For any knot K,
$|\tau (K)|\leq g_4(K)$
.
The
$\tau $
invariant is not easy to compute. For some specific cases such as in Theorem 2.3, there is a straightforward computational method (although for larger grid diagrams, the computation is still quite lengthy). First, we define
$\mathcal {J}(A, B)$
as a symmetric, bilinear function on sets in
$\mathbb {R}^2$
. The function
$\mathcal {J}(\{a\}, B)$
is half the number of points in B which are to the top right and bottom left of a (that is, if
$a = (a_1,a_2)$
, then
$\mathcal {J}(\{a\}, B) = \tfrac 12 |\lbrace (x,y) \in B : (x> a_1 \text { and } y > a_2) \text { or } (x < a_1 \text { and } y < a_2) \rbrace |$
), and
$$ \begin{align*} \mathcal{J}(A,B)=\sum_{a\in A} \mathcal{J}(\{a\}, B). \end{align*} $$
Definition 2.2. A diagonal knot is a knot which can be represented on a grid diagram with all of the Os on the diagonal from top left to bottom right.
Theorem 2.3 [Reference Sarkar9].
If K is a diagonal knot, then
$$ \begin{align*}\tau(K)=\mathcal{J}\bigg(\mathbf{x}-\frac{1}{2}(\mathbb{X}+\mathbb{O}),(\mathbb{X}-\mathbb{O})\bigg)-\frac{n-1}{2}, \end{align*} $$
where
$\mathbb {X}$
and
$\mathbb {O}$
are the sets of X- and O-markings in a diagonal grid diagram for K,
$\mathbf {x}$
is the set of points in between the Os on the grid diagram along with one point on the bottom left corner of the grid, as shown in Figure 2, and n is the size of the grid.
Figure 1 A grid diagram representing the trefoil, and the knot diagram recovered.
Figure 2 An example of a grid diagram where the points used to calculate
$\tau $
are indicated with dots.
2.2 Computational methods
In our investigation of diagonal knot grid diagrams, we wrote code in Java and Mathematica to generate and simplify diagonal knot grid diagrams and to attempt to identify the knots they represent. This code is available on request from the corresponding author.
2.2.1 Generating diagonal grid diagrams
To see which knots can be represented using diagonal grid diagrams, we wrote a program that generates all of the X permutations of diagonal knot grid diagrams of a given size, n. Once we had generated these, we could calculate
$\tau $
and other invariants of the knots they represented, with the goal of identifying those knots.
The program generates all X permutations of diagonal grid diagrams which represent knots systematically using recursion. The function takes as its argument the size of the grid diagrams we wish to generate, then outputs a tab separated value (TSV) file containing a list of the X-permutations of all of the diagonal knot grid diagrams of the given size.
2.2.2 Calculating tau
We wrote code in Java that implements Sarkar’s method [Reference Sarkar9] for calculating the
$\tau $
invariant of the knot represented by a given diagonal grid diagram. The program takes just one argument, a permutation specifying the locations of the X-markings in the grid diagram (because this method for computing tau will only work on diagonal grid diagrams, where we know that the Os will be on the diagonal). The program outputs the
$\tau $
invariant of the knot represented by the grid diagram with the given X-permutation. To our knowledge, no other implementation of this algorithm for computing the
$\tau $
invariant exists, but one could instead use Ozsváth and Szabó’s knot Floer homology calculator [Reference Ozsváth and Szabó8].
2.2.3 Simplifying grid diagrams
To make it easier to identify the knots represented by the diagonal grid diagrams we had generated, we used a program to simplify grid diagrams. Implemented in Java, this program takes as arguments the grid size, X-permutation and O-permutation of a grid diagram, and returns the X- and O-permutations of the simplified grid diagram. We started with code written by Mikels and Guerra [Reference Mikels and Guerra6] that used commutations to find adjacent Xs and Os in the grid diagram, leading to a destabilisation opportunity. Their code, however, did not include cyclic permutations when searching for adjacent Xs and Os. We added code that performed cyclic permutations and looped through their code again with the cyclically permuted grid diagram, which slightly increased the number of grid diagrams the program could simplify. Our code was neither the first nor the best program that performs this task (see, for example, Barbensi and Celoria’s GridPyM [Reference Barbensi and Celoria1]), but it was good enough for our purposes.
2.2.4 Alexander polynomial
The last program we wrote calculates the Alexander polynomial of knots given their grid diagram representations. We coded this in Mathematica, using the minesweeper matrix algorithm outlined in [Reference Manolescu, Ozsváth, Szabó and Thurston5] to calculate the Alexander polynomial. The program takes the output TSV file from the diagonal knot grid diagram generator described in Section 2.2.1 and adds a new column containing Alexander polynomials. Again, our code was neither the first nor the best program to implement this algorithm; one could instead use SnapPy [Reference Culler, Dunfield, Goerner and Weeks3], for example.
3 The class of diagonal knots
3.1 Nonnegativity of
$\tau $
for diagonal knots
While using Sarkar’s method to calculate
$\tau $
for the knots represented by the diagonal grid diagrams generated by our program (described in Section 2.2.1), we noticed that all of the computed values are greater than or equal to zero. This observation inspired us to prove Theorem 3.3, which implies that the
$\tau $
invariant of a diagonal knot is nonnegative.
Definition 3.1. A crossing in a knot is a positive crossing if the crossing follows the right-hand rule, which means that if we point our right thumb in the direction of the orientation of the overstrand of the crossing and then sweep our fingers into a fist, our fingers move in the direction of the orientation of the undercrossing strand. Examples of positive and negative crossings can be seen in Figure 3.
Definition 3.2. A knot K is considered to be a positive knot if there exists a diagram for K that contains only positive crossings.
For example, all three of the crossings in the standard diagram of the right-handed trefoil (Figure 4) are positive, so the right-handed trefoil is a positive knot.
Figure 3 Examples of positive and negative crossings.
Figure 4 The standard diagram for the right-handed trefoil contains all positive crossings, and therefore the right-handed trefoil is a positive knot.
Theorem 3.3. Every diagonal knot is a positive knot.
Proof. A diagonal knot K can be represented using a diagonal grid diagram. In a grid diagram, the Xs connect vertically to the Os and the Os connect horizontally to the Xs. Above the diagonal in the diagonal grid diagram, at every crossing, the overstrand will be a vertical strand oriented downwards and the understrand will be a horizontal strand oriented from left to right. Below the diagonal, at every crossing, the overstrand will be a vertical strand oriented upwards and the understrand will be a horizontal strand oriented from right to left. Therefore, all of the crossings in a diagonal grid diagram will follow the right-hand rule, and so every crossing in the knot diagram for K obtained from the diagonal grid diagram for K is positive. Thus, K is a positive knot.
Corollary 3.4. If K is a diagonal knot, then
$\tau (K) \geq 0$
.
Proof. By Theorem 3.3, K is a positive knot. Because all positive knots are quasipositive knots, then K is a quasipositive knot. By a result of Livingston [Reference Livingston4], if K is quasipositive, then
$\tau (K) = g(K) = g_4(K)$
. Therefore,
$\tau (K) \geq 0$
.
Theorem 3.5. The set of positive torus knots is a proper subset of the set of diagonal knots. In particular, there exists a diagonal knot which is neither a torus knot nor a connected sum of torus knots.
Proof. Any positive torus knot
$T_{p,q}$
can be represented on a diagonal grid diagram of size
$n = p+q$
, with p X-markings in a diagonal line parallel to and above the O-markings, and q X-markings in a diagonal line parallel to and below the O-markings. Figure 2 shows this diagonal grid diagram representation of the right-handed trefoil,
$T_{2,3}$
. Thus, the set of positive torus knots is a subset of the set of diagonal knots.
It remains to show that not all diagonal knots are torus knots. In the output of the code we wrote to generate diagonal grid diagrams (see Section 2.2.1), we discovered a knot represented diagonally with grid size
$n = 11$
that is not a torus knot or a connected sum of torus knots. The X permutation for this grid is
${\sigma _{\mathbb {X}} = \{5, 4, 3, 2, 11, 1, 10, 9, 8, 6, 7\}}$
and its grid diagram is shown in Figure 5. We used SnapPy to identify this knot as SnapPy census knot m211 [Reference Culler, Dunfield, Goerner and Weeks3]. Through a series of grid diagram commutations, it is straightforward to reduce the number of crossings in the knot diagram from 22 to 21, but it is not obvious whether the number of crossings can be reduced further; if so, this knot would also appear in Burton’s list of knots with up to 19 crossings [Reference Burton, Cabello and Chen2]. This knot has a
$\tau $
invariant of 9 and an Alexander polynomial of
$t^{18} - t^{17} + t^{14} - t^{13} + t^{12} - t^{11} + t^9 - t^7 + t^6 - t^5 + t^4 - t + 1$
(calculated using our Mathematica code and verified with SnapPy [Reference Culler, Dunfield, Goerner and Weeks3]).
Figure 5 A diagonal knot that is not a torus knot.
We use two methods to show that the knot represented in Figure 5 is not a torus knot. First, we note that there are 11 torus knots with a grid index less than or equal to 11, since the grid index of
$T_{p,q}$
is
$p+q$
. Since the grid index of a connected sum of two knots K and J with grid indices
$n_K$
and
$n_J$
, respectively, is
$n_K + n_J -1$
, there are three connected sums of torus knots with grid index at most 11 (these are
$T_{2,3} \# T_{2,3}$
,
$T_{2,3} \# T_{2,5}$
and
$T_{2,3} \# T_{3,4}$
). Comparing the Alexander polynomial of the knot represented in Figure 5 to the Alexander polynomials of the torus knots (as listed in [10]) that can be represented on a size 11 grid diagram, we see that this knot is not a torus knot. Since the Alexander polynomial of a connected sum of knots is the product of the Alexander polynomials of the summand knots, we computed the Alexander polynomials of
$T_{2,3} \# T_{2,3}$
,
$T_{2,3} \# T_{2,5}$
and
$T_{2,3} \# T_{3,4}$
, and saw that each of them was distinct from the Alexander polynomial of the knot represented in Figure 5. Therefore, this knot is neither a torus knot nor a connected sum of torus knots. Alternately, we can use SnapPy [Reference Culler, Dunfield, Goerner and Weeks3] to show that this knot is hyperbolic and therefore not a torus knot [Reference Thurston11].
Acknowledgements
We are grateful to Park Mikels and Orlando Guerra, who wrote a program as part of their Spring 2017 senior capstone project that was very helpful as we began writing our grid diagram programs. The fourth author thanks Danmarks Tekniske Universitet (DTU) Compute Institute for Mathematics and Computer Science for welcoming her as a visitor to the Mathematics Section, and allowing the use of their library and office resources during the Spring 2024 semester. We thank the anonymous reviewer for their helpful comments and suggestions.
