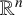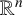1 Introduction
March [Reference March10] gave a criterion for the transience of a rotationally symmetric Riemannian manifold, that is, for a metric on
$\mathbb {R}^n$
of the form
$$ \begin{align*} g=dr^2+\phi^2(r)g_{\mathbb{S}^{n-1}}, \end{align*} $$
with
$\phi $
a smooth function such that
$\phi>0$
for
$r>0$
,
$\phi (0)=0$
and
$\phi '(0)=1$
, and where
$g_{\mathbb {S}^{n-1}}$
is the standard round metric on
$\mathbb {S}^{n-1}$
;
$M_g=(\mathbb {R}^n, g)$
is called a weak model. March proved that
$M_g$
supports bounded nonconstant harmonic functions if and only if
$$ \begin{align} \int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\sigma}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma <\infty. \end{align} $$
The behaviour of the Brownian motion on a manifold and the existence of bounded nontrivial harmonic functions are closely related (see the excellent survey [Reference Grigor’yan8]).
We go beyond the result of March and show that for metrics of the form
$$ \begin{align} g=dr^2+\phi^2(r)g_{\omega}, \end{align} $$
where
$g_{\omega }$
is any metric on
$\mathbb {S}^{n-1}$
, March’s criterion (1.1) implies the solvability on M of the Dirichlet problem at infinity. It is important to clarify that g is defined in
$\mathbb {R}^n\setminus \{0\}$
and it can only be smoothly extended to the origin when
$g_{\omega }=g_{\mathbb {S}^{n-1}}$
if it is also assumed that all derivatives of even order vanish at
$r=0$
. Because g might not be smoothly extendable to the origin, our definition of harmonicity in
$(\mathbb {R}^n,g)$
has the following nuance (see also [Reference Colding and Minicozzi6, Section 1]): we say that u is harmonic if
$u\in C(\mathbb {R}^{n})\cap C^{2}(\mathbb {R}^n\setminus \{0\})$
, and in
$\mathbb {R}^n\setminus \{0\}$
, it satisfies
$$ \begin{align*} \Delta_g u=0, \quad \mbox{where } \Delta_g=\frac{\partial^2}{\partial r^2}+(n-1)\frac{\phi'}{\phi}\frac{\partial}{\partial r} +\frac{1}{\phi^2}\Delta_{g_{\omega}}. \end{align*} $$
Thus, we establish conditions on a class of metrics that generalise the case of weak models, not necessarily rotationally symmetric, for which the Dirichlet problem at infinity is solvable and, as a bonus, we give some quantitative results. That is, we shall prove the following result.
Theorem 1.1. Let
$M=(\mathbb {R}^n, g)$
,
$n\geq 3$
, with g of the form (1.2).
-
(i) For any continuous data
$f\in C(\mathbb {S}^{n-1})$
, if then the Dirichlet problem at infinity is uniquely solvable on M.
$$ \begin{align*} \int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\sigma}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma <\infty, \end{align*} $$
-
(ii) If there is an
$\eta>0$
such that
$\phi '(r)\geq \eta $
outside of a compact subset of M and then there is a constant
$$ \begin{align*} \int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\sigma}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma =\infty, \end{align*} $$
$c>0$
such that a nonconstant harmonic function
$u:\mathbb {R}^n\longrightarrow \mathbb {R}$
must satisfy (1.3)
$$ \begin{align} \max_{r\leq R}|u(\omega, r)|\gtrsim \exp\bigg(c\int_1^R \phi^{n-3}(\sigma) \int_{\sigma}^{R} \frac{1}{\phi^{n-1}(\tau)}\,d\tau\,\, d\sigma\bigg). \end{align} $$
The constant c depends on
$\eta $
and
$\lambda _1$
, the first eigenvalue of the Laplacian
$\Delta _{g_{\omega }}$
on
$(\mathbb {S}^{n-1},g_{\omega })$
. (For example,
$c ={\lambda _1^2}/{(2\lambda _1+4)}$
if the radial curvature of the cone is everywhere nonpositive.) In particular, the Dirichlet problem at infinity is not solvable in M. -
(iii) If
$\phi '(r)\leq \beta $
, for a positive constant
$\beta $
, then any bounded harmonic function must be constant. In fact, there is a constant
$l:=l(\beta ,\lambda _1,n)>0$
such that a nonconstant harmonic function u must satisfy (1.4)
$$ \begin{align} \max_{r\leq R}|u(\omega, r)|\gtrsim r^{l}. \end{align} $$
Some observations are in place here. The hypotheses of the second part of the theorem are satisfied whenever outside a compact set of M,
$\phi '>0$
and the radial curvature
$-\phi "/\phi $
is nonpositive, or just when the radial curvature is nonpositive. Regarding condition (iii), the hypothesis on
$\phi $
holds as soon as the radial curvature is nonnegative. In this case (when
$g_{\omega }=g_{\mathbb {S}^{n-1}}$
), Liouville’s theorem holds, as proved by Yau for metrics of nonnegative Ricci curvature. However, the reader can readily check that if
$\phi (r)=\tfrac 12(r+\sin r)$
, the radial curvature has no definite sign, and in this case, condition (iii) still applies. A proof of condition (iii) is presented in [Reference Bravo and Cortissoz4], and we have included it here because it gives a nice complement to condition (ii).
The study of the Dirichlet problem at infinity has a history of many deep and beautiful results (see, for instance, [Reference Ancona1–Reference Anderson and Schoen3, Reference Choi5, Reference Milnor11, Reference Neel12, Reference Sullivan14]). In particular, Theorem 1.1 was proved by Hsu [Reference Hsu9] in the case where
$g_{w}=g_{\mathbb {S}^{n-1}}$
, the standard round metric on the sphere, for Cartan–Hadamard manifolds. However, it is not clear that his methods, which are probabilistic in nature, extend to arbitrary metrics on
$\mathbb {S}^{n-1}$
, as he uses the symmetry of the heat kernel in the case of a rotationally invariant metric. Our proof is elementary and relies on separation of variables, estimating solutions to a Ricatti equation and some Fourier analysis. We not only generalise Hsu’s result but also provide an alternative to the probabilistic methods employed by him. Also, our estimate on the minimal growth of a nonconstant harmonic function (when the Dirichlet problem at infinity is not solvable) seems to be new.
Following March’s arguments, Theorem 1.1 implies an almost sharp restriction on the curvature of a Cartan–Hadamard manifold whose metric is of the form (1.2) and where the Dirichlet problem at infinity is solvable (see [Reference March10, Theorem 2]).
Corollary 1.2. Let
$M=(\mathbb {R}^n,g)$
with a metric of the form (1.2), such that
$\phi '$
is eventually nonnegative, and let
$k(r)=-\phi "/\phi (r)$
be its radial curvature, with
$k(r)\leq 0$
outside a compact subset of
$\mathbb {R}^n$
. Let
$c_2=1$
and
$c_n=\tfrac 12$
for
$n\geq 3$
. If
$k(r)\leq -c/(r^2\log r)$
outside a compact set for some
$c>c_n$
, then the Dirichlet problem at infinity is solvable. If
$k(r)\geq -c/(r^2\log r)$
for some
$c<c_n$
outside a compact set, then the Dirichlet problem at infinity is not solvable.
In March’s original result (and in Hsu’s result), it is required that the radial curvature
$k(r)$
is nonpositive: in such a case,
$\phi '>0$
holds automatically everywhere.
The layout of this paper is as follows. In Section 2, we define what we understand by solving the Dirichlet problem at infinity; in Section 3, we prove our main result.
2 Preliminaries
To define what we mean by the Dirichlet problem being solvable at infinity, we represent
$\mathbb {R}^n$
as a cone over the sphere
$\mathbb {S}^{n-1}$
, that is,
$$ \begin{align*} \mathbb{R}^n \sim [0,\infty)\times \mathbb{S}^{n-1}/(\{0\}\times \mathbb{S}^{n-1}). \end{align*} $$
The equivalence class of the origin (the pole) will be denoted by O, that is,
$$ \begin{align*} O=\{0\}\times \mathbb{S}^{n-1}/(\{0\}\times \mathbb{S}^{n-1}). \end{align*} $$
We can compactify
$\mathbb {R}^n$
by defining
$$ \begin{align*} \overline{\mathbb{R}^n}= [0,\infty]\times \mathbb{S}^{n-1}/(\{0\}\times\mathbb{S}^{n-1}), \end{align*} $$
where
$[0,\infty ]$
is a compactification of
$[0,\infty )$
.
We say that the Dirichlet problem on
$M=(\mathbb {R}^n,g)$
is solvable at infinity for boundary data
$f\in C(\mathbb {S}^{n-1}_{\infty })$
if there is a harmonic function u on M, that is,
$\Delta _g u= 0$
on
$\mathbb {R}^n\setminus \{0\}$
, which extends continuously to a function
$\overline {u}:\overline {\mathbb {R}^n}\longrightarrow \mathbb {R}$
and such that
$\overline {u}(\infty ,\cdot )=f(\cdot )$
.
Our definition of solvability at infinity coincides with that of Choi [Reference Choi5] on Cartan–Hadamard manifolds. Indeed, for a Cartan–Hadamard manifold, the sphere at infinity given by the Eberlein–O’Neill compactification is obtained by adding at infinity the equivalence classes of geodesic rays starting at the pole (a point around which the metric can be written as in (1.2)), where two geodesic rays are equivalent if
$\limsup _{t\rightarrow \infty } d(\gamma _1(t),\gamma _2(t))<\infty $
, and then endowing this set with the cone topology (see [Reference Choi5]). If we identify the pole of the manifold with the vertex of the cone (or pole, that is, the equivalence class of
$\{0\}\times \mathbb {S}^{n-1}$
), the set of equivalence classes of geodesics can be identified with the unit sphere on
$T_p M$
, where p is a pole of the manifold, which in turn implies that it can be identified with
$\mathbb {S}^{n-1}_{\infty }= \{\infty \}\times \mathbb {S}^{n-1}$
.
3 Proof of the main result
3.1 Proof of part (i)
In this section, we will show that
$$ \begin{align*} J=\int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\sigma}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma <\infty \end{align*} $$
implies the solvability of the Dirichlet problem at infinity. (In Section 3.2, we will show nonsolvability in the case where
$J=\infty $
.)
We will follow the approach implemented in [Reference Cortissoz7], so we use separation of variables to find solutions to the equation
$$ \begin{align*} \Delta_g u=0 \quad \mbox{on } \mathbb{R}^n\setminus\{0\}, \end{align*} $$
which extend continuously to
$\overline {\mathbb {R}^n}$
and satisfy some given data at infinity. With this in mind, we let
$f_{m,k}$
,
$k=0,1,2,\ldots , k_m$
, be eigenfunctions of the mth eigenvalue,
$\lambda _m^2$
(
$\lambda _m\geq 0$
,
$m=0,1,2,\ldots $
), of the Laplacian
$\Delta _{g_{\omega }}$
on
$(\mathbb {S}^{n-1},g_{\omega })$
, such that the set
$\{f_{m,k}\}_{m,k}$
is an orthonormal basis for
$L^{2}(\mathbb {S}^{n-1})$
with respect to the inner product induced by the metric
$g_{\omega }$
. If
$\varphi _m$
is such that
$$ \begin{align*} \Delta_g (\varphi_m f_{m,k})=0, \end{align*} $$
then
$\varphi _m$
must satisfy the radial Laplacian equation
$$ \begin{align} \varphi_m"+(n-1)\frac{\phi'}{\phi}\varphi_m'-\frac{\lambda_m^2}{\phi^2}\varphi_m=0. \end{align} $$
It is proved in [Reference Cortissoz7] that we may assume
$\varphi _0=1$
and that
$\varphi _m$
for
$m>0$
has the form
$$ \begin{align*} \varphi_m(r)=r^l \alpha(r), \end{align*} $$
where
$l=\tfrac 12(-(n-2)+\sqrt {(n-2)^2+4\lambda _m^2})>0$
satisfies the indicial equation
$$ \begin{align*} l(l-1)+(n-1)l-\lambda_m^2=0 \end{align*} $$
and
$\alpha $
is a smooth function. Also, it is shown that
$\varphi _m$
can be chosen so that it is nondecreasing and thus,
$\varphi _m\geq 0$
. Therefore, as argued in [Reference Cortissoz7], to show solvability of the Dirichlet problem at infinity, it suffices to show that the
$\varphi _m$
are bounded.
Indeed, let us sketch why this is so (for details, we refer the reader to [Reference Cortissoz7]). Once we have proved that the
$\varphi _m$
are bounded, we may without loss of generality assume that
$0\leq \varphi _m\leq 1$
and that
$\lim _{r\rightarrow \infty }\varphi _m(r)=1$
. Given
$f\in C(\mathbb {S}^{n-1}_{\infty })$
, we can expand it in a Fourier series,
$$ \begin{align*} f(\omega) = \sum_{m,k} c_{m,k}f_{m,k}(\omega). \end{align*} $$
If f is smooth, a theorem of Peetre [Reference Peetre13] guarantees that this series converges absolutely and uniformly to f (not just in
$L^2(\mathbb {S}^{n-1})$
as it always does). Thus, a harmonic function solving the Dirichlet problem at infinity with boundary data f is given by
$$ \begin{align*} u(r,\omega)=\sum_{m} \varphi_m(r) \sum_{k} c_{m,k}f_{m,k}(\omega). \end{align*} $$
We call u a harmonic extension of f. If f is just continuous, an approximation argument using smooth functions gives the existence of a harmonic extension for f. Uniqueness follows from the maximum principle (see [Reference Cortissoz7]).
In the case of
$f\in L^2$
, again, as proved in [Reference Cortissoz7], the boundedness of
$\varphi _m$
implies solvability. All we are left to do to show solvability is the boundedness of the
$\varphi _m$
, which we do next. (Uniqueness, in the case of continuous f, follows from the maximum principle.)
Lemma 3.1. Given a solution
$\varphi _{m}$
to the radial Laplacian (3.1), there are constants
$A, B>0$
such that the bound
$$ \begin{align*} \varphi_{m}(s)\leq B\exp\bigg(\int_{1}^{s}\frac{\lambda_m^2}{\phi^{n-1}(\tau)}\bigg(A+\int_{1}^{\tau}\phi^{n-3}(\sigma)\, d\sigma \bigg)\, d\tau\bigg) \end{align*} $$
holds for all
$s\geq 1$
.
Proof. Write
$$ \begin{align} \varphi_m(s) = B\exp\bigg(\int_1^s \frac{\lambda_m^2}{\phi^{n-1}(\tau)}x_m(\tau)\, d\tau\bigg) \end{align} $$
for
$s\geq 1$
, with
$B=\varphi _m(1)$
and
$x_m(t)$
a smooth function. From the equation satisfied by
$\varphi _m$
, we arrive at an equation for
$x_m$
, that is,
$$ \begin{align} x_m'(s)+\frac{\lambda_m^2}{\phi^{n-1}(s)}x_m^2(s)=\phi^{n-3}(s), \end{align} $$
which leads to the inequality
$$ \begin{align*} x_m'(s)\leq \phi^{n-3}(s). \end{align*} $$
This yields the estimate
$$ \begin{align*} x_m(s)\leq A+ \int_{1}^{s} \phi^{n-3}(\sigma)\, d\sigma \end{align*} $$
for an appropriately chosen constant
$A>0$
, and the lemma follows.
From Lemma 3.1, it follows that if
$$ \begin{align*} \int_{1}^{\infty}\frac{1}{\phi^{n-1}(\tau)}\, d\tau+ \int_{1}^{\infty}\frac{1}{\phi^{n-1}(\tau)}\int_{1}^{\tau}\phi^{n-3}(\sigma)\, d\sigma \, d\tau < \infty, \end{align*} $$
then
$\varphi _m$
is bounded. The second integral can be rewritten as
$$ \begin{align*} \int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\sigma}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma. \end{align*} $$
Since the inner integral must converge for almost all
$\tau $
, the convergence of the second integral implies the convergence of the integral
$$ \begin{align*} \int_{1}^{\infty}\frac{1}{\phi^{n-1}(\tau)}\, d\tau. \end{align*} $$
So we see that
$$ \begin{align*} \int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\tau}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma <\infty \end{align*} $$
implies that
$\varphi _m$
is bounded, which, by the results in [Reference Cortissoz7], gives the solvability of the Dirichlet problem at infinity.
3.2 Proof of part (ii)
Next, we show that if
$$ \begin{align*} J=\int_{1}^{\infty} \phi^{n-3}(\sigma) \int_{\sigma}^{\infty}\phi^{1-n}(\tau)\,d\tau\,d\sigma =\infty \end{align*} $$
and there is an
$\eta>0$
such that
$\phi '(r)\geq \eta $
outside of a compact set, then the Dirichlet problem at infinity is not solvable. The idea is to bound
$\varphi _m$
from below, and then use Plancherel’s theorem to obtain estimate (1.3).
Let us estimate
$\varphi _m$
. Again, we write
$\varphi _m$
as in (3.2) for
$s\geq 1$
and
$x_m$
a smooth function. We should make an important observation. Since the
$\varphi _m$
are nondecreasing (by the arguments in [Reference Cortissoz7]), it follows that
$x_m(t)\geq 0$
. This fact will be used below. Since
$x_m$
satisfies (3.3), for any
$s\geq 1$
, we must have either
$$ \begin{align} x_m'(s)> \tfrac{1}{4}\phi^{n-3}(s) \end{align} $$
or
$$ \begin{align} \frac{\lambda_m^2}{\phi^{n-1}(s)}x_m^2(s)>\frac{1}{4}\phi^{n-3}(s). \end{align} $$
By hypothesis, there are
$\eta>0$
and
$r_0>0$
such that
$\phi '(r)\geq \eta $
for
$r\geq r_0$
(in the case of a Cartan–Hadamard manifold, we can take
$\eta =1$
). Without loss of generality, we will assume that
$r_0=1$
. We shall prove that these two conditions imply that for
${\overline {\eta }=\min \{1,\eta \}}$
,
$$ \begin{align} x_m(t)\geq \frac{\overline{\eta}}{2\lambda_m+4}\int_{1}^t\phi^{n-3}(s)\,ds. \end{align} $$
Let
$$ \begin{align*} I=\{q\geq 1:\, \mbox{(3.6) holds for } t\in[1, q] \}. \end{align*} $$
It is clear that
$1\in I$
since
$$ \begin{align*} x_m(1)\geq \frac{\overline{\eta}}{2\lambda_m+4}\int_{1}^1\phi^{n-3}(s)\,ds=0. \end{align*} $$
Define
$t_0=\mathrm{sup}\ I$
and let us show that
$t_0=\infty $
. To this end, assume that
$t_0<\infty $
. By continuity, it is clear that
$t_0\in I$
. To reach a contradiction, we will show that for
$\rho>0$
small enough,
$[t_0,t_0+\rho )\subset I$
.
First, we estimate
$$ \begin{align*} \phi^{n-2}(t)= \phi^{n-2}(1)+(n-3)\int_{1}^t \phi^{n-3}(s)\phi'(s)\,ds \geq \eta\int_{1}^t \phi^{n-3}(s)\,ds. \end{align*} $$
Let
$\rho>0$
be small enough so that either (3.4) or (3.5) holds. If (3.4) holds, then we can estimate
$x_m(t)$
for
$t\in [t_0,t_0+\rho )$
by
$$ \begin{align*} x_m(t)\geq x_m(t_0)+\frac{1}{4}\int_{t_0}^{t} \phi^{n-3}(s)\,ds \geq \frac{\overline{\eta}}{2\lambda_m+4}\int_{1}^{t}\phi^{n-3}(s)\,ds. \end{align*} $$
If (3.5) holds (here, we use the observation made above that
$x_m\geq 0$
), then
$$ \begin{align*} x_m(t) \geq \frac{1}{2\lambda_m+4}\phi^{n-2}(t) \geq \frac{n-2}{2\lambda_m+4}\int_1^t\phi^{n-3}(s)\phi'(s)\,ds\ \geq \frac{\eta}{2\lambda_m+4}\int_1^t \phi^{n-3}(s)\,ds, \end{align*} $$
and, hence, (3.6) holds up to
$t<t_0+\rho $
, and
$t_0$
, if finite, cannot be the supremum of I. Thus, we have proved that (3.6) holds, and then we can estimate
$$ \begin{align*} \varphi_m(s)&\geq \exp\bigg( \frac{\lambda_m^2\overline{\eta}}{2\lambda_m+4}\int_1^s \frac{1}{\phi^{n-1}(\tau)} \int_1^{\tau} \phi^{n-3}(\sigma)\,d\sigma\, d\tau\bigg)\\ &= \exp\bigg( \frac{\lambda_m^2 \overline{\eta}}{2\lambda_m+4}\int_1^s \phi^{n-3}(\sigma) \int_{\sigma}^{s} \frac{1}{\phi^{n-1}(\tau)}\,d\tau\, d\sigma\bigg)\\ &\geq \exp\bigg( \frac{\lambda_1^2 \overline{\eta}}{2\lambda_1+4}\int_1^s \phi^{n-3}(\sigma) \int_{\sigma}^{s} \frac{1}{\phi^{n-1}(\tau)}\,d\tau\, d\sigma\bigg). \end{align*} $$
This estimate shows that
$\varphi _m(s)\rightarrow \infty $
as
$s\rightarrow \infty $
for
$m\neq 0$
, under the assumption that
$J=\infty $
. Using this, we will show that the Dirichlet problem at infinity cannot be solved. In fact, we shall show that any bounded harmonic function must be constant. So, let
$u:\mathbb {R}^n\longrightarrow \mathbb {R}$
be a harmonic function. For
$R>0$
arbitrary, we let
$B_R$
be the ball of radius R centred at the origin and
$$ \begin{align*} u_R(\omega)=u|_{\partial B_R}. \end{align*} $$
Since
$u_R$
is smooth, we can expand it as the Fourier series
$$ \begin{align*} u_R(\omega)=\sum_m\sum_k c_{m,k,R}f_{m,k}(\omega), \end{align*} $$
where
$f_{m,k}$
is an eigenfunction of the eigenvalue
$\lambda _m^2$
of the Laplacian
$\Delta _{\omega }$
of
$\mathbb {S}^{n-1}$
. From now on, we shall assume that
$\{f_{m,k}\}$
is an orthonormal basis for
$L^{2}(\mathbb {S}^{n-1})$
.
The harmonic extension of
$u_R$
to
$B_R$
, and thus, by uniqueness, u on
$B_R$
(see [Reference Cortissoz7, Theorem 3]), is given by
$$ \begin{align} u(r,\omega)=\sum_m \frac{\varphi_m(r)}{\varphi_m(R)} \sum_k c_{m,k,R}f_{m,k}(\omega). \end{align} $$
Indeed, the proof is exactly the same as that given in [Reference Cortissoz7] for the Dirichlet problem at infinity. First, we must show that the sum converges in the
$L^2$
-sense for every
$r\leq R$
. Here, we need the fact that the
$\varphi _m$
can be chosen to be nonnegative and nondecreasing: that this can be done is shown in [Reference Cortissoz7]. Therefore,
$0\leq \varphi _m(r)/\varphi _m(R)\leq 1$
for
$0\leq r\le R$
and, from having convergence at R, our assertion follows. Next, we must show that the boundary condition at
$\partial M_R$
is met as
$r\rightarrow R$
, and for this, we also ask the reader to consult [Reference Cortissoz7]. From now on, we shall assume, without loss of generality, that
$c_{0,0}=0$
.
Thus far, we have shown that in
$M_R$
, u can be written as given in (3.7). We shall prove that u can be represented, in the whole of M, as
$$ \begin{align} \sum_m\frac{\varphi_m(r)}{\varphi_m(1)}\sum_k c_{m,k,1}f_{m,k}(\omega), \end{align} $$
where
$$ \begin{align*} \sum_{m,k}c_{m,k,1}f_{m,k}(\omega) \end{align*} $$
is the Fourier expansion of u restricted to
$\partial M_1$
. First, observe that by taking
$R=1$
in (3.7), we obtain (3.8). Now consider (3.7) at any fixed
$R>1$
, evaluate at
$r=1$
and then compare with (3.8) when evaluated at
$r=1$
. By uniqueness,
$$ \begin{align*} c_{m,k,R}=\frac{\varphi_m(R)}{\varphi_m(1)}c_{m,k,1}. \end{align*} $$
However, then it follows that (3.8) represents u for any
$R\geq 1$
and, as this representation is already valid for
$R<1$
, our claim is proved.
Now, we can use Plancherel’s theorem to compute
$$ \begin{align*} \|u\|^2_{L^2(\partial B_R)} = \sum_m\bigg(\frac{\varphi_m(R)}{\varphi_m(1)}\bigg)^2\sum_k |c_{m,k,1}|^2\phi^{n-1}(R). \end{align*} $$
If we assume that
$u(\omega , R)=O(1)$
, then
$$ \begin{align*} \sum_m\bigg(\frac{\varphi_m(R)}{\varphi_m(1)}\bigg)^2\sum_k |c_{m,k,1}|^2\phi^{n-1}(R) = O(1)\phi^{n-1}(R), \end{align*} $$
that is,
$$ \begin{align*} \sum_m\bigg(\frac{\varphi_m(R)}{\varphi_m(1)}\bigg)^2\sum_k |c_{m,k,1}|^2 = O(1), \end{align*} $$
which contradicts the fact that
$\varphi _m(R)\rightarrow \infty $
as
$R\rightarrow \infty $
.
Next, we derive the estimate (1.3). We have
$$ \begin{align*} \max_{r\leq R}|u(r,\omega)|^2&= \max_{r=R}|u(r,\omega)|^2 \quad \mbox{(by the maximum principle)}\\ &\geq \sum_m\bigg(\frac{\varphi_m(R)}{\varphi_m(1)}\bigg)^2\sum_k |c_{m,k,1}|^2\\ &\gtrsim \exp\bigg( \frac{2\lambda_1^2 \overline{\eta}}{2\lambda_1+4}\int_1^s \phi^{n-3}(\sigma) \int_{\sigma}^{s} \frac{1}{\phi^{n-1}(\tau)}\,d\tau\, d\sigma\bigg) \end{align*} $$
and the estimate follows.
3.3 Proof of part (iii)
Assume that for all
$r>0$
,
$\phi '(r)\leq \beta $
, for a positive constant
$\beta $
. Again, write
$\varphi _m$
as in (3.2) for
$s\geq 1$
and
$x_m(t)$
a smooth function. Let
$$ \begin{align*} \eta_m=\frac{1}{2}\bigg(-\frac{\beta(n-2)}{\lambda_m}+\sqrt{\frac{\beta^2(n-2)^2}{\lambda_m^2}+4}\bigg). \end{align*} $$
Since
$x_m$
satisfies (3.3), at any given s, either
$$ \begin{align*} \frac{\lambda_m^2}{\phi^{n-1}(s)}x_m^2(s)> \eta_m^2\phi^{n-3}(s), \end{align*} $$
that is (since
$x_m\geq 0$
),
$$ \begin{align} x_m(s)\geq \frac{\eta_m}{\lambda_m}\phi^{n-2}, \end{align} $$
or
$$ \begin{align} x_m'(s)> (1-\eta_m^2) \phi^{n-3}(s). \end{align} $$
Our choice of
$\eta _m$
guarantees
$$ \begin{align*} \frac{1-\eta_m^2}{\beta(n-2)}=\frac{\eta_m}{\lambda_m}. \end{align*} $$
We shall show the following. Assume that at time
$t=t_0$
, we have the estimate
$$ \begin{align} x_m(t)\geq \frac{1-\eta_m^2}{\beta(n-2)}\phi^{n-2}(t). \end{align} $$
Then, there is an
$\epsilon>0$
such that the same estimate is valid on
$(t_0,t_0+\epsilon )$
. To do so, choose
$\epsilon>0$
such that either (3.9) or (3.10) is valid. In the first case, (3.11) follows immediately. In the second case, we estimate
$x_m(\tau )$
as follows. For
$\tau \in (t_0,t_0+\epsilon )$
,
$$ \begin{align*} x_m(\tau)&= x_m(t_0)+\int_{t_0}^{\tau}\phi^{n-3}(s)\,ds\\[4pt] &\geq x_m(t_0)+ (1-\eta_m^2)\int_{t_0}^{\tau}\phi^{n-3}(s)\frac{\phi'(s)}{\beta}\,ds\\[4pt] &= x_m(t_0)+\frac{1-\eta_m^2}{\beta(n-2)}(\phi^{n-2}(\tau) -\phi^{n-2}(t_0))\\[4pt] &\geq \frac{1-\eta_m^2}{\beta(n-2)}\phi^{n-2}(\tau). \end{align*} $$
By continuity, the estimate (3.11) holds on a closed set and this set is nonempty since the estimate is satisfied when
$t=0$
(again, we are using
$x_m\geq 0$
and
$\phi (0)=0$
). Therefore, the estimate holds for all
$t\in [0,\infty )$
and we obtain
$$ \begin{align*} x_m(t)\geq \frac{\eta_m}{\lambda_m}\phi^{n-2}(t). \end{align*} $$
Thus, we can take
$$ \begin{align*} \eta_m=\frac{1}{2}\frac{\lambda_m^2}{\beta(n-2)}\bigg[\sqrt{1+\frac{4\lambda_m^2}{\beta^2(n-2)^2}}-1\bigg] \end{align*} $$
and hence,
$$ \begin{align*} x_m(t)\geq a_m \phi^{n-2}(t), \end{align*} $$
where
$$ \begin{align*} a_m=\frac{1}{2}\frac{\lambda_m}{\beta(n-2)}\bigg[\sqrt{1+\frac{4\lambda_m^2}{\beta^2(n-2)^2}}-1\bigg]. \end{align*} $$
This shows that
$$ \begin{align*} \varphi_m(r) \gtrsim \exp\bigg(a_m\int_1^r\frac{1}{\phi(s)}\,ds\bigg) \end{align*} $$
and, since the
$a_m$
form an increasing sequence, we have the estimate
$$ \begin{align*} \varphi_m(r) \gtrsim \exp\bigg(a_1\int_1^r\frac{1}{\phi(s)}\,ds\bigg). \end{align*} $$
From Plancherel’s theorem, as we reasoned above, if u is bounded and if
$$ \begin{align*}\int_1^{\infty} \frac{1}{\phi(s)}\,ds =\infty,\end{align*} $$
then u must be constant. However, if
$\phi '(r)\leq \beta $
, then
$\phi \leq \beta r$
. Consequently, the integral above is divergent and Liouville’s theorem holds in this case. Again, an argument using Plancherel’s theorem shows that any nonconstant harmonic u function must satisfy
$$ \begin{align*} \max_{r\leq R}|u(\omega, r)|\gtrsim \exp\bigg(a_1\int_1^r\frac{1}{\phi(s)}\,ds\bigg) \geq r^{{a_1}/{\beta}}, \end{align*} $$
which proves (1.4).
