We use well resolved numerical simulations with the lattice Boltzmann method to study Rayleigh–Bénard convection in cells with a fractal boundary in two dimensions for 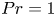 $Pr = 1$ and
$Pr = 1$ and 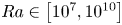 $Ra \in \left [10^7, 10^{10}\right ]$, where Pr and Ra are the Prandtl and Rayleigh numbers. The fractal boundaries are functions characterized by power spectral densities
$Ra \in \left [10^7, 10^{10}\right ]$, where Pr and Ra are the Prandtl and Rayleigh numbers. The fractal boundaries are functions characterized by power spectral densities 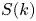 $S(k)$ that decay with wavenumber,
$S(k)$ that decay with wavenumber,  $k$, as
$k$, as 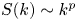 $S(k) \sim k^{p}$ (
$S(k) \sim k^{p}$ (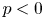 $p < 0$). The degree of roughness is quantified by the exponent
$p < 0$). The degree of roughness is quantified by the exponent 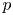 $p$ with
$p$ with 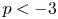 $p < -3$ for smooth (differentiable) surfaces and
$p < -3$ for smooth (differentiable) surfaces and 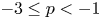 $-3 \le p < -1$ for rough surfaces with Hausdorff dimension
$-3 \le p < -1$ for rough surfaces with Hausdorff dimension 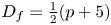 $D_f=\frac {1}{2}(p+5)$. By computing the exponent
$D_f=\frac {1}{2}(p+5)$. By computing the exponent  $\beta$ using power law fits of
$\beta$ using power law fits of 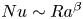 $Nu \sim Ra^{\beta }$, where
$Nu \sim Ra^{\beta }$, where 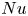 $Nu$ is the Nusselt number, we find that the heat transport scaling increases with roughness through the top two decades of
$Nu$ is the Nusselt number, we find that the heat transport scaling increases with roughness through the top two decades of 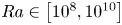 $Ra \in \left [10^8, 10^{10}\right ]$. For
$Ra \in \left [10^8, 10^{10}\right ]$. For 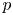 $p$
$p$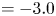 $= -3.0$,
$= -3.0$, 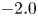 $-2.0$ and
$-2.0$ and  $-1.5$ we find
$-1.5$ we find 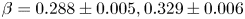 $\beta = 0.288 \pm 0.005, 0.329 \pm 0.006$ and
$\beta = 0.288 \pm 0.005, 0.329 \pm 0.006$ and  $0.352 \pm 0.011$, respectively. We also find that the Reynolds number,
$0.352 \pm 0.011$, respectively. We also find that the Reynolds number, 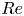 $Re$, scales as
$Re$, scales as 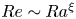 $Re \sim Ra^{\xi }$, where
$Re \sim Ra^{\xi }$, where 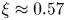 $\xi \approx 0.57$ over
$\xi \approx 0.57$ over  $Ra \in \left [10^7, 10^{10}\right ]$, for all
$Ra \in \left [10^7, 10^{10}\right ]$, for all 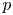 $p$ used in the study. For a given value of
$p$ used in the study. For a given value of 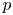 $p$, the averaged
$p$, the averaged 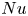 $Nu$ and
$Nu$ and 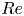 $Re$ are insensitive to the specific realization of the roughness.
$Re$ are insensitive to the specific realization of the roughness.