 $\mathbb{Q}$
$\mathbb{Q}$
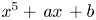
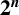 $\boldsymbol {2^n}$
$\boldsymbol {2^n}$
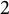 $2$
-towers
$2$
-towers
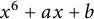 $x^6+ax+b$
$x^6+ax+b$