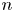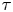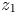1. Introduction
Modular forms appear in various areas of mathematics including geometry, and in physics (see, for instance, Alvarez-Gaumé–Moore–Vafa [Reference Alvarez-Gaumé, Moore and Vafa1]). In this paper, we consider one example called Hilbert schemes, which are related to all of these areas.
Hilbert schemes are an object arising from algebraic geometry. They were defined by Grothendieck [Reference Grothendieck14] as a moduli space of closed subschemes of an algebraic variety. Since moduli spaces parametrizing objects associated with a given space $X$
are a rich source of spaces with interesting structures in general, Hilbert schemes are usually considered as important objects and have been a source of continuous investigations. For the basic references, we refer to Göttsche [Reference Göttsche10] and Nakajima [Reference Nakajima21].
It is interesting to note that modular forms and Hilbert schemes have a connection in relation to physics. In [Reference Vafa and Witten23], it was pointed out that the S-duality conjecture in the string theory implies the modularity of the generating function of Euler numbers of moduli spaces of instanton. Then, using the fact that the Euler numbers of moduli spaces of instantons are equal to those of Hilbert schemes of points in the K3 case, it became possible to obtain the desired answer using the following beautiful formula given by Göttsche [Reference Göttsche10]
Here, $P_t(X):=\sum \nolimits _{i=0}^{2\dim _{\mathbb {C}}(X)}b_i(X)t^{i}$
and $b_i(X)$
is the $i^{th}$
Betti number of $X$
. However, despite the relationship to modular forms, Hilbert schemes have not been extensively studied from the number-theoretic point of view.
Recently, some investigations from number theorists appeared, after the work by Bringmann and Manschot [Reference Bringmann and Manschot7]. In their paper, they found the asymptotic behaviour of the Betti numbers of the Hilbert schemes of points on an algebraic surface that is related to the counting of BPS states in physics. Subsequently, their work was continued by the work of Manschot and Rolon [Reference Manschot and Rolon20], where the following Göttsche's new formula about the Hodge numbers of the Hilbert schemes of $n$
points on algebraic surfaces was considered:
Theorem 1.1 Göttsche [Reference Göttsche10, Theorem 2.3.14]
If $S$
is a smooth projective complex surface, then we have that
We remark that the two generating functions used in the above two papers [Reference Bringmann and Manschot7, Reference Manschot and Rolon20] can be combined mathematically to a general generating series, as was later given by the authors [Reference Jin and Jo16] where the general asymptotic formula was obtained. We also refer the reader, to the papers written by Gillman–Gonzalez–Schoenbauer [Reference Gillman, Gonzalez and Schoenbauer8] and Gillman–Gonzalez–Ono–Rolen–Schoenbauer [Reference Gillman, Gonzalez, Ono, Rolen and Schoenbauer9], respectively, where some specialized cases corresponding to $(x,\,y)=(\pm 1,\,\pm 1)$
(respectively $(x,\,y)=(e^{\frac {2\pi ij_1}{l_1}},\, e^{\frac {2\pi ij_2}{l_2}})$
) in Göttsche's Hodge number generating formula for the Hilbert schemes of $n$
points were thoroughly studied, to obtain exact formulas and asymptotic formulas of the Euler characteristic and the signature of $S^{[n]}$
. Finally, we refer to two recent interesting papers by Bringmann–Craig–Males–Ono [Reference Bringmann, Craig, Males and Ono6] and Griffin–Ono–Rolen–Tsai [Reference Griffin, Ono, Rolen and Tsai11] about Betti distributions of Hilbert schemes.
In this paper, we further consider and study Göttsche's Hodge number generating function of the Hilbert schemes of $n$
points of an algebraic surface to study another property, the algebraicity. Algebraicity has been an important property in mathematics, and in particular, the algebraicity of modular forms (and in general $q$
-series) has been also extensively studied (see, for instance, [Reference Berndt, Chan and Zhang3, Reference Berndt, Chan and Zhang4, Reference Griffin, Ono and Warnaar12, Reference Koo, Shin and Yoon18, Reference Ramanujan22]). It is also interesting that there also has been interest from physicists, including investigations from [Reference Beliakova, Chen and Le2, Reference Bonora, Bytsenko and Elizalde5, Reference Gukov and Vafa15, Reference Kanno and Watari17]. For example, in [Reference Beliakova, Chen and Le2], Beliakova–Chen–Le gave a complete solution to the integrality problem of the Witten–Reshetikhin–Turaev invariant in the SU(2) case by proving that the WRT invariant is an algebraic integer for any three-manifold with any coloured link inside at any root of unity.
In our previous work [Reference Jin and Jo16], it was shown that for a smooth projective surface $S$
the value
is an algebraic number, at any rational number $z$
and any CM point Footnote 1 $\tau$
, where $f_S(z;\tau )$
is the left-hand side of (1.1) with $q=e^{2\pi i (\tau -z)}$
and $t=e^{\pi i z},$
$\chi (S)$
is the Euler characteristic of $S$
, and $\eta (\tau )=e^{\frac {\pi i\tau }{12}}\prod _{n=1}^{\infty }(1-e^{2\pi i n \tau })$
is the Dedekind eta function. Moreover, under some condition on $z$
, (1.3) is an algebraic integer.
In this paper, we give a more refined explanation of our previous work. We study the algebraicity of Göttsche's Hodge number generating function involving the Hodge numbers of the Hilbert schemes of points and see whether some algebraicity holds for the refined subclasses (since in the Kähler case, Betti numbers can be expressed in terms of the Hodge numbers). The result is positive. We consider, in relation to Göttsche's Hodge number generating function, the following generating function
In fact, this is the left-hand side of Theorem 1.1 with $x=e^{2\pi i z_1},\, \ y=e^{2\pi i z_2}$
, and ${q=e^{2\pi i \tau}}$
.
Our first theorem is a generalization of our previous result [Reference Jin and Jo16, Theorem 1.2]. We say that $\alpha$
is a unit over a commutative ring $R$
with unity, if $\alpha$
and $\alpha ^{-1}$
are integral over $R$
.
Theorem 1.2 Let $S$
be a smooth projective complex surface with the Euler characteristic $\chi (S)$
. Let $z_1,\,z_2$
be rational numbers, and let $\tau$
be a CM point.
(1) If $z_1\neq 0$
, $z_2\neq 0$
and $z_1=z_2=z,$
then
is an algebraic number.
(2) If $z_1\neq 0,$
$z_2\neq 0$
and $z_1=-z_2=z,$
then
is an algebraic number.
(3) If $z\neq 0,$
then
is an algebraic number. (Note that $F_S(z,\,0,\,\tau )=F_S(0,\,z,\,\tau$
).)
(4) Let $\mathrm {den}(a)$
be the smallest $N\in \mathbb {N}$
such that $Na\in \mathbb {Z}$
. If $\mathrm {den}(2z)$
(respectively, $\mathrm {den}(z)$
) has at least two distinct prime factors, then the numbers (1.5) and (1.6), respectively (respectively, (1.7)) for each corresponding $z,$
are units over $\mathbb {Z}$
.
In general, the numbers (1.5), (1.6), and (1.7), respectively for each corresponding $z,$
are units over $\mathbb {Z}[\frac { 1}{\mathrm {den}(2z)}],$
$\mathbb {Z}[\frac { 1}{\mathrm {den}(2z)}],$
and $\mathbb {Z}[\frac { 1}{\mathrm {den}(z)}],$
respectively.
One may notice that the exponents of the Dedekind eta function $\eta (\tau )$
vary in (1.5), (1.6), and (1.7), according to the assumptions of the theorem. The point is that these exponents are in fact very special, in the sense that they make expressions (1.5), (1.6), and (1.7) respectively have special algebraic properties at a CM point $\tau$
.
Remark 1.3
(i) If $z_1=z_2=0$
, then we have
\[ F_S(z_1,z_2,\tau)=e^{\frac{\pi i\tau}{12}\chi(S)}\eta(\tau) ^ {-\chi(S)}. \]Therefore we have that
\[ e^{-\frac{\pi i \tau}{12}\chi(S)}\eta(\tau)^{\chi(S)}F_S(z_1,z_2,\tau)=1, \]which is clearly an algebraic number.
(ii) Note that $f_S(z;\tau )$
in (1.3) coincides with $F_S(\frac {z+1}{2},\,\frac {z+1}{2};\tau )$ in (1.4), and hence the result (1) of Theorem 1.2 implies the algebraicity of the number given by (1.3). In fact, Theorem 1.2 (1) improves the results (1) and (3) of [Reference Jin and Jo16, Theorem 1.2]. We also have an improvement of (2) of [Reference Jin and Jo16, Theorem 1.2], but for simplicity, we include it in the proof of the theorem.
Note that Theorem 1.2 corresponds to some special cases of $z_1$
and $z_2$
, namely, when $z_1=\pm z_2$
or $z_1z_2=0$
, and therefore, it is natural to ask about the general case. In the following theorem, we also have the algebraicity result for the generic $z_1$
and $z_2$
, which complete the whole picture.
Theorem 1.4 Let $S$
be a smooth complex projective surface with the Euler characteristic $\chi (S)$
. Let $z_1,\,z_2$
be rational numbers, and let $\tau$
be a CM point.
If $z_1\neq 0$
, $z_2 \neq 0$
, and $z_1\neq \pm z_2$
, then
is an algebraic number, where $\chi (S)$
is the Euler characteristic of $S$
. In fact, (1.8) is a unit over $\mathbb {Z}[\frac {1}{\mathrm {lcm}(\mathrm {den}(z_1),\,\mathrm {den}(z_2))}]$
.
Moreover, if each of $\mathrm {den}(z_1),\, \ \mathrm {den}(z_2)$
, $\mathrm {den}(z_1+ z_2)$
, and $\mathrm {den}(z_1- z_2)$
has at least two distinct prime factors, then (1.8) is an algebraic integer.
One may wonder why the object in Theorem 1.4 contains only ${h^{1,1}(S)}$
in the exponent of $\eta (\tau )$
, simpler than the objects in Theorem 1.2. It is mainly because of the applicability of the algebraicity result on Siegel functions.
This paper is organized as follows: In §2, we state important properties needed to prove Theorem 1.2 and 1.4. In §3, we prove Theorem 1.2 and 1.4.
2. Preliminaries
In this section, we summarize some facts needed to prove our theorems.
2.1. Hodge numbers
The Hodge numbers $h^{p,q}(X)$
of a compact complex manifold $X$
are defined as the complex dimensions of the Dolbeault cohomology groups $H^{q}(X,\,\Omega _X^{p})$
, namely the $q^{th}$
cohomology group of $X$
with values in the sheaf $\Omega _X^{p}$
of holomorphic differential forms of degree $p$
. If $\mathrm { dim}_{\mathbb {C}}(X)=n$
, it is known by the Serre duality that $h^{p,q}(X)=h^{n-p,n-q}(X)$
, and in particular $h^{n,n}(X)=h^{0,0}(X)=1$
. Furthermore, if $X$
is a Kähler manifold, the Hodge numbers are known to satisfy the following further properties (see [Reference Griffiths and Harris13]):
Applying these, we see for a compact complex surface $X$
that
Hodge numbers in fact have a close connection to the celebrated Betti numbers when $X$
is Kähler. The $i^{th}$
Betti number of a manifold $X$
, denoted by $b_i(X)$
, is the rank of its $i^{th}$
singular cohomology group $H^{i}(X,\,\mathbb {C})$
. If a compact complex manifold $X$
is Kähler, then we have the following equality, by the existence of the Hodge decomposition.
It is easily seen that the following holds for the Euler characteristic $\chi (X)$
of $X$
:
2.2. Siegel functions
To deal with the algebraicity of $q$
-series given by infinite products, we need the theory of the so-called Siegel functions.
Let $\mathbf {B}_2(x):=x^{2}-x+\frac {1}{6}$
be the second Bernoulli polynomial and let $e(x):=e^{2\pi ix}$
. If $a=(a_1,\,a_2)\in \mathbb {Q}^{2}$
, then the Siegel function is defined as
where $q=e^{2\pi i\tau }$
.
One of the main use of the Siegel functions comes from the fact that $g_a$
is modular function (of some multiplier system and some subgroup of $\mathrm {SL}_2(\mathbb {Z})$
). Furthermore, if $N\cdot a\in \mathbb {Z}^{2}$
, then $g_a(\tau )^{12N}$
is known to be modular on $\Gamma (N)$
with the trivial multiplier system, where $\Gamma (N)=\{\gamma \in \mathrm {SL}_2(\mathbb {Z}) : \gamma \equiv 1\pmod N \}$
is the $N$
th principal congruence subgroup of $\mathrm {SL}_2(\mathbb {Z})$
(see [Reference Kubert and Lang19, Theorem 1.2]). Let $\mathrm {Den}(a)$
be the smallest $N\in \mathbb {N}$
such that $N\cdot a\in \mathbb {Z}^{2}$
.
What we need about the Siegel functions in this paper is the following theorem about the algebraicity of Siegel functions in relation to the $j$
-invariant $j(\tau ):=\frac {(1+240\sum \nolimits _{n=1}^{\infty }\sum \nolimits _{d|n}d^{3}q^{n})^{3}}{q\prod _{n=1}^{\infty }(1-q^{n})^{24}}$
that is in fact an $\mathrm {SL}_2(\mathbb {Z})$
-modular function.
Theorem 2.1 Kubert and Lang [Reference Kubert and Lang19, chapter 2, Theorem 2.2]
Let $a\in \mathbb {Q}^{2}\backslash \mathbb {Z}^{2}$
. If $\tau$
is in the upper half-plane and $N=\mathrm {Den}(a),$
then the following are true.
(1) If $N$
has at least two prime factors, then $g_a(\tau )$ is a unit over $\mathbb {Z}[j(\tau )]$.(2) If $N=p^{r}$
is a prime power, then $g_a(\tau )$ is a unit over $\mathbb {Z}[1/p][j(\tau )]$.(3) If $c\in \mathbb {Z}$
and $(c,\,N)=1,$ then $(g_{ca}/g_a)$ is a unit over $\mathbb {Z}[j(\tau )].$(4) If $\tau$
is a CM point, then $g_a(\tau )$ is an algebraic integer.
Remark 2.2 In fact, more can be said when $\tau$
is a CM point: if $g_a(\tau )$
is a unit over $\mathbb {Z}[j(\tau )]$
, then $g_a(\tau )$
is an algebraic integer unit, because $j(\tau )$
is an algebraic integer. Similarly, if $g_a(\tau )$
is a unit over $\mathbb {Z}[1/p][j(\tau )]$
then $g_a(\tau )$
is a unit over $\mathbb {Z}[1/p]$
.
2.3. Root of unity
To prove Theorems 1.2 and 1.4, we need some properties about roots of unity. Let $\Phi _n(z)$
be the $n$
th cyclotomic polynomial given by
where $z_1,\,z_2,\,\cdots,\,z_{\varphi (n)}$
are the primitive $n$
th roots of unity and $\mu (n)$
is the Möbius function.
Note that, for $n\geq 2$
,
Therefore we have that, for $n\geq 2$
,
We can check that
From this formula, for $n\geq 2$
, we have that
Using these observations, we have the following well-known fact (see, for instance, [Reference Kubert and Lang19, p.37]).
Lemma 2.3 Let $\zeta$
be a primitive $n$
th root of unity. Then the following are true.
(1) If $n$
has at least two distinct prime factor, then $1-\zeta$ is a unit over $\mathbb {Z}$.(2) If $n=p^{r}$
is a prime power, then $1-\zeta$ is a unit over $\mathbb {Z}[1/p]$.
3. Proofs of the main theorems
In this section, we give proofs of Theorem 1.2 and Theorem 1.4. We use the notation $q=e^{2\pi i\tau }$
in this section.
First, we note that if $(a_1,\,a_2)=(0,\,\alpha )\in \mathbb {Q}^{2}$
, then we have
Note also that the Dedekind eta function has the $q$
-expansion $\eta (\tau )=q^{\frac {1}{24}}\prod _{n=1}^{\infty }(1-q^{n})$
.
Proof of Theorem 1.2. Proof of Theorem 1.2
Let $\zeta _{\ell }^{r}:=e( r/\ell )$
, where $r,\,\ell \in \mathbb {Z}$
and $\gcd (r,\,\ell ) = 1$
. (1) If $z_1=z_2=z=\frac {r}{\ell }$
, then $x=y=\zeta _{\ell }^{r}$
. Using the fact $h^{p,q}(S)=h^{2-p,2-q}(X)$
, one can rephrase the given infinite product as follows:
Therefore, the given infinite product can be expressed in terms of the Euler characteristic $\chi (S)$
, the Dedekind eta function, the Siegel functions, and roots of unity.
Then, one can see from Theorem 2.1(4) that $\frac {g_{(0,r/\ell )}(\tau )^{h^{0,1}(S)+h^{1,0}(S)} }{g_{(0,2r/\ell )}(\tau )^{h^{0,0}(S)}}$
takes an algebraic number at a CM point $\tau$
, and from Lemma 2.3, we also know that $\frac {(1-\zeta ^{-2r}_{\ell } )^{h^{0,0}(S)} }{(1-\zeta ^{-r}_{\ell })^{h^{0,1}(S)+h^{1,0}(S)} }$
takes an algebraic number. Therefore, the algebraicity of
for a CM point $\tau$
follows.
(2) If $z_1=-z_2=z=\frac {r}{\ell }$
, then $x=y^{-1}=e(r/\ell )=\zeta _{\ell }^{r}$
. Then using $h^{p,q}(X)=h^{2-p,2-q}(X)$
, we can rephrase the given infinite product as follows:
Similarly, as in (1), we have that
is an algebraic number for a CM point $\tau$
.
(3) If $z_1=z=\frac {r}{\ell },\, z_2=0$
, then $x=\zeta _{\ell }^{r}$
and $y=1$
. In this case, we have the following rephrasement of the given infinite product:
Then, as before, we conclude that the number
is an algebraic number for a CM point $\tau$
.
(4) Now we prove that if $\mathrm {den}(2z)$
(respectively, $\mathrm {den}(z)$
) has at least two distinct prime divisors, then the above expressions (1.5) and (1.6)(respectively, (1.7)) are units over $\mathbb {Z}$
at the corresponding rational numbers $z$
and a CM point $\tau$
, and, in general, (1.5) and (1.6)(respectively, (1.7)) are units over $\mathbb {Z}[\frac { 1}{\mathrm {den}(2z)}]$
(respectively, $\mathbb {Z}[\frac { 1}{\mathrm {den}(z)}]$
) at the corresponding rational numbers $z$
and a CM point $\tau$
.
First, we consider the cases of (1.5) and (1.6). We only prove the statement about (1.5) here, since the proof of (1.6) is similar. To do this, we divide the proof into two cases, namely when $\mathrm {den}(\frac {2r}{\ell })$
has at least two distinct prime factors and $\mathrm {den}(\frac {2r}{\ell })$
has only one prime factor, i.e., is a prime power.
Let us first consider the case when $\mathrm {den}(\frac {2r}{\ell })$
has at least two distinct prime factors. In this case, first, from Theorem 2.1(1) and Remark 2.2, we can see that $g_{(0,r/\ell )}(\tau )^{\pm (h^{0,1}(S)+h^{1,0}(S))}$
and $g_{(0,2r/\ell )}(\tau )^{\pm h^{0,0}(S)}$
take an algebraic integer at a CM point $\tau$
.
We also need to control the roots of unity part. First, since $1-\zeta _\ell ^{-2r}$
and $1-\zeta _{\ell }^{-r}$
are algebraic integers, it is clear that $(1-\zeta ^{-2r}_{\ell } )^{h^{0,0}(S)}$
and $(1-\zeta ^{-r}_{\ell })^{h^{0,1}(S)+h^{1,0}(S)}$
are also algebraic integers. Furthermore, if $\mathrm {den}(\frac {2r}{\ell })$
has at least two distinct primes, we see from Lemma 2.3(1) that $(1-\zeta ^{-2r}_{\ell } )^{-h^{0,0}(S)}$
and $(1-\zeta ^{-r}_{\ell })^{-h^{0,1}(S)-h^{1,0}(S)}$
are algebraic integers. Combining these two facts, we conclude that if $\frac {r}{\ell }\neq 0$
and $\mathrm {den}(\frac {2r}{\ell })$
has at least two distinct prime factors, then (1.5) is an algebraic unit over $\mathbb {Z}$
for a CM point $\tau$
.
The other remaining case is the case when $\mathrm {den}(\frac {2r}{\ell })=p^{l}$
is a prime power. In this case, similarly, one can get using Theorem 2.1(2) and Lemma 2.3(2) that if $\mathrm {den}(\frac {2r}{\ell })=p^{l}$
is a prime power, then (1.5) is a unit over $\mathbb {Z}[\frac {1}{p}]$
for a CM point $\tau$
.
Therefore, combining the above two cases, we can see that (1.5) is a unit over $\mathbb {Z}[\frac {1}{\mathrm {den}(\frac {2r}{\ell })}]$
for a CM point $\tau$
.
Now, we consider the case of (1.7). In this case, it is sufficient to consider $g_{(0,r/ \ell )}(\tau )$
and $(1-\zeta _\ell ^{r})$
. If $\mathrm {den}(\frac {r}{\ell })$
has at least two distinct prime factors, from Theorem 2.1(1) and Lemma 2.3(1), we see that the Siegel function $g_{(0,r/\ell )}(\tau )^{\pm (h^{0,1}(S)-h^{0,0}(S))}$
takes an algebraic integer and $(1-\zeta _{\ell }^{r})^{\pm (h^{0,1}(S)-h^{0,0}(S)-h^{0,2}(S))}$
is an algebraic integer at a CM point $\tau$
. On the other hand, if $\mathrm {den}(\frac {r}{\ell })=p^{l}$
is a prime power, then $g_{(0,r/\ell )}(\tau )^{\pm (h^{0,1}(S)-h^{0,0}(S))}$
and $(1-\zeta _{\ell }^{r})^{\pm (h^{0,1}(S)-h^{0,0}(S)-h^{0,2}(S))}$
are units over $\mathbb {Z}[\frac {1}{p}]$
using Theorem 2.1(2) and Lemma 2.3(2). Therefore (1.7) is a unit over $\mathbb {Z}[\frac {1}{\mathrm {den}(\frac {r}{\ell })}]$
and an algebraic integer when $\mathrm {den}(\frac {r}{\ell })$
has at least two distinct prime divisors.
Now, we prove Theorem 1.4 in the generic case, i.e., when $z_1\neq \pm z_2$
with non-zero $z_1,\, z_2$
. Note that in this case, the exponent of $\eta (\tau )$
in (1.8) is simpler than those of $\eta (\tau )$
in (1.5), (1.6), and (1.7). At first sight, this phenomenon may seem somewhat strange, since Theorem 1.4 is about the generic case. However, this can be understood from Göttsche's formula (1.2), since the cases of Theorem 1.2 correspond to those when some of the products of the form $\prod _{n=1}^{\infty }(1-x^{a}y^{b} q^{n})$
are simplified to $\prod _{n=1}^{\infty }(1-q^{n})=q^{-\frac {1}{24}}\eta (\tau )$
, which in turn explains powers of $\eta (\tau )$
being more than those of exponent $h^{1,1}(S)$
in Theorem 1.4.
On the other hand, we have to deal with the algebraicity of general infinite products of the form $\prod _{n=1}^{\infty }(1-x^{a}y^{b} q^{n})$
, which are more complex than the exponent of $\eta (\tau )$
in Theorem 1.4. Fortunately, this can be achieved using the theory of Siegel functions, as we see below, but here we have to deal with more Siegel functions than we did in Theorem 1.2. This makes the proof of Theorem 1.4 more involved than that of Theorem 1.2.
Proof of Theorem 1.4. Proof of Theorem 1.4
Let $\zeta _{\ell }^{r}=e(r/\ell )$
, where $r,\,\ell \in \mathbb {Z}$
and $\gcd (r,\,\ell )=1$
. If $x=\zeta _{\ell _1}^{r_1}$
and $y=\zeta _{\ell _2}^{r_2}$
, then
and
From $xy=e((r_1\ell _2+r_2\ell _1)/(\ell _1\ell _2))$
and $x/y=e( (r_1\ell _2-r_2\ell _1)/(\ell _1\ell _2))$
, we have
and
Because of the formula $h^{p,q}(X)=h^{n-p,n-q}(X)$
, we have
Therefore, using (2.1), we have
Because $1-\zeta _{\ell _1\ell _2}^{-r_1\ell _2-r_2\ell _1}$
and $1-\zeta _{\ell _1\ell _2}^{-r_1\ell _2+r_2\ell _1}$
are algebraic integers, we see that
is an algebraic integer. From Lemma 2.3(1), we see that
is an algebraic integer if both $\mathrm {den}(\frac {r_1}{\ell _1})$
and $\mathrm {den}(\frac {r_2}{\ell _2} )$
have at least two distinct prime factors. From Theorem 2.1(4), we have that
takes an algebraic integer at a CM point $\tau$
. Also, from Theorem 2.1(1), if both $\mathrm {den}(\frac {r_1}{\ell _1}+\frac {r_2}{\ell _2})$
and $\mathrm {den}(\frac {r_1}{\ell _1}-\frac {r_2}{\ell _2} )$
have at least two prime factors then
takes an algebraic integer at a CM point $\tau$
.
Therefore, for $\frac {r_1}{\ell _1}\neq 0$
, $\frac {r_2}{\ell _2} \neq 0$
and $\frac {r_1}{\ell _1}\neq \pm \frac {r_2}{\ell _2}$
, if each of $\mathrm {den}(\frac {r_1}{\ell _1})$
, $\mathrm {den}(\frac {r_2}{\ell _2})$
, $\mathrm {den}(\frac {r_1}{\ell _1}+\frac {r_2}{\ell _2})$
and $\mathrm {den}(\frac {r_1}{\ell _1}-\frac {r_2}{\ell _2} )$
has at least two distinct prime factors, then
is an algebraic integer for a CM point $\tau$
.
Generally, from Lemma 2.3 and Theorem 2.1, we can check that $(1-\zeta _{\ell }^{-r})^{\pm 1}$
is a unit over $\mathbb {Z} [\frac {1}{\mathrm {den}(\frac {r}{\ell })} ]$
and $g_{(0,r/\ell )}(\tau )$
is a unit over $\mathbb {Z} [\frac {1}{\mathrm {den}(\frac {r}{\ell })} ]$
for a CM point $\tau$
. Hence for the case that $\frac {r_1}{\ell _1}\neq 0$
, $\frac {r_2}{\ell _2} \neq 0$
and $\frac {r_1}{\ell _1}\neq \pm \frac {r_2}{\ell _2}$
, we conclude that
is a unit over $\mathbb {Z}[\frac {1}{\mathrm {lcm}(\mathrm {den}(\frac {r_1}{\ell _1}),\,\mathrm {den}( \frac {r_2}{\ell _2}))}]$
and an algebraic number for a CM point $\tau$
.
Acknowledgements
The first author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1F1A1A01076646). The second author was supported by the NRF grant funded by the Korea government (MSIT) (No. 2020R1C1C1A01010671).
