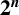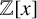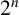1 Introduction
Throughout this paper, for
$f(x)\in {\mathbb Z}[x]$
, when we say that ‘
$f(x)$
is irreducible’ without reference to a particular field, we mean that ‘
$f(x)$
is irreducible over
${\mathbb Q}$
’. We say that
$f(x)$
is reciprocal if
$f(x)=x^{\deg (f)}f(1/x)$
. We let
$\Delta (f)$
and
$\Delta (K)$
denote the discriminants over
${\mathbb Q}$
, respectively, of
$f(x)$
and a number field K. If
$f(x)$
is irreducible, with
$f(\theta )=0$
and
$K={\mathbb Q}(\theta )$
, then
$$ \begin{align} \Delta(f)=[{\mathbb Z}_K:{\mathbb Z}[\theta]]^2\Delta(K), \end{align} $$
where
${\mathbb Z}_K$
is the ring of integers of K [Reference Cohen1]. We say that
$f(x)$
is monogenic if
$f(x)$
is irreducible and
${\mathbb Z}_K={\mathbb Z}[\theta ]$
, or equivalently from (1.1), that
$\Delta (f)=\Delta (K)$
. In this situation,
$\{1,\theta ,\theta ^2,\ldots ,\theta ^{\deg {f}-1}\}$
is a basis for
${\mathbb Z}_K$
, often referred to as a power basis. The existence of a power basis makes computations in
${\mathbb Z}_K$
easier, as in the case of the cyclotomic polynomials
$\Phi _n(x)$
[Reference Washington12]. We see from (1.1) that if
$\Delta (f)$
is squarefree, then
$f(x)$
is monogenic. However, the converse is false in general. Indeed, when
$\Delta (f)$
is not squarefree, it can be quite difficult to determine whether
$f(x)$
is monogenic.
Reciprocal monogenic quintinomials are scarce in the literature. One such infinite family of quartics can be found in [Reference Gaál4]. More recently [Reference Jones9], infinite families of reciprocal monogenic quintinomials of degree
$2^n$
, for every integer
$n\ge 2$
, were constructed by perturbing the middle coefficient of certain cyclotomic polynomials. In this paper, we take a different approach to construct new infinite families of reciprocal monogenic quintinomials of degree
$2^n$
, for every integer
$n\ge 2$
.
Theorem 1.1. Let
$n,A,B\in {\mathbb Z}$
, with
$n\ge 2$
and
$AB\not \equiv 0 \pmod {2}$
. Define the reciprocal quintinomial
$$ \begin{align*} {\mathcal F}_{n,A,B}(x):=x^{2^n}+Ax^{3\cdot 2^{n-2}}+Bx^{2^{n-1}}+Ax^{2^{n-2}}+1. \end{align*} $$
Suppose that
${\mathcal D}:=(2A+B+2)(2A-B-2)(A^2-4B+8) \mbox { is squarefree,}$
and that
$$ \begin{align*}(\widehat{A},\widehat{B})\in {\mathcal C}:=\{(1,3),(3,1),(3,3)\},\end{align*} $$
where
$\widehat {*}\in \{0,1,2,3\}$
is the reduction modulo
$4$
of
$*$
. Then
${\mathcal F}_{n,A,B}(x)$
is monogenic for all
$n\ge 2$
.
Corollary 1.2. Let
${\mathcal C}$
be as defined in Theorem 1.1. Then there exist infinitely many prime pairs
$(p,q)$
with
$(\widehat {p},\widehat {q})\in {\mathcal C}$
, such that
${\mathcal F}_{n,p,q}(x)$
is monogenic for all
$n\ge 2$
.
2 Preliminaries
Definition 2.1 [Reference Cohen1].
Let
$\mathcal{R}$
be an integral domain with quotient field K and let
$\overline {K}$
be an algebraic closure of K. Let
$f(x), g(x)\in \mathcal{R}[x]$
, with the respective factorisations
$f(x)=a\prod _{i=1}^m(x-\alpha _i)\in \overline {K}[x]$
and
$g(x)=b\prod _{i=1}^n(x-\beta _i)\in \overline {K}[x]$
. Then the resultant
$R(f,g)$
of f and g is
$$ \begin{align*}R(f,g)=a^n\prod_{i=1}^mg(\alpha_i)=(-1)^{mn}b^m\prod_{i=1}^nf(\beta_i).\end{align*} $$
Theorem 2.2. Let
$f(x)$
and
$g(x)$
be polynomials in
$\mathbb {Q}[x]$
, with respective leading coefficients a and b and respective degrees m and n. Then
$$ \begin{align*}\Delta(f\circ g)=(-1)^{m^2n(n-1)/2}\cdot a^{n-1}b^{m(mn-n-1)}\Delta(f)^{n}R(f\circ g,g').\end{align*} $$
Remark 2.3. As far as we can determine, Theorem 2.2 is originally due to Cullinan [Reference Cullinan2]. A proof of Theorem 2.2 can be found in [Reference Harrington and Jones6].
The following theorem, known as Dedekind’s index criterion, or simply Dedekind’s criterion if the context is clear, is a standard tool used in determining the monogeneity of a polynomial.
Theorem 2.4 (Dedekind; see [Reference Cohen1]).
Let
$K={\mathbb Q}(\theta )$
be a number field,
$T(x)\in {\mathbb Z}[x]$
the monic minimal polynomial of
$\theta $
and
${\mathbb Z}_K$
the ring of integers of K. Let q be a prime number and let
$\overline { * }$
denote reduction of
$*$
modulo q (in
${\mathbb Z}$
,
${\mathbb Z}[x]$
or
${\mathbb Z}[\theta ]$
). Let
$$ \begin{align*}\overline{T}(x)=\prod_{i=1}^k\overline{\tau_i}(x)^{e_i}\end{align*} $$
be the factorisation of
$T(x)$
modulo q in
${\mathbb F}_q[x]$
and set
$$ \begin{align*}g(x)=\prod_{i=1}^k\tau_i(x),\end{align*} $$
where the
$\tau _i(x)\in {\mathbb Z}[x]$
are arbitrary monic lifts of the
$\overline {\tau _i}(x)$
. Let
$h(x)\in {\mathbb Z}[x]$
be a monic lift of
$\overline {T}(x)/\overline {g}(x)$
and set
$$ \begin{align*}F(x)=\dfrac{g(x)h(x)-T(x)}{q}\in {\mathbb Z}[x].\end{align*} $$
Then
$$ \begin{align*}[{\mathbb Z}_K:{\mathbb Z}[\theta]]\not \equiv 0 \pmod{q} \Longleftrightarrow \gcd(\overline{F},\overline{g},\overline{h})=1 \mbox{ in } {\mathbb F}_q[x].\end{align*} $$
The next theorem follows from [Reference Neukirch10, Corollary 2.10].
Theorem 2.5. Let K and L be number fields with
$K\subset L$
. Then
$$ \begin{align*}\Delta(K)^{[L:K]} \mid\Delta(L).\end{align*} $$
Theorem 2.6. Let
$G(t)\in {\mathbb Z}[t]$
, and suppose that
$G(t)$
factors into a product of distinct irreducibles, such that the degree of each irreducible is at most
$3$
. Define
$$ \begin{align*}N_G(X)=|{\{p\le X : p \mbox{ is prime and } G(p) \mbox{ is squarefree}\}}|.\end{align*} $$
Then
$$ \begin{align*}N_G(X)\sim C_G\dfrac{X}{\log(X)},\end{align*} $$
where
$$ \begin{align*}C_G=\prod_{\ell {\text {prime}}}\bigg(1-\dfrac{\rho_G(\ell^2)}{\ell(\ell-1)}\bigg)\end{align*} $$
and
$\rho _G(\ell ^2)$
is the number of
$z\in ({\mathbb Z}/\ell ^2{\mathbb Z})^{*}$
such that
$G(z)\equiv 0 \pmod {\ell ^2}$
.
Remark 2.7. Theorem 2.6 follows from the work of Helfgott [Reference Helfgott7], Hooley [Reference Hooley8] and Pasten [Reference Pasten11]. For more details, see [Reference Jones9].
Definition 2.8. In the context of Theorem 2.6, for
$G(t)\in {\mathbb Z}[t]$
and a prime
$\ell $
, if
$G(z)\equiv 0 \pmod {\ell ^2}$
for all
$z\in ({\mathbb Z}/\ell ^2{\mathbb Z})^{*}$
, we say that
$G(t)$
has a local obstruction at
$\ell $
.
The following immediate corollary of Theorem 2.6 is used to establish Corollary 1.2.
Corollary 2.9. Let
$G(t)\in {\mathbb Z}[t]$
and suppose that
$G(t)$
factors into a product of distinct irreducibles, such that the degree of each irreducible is at most
$3$
. To avoid the situation where
$C_G=0$
, we suppose further that
$G(t)$
has no local obstructions. Then there exist infinitely many primes q such that
$G(q)$
is squarefree.
We make the following observation concerning
$G(t)$
from Corollary 2.9 in the special case where each of the distinct irreducible factors of
$G(t)$
is of the form
$a_it+b_i$
with
$\gcd (a_i,b_i)=1$
. In this situation, it follows that the minimum number of distinct factors required in
$G(t)$
so that
$G(t)$
has a local obstruction at the prime
$\ell $
is
$2(\ell -1)$
. More precisely, in this minimum scenario,
$$ \begin{align*}G(t)=\prod_{i=1}^{2(\ell-1)}(a_it+b_i)\equiv C(t-1)^2(t-2)^2\cdots (t-(\ell-1))^2 \pmod{\ell},\end{align*} $$
where
$C\not \equiv 0 \pmod {\ell }$
. Then each zero r of
$G(t)$
modulo
$\ell $
lifts to the
$\ell $
distinct zeros
$$ \begin{align*}r,\ r+\ell,\ r+2\ell,\ \ldots , \ r+(\ell-1)\ell \in ({\mathbb Z}/\ell^2{\mathbb Z})^{*}\end{align*} $$
of
$G(t)$
modulo
$\ell ^2$
[Reference Dence and Dence3, Theorem 4.11]. That is,
$G(t)$
has exactly
$\ell (\ell -1)=\phi (\ell ^2)$
distinct zeros
$z\in ({\mathbb Z}/\ell ^2{\mathbb Z})^{*}$
. Therefore, if the number of factors k of
$G(t)$
satisfies
$k<2(\ell -1)$
, then there must exist
$z\in ({\mathbb Z}/\ell ^2{\mathbb Z})^{*}$
for which
$G(z)\not \equiv 0 \pmod {\ell ^2}$
, and we do not need to check such primes
$\ell $
for a local obstruction. Consequently, only finitely many primes need to be checked for local obstructions. They are precisely the primes
$\ell $
such that
$\ell \le (k+2)/2$
.
The following proposition, which follows from a generalisation of a theorem of Capelli, is a special case of the results in [Reference Guersenzvaig5], and gives simple necessary and sufficient conditions for the irreducibility of polynomials of the form
$w(x^{2^k})\in {\mathbb Z}[x]$
, when
$w(x)$
is monic and irreducible.
Proposition 2.10 [Reference Guersenzvaig5].
Let
$w(x)\in {\mathbb Z}[x]$
be monic and irreducible, with
$\deg (w)=m$
. Then
$w(x^{2^k})$
is reducible if and only if there exist
$S_0(x),S_1(x)\in {\mathbb Z}[x]$
such that either
$$ \begin{align*} (-1)^mw(x)=(S_0(x))^2-x(S_1(x))^2 \end{align*} $$
or
$$ \begin{align*} k\ge 2 \quad\mbox{and}\quad w(x^2)=(S_0(x))^2-x(S_1(x))^2. \end{align*} $$
3 Proof of Theorem 1.1
For the proof of Theorem 1.1, we require some special cases of the following lemma, which is of some interest in its own right.
Lemma 3.1. Let
$n,A,B\in {\mathbb Z}$
, with
$n\ge 2$
, and let
$$ \begin{align} {\mathcal F}_{n,A,B}(x)=x^{2^n}+Ax^{3\cdot 2^{n-2}}+Bx^{2^{n-1}}+Ax^{2^{n-2}}+1. \end{align} $$
Then
${\mathcal F}_{n,A,B}(x)$
is irreducible for all
$n\ge 2$
if and only if
$$ \begin{align*}(\widehat{A},\widehat{B})\in \Gamma=\{(0,0),(0,3),(1,3),(2,0),(2,1),(3,1),(3,3)\},\end{align*} $$
where
$\widehat {*}\in \{0,1,2,3\}$
is the reduction modulo
$4$
of
$*$
.
Proof. Suppose first that
$(\widehat {A},\widehat {B})\in \Gamma $
. Since the methods required in all cases of
$(\widehat {A},\widehat {B})$
are similar, we assume that
$(\widehat {A},\widehat {B})=(1,3)$
and give details only for this particular case.
We begin by showing that
${\mathcal F}_{2,A,B}(x)$
is irreducible. Observe that
${\mathcal F}_{2,A,B}(1)\ne 0$
since
${\mathcal F}_{2,A,B}(1)=2A+B+2\equiv 1 \pmod {2}$
. Similarly,
${\mathcal F}_{2,A,B}(-1)\ne 0$
. Thus,
${\mathcal F}_{2,A,B}(x)$
has no zeros by the rational zero theorem. Suppose then that
$$ \begin{align*} {\mathcal F}_{2,A,B}(x)&=(x^2+ax+b)(x^2+cx+d)\\ &=x^4+(c+a)x^3+(d+ac+b)x^2+(ad+bc)x+bd, \end{align*} $$
where
$a,b,c,d\in {\mathbb Z}$
. Equating coefficients yields the system of equations
$$ \begin{align*} a+c&=A,\\ ac+b+d&=B,\\ ad+bc&=A,\\ bd&=1. \end{align*} $$
Letting
$b=d=1$
and reducing this system modulo 4, we arrive at the system of congruences
$$ \begin{align*} a+c&\equiv 1\pmod{4},\\ ac&\equiv 1 \pmod{4}, \end{align*} $$
which produces the insoluble congruence
$c^2\equiv 3 \pmod {4}$
. The situation
$b=d=-1$
is also easily seen to be impossible. Hence,
${\mathcal F}_{2,A,B}(x)$
is irreducible.
Observing that
${\mathcal F}_{n,A,B}(x)={\mathcal F}_{2,A,B}(x^{2^{n-2}})$
for
$n\ge 2$
, we apply Proposition 2.10 with
$w(x)={\mathcal F}_{2,A,B}(x)$
and
$m=4$
. We treat separately the case
$n=3$
, which corresponds to
$k=1$
in Proposition 2.10. By way of contradiction, we assume that
${\mathcal F}_{3,A,B}(x)={\mathcal F}_{2,A,B}(x^2)$
is reducible. Then, by Proposition 2.10, there exist
$S_0(x), S_1(x)\in {\mathbb Z}[x]$
such that
$$ \begin{align*}{\mathcal F}_{2,A,B}(x)=(S_0(x))^2-x(S_1(x))^2.\end{align*} $$
Since
$\deg ({\mathcal F}_{2,A,B})=4$
, it follows that
$$ \begin{align*}S_0(x)=x^2+ax+b \quad \mbox{and}\quad S_1(x)=cx+d\end{align*} $$
for some
$a,b,c,d\in {\mathbb Z}$
. Then
$$ \begin{align} \hspace{-16pt}(S_0(x))^2\kern1.5pt{-}\kern1.5pt x(S_1(x))^2\kern1.5pt{=}\kern1.5pt x^4\kern1.5pt{+}\kern1.5pt(2a\kern1.5pt{-}\kern1.5ptc^2)x^3\kern1.5pt{+}\kern1.5pt(2b\kern1.5pt{+}\kern1.5pta^2\kern1.5pt{-}\kern1.5pt2cd)x^2\kern1.5pt{+}\kern1.5pt(2ab\kern1.5pt{-}\kern1.5ptd^2)x\kern1.5pt{+}\kern1.5ptb^2.\quad \end{align} $$
Equating the coefficients of (3.2) and
${\mathcal F}_{2,A,B}(x)$
, we arrive at the three solutions:
-
(1)
$\{b = -1, 4a=c^2-d^2, 2A=-c^2-d^2, 16B=c^4-2c^2d^2+d^4-8cd-32\}$
, -
(2)
$\{b = 1, c=d, A=2a-d^2, B=a^2-2d^2+2\}$
, -
(3)
$\{b = 1, c = -d, A=2a-d^2, B=a^2+2d^2+2\}$
.
In (1), reduction modulo 4 of the second and third equations implies that both c and d are odd. But then the fourth equation yields the contradiction
$$ \begin{align*}16B=c^4-2c^2d^2+d^4-8cd-32\equiv 8 \pmod{16}.\end{align*} $$
In both (2) and (3), the third and fourth equations produce the system of congruences
$$ \begin{align*} 2a-d^2&\equiv 1\pmod{4},\\ a^2+2d^2&\equiv 1 \pmod{4}, \end{align*} $$
from which it is straightforward to derive the insoluble congruence
$a^2\equiv 3 \pmod {4}$
. Therefore,
${\mathcal F}_{3,A,B}(x)$
is irreducible.
Now suppose that
$n\ge 4$
, which corresponds to
$k\ge 2$
in Proposition 2.10. Assume, by way of contradiction, that
${\mathcal F}_{n,A,B}(x)$
is reducible. Then, by Proposition 2.10, there exist
$S_0(x),S_1(x)\in {\mathbb Z}[x]$
such that
$$ \begin{align} {\mathcal F}_{3,A,B}(x)={\mathcal F}_{2,A,B}(x^2)=(S_0(x))^2-x(S_1(x))^2, \end{align} $$
where
$$ \begin{align*}S_0(x)=x^4+\sum_{j=0}^3c_jx^j \quad \mbox{and} \quad S_1(x)=\sum_{j=0}^3d_jx^j.\end{align*} $$
Equating coefficients in (3.3) on x and
$x^2$
, along with the constant term, yields the system of equations
$$ \begin{align*} \begin{array}{rl} x:& 2c_0c_1-d_0^2=0,\\ x^2:& c_1^2-2d_0d_1+2c_0c_2=A,\\[2pt] \mbox{constant term}:& c_0^2=1. \end{array} \end{align*} $$
Examination of the equation corresponding to the coefficient on x reveals that
$d_0\equiv 0\pmod {2}$
. Then reduction modulo 4 of this same equation implies that
$c_1\equiv 0 \pmod {2}$
, since
$c_0=\pm 1$
from the constant-term equation. Consequently, we arrive at a contradiction in the equation corresponding to
$x^2$
, since then the left-hand side is even, while the right-hand side is odd. We deduce, by Proposition 2.10, that
${\mathcal F}_{n,A,B}(x)={\mathcal F}_{2,A,B}(x^{2^{n-2}})$
is irreducible, for all
$n\ge 2$
.
Finally, for the other direction of the proof, suppose that
$(\widehat {A},\widehat {B})\not \in \Gamma $
. That is, assume
$$ \begin{align} (\widehat{A},\widehat{B})\in \{(0,1),(0,2),(1,0),(1,1),(1,2),(2,2),(2,3),(3,0),(3,2)\}. \end{align} $$
For each of these cases of
$(\widehat {A},\widehat {B})\ne (1,1)$
, we provide in Table 1 an explicit example of
$(A,B)$
such that
${\mathcal F}_{n,A,B}(x)$
is reducible, not only for some n, but for all
$n\ge 2$
. For the special case of
$(\widehat {A},\widehat {B})=(1,1)$
, the example in Table 1 is irreducible for
$n=2$
, but reducible for all
$n\ge 3$
. We let
$\Phi _N(x)$
denote the cyclotomic polynomial of index N in Table 1.
Table 1 Examples for (3.4) and their factorisations.
Proof of Theorem 1.1.
Since
${\mathcal C}\subset \Gamma $
, it follows from Lemma 3.1 that
${\mathcal F}_{n,A,B}(x)$
is irreducible for all
$n\ge 2$
. A computation in Maple yields
$$ \begin{align} \Delta({\mathcal F}_{2,A,B})=-(2A+B+2)(2A-B-2)(A^2-4B+8)^2. \end{align} $$
Making the observation that
${\mathcal F}_{n,A,B}(x)={\mathcal F}_{2,A,B}(x^{2^{n-2}})$
for
$n\ge 2$
, we then use Theorem 2.2 and Definition 2.1 to calculate
$$ \begin{align} \Delta({\mathcal F}_{n,A,B})&=\Delta({\mathcal F}_{2,A,B}\circ x^{2^{n-2}})\nonumber \\ &=(-1)^{2^{n+1}(2^{n-2}-1)}\Delta({\mathcal F}_{2,A,B})^{2^{n-2}}R({\mathcal F}_{n,A,B},2^{n-2}x^{2^{n-2}-1})\nonumber \\ &=2^{2^n(n-2)}\Delta({\mathcal F}_{2,A,B})^{2^{n-2}}\nonumber \\ &=2^{2^n(n-2)}(-(2A+B+2)(2A-B-2)(A^2-4B+8)^2)^{2^{n-2}}. \end{align} $$
To establish that
${\mathcal F}_{n,A,B}(x)$
is monogenic, we begin with the case
$n=2$
. Suppose that
${\mathcal F}_{2,A,B}(\theta )=0$
. We use Theorem 2.4 to show that
$[{\mathbb Z}_{K}:{\mathbb Z}[\theta ]]\not \equiv 0 \pmod {q}$
, for every prime q dividing
${\mathcal D}$
, where
${\mathbb Z}_{K}$
is the ring of integers of
$K={\mathbb Q}(\theta )$
. Because
${\mathcal D}$
is squarefree, it follows from (3.5) that no prime dividing
$(2A+B+2)(2A-B-2)$
can divide the index
$[{\mathbb Z}_{K}:{\mathbb Z}[\theta ]]$
. Hence, we only need to focus on primes dividing
$A^2-4B+8$
. Suppose then that q is such a prime. We apply Theorem 2.4 to q with
$T(x):={\mathcal F}_{2,A,B}(x)$
. Since
$B\equiv (A^2+8)/4 \pmod {q}$
, we have
$$ \begin{align*}\overline{T}(x)=(x^2+(A/2)x+1)^2=\overline{\tau}(x)^2.\end{align*} $$
Then, using the quadratic formula, we see that there are three cases to consider:
-
(i)
$\overline {\tau }(x)\equiv (x+A/4)^2 \pmod {q}$
; -
(ii)
$\overline {\tau }(x)$
is irreducible over
${\mathbb F}_q$
; -
(iii)
$\overline {\tau }(x)\equiv (x-(-A+w)/4)(x-(-A-w)/4) \pmod {q}$
, where
$w^2\equiv A^2-16 \pmod {q}$
.
We claim first that case (i) cannot happen. In this case, we see from the quadratic formula that
$A^2-16 \equiv 0 \pmod {q}$
. Then
$B\equiv 6\pmod {q}$
since
$$ \begin{align*}-4(B-6)\equiv -4B+24\equiv A^2-4B+8\equiv 0\pmod{q}.\end{align*} $$
Consequently,
$$ \begin{align*}(2A+B+2)(2A-B-2)=4A^2-B^2-4B-4\equiv 0 \pmod{q},\end{align*} $$
which contradicts the fact that
${\mathcal D}$
is squarefree. Therefore, case (i) is vacuous.
Suppose next that we are in case (ii). Since
$A\equiv 1 \pmod {2}$
, we can let
$$ \begin{align*} g(x)=h(x)=\tau(x)=x^2+((A+q)/2)x+1. \end{align*} $$
Then
$$ \begin{align*} F(x)&=\dfrac{g(x)h(x)-T(x)}{q}\\ &=\dfrac{(x^2+((A+q)/2)x+1)^2-{\mathcal F}_{2,A,B}(x)}{q}\\ &=x\bigg(x^2+\bigg(\dfrac{\textstyle{\frac{A^2-4B+8}{q}}+2A+q}{4}\bigg)x+1\bigg), \end{align*} $$
so that
$$ \begin{align} \overline{F}(x)=x\bigg(x^2+\bigg(\dfrac{\overline{\bigg(\textstyle{\frac{A^2-4B+8}{q}}\bigg)}+2A}{4}\bigg)x+1\bigg). \end{align} $$
If
$\gcd (\overline {g},\overline {F})>1$
, then, since
$\overline {g}(x)$
is irreducible over
${\mathbb F}_q$
, it follows that
$\overline {F}(x)$
is divisible by
$\overline {g}(x)$
. Thus, equating coefficients on
$\overline {g}(x)$
and the quadratic factor of
$\overline {F}(x)$
in (3.7) yields
$$ \begin{align*}\dfrac{A}{2}\equiv \dfrac{\overline{\bigg(\textstyle{\frac{A^2-4B+8}{q}}\bigg)}+2A}{4}\equiv \overline{\bigg(\dfrac{A^2-4B+8}{4q}\bigg)}+\dfrac{A}{2} \pmod{q},\end{align*} $$
so that
$$ \begin{align*}\overline{\bigg(\dfrac{A^2-4B+8}{4q}\bigg)}\equiv 0 \pmod{q}.\end{align*} $$
Hence,
$A^2-4B+8\equiv 0 \pmod {q^2}$
, which contradicts the fact that
$A^2-4B+8$
is squarefree. Therefore,
$\gcd (\overline {g},\overline {F})=1$
, which implies that
$[{\mathbb Z}_K:{\mathbb Z}[\theta ]]\not \equiv 0 \pmod {q}$
by Theorem 2.4, and
${\mathcal F}_{2,A,B}(x)$
is monogenic in this case.
Finally, suppose that we are in case (iii). Without loss of generality, assume that
$w\equiv 0 \pmod {2}$
. Then
$$ \begin{align*}-A+w+\epsilon q\equiv -A-w+\epsilon q\equiv 0 \pmod{4} \quad \mbox{ for some}\ \epsilon\in \{-1,1\},\end{align*} $$
where the value of
$\epsilon $
depends on the congruence classes of A and q modulo 4. Since both of these possibilities for
$\epsilon $
are handled identically, we give details only for
$\epsilon =1$
. Thus, we can let
$$ \begin{align*}g(x)=h(x)=(x-(-A+w+q)/4)(x-(-A-w+q)/4).\end{align*} $$
Therefore, to prove that
$\gcd(\overline{F},\overline{g})=1$
, we only have to show
$\overline{F}((-A\pm w+q)/4)\ne 0$
. Because the methods are the same, we give details only for
$x=(-A+w+q)/4$
. Noting that
$\overline{F}((-A+w+q)/4)\ne 0$
if and only if
$qF((-A+w+q)/4)\not \equiv 0 \pmod{q^2}$
, we examine
$qF((-A+w+q)/4)$
. Since
$w^2\equiv A^2-16\pmod{q}$
, we can write
$w^2=A^2-16+qk$
, for some
$k\in \mathbb{Z}$
. Using this substitution for
$w^2$
and the fact that q divides
$A^2-4B+8$
, a straightforward calculation in Maple reveals that
$$ \begin{align*} 256qF((-A+w+q)/4)&=-q^4-(4w+6k)q^3+(96-k^2-4kw-16B)q^2\\ &\quad -4(2A-2w-k)(A^2-4B+8)q\\ &\quad +8(A^2-Aw-8)(A^2-4B+8)\\ &\equiv 8(A^2-Aw-8)(A^2-4B+8)\quad \pmod{q^2}.\end{align*} $$
If
$A^2-Aw-8\equiv 0 \pmod{q}$
, then, since
$q\equiv 1 \pmod{2}$
, we see that
$A\not \equiv 0 \pmod{q}$
. Thus,
$w\equiv (A^2-8)/A \pmod{q}$
. But
$w^2\equiv A^2-16 \pmod{q}$
, so that
$$ \begin{align*} \bigg(\dfrac{A^2-8}{A}\bigg)^2\equiv A^2-16\quad \pmod{q}, \end{align*} $$
which yields the impossible congruence
$64\equiv 0 \pmod{q}$
. Since
$A^2-4B+8$
is squarefree, we conclude that
$qF((-A+w+q)/4)\not \equiv 0 \pmod{q^2}$
, completing the proof that
$\mathcal{F}_{2,A,B}(x)$
is monogenic.
For
$n\ge 2$
, define
$$ \begin{align*} \theta_n:=\theta^{1/2^{n-2}} \quad \mbox{and} \quad K_n:={\mathbb Q}(\theta_n), \end{align*} $$
noting that
$\theta _2=\theta $
and
$K_2=K$
. Furthermore, observe that
${\mathcal F}_{n,A,B}(\theta _n)=0$
and that
${[K_{n+1}:K_n]=2}$
. Thus, if
${\mathcal F}_{n,A,B}(x)$
is monogenic, then
$\Delta ({\mathcal F}_{n,A,B})=\Delta (K_n)$
, and we deduce from Theorem 2.5 that
$$ \begin{align*}\Delta(K_{n+1})\equiv 0 \pmod{\Delta({\mathcal F}_{n,A,B})^2}.\end{align*} $$
By (3.6),
$$ \begin{align*}\Delta({\mathcal F}_{n+1,A,B})/\Delta({\mathcal F}_{n,A,B})^2=2^{2^{n+1}}.\end{align*} $$
Hence, to show that
${\mathcal F}_{n+1,A,B}(x)$
is monogenic, we only have to show that
$$ \begin{align} [{\mathbb Z}_{K_{n+1}}:{\mathbb Z}[\theta_{n+1}]]\not \equiv 0 \pmod{2}. \end{align} $$
We apply Theorem 2.4 with
$$ \begin{align*}T(x):={\mathcal F}_{n+1,A,B}(x)=x^{2^{n+1}}+Ax^{3\cdot2^{n-1}}+Bx^{2^n}+Ax^{2^{n-1}}+1.\end{align*} $$
Then
$$ \begin{align*}\overline{T}(x)=(x^4+x^3+x^2+x+1)^{2^{n-1}}=\Phi_5(x)^{2^{n-1}},\end{align*} $$
where
$\Phi _5(x)$
is easily seen to be irreducible over
${\mathbb F}_2$
. Therefore, we can let
$$ \begin{align*}g(x)=\Phi_5(x) \quad \mbox{and} \quad h(x)=\Phi_5(x)^{2^{n-1}-1}.\end{align*} $$
A straightforward induction argument shows that
$$ \begin{align*}g(x)h(x)\equiv x^{2^{n+1}}+2x^{7\cdot 2^{n-2}}+3x^{3\cdot 2^{n-1}}+x^{2^n}+3x^{2^{n-1}}+2x^{2^{n-2}}+1 \pmod{4}\end{align*} $$
for
$n\ge 2$
. Thus,
$$ \begin{align*} &g(x)h(x)-T(x)\\ &\quad = \left\{ \begin{array}{ll} 2x^{2^{n-2}}(x^{6\cdot 2^{n-2}}+x^{5\cdot 2^{n-2}}-x^{3\cdot 2^{n-2}}+x^{2^{n-2}}+1)+4E_1(x) & \mbox{if}\ (\widehat{A},\widehat{B})=(1,3),\\[.5em] 2x^{2^{n-2}}(x^{6\cdot 2^{n-2}}+1)+4E_2(x) & \mbox{if}\ (\widehat{A},\widehat{B})=(3,1),\\[.5em] 2x^{2^{n-2}}(x^{6\cdot 2^{n-2}}-x^{3\cdot 2^{n-2}}+1)+4E_3(x) & \mbox{if}\ (\widehat{A},\widehat{B})=(3,3), \end{array} \right. \end{align*} $$
for some
$E_i(x)\in {\mathbb Z}[x]$
. It follows that
$$ \begin{align*}\overline{F}(x)=\overline{\dfrac{g(x)h(x)-T(x)}{2}}= \left\{\begin{array}{ll} x^{2^{n-2}}(x^2+x+1)^{3\cdot2^{n-2}} & \mbox{if}\ (\widehat{A},\widehat{B})=(1,3),\\[.5em] x^{2^{n-2}}(x+1)^{2^{n-1}}(x^2+x+1)^{2^{n-1}} & \mbox{if}\ (\widehat{A},\widehat{B})=(3,1),\\[.5em] x^{2^{n-2}}(x^6+x^3+1)^{2^{n-2}} & \mbox{if}\ (\widehat{A},\widehat{B})=(3,3). \end{array}\right.\end{align*} $$
It is then apparent that
$\gcd (\overline {F},\overline {g})=1$
in each case of
$(\widehat {A},\widehat {B})\in {\mathcal C}$
, from which we conclude by Theorem 2.4 that (3.8) holds. Hence,
${\mathcal F}_{n+1,A,B}(x)$
is monogenic, and consequently,
${\mathcal F}_{n,A,B}(x)$
is monogenic for all
$n\ge 2$
by induction.
4 Proof of Corollary 1.2
We conclude with the proof of Corollary 1.2.
Proof. Let p be a prime with
$p\equiv 3 \pmod {4}$
and define the polynomial
$$ \begin{align*}G(t):=(t+2p+2)(t-2p+2)(4t-p^2-8)\in {\mathbb Z}[t].\end{align*} $$
We wish to apply Corollary 2.9 to
$G(t)$
. According to the discussion following Corollary 2.9, we only need to check for local obstructions at the primes
$\ell $
satisfying
$\ell \le (k+2)/1=5/2$
. That is, we only need to check the prime
$\ell =2$
. Since
$G(1)\equiv 3 \pmod {4}$
, we see that there is no local obstruction at
$\ell =2$
. Hence, by Corollary 2.9, there exist infinitely many primes q such that
$G(q)$
is squarefree. Thus, for any such prime q, we deduce from Theorem 1.1 that
${\mathcal F}_{n,p,q}(x)$
is monogenic for all
$n\ge 2$
.
Acknowledgement
The author thanks the anonymous referee for a careful reading of this paper.
