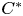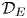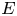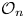1. Introduction
This paper is devoted to investigations of conjugacy of MASAs in the $C^*$![]() -algebras of finite directed graphs. The problem of conjugacy of MASAs in factor von Neumann algebras has been extensively investigated for many years, in particular with relation to Cartan subalgebras. Variety of different situations may occur. There exist factors with a unique Cartan subalgebra or with (uncountably) many ones, e.g. see [Reference Houdayer and Vaes17, Reference Packer21, Reference Speelman and Vaes23].
-algebras of finite directed graphs. The problem of conjugacy of MASAs in factor von Neumann algebras has been extensively investigated for many years, in particular with relation to Cartan subalgebras. Variety of different situations may occur. There exist factors with a unique Cartan subalgebra or with (uncountably) many ones, e.g. see [Reference Houdayer and Vaes17, Reference Packer21, Reference Speelman and Vaes23].
This problem has received much less attention by researchers working with $C^*$![]() -algebras. In particular, the literature on the conjugacy of subalgebras in simple purely infinite $C^*$
-algebras. In particular, the literature on the conjugacy of subalgebras in simple purely infinite $C^*$![]() -algebras is rather scarce. The present paper is the continuation of investigations of this problem initiated in [Reference Conti, Hong and Szymański5, Reference Hayashi, Hong, Mikkelsen and Szymański14], where the question of inner conjugacy to the diagonal MASA of its images under quasi-free automorphisms was looked at in the Cuntz algebras and more generally graph $C^*$
-algebras is rather scarce. The present paper is the continuation of investigations of this problem initiated in [Reference Conti, Hong and Szymański5, Reference Hayashi, Hong, Mikkelsen and Szymański14], where the question of inner conjugacy to the diagonal MASA of its images under quasi-free automorphisms was looked at in the Cuntz algebras and more generally graph $C^*$![]() -algebras. The arguments from [Reference Conti, Hong and Szymański5, Reference Hayashi, Hong, Mikkelsen and Szymański14] where based on rather ad hoc estimations, tailor made for the cases at hand. Now, we aim at developing a more general technique that may be applicable in many diverse instances. The idea is simple, see Lemma 2.3, and it is inspired by Popa's intertwining-by-bimodules technique, see Theorem 2.2. We believe that this approach is conceptually sound and may be useful in many a different situation.
-algebras. The arguments from [Reference Conti, Hong and Szymański5, Reference Hayashi, Hong, Mikkelsen and Szymański14] where based on rather ad hoc estimations, tailor made for the cases at hand. Now, we aim at developing a more general technique that may be applicable in many diverse instances. The idea is simple, see Lemma 2.3, and it is inspired by Popa's intertwining-by-bimodules technique, see Theorem 2.2. We believe that this approach is conceptually sound and may be useful in many a different situation.
Our paper is organized as follows. Section 2 contains rather extensive preliminaries on graph $C^*$![]() -algebras, traces on them, and their endomorphisms. In particular, a discussion of aspects of the classical Perron–Frobenius theory is included, in so far as it is relevant for our purpose. At the end of this section, we briefly state the key technical device we intend to use for distinguishing non-inner conjugate subalgebras. Section 3 contains a discussion of quasi-free automorphisms in relation to aspects of the Perron–Frobenius theory. In this section, we give a new, and hopefully conceptually more interesting, proof of non-inner conjugacy to the diagonal of its images under non-trivial quasi-free automorphisms, see Theorem 3.3. In Section 4, we show that by changing the graph representing the algebra in question our main result on quasi-free automorphism becomes applicable to some non quasi-free automorphisms as well. In Section 5, we exhibit a large class of MASAs of the Cuntz algebra ${\mathcal {O}}_n$
-algebras, traces on them, and their endomorphisms. In particular, a discussion of aspects of the classical Perron–Frobenius theory is included, in so far as it is relevant for our purpose. At the end of this section, we briefly state the key technical device we intend to use for distinguishing non-inner conjugate subalgebras. Section 3 contains a discussion of quasi-free automorphisms in relation to aspects of the Perron–Frobenius theory. In this section, we give a new, and hopefully conceptually more interesting, proof of non-inner conjugacy to the diagonal of its images under non-trivial quasi-free automorphisms, see Theorem 3.3. In Section 4, we show that by changing the graph representing the algebra in question our main result on quasi-free automorphism becomes applicable to some non quasi-free automorphisms as well. In Section 5, we exhibit a large class of MASAs of the Cuntz algebra ${\mathcal {O}}_n$![]() that are not inner conjugate to the diagonal MASA ${\mathcal {D}}_n$
that are not inner conjugate to the diagonal MASA ${\mathcal {D}}_n$![]() , thus generalizing the case resulting from quasi-free automorphisms. In the final Section 6, we collected proofs of a few technical lemmas needed in the preceding parts of the paper.
, thus generalizing the case resulting from quasi-free automorphisms. In the final Section 6, we collected proofs of a few technical lemmas needed in the preceding parts of the paper.
2. Preliminaries
2.1. Finite-directed graphs and their $C^*$ -algebras
-algebras
Let $E=(E^0,\,E^1,\,r,\,s)$![]() be a directed graph, where $E^0$
be a directed graph, where $E^0$![]() and $E^1$
and $E^1$![]() are finite sets of vertices and edges, respectively, and $r,\,s:E^1\to E^0$
are finite sets of vertices and edges, respectively, and $r,\,s:E^1\to E^0$![]() are range and source maps, respectively. A path $\mu$
are range and source maps, respectively. A path $\mu$![]() of length $|\mu |=k\geq 1$
of length $|\mu |=k\geq 1$![]() is a sequence $\mu =(\mu _1,\,\ldots,\,\mu _k)$
is a sequence $\mu =(\mu _1,\,\ldots,\,\mu _k)$![]() of $k$
of $k$![]() edges $\mu _j$
edges $\mu _j$![]() such that $r(\mu _j)=s(\mu _{j+1})$
such that $r(\mu _j)=s(\mu _{j+1})$![]() for $j=1,\,\ldots,\, k-1$
for $j=1,\,\ldots,\, k-1$![]() . We view the vertices as paths of length $0$
. We view the vertices as paths of length $0$![]() . The set of all paths of length $k$
. The set of all paths of length $k$![]() is denoted $E^k$
is denoted $E^k$![]() , and $E^*$
, and $E^*$![]() denotes the collection of all finite paths (including paths of length zero). The range and source maps naturally extend from edges $E^1$
denotes the collection of all finite paths (including paths of length zero). The range and source maps naturally extend from edges $E^1$![]() to paths $E^k$
to paths $E^k$![]() . A sink is a vertex $v$
. A sink is a vertex $v$![]() which emits no edges, i.e. $s^{-1}(v)=\emptyset$
which emits no edges, i.e. $s^{-1}(v)=\emptyset$![]() . A source is a vertex $w$
. A source is a vertex $w$![]() which receives no edges, i.e. $r^{-1}(w)=\emptyset$
which receives no edges, i.e. $r^{-1}(w)=\emptyset$![]() . By a cycle we mean a path $\mu$
. By a cycle we mean a path $\mu$![]() of length $|\mu |\geq 1$
of length $|\mu |\geq 1$![]() such that $s(\mu )=r(\mu )$
such that $s(\mu )=r(\mu )$![]() . A cycle $\mu =(\mu _1,\,\ldots,\,\mu _k)$
. A cycle $\mu =(\mu _1,\,\ldots,\,\mu _k)$![]() has an exit if there is a $j$
has an exit if there is a $j$![]() such that $s(\mu _j)$
such that $s(\mu _j)$![]() emits at least two distinct edges. If $\alpha$
emits at least two distinct edges. If $\alpha$![]() is an initial subpath of $\beta$
is an initial subpath of $\beta$![]() then we write $\alpha \prec \beta$
then we write $\alpha \prec \beta$![]() . Graph $E$
. Graph $E$![]() is transitive if for any two vertices $v,\,w$
is transitive if for any two vertices $v,\,w$![]() there exists a path $\mu \in E^*$
there exists a path $\mu \in E^*$![]() from $v$
from $v$![]() to $w$
to $w$![]() of non-zero length. Thus, a transitive graph does not contain any sinks or sources. Given a graph $E$
of non-zero length. Thus, a transitive graph does not contain any sinks or sources. Given a graph $E$![]() , we will denote by $A=[A(v,\,w)]_{v,w\in E^0}$
, we will denote by $A=[A(v,\,w)]_{v,w\in E^0}$![]() its adjacency matrix. That is, $A$
its adjacency matrix. That is, $A$![]() is a matrix with rows and columns indexed by the vertices of $E$
is a matrix with rows and columns indexed by the vertices of $E$![]() , such that $A(v,\,w)$
, such that $A(v,\,w)$![]() is the number of edges with source $v$
is the number of edges with source $v$![]() and range $w$
and range $w$![]() . If the graph $E$
. If the graph $E$![]() is transitive then the corresponding matrix $A$
is transitive then the corresponding matrix $A$![]() is irreducible, in the sense that for any two vertices $v,\,w$
is irreducible, in the sense that for any two vertices $v,\,w$![]() there is a positive integer $k$
there is a positive integer $k$![]() such that $A^k(v,\,w)>0$
such that $A^k(v,\,w)>0$![]() . Here $A^k$
. Here $A^k$![]() is the $k$
is the $k$![]() ’th power of matrix $A$
’th power of matrix $A$![]() and hence $A^k(w,\, v)$
and hence $A^k(w,\, v)$![]() gives the number of paths from vertex $w$
gives the number of paths from vertex $w$![]() to vertex $v$
to vertex $v$![]() .
.
The $C^*$![]() -algebra $C^*(E)$
-algebra $C^*(E)$![]() corresponding to a graph $E$
corresponding to a graph $E$![]() is by definition, [Reference Kumjian, Pask and Raeburn19, Reference Kumjian, Pask, Raeburn and Renault20], the universal $C^*$
is by definition, [Reference Kumjian, Pask and Raeburn19, Reference Kumjian, Pask, Raeburn and Renault20], the universal $C^*$![]() -algebra generated by mutually orthogonal projections $P_v$
-algebra generated by mutually orthogonal projections $P_v$![]() , $v\in E^0$
, $v\in E^0$![]() , and partial isometries $S_e$
, and partial isometries $S_e$![]() , $e\in E^1$
, $e\in E^1$![]() , subject to the following two relations:
, subject to the following two relations:
(GA1) $S_e^*S_e=P_{r(e)}$
 ,
,(GA2) $P_v=\sum \nolimits _{s(e)=v}S_e S_e^*$
 if $v\in E^0$
if $v\in E^0$ emits at least one edge.
emits at least one edge.
For a path $\mu =(\mu _1,\,\ldots,\,\mu _k)$![]() , we denote by $S_\mu = S_{\mu _1}\cdots S_{\mu _k}$
, we denote by $S_\mu = S_{\mu _1}\cdots S_{\mu _k}$![]() the corresponding partial isometry in $C^*(E)$
the corresponding partial isometry in $C^*(E)$![]() . We agree to write $S_v=P_v$
. We agree to write $S_v=P_v$![]() for a $v\in E^0$
for a $v\in E^0$![]() . Each $S_\mu$
. Each $S_\mu$![]() is non-zero with the domain projection $P_{r(\mu )}$
is non-zero with the domain projection $P_{r(\mu )}$![]() . Then $C^*(E)$
. Then $C^*(E)$![]() is the closed span of $\{S_\mu S_\nu ^*:\mu,\,\nu \in E^*\}$
is the closed span of $\{S_\mu S_\nu ^*:\mu,\,\nu \in E^*\}$![]() . Note that $S_\mu S_\nu ^*$
. Note that $S_\mu S_\nu ^*$![]() is non-zero if and only if $r(\mu )=r(\nu )$
is non-zero if and only if $r(\mu )=r(\nu )$![]() . In that case, $S_\mu S_\nu ^*$
. In that case, $S_\mu S_\nu ^*$![]() is a partial isometry with domain and range projections equal to $S_\nu S_\nu ^*$
is a partial isometry with domain and range projections equal to $S_\nu S_\nu ^*$![]() and $S_\mu S_\mu ^*$
and $S_\mu S_\mu ^*$![]() , respectively.
, respectively.
The range projections $P_\mu =S_\mu S_\mu ^*$![]() of all partial isometries $S_\mu$
of all partial isometries $S_\mu$![]() mutually commute, and the abelian $C^*$
mutually commute, and the abelian $C^*$![]() -subalgebra of $C^*(E)$
-subalgebra of $C^*(E)$![]() generated by all of them is called the diagonal subalgebra and denoted ${\mathcal {D}}_E$
generated by all of them is called the diagonal subalgebra and denoted ${\mathcal {D}}_E$![]() . We set ${\mathcal {D}}^0_E = {\rm span}\{P_v : v\in E^0 \}$
. We set ${\mathcal {D}}^0_E = {\rm span}\{P_v : v\in E^0 \}$![]() and, more generally, ${\mathcal {D}}_E^k= {\rm span}\{P_\mu : \mu \in E^k \}$
and, more generally, ${\mathcal {D}}_E^k= {\rm span}\{P_\mu : \mu \in E^k \}$![]() for $k\geq 0$
for $k\geq 0$![]() . $C^*$
. $C^*$![]() -algebra ${\mathcal {D}}_E$
-algebra ${\mathcal {D}}_E$![]() coincides with the norm closure of $\bigcup _{k=0}^\infty {\mathcal {D}}_E^k$
coincides with the norm closure of $\bigcup _{k=0}^\infty {\mathcal {D}}_E^k$![]() . If $E$
. If $E$![]() does not contain sinks and all cycles have exits then ${\mathcal {D}}_E$
does not contain sinks and all cycles have exits then ${\mathcal {D}}_E$![]() is a MASA (maximal abelian subalgebra) in $C^*(E)$
is a MASA (maximal abelian subalgebra) in $C^*(E)$![]() by [Reference Hopenwasser, Peters and Power15, Theorem 5.2]. Throughout this paper, we make the following
by [Reference Hopenwasser, Peters and Power15, Theorem 5.2]. Throughout this paper, we make the following
standing assumption: all graphs we consider are finite, transitive and all cycles in these graphs admit exits.
There exists a strongly continuous action $\gamma$![]() of the circle group $U(1)$
of the circle group $U(1)$![]() on $C^*(E)$
on $C^*(E)$![]() , called the gauge action, such that $\gamma _z(S_e)=zS_e$
, called the gauge action, such that $\gamma _z(S_e)=zS_e$![]() and $\gamma _z(P_v)=P_v$
and $\gamma _z(P_v)=P_v$![]() for all $e\in E^1$
for all $e\in E^1$![]() , $v\in E^0$
, $v\in E^0$![]() and $z\in U(1)\subseteq {\mathbb {C}}$
and $z\in U(1)\subseteq {\mathbb {C}}$![]() . The fixed-point algebra $C^*(E)^\gamma$
. The fixed-point algebra $C^*(E)^\gamma$![]() for the gauge action is an AF-algebra, denoted ${\mathcal {F}}_E$
for the gauge action is an AF-algebra, denoted ${\mathcal {F}}_E$![]() and called the core AF-subalgebra of $C^*(E)$
and called the core AF-subalgebra of $C^*(E)$![]() . ${\mathcal {F}}_E$
. ${\mathcal {F}}_E$![]() is the closed span of $\{S_\mu S_\nu ^*:\mu,\,\nu \in E^*,\,\;|\mu |=|\nu |\}$
is the closed span of $\{S_\mu S_\nu ^*:\mu,\,\nu \in E^*,\,\;|\mu |=|\nu |\}$![]() . For $k\in {\mathbb {N}}=\{0,\,1,\,2,\,\ldots \}$
. For $k\in {\mathbb {N}}=\{0,\,1,\,2,\,\ldots \}$![]() we denote by ${\mathcal {F}}_E^k$
we denote by ${\mathcal {F}}_E^k$![]() the linear span of $\{S_\mu S_\nu ^*:\mu,\,\nu \in E^*,\,\;|\mu |=|\nu |= k\}$
the linear span of $\{S_\mu S_\nu ^*:\mu,\,\nu \in E^*,\,\;|\mu |=|\nu |= k\}$![]() . $C^*$
. $C^*$![]() -algebra ${\mathcal {F}}_E$
-algebra ${\mathcal {F}}_E$![]() coincides with the norm closure of $\bigcup _{k=0}^\infty {\mathcal {F}}_E^k$
coincides with the norm closure of $\bigcup _{k=0}^\infty {\mathcal {F}}_E^k$![]() .
.
We consider the usual shift on $C^*(E)$![]() , [Reference Cuntz and Krieger10], given by
, [Reference Cuntz and Krieger10], given by
In general, for finite graphs without sinks and sources, the shift is a unital, completely positive map. However, it is an injective $*$![]() -homomorphism when restricted to the relative commutant $({\mathcal {D}}_E^0)'\cap C^*(E)$
-homomorphism when restricted to the relative commutant $({\mathcal {D}}_E^0)'\cap C^*(E)$![]() of ${\mathcal {D}}_E^0$
of ${\mathcal {D}}_E^0$![]() in $C^*(E)$
in $C^*(E)$![]() .
.
We observe that for each $v\in E^0$![]() projection $\varphi ^k(P_v)$
projection $\varphi ^k(P_v)$![]() is minimal in the centre of ${\mathcal {F}}_E^k$
is minimal in the centre of ${\mathcal {F}}_E^k$![]() . The $C^*$
. The $C^*$![]() -algebra ${\mathcal {F}}_E^k\varphi ^k(P_v)$
-algebra ${\mathcal {F}}_E^k\varphi ^k(P_v)$![]() is the linear span of partial isometries $S_\mu S_\nu ^*$
is the linear span of partial isometries $S_\mu S_\nu ^*$![]() with $|\mu |=|\nu |=k$
with $|\mu |=|\nu |=k$![]() and $r(\mu )=r(\nu )=v$
and $r(\mu )=r(\nu )=v$![]() . It is isomorphic to the full matrix algebra of size $\sum \nolimits _{w\in E^0} A^k(w,\, v)$
. It is isomorphic to the full matrix algebra of size $\sum \nolimits _{w\in E^0} A^k(w,\, v)$![]() . The multiplicity of ${\mathcal {F}}_E^k\varphi ^k(P_v)$
. The multiplicity of ${\mathcal {F}}_E^k\varphi ^k(P_v)$![]() in ${\mathcal {F}}_E^{k+1}\varphi ^{k+1}(P_w)$
in ${\mathcal {F}}_E^{k+1}\varphi ^{k+1}(P_w)$![]() is $A(v,\,w)$
is $A(v,\,w)$![]() , so the Bratteli diagram for ${\mathcal {F}}_E$
, so the Bratteli diagram for ${\mathcal {F}}_E$![]() is induced from the graph $E$
is induced from the graph $E$![]() , see [Reference Bates, Pask, Raeburn and Szymański3, Reference Cuntz and Krieger10, Reference Kumjian, Pask, Raeburn and Renault20].
, see [Reference Bates, Pask, Raeburn and Szymański3, Reference Cuntz and Krieger10, Reference Kumjian, Pask, Raeburn and Renault20].

We denote
That is, $\mathfrak B$![]() is the linear span of elements $S_e S_f^*$
is the linear span of elements $S_e S_f^*$![]() , $e,\,f\in E^1$
, $e,\,f\in E^1$![]() , with $s(e)=s(f)$
, with $s(e)=s(f)$![]() . We note that $\mathfrak B$
. We note that $\mathfrak B$![]() is contained in the multiplicative domain of $\varphi$
is contained in the multiplicative domain of $\varphi$![]() . We have ${\mathcal {D}}_E^1 \subseteq \mathfrak B \subseteq {\mathcal {F}}_E^1$
. We have ${\mathcal {D}}_E^1 \subseteq \mathfrak B \subseteq {\mathcal {F}}_E^1$![]() and
and
for all $k$![]() . For $v,\,w\in E^0$
. For $v,\,w\in E^0$![]() , we denote
, we denote
Each $_vQ_w$![]() is a minimal projection in the centre of $\mathfrak B$
is a minimal projection in the centre of $\mathfrak B$![]() and $\mathfrak B_vQ_w\cong M_{A(v,w)}({\mathbb {C}})$
and $\mathfrak B_vQ_w\cong M_{A(v,w)}({\mathbb {C}})$![]() . We put
. We put

for $k\geq 1$![]() , the $C^*$
, the $C^*$![]() -algebra generated by $\bigcup _{j=0}^{k-1}\varphi ^j(\mathfrak B)$
-algebra generated by $\bigcup _{j=0}^{k-1}\varphi ^j(\mathfrak B)$![]() . In general, if $A$
. In general, if $A$![]() and $B$
and $B$![]() are both $C^*$
are both $C^*$![]() -subalgebras of a $C^*$
-subalgebras of a $C^*$![]() -algebra $C$
-algebra $C$![]() , then we denote by $A\vee B$
, then we denote by $A\vee B$![]() the $C^*$
the $C^*$![]() -subalgebra of $C$
-subalgebra of $C$![]() generated by $A$
generated by $A$![]() and $B$
and $B$![]() . Since for all $k$
. Since for all $k$![]() , we have
, we have

it is easy to see that
We observe that
This implies that

There exist faithful conditional expectations $\varPhi _{{\mathcal {F}}}:C^*(E)\to {\mathcal {F}}_E$![]() and $\varPhi _{{\mathcal {D}}}:C^*(E)\to {\mathcal {D}}_E$
and $\varPhi _{{\mathcal {D}}}:C^*(E)\to {\mathcal {D}}_E$![]() such that $\varPhi _{{\mathcal {F}}}(S_\mu S_\nu ^*)=0$
such that $\varPhi _{{\mathcal {F}}}(S_\mu S_\nu ^*)=0$![]() for $|\mu |\neq |\nu |$
for $|\mu |\neq |\nu |$![]() and $\varPhi _{{\mathcal {D}}}(S_\mu S_\nu ^*)=0$
and $\varPhi _{{\mathcal {D}}}(S_\mu S_\nu ^*)=0$![]() for $\mu \neq \nu$
for $\mu \neq \nu$![]() . We note that $\varPhi _{{\mathcal {D}}} = \varPhi _{{\mathcal {D}}}\circ \varPhi _{{\mathcal {F}}}$
. We note that $\varPhi _{{\mathcal {D}}} = \varPhi _{{\mathcal {D}}}\circ \varPhi _{{\mathcal {F}}}$![]() and
and
For an integer $m\in {\mathbb {Z}}$![]() , we denote by $C^*(E)^{(m)}$
, we denote by $C^*(E)^{(m)}$![]() the spectral subspace of the gauge action corresponding to $m$
the spectral subspace of the gauge action corresponding to $m$![]() . That is,
. That is,
In particular, $C^*(E)^{(0)}=C^*(E)^\gamma$![]() . For each $m\in {\mathbb {Z}}$
. For each $m\in {\mathbb {Z}}$![]() there is a unital, contractive and completely bounded map $\varPhi ^m:C^*(E)\to C^*(E)^{(m)}$
there is a unital, contractive and completely bounded map $\varPhi ^m:C^*(E)\to C^*(E)^{(m)}$![]() given by
given by
In particular, $\varPhi ^0=\varPhi _{\mathcal {F}}$![]() . We have $\varPhi ^m(x)=x$
. We have $\varPhi ^m(x)=x$![]() for all $x\in C^*(E)^{(m)}$
for all $x\in C^*(E)^{(m)}$![]() . If $x\in C^*(E)$
. If $x\in C^*(E)$![]() and $\varPhi ^m(x)=0$
and $\varPhi ^m(x)=0$![]() for all $m\in {\mathbb {Z}}$
for all $m\in {\mathbb {Z}}$![]() then $x=0$
then $x=0$![]() .
.
2.2. The trace on the core AF-subalgebra
We recall the definition of a natural trace on the core $AF$![]() -subalgebra ${\mathcal {F}}_E$
-subalgebra ${\mathcal {F}}_E$![]() . For relevant facts from the Perron–Frobenius theory, see for example [Reference Goodman, de la Harpe and Jones12, Reference Graham13].
. For relevant facts from the Perron–Frobenius theory, see for example [Reference Goodman, de la Harpe and Jones12, Reference Graham13].
Let $\beta$![]() be the Perron–Frobenius eigenvalue of the matrix $A$
be the Perron–Frobenius eigenvalue of the matrix $A$![]() and let $(x(v))_{v\in E^0}$
and let $(x(v))_{v\in E^0}$![]() be the corresponding Perron–Frobenius eigenvector. That is, $\beta >0$
be the corresponding Perron–Frobenius eigenvector. That is, $\beta >0$![]() , for each $v\in E^0$
, for each $v\in E^0$![]() we have $x(v)>0$
we have $x(v)>0$![]() , and
, and
We set $X:=\sum \nolimits _{v\in E^0} x(v)$![]() and define a tracial state $\tau$
and define a tracial state $\tau$![]() on ${\mathcal {F}}_E$
on ${\mathcal {F}}_E$![]() so that
so that
for $\mu,\,\nu \in E^k$![]() . We have $\tau (\varPhi _{{\mathcal {D}}}(x)) = \tau (x)$
. We have $\tau (\varPhi _{{\mathcal {D}}}(x)) = \tau (x)$![]() for all $x\in {\mathcal {F}}_E$
for all $x\in {\mathcal {F}}_E$![]() .
.
Remark 2.1 Trace $\tau$![]() defined above is not shift invariant, in general. That is, it may happen that $\tau (\varphi (x))\neq \tau (x)$
defined above is not shift invariant, in general. That is, it may happen that $\tau (\varphi (x))\neq \tau (x)$![]() for some $x\in {\mathcal {F}}_E$
for some $x\in {\mathcal {F}}_E$![]() . In fact, $\tau$
. In fact, $\tau$![]() is $\varphi$
is $\varphi$![]() -invariant if and only if
-invariant if and only if
for each $w\in E^0$![]() . For example, the matrix
. For example, the matrix
does not satisfy this condition.
2.3. Endomorphisms determined by unitaries
Cuntz's classical approach to the study of endomorphisms of ${\mathcal {O}}_n$![]() , [Reference Cuntz9], has been developed further in [Reference Conti and Szymański7] and extended to graph $C^*$
, [Reference Cuntz9], has been developed further in [Reference Conti and Szymański7] and extended to graph $C^*$![]() -algebras in [Reference Avery, Johansen and Szymański1, Reference Conti, Hong and Szymański4, Reference Johansen, Sørensen and Szymański18].
-algebras in [Reference Avery, Johansen and Szymański1, Reference Conti, Hong and Szymański4, Reference Johansen, Sørensen and Szymański18].
We denote by ${\mathcal {U}}_E$![]() the collection of all those unitaries in $C^*(E)$
the collection of all those unitaries in $C^*(E)$![]() which commute with all vertex projections $P_v$
which commute with all vertex projections $P_v$![]() , $v\in E^0$
, $v\in E^0$![]() . That is
. That is
If $u\in {\mathcal {U}}_E$![]() then $uS_e$
then $uS_e$![]() , $e\in E^1$
, $e\in E^1$![]() , are partial isometries in $C^*(E)$
, are partial isometries in $C^*(E)$![]() which together with projections $P_v$
which together with projections $P_v$![]() , $v\in E^0$
, $v\in E^0$![]() , satisfy (GA1) and (GA2). Thus, by the universality of $C^*(E)$
, satisfy (GA1) and (GA2). Thus, by the universality of $C^*(E)$![]() , there exists a unital $*$
, there exists a unital $*$![]() -homomorphism $\lambda _u:C^*(E)\to C^*(E)$
-homomorphism $\lambda _u:C^*(E)\to C^*(E)$![]() such thatFootnote 1
such thatFootnote 1
The mapping $u\mapsto \lambda _u$![]() establishes a bijective correspondence between ${\mathcal {U}}_E$
establishes a bijective correspondence between ${\mathcal {U}}_E$![]() and the semigroup of those unital endomorphisms of $C^*(E)$
and the semigroup of those unital endomorphisms of $C^*(E)$![]() which fix all $P_v$
which fix all $P_v$![]() , $v\in E^0$
, $v\in E^0$![]() . As observed in [Reference Conti, Hong and Szymański4, Proposition 2.1], if $u\in {\mathcal {U}}_E\cap {\mathcal {F}}_E$
. As observed in [Reference Conti, Hong and Szymański4, Proposition 2.1], if $u\in {\mathcal {U}}_E\cap {\mathcal {F}}_E$![]() then $\lambda _u$
then $\lambda _u$![]() is automatically injective. We say $\lambda _u$
is automatically injective. We say $\lambda _u$![]() is invertible if $\lambda _u$
is invertible if $\lambda _u$![]() is an automorphism of $C^*(E)$
is an automorphism of $C^*(E)$![]() . If $u$
. If $u$![]() belongs to ${\mathcal {U}}_E\cap {\mathcal {F}}_E^k$
belongs to ${\mathcal {U}}_E\cap {\mathcal {F}}_E^k$![]() for some $k$
for some $k$![]() , then the corresponding endomorphism $\lambda _u$
, then the corresponding endomorphism $\lambda _u$![]() is called localized, [Reference Conti, Hong and Szymański4, Reference Conti and Pinzari6].
is called localized, [Reference Conti, Hong and Szymański4, Reference Conti and Pinzari6].
If $u\in {\mathcal {U}}(\mathfrak B)$![]() then $\lambda _u$
then $\lambda _u$![]() is automatically invertible with inverse $\lambda _{u^*}$
is automatically invertible with inverse $\lambda _{u^*}$![]() and the map
and the map
is a group homomorphism with a range inside the subgroup of quasi-free automorphisms of $C^*(E)$![]() , see [Reference Zacharias24]. Note that this group is almost never trivial and it is non-commutative if graph $E$
, see [Reference Zacharias24]. Note that this group is almost never trivial and it is non-commutative if graph $E$![]() contains two edges $e,\,f\in E^1$
contains two edges $e,\,f\in E^1$![]() such that $s(e)=s(f)$
such that $s(e)=s(f)$![]() and $r(e)=r(f)$
and $r(e)=r(f)$![]() .
.
The shift $\varphi$![]() globally preserves ${\mathcal {U}}_E$
globally preserves ${\mathcal {U}}_E$![]() , ${\mathcal {F}}_E$
, ${\mathcal {F}}_E$![]() and ${\mathcal {D}}_E$
and ${\mathcal {D}}_E$![]() . For $k\geq 1$
. For $k\geq 1$![]() , we denote
, we denote
For each $u\in {\mathcal {U}}_E$![]() and all $e\in E^1$
and all $e\in E^1$![]() , we have $S_e u = \varphi (u) S_e$
, we have $S_e u = \varphi (u) S_e$![]() , and thus
, and thus
for any two paths $\mu,\,\nu \in E^*$![]() .
.
2.4. The Popa criterion
In the analysis of uniqueness of Cartan subalgebras of tracial von Neumann algebras, Popa's intertwining-by-bimodules technique has been extremely successful. This method goes back to [Reference Popa22], but has been polished over the years and recently even extended to type $III$![]() case [Reference Houdayer and Isono16]. The following result contains its essential ingredient.
case [Reference Houdayer and Isono16]. The following result contains its essential ingredient.
Theorem 2.2 S. Popa
Let $M$![]() be a von Neumann algebra equipped with a faithful normal trace $\tau$
be a von Neumann algebra equipped with a faithful normal trace $\tau$![]() . Let $A,\,B$
. Let $A,\,B$![]() be von Neumann subalgebras of $M,$
be von Neumann subalgebras of $M,$![]() and let $\varPhi _B:M\to B$
and let $\varPhi _B:M\to B$![]() be a $\tau$
be a $\tau$![]() -preserving conditional expectation. Then the following two conditions are equivalent.
-preserving conditional expectation. Then the following two conditions are equivalent.
(1) There exist non-zero projections $p\in A$
 , $q\in B$
, $q\in B$ , a non-zero partial isometry $v\in pMq$
, a non-zero partial isometry $v\in pMq$ and a $*$
and a $*$ -homomorphism $\varPhi :pAp\to qBq$
-homomorphism $\varPhi :pAp\to qBq$ such that $xv=v\varPhi (x)$
such that $xv=v\varPhi (x)$ for all $x\in pAp$
for all $x\in pAp$ .
.(2) There is no sequence of unitaries $w_n\in {\mathcal {U}}(A)$
 such that
(18)\begin{equation} || \varPhi_B(xw_n y)||_2 \underset{n\to\infty}{\longrightarrow} 0, \quad \forall x,y\in M. \end{equation}
such that
(18)\begin{equation} || \varPhi_B(xw_n y)||_2 \underset{n\to\infty}{\longrightarrow} 0, \quad \forall x,y\in M. \end{equation}
This beautiful theorem is inapplicable to graph $C^*$![]() -algebras, of course. However, the following simple fact remains valid in the $C^*$
-algebras, of course. However, the following simple fact remains valid in the $C^*$![]() -algebraic setting.
-algebraic setting.
Lemma 2.3 Let $M$![]() be a unital $C^*$
be a unital $C^*$![]() -algebra, and let $A,\,B$
-algebra, and let $A,\,B$![]() be its $C^*$
be its $C^*$![]() -subalgebras containing the unit of $M$
-subalgebras containing the unit of $M$![]() . Let $\varPhi _B:M\to B$
. Let $\varPhi _B:M\to B$![]() be a conditional expectation, and let $\tau$
be a conditional expectation, and let $\tau$![]() be a trace on $B$
be a trace on $B$![]() . If there is a sequence of unitaries $w_n\in {\mathcal {U}}(A)$
. If there is a sequence of unitaries $w_n\in {\mathcal {U}}(A)$![]() such that (18) holds then there is no unitary $v\in {\mathcal {U}}(M)$
such that (18) holds then there is no unitary $v\in {\mathcal {U}}(M)$![]() such that $vAv^*\subseteq B$
such that $vAv^*\subseteq B$![]() .
.
Proof. Indeed, let $w_n\in {\mathcal {U}}(A)$![]() be as in the lemma and suppose $v\in {\mathcal {U}}(M)$
be as in the lemma and suppose $v\in {\mathcal {U}}(M)$![]() is such that $vAv^*\subseteq B$
is such that $vAv^*\subseteq B$![]() . Then
. Then
which gives a contradiction.
3. Quasi-free automorphisms
In this section, we apply Lemma 2.3 with $M=C^*(E)$![]() , $\tau$
, $\tau$![]() the canonical trace on ${\mathcal {F}}_E$
the canonical trace on ${\mathcal {F}}_E$![]() , $B={\mathcal {D}}_E$
, $B={\mathcal {D}}_E$![]() , and $\varPhi _B=\varPhi _{\mathcal {D}}$
, and $\varPhi _B=\varPhi _{\mathcal {D}}$![]() . We keep the standing assumptions on the graph $E$
. We keep the standing assumptions on the graph $E$![]() . Note that for unitaries $u\in \mathfrak B$
. Note that for unitaries $u\in \mathfrak B$![]() and $d\in {\mathcal {D}}_E^1$
and $d\in {\mathcal {D}}_E^1$![]() , we have
, we have
Lemma 3.1 Let $u\in \mathfrak B$![]() be a unitary such that $u{\mathcal {D}}_E^1u^*\neq {\mathcal {D}}_E^1,$
be a unitary such that $u{\mathcal {D}}_E^1u^*\neq {\mathcal {D}}_E^1,$![]() and let $d\in {\mathcal {D}}_E^1$
and let $d\in {\mathcal {D}}_E^1$![]() be a unitary such that $u{\rm d}u^*\not \in {\mathcal {D}}_E^1$
be a unitary such that $u{\rm d}u^*\not \in {\mathcal {D}}_E^1$![]() . Then we have
. Then we have
Proof. We set $d_{v,w}:=d\cdot _vQ_w$![]() . Since $\mathfrak B\cdot _vQ_w$
. Since $\mathfrak B\cdot _vQ_w$![]() is a full matrix algebra, it has a unique tracial state $\tau _{v,w}$
is a full matrix algebra, it has a unique tracial state $\tau _{v,w}$![]() . We denote by $||\cdot ||_{2,v,w}$
. We denote by $||\cdot ||_{2,v,w}$![]() the 2-norm induced by this trace. In view of Corollary 6.2, we have
the 2-norm induced by this trace. In view of Corollary 6.2, we have

We define non-negative numbers $\{ \lambda _{v_1,v_2,\ldots,v_{k+1}} \}_{v_1,v_2,\ldots,v_{k+1}\in E^0}$![]() by
by

We remark that $A(v_1,\,v_2) A(v_2,\,v_3) \cdots A(v_k,\,v_{k+1})$![]() is the total number of paths of length $k$
is the total number of paths of length $k$![]() which pass through $v_1,\,v_2,\,\ldots,\,v_{k+1}$
which pass through $v_1,\,v_2,\,\ldots,\,v_{k+1}$![]() in this order. Since $_{v_1}Q_{v_2} \varphi (_{v_2}Q_{v_3}) \cdots \varphi ^{k-1}(_{v_k}Q_{v_{k+1}})$
in this order. Since $_{v_1}Q_{v_2} \varphi (_{v_2}Q_{v_3}) \cdots \varphi ^{k-1}(_{v_k}Q_{v_{k+1}})$![]() is a central minimal projection of $\mathfrak B_E^k$
is a central minimal projection of $\mathfrak B_E^k$![]() , for any $x\in \mathfrak B_E^k$
, for any $x\in \mathfrak B_E^k$![]() , we have
, we have
where $\tau _{{v_1,v_2,\ldots,v_{k+1}}}$![]() is a unique tracial state on a full matrix algebra
is a unique tracial state on a full matrix algebra
Then since

for all $a_1,\,a_2,\,\ldots,\,a_k\in \mathfrak B$![]() , we have
, we have

Thus, we see that

By the hypothesis of the lemma, there exist two vertices $w_1,\,w_2$![]() such that
such that

and hence
For $i=0,\,1,\,\ldots,\,k$![]() , we denote by $M_{k,v}^i$
, we denote by $M_{k,v}^i$![]() the set of all paths $\mu$
the set of all paths $\mu$![]() such that
such that
(i) $|\mu |=k$
 ,
,(ii) $r(\mu )=v$
 ,
,(iii) in path $\mu$
 , edges from $w_1$
, edges from $w_1$ to $w_2$
to $w_2$ occur exactly $i$
occur exactly $i$ times.
times.
We remark that $M_{k,v}^i \cap M_{k,v}^j=\emptyset$![]() if $i\neq j$
if $i\neq j$![]() . Thus, we have $\sum \nolimits _{i=0}^k|M_{k,v}^i| = \sum \nolimits _{w\in E^0}A^k(w,\,v)$
. Thus, we have $\sum \nolimits _{i=0}^k|M_{k,v}^i| = \sum \nolimits _{w\in E^0}A^k(w,\,v)$![]() , where $|M_{k,v}^i|$
, where $|M_{k,v}^i|$![]() denotes the cardinality of $M_{k,v}^i$
denotes the cardinality of $M_{k,v}^i$![]() . We claim that for all $v$
. We claim that for all $v$![]() and $i$
and $i$![]()
At first, we note that because of (19) the full matrix algebra $\mathfrak B\cdot _{w_1}Q_{w_2}$![]() is not isomorphic to ${\mathbb {C}}$
is not isomorphic to ${\mathbb {C}}$![]() , and hence $A(w_1,\,w_2)\geq 2$
, and hence $A(w_1,\,w_2)\geq 2$![]() . Let $A_1$
. Let $A_1$![]() be the matrix defined in (26) in § 6 for $(i_1,\,j_1)=(w_1,\,w_2)$
be the matrix defined in (26) in § 6 for $(i_1,\,j_1)=(w_1,\,w_2)$![]() , and let $E_1$
, and let $E_1$![]() be the corresponding graph. $E_1$
be the corresponding graph. $E_1$![]() may be viewed as a subgraph of $E$
may be viewed as a subgraph of $E$![]() obtained by removing all but one edge in $E^1$
obtained by removing all but one edge in $E^1$![]() that begin at $w_1$
that begin at $w_1$![]() and end at $w_2$
and end at $w_2$![]() . Set $N_{k,v}^i := M_{k,v}^i\cap E_1^*$
. Set $N_{k,v}^i := M_{k,v}^i\cap E_1^*$![]() . It is easy to see that
. It is easy to see that
But now, by virtue of Theorem 6.6, we have
and the claim holds.
Now, since $||\varphi ^{j-1}(\varPhi _{\mathcal {D}}(ud_{v_j,v_{j+1}}u^*)) ||^2_{2,v_j,v_{j+1}}\leq 1$![]() and $c= || \varPhi _{\mathcal {D}}( u{\rm d}u^*\cdot _{w_1}Q_{w_2}) ||^2_{2,w_1,w_2}$
and $c= || \varPhi _{\mathcal {D}}( u{\rm d}u^*\cdot _{w_1}Q_{w_2}) ||^2_{2,w_1,w_2}$![]() , for each $i_0$
, for each $i_0$![]() , we have
, we have

and hence

Since

we may conclude that
Since $i_0$![]() was arbitrary, the lemma is proved.
was arbitrary, the lemma is proved.
Keeping the hypothesis of Lemma 3.1, we have the following.
Lemma 3.2 For all $x,\,y\in {\mathcal {F}}_E$![]() we have
we have
Proof. To prove the lemma, it suffices to consider elements $x,\,y\in {\mathcal {F}}_E^p$![]() for an arbitrary positive integer $p$
for an arbitrary positive integer $p$![]() . We have
. We have

Therefore, it is enough to show that
for all $x\in {\mathcal {F}}_E^p$![]() . However, we have
. However, we have

by Lemma 6.1 and
Now we are ready to prove the main result of this section. We keep the standard assumptions on the graph $E$![]() .
.
Theorem 3.3 Let $u\in \mathfrak B$![]() be a unitary such that $u{\mathcal {D}}_E^1u^*\neq {\mathcal {D}}_E^1,$
be a unitary such that $u{\mathcal {D}}_E^1u^*\neq {\mathcal {D}}_E^1,$![]() and let $d\in {\mathcal {D}}_E^1$
and let $d\in {\mathcal {D}}_E^1$![]() be a unitary such that $u{\rm d}u^*\not \in {\mathcal {D}}_E^1$
be a unitary such that $u{\rm d}u^*\not \in {\mathcal {D}}_E^1$![]() . Then for all $x,\,y\in C^*(E)$
. Then for all $x,\,y\in C^*(E)$![]() , we have
, we have
Thus, in view of Lemma 2.3, ${\mathcal {D}}_E$![]() and $\lambda _u({\mathcal {D}}_E)$
and $\lambda _u({\mathcal {D}}_E)$![]() are not inner conjugate in $C^*(E)$
are not inner conjugate in $C^*(E)$![]() .
.
Proof. By the polarization identity, it suffices to compute the above limit in the case $y=x^*$![]() . Furthermore, we may assume that $x$
. Furthermore, we may assume that $x$![]() belongs to the dense $*$
belongs to the dense $*$![]() -subalgebra of $C^*(E)$
-subalgebra of $C^*(E)$![]() generated by partial isometries corresponding to finite paths. That is, in the case, $x$
generated by partial isometries corresponding to finite paths. That is, in the case, $x$![]() is a finite sum of the form
is a finite sum of the form
with $x_0,\,a_\mu,\,b_\nu \in {\mathcal {F}}_E$![]() . Applying conditional expectation $\varPhi _{\mathcal {F}}$
. Applying conditional expectation $\varPhi _{\mathcal {F}}$![]() on the core AF-subalgebra first, we get
on the core AF-subalgebra first, we get

Thus, we must show the following three cases:

Ad (1). Consider two paths $\mu$![]() and $\mu '$
and $\mu '$![]() with $|\mu |=|\mu '|$
with $|\mu |=|\mu '|$![]() . For any $x\in \mathfrak B$
. For any $x\in \mathfrak B$![]() and for any $l-1\geq |\mu |=|\mu '|$
and for any $l-1\geq |\mu |=|\mu '|$![]() , we see that
, we see that
On the other hand, for any $l-1<|\mu |=|\mu '|$![]() , since both $S_\mu S_\mu ^*$
, since both $S_\mu S_\mu ^*$![]() and $S_{\mu '} S_{\mu '}^*$
and $S_{\mu '} S_{\mu '}^*$![]() are minimal projections of $\mathfrak B_E^{|\mu |}$
are minimal projections of $\mathfrak B_E^{|\mu |}$![]() and $x\varphi (x)\cdots \varphi ^{l-1}(x)\in \mathfrak B_E^{|\mu |}$
and $x\varphi (x)\cdots \varphi ^{l-1}(x)\in \mathfrak B_E^{|\mu |}$![]() , we have
, we have

for some scalar $t\in {\mathbb {C}}$![]() with $|t|\leq ||x||^{l-1}$
with $|t|\leq ||x||^{l-1}$![]() . Therefore, for any $k>|\mu |=|\mu '|$
. Therefore, for any $k>|\mu |=|\mu '|$![]() , we see that
, we see that
for some scalar $t\in {\mathbb {C}}$![]() with $|t|\leq ||u{\rm d}u^*||^{k-1}=1$
with $|t|\leq ||u{\rm d}u^*||^{k-1}=1$![]() . Since $P_{r(\mu )}\in {\mathcal {D}}$
. Since $P_{r(\mu )}\in {\mathcal {D}}$![]() , the claim follows from Lemma 3.1.
, the claim follows from Lemma 3.1.
Ad (2). This is shown in Lemma 3.2.
Ad (3). If $\nu \neq \nu '$![]() then
then
Thus

and this tends to $0$![]() as $k$
as $k$![]() increases to infinity by the same argument as in the proof of Lemma 3.2.
increases to infinity by the same argument as in the proof of Lemma 3.2.
4. An application — changing graphs
The same graph $C^*$![]() -algebra may often be presented by many different graphs, and the property of being quasi-free is usually not preserved when passing from one graph to another. This makes Theorem 3.3 applicable to a much wider class of automorphisms than quasi-free ones. We illustrate this phenomenon with the following two examples.
-algebra may often be presented by many different graphs, and the property of being quasi-free is usually not preserved when passing from one graph to another. This makes Theorem 3.3 applicable to a much wider class of automorphisms than quasi-free ones. We illustrate this phenomenon with the following two examples.
4.1. Out-splitting
Given a graph $E$![]() satisfying our standing assumption, we consider its out-split graph $E_s({\mathcal {P}})$
satisfying our standing assumption, we consider its out-split graph $E_s({\mathcal {P}})$![]() , as defined by Bates and Pask in [Reference Bates and Pask2]. Namely, for each vertex $v\in E^0$
, as defined by Bates and Pask in [Reference Bates and Pask2]. Namely, for each vertex $v\in E^0$![]() , we partition the set of edges emitted by $v$
, we partition the set of edges emitted by $v$![]() , that is $s^{-1}(v)$
, that is $s^{-1}(v)$![]() , into $m(v)$
, into $m(v)$![]() non-empty disjoint subsets $E^1_v,\, \ldots,\, E^{m(v)}_v$
non-empty disjoint subsets $E^1_v,\, \ldots,\, E^{m(v)}_v$![]() . Denote by ${\mathcal {P}}$
. Denote by ${\mathcal {P}}$![]() the resulting partition of $E^1$
the resulting partition of $E^1$![]() . The out-split graph $E_s({\mathcal {P}})$
. The out-split graph $E_s({\mathcal {P}})$![]() has the following vertices, edges, source and range functions:
has the following vertices, edges, source and range functions:

As shown in [Reference Bates and Pask2, Theorem 3.2], the $C^*$![]() –algebras $C^*(E)$
–algebras $C^*(E)$![]() and $C^*(E_s({\mathcal {P}}))$
and $C^*(E_s({\mathcal {P}}))$![]() are isomorphic by an isomorphism which maps the diagonal MASA ${\mathcal {D}}_E$
are isomorphic by an isomorphism which maps the diagonal MASA ${\mathcal {D}}_E$![]() of $C^*(E)$
of $C^*(E)$![]() onto the diagonal MASA ${\mathcal {D}}_{E_s({\mathcal {P}})}$
onto the diagonal MASA ${\mathcal {D}}_{E_s({\mathcal {P}})}$![]() of $C^*(E_s({\mathcal {P}}))$
of $C^*(E_s({\mathcal {P}}))$![]() . However, the groups of quasi-free automorphims of $C^*(E)$
. However, the groups of quasi-free automorphims of $C^*(E)$![]() and $C^*(E_s({\mathcal {P}}))$
and $C^*(E_s({\mathcal {P}}))$![]() may be different. For example, in the following case
may be different. For example, in the following case

the groups ${\mathcal {U}}(\mathfrak B)$![]() in $C^*(E_s({\mathcal {P}}))$
in $C^*(E_s({\mathcal {P}}))$![]() and $C^*(E)$
and $C^*(E)$![]() are isomorphic to $U(1)\times U(1)\times U(1)\times U(1)$
are isomorphic to $U(1)\times U(1)\times U(1)\times U(1)$![]() and $U(2)$
and $U(2)$![]() , respectively.
, respectively.
Thus, the isomorphism $C^*(E)\cong C^*(E_s({\mathcal {P}}))$![]() may identify a quasi-free automorphism of one of the two algebras with a non quasi-free automorphism of the other. In this way, our Theorem 3.3 leads to non-trivial examples of non quasi-free automorphisms of graph algebras that map the diagonal MASA onto another MASA that is not inner conjugate to it.
may identify a quasi-free automorphism of one of the two algebras with a non quasi-free automorphism of the other. In this way, our Theorem 3.3 leads to non-trivial examples of non quasi-free automorphisms of graph algebras that map the diagonal MASA onto another MASA that is not inner conjugate to it.
4.2. Two graphs for ${\mathcal {O}}_2$
Consider the following graph:

Then the graph algebra $C^*(E)$![]() is isomorphic to the Cuntz algebra ${\mathcal {O}}_2=C^*(T_1,\,T_2)$
is isomorphic to the Cuntz algebra ${\mathcal {O}}_2=C^*(T_1,\,T_2)$![]() , [Reference Cuntz8]. Here $C^*(T_1,\,T_2)$
, [Reference Cuntz8]. Here $C^*(T_1,\,T_2)$![]() is the universal $C^*$
is the universal $C^*$![]() -algebra for the relations $1 = T_1T_1^* + T_2T_2^* = T_1^*T_1 = T_2^*T_2$
-algebra for the relations $1 = T_1T_1^* + T_2T_2^* = T_1^*T_1 = T_2^*T_2$![]() . That is, it is a graph algebra for the graph consisting of one vertex and two edges attached to it. The isomorphism between $C^*(E) = C^*(S_a,\,S_b,\,S_c,\,S_d,\,S_e)$
. That is, it is a graph algebra for the graph consisting of one vertex and two edges attached to it. The isomorphism between $C^*(E) = C^*(S_a,\,S_b,\,S_c,\,S_d,\,S_e)$![]() and ${\mathcal {O}}_2=C^*(T_1,\,T_2)$
and ${\mathcal {O}}_2=C^*(T_1,\,T_2)$![]() is obtained by the identification
is obtained by the identification
The inverse map is given by
Note that this isomorphism carries the diagonal MASA ${\mathcal {D}}_E$![]() of $C^*(E)$
of $C^*(E)$![]() onto the standard diagonal MASA ${\mathcal {D}}_2$
onto the standard diagonal MASA ${\mathcal {D}}_2$![]() of ${\mathcal {O}}_2$
of ${\mathcal {O}}_2$![]() . Indeed, it follows from the above definition that every product $x$
. Indeed, it follows from the above definition that every product $x$![]() of the generators of $C^*(E)$
of the generators of $C^*(E)$![]() is mapped onto an element of the form $T_\alpha T_\beta ^*$
is mapped onto an element of the form $T_\alpha T_\beta ^*$![]() in ${\mathcal {O}}_2$
in ${\mathcal {O}}_2$![]() , with $\alpha,\,\beta$
, with $\alpha,\,\beta$![]() some words on the alphabet $\{1,\,2\}$
some words on the alphabet $\{1,\,2\}$![]() . Thus, the range projection $xx^*$
. Thus, the range projection $xx^*$![]() of that product is mapped onto a projection in the diagonal MASA ${\mathcal {D}}_2$
of that product is mapped onto a projection in the diagonal MASA ${\mathcal {D}}_2$![]() of ${\mathcal {O}}_2$
of ${\mathcal {O}}_2$![]() . Hence, the image of ${\mathcal {D}}_E$
. Hence, the image of ${\mathcal {D}}_E$![]() is contained in ${\mathcal {D}}_2$
is contained in ${\mathcal {D}}_2$![]() . But under an isomorphism, the image of a MASA in $C^*(E)$
. But under an isomorphism, the image of a MASA in $C^*(E)$![]() is a MASA in ${\mathcal {O}}_2$
is a MASA in ${\mathcal {O}}_2$![]() . Thus, the image of MASA ${\mathcal {D}}_E$
. Thus, the image of MASA ${\mathcal {D}}_E$![]() of $C^*(E)$
of $C^*(E)$![]() is the entire MASA ${\mathcal {D}}_2$
is the entire MASA ${\mathcal {D}}_2$![]() of ${\mathcal {O}}_2$
of ${\mathcal {O}}_2$![]() , as claimed.
, as claimed.
Now, using the isomorphism above, we may find a quasi-free automorphism of $C^*(E)$![]() such that the corresponding automorphism of ${\mathcal {O}}_2$
such that the corresponding automorphism of ${\mathcal {O}}_2$![]() is not quasi-free and yet carries the diagonal MASA ${\mathcal {D}}_2$
is not quasi-free and yet carries the diagonal MASA ${\mathcal {D}}_2$![]() of ${\mathcal {O}}_2$
of ${\mathcal {O}}_2$![]() onto a MASA which is not inner conjugate to ${\mathcal {D}}_2$
onto a MASA which is not inner conjugate to ${\mathcal {D}}_2$![]() . Indeed, let
. Indeed, let
be a unitary matrix whose all entries are non-zero complex numbers. Then
is a unitary in ${\mathcal {F}}_E^1$![]() satisfying the hypothesis of Theorem 3.3. The above isomorphism transports the quasi-free automorphism $\lambda _u$
satisfying the hypothesis of Theorem 3.3. The above isomorphism transports the quasi-free automorphism $\lambda _u$![]() of $C^*(E)$
of $C^*(E)$![]() onto an automorphism $\lambda _U$
onto an automorphism $\lambda _U$![]() of ${\mathcal {O}}_2$
of ${\mathcal {O}}_2$![]() corresponding to the unitary
corresponding to the unitary
Clearly, $\lambda _U$![]() is not a quasi-free automorphism of ${\mathcal {O}}_2$
is not a quasi-free automorphism of ${\mathcal {O}}_2$![]() , since $U$
, since $U$![]() does not belong to the linear span of $T_iT_j^*$
does not belong to the linear span of $T_iT_j^*$![]() , $i,\,j=1,\,2$
, $i,\,j=1,\,2$![]() . Theorem 3.3 implies that there is no unitary $w\in {\mathcal {O}}_2$
. Theorem 3.3 implies that there is no unitary $w\in {\mathcal {O}}_2$![]() satisfying $w{\mathcal {D}}_2w^*=\lambda _U({\mathcal {D}}_2)$
satisfying $w{\mathcal {D}}_2w^*=\lambda _U({\mathcal {D}}_2)$![]() .
.
5. Certain MASAs in ${\mathcal {O}}_n$ not inner conjugate to the diagonal ${\mathcal {D}}_n$
not inner conjugate to the diagonal ${\mathcal {D}}_n$
In this section, we consider the Cuntz algebra ${\mathcal {O}}_n$![]() , with $2\leq n<\infty$
, with $2\leq n<\infty$![]() . As usual, we view it as the graph $C^*$
. As usual, we view it as the graph $C^*$![]() -algebra of the graph $E_n$
-algebra of the graph $E_n$![]() with one vertex and $n$
with one vertex and $n$![]() edges. Let $\lambda _u\in \operatorname {End}({\mathcal {O}}_n)$
edges. Let $\lambda _u\in \operatorname {End}({\mathcal {O}}_n)$![]() . Suppose $w_k$
. Suppose $w_k$![]() is a sequence of unitaries in a commutative $C^*$
is a sequence of unitaries in a commutative $C^*$![]() -subalgebra $A$
-subalgebra $A$![]() of ${\mathcal {O}}_n$
of ${\mathcal {O}}_n$![]() . We ask under what circumstances the sequence $w_k$
. We ask under what circumstances the sequence $w_k$![]() satisfies the condition of Lemma 2.3 for $M={\mathcal {O}}_n$
satisfies the condition of Lemma 2.3 for $M={\mathcal {O}}_n$![]() , $A$
, $A$![]() , $B={\mathcal {D}}_n$
, $B={\mathcal {D}}_n$![]() , and $\tau$
, and $\tau$![]() the canonical trace on the UHF-subalgebra ${\mathcal {F}}_n$
the canonical trace on the UHF-subalgebra ${\mathcal {F}}_n$![]() . Clearly, this is the case if and only if
. Clearly, this is the case if and only if
for all paths $\alpha,\,\beta,\,\mu,\,\nu$![]() . Let
. Let
be the standard Fourier series of $w_k$![]() (with respect to the decomposition of ${\mathcal {O}}_n$
(with respect to the decomposition of ${\mathcal {O}}_n$![]() into spectral subspaces ${\mathcal {O}}_n^{(m)}$
into spectral subspaces ${\mathcal {O}}_n^{(m)}$![]() for the gauge action). Then (21) is equivalent to the requirement that
for the gauge action). Then (21) is equivalent to the requirement that
for all paths $\alpha,\,\beta,\,\mu,\,\nu$![]() , and all $m\in {\mathbb {Z}}$
, and all $m\in {\mathbb {Z}}$![]() . Of course, it suffices to consider the case $m=|\beta |+|\nu |-|\alpha |-|\mu |$
. Of course, it suffices to consider the case $m=|\beta |+|\nu |-|\alpha |-|\mu |$![]() . Clearly, for all $x\in {\mathcal {O}}_n$
. Clearly, for all $x\in {\mathcal {O}}_n$![]() and all paths $\alpha$
and all paths $\alpha$![]() we have
we have
Thus, it suffices to consider condition (23) in the following three cases:
(ZL1) $\nu =\emptyset$![]() , $\beta \neq \emptyset$
, $\beta \neq \emptyset$![]() and $m=|\beta | - |\alpha | - |\mu |$
and $m=|\beta | - |\alpha | - |\mu |$![]() ,
,
(ZL2) $\alpha =\emptyset$![]() , $\mu \neq \emptyset$
, $\mu \neq \emptyset$![]() and $m=|\beta |+|\nu |-|\mu |$
and $m=|\beta |+|\nu |-|\mu |$![]() ,
,
(ZL3) $\alpha =\nu =\emptyset$![]() and $m=|\beta |-|\mu |$
and $m=|\beta |-|\mu |$![]() .
.
Lemma 5.1 If (23) holds for all $\alpha,$![]() $\beta,$
$\beta,$![]() $\mu,$
$\mu,$![]() $\nu$
$\nu$![]() as in (ZL3), it holds for all $\alpha,$
as in (ZL3), it holds for all $\alpha,$![]() $\beta,$
$\beta,$![]() $\mu,$
$\mu,$![]() $\nu$
$\nu$![]() as in (ZL1) and (ZL2).
as in (ZL1) and (ZL2).
Proof. Consider condition (ZL1) first. By (ZL3), we have
Thus, by identity (24), we also have

Now, consider condition (ZL2). By (ZL3), we have
Thus, by identity (24), we also have

Now, we describe a construction of a large family of MASAs of the Cuntz algebra ${\mathcal {O}}_n$![]() which are contained in the core UHF-subalgebra ${\mathcal {F}}_n$
which are contained in the core UHF-subalgebra ${\mathcal {F}}_n$![]() and are not inner conjugate to the diagonal MASA ${\mathcal {D}}_n$
and are not inner conjugate to the diagonal MASA ${\mathcal {D}}_n$![]() . MASAs obtained by applying to ${\mathcal {D}}_n$
. MASAs obtained by applying to ${\mathcal {D}}_n$![]() quasi-free automorphisms not preserving ${\mathcal {D}}_n$
quasi-free automorphisms not preserving ${\mathcal {D}}_n$![]() provide very special examples of this more general construction.
provide very special examples of this more general construction.
We start with a sequence $\{r_k\}_{k=1}^\infty$![]() of positive integers and denote $R_1:=0$
of positive integers and denote $R_1:=0$![]() and $R_k:=\sum \nolimits _{j=1}^{k-1}r_j$
and $R_k:=\sum \nolimits _{j=1}^{k-1}r_j$![]() for $k\geq 2$
for $k\geq 2$![]() . For each $k$
. For each $k$![]() pick a $0< c_k<1$
pick a $0< c_k<1$![]() so that
so that

For each $k$![]() let $d_k$
let $d_k$![]() be a unitary in $\varphi ^{R_k}({\mathcal {D}}_n^{r_k})$
be a unitary in $\varphi ^{R_k}({\mathcal {D}}_n^{r_k})$![]() and $U_k$
and $U_k$![]() a unitary in $\varphi ^{R_k}({\mathcal {F}}_n^{r_k})$
a unitary in $\varphi ^{R_k}({\mathcal {F}}_n^{r_k})$![]() such that
such that
Such unitaries may be found through easy matrix considerations. Given these data, we define ${\mathcal {A}}$![]() to be the $C^*$
to be the $C^*$![]() -subalgebra of ${\mathcal {O}}_n$
-subalgebra of ${\mathcal {O}}_n$![]() generated by the union of all algebras $U_k \varphi ^{R_k}({\mathcal {D}}_n^{r_k}) U_k^*$
generated by the union of all algebras $U_k \varphi ^{R_k}({\mathcal {D}}_n^{r_k}) U_k^*$![]() .
.
Theorem 5.2 Every $C^*$![]() -algebra ${\mathcal {A}}$
-algebra ${\mathcal {A}}$![]() , defined as above, is a MASA in ${\mathcal {O}}_n$
, defined as above, is a MASA in ${\mathcal {O}}_n$![]() that is not inner conjugate to ${\mathcal {D}}_n$
that is not inner conjugate to ${\mathcal {D}}_n$![]() .
.
Proof. Let ${\mathcal {A}}$![]() be as above. Then clearly ${\mathcal {A}}$
be as above. Then clearly ${\mathcal {A}}$![]() is a MASA in the core UHF-subalgebra ${\mathcal {F}}_n$
is a MASA in the core UHF-subalgebra ${\mathcal {F}}_n$![]() of ${\mathcal {O}}_n$
of ${\mathcal {O}}_n$![]() , for example see [Reference Donsig and Power11]. We will show that ${\mathcal {A}}$
, for example see [Reference Donsig and Power11]. We will show that ${\mathcal {A}}$![]() is a MASA in the entire ${\mathcal {O}}_n$
is a MASA in the entire ${\mathcal {O}}_n$![]() as well.
as well.
Indeed, let $x$![]() be in ${\mathcal {A}}'\cap {\mathcal {O}}_n$
be in ${\mathcal {A}}'\cap {\mathcal {O}}_n$![]() , and let $x = \sum \nolimits _{m\in {\mathbb {Z}}}x^{(m)}$
, and let $x = \sum \nolimits _{m\in {\mathbb {Z}}}x^{(m)}$![]() be its standard Fourier series. Then for each $m$
be its standard Fourier series. Then for each $m$![]() we have $x^{(m)}\in {\mathcal {A}}'\cap {\mathcal {O}}_n$
we have $x^{(m)}\in {\mathcal {A}}'\cap {\mathcal {O}}_n$![]() . Consider a fixed $m>0$
. Consider a fixed $m>0$![]() . Both $x^{(m)*}x^{(m)}$
. Both $x^{(m)*}x^{(m)}$![]() and $x^{(m)}x^{(m)*}$
and $x^{(m)}x^{(m)*}$![]() are in ${\mathcal {A}}'\cap {\mathcal {F}}_n = {\mathcal {A}}$
are in ${\mathcal {A}}'\cap {\mathcal {F}}_n = {\mathcal {A}}$![]() . Since both these elements are positive and for every projection $q\in {\mathcal {A}}$
. Since both these elements are positive and for every projection $q\in {\mathcal {A}}$![]() we have $||qx^{(m)}x^{(m)*}|| = ||qx^{(m)}x^{(m)*}q|| = ||x^{(m)*}qx^{(m)}|| = ||qx^{(m)*}x^{(m)}||$
we have $||qx^{(m)}x^{(m)*}|| = ||qx^{(m)}x^{(m)*}q|| = ||x^{(m)*}qx^{(m)}|| = ||qx^{(m)*}x^{(m)}||$![]() , it easily follows that $x^{(m)*}x^{(m)} = x^{(m)}x^{(m)*}$
, it easily follows that $x^{(m)*}x^{(m)} = x^{(m)}x^{(m)*}$![]() . That is, the element $x^{(m)}$
. That is, the element $x^{(m)}$![]() of ${\mathcal {O}}_n$
of ${\mathcal {O}}_n$![]() is normal. Now, denote $v=S_1^m$
is normal. Now, denote $v=S_1^m$![]() and $a=x^{(m)}(S_1^m)^*$
and $a=x^{(m)}(S_1^m)^*$![]() . Then $a\in {\mathcal {F}}_n$
. Then $a\in {\mathcal {F}}_n$![]() and we have $x^{(m)}=av$
and we have $x^{(m)}=av$![]() . Since $av$
. Since $av$![]() is normal, we have
is normal, we have
Thus, $\tau (a^*a)=0$![]() and hence $a=0$
and hence $a=0$![]() . Consequently, $x^{(m)}=0$
. Consequently, $x^{(m)}=0$![]() for all $m>0$
for all $m>0$![]() . A similar argument shows that $x^{(m)} = 0$
. A similar argument shows that $x^{(m)} = 0$![]() for all $m<0$
for all $m<0$![]() . Thus, $x=x^{(0)}$
. Thus, $x=x^{(0)}$![]() belongs to ${\mathcal {A}}'\cap {\mathcal {F}}_n = {\mathcal {A}}$
belongs to ${\mathcal {A}}'\cap {\mathcal {F}}_n = {\mathcal {A}}$![]() , and ${\mathcal {A}}$
, and ${\mathcal {A}}$![]() is a MASA in ${\mathcal {O}}_n$
is a MASA in ${\mathcal {O}}_n$![]() as claimed.
as claimed.
To show that ${\mathcal {A}}$![]() is not inner conjugate in ${\mathcal {O}}_n$
is not inner conjugate in ${\mathcal {O}}_n$![]() to ${\mathcal {D}}_n$
to ${\mathcal {D}}_n$![]() , we verify that condition (ZL3) holds for
, we verify that condition (ZL3) holds for

Since each $w_k$![]() is in ${\mathcal {F}}_n$
is in ${\mathcal {F}}_n$![]() , it suffices to check it with $m=0$
, it suffices to check it with $m=0$![]() . So fix $\beta,\,\mu$
. So fix $\beta,\,\mu$![]() with $|\beta |=|\mu |$
with $|\beta |=|\mu |$![]() . Take $t$
. Take $t$![]() so large that $t\geq |\beta |$
so large that $t\geq |\beta |$![]() and consider $k> t$
and consider $k> t$![]() . Since $\prod _{j=t+1}^k U_j d_j U_j^*$
. Since $\prod _{j=t+1}^k U_j d_j U_j^*$![]() is in the range of injective endomorphism $\varphi ^{|\mu |}$
is in the range of injective endomorphism $\varphi ^{|\mu |}$![]() , we have
, we have

Thus, we have by Lemma 6.1, that

We remark that it is not immediately clear which of the MASAs considered in Proposition 5.2 are outer conjugate in ${\mathcal {O}}_n$![]() to ${\mathcal {D}}_n$
to ${\mathcal {D}}_n$![]() .
.
6. Technical lemmas
In this section, we collect a few technical facts used in the proofs above.
6.1. The conditional expectations
Lemma 6.1 Let $A$![]() and $B$
and $B$![]() be unital $C^*$
be unital $C^*$![]() -subalgebras of a finite-dimensional $C^*$
-subalgebras of a finite-dimensional $C^*$![]() -algebra, such that $ab=ba$
-algebra, such that $ab=ba$![]() for all $a\in A,$
for all $a\in A,$![]() $b\in B$
$b\in B$![]() . Let $D_A$
. Let $D_A$![]() and $D_B$
and $D_B$![]() be MASAs of $A$
be MASAs of $A$![]() and $B,$
and $B,$![]() respectively, so that $D:=D_A\vee D_B$
respectively, so that $D:=D_A\vee D_B$![]() is a MASA of $A\vee B$
is a MASA of $A\vee B$![]() . Let $\tau$
. Let $\tau$![]() be a faithful tracial state on $A\vee B,$
be a faithful tracial state on $A\vee B,$![]() and let $E_D,$
and let $E_D,$![]() $E_{D_A}$
$E_{D_A}$![]() and $E_{D_B}$
and $E_{D_B}$![]() be $\tau$
be $\tau$![]() -preserving conditional expectations from $A\vee B$
-preserving conditional expectations from $A\vee B$![]() onto $D,$
onto $D,$![]() $D_A$
$D_A$![]() and $D_B,$
and $D_B,$![]() respectively. Then we have
respectively. Then we have
for all $a\in A,$![]() $b\in B$
$b\in B$![]() .
.
Proof. If $A$![]() is a full matrix algebra (i.e., the centre of $A$
is a full matrix algebra (i.e., the centre of $A$![]() is trivial) then $A\vee B\cong A\otimes B$
is trivial) then $A\vee B\cong A\otimes B$![]() and $\tau (ab)=\tau (a)\tau (b)$
and $\tau (ab)=\tau (a)\tau (b)$![]() for all $a\in A$
for all $a\in A$![]() , $b\in B$
, $b\in B$![]() . Thus, in this case, the claim obviously holds.
. Thus, in this case, the claim obviously holds.
In the general case, let $\{p_1,\,\ldots,\,p_n\}$![]() be the minimal central projections in $A$
be the minimal central projections in $A$![]() . Then
. Then

The $\tau$![]() -preserving conditional expectation $E_i$
-preserving conditional expectation $E_i$![]() from $(A\vee B){p_i}$
from $(A\vee B){p_i}$![]() onto $(D_A\vee D_B){p_i}$
onto $(D_A\vee D_B){p_i}$![]() satisfies
satisfies
for all $a\in Ap_i$![]() and $b\in Bp_i$
and $b\in Bp_i$![]() , by the preceding argument. Since
, by the preceding argument. Since

the claim follows.
Corollary 6.2 For all $x_1,\,x_2,\,\ldots,\,x_k\in \mathfrak B$![]() , we have
, we have
Proof. Since $\mathfrak B$![]() , $\varphi (\mathfrak B)$
, $\varphi (\mathfrak B)$![]() , …, $\varphi ^{k-1}(\mathfrak B)$
, …, $\varphi ^{k-1}(\mathfrak B)$![]() are mutually commuting unital finite-dimensional $C^*$
are mutually commuting unital finite-dimensional $C^*$![]() -algebras, by Lemma 6.1, we have
-algebras, by Lemma 6.1, we have
The claims follow since the conditional expectation $\varPhi _{{\mathcal {D}}}$![]() commutes with the shift $\varphi$
commutes with the shift $\varphi$![]() .
.
6.2. The Perron-frobenius theory
Let $A$![]() be an $n\times n$
be an $n\times n$![]() matrix with non-negative integer entries. We assume that $A$
matrix with non-negative integer entries. We assume that $A$![]() is irreducible in the sense that for each pair of indices $(i,\,j)$
is irreducible in the sense that for each pair of indices $(i,\,j)$![]() there exists a positive integer $k$
there exists a positive integer $k$![]() such that $A^k(i,\,j)>0$
such that $A^k(i,\,j)>0$![]() . Let $\beta$
. Let $\beta$![]() be the Perron–Frobenius eigenvalue and let $(x(1),\,x(2),\,\ldots,\,x(n))$
be the Perron–Frobenius eigenvalue and let $(x(1),\,x(2),\,\ldots,\,x(n))$![]() be the corresponding Perron–Frobenius eigenvector. That is, $\beta >0$
be the corresponding Perron–Frobenius eigenvector. That is, $\beta >0$![]() , $x(i)>0$
, $x(i)>0$![]() for all indices $i=1,\,\ldots,\,n$
for all indices $i=1,\,\ldots,\,n$![]() , and
, and
In this subsection, for a (not necessary square) matrix $B$![]() we write $B\geq 0$
we write $B\geq 0$![]() if $B(i,\,j)\geq 0$
if $B(i,\,j)\geq 0$![]() for all $(i,\,j)$
for all $(i,\,j)$![]() . Likewise, we write $B> 0$
. Likewise, we write $B> 0$![]() if $B(i,\,j)> 0$
if $B(i,\,j)> 0$![]() for all $(i,\,j)$
for all $(i,\,j)$![]() . For a column vector $y\geq 0$
. For a column vector $y\geq 0$![]() , we set
, we set
The following lemma is part of the classical Perron–Frobenius theory, hence its proof is omitted.
Lemma 6.3 For an irreducible matrix $A,$![]() as above, we have
as above, we have
Lemma 6.4 Let $\beta '>0$![]() be the Perron–Frobenius eigenvalue of the transpose matrix ${^t}A$
be the Perron–Frobenius eigenvalue of the transpose matrix ${^t}A$![]() . Let $\{y(v)\}_v$
. Let $\{y(v)\}_v$![]() be the Perron–Frobenius eigenvector of ${^t}A$
be the Perron–Frobenius eigenvector of ${^t}A$![]() . That is,
. That is,
Set $m=\min _v y(v)$![]() and $M=\max _v y(v)$
and $M=\max _v y(v)$![]() . For any $f\in {\mathcal {D}}_E$
. For any $f\in {\mathcal {D}}_E$![]() , we have
, we have
Hence we have
Proof. We may assume that $f=S_\mu S_\mu ^*$![]() . We see that
. We see that

Lemma 6.5 For an irreducible matrix $A,$![]() as above, we set $X=\sum \nolimits _i x(i),$
as above, we set $X=\sum \nolimits _i x(i),$![]() $\alpha = \min _i x(i),$
$\alpha = \min _i x(i),$![]() and $\alpha '=\max _i x(i)$
and $\alpha '=\max _i x(i)$![]() . Then, for every positive integer $k$
. Then, for every positive integer $k$![]() , we have
, we have
Proof. Since $x(j)/\alpha ' \leq 1 \leq x(j)/\alpha$![]() for all $j$
for all $j$![]() and $\sum \nolimits _j A^k(i,\,j)x(j)=\beta ^k x(i)$
and $\sum \nolimits _j A^k(i,\,j)x(j)=\beta ^k x(i)$![]() for all $i$
for all $i$![]() , we have
, we have
For an irreducible matrix $A$![]() , as above, and a fixed pair of indices $(i_1,\,j_1)$
, as above, and a fixed pair of indices $(i_1,\,j_1)$![]() we set
we set
Theorem 6.6 Let $A$![]() be an irreducible matrix, as above. Assume that $A(i_1,\,j_1)\geq 2$
be an irreducible matrix, as above. Assume that $A(i_1,\,j_1)\geq 2$![]() . Then $A_1$
. Then $A_1$![]() is an irreducible matrix such that $A_1\leq A$
is an irreducible matrix such that $A_1\leq A$![]() and we have
and we have
with $\beta$![]() the Perron–Frobenius eigenvalue of $A$
the Perron–Frobenius eigenvalue of $A$![]() .
.
Proof. It is clear that $A_1$![]() is irreducible and $A_1\leq A$
is irreducible and $A_1\leq A$![]() . Let $\beta _1$
. Let $\beta _1$![]() be the Perron–Frobenius eigenvalue of $A_1$
be the Perron–Frobenius eigenvalue of $A_1$![]() , with the corresponding Perron–Frobenius eigenvector $(x_1(1),\,\ldots,\,x_1(n))$
, with the corresponding Perron–Frobenius eigenvector $(x_1(1),\,\ldots,\,x_1(n))$![]() . We have
. We have

Thus, in view of Lemma 6.5, it suffices to show that $\beta _1<\beta$![]() .
.
Now, for each pair of indices $(i,\,j)$![]() we can find an $l_{i,j}$
we can find an $l_{i,j}$![]() such that $A_1^{l_{i,j}}(i,\,j) < A^{l_{i,j}}(i,\,j)$
such that $A_1^{l_{i,j}}(i,\,j) < A^{l_{i,j}}(i,\,j)$![]() . Indeed, denote by $E_1$
. Indeed, denote by $E_1$![]() a graph with the adjacency matrix $A_1$
a graph with the adjacency matrix $A_1$![]() . We may view $E_1$
. We may view $E_1$![]() as a subgraph of $E$
as a subgraph of $E$![]() . Given $(i,\,j)$
. Given $(i,\,j)$![]() we can find a path $\mu \in E^*\setminus E_1^*$
we can find a path $\mu \in E^*\setminus E_1^*$![]() with source in vertex $i$
with source in vertex $i$![]() and range in vertex $j$
and range in vertex $j$![]() . To this end, take a path $\mu _1$
. To this end, take a path $\mu _1$![]() from $i$
from $i$![]() to $i_1$
to $i_1$![]() , a path $\mu _2$
, a path $\mu _2$![]() from $j_1$
from $j_1$![]() to $j$
to $j$![]() , and an edge $e\in E^1\setminus E_1^1$
, and an edge $e\in E^1\setminus E_1^1$![]() from $i_1$
from $i_1$![]() to $j_1$
to $j_1$![]() . Then put $\mu :=\mu _1 e\mu _2$
. Then put $\mu :=\mu _1 e\mu _2$![]() . Setting $l_{i,j}:=|\mu |$
. Setting $l_{i,j}:=|\mu |$![]() we have $A_1^{l_{i,j}}(i,\,j) < A^{l_{i,j}}(i,\,j)$
we have $A_1^{l_{i,j}}(i,\,j) < A^{l_{i,j}}(i,\,j)$![]() , as desired. Let $k$
, as desired. Let $k$![]() be an integer such that $k > l_{i,j}$
be an integer such that $k > l_{i,j}$![]() for all $i,\,j$
for all $i,\,j$![]() . Then we have
. Then we have

Now, we set $\overline {A}=\sum \nolimits _{j=1}^k A^j$![]() , $\overline {A}_1=\sum \nolimits _{j=1}^k A^j_1$
, $\overline {A}_1=\sum \nolimits _{j=1}^k A^j_1$![]() , $\overline {\beta }=\sum \nolimits _{j=1}^k \beta ^j$
, $\overline {\beta }=\sum \nolimits _{j=1}^k \beta ^j$![]() , and $\overline {\beta }_1=\sum \nolimits _{j=1}^k \beta ^j_1$
, and $\overline {\beta }_1=\sum \nolimits _{j=1}^k \beta ^j_1$![]() . We have $\overline {A}x=\overline {\beta }x$
. We have $\overline {A}x=\overline {\beta }x$![]() and $\overline {A}_1x_1=\overline {\beta }_1x_1$
and $\overline {A}_1x_1=\overline {\beta }_1x_1$![]() . To prove the theorem, it suffices to show that $\overline {\beta }_1 < \overline {\beta }$
. To prove the theorem, it suffices to show that $\overline {\beta }_1 < \overline {\beta }$![]() . Thus, without loss of generality, we may simply assume that $A_1 < A$
. Thus, without loss of generality, we may simply assume that $A_1 < A$![]() .
.
Let $I$![]() be the $n\times n$
be the $n\times n$![]() matrix with $I(i,\,j)=1$
matrix with $I(i,\,j)=1$![]() for all $i,\,j$
for all $i,\,j$![]() . Since $A > A_1$
. Since $A > A_1$![]() , we have
, we have
With $X_1:=\sum \nolimits _j x_1(j) >0$![]() , we see that
, we see that

We can take a small $\epsilon >0$![]() such that
such that

This means that $\lambda (x_1,\,A) \geq \beta _1+\epsilon > \beta _1$![]() . Since $\beta \geq \lambda (x_1,\,A)$
. Since $\beta \geq \lambda (x_1,\,A)$![]() , we may finally conclude that $\beta >\beta _1$
, we may finally conclude that $\beta >\beta _1$![]() .
.
Acknowledgements
W. Szymański was supported by the DFF-Research Project 2 on ‘Automorphisms and invariants of operator algebras’, Nr. 7014–00145B.
Conflict of interest
The authors declare none.