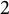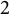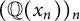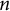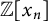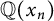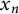1 Introduction
Let
$$ \begin{align*}\mathbb{Z}^{(\nu,x_0)}=\bigcup_{n\ge0}R_n, \end{align*} $$
where
$R_0=\mathbb {Z}$
and
$R_n=R_{n-1}[x_n]$
, for some fixed rational integers
$\nu \ge 2$
and
$x_0\ge 0$
such that
$\nu +x_0$
is not a square and
$x_{n}$
is the positive square root of
$\nu +x_{n-1}$
. Note that
$R_n=\mathbb {Z}[x_n]$
. Let
$\mathbb {Q}^{(\nu ,x_0)}$
be the fraction field of
$\mathbb {Z}^{(\nu ,x_0)}$
.
In this paper, we give a characterization for the ring
$\mathbb {Z}^{(\nu ,x_0)}$
to be the ring of integers of
$\mathbb {Q}^{(\nu ,x_0)}$
, answering partially a question raised by Vidaux and Videla in [Reference Vidaux and Videla10, Question 1.1, and the paragraph above Question 1.5]. The original motivation comes from a question in mathematical logic raised by Julia Robinson (see [Reference Vidaux and Videla10]).
For each
$n$
, let
$P_n$
denote the minimal polynomial of
$x_n$
over
$\mathbb {Q}$
. In Section 3 we prove the following result.
Theorem 1.1 Assume that
$\nu +x_0$
is congruent to
$2$
or
$3$
modulo
$4$
and is square-free. The ring
$\mathbb {Z}^{(\nu ,x_0)}$
is the ring of integers of
$\mathbb {Q}^{(\nu ,x_0)}$
if and only if
$P_n(0)$
is square-free for all
$n\ge 1$
.
The only pairs for which we know that our theorem applies are
$(2,0)$
and
$(2,1)$
, which corresponds to known cases (see Liang [Reference Liang4]). To determine any other pair for which the above result applies appears to be a very difficult problem. However, numerically we have established that for many pairs
$(\nu ,x_0)$
and values of
$n$
,
$P_n(0)$
is square-free, and therefore we are able to produce new examples of monogenic number fields. It should be noted that the problem of determining whether or not a number field is monogenic goes back to Dedekind, who showed that cyclotomic number fields are monogenic (see [Reference Gaál2] for a modern presentation of the subject).
For our proof to work, we need that the tower increases at each step, meaning that for every
$n$
,
$\mathbb {Q}(x_{n})$
has degree
$2$
over
$\mathbb {Q}(x_{n-1})$
(in particular, this implies that
$P_n$
has degree
$2^n$
). In [Reference Vidaux and Videla10, Proposition 2.15], it is shown that this happens whenever
$\nu +x_0$
is congruent to
$2$
or
$3$
modulo
$4$
. We observe that if
$x_0=0$
and
$\nu $
is not a square, the tower also increases at each step (apply [Reference Stoll8, Corollary 1.3] to the iterated of
$f(t)=t^2-\nu $
.
Assuming
$x_0=0$
, we computed
$P_n(0)$
for
$n$
from
$1$
to
$6$
and for
$\nu $
up to
$100$
. Considering only the relevant values of
$\nu $
, in the Table 1 an X in the cell
$(\nu ,n)$
means that
$P_k(0)$
is square-free for
$k$
up to
$n$
. It is remarkable that there is no X for
$n=3,4,5$
. From this, we obtain new monogenic number fields up to degree
$2^6$
. One can go further for some given value of
$\nu $
. Could it be true that for
$\nu =3$
,
$P_n(0)$
is always square-free?
Table 1 Values of
$n$
such that
$P_k(0)$
is square-free for
$k$
up to
$n$
.
In Section 4, we give some more evidence for the existence of pairs
$(\nu ,0)\ne (2,0)$
for which Theorem 1.1 applies. In particular, under the ABC-Conjecture, and assuming that
$x_0=0$
, we prove that for each
$n$
, there exist infinitely many values of
$\nu $
for which
$P_n(0)$
is square-free. We will also prove that, for
$\nu \ge 3$
, the largest prime divisor of
$P_n(0)$
tends to infinity as
$n$
tends to infinity.
We finish this introduction by a remark. Indeed, in order to prove Theorem 1.1, we will prove that for each
$n\ge 1$
,
$P_n(0)$
is square-free if and only if
$\mathbb {Z}[x_n]$
is the ring of integers of
$\mathbb {Q}(x_n)$
. Because of the latter, the condition that
$\nu +x_0$
is congruent to 2 or 3 modulo 4 cannot be dropped, because
-
(1) if
$\mathbb {Z}[x_n]=\mathcal {O}_{\mathbb {Q}(x_n)}$
for some
$n\ge 2$
, then also
$\mathbb {Z}[x_{n-1}]=\mathcal {O}_{\mathbb {Q}(x_{n-1})}$
; and -
(2) for square-free
$\nu +x_0$
, the ring
$\mathbb {Z}[x_1]$
is equal to the ring of integers
$\mathcal {O}_{\mathbb {Q}(x_1)}$
of
$\mathbb {Q}(x_1)$
if and only if
$\nu +x_0$
is congruent to
$2$
or
$3$
modulo
$4$
.
To see why item 1 is true, let
$\alpha \in \mathcal {O}_{\mathbb {Q}(x_{n-1})}$
. If
$\mathbb {Z}[x_n]=\mathcal {O}_{\mathbb {Q}(x_n)}$
, then we have
$$ \begin{align*}\alpha=a_0+a_1x_n+a_2x_n^2+\cdots+a_{2^n-1}x_n^{2^n-1}, \end{align*} $$
for some
$a_i\in \mathbb {Z}$
. Separating even and odd powers of
$x_n$
, since
$x_n^2=\nu +x_{n-1}$
, we have
$$ \begin{align*}\alpha=a+bx_n, \end{align*} $$
for some
$a,b\in \mathbb {Z}[x_{n-1}]$
. Since the tower increases at each step, we have
$x_n\notin \mathbb {Q}(x_{n-1})$
, and we deduce that
$b$
is
$0$
. Hence,
$\alpha \in \mathbb {Z}[x_{n-1}]$
.
2 Discriminant of
$x_n$
In this section we assume that the integer
$\nu +x_0$
is square-free and congruent to
$2$
or
$3$
modulo
$4$
. We will prove the following result.
Proposition 2.1 Assume that
$\mathbb {Q}(x_n)$
has degree
$2^n$
over
$\mathbb {Q}$
. We have
$$ \begin{align*}{\mathrm{disc}}(x_0)=1 \text{ and } {\mathrm{disc}}(x_1)=2^2(\nu+x_0), \end{align*} $$
and for
$n\geq 2$
we have
$$ \begin{align*}{\mathrm{disc}}(x_n)=({\mathrm{disc}}(x_{n-1}))^2\cdot 2^{2^n} P_n(0). \end{align*} $$
In our situation, the assumption that
$\mathbb {Q}(x_n)$
has degree
$2^n$
over
$\mathbb {Q}$
is fulfilled because
$\nu +x_0$
is congruent to
$2$
or
$3$
modulo
$4$
(see [Reference Vidaux and Videla10, Proposition 2.15]). Under this assumption,
$\mathbb {Q}(x_n)$
has basis
$$ \begin{align*}B_n:=\{1,x_n,x_n^2,\ldots,x_n^{2^n-1}\} \end{align*} $$
over
$\mathbb {Q}$
. Note that the field extension
$\mathbb {Q}(x_n)/\mathbb {Q}(x_m)$
has degree
$2^{n-m}$
. We will denote by
${\mathrm{disc}}_{n/n-1}(x_n)$
the discriminant of
$x_n$
from
$\mathbb {Q}(x_n)$
to
$\mathbb {Q}(x_{n-1})$
. Hence, for
$n\geq 1$
, we have
$$ \begin{align*}{\mathrm{disc}}_{n/n-1}(x_n) =\left| \begin{array}{cc} 1 & x_n\\ 1 & -x_n \end{array}\right|{}^2 =4(x_n)^2=4(\nu+x_{n-1}). \end{align*} $$
Notation 2.2 For
$n\geq 1$
, we denote by
$N_n$
the norm from
$\mathbb {Q}(x_n)$
to
$\mathbb {Q}$
of
${\mathrm{disc}}_{n+1/n}(x_{n+1})$
, and by
$N_0$
the discriminant of
$x_1$
from
$\mathbb {Q}(x_1)$
to
$\mathbb {Q}$
.
Proposition 2.3 We have
-
(1)
$N_0=2^2(\nu +x_0)$
, and -
(2)
$N_n=2^{2^{n+1}} P_{n+1}(0)$
for any
$n\geq 1$
.
Proof Item 1 is immediate from our above computation, so we prove item 2. Let
$n\geq 1$
. We have
$$ \begin{align*}\begin{aligned} N_n &={\mathrm{Norm}}_{\mathbb{Q}(x_n)/\mathbb{Q}} \left( {\mathrm{disc}} _{n+1/n}(x_{n+1})\right)\\ &={\mathrm{Norm}}_{\mathbb{Q}(x_n)/\mathbb{Q}} ( 4(\nu+x_n))\\ &=2^{2^{n+1}}{\mathrm{Norm}}_{\mathbb{Q}(x_n)/\mathbb{Q}} (\nu+x_n)\\ &=2^{2^{n+1}}{\mathrm{Norm}}_{\mathbb{Q}(x_n)/\mathbb{Q}} (-{\mathrm{Norm}}_{\mathbb{Q}(x_{n+1})/\mathbb{Q}(x_n)}(x_{n+1}))\\ &=2^{2^{n+1}}{\mathrm{Norm}}_{\mathbb{Q}(x_{n+1})/\mathbb{Q}} (x_{n+1})\\ &=2^{2^{n+1}} P_{n+1}(0) \end{aligned}\\[-34pt] \end{align*} $$
▪
We need the following proposition (see [Reference Marcus5, Chapter 2, Exercise 23, p. 43]).
Proposition 2.4 Let
$K\subset L\subset M$
be number fields,
$\left [L \colon K\right ]=n$
,
$\left [M \colon L\right ]=m$
, and let
$\left \{\alpha _1,\ldots , \alpha _n\right \}$
and
$\left \{\beta _1,\ldots , \beta _m\right \}$
be bases for
$L$
over
$K$
and
$M$
over
$L$
, respectively. We have
$$ \begin{align*}{\mathrm{disc}} _{{M/K}} \left(\alpha_1\beta_1,\ldots,\alpha_n\beta_m\right) &=\left({\mathrm{disc}} _{{L/K}}(\alpha_1,\ldots,\alpha_n)\right)^m\\ &\quad\cdot {\mathrm{Norm}}_{{L/K}}\left({\mathrm{disc}} _{{M/L}}(\beta_1,\ldots,\beta_m)\right). \end{align*} $$
Proposition 2.1 follows from Propositions 2.3 and 2.4 in the following way. Take
$$ \begin{align*}K=\mathbb{Q},\quad L=\mathbb{Q}(x_{n-1}),\quad\mathrm{and}\quad M=\mathbb{Q}(x_n). \end{align*} $$
The degree of
$L$
over
$K$
is
$2^{n-1}$
and
$L$
has basis
$$ \begin{align*}\left\{1,x_{n-1}, x^{2}_{n-1},\ldots, x^{2^{n-1}-1}_{n-1}\right\} \end{align*} $$
over
$K$
, while the degree of
$M$
over
$L$
is
$2$
and
$M$
has basis
$\left \{1, x_n\right \}$
over
$L$
. The set
$\left \{\alpha _1\beta _1,\ldots , \alpha _n\beta _m\right \}$
in Proposition 2.4 corresponds to the set
$$ \begin{align*}B'=\left\{1,x_{n-1}, x^{2}_{n-1},\ldots, x^{2^{n-1}-1}_{n-1}, x_n,x_{n-1}x_n, x^{2}_{n-1}x_n,\ldots, x^{2^{n-1}-1}_{n-1}x_n\right\}. \end{align*} $$
This set
$B'$
is a basis for
$M$
over
$K$
. Indeed, we have
$$ \begin{align*}|B'|=2\left(2^{n-1}-1\right)+2=2^n=|B_n|, \end{align*} $$
and since
$x^2_n=\nu +x_{n-1}$
, each element of
$B_n$
can be written as a
$\mathbb {Z}$
-linear combination of elements of
$B'$
. Similarly, each element of
$B'$
is a
$\mathbb {Z}$
-linear combination of elements of
$B_n$
. Since the base change matrices from
$B_n$
to
$B'$
and from
$B'$
to
$B_n$
have an integral determinant and because the discriminants are also integers, we deduce
$$ \begin{align*}{\mathrm{disc}} _{{M/K}}(B')={\mathrm{disc}} _{{M/K}}(B_n)={\mathrm{disc}} _{{M/K}}(x_n). \end{align*} $$
One obtains the formula in Proposition 2.1 by using in Proposition 2.4 the formulas from Proposition 2.3.
3 Proof of Theorem 1.1
In this section we assume that the integer
$\nu +x_0$
is square-free and congruent to
$2$
or
$3$
modulo
$4$
.
We start by a lemma that we will need at the end of the section in order to finish the proof of Theorem 1.1.
Lemma 3.1 If
$\mathbb {Z}^{(\nu ,x_0)}$
is the ring of integers of its fraction field, then
$\mathbb {Z}[x_n]=\mathcal {O}_{\mathbb {Q}(x_n)}$
for every
$n\geq 1$
.
Proof For
$n$
fixed, let
$\alpha \in \mathcal {O}_{\mathbb {Q}(x_{n})}$
, hence
$\alpha $
can be written as
$a+bx_n$
, for some
$a, b \in \mathbb {Q}(x_{n-1})$
. Since
$\alpha \in \mathbb {Z}^{(\nu ,x_0)}$
, there exists
$m\ge 0$
such that
$\alpha \in \mathbb {Z}[x_m]$
. If
$m=0$
, then
$\alpha \in \mathbb {Z}$
, so we assume
$m>0$
. Choose
$m>0$
minimal such that
$\alpha \in \mathbb {Z}[x_m]$
. Note that there exist
$c,d\in \mathbb {Z}[x_{m-1}]$
such that
$\alpha =c+dx_m$
and
$d\ne 0$
(by minimality of
$m$
). Therefore, we have
$$ \begin{align*}a+bx_n=c+dx_m, \end{align*} $$
hence
$x_m\in \mathbb {Q}(x_{n})$
, so
$m\le n$
and
$\alpha \in \mathbb {Z}[x_n]$
.▪
We will also use the following result from [Reference Uchida9].
Theorem 3.2 [Reference Uchida9]
Let
$R$
be a Dedeking ring. Let
$\theta $
be an element of some integral domain which contains
$R$
and let
$\theta $
be integral over
$R$
. Then
$R[\theta ]$
is a Dedekind ring if and only if the defining polynomial
$f(t)$
of
$\theta $
is not contained in
$\frak {m}^2$
for any maximal ideal
$\frak {m}$
of the polynomial ring
$R[t]$
.
Before we go to the proof of the theorem, we need to recall a few facts.
Proposition 3.3 [Reference Narkiewicz6, Proposition 2.13]
Let
$\theta $
be an algebraic integer. We have
$$ \begin{align*}{\mathrm{disc}} (\theta)=m^2{\mathrm{disc}} (\mathbb{Q}(\theta)), \end{align*} $$
where
$m$
is the index in
$\mathcal {O}_{\mathbb {Q}(\theta )}$
of the
$\mathbb {Z}$
-module
$\mathbb {Z}[\theta ]$
.
Definition 3.1 We say that a monic polynomial
$$ \begin{align*}x^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0 \end{align*} $$
with coefficients in
$\mathbb {Z}$
is p-Eisenstein with respect to the prime number
$p$
, if
$a_0,a_1,\ldots ,a_{n-1}$
are divisible by
$p$
, and
$p^2$
does not divide
$a_0$
.
Lemma 3.4 [Reference Narkiewicz6, Lemma 2.17]
Let
$\theta $
be an algebraic integer and
$p$
be a prime number. If the minimal polynomial of
$\theta $
over
$\mathbb {Q}$
is
$p$
-Eisenstein, then the index of
$\theta $
in
$\mathbb {Q}(\theta )$
is not divisible by
$p$
.
In the proof of Proposition 2.15 in [Reference Vidaux and Videla10], Vidaux and Videla proved the following result.
Proposition 3.5 [Reference Vidaux and Videla10]
For each
$n\geq 1$
, let
$P_n$
be the minimal polynomial of
$x_n$
. Suppose that
$\nu +x_0$
is congruent to
$2$
or
$3$
modulo
$4$
. We have
-
(1) if
$n$
is odd, then
$P_n(t+a)$
is
$2$
-Eisenstein, where and
$$ \begin{align*}a=\left\{ \begin{aligned} 0 &\text{ if } \nu+x_0\equiv 2 \mod 4,\\ 1 &\text{ if } \nu+x_0\equiv 3 \mod 4, \end{aligned} \right. \end{align*} $$
-
(2) if
$n$
is even, then
$P_n(t+x_0)$
is
$2$
-Eisenstein.
Moreover, writing
$f(t)=t^2-\nu $
, we have
$P_n(t)=f^{\circ n}(t)-x_0$
, hence in particular
$P_n$
has no monomial of odd degree (here,
$f^{\circ n}$
stands for the composition of
$f$
with itself
$n$
times).
Proposition 3.6 For all
$n\geq 1$
, if
$\nu +x_0$
is congruent to 2 or 3 modulo 4, then the index in
$\mathcal {O}_{\mathbb {Q}(x_n)}$
of the
$\mathbb {Z}$
module
$\mathbb {Z}[x_n]$
is not divisible by 2.
Proof It is an immediate consequence of Proposition 3.5 and Lemma 3.4, since for any rational integer
$c$
,
$P_n(t+c)$
is the minimal polynomial of
$x_n-c$
,
$\mathbb {Z}[x_n-c]=\mathbb {Z}[x_n]$
, and
$\mathbb {Q}(x_n-c)=\mathbb {Q}(x_n)$
.▪
3.1 Proof of Theorem 1.1
Assume first that there exists
$n\ge 1$
such that
$P_n(0)$
is not square-free. Let
$p$
be a prime such that
$p^2$
divides
$P_n(0)$
and write
$P_n(0)=p^2s$
, where
$s\in \mathbb {Z}-\{0\}$
. Since
$P_n$
has only monomials of even degree, we have
$$ \begin{align*}P_n(t)=p^2s+pt\cdot 0+t^2g(t), \end{align*} $$
for some
$g(t)\in \mathbb {Z}[t]$
. Hence
$P_n(t)\in (p,t)^2\subseteq \mathbb {Z}[t]$
. Since the ideal
$(p,t)$
is a maximal ideal of
$\mathbb {Z}[x_n]$
(the quotient ring is the field
$\mathbb {F}_p$
),
$\mathbb {Z}[x_n]$
is not the ring of integers of
$\mathbb {Q}(x_n)$
by Theorem 3.2. We deduce from Lemma 3.1 that
$\mathbb {Z}^{\nu ,x_0}$
is not the ring of integers of its fraction field.
We will show by induction on
$n$
that if
$P_n(0)$
is square-free, then
$\mathbb {Z}[x_n]=\mathcal {O}_{\mathbb {Q}(x_n)}$
. This is enough to prove the other direction in Theorem 1.1. Indeed, if
$\alpha \in \mathcal {O}_{\mathbb {Q}^{(\nu ,x_0)}}$
, then there exists
$n\ge 0$
such that
$\alpha \in \mathcal {O}_{\mathbb {Q}(x_n)}=\mathbb {Z}[x_n]$
.
Let
$m_n$
be the index in
$\mathcal {O}_{\mathbb {Q}(x_n)}$
of the
$\mathbb {Z}$
-module
$\mathbb {Z}[x_n]$
, so that
$$ \begin{align*}{\mathrm{disc}} (x_n)=m_n^2 {\mathrm{disc}}\: \mathbb{Q}(x_n) \end{align*} $$
by Proposition 3.3. We prove that
$m_n=1$
.
For
$n=1$
, we have
${\mathrm{disc}} (x_1)=4(\nu +x_0)={\mathrm{disc}}\: \mathbb {Q}(x_1)$
, because
$\nu +x_0\equiv 2,3 \pmod 4$
.
For
$n\geq 2$
, suppose that
$m_{n-1}=1$
, that is
${\mathrm{disc}} (x_{n-1})={\mathrm{disc}}\: \mathbb {Q}(x_{n-1})$
. By Proposition 2.1 and by induction hypothesis we have
$$ \begin{align*}2^{2^{n}}P_n(0)= \frac{{\mathrm{disc}} (x_{n})}{({\mathrm{disc}} (x_{n-1}))^2}=\frac{m_n^2 {\mathrm{disc}}\: \mathbb{Q}(x_n)}{({\mathrm{disc}}\: \mathbb{Q}(x_{n-1}))^2}. \end{align*} $$
On the one hand, by Proposition 3.6 we have that
$2$
does not divide
$m_n$
, and on the other hand, by [Reference Narkiewicz6, Corollary 1 of Proposition 4.15], the discriminant of
$\mathbb {Q}(x_n)$
is divisible by
$$ \begin{align*}({\mathrm{disc}}\: \mathbb{Q}(x_{n-1}))^{[\mathbb{Q}(x_n):\mathbb{Q}(x_{n-1})]}=({\mathrm{disc}}\: \mathbb{Q}(x_{n-1}))^2. \end{align*} $$
Hence,
$P_n(0)=m_n^2\ell $
for some
$\ell \in \mathbb {Z}$
. We deduce that
$m_n=1$
because
$P_n(0)$
is assumed to be square-free.
4 Monogenity up to any level assuming ABC
In all this section, we assume
$x_0=0$
.
Given an integer
$r\geq 2$
and a polynomial
$h\in \mathbb {Z}[X]$
of degree
$r$
, we consider
$$ \begin{align*}N_h(x)= \#\left\{n\leq x \colon h(n) \text{ is square-free} \right\}, \end{align*} $$
and
$$ \begin{align*}G_h=\gcd\{h(n) \colon n \geq 1\}. \end{align*} $$
Theorem 4.1 [Reference Granville3, Theorem 1]
Assume the ABC-Conjecture. Let
$h\in \mathbb {Z}[t]$
be a polynomial with integer coefficients, of degree at least
$2$
, without repeated factors. If
$G_h$
is square-free, then
$$ \begin{align*}N_h(x) \sim c_h x, \end{align*} $$
for some
$c_h>0$
.
Recall that since
$x_0=0$
, we have
$P_n(t)=f^{\circ n}(t)$
, where
$f(t)=t^2-\nu $
. We define the polynomials
$g_n(t)\in \mathbb {Z}[t]$
by induction on
$n$
:
-
•
$g_1(t)=-t$
, and -
•
$g_{n+1}(t)=(g_{n}(t))^2-t$
, for each
$n\geq 2$
.
So in particular we have
$P_1(0)=-\nu =g_1(\nu )$
, and if
$P_n(0)=g_n(\nu )$
, then
$$ \begin{align*}P_{n+1}(0)=(f\circ f^{\circ n})(0)=(f^{\circ n}(0))^2-\nu=P_n(0)^2-\nu=g_n(\nu)^2-\nu=g_{n+1}(\nu). \end{align*} $$
Therefore, for each
$n\ge 1$
, we have
$$ \begin{align*}P_n(0)=g_n(\nu). \end{align*} $$
Given
$\ell \ge 1$
, we consider
$$ \begin{align*}h_\ell(t)=\mbox{lcm } \{g_n(t)\colon 1\le n\le \ell\}. \end{align*} $$
Lemma 4.2 For every
$\ell \geq 1$
,
$G_{h_\ell }$
is square-free.
Proof Since
$2^2-2=2$
, for all
$n\geq 1$
we have
$g_n(2)=\pm 2$
. Also, it is immediate from the definition of
$g$
that there exists a polynomial
$q_n(t)$
in
$\mathbb {Z}[t]$
such that
$g_n(t)=t q_n(t)$
. Hence for each
$n\geq 1$
we have
$q_n(2)=\pm 1$
, and for each polynomial
$p(t)$
in
$\mathbb {Z}[t]$
which divides
$q_n(t)$
, we have
$p(2)=\pm 1$
. Hence for each
$\ell \geq 1$
, we have
$h_\ell (2)=\pm 2$
. Since
$g_2(t)=t(t-1)$
, the product
$t(t-1)$
divides
$h_\ell (t)$
for each
$\ell \ge 2$
, so
$2$
divides
$h_\ell (t)$
for any
$t\ge 2$
and for each
$\ell \ge 2$
, hence for each
$\ell \ge 1$
. We have
$h_\ell (1)=-1$
for odd
$\ell $
, in which case
$G_{h_\ell }=1$
, and
$h_\ell (1)=0$
for even
$\ell $
, in which case
$G_{h_\ell }=\pm 2$
.▪
Lemma 4.3 For every
$\ell \geq 1$
, the polynomial
$h_\ell \in \mathbb {Z}[t]$
has degree
$\ge 2$
and no repeated factors.
Proof The fact that
$h_\ell $
has degree
$\ge 2$
is immediate from its definition. It is enough to show that each
$g_n$
has no repeated factor. The derivative of
$g_n(t)$
is
$$ \begin{align*}g_n'(t)=2(g_{n-1}(t))\cdot((g_{n-1})'(t))-1. \end{align*} $$
Hence the reduction modulo
$2$
of
$g_n'(t)$
is equal to
$1$
. If there were a root
$\alpha $
in common between
$g_n(t)$
and
$g_n'(t)$
, then
$g_n'(t)$
would have the form
$A(t)B(t)$
, with
$A(t)$
the minimal polynomial of
$\alpha $
. Since
$g_n(t)$
is monic with integer coefficients,
$\alpha $
would be an algebraic integer, hence
$A(t)$
also would be a monic polynomial with integer coefficients. By Gauss’ Lemma,
$B(t)$
also has integer coefficients. Reducing modulo
$2$
, we get
$A(t)B(t)\equiv 1$
, hence in particular
$A(t)\equiv 1$
, which contradicts the fact that it is monic and non-constant.▪
Corollary 4.4 Assume
$x_0=0$
and fix an integer
$\ell \ge 2$
. Under the ABC Conjecture, there exist infinitely many values of
$\nu $
such that, for all
$1\le n\le \ell $
,
$P_n(0)$
is square-free. Moreover, all these
$\nu $
are congruent to
$2$
or
$3$
modulo
$4$
.
Proof By Theorem 4.1 and Lemmas 4.2 and 4.3, we know that
$h_\ell (\nu )$
infinitely many
$\nu $
. For each of those
$\nu $
, given
$1\le n\le \ell $
, since
$g_n$
divides
$h_\ell $
in
$\mathbb {Z}[t]$
, also
$g_n(\nu )=P_n(0)$
is square-free. Let
$\nu $
be such that
$P_n(0)$
each
$1\le n\le \ell $
. In particular,
$P_1(0)=-\nu $
and
$P_2(0)=\nu ^2-\nu $
are square-free, so
$\nu $
cannot be congruent to
$0$
or
$1$
modulo
$4$
.▪
We finish with a simple remark.
Assume
$\nu \ge 3$
. Note that under this condition, the sequence
$(P_n(0))_n$
is strictly increasing. We prove that the largest prime of
$P_n(0)$
tends to infinity as
$n$
tends to infinity. If this were not true, then there would be no hope for
$P_n(0)$
to be square-free for every
$n$
.
We adapt an argument that we saw in [Reference Serre7, Section 7.6, p. 105]. For the sake of contradiction, assume that there exists a sequence
$(n_i)_i$
tending to infinity and there exists
$M$
such that
$P_{n_i}(0)=p_1^{h_1},\ldots , p_j^{h_j}$
, with the
$h_k\ge 1$
and the
$p_k$
primes less than
$M$
. Let
$\theta _k$
be the remainder of the division of
$h_k$
by
$3$
, so that
$P_{n_i}(0)=p_1^{\theta _1},\ldots , p_j^{\theta _j}y^3$
, so
$f(P_{n_i-1}(0))=p_1^{\theta _1},\ldots , p_j^{\theta _j}x^3$
. The curve
$f(Y)=Y^2-\nu =p_1^{\theta _1},\ldots , p_j^{\theta _j}X^3$
is an elliptic curve, so by Siegel’s Theorem it has finitely many integral points. Since there are finitely many choices for the
$\theta _k$
and for the primes, there are finitely many such curves, hence finitely many possible values for
$P_{n_i}(0)$
.
