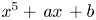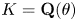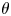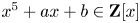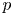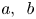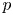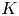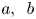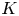1. Introduction and statements of results
Let $K={\mathbf {Q}}(\theta )$![]() be an algebraic number field with $\theta$
be an algebraic number field with $\theta$![]() in the ring $A_K$
in the ring $A_K$![]() of algebraic integers of $K$
of algebraic integers of $K$![]() . Let $f(x)\in {\mathbf {Z}}[x]$
. Let $f(x)\in {\mathbf {Z}}[x]$![]() be the minimal polynomial of $\theta$
be the minimal polynomial of $\theta$![]() having degree $n$
having degree $n$![]() over the field ${\mathbf {Q}}$
over the field ${\mathbf {Q}}$![]() of rational numbers. It is well known that $A_K$
of rational numbers. It is well known that $A_K$![]() is a free ${\mathbf {Z}}$
is a free ${\mathbf {Z}}$![]() -module of rank $n$
-module of rank $n$![]() . An algebraic number field $K$
. An algebraic number field $K$![]() is said to be monogenic if there exists some $\alpha \in A_K$
is said to be monogenic if there exists some $\alpha \in A_K$![]() such that $A_K={\mathbf {Z}}[\alpha ]$
such that $A_K={\mathbf {Z}}[\alpha ]$![]() . In this case, $\{1,\, \alpha,\,\cdots,\,\alpha ^{n-1}\}$
. In this case, $\{1,\, \alpha,\,\cdots,\,\alpha ^{n-1}\}$![]() is an integral basis of $K$
is an integral basis of $K$![]() ; such an integral basis of $K$
; such an integral basis of $K$![]() is called a power integral basis or briefly a power basis of $K$
is called a power integral basis or briefly a power basis of $K$![]() . If $K$
. If $K$![]() does not possess any power basis, we say that $K$
does not possess any power basis, we say that $K$![]() is non-monogenic. It is well known that every quadratic and cyclotomic field is monogenic. In algebraic number theory, it is important to know whether a number field is monogenic or not. The first non-monogenic number field was given by Dedekind in $1878$
is non-monogenic. It is well known that every quadratic and cyclotomic field is monogenic. In algebraic number theory, it is important to know whether a number field is monogenic or not. The first non-monogenic number field was given by Dedekind in $1878$![]() . He proved that the cubic field ${\mathbf {Q}}(\xi )$
. He proved that the cubic field ${\mathbf {Q}}(\xi )$![]() is not monogenic when $\xi$
is not monogenic when $\xi$![]() is a root of the polynomial $x^3-x^2-2x-8$
is a root of the polynomial $x^3-x^2-2x-8$![]() (cf. [Reference Narkiewicz14, p. 64]). The problem of testing the monogenity of number fields and constructing power integral bases have been intensively studied (cf. [Reference Ahmad, Nakahara and Husnine1,Reference Ahmad, Nakahara and Hameed2,Reference Gaál and Remete7,Reference Jakhar and Kaur9,Reference Jakhar and Kumar10,Reference MacKenzie and Scheuneman13,Reference Soullami and Sahmoudi17]). In $1984$
(cf. [Reference Narkiewicz14, p. 64]). The problem of testing the monogenity of number fields and constructing power integral bases have been intensively studied (cf. [Reference Ahmad, Nakahara and Husnine1,Reference Ahmad, Nakahara and Hameed2,Reference Gaál and Remete7,Reference Jakhar and Kaur9,Reference Jakhar and Kumar10,Reference MacKenzie and Scheuneman13,Reference Soullami and Sahmoudi17]). In $1984$![]() , Funakura [Reference Funakura5] gave necessary and sufficient condition on those integers $m$
, Funakura [Reference Funakura5] gave necessary and sufficient condition on those integers $m$![]() for which the quartic field ${\mathbf {Q}}(m^{1/4})$
for which the quartic field ${\mathbf {Q}}(m^{1/4})$![]() is monogenic. Ahmad et al. [Reference Ahmad, Nakahara and Husnine1,Reference Ahmad, Nakahara and Hameed2] proved that for a square-free integer, $m$
is monogenic. Ahmad et al. [Reference Ahmad, Nakahara and Husnine1,Reference Ahmad, Nakahara and Hameed2] proved that for a square-free integer, $m$![]() is not congruent to $\pm 1\mod 9$
is not congruent to $\pm 1\mod 9$![]() , a pure field ${\mathbf {Q}}(m^{1/6})$
, a pure field ${\mathbf {Q}}(m^{1/6})$![]() having degree six over ${\mathbf {Q}}$
having degree six over ${\mathbf {Q}}$![]() is monogenic when $m\equiv 2$
is monogenic when $m\equiv 2$![]() or $3\mod 4$
or $3\mod 4$![]() and it is non-monogenic when $m\equiv 1\mod 4$
and it is non-monogenic when $m\equiv 1\mod 4$![]() . In $2017$
. In $2017$![]() , Gaál and Remete [Reference Gaál and Remete7] studied monogenity of algebraic number fields of the type ${\mathbf {Q}}(m^{1/n})$
, Gaál and Remete [Reference Gaál and Remete7] studied monogenity of algebraic number fields of the type ${\mathbf {Q}}(m^{1/n})$![]() where $3\leq n\leq 9$
where $3\leq n\leq 9$![]() and $m$
and $m$![]() is square free. In [Reference Gaál6], Gaál studied monogenity of number fields defined by some sextic irreducible trinomials. El. Fadil characterized when a prime $p$
is square free. In [Reference Gaál6], Gaál studied monogenity of number fields defined by some sextic irreducible trinomials. El. Fadil characterized when a prime $p$![]() is a common index divisor of the number field defined by $x^6+ax^3+b\in {\mathbf {Z}}[x]$
is a common index divisor of the number field defined by $x^6+ax^3+b\in {\mathbf {Z}}[x]$![]() in [Reference Fadil4].
in [Reference Fadil4].
Recall that for an algebraic number field $L={\mathbf {Q}}(\xi )$![]() with $\xi$
with $\xi$![]() an algebraic integer satisfying a monic irreducible polynomial $g(x)$
an algebraic integer satisfying a monic irreducible polynomial $g(x)$![]() over ${\mathbf {Q}}$
over ${\mathbf {Q}}$![]() , the discriminant $D$
, the discriminant $D$![]() of $g(x)$
of $g(x)$![]() and the discriminant $d_L$
and the discriminant $d_L$![]() of $L$
of $L$![]() are related by the formula
are related by the formula
In what follows, let $K={\mathbf {Q}}(\theta )$![]() be an algebraic number field with $\theta$
be an algebraic number field with $\theta$![]() a root of an irreducible trinomial $f(x)=x^5+ax+b\in {\mathbf {Z}}[x]$
a root of an irreducible trinomial $f(x)=x^5+ax+b\in {\mathbf {Z}}[x]$![]() . Then for every rational prime $p$
. Then for every rational prime $p$![]() , we provide necessary and sufficient conditions on $a,\,~b$
, we provide necessary and sufficient conditions on $a,\,~b$![]() , so that $p$
, so that $p$![]() is a common index divisor of $K$
is a common index divisor of $K$![]() . In particular, under these conditions $K$
. In particular, under these conditions $K$![]() is non-monogenic. As an application of our results, we provide some classes of algebraic number fields which are non-monogenic.
is non-monogenic. As an application of our results, we provide some classes of algebraic number fields which are non-monogenic.
Throughout this paper, $\mathop {\mathrm {ind}} \theta$![]() denotes the index of the subgroup ${\mathbf {Z}}[\theta ]$
denotes the index of the subgroup ${\mathbf {Z}}[\theta ]$![]() in $A_K$
in $A_K$![]() and $i(K)$
and $i(K)$![]() will stand for the index of the field $K$
will stand for the index of the field $K$![]() defined by
defined by
A prime number $p$![]() dividing $i(K)$
dividing $i(K)$![]() is called a prime common index divisor of $K$
is called a prime common index divisor of $K$![]() . Note that if $K$
. Note that if $K$![]() is monogenic then $i(K)=1$
is monogenic then $i(K)=1$![]() . Therefore, a number field having a prime common index divisor is non-monogenic. There exist non-monogenic number fields having $i(K)=1$
. Therefore, a number field having a prime common index divisor is non-monogenic. There exist non-monogenic number fields having $i(K)=1$![]() , e.g., $K={\mathbf {Q}}(\sqrt [3]{175})$
, e.g., $K={\mathbf {Q}}(\sqrt [3]{175})$![]() is not monogenic with $i(K)=1$
is not monogenic with $i(K)=1$![]() . In what follows, for a prime $p$
. In what follows, for a prime $p$![]() and a non-zero $m$
and a non-zero $m$![]() belonging to the ring ${\mathbf {Z}}_p$
belonging to the ring ${\mathbf {Z}}_p$![]() of $p$
of $p$![]() -adic integers, $v_p(m)$
-adic integers, $v_p(m)$![]() will denote the highest power of $p$
will denote the highest power of $p$![]() dividing $m$
dividing $m$![]() . For a non-zero integer $l$
. For a non-zero integer $l$![]() , let $l_p$
, let $l_p$![]() denote $\frac {l}{p^{v_p(l)}}$
denote $\frac {l}{p^{v_p(l)}}$![]() . If a rational prime $p$
. If a rational prime $p$![]() is such that $p^4$
is such that $p^4$![]() divides $a$
divides $a$![]() and $p^5$
and $p^5$![]() divides $b$
divides $b$![]() , then $\theta /p$
, then $\theta /p$![]() is a root of the polynomial $x^5+(a/p^4)x+(b/p^5)$
is a root of the polynomial $x^5+(a/p^4)x+(b/p^5)$![]() having integer coefficients. So we may assume that for each prime $p$
having integer coefficients. So we may assume that for each prime $p$![]()
In this paper, $D$![]() will stand for the discriminant of $f(x)$
will stand for the discriminant of $f(x)$![]() . One can check that
. One can check that
We abbreviate $a\equiv b\mod n$![]() by $a\equiv b(n)$
by $a\equiv b(n)$![]() . For integers $u,\,v,\,w,\,z$
. For integers $u,\,v,\,w,\,z$![]() and prime number $p$
and prime number $p$![]() , by notation $(u,\,v)\equiv (w,\,z)(p)$
, by notation $(u,\,v)\equiv (w,\,z)(p)$![]() , we mean $u\equiv w(p)$
, we mean $u\equiv w(p)$![]() and $v\equiv z(p)$
and $v\equiv z(p)$![]() . Also, $(u,\,v)\in I(p)$
. Also, $(u,\,v)\in I(p)$![]() means that $(u,\,v)\equiv (w,\,z)(p)$
means that $(u,\,v)\equiv (w,\,z)(p)$![]() for some $(w,\,z) \in I$
for some $(w,\,z) \in I$![]() .
.
With the above notation and assumption (1.2), we prove
Theorem 1.1 Let $K={\mathbf {Q}}(\theta )$![]() with $\theta$
with $\theta$![]() a root of an irreducible polynomial $f(x) = x^5+ax+b \in {\mathbf {Z}}[x]$
a root of an irreducible polynomial $f(x) = x^5+ax+b \in {\mathbf {Z}}[x]$![]() . Then for any odd rational prime $p$
. Then for any odd rational prime $p$![]() , $p\nmid i(K)$
, $p\nmid i(K)$![]() .
.
Theorem 1.2 Let $K={\mathbf {Q}}(\theta )$![]() be an algebraic number field with $\theta$
be an algebraic number field with $\theta$![]() a root of an irreducible polynomial $f(x)=x^5+ax+b$
a root of an irreducible polynomial $f(x)=x^5+ax+b$![]() . If $u=\frac {v_2(f(-\frac {5b}{4a}))-1}{2}$
. If $u=\frac {v_2(f(-\frac {5b}{4a}))-1}{2}$![]() and $\delta =2^u-\frac {5b}{4a}$
and $\delta =2^u-\frac {5b}{4a}$![]() , then the prime ideal factorization of $2A_K$
, then the prime ideal factorization of $2A_K$![]() is given in Table 1. Furthermore, $2\mid i(K)$
is given in Table 1. Furthermore, $2\mid i(K)$![]() if and only if one of the conditions A$7$
if and only if one of the conditions A$7$![]() , A$9$
, A$9$![]() , A$13$
, A$13$![]() , A$15$
, A$15$![]() , A$18$
, A$18$![]() , A$19$
, A$19$![]() , A$21$
, A$21$![]() , A$22$
, A$22$![]() , A$24$
, A$24$![]() , A$29$
, A$29$![]() hold.
hold.
Table 1. Factorization of $2A_K$![]() .
.

Table 2. Factorization of $3A_K$![]() .
.

In particular, if any one of the conditions A$7$![]() , A$9$
, A$9$![]() , A$13$
, A$13$![]() , A$15$
, A$15$![]() , A$18$
, A$18$![]() , A$19$
, A$19$![]() , A$21$
, A$21$![]() , A$22$
, A$22$![]() , A$24$
, A$24$![]() , A$29$
, A$29$![]() hold, then $K$
hold, then $K$![]() is non-monogenic, otherwise $i(K)=1$
is non-monogenic, otherwise $i(K)=1$![]() .
.
The following corollaries follow immediately from the above theorem.
Corollary 1.3 Let $K={\mathbf {Q}}(\theta )$![]() where $\theta$
where $\theta$![]() satisfies the polynomial $x^5+ax+b$
satisfies the polynomial $x^5+ax+b$![]() . If $a,\,~b$
. If $a,\,~b$![]() are such that $a=1088r+68$
are such that $a=1088r+68$![]() and $b=18496s+ 1088$
and $b=18496s+ 1088$![]() with $r,\,~s\in {\mathbf {Z}}$
with $r,\,~s\in {\mathbf {Z}}$![]() , then $K$
, then $K$![]() is non-monogenic in view of Case A$13$
is non-monogenic in view of Case A$13$![]() of Table 1 of Theorem 1.2.
of Table 1 of Theorem 1.2.
Corollary 1.4 Let $a,\,~b$![]() be such that $a=20r+5$
be such that $a=20r+5$![]() and $b=100s+10$
and $b=100s+10$![]() with $r,\,~s\in {\mathbf {Z}}$
with $r,\,~s\in {\mathbf {Z}}$![]() . Let $K={\mathbf {Q}}(\theta )$
. Let $K={\mathbf {Q}}(\theta )$![]() where $\theta$
where $\theta$![]() is a root of a polynomial $x^5+ax+b$
is a root of a polynomial $x^5+ax+b$![]() . Then $K$
. Then $K$![]() is non-monogenic by Case A$15$
is non-monogenic by Case A$15$![]() of Table 1 of Theorem 1.2.
of Table 1 of Theorem 1.2.
We now provide some examples of non-monogenic number fields.
Example 1.5 Let $K={\mathbf {Q}}(\theta )$![]() where $\theta$
where $\theta$![]() is a root of $f(x)=x^5+68x+1088$
is a root of $f(x)=x^5+68x+1088$![]() . Note that $f(x)$
. Note that $f(x)$![]() satisfies Eisenstein criterion with respect to $17$
satisfies Eisenstein criterion with respect to $17$![]() , hence, it is irreducible over ${\mathbf {Q}}$
, hence, it is irreducible over ${\mathbf {Q}}$![]() . So $K$
. So $K$![]() is non-monogenic by Corollary 1.3.
is non-monogenic by Corollary 1.3.
Example 1.6 Let $K={\mathbf {Q}}(\theta )$![]() with $\theta$
with $\theta$![]() satisfying $f(x)=x^5+5x+10$
satisfying $f(x)=x^5+5x+10$![]() . It can be easily seen that $f(x)$
. It can be easily seen that $f(x)$![]() is $5$
is $5$![]() -Eisenstein. Hence, $K$
-Eisenstein. Hence, $K$![]() is non-monogenic by Corollary 1.4.
is non-monogenic by Corollary 1.4.
2. Preliminary results
Let $K={\mathbf {Q}}(\theta )$![]() be an algebraic number field with $\theta$
be an algebraic number field with $\theta$![]() a root of a monic irreducible polynomial $f(x)$
a root of a monic irreducible polynomial $f(x)$![]() belonging to ${\mathbf {Z}}[x]$
belonging to ${\mathbf {Z}}[x]$![]() . In what follows, $A_K$
. In what follows, $A_K$![]() will stand for the ring of algebraic integers of $K$
will stand for the ring of algebraic integers of $K$![]() . For a rational prime $p$
. For a rational prime $p$![]() , let $\mathbb {F}_p$
, let $\mathbb {F}_p$![]() denote the finite field with $p$
denote the finite field with $p$![]() elements. The following lemma (cf. [Reference Smith16, Theorem 2.2]) will play an important role in the proof of Theorems 1.1, 1.2.
elements. The following lemma (cf. [Reference Smith16, Theorem 2.2]) will play an important role in the proof of Theorems 1.1, 1.2.
Lemma 2.1 Let $K$![]() be an algebraic number field and $p$
be an algebraic number field and $p$![]() be a rational prime. Then $p$
be a rational prime. Then $p$![]() is a common index divisor of $K$
is a common index divisor of $K$![]() if and only if for some positive integer $h$
if and only if for some positive integer $h$![]() , the number of distinct prime ideals of $A_K$
, the number of distinct prime ideals of $A_K$![]() lying above $p$
lying above $p$![]() having residual degree $h$
having residual degree $h$![]() is greater than the number of monic irreducible polynomials of degree $h$
is greater than the number of monic irreducible polynomials of degree $h$![]() in $\mathbb {F}_p[x]$
in $\mathbb {F}_p[x]$![]() .
.
We shall first introduce the notion of Gauss valuation, $\phi$![]() -Newton polygon and Newton polygon of second order, where $\phi (x)$
-Newton polygon and Newton polygon of second order, where $\phi (x)$![]() belonging to ${\mathbf {Z}}_p[x]$
belonging to ${\mathbf {Z}}_p[x]$![]() is a monic polynomial with $\overline {\phi }(x)$
is a monic polynomial with $\overline {\phi }(x)$![]() irreducible over $\mathbb {F}_p$
irreducible over $\mathbb {F}_p$![]() .
.
Definition 2.2 The Gauss valuation of the field ${\mathbf {Q}}_p(x)$![]() of rational functions in an indeterminate $x$
of rational functions in an indeterminate $x$![]() which extends the valuation $v_p$
which extends the valuation $v_p$![]() of ${\mathbf {Q}}_p$
of ${\mathbf {Q}}_p$![]() and is defined on ${\mathbf {Q}}_p[x]$
and is defined on ${\mathbf {Q}}_p[x]$![]() by
by
Definition 2.3 Let $p$![]() be a rational prime. Let $\phi (x)\in {\mathbf {Z}}_p[x]$
be a rational prime. Let $\phi (x)\in {\mathbf {Z}}_p[x]$![]() be a monic polynomial which is irreducible modulo $p$
be a monic polynomial which is irreducible modulo $p$![]() and $f(x)\in {\mathbf {Z}}_p[x]$
and $f(x)\in {\mathbf {Z}}_p[x]$![]() be a monic polynomial not divisible by $\phi (x)$
be a monic polynomial not divisible by $\phi (x)$![]() . Let $\displaystyle \sum \nolimits _{i=0}^{n}a_i(x)\phi (x)^i$
. Let $\displaystyle \sum \nolimits _{i=0}^{n}a_i(x)\phi (x)^i$![]() with $\deg a_i(x)<\deg \phi (x)$
with $\deg a_i(x)<\deg \phi (x)$![]() , $a_n(x)\neq 0$
, $a_n(x)\neq 0$![]() be the $\phi (x)$
be the $\phi (x)$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() obtained on dividing it by the successive powers of $\phi (x)$
obtained on dividing it by the successive powers of $\phi (x)$![]() . Let $P_i$
. Let $P_i$![]() stand for the point in the plane having coordinates $(i,\,v_{p,x}(a_{n-i}(x)))$
stand for the point in the plane having coordinates $(i,\,v_{p,x}(a_{n-i}(x)))$![]() when $a_{n-i}(x)\neq 0$
when $a_{n-i}(x)\neq 0$![]() , $0\leq i\leq n$
, $0\leq i\leq n$![]() . Let $\mu _{ij}$
. Let $\mu _{ij}$![]() denote the slope of the line joining the point $P_i$
denote the slope of the line joining the point $P_i$![]() with $P_j$
with $P_j$![]() if $a_{n-i}(x)a_{n-j}(x)\neq 0$
if $a_{n-i}(x)a_{n-j}(x)\neq 0$![]() . Let $i_1$
. Let $i_1$![]() be the largest positive index not exceeding $n$
be the largest positive index not exceeding $n$![]() such that
such that
If $i_1< n,$![]() let $i_2$
let $i_2$![]() be the largest index such that $i_1< i_2\leq n$
be the largest index such that $i_1< i_2\leq n$![]() with
with
and so on. The $\phi$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() with respect to $p$
with respect to $p$![]() is the polygonal path having segments $P_{0}P_{i_1},\,P_{i_1}P_{i_2},\,\ldots,\,P_{i_{k-1}}P_{i_k}$
is the polygonal path having segments $P_{0}P_{i_1},\,P_{i_1}P_{i_2},\,\ldots,\,P_{i_{k-1}}P_{i_k}$![]() with $i_k=n$
with $i_k=n$![]() . These segments are called the edges of the $\phi$
. These segments are called the edges of the $\phi$![]() -Newton polygon and their slopes form a strictly increasing sequence; these slopes are non-negative as $f(x)$
-Newton polygon and their slopes form a strictly increasing sequence; these slopes are non-negative as $f(x)$![]() is a monic polynomial with coefficients in ${\mathbf {Z}}_p$
is a monic polynomial with coefficients in ${\mathbf {Z}}_p$![]() .
.
Definition 2.4 Let $\phi (x) \in {\mathbf {Z}}_p[x]$![]() be a monic polynomial which is irreducible modulo a rational prime $p$
be a monic polynomial which is irreducible modulo a rational prime $p$![]() having a root $\alpha$
having a root $\alpha$![]() in the algebraic closure $\widetilde {{\mathbf {Q}}}_{p}$
in the algebraic closure $\widetilde {{\mathbf {Q}}}_{p}$![]() of ${\mathbf {Q}}_p$
of ${\mathbf {Q}}_p$![]() . Let $f(x) \in {\mathbf {Z}}_p[x]$
. Let $f(x) \in {\mathbf {Z}}_p[x]$![]() be a monic polynomial not divisible by $\phi (x)$
be a monic polynomial not divisible by $\phi (x)$![]() with $\phi (x)$
with $\phi (x)$![]() -expansion $\phi (x)^n + a_{n-1}(x)\phi (x)^{n-1} + \cdots + a_0(x)$
-expansion $\phi (x)^n + a_{n-1}(x)\phi (x)^{n-1} + \cdots + a_0(x)$![]() such that $\overline {f}(x)$
such that $\overline {f}(x)$![]() is a power of $\overline {\phi }(x)$
is a power of $\overline {\phi }(x)$![]() . Suppose that the $\phi$
. Suppose that the $\phi$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() consists of a single edge, say $S$
consists of a single edge, say $S$![]() , having a positive slope denoted by $\frac {l}{e}$
, having a positive slope denoted by $\frac {l}{e}$![]() with $l,\, e$
with $l,\, e$![]() coprime, i.e.,
coprime, i.e.,
so that $n$![]() is divisible by $e$
is divisible by $e$![]() , say $n=et$
, say $n=et$![]() and $v_{p,x}(a_{n-ej}(x)) \geq lj$
and $v_{p,x}(a_{n-ej}(x)) \geq lj$![]() for $1\leq j\leq t$
for $1\leq j\leq t$![]() . Thus, the polynomial $b_j(x):=\frac {a_{n-ej}(x)}{p^{lj}}$
. Thus, the polynomial $b_j(x):=\frac {a_{n-ej}(x)}{p^{lj}}$![]() has coefficients in ${\mathbf {Z}}_p$
has coefficients in ${\mathbf {Z}}_p$![]() and hence $b_j(\alpha )\in {\mathbf {Z}}_p[\alpha ]$
and hence $b_j(\alpha )\in {\mathbf {Z}}_p[\alpha ]$![]() for $1\leq j \leq t$
for $1\leq j \leq t$![]() . The polynomial $T(Y)$
. The polynomial $T(Y)$![]() in an indeterminate $Y$
in an indeterminate $Y$![]() defined by $T(Y) = Y^t + \sum \nolimits \limits _{j=1}^{t} \overline {b_j}(\overline {\alpha })Y^{t-j}$
defined by $T(Y) = Y^t + \sum \nolimits \limits _{j=1}^{t} \overline {b_j}(\overline {\alpha })Y^{t-j}$![]() having coefficients in $\mathbb {F}_p[\overline {\alpha }]\cong \frac {\mathbb {F}_p[x]}{\langle \phi (x)\rangle }$
having coefficients in $\mathbb {F}_p[\overline {\alpha }]\cong \frac {\mathbb {F}_p[x]}{\langle \phi (x)\rangle }$![]() is called residual polynomial of $f (x)$
is called residual polynomial of $f (x)$![]() with respect to $(\phi,\,S)$
with respect to $(\phi,\,S)$![]() .
.
The following definition gives the notion of a residual polynomial when $f(x)$![]() is more general.
is more general.
Definition 2.5 Let $\phi (x),\, \alpha$![]() be as in Definition 2.4. Let $g(x)\in {\mathbf {Z}}_p[x]$
be as in Definition 2.4. Let $g(x)\in {\mathbf {Z}}_p[x]$![]() be a monic polynomial not divisible by $\phi (x)$
be a monic polynomial not divisible by $\phi (x)$![]() such that $\overline {g}(x)$
such that $\overline {g}(x)$![]() is a power of $\overline {\phi }(x)$
is a power of $\overline {\phi }(x)$![]() . Let $\lambda _1 < \cdots < \lambda _k$
. Let $\lambda _1 < \cdots < \lambda _k$![]() be the slopes of the edges of the $\phi$
be the slopes of the edges of the $\phi$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() and $S_i$
and $S_i$![]() denote the edge with slope $\lambda _i$
denote the edge with slope $\lambda _i$![]() . In view of a classical result proved by Ore (cf. [Reference Cohen, Movahhedi and Salinier3, Theorem 1.5], [Reference Khanduja and Kumar12, Theorem 1.1]), we can write $g(x) = g_1(x)\cdots g_k(x)$
. In view of a classical result proved by Ore (cf. [Reference Cohen, Movahhedi and Salinier3, Theorem 1.5], [Reference Khanduja and Kumar12, Theorem 1.1]), we can write $g(x) = g_1(x)\cdots g_k(x)$![]() , where the $\phi$
, where the $\phi$![]() -Newton polygon of $g_i(x) \in {\mathbf {Z}}_{p}[x]$
-Newton polygon of $g_i(x) \in {\mathbf {Z}}_{p}[x]$![]() has a single edge, say $S_i'$
has a single edge, say $S_i'$![]() , which is a translate of $S_i$
, which is a translate of $S_i$![]() . Let $T_i(Y)$
. Let $T_i(Y)$![]() belonging to ${\mathbb {F}}_{p}[\overline {\alpha }][Y]$
belonging to ${\mathbb {F}}_{p}[\overline {\alpha }][Y]$![]() denote the residual polynomial of $g_i(x)$
denote the residual polynomial of $g_i(x)$![]() with respect to ($\phi,\,~S_i'$
with respect to ($\phi,\,~S_i'$![]() ) described as in Definition 2.4. For convenience, the polynomial $T_i(Y)$
) described as in Definition 2.4. For convenience, the polynomial $T_i(Y)$![]() will be referred to as the residual polynomial of $g(x)$
will be referred to as the residual polynomial of $g(x)$![]() with respect to $(\phi,\,S_i)$
with respect to $(\phi,\,S_i)$![]() . The polynomial $g(x)$
. The polynomial $g(x)$![]() is said to be $p$
is said to be $p$![]() -regular with respect to $\phi$
-regular with respect to $\phi$![]() if none of the polynomials $T_i(Y)$
if none of the polynomials $T_i(Y)$![]() has a repeated root in the algebraic closure of $\mathbb {F}_p$
has a repeated root in the algebraic closure of $\mathbb {F}_p$![]() , $1\leq i\leq k$
, $1\leq i\leq k$![]() . In general, if $F(x)$
. In general, if $F(x)$![]() belonging to ${\mathbf {Z}}_p[x]$
belonging to ${\mathbf {Z}}_p[x]$![]() is a monic polynomial and $\overline {f}(x) = \overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$
is a monic polynomial and $\overline {f}(x) = \overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$![]() is its factorization modulo $p$
is its factorization modulo $p$![]() into irreducible polynomials with each $\phi _i(x)$
into irreducible polynomials with each $\phi _i(x)$![]() belonging to ${\mathbf {Z}}_p[x]$
belonging to ${\mathbf {Z}}_p[x]$![]() monic and $e_i > 0$
monic and $e_i > 0$![]() , then by Hensel's Lemma there exist monic polynomials $f_1(x),\, \cdots,\, f_r(x)$
, then by Hensel's Lemma there exist monic polynomials $f_1(x),\, \cdots,\, f_r(x)$![]() belonging to ${\mathbf {Z}}_{p}[x]$
belonging to ${\mathbf {Z}}_{p}[x]$![]() such that $f(x) = f_1(x)\cdots f_r(x)$
such that $f(x) = f_1(x)\cdots f_r(x)$![]() and $\overline {f}_i(x) = \overline {\phi }_i(x)^{e_i}$
and $\overline {f}_i(x) = \overline {\phi }_i(x)^{e_i}$![]() for each $i$
for each $i$![]() . The polynomial $f(x)$
. The polynomial $f(x)$![]() is said to be $p$
is said to be $p$![]() -regular (with respect to $\phi _1,\, \cdots,\, \phi _r$
-regular (with respect to $\phi _1,\, \cdots,\, \phi _r$![]() ) if each $f_i(x)$
) if each $f_i(x)$![]() is ${p}$
is ${p}$![]() -regular with respect to $\phi _i$
-regular with respect to $\phi _i$![]() .
.
To determine the number of distinct prime ideals of $A_K$![]() lying above a rational prime $p$
lying above a rational prime $p$![]() , we will use the Newton polygon of second order and the following theorem which is a weaker version of Theorem 1.2 of [Reference Khanduja and Kumar12].
, we will use the Newton polygon of second order and the following theorem which is a weaker version of Theorem 1.2 of [Reference Khanduja and Kumar12].
Theorem 2.6 Let $L={\mathbf {Q}}(\xi )$![]() be an algebraic number field with $\xi$
be an algebraic number field with $\xi$![]() satisfying an irreducible polynomial $g(x)\in {\mathbf {Z}}[x]$
satisfying an irreducible polynomial $g(x)\in {\mathbf {Z}}[x]$![]() and $p$
and $p$![]() be a rational prime. Let $\overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$
be a rational prime. Let $\overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$![]() be the factorization of $g(x)$
be the factorization of $g(x)$![]() modulo $p$
modulo $p$![]() into powers of distinct irreducible polynomials over $\mathbb {F}_p$
into powers of distinct irreducible polynomials over $\mathbb {F}_p$![]() with each $\phi _i(x)\neq g(x)$
with each $\phi _i(x)\neq g(x)$![]() belonging to ${\mathbf {Z}}[x]$
belonging to ${\mathbf {Z}}[x]$![]() monic. Suppose that the $\phi _i$
monic. Suppose that the $\phi _i$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() has $k_i$
has $k_i$![]() edges, say $S_{ij}$
edges, say $S_{ij}$![]() having slopes $\lambda _{ij}=\frac {l_{ij}}{e_{ij}}$
having slopes $\lambda _{ij}=\frac {l_{ij}}{e_{ij}}$![]() with $\gcd (l_{ij},\,~e_{ij})=1$
with $\gcd (l_{ij},\,~e_{ij})=1$![]() for $1\leq j\leq k_i$
for $1\leq j\leq k_i$![]() . If $T_{ij}(Y) = \prod \limits _{s=1}^{s_{ij}}U_{ijs}(Y)$
. If $T_{ij}(Y) = \prod \limits _{s=1}^{s_{ij}}U_{ijs}(Y)$![]() is the factorization of the residual polynomial $T_{ij}(Y)$
is the factorization of the residual polynomial $T_{ij}(Y)$![]() into distinct irreducible factors over $\mathbb {F}_p$
into distinct irreducible factors over $\mathbb {F}_p$![]() with respect to $(\phi _i,\,~S_{ij})$
with respect to $(\phi _i,\,~S_{ij})$![]() for $1\leq j\leq k_i,$
for $1\leq j\leq k_i,$![]() then
then

where $\mathfrak p_{ijs}$![]() are distinct prime ideals of $A_L$
are distinct prime ideals of $A_L$![]() having residual degree $\deg \phi _i(x)\times \deg U_{ijs}(Y).$
having residual degree $\deg \phi _i(x)\times \deg U_{ijs}(Y).$![]()
Let $L={\mathbf {Q}}(\gamma )$![]() where $\gamma$
where $\gamma$![]() is a root of a monic polynomial $g(x)=a_nx^n+\cdots +a_0\in {\mathbf {Z}}[x],\,~a_0\neq 0$
is a root of a monic polynomial $g(x)=a_nx^n+\cdots +a_0\in {\mathbf {Z}}[x],\,~a_0\neq 0$![]() . Let $p$
. Let $p$![]() be a prime number such that $g(x)\equiv x^n(p)$
be a prime number such that $g(x)\equiv x^n(p)$![]() . Suppose that the $p$
. Suppose that the $p$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() consists of a single edge with positive slope $\lambda =\frac {l}{e},$
consists of a single edge with positive slope $\lambda =\frac {l}{e},$![]() where $\gcd (l,\,~e)=1$
where $\gcd (l,\,~e)=1$![]() . Let the residual polynomial $T_g(Y)\in \mathbb {F}_p[Y]$
. Let the residual polynomial $T_g(Y)\in \mathbb {F}_p[Y]$![]() of $g(x)$
of $g(x)$![]() is a power of monic irreducible polynomial $\psi (Y)$
is a power of monic irreducible polynomial $\psi (Y)$![]() over $\mathbb {F}_p$
over $\mathbb {F}_p$![]() , i.e., $T_g(Y)=\psi (Y)^s$
, i.e., $T_g(Y)=\psi (Y)^s$![]() in $\mathbb {F}_p[Y]$
in $\mathbb {F}_p[Y]$![]() , where $s\geq 2$
, where $s\geq 2$![]() . In this case, we construct a key polynomial $\varPhi (x)$
. In this case, we construct a key polynomial $\varPhi (x)$![]() attached with the slope $\lambda$
attached with the slope $\lambda$![]() such that the following hold:
such that the following hold:
(i) $\varPhi (x)$
 is congruent to a power of $x$
is congruent to a power of $x$ modulo $p$
modulo $p$ .
.(ii) The $p$
 -Newton polygon of $\varPhi (x)$
-Newton polygon of $\varPhi (x)$ of first order is one-sided with slope $\lambda$
of first order is one-sided with slope $\lambda$ .
.(iii) The residual polynomial of $\varPhi (x)$
 with respect to $p$
with respect to $p$ is $\psi (Y)$
is $\psi (Y)$ in $\mathbb {F}_p[Y]$
in $\mathbb {F}_p[Y]$ .
.(iv) $\deg \varPhi (x)= e\deg \psi (Y)$
 .
.
As described in [Reference Guárdia, Montes and Nart8, Section 2.2], the data $(x;~\lambda,\,~\psi (Y))$![]() determine a $p$
determine a $p$![]() -adic valuation $V$
-adic valuation $V$![]() of the field ${\mathbf {Q}}_p(x)$
of the field ${\mathbf {Q}}_p(x)$![]() which satisfies the following properties:
which satisfies the following properties:
(i) $V(x)=l$
 where $\lambda =\frac {l}{e}~$
where $\lambda =\frac {l}{e}~$ with $\gcd (l,\,~e)=1$
with $\gcd (l,\,~e)=1$ .
.(ii) If $p(x)=\displaystyle \sum \nolimits _{0\leq i}^{}b_ix^i\in {\mathbf {Z}}_p[x]$
 is any polynomial, then
(2.1)\begin{equation} V(p(x))=e\displaystyle\min_{ i\geq 0}^{}\{v_p(b_i)+i \lambda\}. \end{equation}
is any polynomial, then
(2.1)\begin{equation} V(p(x))=e\displaystyle\min_{ i\geq 0}^{}\{v_p(b_i)+i \lambda\}. \end{equation}
We define the above valuation $V$![]() to the valuation of the second order.
to the valuation of the second order.
If $g(x)=\displaystyle \sum \nolimits _{i=0}^{u} a_i(x)\varPhi (x)^i\in {\mathbf {Z}}_p[x]$![]() is a $\varPhi$
is a $\varPhi$![]() -adic expansion of $g(x)$
-adic expansion of $g(x)$![]() , then the Newton polygon of $g(x)$
, then the Newton polygon of $g(x)$![]() with respect to $V$
with respect to $V$![]() (also called $V$
(also called $V$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() of second order) is the lower convex hull of the set of the points $(i,\, V(a_{u-i}(x)\varPhi (x)^{i}))$
of second order) is the lower convex hull of the set of the points $(i,\, V(a_{u-i}(x)\varPhi (x)^{i}))$![]() of the Euclidean plane.
of the Euclidean plane.
Let the $V$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() of second order has $k$
of second order has $k$![]() -sides $E_1,\,\cdots,\, E_k$
-sides $E_1,\,\cdots,\, E_k$![]() with positive slopes $\lambda _1,\,\cdots,\,\lambda _k$
with positive slopes $\lambda _1,\,\cdots,\,\lambda _k$![]() . Let $\lambda _t=\frac {l_t}{e_t}$
. Let $\lambda _t=\frac {l_t}{e_t}$![]() with $\gcd (l_t,\,~e_t)=1$
with $\gcd (l_t,\,~e_t)=1$![]() and $[a_t,\, b_t]$
and $[a_t,\, b_t]$![]() denote the projection to the horizontal axis of the side of slope $\lambda _t$
denote the projection to the horizontal axis of the side of slope $\lambda _t$![]() for $1\leq t \leq k.$
for $1\leq t \leq k.$![]() Then, there is a natural residual polynomial $\psi _t(Y)$
Then, there is a natural residual polynomial $\psi _t(Y)$![]() of second order attached to each side $E_t,$
of second order attached to each side $E_t,$![]() whose degree coincides with the degree of the side (i.e., $\frac {b_t-a_t}{e_t}$
whose degree coincides with the degree of the side (i.e., $\frac {b_t-a_t}{e_t}$![]() ) [Reference Guárdia, Montes and Nart8, Section 2.5]. Only those integral points of the $V$
) [Reference Guárdia, Montes and Nart8, Section 2.5]. Only those integral points of the $V$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() which lie on the side, determine a non-zero coefficient of this second-order residual polynomial. We define $g(x)$
which lie on the side, determine a non-zero coefficient of this second-order residual polynomial. We define $g(x)$![]() to be $\psi _t$
to be $\psi _t$![]() -regular when the second order residual polynomial $\psi _t(Y)$
-regular when the second order residual polynomial $\psi _t(Y)$![]() attached to the side $E_t$
attached to the side $E_t$![]() of the $V$
of the $V$![]() -Newton polygon of $g(x)$
-Newton polygon of $g(x)$![]() of second order is separable in $\frac {\mathbb {F}_p[Y ]}{\langle \psi (Y)\rangle }$
of second order is separable in $\frac {\mathbb {F}_p[Y ]}{\langle \psi (Y)\rangle }$![]() . We define $g(x)$
. We define $g(x)$![]() to be $V$
to be $V$![]() -regular if $g(x)$
-regular if $g(x)$![]() is $\psi _t$
is $\psi _t$![]() -regular for each $t$
-regular for each $t$![]() , $1\leq t\leq k$
, $1\leq t\leq k$![]() . Further, if each residual polynomial $\psi _t(Y)$
. Further, if each residual polynomial $\psi _t(Y)$![]() , $t\in \{1,\,~2,\,\cdots,\,k\}$
, $t\in \{1,\,~2,\,\cdots,\,k\}$![]() , is irreducible in $\frac {\mathbb {F}_p[Y ]}{\langle \psi (Y)\rangle }$
, is irreducible in $\frac {\mathbb {F}_p[Y ]}{\langle \psi (Y)\rangle }$![]() , then each $\psi _t(Y)$
, then each $\psi _t(Y)$![]() provides a prime ideal having residual degree $\deg \psi \cdot \deg \psi _t$
provides a prime ideal having residual degree $\deg \psi \cdot \deg \psi _t$![]() and ramification index $e\cdot e_t$
and ramification index $e\cdot e_t$![]() .
.
3. Proof of Theorems 1.1 and 1.2
Proof of Theorem 1.1. Since the degree of the extension $K/{\mathbf {Q}}$![]() is $5$
is $5$![]() , to prove this theorem it is sufficient to show that $3\nmid i(K)$
, to prove this theorem it is sufficient to show that $3\nmid i(K)$![]() and $5\nmid i(K)$
and $5\nmid i(K)$![]() . If $3\mid i(K)$
. If $3\mid i(K)$![]() , then by (1.3), $a^5\equiv b^4(3)$
, then by (1.3), $a^5\equiv b^4(3)$![]() . Therefore, $(a,\,~b)\in \{(0,\,~0),\, (1,\,~-1),\,~(1,\,~1)\}(3)$
. Therefore, $(a,\,~b)\in \{(0,\,~0),\, (1,\,~-1),\,~(1,\,~1)\}(3)$![]() . Note that if $3$
. Note that if $3$![]() divides both $a,\,b$
divides both $a,\,b$![]() and $5v_3(a)<4v_3(b)$
and $5v_3(a)<4v_3(b)$![]() , then $v_3(a)\in \{1,\,2,\,3\}$
, then $v_3(a)\in \{1,\,2,\,3\}$![]() by (1.2).
by (1.2).
Case B1: $a\equiv 0(3),\,b\equiv 0(3)$![]() , $5v_3(a)<4v_3(b)$
, $5v_3(a)<4v_3(b)$![]() , $v_3(a)\in \{1,\,3\}$
, $v_3(a)\in \{1,\,3\}$![]() . Here $f(x)\equiv x ^5(3)$
. Here $f(x)\equiv x ^5(3)$![]() and the $x$
and the $x$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges. The first edge, say $S_1$
has two edges. The first edge, say $S_1$![]() , is the line segment joining the points $(0,\,0)$
, is the line segment joining the points $(0,\,0)$![]() and $(4,\,v_3(a))$
and $(4,\,v_3(a))$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , is the line segment that joins $(4,\,v_3(a))$
, is the line segment that joins $(4,\,v_3(a))$![]() to $(5,\,v_3(b))$
to $(5,\,v_3(b))$![]() . For each $i=1,\,2$
. For each $i=1,\,2$![]() , the residual polynomial of $f(x)$
, the residual polynomial of $f(x)$![]() with respect to $(x,\,S_i)$
with respect to $(x,\,S_i)$![]() is linear. So Theorem 2.6 is applicable. Using this theorem, $3A_K=\mathfrak { p_1^4}\mathfrak { p_2}$
is linear. So Theorem 2.6 is applicable. Using this theorem, $3A_K=\mathfrak { p_1^4}\mathfrak { p_2}$![]() , where the residual degree of each prime ideal $\mathfrak {p_i}$
, where the residual degree of each prime ideal $\mathfrak {p_i}$![]() for $i=1,\,2,$
for $i=1,\,2,$![]() is $1$
is $1$![]() . Hence, in view of Lemma 2.1, $3\nmid i(K)$
. Hence, in view of Lemma 2.1, $3\nmid i(K)$![]() .
.
Case B2: $a\equiv 0(3),\,b\equiv 0(3)$![]() , $5v_3(a)<4v_3(b)$
, $5v_3(a)<4v_3(b)$![]() , $v_3(a)=2$
, $v_3(a)=2$![]() , $a_3\equiv 1(3)$
, $a_3\equiv 1(3)$![]() . In this case, $f(x)\equiv x ^5(3)$
. In this case, $f(x)\equiv x ^5(3)$![]() . The $x$
. The $x$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges. The first edge, say $S_1$
has two edges. The first edge, say $S_1$![]() , is the line segment joining the points $(0,\,0)$
, is the line segment joining the points $(0,\,0)$![]() and $(4,\,2)$
and $(4,\,2)$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , is the line segment that join $(4,\,2)$
, is the line segment that join $(4,\,2)$![]() to $(5,\,v_3(b))$
to $(5,\,v_3(b))$![]() . The residual polynomial of $f(x)$
. The residual polynomial of $f(x)$![]() with respect to $(x,\,S_1)$
with respect to $(x,\,S_1)$![]() is $Y^2+\bar {1}\in \mathbb {F}_3[Y]$
is $Y^2+\bar {1}\in \mathbb {F}_3[Y]$![]() and with respect to $(x,\,S_2)$
and with respect to $(x,\,S_2)$![]() is linear. So by Theorem 2.6, $3A_K=\mathfrak { p_1^2}\mathfrak { p_2}$
is linear. So by Theorem 2.6, $3A_K=\mathfrak { p_1^2}\mathfrak { p_2}$![]() , where the residual degree of the prime ideals $\mathfrak {p_1}$
, where the residual degree of the prime ideals $\mathfrak {p_1}$![]() and $\mathfrak { p_2}$
and $\mathfrak { p_2}$![]() is $2$
is $2$![]() and $1$
and $1$![]() , respectively. Therefore, $3\nmid i(K)$
, respectively. Therefore, $3\nmid i(K)$![]() .
.
Case B3: $a\equiv 0(3),\, b\equiv 0(3)$![]() , $5v_3(a)<4v_3(b)$
, $5v_3(a)<4v_3(b)$![]() , $v_3(a)=2$
, $v_3(a)=2$![]() , $a_3\equiv -1(3)$
, $a_3\equiv -1(3)$![]() . Here $f(x)\equiv x ^5(3)$
. Here $f(x)\equiv x ^5(3)$![]() . The $x$
. The $x$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges. The first edge, say $S_1$
has two edges. The first edge, say $S_1$![]() , is the line segment joining the points $(0,\,0)$
, is the line segment joining the points $(0,\,0)$![]() and $(4,\,2)$
and $(4,\,2)$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , is the line segment joining the points $(4,\,2)$
, is the line segment joining the points $(4,\,2)$![]() and $(5,\,v_3(b))$
and $(5,\,v_3(b))$![]() . The residual polynomial of $f(x)$
. The residual polynomial of $f(x)$![]() with respect to $(x,\,S_1)$
with respect to $(x,\,S_1)$![]() is $(Y-\bar {1})(Y+\bar {1})$
is $(Y-\bar {1})(Y+\bar {1})$![]() and with respect to $(x,\,S_2)$
and with respect to $(x,\,S_2)$![]() is linear. Therefore, we have $3A_K=\mathfrak { p_1^2}\mathfrak { p_2^2}\mathfrak { p_3}$
is linear. Therefore, we have $3A_K=\mathfrak { p_1^2}\mathfrak { p_2^2}\mathfrak { p_3}$![]() , where the residual degree of each prime ideal $\mathfrak { p_i}$
, where the residual degree of each prime ideal $\mathfrak { p_i}$![]() for $i=1,\,2,\,3$
for $i=1,\,2,\,3$![]() , is $1$
, is $1$![]() . Hence, $3\nmid i(K)$
. Hence, $3\nmid i(K)$![]() .
.
Keeping in mind (1.2), we see that the case $5v_3(a)=4v_3(b)$![]() is not possible.
is not possible.
Case B4: $a\equiv 0(3),\, b\equiv 0(3)$![]() , $5v_3(a)>4v_3(b)$
, $5v_3(a)>4v_3(b)$![]() . Here $v_3(b)\in \{1,\,2,\,3,\,4\}$
. Here $v_3(b)\in \{1,\,2,\,3,\,4\}$![]() . The $x$
. The $x$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has a single edge, say $S$
has a single edge, say $S$![]() , which join the points $(0,\,0)$
, which join the points $(0,\,0)$![]() and $(5,\,v_3(b))$
and $(5,\,v_3(b))$![]() . The residual polynomial of $f(x)$
. The residual polynomial of $f(x)$![]() with respect to $(x,\,S)$
with respect to $(x,\,S)$![]() is linear. So $3A_K=\mathfrak { p^5}$
is linear. So $3A_K=\mathfrak { p^5}$![]() , where the residual degree of $\mathfrak { p}$
, where the residual degree of $\mathfrak { p}$![]() is $1$
is $1$![]() . Thus, $3\nmid i(K)$
. Thus, $3\nmid i(K)$![]() .
.
Case B5: $a\equiv 1(3),\,~b\equiv \tau (3)$![]() , where $\tau \in \{-1,\,1\}$
, where $\tau \in \{-1,\,1\}$![]() . Note that $f(x)\equiv (x^3- x^2\tau +\tau ) (x- \tau )^2(3)$
. Note that $f(x)\equiv (x^3- x^2\tau +\tau ) (x- \tau )^2(3)$![]() . In this case, there is only one prime ideal, say $\mathfrak { p_1}$
. In this case, there is only one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $3$
, of residual degree $3$![]() . Hence, in view of the Fundamental Equality, there can be either atmost two prime ideals of residual degree $1$
. Hence, in view of the Fundamental Equality, there can be either atmost two prime ideals of residual degree $1$![]() each or one prime ideal of residual degree $2$
each or one prime ideal of residual degree $2$![]() . Hence, $3\nmid i(K)$
. Hence, $3\nmid i(K)$![]() .
.
It remains to show that $5\nmid i(K)$![]() . Suppose there exist distinct non-zero prime ideals $\mathfrak {p}_1$
. Suppose there exist distinct non-zero prime ideals $\mathfrak {p}_1$![]() , $\cdots$
, $\cdots$![]() , $\mathfrak {p}_r$
, $\mathfrak {p}_r$![]() of $A_K$
of $A_K$![]() such that $5A_K=\mathfrak {p}_1^{e_1}\cdots \mathfrak {p}_r^{e_r}$
such that $5A_K=\mathfrak {p}_1^{e_1}\cdots \mathfrak {p}_r^{e_r}$![]() , where $e_i \geq 1$
, where $e_i \geq 1$![]() , then by the Fundamental Equality, $e_1f_1+\cdots +e_rf_r=5$
, then by the Fundamental Equality, $e_1f_1+\cdots +e_rf_r=5$![]() where $f_i$
where $f_i$![]() is the residual degree of $\mathfrak p_i$
is the residual degree of $\mathfrak p_i$![]() for $i=1,\,2,\,\cdots,\,r$
for $i=1,\,2,\,\cdots,\,r$![]() . Since $e_i\ge 1$
. Since $e_i\ge 1$![]() for all $i=1,\,2,\,\cdots,\,r$
for all $i=1,\,2,\,\cdots,\,r$![]() , therefore, there can be at most $5$
, therefore, there can be at most $5$![]() prime ideals lying above $5$
prime ideals lying above $5$![]() , but for every positive integer $h$
, but for every positive integer $h$![]() the number of monic irreducible polynomials of degree $h$
the number of monic irreducible polynomials of degree $h$![]() in $\mathbb {F}_5[x]$
in $\mathbb {F}_5[x]$![]() is greater than or equal to $5$
is greater than or equal to $5$![]() . So by Lemma 2.1, $5\nmid i(K)$
. So by Lemma 2.1, $5\nmid i(K)$![]() . This completes the proof.
. This completes the proof.
Proof of Theorem 1.2. Case A1: $a\equiv 0(2)$![]() , $b\equiv 1(2)$
, $b\equiv 1(2)$![]() . In this case, $f(x)\equiv (x+1) (x^4+x^3+x^2+x+1)$
. In this case, $f(x)\equiv (x+1) (x^4+x^3+x^2+x+1)$![]() (2). Using hypothesis and Equations (1.1) and (1.3), we see that $2\nmid \mathop {\mathrm {ind}}(\theta )$
(2). Using hypothesis and Equations (1.1) and (1.3), we see that $2\nmid \mathop {\mathrm {ind}}(\theta )$![]() . So, by Dedekind's Theorem on splitting of primes [Reference Khanduja11, Theorem 4.3], we have $2A_K=\mathfrak { p_1}\mathfrak { p_2}$
. So, by Dedekind's Theorem on splitting of primes [Reference Khanduja11, Theorem 4.3], we have $2A_K=\mathfrak { p_1}\mathfrak { p_2}$![]() , where residual degree of $\mathfrak { p_1}$
, where residual degree of $\mathfrak { p_1}$![]() is $1$
is $1$![]() and residual degree of $\mathfrak { p_2}$
and residual degree of $\mathfrak { p_2}$![]() is $4$
is $4$![]() . Hence, in view of Lemma 2.1, $2\nmid i(K)$
. Hence, in view of Lemma 2.1, $2\nmid i(K)$![]() .
.
Case A2: $a\equiv 1(2)$![]() , $b\equiv 1(2)$
, $b\equiv 1(2)$![]() . Here $f(x)\equiv (x^2+x+1)(x^3+x^2+1)$
. Here $f(x)\equiv (x^2+x+1)(x^3+x^2+1)$![]() (2). Arguing as in Case A1, one can easily check that $2A_K=\mathfrak { p_1}\mathfrak { p_2}$
(2). Arguing as in Case A1, one can easily check that $2A_K=\mathfrak { p_1}\mathfrak { p_2}$![]() , where the residual degree of $\mathfrak { p_1}$
, where the residual degree of $\mathfrak { p_1}$![]() is $2$
is $2$![]() and residual degree of $\mathfrak { p_2}$
and residual degree of $\mathfrak { p_2}$![]() is $3$
is $3$![]() . Thus, by Lemma 2.1, $2\nmid i(K)$
. Thus, by Lemma 2.1, $2\nmid i(K)$![]() .
.
Case A3: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)\geq 4v_2(b)$
, $5v_2(a)\geq 4v_2(b)$![]() . By (1.2), we have $v_2(b)\leq 4$
. By (1.2), we have $v_2(b)\leq 4$![]() . The $x$
. The $x$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has a single edge, say $S$
has a single edge, say $S$![]() , having slope $\frac {v_2(b)}{5}$
, having slope $\frac {v_2(b)}{5}$![]() . The residual polynomial of $f(x)$
. The residual polynomial of $f(x)$![]() with respect to $(x,\,S)$
with respect to $(x,\,S)$![]() is linear. So $2A_K=\mathfrak {p}^5$
is linear. So $2A_K=\mathfrak {p}^5$![]() , where the residual degree of $\mathfrak { p}$
, where the residual degree of $\mathfrak { p}$![]() is $1$
is $1$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Note that when $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() and $5v_2(a)<4v_2(b)$
and $5v_2(a)<4v_2(b)$![]() , then $v_2(a)\in \{1,\,2,\,3\}$
, then $v_2(a)\in \{1,\,2,\,3\}$![]() and $v_2(b)\ge 2$
and $v_2(b)\ge 2$![]() by (1.2).
by (1.2).
Case A4: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)\in \{1,\,3\}$
, $v_2(a)\in \{1,\,3\}$![]() . In this case, $f(x)\equiv x^5(2)$
. In this case, $f(x)\equiv x^5(2)$![]() . Set $\phi (x)=x$
. Set $\phi (x)=x$![]() . The $\phi$
. The $\phi$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges. The first edge, say $S_1$
has two edges. The first edge, say $S_1$![]() , is the line segment joining the point $(0,\,0)$
, is the line segment joining the point $(0,\,0)$![]() and $(4,\,v_2(a))$
and $(4,\,v_2(a))$![]() with slope $\frac {v_2(a)}{4}$
with slope $\frac {v_2(a)}{4}$![]() and the second edge, say $S_2$
and the second edge, say $S_2$![]() , join the point $(4,\,v_2(a))$
, join the point $(4,\,v_2(a))$![]() to $(5,\, v_2(b))$
to $(5,\, v_2(b))$![]() . So for each $i=1,\,2$
. So for each $i=1,\,2$![]() , the residual polynomial of $f(x)$
, the residual polynomial of $f(x)$![]() with respect to $(\phi,\,S_i)$
with respect to $(\phi,\,S_i)$![]() is linear. Therefore, $f(x)$
is linear. Therefore, $f(x)$![]() is $2$
is $2$![]() -regular. Thus, Theorem 2.6 is applicable. Using this theorem, we have $2A_K=\mathfrak { p_1^4}\mathfrak { p_2}$
-regular. Thus, Theorem 2.6 is applicable. Using this theorem, we have $2A_K=\mathfrak { p_1^4}\mathfrak { p_2}$![]() , where the residual degree of prime ideals $\mathfrak { p_1}$
, where the residual degree of prime ideals $\mathfrak { p_1}$![]() and $\mathfrak { p_2}$
and $\mathfrak { p_2}$![]() is $1$
is $1$![]() . Since there are only two monic irreducible polynomials of degree $1$
. Since there are only two monic irreducible polynomials of degree $1$![]() over $\mathbb {F}_2$
over $\mathbb {F}_2$![]() , by Lemma 2.1 we see that $2\nmid i(K)$
, by Lemma 2.1 we see that $2\nmid i(K)$![]() .
.
One can easily check that when $v_2(a)=2$![]() , then $5v_2(a)<4v_2(b)$
, then $5v_2(a)<4v_2(b)$![]() implies $v_2(b)\ge 3$
implies $v_2(b)\ge 3$![]() .
.
Case A5: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\in \{3,\,4\}$
, $v_2(b)\in \{3,\,4\}$![]() , $a_2\equiv 3(4)$
, $a_2\equiv 3(4)$![]() . In this case, $f(x)\equiv x^5(2)$
. In this case, $f(x)\equiv x^5(2)$![]() . Set $\phi (x)=x$
. Set $\phi (x)=x$![]() . The $\phi$
. The $\phi$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges. The first edge, say $S_1$
has two edges. The first edge, say $S_1$![]() , is the line segment joining the points $(0,\,0)$
, is the line segment joining the points $(0,\,0)$![]() and $(4,\,2)$
and $(4,\,2)$![]() with slope $\lambda _1=\frac {1}{2}$
with slope $\lambda _1=\frac {1}{2}$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , join the point $(4,\,2)$
, join the point $(4,\,2)$![]() to $(5,\,v_2(b))$
to $(5,\,v_2(b))$![]() and has slope $\lambda _2=v_2(b)-2$
and has slope $\lambda _2=v_2(b)-2$![]() . The residual polynomial of $f(x)$
. The residual polynomial of $f(x)$![]() with respect to $(\phi,\,S_1)$
with respect to $(\phi,\,S_1)$![]() is $(Y+\bar {1})^2$
is $(Y+\bar {1})^2$![]() and with respect to $(\phi,\,S_2)$
and with respect to $(\phi,\,S_2)$![]() is $Y+\bar {1}$
is $Y+\bar {1}$![]() . The edge $S_2$
. The edge $S_2$![]() provides one prime ideal of $A_K$
provides one prime ideal of $A_K$![]() , say $\mathfrak { p_1}$
, say $\mathfrak { p_1}$![]() , with residual degree $1$
, with residual degree $1$![]() . Set $\psi (Y)=Y+\bar {1}$
. Set $\psi (Y)=Y+\bar {1}$![]() .
.
Consider the numerical invariants $l=1,\,~e=2$![]() and $f=\deg \psi =1$
and $f=\deg \psi =1$![]() , where $\lambda _1 = \frac {l}{e}$
, where $\lambda _1 = \frac {l}{e}$![]() with $\gcd (l,\,e) = 1$
with $\gcd (l,\,e) = 1$![]() . In this case, $2A_K=\mathfrak p_1\mathfrak a$
. In this case, $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak a$
, where $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . All prime ideals dividing $\mathfrak a$
. All prime ideals dividing $\mathfrak a$![]() has ramification index a multiple of $e=2$
has ramification index a multiple of $e=2$![]() and residual degree a multiple of $f=1$
and residual degree a multiple of $f=1$![]() . Since $e>1$
. Since $e>1$![]() , so we analyse second-order Newton polygons. Keeping in mind Lemma 2.1, $2$
, so we analyse second-order Newton polygons. Keeping in mind Lemma 2.1, $2$![]() divides $i(K)$
divides $i(K)$![]() if and only if the key polynomial, say $\varPhi$
if and only if the key polynomial, say $\varPhi$![]() , attached with the slope $\lambda _1$
, attached with the slope $\lambda _1$![]() provides two prime ideals of residual degree $1$
provides two prime ideals of residual degree $1$![]() each. Recall that the second-order valuation on ${\mathbf {Q}}_2(x)$
each. Recall that the second-order valuation on ${\mathbf {Q}}_2(x)$![]() is defined as $V(\displaystyle \sum \nolimits _{i\geq 0}^{}a_ix^i)=e\cdot \min \{v_2(a_i)+i\lambda _1\}$
is defined as $V(\displaystyle \sum \nolimits _{i\geq 0}^{}a_ix^i)=e\cdot \min \{v_2(a_i)+i\lambda _1\}$![]() . In particular, $V(x)=l=1$
. In particular, $V(x)=l=1$![]() , $V(2)=e=2$
, $V(2)=e=2$![]() . Since $v_2(a)=2$
. Since $v_2(a)=2$![]() and $v_2(b)\in \{3,\,4\}$
and $v_2(b)\in \{3,\,4\}$![]() , so we can write
, so we can write
where $m\in \{0,\,1\}$![]() . Take $\varPhi (x)=x^2-2$
. Take $\varPhi (x)=x^2-2$![]() . One can easily check that $\varPhi (x)$
. One can easily check that $\varPhi (x)$![]() is a key polynomial attached with the slope $\lambda _1$
is a key polynomial attached with the slope $\lambda _1$![]() . Note that $V(\varPhi (x))=2$
. Note that $V(\varPhi (x))=2$![]() . The $\varPhi$
. The $\varPhi$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is
is
The $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order is the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,7),\,(2,\, \min \{2v_2(a_2+1)+5,\,2m+6\})\}$
of second order is the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,7),\,(2,\, \min \{2v_2(a_2+1)+5,\,2m+6\})\}$![]() . The $V$
. The $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order has a single edge of a positive slope $\frac {2m+1}{2}(=\frac {l_1}{e_1})$
of second order has a single edge of a positive slope $\frac {2m+1}{2}(=\frac {l_1}{e_1})$![]() joining the points $(0,\,5)$
joining the points $(0,\,5)$![]() and $(2,\,2m+6)$
and $(2,\,2m+6)$![]() . The residual polynomial, say $\psi _1(Y)$
. The residual polynomial, say $\psi _1(Y)$![]() , attached to this edge is linear. At this stage the numerical invariants are $l_1=2m+1$
, attached to this edge is linear. At this stage the numerical invariants are $l_1=2m+1$![]() , $e_1=2$
, $e_1=2$![]() and $f_1=\deg \psi _1=1$
and $f_1=\deg \psi _1=1$![]() . Hence, $2A_K=\mathfrak {p}_1\mathfrak {p_2^4}$
. Hence, $2A_K=\mathfrak {p}_1\mathfrak {p_2^4}$![]() , where the residual degree of the prime ideal $\mathfrak p_2$
, where the residual degree of the prime ideal $\mathfrak p_2$![]() is $ff_1=1$
is $ff_1=1$![]() . So $2\nmid i(K)$
. So $2\nmid i(K)$![]() .
.
Case A6: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\ge 5$
, $v_2(b)\ge 5$![]() , $a_2\equiv 3(8)$
, $a_2\equiv 3(8)$![]() . With the notation as in Case A5, it can be seen that $2A_K=\mathfrak p_1\mathfrak a$
. With the notation as in Case A5, it can be seen that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Let key polynomial $\varPhi (x)$
. Let key polynomial $\varPhi (x)$![]() and valuation $V$
and valuation $V$![]() be the same as in the Case A5. The $\varPhi$
be the same as in the Case A5. The $\varPhi$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is
is
The $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order being the lower convex hull of the points $(0,\,5)$
of second order being the lower convex hull of the points $(0,\,5)$![]() , $(1,\,7)$
, $(1,\,7)$![]() , $(2,\,9)$
, $(2,\,9)$![]() has a single edge joining $(0,\,~5)$
has a single edge joining $(0,\,~5)$![]() and $(2,\,~9)$
and $(2,\,~9)$![]() with a lattice point $(1,\,~7)$
with a lattice point $(1,\,~7)$![]() lying on it. The residual polynomial corresponding to this edge is $Y^2+Y+\bar 1\in \mathbb {F}_2[Y]$
lying on it. The residual polynomial corresponding to this edge is $Y^2+Y+\bar 1\in \mathbb {F}_2[Y]$![]() . So $2A_K=\mathfrak {p}_1\mathfrak {p_2^2}$
. So $2A_K=\mathfrak {p}_1\mathfrak {p_2^2}$![]() , where the residual degree of $\mathfrak p_2$
, where the residual degree of $\mathfrak p_2$![]() is $2$
is $2$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Case A7: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\ge 5$
, $v_2(b)\ge 5$![]() , $a_2\equiv 7(8)$
, $a_2\equiv 7(8)$![]() . Proceeding as in Case A5, one can check that $2A_K=\mathfrak p_1\mathfrak a$
. Proceeding as in Case A5, one can check that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Take $\varPhi (x)$
. Take $\varPhi (x)$![]() and $V$
and $V$![]() same as in Case A5. Keeping in mind (3.3), we observe that the $V$
same as in Case A5. Keeping in mind (3.3), we observe that the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order being the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,7),\,(2,\, \min \{2v_2(a_2+1)+5,\,2v_2(b)\})\}$
of second order being the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,7),\,(2,\, \min \{2v_2(a_2+1)+5,\,2v_2(b)\})\}$![]() has two edges of positive slope. The residual polynomial attached to each edge is linear. So $2A_K=\mathfrak { p_1}\mathfrak {p_2^2}\mathfrak {p_3^2}$
has two edges of positive slope. The residual polynomial attached to each edge is linear. So $2A_K=\mathfrak { p_1}\mathfrak {p_2^2}\mathfrak {p_3^2}$![]() , where the residual degree of $\mathfrak p_i$
, where the residual degree of $\mathfrak p_i$![]() is $1$
is $1$![]() , for each $i=2,\,3$
, for each $i=2,\,3$![]() . Hence, in this case, $2\mid i(K)$
. Hence, in this case, $2\mid i(K)$![]() .
.
Note that if $a_2\equiv 1(4)$![]() and $v_2(b)\ge 4$
and $v_2(b)\ge 4$![]() , then the $V$
, then the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() is the lower convex hull of the points $(0,\,5),\,(1,\,7)$
is the lower convex hull of the points $(0,\,5),\,(1,\,7)$![]() and $(2,\,7)$
and $(2,\,7)$![]() . In this case, the residual polynomial with respect to $x^2-2$
. In this case, the residual polynomial with respect to $x^2-2$![]() is not square-free, so we use another key polynomial $\varPhi (x)=x^2-2x-2$
is not square-free, so we use another key polynomial $\varPhi (x)=x^2-2x-2$![]() .
.
Case A8: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\in \{3,\,4\}$
, $v_2(b)\in \{3,\,4\}$![]() , $a_2\equiv 1(4)$
, $a_2\equiv 1(4)$![]() . Let $\phi (x)$
. Let $\phi (x)$![]() , $\lambda _1$
, $\lambda _1$![]() , $\psi (Y)$
, $\psi (Y)$![]() be same as in Case A5. Arguing as in Case A5, it is easy to verify that $2A_K=\mathfrak p_1\mathfrak a$
be same as in Case A5. Arguing as in Case A5, it is easy to verify that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal with residual degree $1$
is a prime ideal with residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Let $\varPhi (x)=x^2-2x-2$
. Let $\varPhi (x)=x^2-2x-2$![]() . Then $\varPhi (x)$
. Then $\varPhi (x)$![]() works as a key polynomial attached with slope $\lambda _1$
works as a key polynomial attached with slope $\lambda _1$![]() . The data $(x,\,\lambda _1,\, \psi (Y))$
. The data $(x,\,\lambda _1,\, \psi (Y))$![]() define a valuation $V$
define a valuation $V$![]() of second order given in (2.1), such that $V(x)=1$
of second order given in (2.1), such that $V(x)=1$![]() , $V(2)=2$
, $V(2)=2$![]() and $V(\varPhi (x))=2$
and $V(\varPhi (x))=2$![]() . The $\varPhi$
. The $\varPhi$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is given by
is given by
where $m\in \{0,\,1\}$![]() . The $V$
. The $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order being the lower convex hull of the points $(0,\,5)$
of second order being the lower convex hull of the points $(0,\,5)$![]() , $(1,\,8)$
, $(1,\,8)$![]() , $(2,\,2m+6)$
, $(2,\,2m+6)$![]() has a single edge of positive slope. The residual polynomial attached to this edge is linear. Hence, $2A_K=\mathfrak {p_1}\mathfrak {p_2^4}$
has a single edge of positive slope. The residual polynomial attached to this edge is linear. Hence, $2A_K=\mathfrak {p_1}\mathfrak {p_2^4}$![]() , where the residual degree of $\mathfrak {p_2}$
, where the residual degree of $\mathfrak {p_2}$![]() is $1$
is $1$![]() . So $2\nmid i(K)$
. So $2\nmid i(K)$![]() .
.
Case A9: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)=5$
, $v_2(b)=5$![]() , $a_2\equiv 5(16)$
, $a_2\equiv 5(16)$![]() . Proceeding as in Case A5, we see that, $2A_K=\mathfrak p_1\mathfrak a$
. Proceeding as in Case A5, we see that, $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Let $\varPhi (x)$
. Let $\varPhi (x)$![]() and $V$
and $V$![]() be same as in Case A8. The $\varPhi$
be same as in Case A8. The $\varPhi$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is given by
is given by
The $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order is the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,8),\,(2,\,\min \{5+2v_2(a_2+11),\,10+2v_2(1+b_2)\})\}$
of second order is the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,8),\,(2,\,\min \{5+2v_2(a_2+11),\,10+2v_2(1+b_2)\})\}$![]() . The $V$
. The $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order has two edges of positive slope and the residual polynomial attached to each edge is linear. Hence, $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}\mathfrak {p_3^2}$
of second order has two edges of positive slope and the residual polynomial attached to each edge is linear. Hence, $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}\mathfrak {p_3^2}$![]() , where the residual degree of $\mathfrak {p}_i$
, where the residual degree of $\mathfrak {p}_i$![]() is $1$
is $1$![]() , for each $i=2,\,3$
, for each $i=2,\,3$![]() . Thus, $2\mid i(K)$
. Thus, $2\mid i(K)$![]() .
.
Case A10: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)=5$
, $v_2(b)=5$![]() , $a_2\equiv 13(16)$
, $a_2\equiv 13(16)$![]() . Arguing as in Case A5, we see that $2A_K=\mathfrak p_1\mathfrak a$
. Arguing as in Case A5, we see that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Let $\varPhi (x)$
. Let $\varPhi (x)$![]() and $V$
and $V$![]() be same as in Case A8. Keeping in mind (3.5), one can easily check that the $V$
be same as in Case A8. Keeping in mind (3.5), one can easily check that the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order being the lower convex hull of the points $(0,\,5)$
of second order being the lower convex hull of the points $(0,\,5)$![]() , $(1,\,8)$
, $(1,\,8)$![]() , $(2,\,11)$
, $(2,\,11)$![]() has a single edge of the positive slope and the residual polynomial attached to this edge is $Y^2+Y+\bar 1\in \mathbb {F}_2[Y]$
has a single edge of the positive slope and the residual polynomial attached to this edge is $Y^2+Y+\bar 1\in \mathbb {F}_2[Y]$![]() . So $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}$
. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}$![]() , where the residual degree of $\mathfrak {p_2}$
, where the residual degree of $\mathfrak {p_2}$![]() is $2$
is $2$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Case A11: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\ge 6$
, $v_2(b)\ge 6$![]() , $a_2\equiv 5(8)$
, $a_2\equiv 5(8)$![]() . Proceeding as in Case A5, one can verify that $2A_K=\mathfrak p_1\mathfrak a$
. Proceeding as in Case A5, one can verify that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal with residual degree $1$
is a prime ideal with residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Take $\varPhi (x)$
. Take $\varPhi (x)$![]() and $V$
and $V$![]() same as in Case A8. Using the $\varPhi (x)$
same as in Case A8. Using the $\varPhi (x)$![]() expansion of $f(x)$
expansion of $f(x)$![]() given in (3.5), we see that the $V$
given in (3.5), we see that the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order being the lower convex hull of the points $(0,\,5)$
of second order being the lower convex hull of the points $(0,\,5)$![]() , $(1,\,8)$
, $(1,\,8)$![]() , $(2,\,10)$
, $(2,\,10)$![]() has a single edge of positive slope. The residual polynomial attached to this edge is linear. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^4}$
has a single edge of positive slope. The residual polynomial attached to this edge is linear. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^4}$![]() , where the residual degree of $\mathfrak { p_2}$
, where the residual degree of $\mathfrak { p_2}$![]() is $1$
is $1$![]() . Thus, $2\nmid i(K)$
. Thus, $2\nmid i(K)$![]() .
.
Keeping in mind (3.5), it is easy to observe that when $a_2\equiv 1(8)$![]() and $m\ge 2$
and $m\ge 2$![]() , then the $V$
, then the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order being the lower convex hull of the points $(0,\,5),\,(1,\,8),\,(2,\,9)$
of second order being the lower convex hull of the points $(0,\,5),\,(1,\,8),\,(2,\,9)$![]() has a single edge of positive slope. The residual polynomial attached with this edge is not square-free. So we shall use a different key polynomial.
has a single edge of positive slope. The residual polynomial attached with this edge is not square-free. So we shall use a different key polynomial.
Case A12: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)=5$
, $v_2(b)=5$![]() , $a_2\equiv 1(8)$
, $a_2\equiv 1(8)$![]() . Here $f(x)\equiv x^5(2)$
. Here $f(x)\equiv x^5(2)$![]() . Set $\phi (x)=x$
. Set $\phi (x)=x$![]() . Arguing as in Case A5, we have $2A_K=\mathfrak p_1\mathfrak a$
. Arguing as in Case A5, we have $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Let $\varPhi (x)=x^2-2x+2$
. Let $\varPhi (x)=x^2-2x+2$![]() . As in (2.1), we can define valuation $V$
. As in (2.1), we can define valuation $V$![]() of second order such that $V(x)=1$
of second order such that $V(x)=1$![]() , $V(2)=2$
, $V(2)=2$![]() and $V(\varPhi (x))=2$
and $V(\varPhi (x))=2$![]() . The $\varPhi$
. The $\varPhi$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is given by
is given by
Keeping in mind the above expansion of $f(x)$![]() , we see that the $V$
, we see that the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() of second order has a single edge of positive slope. The residual polynomial attached with this edge is linear. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^4}$
of second order has a single edge of positive slope. The residual polynomial attached with this edge is linear. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^4}$![]() , where the residual degree of $\mathfrak { p_2}$
, where the residual degree of $\mathfrak { p_2}$![]() is $1$
is $1$![]() . Thus, $2\nmid i(K)$
. Thus, $2\nmid i(K)$![]() .
.
Case A13: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\ge 6$
, $v_2(b)\ge 6$![]() , $a_2\equiv 1(16)$
, $a_2\equiv 1(16)$![]() . Proceeding as in Case A5, we observe that $2A_K=\mathfrak p_1\mathfrak a$
. Proceeding as in Case A5, we observe that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Take $\varPhi (x)$
. Take $\varPhi (x)$![]() and $V$
and $V$![]() same as in Case A12. Keeping in mind (3.6), we see that the $V$
same as in Case A12. Keeping in mind (3.6), we see that the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() being the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,8),\,(2,\,\min \{5+2v_2(a_2-1),\,2v_2(b)\})\}$
being the lower convex hull of the points of the set $T=\{(0,\,5),\,(1,\,8),\,(2,\,\min \{5+2v_2(a_2-1),\,2v_2(b)\})\}$![]() has two edges of positive slope. The residual polynomial attached to each edge is linear. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}\mathfrak {p_3^2}$
has two edges of positive slope. The residual polynomial attached to each edge is linear. So $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}\mathfrak {p_3^2}$![]() , where the residual degree of each prime ideal $\mathfrak {p_i}$
, where the residual degree of each prime ideal $\mathfrak {p_i}$![]() for $i=2,\,3$
for $i=2,\,3$![]() is $1$
is $1$![]() . Thus, $2\mid i(K)$
. Thus, $2\mid i(K)$![]() .
.
Case A14: $a\equiv 0(2)$![]() , $b\equiv 0(2)$
, $b\equiv 0(2)$![]() , $5v_2(a)<4v_2(b)$
, $5v_2(a)<4v_2(b)$![]() , $v_2(a)=2$
, $v_2(a)=2$![]() , $v_2(b)\ge 6$
, $v_2(b)\ge 6$![]() , $a_2\equiv 9(16)$
, $a_2\equiv 9(16)$![]() . Arguing as in Case A5, we see that $2A_K=\mathfrak p_1\mathfrak a$
. Arguing as in Case A5, we see that $2A_K=\mathfrak p_1\mathfrak a$![]() , where $\mathfrak p_1$
, where $\mathfrak p_1$![]() is a prime ideal of residual degree $1$
is a prime ideal of residual degree $1$![]() and $\mathfrak a$
and $\mathfrak a$![]() is an ideal of $A_K$
is an ideal of $A_K$![]() . Let $\varPhi (x)$
. Let $\varPhi (x)$![]() and $V$
and $V$![]() be same as in Case A12. Using the $\varPhi (x)$
be same as in Case A12. Using the $\varPhi (x)$![]() expansion of $f(x)$
expansion of $f(x)$![]() given in (3.6), we see that the $V$
given in (3.6), we see that the $V$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() being the lower convex hull of the points $(0,\,5)$
being the lower convex hull of the points $(0,\,5)$![]() , $(1,\,8)$
, $(1,\,8)$![]() , $(2,\,11)$
, $(2,\,11)$![]() has one edge of positive slope. In this case, $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}$
has one edge of positive slope. In this case, $2A_K=\mathfrak {p_1}\mathfrak {p_2^2}$![]() , where the residual degree of $\mathfrak {p_2}$
, where the residual degree of $\mathfrak {p_2}$![]() is $2$
is $2$![]() . So $2\nmid i(K)$
. So $2\nmid i(K)$![]() .
.
Case A15: $a\equiv 1(4)$![]() , $b\equiv 2(4)$
, $b\equiv 2(4)$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . The $\phi _1$
. The $\phi _1$![]() -Newton polygon of $f$
-Newton polygon of $f$![]() has a single edge, say $S$
has a single edge, say $S$![]() , of positive slope joining the points $(4,\, 0)$
, of positive slope joining the points $(4,\, 0)$![]() and $(5,\,1)$
and $(5,\,1)$![]() . The residual polynomial of $f(x)$
. The residual polynomial of $f(x)$![]() with respect to $(x,\,S)$
with respect to $(x,\,S)$![]() is linear. Thus, $\phi _1$
is linear. Thus, $\phi _1$![]() provides one prime ideal of residual degree $1$
provides one prime ideal of residual degree $1$![]() . The $\phi _2$
. The $\phi _2$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() can be written as
can be written as
The $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() is the lower convex hull of the points of the set $T=\{(0,\,0),\, (1,\,0),\, (2,\,1) ,\,(3,\,1),\, (4,\,1),\, (5,\,v_2(b-a-1))\}$
is the lower convex hull of the points of the set $T=\{(0,\,0),\, (1,\,0),\, (2,\,1) ,\,(3,\,1),\, (4,\,1),\, (5,\,v_2(b-a-1))\}$![]() . By hypothesis, $v_2(b-a-1)\ge 2$
. By hypothesis, $v_2(b-a-1)\ge 2$![]() . Therefore, $\phi _2$
. Therefore, $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges of positive slope. The first edge, say $S_1,$
has two edges of positive slope. The first edge, say $S_1,$![]() is the line segment joining the point $(1,\, 0)$
is the line segment joining the point $(1,\, 0)$![]() to $(4,\, 1)$
to $(4,\, 1)$![]() and the second edge, say $S_2,$
and the second edge, say $S_2,$![]() join the point $(4,\, 1)$
join the point $(4,\, 1)$![]() to $(5,\, v_2(b-a-1))$
to $(5,\, v_2(b-a-1))$![]() . For each $i=1,\,2$
. For each $i=1,\,2$![]() , the residual polynomial of $f(x)$
, the residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_i)$
with respect to $(\phi _2,\,S_i)$![]() is linear. So $\phi _2$
is linear. So $\phi _2$![]() provides two prime ideals, say $\mathfrak { p_2}$
provides two prime ideals, say $\mathfrak { p_2}$![]() and $\mathfrak { p_3}$
and $\mathfrak { p_3}$![]() , of residual degree $1$
, of residual degree $1$![]() each. Using Theorem 2.6, we have $2A_K=\mathfrak { p_1}\mathfrak { p_2^3}\mathfrak { p_3}$
each. Using Theorem 2.6, we have $2A_K=\mathfrak { p_1}\mathfrak { p_2^3}\mathfrak { p_3}$![]() . Hence, $2\mid i(K)$
. Hence, $2\mid i(K)$![]() .
.
Case A16: $a\equiv 1(4)$![]() , $b\equiv 0(4)$
, $b\equiv 0(4)$![]() . Here $f(x)\equiv x(x+1)^4(2)$
. Here $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Proceeding as in Case A15, it is easy to verify that $\phi _1$
. Proceeding as in Case A15, it is easy to verify that $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() and $\phi _2$
and $\phi _2$![]() provides one prime ideal, say $\mathfrak { p_2}$
provides one prime ideal, say $\mathfrak { p_2}$![]() , of residual degree $1$
, of residual degree $1$![]() . In this case, we have $2A_K=\mathfrak { p_1}\mathfrak { p_2^4}$
. In this case, we have $2A_K=\mathfrak { p_1}\mathfrak { p_2^4}$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Case A17: $a\equiv 3(8)$![]() , $b\equiv 2(4)$
, $b\equiv 2(4)$![]() . We have $f(x)\equiv x(x+1)^4(2)$
. We have $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Arguing as in Case A15, we see that $\phi _1$
. Arguing as in Case A15, we see that $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() and $\phi _2$
and $\phi _2$![]() gives one prime ideal, say $\mathfrak { p_2}$
gives one prime ideal, say $\mathfrak { p_2}$![]() , of residual degree $1$
, of residual degree $1$![]() . Here $2A_K=\mathfrak { p_1}\mathfrak { p_2^4}$
. Here $2A_K=\mathfrak { p_1}\mathfrak { p_2^4}$![]() . So $2\nmid i(K)$
. So $2\nmid i(K)$![]() in this case.
in this case.
Case A18: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)$
, $v_2(D)$![]() is even. In this case, $f(x)\equiv x(x+1)^4(2)$
is even. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Arguing as in Case A15, we see that $\phi _1$
. Arguing as in Case A15, we see that $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . Keeping in mind (3.7) and the hypothesis, we note that the number of edges of the $(x+1)$
. Keeping in mind (3.7) and the hypothesis, we note that the number of edges of the $(x+1)$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() is not specific. So we choose a rational number $\beta$
is not specific. So we choose a rational number $\beta$![]() of zero valuation such that $f(x)$
of zero valuation such that $f(x)$![]() is regular with respect to $x-\beta$
is regular with respect to $x-\beta$![]() . In this case, one can easily check that $v_2(D)\geq 12$
. In this case, one can easily check that $v_2(D)\geq 12$![]() . Define $\beta =\frac {-5b}{4a}$
. Define $\beta =\frac {-5b}{4a}$![]() . Set $\phi _2(x)=x-\beta$
. Set $\phi _2(x)=x-\beta$![]() . The $\phi _2$
. The $\phi _2$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is
is
Keeping in mind (1.3), it can be verified that
Since $v_2(a)=0$![]() and $v_2(b)=2$
and $v_2(b)=2$![]() , so $v_2(f(\beta ))=v_2(f'(\beta ))=v_2(D)-8$
, so $v_2(f(\beta ))=v_2(f'(\beta ))=v_2(D)-8$![]() . The $\phi _2$
. The $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() is the lower convex hull of the points $(0,\,0),\,(1,\,0),\,(2,\,1),\,(3,\,1), (4,\,v_2(D)-8)$
is the lower convex hull of the points $(0,\,0),\,(1,\,0),\,(2,\,1),\,(3,\,1), (4,\,v_2(D)-8)$![]() and $(5,\,v_2(D)-8)$
and $(5,\,v_2(D)-8)$![]() . As $v_2(D)\ge 12$
. As $v_2(D)\ge 12$![]() and even, therefore, $v_2(D)-8\ge 4$
and even, therefore, $v_2(D)-8\ge 4$![]() . Thus, the $\phi _2$
. Thus, the $\phi _2$![]() - Newton polygon of $f(x)$
- Newton polygon of $f(x)$![]() has two edges of positive slope. The first edge, say $S_1$
has two edges of positive slope. The first edge, say $S_1$![]() , is the line segment joining the point $(1,\,0)$
, is the line segment joining the point $(1,\,0)$![]() with $(3,\,1)$
with $(3,\,1)$![]() and has slope $\frac {1}{2}$
and has slope $\frac {1}{2}$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , is the line segment joining the point $(3,\,1)$
, is the line segment joining the point $(3,\,1)$![]() with $(5,\,v_2(D)-8)$
with $(5,\,v_2(D)-8)$![]() and has slope $\frac {v_2(D)-9}{2}$
and has slope $\frac {v_2(D)-9}{2}$![]() . For each $i=1,\,2$
. For each $i=1,\,2$![]() , the residual polynomial of $f(x)$
, the residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_i)$
with respect to $(\phi _2,\,S_i)$![]() is linear. Thus $2A_K= \mathfrak { p_1}\mathfrak { p_2^2} \mathfrak { p_3^2}$
is linear. Thus $2A_K= \mathfrak { p_1}\mathfrak { p_2^2} \mathfrak { p_3^2}$![]() , where for each $i=1,\,2,\,3$
, where for each $i=1,\,2,\,3$![]() , the residual degree of $\mathfrak { p_i}$
, the residual degree of $\mathfrak { p_i}$![]() is $1$
is $1$![]() . Hence, $2\mid i(K)$
. Hence, $2\mid i(K)$![]() .
.
Note that if $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() and $v_2(D)$
and $v_2(D)$![]() is odd, then the residual polynomial of $f(x)$
is odd, then the residual polynomial of $f(x)$![]() with respect to $(x-\beta,\,S_2)$
with respect to $(x-\beta,\,S_2)$![]() is not square-free and $f(x)$
is not square-free and $f(x)$![]() is not $(x-\beta )$
is not $(x-\beta )$![]() -regular. So we choose another rational number $\delta$
-regular. So we choose another rational number $\delta$![]() such that $f(x)$
such that $f(x)$![]() is $(x-\delta )$
is $(x-\delta )$![]() -regular.
-regular.
In what follows, when $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() and $v_2(D)$
and $v_2(D)$![]() is odd, then $\delta$
is odd, then $\delta$![]() will stand for $2^u-\frac {5b_2}{a}$
will stand for $2^u-\frac {5b_2}{a}$![]() , where $u=\frac {v_2(D)-9}{2}$
, where $u=\frac {v_2(D)-9}{2}$![]() . It can be verified that $v_2(f(\delta ))\ge 2u+2$
. It can be verified that $v_2(f(\delta ))\ge 2u+2$![]() and $v_2(f'(\delta ))=u+2$
and $v_2(f'(\delta ))=u+2$![]() .
.
Case A19: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)\neq 11$
, $v_2(D)\neq 11$![]() is odd, $v_2(f(\delta ))=2u+2$
is odd, $v_2(f(\delta ))=2u+2$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() and $v_2(D)\ge 13$
and $v_2(D)\ge 13$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() . Then, $\phi _1$
. Then, $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . Arguing as in Case A18, we see that $f(x)$
. Arguing as in Case A18, we see that $f(x)$![]() is not $2$
is not $2$![]() -regular always. Consider $\phi _2(x)=x-\delta$
-regular always. Consider $\phi _2(x)=x-\delta$![]() . The $\phi _2(x)$
. The $\phi _2(x)$![]() -expansion of $f(x)$
-expansion of $f(x)$![]() is
is
The $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() is the lower convex hull of the points $(0,\,0)$
is the lower convex hull of the points $(0,\,0)$![]() , $(1,\,0)$
, $(1,\,0)$![]() , $(2,\,1)$
, $(2,\,1)$![]() , $(3,\,1)$
, $(3,\,1)$![]() , $(4,\,v_2(f'(\delta ))$
, $(4,\,v_2(f'(\delta ))$![]() and $(5,\,v_2(f(\delta ))$
and $(5,\,v_2(f(\delta ))$![]() . Since $v_2(f(\delta ))=2u+2$
. Since $v_2(f(\delta ))=2u+2$![]() and $v_2(f'(\delta ))=u+2$
and $v_2(f'(\delta ))=u+2$![]() , the $\phi _2$
, the $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges, say $S_1$
has two edges, say $S_1$![]() and $S_2$
and $S_2$![]() , of positive slope. For each $i=1,\,2$
, of positive slope. For each $i=1,\,2$![]() , the residual polynomial of $f(x)$
, the residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_i)$
with respect to $(\phi _2,\,S_i)$![]() is linear. Thus, $\phi _2(x)$
is linear. Thus, $\phi _2(x)$![]() provides two prime ideals, say $\mathfrak { p_2}$
provides two prime ideals, say $\mathfrak { p_2}$![]() and $\mathfrak { p_3}$
and $\mathfrak { p_3}$![]() , of residual degree $1$
, of residual degree $1$![]() each. Therefore, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3^2}$
each. Therefore, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3^2}$![]() . Hence, $2\mid i(K)$
. Hence, $2\mid i(K)$![]() .
.
Case A20: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)\neq 11$
, $v_2(D)\neq 11$![]() is odd, $v_2(f(\delta ))=2u+3$
is odd, $v_2(f(\delta ))=2u+3$![]() . Here $f(x)\equiv x(x+1)^4(2)$
. Here $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() . Then $\phi _1$
. Then $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . Take $\phi _2(x)=x-\delta$
. Take $\phi _2(x)=x-\delta$![]() . Arguing as in Case A19, it can be checked that $\phi _2$
. Arguing as in Case A19, it can be checked that $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() being the lower convex hull of the points $(0,\,0)$
being the lower convex hull of the points $(0,\,0)$![]() , $(1,\,0)$
, $(1,\,0)$![]() , $(2,\,1)$
, $(2,\,1)$![]() , $(3,\,1)$
, $(3,\,1)$![]() , $(4,\,u+2)$
, $(4,\,u+2)$![]() and $(5,\,2u+3)$
and $(5,\,2u+3)$![]() has two edges of positive slope. The first edge, say $S_1$
has two edges of positive slope. The first edge, say $S_1$![]() , is the line segment joining the points $(1,\,0)$
, is the line segment joining the points $(1,\,0)$![]() and $(3,\,1)$
and $(3,\,1)$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , is the line segment joining the points $(3,\,1)$
, is the line segment joining the points $(3,\,1)$![]() and $(5,\,2u+3)$
and $(5,\,2u+3)$![]() with a lattice point $(4,\,u+2)$
with a lattice point $(4,\,u+2)$![]() lying on it. The residual polynomial of $f(x)$
lying on it. The residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_1$
with respect to $(\phi _2,\,S_1$![]() ) and $(\phi _2,\,S_2)$
) and $(\phi _2,\,S_2)$![]() is $Y+\bar {1}$
is $Y+\bar {1}$![]() and $Y^2+Y+\bar {1}$
and $Y^2+Y+\bar {1}$![]() respectively. Thus, $\phi _2$
respectively. Thus, $\phi _2$![]() provides two prime ideals, say $\mathfrak { p_2}$
provides two prime ideals, say $\mathfrak { p_2}$![]() and $\mathfrak { p_3}$
and $\mathfrak { p_3}$![]() , of residual degree $1$
, of residual degree $1$![]() and $2$
and $2$![]() respectively. So $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}$
respectively. So $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}$![]() and $2\nmid i(K)$
and $2\nmid i(K)$![]() .
.
Case A21: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)\neq 11$
, $v_2(D)\neq 11$![]() is odd, $v_2(f(\delta ))\ge 2u+4$
is odd, $v_2(f(\delta ))\ge 2u+4$![]() . Here $f(x)\equiv x(x+1)^4(2)$
. Here $f(x)\equiv x(x+1)^4(2)$![]() . Let $\phi _1(x)=x$
. Let $\phi _1(x)=x$![]() . Clearly, $\phi _1$
. Clearly, $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . Let $\phi _2=x-\delta$
. Let $\phi _2=x-\delta$![]() . Keeping in mind (3.10), it is easy to verify that the $\phi _2$
. Keeping in mind (3.10), it is easy to verify that the $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has three edges of positive slope. The first edge, say $S_1$
has three edges of positive slope. The first edge, say $S_1$![]() , is the line segment joining the points $(1,\,0)$
, is the line segment joining the points $(1,\,0)$![]() and $(3,\,1)$
and $(3,\,1)$![]() . The second edge, say $S_2$
. The second edge, say $S_2$![]() , is the line segment joining the points $(3,\,1)$
, is the line segment joining the points $(3,\,1)$![]() and $(4,\,u+2)$
and $(4,\,u+2)$![]() . The third edge, say $S_3$
. The third edge, say $S_3$![]() , is the line segment joining the points $(4,\,u+2)$
, is the line segment joining the points $(4,\,u+2)$![]() and $(5,\,v_2(f(\delta )))$
and $(5,\,v_2(f(\delta )))$![]() . For each $i=1,\,2,\,3$
. For each $i=1,\,2,\,3$![]() , the residual polynomial of $f(x)$
, the residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_i)$
with respect to $(\phi _2,\,S_i)$![]() is linear. So $\phi _2$
is linear. So $\phi _2$![]() provides three prime ideals, say $\mathfrak { p_2}$
provides three prime ideals, say $\mathfrak { p_2}$![]() , $\mathfrak { p_3}$
, $\mathfrak { p_3}$![]() and $\mathfrak { p_4}$
and $\mathfrak { p_4}$![]() , of residual degree $1$
, of residual degree $1$![]() each. Thus, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}\mathfrak { p_4}$
each. Thus, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}\mathfrak { p_4}$![]() . Hence, $2\mid i(K)$
. Hence, $2\mid i(K)$![]() .
.
Note that when $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() and $v_2(D)=11$
and $v_2(D)=11$![]() , then $u=\frac {v_2(D)-9}{2}=1$
, then $u=\frac {v_2(D)-9}{2}=1$![]() . So $v_2(f(\delta ))\ge 4$
. So $v_2(f(\delta ))\ge 4$![]() and $v_2(f'(\delta ))=3$
and $v_2(f'(\delta ))=3$![]() .
.
Case A22: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)=11$
, $v_2(D)=11$![]() , $v_2(f(\delta ))= 4$
, $v_2(f(\delta ))= 4$![]() . We have $f(x)\equiv x(x+1)^4(2)$
. We have $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x-\delta$
and $\phi _2(x)=x-\delta$![]() . Clearly $\phi _1$
. Clearly $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . Keeping in mind (3.10), we see that the $\phi _2$
. Keeping in mind (3.10), we see that the $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges, say $S_1$
has two edges, say $S_1$![]() and $S_2$
and $S_2$![]() , of positive slope. The residual polynomial of $f(x)$
, of positive slope. The residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_i)$
with respect to $(\phi _2,\,S_i)$![]() , for $i=1,\,2$
, for $i=1,\,2$![]() , is linear. Therefore $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3^2}$
, is linear. Therefore $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3^2}$![]() , where the residual degree of each prime ideal $\mathfrak { p_i}$
, where the residual degree of each prime ideal $\mathfrak { p_i}$![]() is $1$
is $1$![]() , for each $i=2,\,3$
, for each $i=2,\,3$![]() . Hence, $2\mid i(K)$
. Hence, $2\mid i(K)$![]() .
.
Case A23: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)=11$
, $v_2(D)=11$![]() , $v_2(f(\delta ))= 5$
, $v_2(f(\delta ))= 5$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x-\delta$
and $\phi _2(x)=x-\delta$![]() . Note that $\phi _1$
. Note that $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . In view of (3.10), we see that the $\phi _2$
. In view of (3.10), we see that the $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has two edges, say $S_1$
has two edges, say $S_1$![]() and $S_2$
and $S_2$![]() , of positive slope. The residual polynomial of $f(x)$
, of positive slope. The residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_1)$
with respect to $(\phi _2,\,S_1)$![]() is linear. The residual polynomial of $f(x)$
is linear. The residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_2)$
with respect to $(\phi _2,\,S_2)$![]() is $Y^2+Y+\bar {1}$
is $Y^2+Y+\bar {1}$![]() . Therefore, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}$
. Therefore, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}$![]() , where the residual degree of $\mathfrak { p_2}$
, where the residual degree of $\mathfrak { p_2}$![]() and $\mathfrak { p_3}$
and $\mathfrak { p_3}$![]() is $1$
is $1$![]() and $2$
and $2$![]() respectively. Hence, $2\nmid i(K)$
respectively. Hence, $2\nmid i(K)$![]() .
.
Case A24: $a\equiv 3(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() , $v_2(D)=11$
, $v_2(D)=11$![]() , $v_2(f(\delta ))\ge 6$
, $v_2(f(\delta ))\ge 6$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x-\delta$
and $\phi _2(x)=x-\delta$![]() . Here $\phi _1$
. Here $\phi _1$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() . In view of (3.10), we observe that the $\phi _2$
. In view of (3.10), we observe that the $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() being the lower convex hull of the points $(0,\,0)$
being the lower convex hull of the points $(0,\,0)$![]() , $(1,\,0)$
, $(1,\,0)$![]() , $(2,\,1)$
, $(2,\,1)$![]() , $(3,\,1)$
, $(3,\,1)$![]() , $(4,\,3)$
, $(4,\,3)$![]() , $(5,\,v_2(f(\delta )))$
, $(5,\,v_2(f(\delta )))$![]() has three edges, say $S_1$
has three edges, say $S_1$![]() , $S_2$
, $S_2$![]() and $S_3$
and $S_3$![]() , of positive slope. The residual polynomial of $f(x)$
, of positive slope. The residual polynomial of $f(x)$![]() with respect to $(\phi _2,\,S_i)$
with respect to $(\phi _2,\,S_i)$![]() , for $i=1,\,2,\,3$
, for $i=1,\,2,\,3$![]() , is linear. So $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}\mathfrak { p_4}$
, is linear. So $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}\mathfrak { p_4}$![]() , where the residual degree of prime ideal $\mathfrak { p_i}$
, where the residual degree of prime ideal $\mathfrak { p_i}$![]() is $1$
is $1$![]() , for each $i=2,\,3,\,4$
, for each $i=2,\,3,\,4$![]() . Thus, $2\mid i(K)$
. Thus, $2\mid i(K)$![]() .
.
Case A25: $a\equiv 3(8)$![]() , $b\equiv 0(8)$
, $b\equiv 0(8)$![]() . Here $f(x)\equiv x(x+1)^4(2)$
. Here $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . The $\phi _1$
. The $\phi _1$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has a single edge of positive slope, say $S$
has a single edge of positive slope, say $S$![]() , joining the points $(4,\,~0)$
, joining the points $(4,\,~0)$![]() and $(5,\,~v_2(b))$
and $(5,\,~v_2(b))$![]() . So the residual polynomial attached to $(\phi _1,\,~S)$
. So the residual polynomial attached to $(\phi _1,\,~S)$![]() is linear. Keeping in mind the $\phi _2$
is linear. Keeping in mind the $\phi _2$![]() expansion of $f(x)$
expansion of $f(x)$![]() given in (3.7), one can see that the $\phi _2$
given in (3.7), one can see that the $\phi _2$![]() -Newton polygon of $f(x)$
-Newton polygon of $f(x)$![]() has a single edge, say $S'$
has a single edge, say $S'$![]() , joining the points $(1,\,~ 0)$
, joining the points $(1,\,~ 0)$![]() and $(5,\, ~2)$
and $(5,\, ~2)$![]() with point $(3,\,~ 1)$
with point $(3,\,~ 1)$![]() lying on it. The polynomial associated to $f(x)$
lying on it. The polynomial associated to $f(x)$![]() with respect to ($\phi _2,\,~S')$
with respect to ($\phi _2,\,~S')$![]() is $Y^2+Y+\overline {1}\in \mathbb {F}_2[Y]$
is $Y^2+Y+\overline {1}\in \mathbb {F}_2[Y]$![]() having no repeated roots. Thus, $f(x)$
having no repeated roots. Thus, $f(x)$![]() is $2$
is $2$![]() -regular. Using Theorem 2.6, one can check that $\phi _1(x)$
-regular. Using Theorem 2.6, one can check that $\phi _1(x)$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() and $\phi _2(x)$
and $\phi _2(x)$![]() provides one prime ideal, say $\mathfrak { p_2}$
provides one prime ideal, say $\mathfrak { p_2}$![]() , of residual degree $2$
, of residual degree $2$![]() . Therefore, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}$
. Therefore, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}$![]() and $2\nmid i(K)$
and $2\nmid i(K)$![]() .
.
Case A26: $a\equiv 7(8)$![]() , $b\equiv 2(4)$
, $b\equiv 2(4)$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Let $\phi _1(x)=x$
. Let $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Arguing as in Case A25, it can be easily seen that $2A_K=\mathfrak { p_1}\mathfrak { p_2^4}$
. Arguing as in Case A25, it can be easily seen that $2A_K=\mathfrak { p_1}\mathfrak { p_2^4}$![]() , where the residual degree of $\mathfrak { p_1}$
, where the residual degree of $\mathfrak { p_1}$![]() and $\mathfrak { p_2}$
and $\mathfrak { p_2}$![]() is $1$
is $1$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Case A27: $a\equiv 7(8)$![]() , $b\equiv 4(8)$
, $b\equiv 4(8)$![]() . Here $f(x)\equiv x(x+1)^4(2)$
. Here $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Proceeding as in Case A25, we can check that $\phi _1(x)$
. Proceeding as in Case A25, we can check that $\phi _1(x)$![]() gives one prime ideal, say $\mathfrak { p_1}$
gives one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() and $\phi _2(x)$
and $\phi _2(x)$![]() provides one prime ideal, say $\mathfrak { p_2}$
provides one prime ideal, say $\mathfrak { p_2}$![]() , of residual degree $2$
, of residual degree $2$![]() . So $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}$
. So $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Case A28: $a\equiv 7(8)$![]() , $b\equiv 0(8)$
, $b\equiv 0(8)$![]() , $v_2(b-a-1)=3$
, $v_2(b-a-1)=3$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Arguing as in Case A25, it can be verified that $\phi _1(x)$
. Arguing as in Case A25, it can be verified that $\phi _1(x)$![]() provides one prime ideal, say $\mathfrak { p_1}$
provides one prime ideal, say $\mathfrak { p_1}$![]() , of residual degree $1$
, of residual degree $1$![]() and $\phi _2$
and $\phi _2$![]() provides two prime ideals say, $\mathfrak { p_2}$
provides two prime ideals say, $\mathfrak { p_2}$![]() and $\mathfrak { p_3}$
and $\mathfrak { p_3}$![]() , of residual degree $1$
, of residual degree $1$![]() and $2$
and $2$![]() , respectively. Thus, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}$
, respectively. Thus, $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}$![]() . Hence, $2\nmid i(K)$
. Hence, $2\nmid i(K)$![]() .
.
Case A29: $a\equiv 7(8)$![]() , $b\equiv 0(8)$
, $b\equiv 0(8)$![]() , $v_2(b-a-1)\ge 4$
, $v_2(b-a-1)\ge 4$![]() . In this case, $f(x)\equiv x(x+1)^4(2)$
. In this case, $f(x)\equiv x(x+1)^4(2)$![]() . Set $\phi _1(x)=x$
. Set $\phi _1(x)=x$![]() and $\phi _2(x)=x+1$
and $\phi _2(x)=x+1$![]() . Arguing as in Case A25, we have $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}\mathfrak { p_4}$
. Arguing as in Case A25, we have $2A_K=\mathfrak { p_1}\mathfrak { p_2^2}\mathfrak { p_3}\mathfrak { p_4}$![]() , where the residual degree of each $\mathfrak {p_i},\,~1\leq i\leq 4$
, where the residual degree of each $\mathfrak {p_i},\,~1\leq i\leq 4$![]() is $1$
is $1$![]() . Hence, $2\mid i(K)$
. Hence, $2\mid i(K)$![]() . This completes the proof of the theorem.
. This completes the proof of the theorem.
Acknowledgements
The first author is thankful to SERB grant SRG/2021/000393. The second author is grateful to the Council of Scientific and Industrial Research, New Delhi for providing financial support in the form of Senior Research Fellowship through Grant No. $09/135(0878)/2019$![]() -EMR-$1$
-EMR-$1$![]() . The third author is grateful to the University Grants Commission, New Delhi for providing financial support in the form of Junior Research Fellowship through Ref No.1129/(CSIR-NET JUNE 2019).
. The third author is grateful to the University Grants Commission, New Delhi for providing financial support in the form of Junior Research Fellowship through Ref No.1129/(CSIR-NET JUNE 2019).