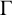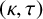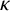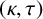A subset R of the vertex set of a graph $\Gamma $ is said to be $(\kappa ,\tau )$-regular if R induces a $\kappa $-regular subgraph and every vertex outside R is adjacent to exactly $\tau $ vertices in R. In particular, if R is a $(\kappa ,\tau )$-regular set of some Cayley graph on a finite group G, then R is called a 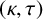$(\kappa ,\tau )$-regular set of G. 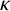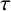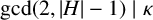Let H be a nontrivial normal subgroup of G, and $\kappa $ and $\tau $ a pair of integers satisfying $0\leq \kappa \leq |H|-1$, $1\leq \tau \leq |H|$ and $\gcd (2,|H|-1)\mid \kappa $. It is proved that (i) if 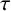$\tau $ is even, then H is a $(\kappa ,\tau )$-regular set of G; (ii) if $\tau $ is odd, then H is a $(\kappa ,\tau )$-regular set of G if and only if it is a $(0,1)$-regular set of G.

We present a Mordell–Weil sieve that can be used to compute points on certain bielliptic modular curves $X_0(N)$ over fixed quadratic fields. We study $X_0(N)(\mathbb {Q}(\sqrt {d}))$ for $N \in \{ 53,61,65,79,83,89,101,131 \}$ and ${\lvert d \rvert < 100}$.

Lin introduced the partition function $\text {PDO}_t(n)$, which counts the total number of tagged parts over all the partitions of n with designated summands in which all parts are odd. Lin also proved some congruences modulo 3 and 9 for $\text {PDO}_t(n)$, and conjectured certain congruences modulo $3^{k+2}$ for $k\geq 0$. He proved the conjecture for $k=0$ and $k=1$ [‘The number of tagged parts over the partitions with designated summands’, J. Number Theory 184 (2018), 216–234]. We prove the conjecture for $k=2$. We also study the lacunarity of $\text {PDO}_t(n)$ modulo arbitrary powers of 2 and 3. Using nilpotency of Hecke operators, we prove that there exists an infinite family of congruences modulo any power of 2 satisfied by $\text {PDO}_t(n)$.

Let $Q(n)$ denote the number of partitions of n into distinct parts. Merca [‘Ramanujan-type congruences modulo 4 for partitions into distinct parts’, An. Şt. Univ. Ovidius Constanţa 30(3) (2022), 185–199] derived some congruences modulo $4$ and $8$ for $Q(n)$ and posed a conjecture on congruences modulo powers of $2$ enjoyed by $Q(n)$. We present an approach which can be used to prove a family of internal congruence relations modulo powers of $2$ concerning $Q(n)$. As an immediate consequence, we not only prove Merca’s conjecture, but also derive many internal congruences modulo powers of $2$ satisfied by $Q(n)$. Moreover, we establish an infinite family of congruence relations modulo $4$ for $Q(n)$.

Let F be a subfield of the complex numbers and $f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$ an irreducible polynomial. We give an elementary characterisation of the Galois group of $f(x)$ as a transitive subgroup of $S_6$. The method involves determining whether three expressions involving a, b and c are perfect squares in F and whether a related quartic polynomial has a linear factor. As an application, we produce one-parameter families of reciprocal sextic polynomials with a specified Galois group.

Let $\alpha $ be a complex-valued $2$-cocycle of a finite group $G.$ A new concept of strict $\alpha $-regularity is introduced and its basic properties are investigated. To illustrate the potential use of this concept, a new proof is offered to show that the number of orbits of G under its action on the set of complex-valued irreducible $\alpha _N$-characters of N equals the number of $\alpha $-regular conjugacy classes of G contained in $N,$ where N is a normal subgroup of $G.$

Let H be a subgroup of a finite group G and let $\alpha $ be a complex-valued $2$-cocycle of $G.$ Conditions are found to ensure there exists a nontrivial element of H that is $\alpha $-regular in $G.$ However, a new result is established allowing a prime by prime analysis of the Sylow subgroups of $C_G(x)$ to determine the $\alpha $-regularity of a given $x\in G.$ In particular, this result implies that every $\alpha _H$-regular element of a normal Hall subgroup H is $\alpha $-regular in $G.$

Let G be a finite group and $\mathrm {Irr}(G)$ the set of all irreducible complex characters of G. Define the codegree of $\chi \in \mathrm {Irr}(G)$ as $\mathrm {cod}(\chi ):={|G:\mathrm {ker}(\chi ) |}/{\chi (1)}$ and denote by $\mathrm {cod}(G):=\{\mathrm {cod}(\chi ) \mid \chi \in \mathrm {Irr}(G)\}$ the codegree set of G. Let H be one of the $26$ sporadic simple groups. We show that H is determined up to isomorphism by cod$(H)$.

A natural operation on numerical semigroups is taking a quotient by a positive integer. If $\mathcal {S}$ is a quotient of a numerical semigroup with k generators, we call $\mathcal {S}$ a k-quotient. We give a necessary condition for a given numerical semigroup $\mathcal {S}$ to be a k-quotient and present, for each $k \ge 3$, the first known family of numerical semigroups that cannot be written as a k-quotient. We also examine the probability that a randomly selected numerical semigroup with k generators is a k-quotient.

We study the arithmeticity of $\mathbb {C}$-Fuchsian subgroups of some nonarithmetic lattices constructed by Deraux et al. [‘New non-arithmetic complex hyperbolic lattices’, Invent. Math. 203 (2016), 681–771]. Our results give an answer to a question raised by Wells [Hybrid Subgroups of Complex Hyperbolic Isometries, Doctoral thesis, Arizona State University, 2019].

For any real polynomial $p(x)$ of even degree k, Shapiro [‘Problems around polynomials: the good, the bad and the ugly$\ldots $’, Arnold Math. J. 1(1) (2015), 91–99] proposed the conjecture that the sum of the number of real zeros of the two polynomials $(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)$ and $p(x)$ is larger than 0. We prove that the conjecture is true except in one case: when the polynomial $p(x)$ has no real zeros, the derivative polynomial $p{'}(x)$ has one real simple zero, that is, $p{'}(x)=C(x)(x-w)$, where $C(x)$ is a polynomial with $C(w)\ne 0$, and the polynomial $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$ has no real zeros.

The sharp bound for the third Hankel determinant for the coefficients of the inverse function of convex functions is obtained, thus answering a recent conjecture concerning invariance of coefficient functionals for convex functions.

We obtain bounds for certain functionals defined on a class of meromorphic functions in the unit disc of the complex plane with a nonzero simple pole. These bounds are sharp in a certain sense. We also discuss possible applications of this result. Finally, we generalise the result to meromorphic functions with more than one simple pole.

The signature four elliptic theory of Ramanujan is provided with a counterpart to the Jacobian modular sine; this counterpart yields natural direct proofs of several hypergeometric identities recorded by Ramanujan, bypassing the signature four transfer principle of Berndt et al. [‘Ramanujan’s theories of elliptic functions to alternative bases’, Trans. Amer. Math. Soc. 347 (1995), 4163–4244].

We consider the growth of the convex viscosity solution of the Monge–Ampère equation $\det D^2u=1$ outside a bounded domain of the upper half space. We show that if u is a convex quadratic polynomial on the boundary $\{x_n=0\}$ and there exists some $\varepsilon>0$ such that $u=O(|x|^{3-\varepsilon })$ at infinity, then $u=O(|x|^2)$ at infinity. As an application, we improve the asymptotic result at infinity for viscosity solutions of Monge–Ampère equations in half spaces of Jia, Li and Li [‘Asymptotic behavior at infinity of solutions of Monge–Ampère equations in half spaces’, J. Differential Equations 269(1) (2020), 326–348].

Niven’s theorem asserts that $\{\cos (r\pi ) \mid r\in \mathbb {Q}\}\cap \mathbb {Q}=\{0,\pm 1,\pm 1/2\}.$ In this paper, we use elementary techniques and results from arithmetic dynamics to obtain an algorithm for classifying all values in the set $\{\cos (r\pi ) \mid r\in \mathbb {Q}\}\cap K$, where K is an arbitrary number field.

Suppose that X and Y are two real normed spaces. A map $f:X\rightarrow Y$ is called a min-phase-isometry if it satisfies

$$ \begin{align*} \min\{\|f(x)+f(y)\|,\|f(x)-f(y)\|\}=\min\{\|x+y\|,\|x-y\|\} \quad (x,y\in X). \end{align*} $$

We present properties of min-phase-isometries in the case that Y is strictly convex and show that if a min-phase-isometry f (not necessarily surjective) fixes the origin, then it is phase-equivalent to a linear isometry, that is, $f(x)=\varepsilon (x)g(x)$ for $x\in X$, where $g:X\rightarrow Y$ is a linear isometry and $\varepsilon $ is a map from X to $\{-1,1\}$.