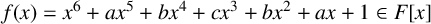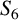1 Introduction
Let F be a subfield of the complex numbers and
![]() $f(x)\in F[x]$
an irreducible polynomial of degree n. Identifying the Galois group,
$f(x)\in F[x]$
an irreducible polynomial of degree n. Identifying the Galois group,
![]() $\operatorname {\mathrm {Gal}}(f)$
, of
$\operatorname {\mathrm {Gal}}(f)$
, of
![]() $f(x)$
as a transitive subgroup of
$f(x)$
as a transitive subgroup of
![]() $S_n$
is a fundamental problem in computational algebra. In general, this is a difficult task; most modern approaches are based on [Reference Soicher and McKay9, Reference Stauduhar10]. However, when
$S_n$
is a fundamental problem in computational algebra. In general, this is a difficult task; most modern approaches are based on [Reference Soicher and McKay9, Reference Stauduhar10]. However, when
![]() $f(x)$
has a special form, the computation can be more straightforward.
$f(x)$
has a special form, the computation can be more straightforward.
For example, Galois groups of even quartic polynomials (
![]() $x^4+ax^2+b$
), even sextic polynomials (
$x^4+ax^2+b$
), even sextic polynomials (
![]() $x^6+ax^4+bx^2+c$
) and doubly even octic polynomials (
$x^6+ax^4+bx^2+c$
) and doubly even octic polynomials (
![]() $x^8+ax^4+b$
) have elementary characterisations (see for example [Reference Altmann, Awtrey, Cryan, Shannon and Touchette1, Reference Awtrey and Jakes2]). In each case, the characterisation leverages information about the index-2 subfield of the field defined by the polynomial.
$x^8+ax^4+b$
) have elementary characterisations (see for example [Reference Altmann, Awtrey, Cryan, Shannon and Touchette1, Reference Awtrey and Jakes2]). In each case, the characterisation leverages information about the index-2 subfield of the field defined by the polynomial.
A natural extension of this technique is to irreducible reciprocal polynomials, which are polynomials satisfying
![]() $f(x) = x^n\cdot f(1/x)$
, since the field extension defined by such a polynomial also has an index-2 subfield (see Theorem 2.1). Note that if
$f(x) = x^n\cdot f(1/x)$
, since the field extension defined by such a polynomial also has an index-2 subfield (see Theorem 2.1). Note that if
![]() $f(x) = \sum _{i=0}^n f_i x^i$
is a reciprocal polynomial, then
$f(x) = \sum _{i=0}^n f_i x^i$
is a reciprocal polynomial, then
![]() $f_i = f_{n-i}$
; that is, the sequence of coefficients
$f_i = f_{n-i}$
; that is, the sequence of coefficients
![]() $\{f_i\}$
forms a palindrome.
$\{f_i\}$
forms a palindrome.
In this setting, some similar characterisations of
![]() $\operatorname {\mathrm {Gal}}(f)$
are known. The following classical result of Dickson determines the Galois group of an irreducible reciprocal quartic polynomial by testing the squareness of two elements of F (see [Reference Dickson4]). In the theorem, as in the rest of the paper, we will use the following standard convention for describing groups:
$\operatorname {\mathrm {Gal}}(f)$
are known. The following classical result of Dickson determines the Galois group of an irreducible reciprocal quartic polynomial by testing the squareness of two elements of F (see [Reference Dickson4]). In the theorem, as in the rest of the paper, we will use the following standard convention for describing groups:
![]() $C_n$
denotes the cyclic group of order n,
$C_n$
denotes the cyclic group of order n,
![]() $D_n$
the dihedral group of order
$D_n$
the dihedral group of order
![]() $2n$
, and
$2n$
, and
![]() $A_n$
and
$A_n$
and
![]() $S_n$
the alternating and symmetric groups on n letters, respectively. We also use
$S_n$
the alternating and symmetric groups on n letters, respectively. We also use
![]() $\times $
to denote a direct product,
$\times $
to denote a direct product,
![]() $\rtimes $
a semidirect product and
$\rtimes $
a semidirect product and
![]() $\wr $
a wreath product.
$\wr $
a wreath product.
Theorem 1.1 (Dickson)
Let
![]() $x^4+ax^3+bx^2+ax+1 \in F[x]$
be irreducible. Then
$x^4+ax^3+bx^2+ax+1 \in F[x]$
be irreducible. Then
![]() $\operatorname {\mathrm {Gal}}(f)$
is isomorphic to:
$\operatorname {\mathrm {Gal}}(f)$
is isomorphic to:
-
•
 $C_2\times C_2$
if and only if
$C_2\times C_2$
if and only if
 $(b+2)^2-4a^2$
is a square in F;
$(b+2)^2-4a^2$
is a square in F; -
•
 $C_4$
if and only if
$C_4$
if and only if
 $((b+2)^2-4a^2)(a^2-4b+8)$
is a square in F;
$((b+2)^2-4a^2)(a^2-4b+8)$
is a square in F; -
•
 $D_4$
if and only if neither
$D_4$
if and only if neither
 $(b+2)^2-4a^2$
nor
$(b+2)^2-4a^2$
nor
 $((b+2)^2-4a^2)(a^2-4b+8)$
is a square in F.
$((b+2)^2-4a^2)(a^2-4b+8)$
is a square in F.
Since reciprocal polynomials of odd degree are reducible (they have
![]() $-1$
as a root), the next logical case to consider is Galois groups of irreducible reciprocal sextic polynomials; that is, those of the form
$-1$
as a root), the next logical case to consider is Galois groups of irreducible reciprocal sextic polynomials; that is, those of the form
![]() $x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$
. The purpose of this paper is to provide a similar characterisation, reflecting the spirit of Theorem 1.1. In doing so, we will generalise the results in [Reference Jones6, Reference Jones7], which verify that certain families of irreducible reciprocal sextic polynomials with rational coefficients have Galois group isomorphic to either
$x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$
. The purpose of this paper is to provide a similar characterisation, reflecting the spirit of Theorem 1.1. In doing so, we will generalise the results in [Reference Jones6, Reference Jones7], which verify that certain families of irreducible reciprocal sextic polynomials with rational coefficients have Galois group isomorphic to either
![]() $S_3$
,
$S_3$
,
![]() $D_6$
or
$D_6$
or
![]() $S_4\times C_2$
.
$S_4\times C_2$
.
The remainder of the paper is organised as follows. In Section 2, we collect several results concerning field extensions defined by reciprocal polynomials and their Galois groups; these will be used to prove our main theorem in Section 3. Our main result, Theorem 3.5, gives a characterisation of the Galois group of
![]() $x^6+ax^5+bx^4+cx^3+bx^2+ax+1$
that depends only on the squareness of three elements whose expressions involve a, b and c, along with whether or not a related quartic polynomial has a linear factor. As an application, we provide one-parameter families of reciprocal sextics for each possible Galois group (see Theorem 3.7).
$x^6+ax^5+bx^4+cx^3+bx^2+ax+1$
that depends only on the squareness of three elements whose expressions involve a, b and c, along with whether or not a related quartic polynomial has a linear factor. As an application, we provide one-parameter families of reciprocal sextics for each possible Galois group (see Theorem 3.7).
2 Preliminary results
In this section, we let
![]() $f(x) \in F[x]$
be a monic irreducible reciprocal polynomial of degree
$f(x) \in F[x]$
be a monic irreducible reciprocal polynomial of degree
![]() $n=2m$
, and we let
$n=2m$
, and we let
![]() $L = F(\alpha )$
where
$L = F(\alpha )$
where
![]() $f(\alpha )=0$
. We collect results about L and
$f(\alpha )=0$
. We collect results about L and
![]() $\operatorname {\mathrm {Gal}}(f)$
that are used later in the paper.
$\operatorname {\mathrm {Gal}}(f)$
that are used later in the paper.
The reader is referred to [Reference Lindstrom8] for an elementary overview of several standard facts about reciprocal polynomials. One such result shows there exists a polynomial
![]() $g(x)$
of degree m such that
$g(x)$
of degree m such that
![]() $f(x) = x^m\cdot g(x+1/x)$
(see [Reference Lindstrom8, Proposition 2.0.16]). It turns out that
$f(x) = x^m\cdot g(x+1/x)$
(see [Reference Lindstrom8, Proposition 2.0.16]). It turns out that
![]() $g(x)$
is the minimal polynomial of
$g(x)$
is the minimal polynomial of
![]() $\alpha +1/\alpha $
. This result is straightforward to establish and shows L has an index-2 subfield. For convenience, we include a proof.
$\alpha +1/\alpha $
. This result is straightforward to establish and shows L has an index-2 subfield. For convenience, we include a proof.
Theorem 2.1. The minimal polynomial,
![]() $g(x)$
, of
$g(x)$
, of
![]() $\beta = \alpha +1/\alpha $
has degree m. Thus, L has a subfield,
$\beta = \alpha +1/\alpha $
has degree m. Thus, L has a subfield,
![]() $K=F(\beta )$
, of index 2.
$K=F(\beta )$
, of index 2.
Proof. Let the roots of
![]() $f(x)$
be
$f(x)$
be
![]() $\{\alpha = r_1, 1/r_1, \ldots , r_m, 1/r_m\}$
, and let
$\{\alpha = r_1, 1/r_1, \ldots , r_m, 1/r_m\}$
, and let
![]() $g(x)$
be the polynomial whose roots are
$g(x)$
be the polynomial whose roots are
![]() $\{r_i+1/r_i\}$
for
$\{r_i+1/r_i\}$
for
![]() $1\leq i\leq m$
. Thus, the degree of
$1\leq i\leq m$
. Thus, the degree of
![]() $g(x)$
is m and
$g(x)$
is m and
![]() $g(\beta )=0$
. Let
$g(\beta )=0$
. Let
![]() $h(x) = x^m\cdot g(x+1/x)$
. It follows that
$h(x) = x^m\cdot g(x+1/x)$
. It follows that
![]() $f(x) = h(x)$
since both polynomials are monic, are of the same degree and have the same roots. If
$f(x) = h(x)$
since both polynomials are monic, are of the same degree and have the same roots. If
![]() $g(x)$
were reducible, say
$g(x)$
were reducible, say
![]() $g(x) = k(x)\cdot l(x)$
, then this would imply
$g(x) = k(x)\cdot l(x)$
, then this would imply
![]() $f(x)$
is reducible since
$f(x)$
is reducible since
However, this contradicts the irreducibility of
![]() $f(x)$
. Thus,
$f(x)$
. Thus,
![]() $g(x)$
is irreducible and is therefore the minimal polynomial of
$g(x)$
is irreducible and is therefore the minimal polynomial of
![]() $\beta $
.
$\beta $
.
Since subfields of L correspond to block systems of
![]() $\operatorname {\mathrm {Gal}}(f)$
(see [Reference Dixon and Mortimer5, Section 1.6] for more information about block systems), it follows that
$\operatorname {\mathrm {Gal}}(f)$
(see [Reference Dixon and Mortimer5, Section 1.6] for more information about block systems), it follows that
![]() $\operatorname {\mathrm {Gal}}(f)$
can be embedded in a suitable wreath product. In particular, the following is an immediate consequence of Theorem 2.1 and [Reference Dixon and Mortimer5, Theorem 2.6 A].
$\operatorname {\mathrm {Gal}}(f)$
can be embedded in a suitable wreath product. In particular, the following is an immediate consequence of Theorem 2.1 and [Reference Dixon and Mortimer5, Theorem 2.6 A].
Corollary 2.2. We have
![]() $\operatorname {\mathrm {Gal}}(f)$
is a subgroup of
$\operatorname {\mathrm {Gal}}(f)$
is a subgroup of
![]() $C_2 \wr \operatorname {\mathrm {Gal}}(g) \simeq C_2^m \rtimes \operatorname {\mathrm {Gal}}(g)$
. Thus,
$C_2 \wr \operatorname {\mathrm {Gal}}(g) \simeq C_2^m \rtimes \operatorname {\mathrm {Gal}}(g)$
. Thus,
![]() $2^m \cdot m!$
is an upper bound for
$2^m \cdot m!$
is an upper bound for
![]() $|\kern-1.5pt\operatorname {\mathrm {Gal}}(f)|$
.
$|\kern-1.5pt\operatorname {\mathrm {Gal}}(f)|$
.
3 Galois groups of reciprocal sextics
For the rest of the paper, we let
![]() $f(x) = x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$
be an irreducible reciprocal polynomial,
$f(x) = x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$
be an irreducible reciprocal polynomial,
![]() $\alpha $
a root of
$\alpha $
a root of
![]() $f(x)$
and
$f(x)$
and
![]() $L = F(\alpha )$
. Let
$L = F(\alpha )$
. Let
![]() $g(x)$
denote the minimal polynomial of
$g(x)$
denote the minimal polynomial of
![]() $\alpha +1/\alpha $
. Thus, we have the following result as a consequence of Theorem 2.1.
$\alpha +1/\alpha $
. Thus, we have the following result as a consequence of Theorem 2.1.
Corollary 3.1. The polynomial
![]() $g(x) = x^3 + ax^2 + (b - 3)x-2a+c$
is irreducible and defines a cubic subfield K of L.
$g(x) = x^3 + ax^2 + (b - 3)x-2a+c$
is irreducible and defines a cubic subfield K of L.
Since
![]() $f(x)$
is irreducible of degree 6, it follows that
$f(x)$
is irreducible of degree 6, it follows that
![]() $\operatorname {\mathrm {Gal}}(f)$
is a transitive subgroup of
$\operatorname {\mathrm {Gal}}(f)$
is a transitive subgroup of
![]() $S_6$
that is also a subgroup of
$S_6$
that is also a subgroup of
![]() $C_2 \wr S_3 \simeq S_4 \times C_2$
, by Corollary 2.2. Among the 16 transitive subgroups of
$C_2 \wr S_3 \simeq S_4 \times C_2$
, by Corollary 2.2. Among the 16 transitive subgroups of
![]() $S_6$
, only 8 are subgroups of
$S_6$
, only 8 are subgroups of
![]() $S_4\times C_2$
. Table 1 gives information about these 8 groups: their transitive numbers (as given in [Reference Butler and McKay3]), their orders, descriptive names and generators for (one representative of the conjugacy class of) each group.
$S_4\times C_2$
. Table 1 gives information about these 8 groups: their transitive numbers (as given in [Reference Butler and McKay3]), their orders, descriptive names and generators for (one representative of the conjugacy class of) each group.
Table 1 Possible Galois groups of irreducible reciprocal sextic polynomials. Size gives the order of the group.

We point out that 6T7 and 6T8 are isomorphic copies of
![]() $S_4$
that are distinguished by their parity; that is, 6T7 contains only even permutations while 6T8 does not; this is reflected in the table by the respective superscripts of each group’s ‘Name’. Note that each of these eight groups does appear as a Galois group over
$S_4$
that are distinguished by their parity; that is, 6T7 contains only even permutations while 6T8 does not; this is reflected in the table by the respective superscripts of each group’s ‘Name’. Note that each of these eight groups does appear as a Galois group over
![]() $\mathbb {Q}$
. See Table 2, which gives one sample irreducible reciprocal sextic polynomial in
$\mathbb {Q}$
. See Table 2, which gives one sample irreducible reciprocal sextic polynomial in
![]() $\mathbb {Q}[x]$
for each possible Galois group.
$\mathbb {Q}[x]$
for each possible Galois group.
Table 2 One sample reciprocal sextic Polynomial in
![]() $\mathbb {Q}[x]$
for each possible Galois group.
$\mathbb {Q}[x]$
for each possible Galois group.

We can determine properties of
![]() $\operatorname {\mathrm {Gal}}(f)$
from properties of
$\operatorname {\mathrm {Gal}}(f)$
from properties of
![]() $\operatorname {\mathrm {Gal}}(g)$
, as our next general result shows.
$\operatorname {\mathrm {Gal}}(g)$
, as our next general result shows.
Theorem 3.2. Let
![]() $\phi (x)\in F[x]$
be irreducible of degree
$\phi (x)\in F[x]$
be irreducible of degree
![]() $6$
and
$6$
and
![]() $\rho $
be a root of
$\rho $
be a root of
![]() $\phi $
. Suppose that
$\phi $
. Suppose that
![]() $F(\rho )$
has a subfield M of degree
$F(\rho )$
has a subfield M of degree
![]() $3$
defined by
$3$
defined by
![]() $\gamma (x)\in F[x]$
. Then:
$\gamma (x)\in F[x]$
. Then:
-
(1)
 $\operatorname {\mathrm {Disc}}(\phi )$
is a perfect square in F if and only if
$\operatorname {\mathrm {Disc}}(\phi )$
is a perfect square in F if and only if
 $\operatorname {\mathrm {Gal}}(\phi )$
is either
$\operatorname {\mathrm {Gal}}(\phi )$
is either
 $A_4$
or
$A_4$
or
 $S_4^+$
;
$S_4^+$
; -
(2)
 $\operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square in F if and only if
$\operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square in F if and only if
 $\operatorname {\mathrm {Gal}}(\phi )$
is either
$\operatorname {\mathrm {Gal}}(\phi )$
is either
 $C_6$
,
$C_6$
,
 $A_4$
or
$A_4$
or
 $A_4\times C_2$
;
$A_4\times C_2$
; -
(3)
 $\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square in F if and only if
$\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square in F if and only if
 $\operatorname {\mathrm {Gal}}(\phi )$
is either
$\operatorname {\mathrm {Gal}}(\phi )$
is either
 $S_3$
,
$S_3$
,
 $A_4$
or
$A_4$
or
 $S_4^-$
.
$S_4^-$
.
Proof. A standard result in Galois theory shows that
![]() $\operatorname {\mathrm {Gal}}(\phi )$
is a subgroup of
$\operatorname {\mathrm {Gal}}(\phi )$
is a subgroup of
![]() $A_6$
if and only if
$A_6$
if and only if
![]() $\operatorname {\mathrm {Disc}}(\phi )$
is a square in F. Of the eight possibilities, only
$\operatorname {\mathrm {Disc}}(\phi )$
is a square in F. Of the eight possibilities, only
![]() $A_4$
and
$A_4$
and
![]() $S_4^+$
are subgroups of
$S_4^+$
are subgroups of
![]() $A_6$
, proving item (1).
$A_6$
, proving item (1).
Since
![]() $\gamma $
is a cubic polynomial, another standard result in Galois theory shows
$\gamma $
is a cubic polynomial, another standard result in Galois theory shows
![]() $\operatorname {\mathrm {Gal}}(\gamma ) \simeq C_3$
if and only if
$\operatorname {\mathrm {Gal}}(\gamma ) \simeq C_3$
if and only if
![]() $\operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square. Under the Galois correspondence, M corresponds to an index 3 subgroup H of
$\operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square. Under the Galois correspondence, M corresponds to an index 3 subgroup H of
![]() $\operatorname {\mathrm {Gal}}(\phi )$
containing the stabiliser of
$\operatorname {\mathrm {Gal}}(\phi )$
containing the stabiliser of
![]() $\rho $
. Let N be the normal core of H in
$\rho $
. Let N be the normal core of H in
![]() $\operatorname {\mathrm {Gal}}(\phi )$
; that is, the largest normal subgroup of
$\operatorname {\mathrm {Gal}}(\phi )$
; that is, the largest normal subgroup of
![]() $\operatorname {\mathrm {Gal}}(\phi )$
contained in H. Therefore,
$\operatorname {\mathrm {Gal}}(\phi )$
contained in H. Therefore,
![]() $\operatorname {\mathrm {Gal}}(\gamma )$
is isomorphic to
$\operatorname {\mathrm {Gal}}(\gamma )$
is isomorphic to
![]() $\operatorname {\mathrm {Gal}}(\phi )/N$
. Using [11] to perform group computations, we see that each of the eight possibilities has a unique such subgroup H of index 3, up to conjugation. This means
$\operatorname {\mathrm {Gal}}(\phi )/N$
. Using [11] to perform group computations, we see that each of the eight possibilities has a unique such subgroup H of index 3, up to conjugation. This means
![]() $M/F$
is the unique cubic subfield of
$M/F$
is the unique cubic subfield of
![]() $F(\rho )/F$
, up to isomorphism. Further group computations show that in the cases of
$F(\rho )/F$
, up to isomorphism. Further group computations show that in the cases of
![]() $C_6$
,
$C_6$
,
![]() $A_4$
and
$A_4$
and
![]() $A_4\times C_2$
,
$A_4\times C_2$
,
![]() $\operatorname {\mathrm {Gal}}(\phi )/N$
is isomorphic to
$\operatorname {\mathrm {Gal}}(\phi )/N$
is isomorphic to
![]() $C_3$
; in all other cases it is isomorphic to
$C_3$
; in all other cases it is isomorphic to
![]() $S_3$
, proving item (2).
$S_3$
, proving item (2).
If both
![]() $\operatorname {\mathrm {Disc}}(\phi )$
and
$\operatorname {\mathrm {Disc}}(\phi )$
and
![]() $\operatorname {\mathrm {Disc}}(\gamma )$
are perfect squares, then
$\operatorname {\mathrm {Disc}}(\gamma )$
are perfect squares, then
![]() $\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square. According to the previous paragraphs, there is only one group among the eight where this occurs; namely,
$\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square. According to the previous paragraphs, there is only one group among the eight where this occurs; namely,
![]() $A_4$
. For the remainder of the proof, we suppose neither
$A_4$
. For the remainder of the proof, we suppose neither
![]() $\operatorname {\mathrm {Disc}}(\phi )$
nor
$\operatorname {\mathrm {Disc}}(\phi )$
nor
![]() $\operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square. Thus, the polynomials
$\operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square. Thus, the polynomials
![]() $x^2-\operatorname {\mathrm {Disc}}(\phi )$
and
$x^2-\operatorname {\mathrm {Disc}}(\phi )$
and
![]() $x^2-\operatorname {\mathrm {Disc}}(\gamma )$
define quadratic subfields of the splitting field of
$x^2-\operatorname {\mathrm {Disc}}(\gamma )$
define quadratic subfields of the splitting field of
![]() $\phi (x)$
. By the Galois correspondence,
$\phi (x)$
. By the Galois correspondence,
![]() $F(\sqrt {\operatorname {\mathrm {Disc}}(\phi )})$
corresponds to
$F(\sqrt {\operatorname {\mathrm {Disc}}(\phi )})$
corresponds to
![]() $H_1=A_6\cap \operatorname {\mathrm {Gal}}(\phi )$
. Similarly, if
$H_1=A_6\cap \operatorname {\mathrm {Gal}}(\phi )$
. Similarly, if
![]() $M'$
is the normal closure of
$M'$
is the normal closure of
![]() $\gamma (x)$
, then the subgroup fixing
$\gamma (x)$
, then the subgroup fixing
![]() $M'$
is N. Thus,
$M'$
is N. Thus,
![]() $F(\sqrt {\operatorname {\mathrm {Disc}}(\gamma )})$
corresponds to the unique subgroup
$F(\sqrt {\operatorname {\mathrm {Disc}}(\gamma )})$
corresponds to the unique subgroup
![]() $H_2$
of
$H_2$
of
![]() $\operatorname {\mathrm {Gal}}(\phi )$
of index 2 that contains N. It follows that
$\operatorname {\mathrm {Gal}}(\phi )$
of index 2 that contains N. It follows that
![]() $\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square if and only if
$\operatorname {\mathrm {Disc}}(\phi )\cdot \operatorname {\mathrm {Disc}}(\gamma )$
is a perfect square if and only if
![]() $H_1=H_2$
. Among the four remaining possible Galois groups, direct computation shows
$H_1=H_2$
. Among the four remaining possible Galois groups, direct computation shows
![]() $S_3$
and
$S_3$
and
![]() $S_4^-$
have
$S_4^-$
have
![]() $H_1=H_2$
. The groups
$H_1=H_2$
. The groups
![]() $D_6$
and
$D_6$
and
![]() $S_4\times C_2$
have
$S_4\times C_2$
have
![]() $H_1\neq H_2$
, proving item (3).
$H_1\neq H_2$
, proving item (3).
Our next result is an immediate consequence of Theorem 3.2 and the fact that
![]() $\operatorname {\mathrm {Disc}}(f) = ((2a+c)^2-(2b+2)^2) \cdot \operatorname {\mathrm {Disc}}(g)^2$
.
$\operatorname {\mathrm {Disc}}(f) = ((2a+c)^2-(2b+2)^2) \cdot \operatorname {\mathrm {Disc}}(g)^2$
.
Corollary 3.3. We have the following:
-
(1)
 $(2a+c)^2-(2b+2)^2$
is a perfect square in F if and only if
$(2a+c)^2-(2b+2)^2$
is a perfect square in F if and only if
 $\operatorname {\mathrm {Gal}}(f)$
is either
$\operatorname {\mathrm {Gal}}(f)$
is either
 $A_4$
or
$A_4$
or
 $S_4^+$
;
$S_4^+$
; -
(2)
 $\operatorname {\mathrm {Disc}}(g)$
is a perfect square in F if and only if
$\operatorname {\mathrm {Disc}}(g)$
is a perfect square in F if and only if
 $\operatorname {\mathrm {Gal}}(f)$
is either
$\operatorname {\mathrm {Gal}}(f)$
is either
 $C_6$
,
$C_6$
,
 $A_4$
or
$A_4$
or
 $A_4\times C_2$
;
$A_4\times C_2$
; -
(3)
 $((2a+c)^2-(2b+2)^2)\cdot \operatorname {\mathrm {Disc}}(g)$
is a perfect square in F if and only if
$((2a+c)^2-(2b+2)^2)\cdot \operatorname {\mathrm {Disc}}(g)$
is a perfect square in F if and only if
 $\operatorname {\mathrm {Gal}}(f)$
is either
$\operatorname {\mathrm {Gal}}(f)$
is either
 $S_3$
,
$S_3$
,
 $A_4$
or
$A_4$
or
 $S_4^-$
.
$S_4^-$
.
Next, we introduce a degree 4 resolvent polynomial that is helpful in determining
![]() $\operatorname {\mathrm {Gal}}(f)$
.
$\operatorname {\mathrm {Gal}}(f)$
.
Theorem 3.4. Let
![]() $h(x) = x^4+Ax^3+Bx^2+Cx+D$
, where
$h(x) = x^4+Ax^3+Bx^2+Cx+D$
, where
-
•
 $A = -4(a^2-2b-6)$
;
$A = -4(a^2-2b-6)$
; -
•
 $B = 2(3a^4 - 4a^2(3b+5) + 8(ac+b^2+4b+9))$
;
$B = 2(3a^4 - 4a^2(3b+5) + 8(ac+b^2+4b+9))$
; -
•
 $C = -4(a^4(a^2 - 6b-2) + 8a^2(ac+b^2 + 5) + 16(ac-2b^2 - b(ac+2) -4))$
;
$C = -4(a^4(a^2 - 6b-2) + 8a^2(ac+b^2 + 5) + 16(ac-2b^2 - b(ac+2) -4))$
; -
•
 $D = (a^4-4a^2(b-1)+8(ac-2b))^2$
.
$D = (a^4-4a^2(b-1)+8(ac-2b))^2$
.
Then,
![]() $h(x)$
is separable and has a linear factor if and only if
$h(x)$
is separable and has a linear factor if and only if
![]() $\operatorname {\mathrm {Gal}}(f)$
is either
$\operatorname {\mathrm {Gal}}(f)$
is either
![]() $C_6$
,
$C_6$
,
![]() $S_3$
or
$S_3$
or
![]() $D_6$
.
$D_6$
.
Proof. Let
![]() $\{\alpha = r, 1/r, s, 1/s, t,1/t\}$
be the roots of
$\{\alpha = r, 1/r, s, 1/s, t,1/t\}$
be the roots of
![]() $f(x)$
. The roots of
$f(x)$
. The roots of
![]() $h(x)$
are
$h(x)$
are
![]() $\{(r-1/r) \pm (s-1/s) \pm (t-1/t)\}$
, which can be verified by using the theory of elementary symmetric functions to express the coefficients of
$\{(r-1/r) \pm (s-1/s) \pm (t-1/t)\}$
, which can be verified by using the theory of elementary symmetric functions to express the coefficients of
![]() $h(x)$
in terms of a, b and c.
$h(x)$
in terms of a, b and c.
If
![]() $h(x)$
were not separable, then two roots would be equal. There are six cases:
$h(x)$
were not separable, then two roots would be equal. There are six cases:
-
(1)
 $(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) + (s-1/s) - (t-1/t)$
;
$(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) + (s-1/s) - (t-1/t)$
; -
(2)
 $(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) + (t-1/t)$
;
$(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) + (t-1/t)$
; -
(3)
 $(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$
;
$(r-1/r) + (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$
; -
(4)
 $(r-1/r) + (s-1/s) - (t-1/t) = (r-1/r) - (s-1/s) + (t-1/t)$
;
$(r-1/r) + (s-1/s) - (t-1/t) = (r-1/r) - (s-1/s) + (t-1/t)$
; -
(5)
 $(r-1/r) + (s-1/s) - (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$
;
$(r-1/r) + (s-1/s) - (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$
; -
(6)
 $(r-1/r) - (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$
.
$(r-1/r) - (s-1/s) + (t-1/t) = (r-1/r) - (s-1/s) - (t-1/t)$
.
We will show each case leads to a contradiction. Cases 2 and 5 imply
![]() $s=1/s$
and Cases 1 and 6 imply
$s=1/s$
and Cases 1 and 6 imply
![]() $t=1/t$
; these contradict the fact that
$t=1/t$
; these contradict the fact that
![]() $f(x)$
is irreducible and thus separable. Case 4 implies
$f(x)$
is irreducible and thus separable. Case 4 implies
![]() $st(s-t)=-(s-t)$
. Since
$st(s-t)=-(s-t)$
. Since
![]() $f(x)$
is separable, this implies
$f(x)$
is separable, this implies
![]() $st=-1$
. Thus,
$st=-1$
. Thus,
![]() $s=-1/t$
and
$s=-1/t$
and
![]() $1/s=-t$
. Therefore,
$1/s=-t$
. Therefore,
![]() $-a = r+1/r+s+1/s+t+1/t = r+1/r$
, which is rational. However, this contradicts Theorem 2.1, which shows
$-a = r+1/r+s+1/s+t+1/t = r+1/r$
, which is rational. However, this contradicts Theorem 2.1, which shows
![]() $r+1/r$
is not rational. Similarly, Case 3 implies
$r+1/r$
is not rational. Similarly, Case 3 implies
![]() $st(s+t)=s+t$
. If
$st(s+t)=s+t$
. If
![]() $s+t\neq 0$
, then
$s+t\neq 0$
, then
![]() $st=1$
; which contradicts the separability of
$st=1$
; which contradicts the separability of
![]() $f(x)$
. If
$f(x)$
. If
![]() $s=-t$
, then
$s=-t$
, then
![]() $1/s=-1/t$
. We again reach the contradiction
$1/s=-1/t$
. We again reach the contradiction
![]() $-a=r+1/r$
. Thus,
$-a=r+1/r$
. Thus,
![]() $h(x)$
is separable.
$h(x)$
is separable.
To prove the rest of the theorem, let
![]() $G = S_4\times C_2$
and
$G = S_4\times C_2$
and
![]() $H = D_6$
be the subgroups of
$H = D_6$
be the subgroups of
![]() $S_6$
as given in Table 1. Then, a complete set of a right coset representatives of
$S_6$
as given in Table 1. Then, a complete set of a right coset representatives of
![]() $G/H$
is
$G/H$
is
![]() $\{\text {id}, (34), (56), (34)(56) \}$
. Further, the only block system of G is
$\{\text {id}, (34), (56), (34)(56) \}$
. Further, the only block system of G is
![]() $R = \{\{1,2\}, \{3,4\}, \{5,6\}\}$
. We identify r as root 1,
$R = \{\{1,2\}, \{3,4\}, \{5,6\}\}$
. We identify r as root 1,
![]() $1/r$
as root 2, s as root 3,
$1/r$
as root 2, s as root 3,
![]() $1/s$
as root 4, t as root 5 and
$1/s$
as root 4, t as root 5 and
![]() $1/t$
as root 6.
$1/t$
as root 6.
A multivariable function stabilised by H is
![]() $T(x_1,x_2,x_3,x_4,x_5,x_6) = x_1-x_2+x_3-x_4+x_5-x_6$
; the action on T is via subscripts. We form the resolvent polynomial corresponding to G, H and T (see [Reference Soicher and McKay9]); this produces the polynomial
$T(x_1,x_2,x_3,x_4,x_5,x_6) = x_1-x_2+x_3-x_4+x_5-x_6$
; the action on T is via subscripts. We form the resolvent polynomial corresponding to G, H and T (see [Reference Soicher and McKay9]); this produces the polynomial
![]() $h(x)$
. By the theory of resolvent polynomials, the factorisation of
$h(x)$
. By the theory of resolvent polynomials, the factorisation of
![]() $h(x)$
corresponds to the orbits of
$h(x)$
corresponds to the orbits of
![]() $\operatorname {\mathrm {Gal}}(f)$
acting on the cosets
$\operatorname {\mathrm {Gal}}(f)$
acting on the cosets
![]() $G/H$
. Direct computation on each possibility for
$G/H$
. Direct computation on each possibility for
![]() $\operatorname {\mathrm {Gal}}(f)$
shows that in the cases of
$\operatorname {\mathrm {Gal}}(f)$
shows that in the cases of
![]() $C_6$
,
$C_6$
,
![]() $S_3$
and
$S_3$
and
![]() $D_6$
, there is an orbit of length 1 and an orbit of length 3. In the other five cases, there is a single orbit of length 4. This means
$D_6$
, there is an orbit of length 1 and an orbit of length 3. In the other five cases, there is a single orbit of length 4. This means
![]() $h(x)$
factors as a linear times a cubic polynomial in those three cases and remains irreducible in the other five cases, proving the theorem.
$h(x)$
factors as a linear times a cubic polynomial in those three cases and remains irreducible in the other five cases, proving the theorem.
We can now state our main result, which gives an elementary characterisation of
![]() $\operatorname {\mathrm {Gal}}(f)$
. This is an immediate consequence of Corollary 3.3 and Theorem 3.4. For convenience, Table 3 summarises this characterisation.
$\operatorname {\mathrm {Gal}}(f)$
. This is an immediate consequence of Corollary 3.3 and Theorem 3.4. For convenience, Table 3 summarises this characterisation.
Table 3 Let
![]() $f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1\in F[x]$
be irreducible,
$f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1\in F[x]$
be irreducible,
![]() $g(x) = x^3 + ax^2 + (b - 3)x-2a+c$
and
$g(x) = x^3 + ax^2 + (b - 3)x-2a+c$
and
![]() $h(x)$
as defined in Theorem 3.4. The table lists whether
$h(x)$
as defined in Theorem 3.4. The table lists whether
![]() $\operatorname {\mathrm {Disc}}(f)$
,
$\operatorname {\mathrm {Disc}}(f)$
,
![]() $\operatorname {\mathrm {Disc}}(g)$
and
$\operatorname {\mathrm {Disc}}(g)$
and
![]() $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
are perfect squares in F, and whether
$\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
are perfect squares in F, and whether
![]() $h(x)$
has a linear factor, according to
$h(x)$
has a linear factor, according to
![]() $\operatorname {\mathrm {Gal}}(f)$
.
$\operatorname {\mathrm {Gal}}(f)$
.

Theorem 3.5. Let
![]() $f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1\in F[x]$
be irreducible,
$f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1\in F[x]$
be irreducible,
![]() $g(x) = x^3 + ax^2 + (b - 3)x-2a+c$
and
$g(x) = x^3 + ax^2 + (b - 3)x-2a+c$
and
![]() $h(x)$
as defined in Theorem 3.4.
$h(x)$
as defined in Theorem 3.4.
-
(1) If
 $\operatorname {\mathrm {Disc}}(f)$
is a perfect square in F, then
$\operatorname {\mathrm {Disc}}(f)$
is a perfect square in F, then
 $\operatorname {\mathrm {Gal}}(f)$
is
$\operatorname {\mathrm {Gal}}(f)$
is
 $A_4$
if
$A_4$
if
 $\operatorname {\mathrm {Disc}}(g)$
is a square and is
$\operatorname {\mathrm {Disc}}(g)$
is a square and is
 $S_4^+$
otherwise.
$S_4^+$
otherwise. -
(2) If
 $\operatorname {\mathrm {Disc}}(f)$
is not a square and
$\operatorname {\mathrm {Disc}}(f)$
is not a square and
 $\operatorname {\mathrm {Disc}}(g)$
is a square, then
$\operatorname {\mathrm {Disc}}(g)$
is a square, then
 $\operatorname {\mathrm {Gal}}(f)$
is
$\operatorname {\mathrm {Gal}}(f)$
is
 $C_6$
if
$C_6$
if
 $h(x)$
has a linear factor and is
$h(x)$
has a linear factor and is
 $A_4\times C_2$
otherwise.
$A_4\times C_2$
otherwise. -
(3) If
 $\operatorname {\mathrm {Disc}}(f)$
and
$\operatorname {\mathrm {Disc}}(f)$
and
 $\operatorname {\mathrm {Disc}}(g)$
are not squares and
$\operatorname {\mathrm {Disc}}(g)$
are not squares and
 $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
is a square, then
$\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
is a square, then
 $\operatorname {\mathrm {Gal}}(f)$
is
$\operatorname {\mathrm {Gal}}(f)$
is
 $S_3$
if
$S_3$
if
 $h(x)$
has a linear factor and is
$h(x)$
has a linear factor and is
 $S_4^-$
otherwise.
$S_4^-$
otherwise. -
(4) If none of
 $\operatorname {\mathrm {Disc}}(f)$
,
$\operatorname {\mathrm {Disc}}(f)$
,
 $\operatorname {\mathrm {Disc}}(g)$
and
$\operatorname {\mathrm {Disc}}(g)$
and
 $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
is a square, then
$\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
is a square, then
 $\operatorname {\mathrm {Gal}}(f)$
is
$\operatorname {\mathrm {Gal}}(f)$
is
 $D_6$
if
$D_6$
if
 $h(x)$
has a linear factor and is
$h(x)$
has a linear factor and is
 $S_4\times C_2$
otherwise.
$S_4\times C_2$
otherwise.
Example 3.6. As an example, we use Theorem 3.5 to compute the Galois group of a family of sextic reciprocal polynomials. Take
![]() $t>-27/4$
and suppose the polynomial
$t>-27/4$
and suppose the polynomial
![]() $f(x) = x^6+3x^5+(t+6)x^4+(2t+7)x^3+(t+6)x^2+3x+1 \in \mathbb {Q}[x]$
is irreducible. Then,
$f(x) = x^6+3x^5+(t+6)x^4+(2t+7)x^3+(t+6)x^2+3x+1 \in \mathbb {Q}[x]$
is irreducible. Then,
![]() $\operatorname {\mathrm {Disc}}(f) = -t^4(4t+27)^3$
, which is not a square. We also have
$\operatorname {\mathrm {Disc}}(f) = -t^4(4t+27)^3$
, which is not a square. We also have
![]() $g(x) = x^3 + 3x^2 + (t + 3)x + (2t + 1)$
. Then,
$g(x) = x^3 + 3x^2 + (t + 3)x + (2t + 1)$
. Then,
![]() $\operatorname {\mathrm {Disc}}(g) = -t^2(4t+27)$
, which is also not a square. However,
$\operatorname {\mathrm {Disc}}(g) = -t^2(4t+27)$
, which is also not a square. However,
![]() $\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
is a square. Further,
$\operatorname {\mathrm {Disc}}(f)\cdot \operatorname {\mathrm {Disc}}(g)$
is a square. Further,
![]() $h(x)$
has
$h(x)$
has
![]() $x+4t+27$
as a linear factor. By item (3) of Theorem 3.5,
$x+4t+27$
as a linear factor. By item (3) of Theorem 3.5,
![]() $\operatorname {\mathrm {Gal}}(f)$
is
$\operatorname {\mathrm {Gal}}(f)$
is
![]() $S_3$
. Note, this also confirms item (3) of [Reference Jones6, Theorem 1].
$S_3$
. Note, this also confirms item (3) of [Reference Jones6, Theorem 1].
As an application of Theorem 3.5, we give one-parameter families of reciprocal sextics defined over
![]() $\mathbb {Q}$
for each possible Galois group.
$\mathbb {Q}$
for each possible Galois group.
Theorem 3.7. The polynomials in Table 4 have the indicated Galois group over
![]() $\mathbb {Q}$
, except for values of t that result in reducible polynomials.
$\mathbb {Q}$
, except for values of t that result in reducible polynomials.
Table 4 One-parameter families of reciprocal sextic polynomials with specified Galois group over
![]() $\mathbf {Q}$
.
$\mathbf {Q}$
.

Verifying each family of polynomials in Table 4 has the indicated Galois group is a straightforward computation using Theorem 3.5 and a computer algebra system. For example, we can consider the polynomial in the first row of Table 4:
![]() $f(x) = (2t^2{\kern-1pt}-2t+{\kern-1pt}13)x^6+(-4t+{\kern-1pt}2)x^5+(-2t^2{\kern-1pt}+{\kern-1pt}2t+19)x^4+(8t-4)x^3+(-2t^2+2t+19)x^2 +(-4t+2)x+(2t^2-2t+13)$
. Then,
$f(x) = (2t^2{\kern-1pt}-2t+{\kern-1pt}13)x^6+(-4t+{\kern-1pt}2)x^5+(-2t^2{\kern-1pt}+{\kern-1pt}2t+19)x^4+(8t-4)x^3+(-2t^2+2t+19)x^2 +(-4t+2)x+(2t^2-2t+13)$
. Then,
![]() $\operatorname {\mathrm {Disc}}(f) = -(t^2-t-1)^4(t^2-t+7)^4$
, which is not a square. We also have
$\operatorname {\mathrm {Disc}}(f) = -(t^2-t-1)^4(t^2-t+7)^4$
, which is not a square. We also have
![]() $g(x) = (2t^2 - 2t + 13)x^3 + (-4t + 2)x^2 + (-8t^2 + 8t - 20)x + (16t - 8)$
. Then,
$g(x) = (2t^2 - 2t + 13)x^3 + (-4t + 2)x^2 + (-8t^2 + 8t - 20)x + (16t - 8)$
. Then,
![]() $\operatorname {\mathrm {Disc}}(g) = (t^2-t-1)^2(t^2-t+7)^2$
, which is a square. Furthermore,
$\operatorname {\mathrm {Disc}}(g) = (t^2-t-1)^2(t^2-t+7)^2$
, which is a square. Furthermore,
![]() $h(x)$
has
$h(x)$
has
![]() $(t^4 - 2t^3 + 14t^2 - 13t + 169/4)x + 4t^4 - 8t^3 + 36t^2 - 32t + 64$
as a linear factor. This proves
$(t^4 - 2t^3 + 14t^2 - 13t + 169/4)x + 4t^4 - 8t^3 + 36t^2 - 32t + 64$
as a linear factor. This proves
![]() $\operatorname {\mathrm {Gal}}(f) = C_6$
, as claimed.
$\operatorname {\mathrm {Gal}}(f) = C_6$
, as claimed.