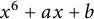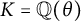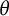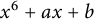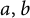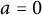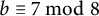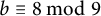1 Introduction
In Algebraic Number Theory, it is an important problem to know whether a given algebraic number field is monogenic. This problem has been widely studied and of interest to several mathematicians (cf. [Reference Ahmad, Nakahara and Hameed1, Reference Bilu, Gaál and Györy2, Reference Fadil4–Reference Gaál and Remete8, Reference Pethö and Pohst10, Reference Yakkou and Fadil11]). Let K be an algebraic number field generated by a complex root
$\theta $
of a monic irreducible polynomial
$f(x)$
having degree n with coefficients from the ring
$\mathbb Z$
of integers. Let
$\mathbb Z_K$
denote the ring of algebraic integers of K. It is well-known that
$\mathbb Z_K$
is a free abelian group of rank n. Let
$\mathop {\mathrm {ind}} \theta $
denote the index of the subgroup
$\mathbb Z[\theta ]$
in
$\mathbb Z_K$
. If
$\mathop {\mathrm {ind}} \alpha = 1$
for some
$\alpha \in \mathbb Z_K$
, then
$\{1, \alpha , \dots , \alpha ^{n-1}\}$
is a power integral basis of
$\mathbb Z_K$
. In such a case, K is called monogenic. If there does not exist any such
$\alpha \in \mathbb Z_K$
, then K is called nonmonogenic. In 2016, Ahmad et al. [Reference Ahmad, Nakahara and Hameed1] proved that the sextic number field generated by
$m^{\frac {1}{6}}$
is not monogenic if
$m\equiv 1 \mod 4$
and
$m\not \equiv \pm 1 \mod 9.$
In 2017, Gaál and Remete [Reference Gaál and Remete8] obtained some new results on monogenity of number fields generated by
$m^{\frac {1}{n}}$
with m a square free integer and
$3\leq n\leq 9$
by applying the explicit form of the index equation. In 2021, Yakkou and Fadil [Reference Yakkou and Fadil11] studied the monogenity of number fields generated by
$m^{\frac {1}{q^r}}$
, where m is a square-free integer and q be a prime number. In this paper, based on prime ideal factorization, we prove some results regarding the nonmonogenity of a number field K defined by an irreducible trinomial of the type
$x^6 + ax + b$
having integer coefficients. As an application of our result, we show that in the special case
$a = 0$
, if
$b\equiv 7 \mod 8$
or
$b\equiv 8 \mod 9$
, then K is not monogenic. We illustrate our results through examples.
Throughout the paper,
$\mathbb Z_K$
denotes the ring of algebraic integers of an algebraic number field K. For a prime number q and a nonzero m belonging to the ring
$\mathbb Z_q$
of q-adic integers,
$v_q(m)$
will be defined to be the highest power of q dividing m.
Precisely, we prove the following result.
Theorem 1.1 Let
$K = \mathbb Q(\theta )$
be an algebraic number field with
$\theta $
a root of an irreducible polynomial
$f(x) = x^6 + ax + b$
having integer coefficients. If a and
$b+1$
are both divisible by either
$8$
or
$9$
, then K is not monogenic.
The following result is an immediate consequence of the above theorem.
Corollary 1.2 Let b be an integer. Let
$f(x) = x^6 + b$
be an irreducible polynomial having a root
$\theta $
and
$K = \mathbb Q(\theta ).$
If
$b \equiv 7 \mod 8$
or
$b\equiv 8 \mod 9$
, then K is not monogenic.
It may be pointed out that the above corollary also follows from the results of [Reference Fadil4].
Theorem 1.3 Let
$K = \mathbb Q(\theta )$
and
$f(x) = x^6 + ax + b$
be as in Theorem 1.1. Let
$a \equiv 2 \mod 4$
and
$b\equiv 1 \mod 4$
. Let D denote the discriminant of
$f(x)$
given by
$5^5a^6-6^6b^5$
and
$D_2 = \frac {D}{v_2(D)}$
. If
$v_2(D)$
is even with
$D_2 \equiv 3 \mod 4$
and
$bD_2 \not \equiv 7 \mod 8$
, then K is not monogenic.
The following corollary is an immediate consequence of Theorem 1.3.
Corollary 1.4 Let
$a,b$
be integers such that
$a = 192r+78$
and
$b= 160r+65$
with
$r\in \mathbb Z$
. Let
$K = \mathbb Q(\theta )$
with
$\theta $
a root of an irreducible polynomial
$x^6 + ax + b$
, then K is not monogenic.
We now provide some examples of nonmonogenic number fields defined by irreducible sextic trinomials.
Example 1.5 Let q be a prime numberFootnote
1
of the form
$8k-1$
with
$k\in \mathbb Z$
. Let m be an odd integer such that q divides m. Consider
$f(x) = x^6 + 8m + q$
. Note that
$f(x)$
is irreducible over
$\mathbb Q$
as
$f(x)$
satisfies Eisenstein criterion with respect to prime q. If
$\theta $
is a root of
$f(x)$
and
$K = \mathbb Q(\theta )$
, then K is not monogenic in view of Theorem 1.1.
Example 1.6 Let
$K = \mathbb Q(\theta )$
with
$\theta $
a root of
$f(x) = x^6 + 78x+65$
. Note that
$f(x)$
satisfies Eisenstein criterion with respect to
$13$
, hence it is irreducible over
$\mathbb Q$
. By Corollary 1.4, we see that K is not monogenic.
2 Preliminary results
Let
$\mathbb Z_K$
denote the ring of algebraic integers of an algebraic number field
$K = \mathbb Q(\theta )$
with
$\theta $
a root of an irreducible polynomial
$f(x)$
having integer coefficients. Let q be a prime number. Suppose q does not divide
$\mathop {\mathrm {ind}} \theta $
. Then, in 1878, Dedekind [Reference Dedekind3] proved a significant theorem which relates the decomposition of
$f(x)$
modulo q with the factorization of
$q\mathbb Z_K$
into a product of prime ideals of
$\mathbb Z_K$
. The following lemma plays an important role in the proof of Theorem 1.1, which is an immediate consequence of Dedekind’s theorem. We shall denote by
$\mathbb F_q$
the field with q elements.
Lemma 2.1 Let K be a number field and q be a prime number. For every positive integer f, let
$N_f$
denote the number of irreducible polynomials of
$\mathbb F_q[x]$
of degree f and
$P_f$
denote the number of distinct prime ideals of
$\mathbb Z_K$
lying above q having residual degree f. If
$P_f> N_f$
for some f, then for every generator
$\alpha \in \mathbb Z_K$
of K, q divides
$\mathop {\mathrm {ind}} \alpha $
.
For a prime number q, to find the number of distinct prime ideals of
$\mathbb Z_K$
lying above q, we shall use a weaker version of the classical Theorem of Ore. Before stating that, we first introduce the notions of Gauss valuation,
$\phi $
-Newton polygon and q-regular where
$\phi (x)$
belonging to
$\mathbb Z_q[x]$
is a monic polynomial with
$\overline {\phi }(x)$
irreducible over
$\mathbb F_q$
.
We shall denote by
$v_{q,x}$
the Gauss valuation of the
$\mathbb Q_q(x)$
of rational functions in an indeterminate x which extends the valuation
$v_q$
of
$\mathbb Q_q$
and is defined on
$\mathbb Q_q[x]$
by
$$ \begin{align} v_{q,x}\left(\sum\limits_{i}b_ix^i\right) = \min\limits_i\{v_q(b_i)\}, b_i \in \mathbb Q_q. \end{align} $$
Now, we define the notion of
$\phi $
-Newton polygon with respect to some prime q.
Definition 2.1 Let q be a prime number and
$\phi (x) \in \mathbb Z_q[x]$
be a monic polynomial, which is irreducible modulo q. Let
$f(x) \in \mathbb Z_q[x]$
be a monic polynomial not divisible by
$\phi (x)$
and
$\sum \limits _{i=0}^{n}a_i(x)\phi (x)^{i}$
with
$\deg a_i(x) < \deg \phi (x), a_n(x) \neq 0$
be the
$\phi $
-expansion of
$f(x)$
obtained on dividing it by successive powers of
$\phi (x).$
To each non-zero term
$a_k(x)\phi (x)^k$
, we associate the point
$(n-k, v_{q,x}(a_k(x)))$
and form the set
$$\begin{align*}P = \{(k, v_{q,x}(a_{n-k}(x))) ~|~0\leq k\leq n, a_{n-k}(x) \neq 0\}.\end{align*}$$
The
$\phi $
-Newton polygon of
$f(x)$
with respect to prime q is the polygonal path formed by the lower edges along the convex hull of the points of P. The slopes of the edges are increasing when calculated from left to right.
Example 2.2 Let
$f(x) = (x+5)^4 - 5$
. Here, take
$\phi (x) = x$
. Then the x-Newton polygon of
$f(x)$
with respect to prime
$2$
consists of only one edge joining the points
$(0,0)$
and
$(4,2)$
with the lattice point
$(2,1)$
lying on it (see Figure 1).
Figure 1
x-Newton polygon of
$f(x)$
with respect to prime
$2$
.
Definition 2.2 Let
$\phi (x) \in \mathbb Z_q[x]$
be a monic polynomial which is irreducible modulo a prime q having a root
$\alpha $
in the algebraic closure
$\widetilde {\mathbb Q}_{q}$
of
$\mathbb Q_q$
. Let
$f(x) \in \mathbb Z_q[x]$
be a monic polynomial not divisible by
$\phi (x)$
having degree a multiple of
$\deg \phi (x)$
with
$\phi (x)$
-expansion
$\phi (x)^n + a_{n-1}(x)\phi (x)^{n-1} + \cdots + a_0(x)$
. Suppose that the
$\phi $
-Newton polygon of
$f(x)$
with respect to q consists of a single edge, say S having positive slope denoted by
$\frac {d}{e}$
with
$d, e$
coprime, i.e.,
$$\begin{align*}\min\left\{\frac{v_{q,x}(a_{n-i}(x))}{i}~\mid~1\leq i\leq n\right\} = \frac{v_{q,x}(a_0(x))}{n} = \frac{d}{e},\end{align*}$$
so that n is divisible by e, say
$n=et$
and
$v_{q,x}(a_{n-ej}(x)) \geq dj$
for
$1\leq j\leq t$
. Thus, the polynomial
$\frac {a_{n-ej}(x)}{q^{dj}}=b_j(x)$
(say) has coefficients in
$\mathbb Z_q$
and hence
$b_j(\alpha )\in \mathbb Z_q[\alpha ]$
for
$1\leq j \leq t$
. The polynomial
$T(y)$
in an indeterminate y defined by
$T(y) = y^t + \sum \limits _{j=1}^{t} \overline {b_j}(\overline {\alpha })y^{t-j}$
having coefficients in
$\mathbb {F}_q[\overline {\alpha }]$
is said to be the polynomial associated to
$f(x)$
with respect to
$(\phi ,S)$
; here, the field
$\mathbb F_q[\overline {\alpha }]$
is isomorphic to the field
$\frac {\mathbb {F}_q[x]}{\langle \overline {\phi }(x)\rangle }$
.
Example 2.3 Consider
$f(x) = (x+5)^4-5$
. Then, as in Example 2.2, the x-Newton polygon of
$f(x)$
with respect to prime
$2$
consists of only one edge joining the points
$(0,0)$
and
$(4,2)$
with the lattice point
$(2,1)$
lying on it. With notations as in the above definition, we see that
$e=2,~d=1$
and the polynomial associated to
$f(x)$
with respect to
$(x,S)$
is
$T(y)=y^2+y+\overline {1}$
belonging to
$\mathbb F_2[y]$
.
The following definition extends the notion of associated polynomial when
$f(x)$
is more general.
Definition 2.3 Let
$\phi (x), \alpha $
be as in Definition 2.2. Let
$g(x)\in \mathbb Z_q[x]$
be a monic polynomial not divisible by
$\phi (x)$
such that
$\overline {g}(x)$
is a power of
$\overline {\phi }(x)$
. Let
$\lambda _1 < \cdots < \lambda _k$
be the slopes of the edges of the
$\phi $
-Newton polygon of
$g(x)$
and
$S_i$
denote the edge with slope
$\lambda _i$
. In view of a classical result proved by Ore (cf. [Reference Khanduja and Kumar9, Theorem 1.1]), we can write
$g(x) = g_1(x)\cdots g_k(x)$
, where the
$\phi $
-Newton polygon of
$g_i(x) \in \mathbb Z_{{q}}[x]$
has a single edge, say
$S_i'$
which is a translate of
$S_i$
. Let
$T_i(y)$
belonging to
${\mathbb F}_{q}[\overline {\alpha }][y]$
denote the polynomial associated to
$g_i(x)$
with respect to (
$\phi ,~S_i'$
) described as in Definition 2.2. For convenience, the polynomial
$T_i(y)$
will be referred to as the polynomial associated to
$g(x)$
with respect to
$(\phi ,S_i)$
. The polynomial
$g(x)$
is said to be q-regular with respect to
$\phi $
if
$T_i(y)$
is irreducible in the algebraic closure of
$\mathbb F_q$
,
$1\leq i\leq k$
. In general, if
$f(x)$
belonging to
$\mathbb Z_q[x]$
is a monic polynomial and
$\overline {f}(x) = \overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$
is its factorization modulo q into irreducible polynomials with each
$\phi _i(x)$
belonging to
$\mathbb Z_q[x]$
monic and
$e_i> 0$
, then by Hensel’s Lemma there exist monic polynomials
$f_1(x), \dots , f_r(x)$
belonging to
$\mathbb Z_{{q}}[x]$
such that
$f(x) = f_1(x)\cdots f_r(x)$
and
$\overline {f}_i(x) = \overline {\phi }_i(x)^{e_i}$
for each i. The polynomial
$f(x)$
is said to be q-regular (with respect to
$\phi _1, \dots , \phi _r$
) if each
$f_i(x)$
is
${q}$
-regular with respect to
$\phi _i$
.
We now state a weaker version of Theorem 1.2 of [Reference Khanduja and Kumar9].
Theorem 2.4 Let
$L = \mathbb Q(\xi )$
be an algebraic number field with
$\xi $
satisfying a monic irreducible polynomial
$g(x) \in \mathbb Z[x]$
and q be a prime number. Let
$ \overline {\phi }_{1}(x)^{e_1}\cdots \overline {\phi }_r{(x)}^{e_r}$
be the factorization of
${g}(x)$
modulo q into a product of powers of distinct irreducible polynomials over
$\mathbb F_q$
with each
$\phi _i(x) \neq g(x)$
belonging to
$\mathbb Z[x]$
monic. Assume that the
$\phi _i$
-Newton polygon of
$g(x)$
has
$k_{i}$
edges, say
$S_{ij}$
having slopes
$\lambda _{ij} = \frac {d_{ij}}{e_{ij}}$
with
$\gcd (d_{ij}, e_{ij}) =1$
for
$1\leq j\leq k_i$
. If
$g(x)$
is q-regular with respect to
$\phi _1, \dots , \phi _r$
, then
$$\begin{align*}q\mathbb Z_L = \prod\limits_{i=1}^{r}\prod\limits_{j=1}^{k_i}\wp_{ij}^{e_{ij}},\end{align*}$$
where
$\wp _{ij}$
s are distinct prime ideals of
$\mathbb Z_L$
having residual degree
$\deg \phi _{i}(x)\times \deg T_{ij}(y)$
and
$T_{ij}(y)$
is the polynomial associated to
$g(x)$
with respect to
$(\phi _i, S_{ij})$
,
$1\leq j\leq k_i$
.
3 Proof of Theorems 1.1, 1.3
Proof of Theorem 1.1
We first consider the case when
$8$
divides both a and
$b+1$
. In this case,
$f(x)\equiv (x^2+x+1)^2(x+1)^2 \mod 2$
. Set
$\phi _1(x)=x^2+x+1$
and
$\phi _2(x)=x+1$
. The
$\phi _1$
-expansion of
$f(x)$
is given by
$$ \begin{align*} f(x)=(x^2+x+1)^3-3x(x^2+x+1)^2+(2x-2)(x^2+x+1)+ax+b+1. \end{align*} $$
Using the fact that
$\min \{v_2(a), v_2(b+1)\} \geq 3$
, it is easy to see that the
$\phi _1$
-Newton polygon of f has two edges of positive slope, say
$S_1 $
and
$S_2$
joining the point
$(1, 0)$
with
$(2, 1)$
and the point
$(2, 1)$
with
$(3, \min \{v_2(a),v_2(b+1)\})$
. The polynomial associated to
$f(x)$
with respect to
$(\phi _1,S_i)$
is linear for
$i=1,~2$
. Note that the
$\phi _2$
-expansion of
$f(x)$
is given by
$$ \begin{align*} f(x)&=(x+1)^6-6(x+1)^5+15(x+1)^4-20(x+1)^3+15(x+1)^2\\&\quad +(a-6)(x+1)+(-a+b+1). \end{align*} $$
It can be easily verified that the
$\phi _2$
-Newton polygon of f has two edges of positive slope, say
$S_1'$
and
$S_2'$
joining the point
$(4, 0)$
with
$(5, 1)$
and the point
$(5, 1)$
with
$(6, v_2(-a+b+1))$
respectively. The polynomial associated to
$f(x)$
with respect to
$(\phi _2,S_i)$
is linear for
$i=1,~2$
. So
$f(x)$
is
$2$
-regular with respect to
$\phi _1,~\phi _2$
. Hence, applying Theorem 2.4, we see that there are two distinct prime ideals of
$\mathbb Z_K$
lying above
$2$
having residual degree two each. Since there is only one irreducible polynomial over
$\mathbb F_2$
of degree two, in view of Lemma 2.1,
$2$
divides
$\mathop {\mathrm {ind}} \alpha $
for every generator
$\alpha \in \mathbb Z_K$
. So K is not monogenic.
Now consider the case when
$9$
divides both a and
$b+1$
. In this case,
$f(x)\equiv (x-1)^3 (x+1)^3 \mod 3$
. Set
$\phi _1(x)=x-1$
and
$\phi _2(x)=x+1$
. It is easy to check that the
$\phi _1$
-expansion of
$f(x)$
is given by
$$ \begin{align*} f(x)&=(x-1)^6+6(x-1)^5+15(x-1)^4+20(x-1)^3+15(x-1)^2\\&\quad +(a+6)(x-1)+(a+b+1). \end{align*} $$
Since
$9$
divides both a and
$b+1$
, we have
$a+6\equiv 6 \mod 9$
and
$a+b+1\equiv 0 \mod 9$
. Therefore, it can be easily seen that the
$\phi _1$
-Newton polygon of
$f(x)$
has two edges of positive slope. The first edge, say
$S_1$
is the line segment joining the point
$(3, 0)$
with
$(5, 1)$
and the second edge, say
$S_2$
is the line segment joining the point
$(5, 1)$
with
$(6, v_3(a+b+1))$
. The polynomial associated to
$f(x)$
with respect to
$(x-1,S_i)$
is linear for
$i=1,~2$
.
Recall that the
$\phi _2$
-expansion of
$f(x)$
is given by
$$ \begin{align*} f(x)&=(x+1)^6-6(x+1)^5+15(x+1)^4-20(x+1)^3+15(x+1)^2\\&\quad +(a-6)(x+1)+(-a+b+1). \end{align*} $$
One can verify that the
$\phi _2$
-Newton polygon of
$f(x)$
has two edges of positive slope. The first edge, say
$S_1'$
is the line segment joining the point
$(3, 0)$
with
$(5, 1)$
and the second edge, say
$S_2'$
is the line segment joining the point
$(5, 1)$
with
$(6, v_3(-a+b+1))$
. The polynomial associated to
$f(x)$
with respect to
$(x+1,S_i')$
is linear for
$i=1,~2$
.
Thus
$f(x)$
is
$3$
-regular with respect to
$\phi _1,~\phi _2$
. Hence, applying Theorem 2.4, we see that there exist four distinct prime ideals of
$\mathbb Z_K$
lying above
$3$
having residual degree one. Since there are only three irreducible polynomials of
$\mathbb F_3[x]$
of degree
$1$
, by Lemma 2.1, K is not monogenic.▪
Proof of Theorem 1.3
By hypothesis, we have
$a \equiv 2 \mod 4,~b\equiv 1 \mod 4$
. In this case,
$f(x)\equiv (x^2+x+1)^2(x+1)^2~ \mod 2.$
Set
$\phi _1(x)=x^2+x+1$
. The
$\phi _1$
-expansion of
$f(x)$
is given by
$$ \begin{align} f(x)=(x^2+x+1)^3-3x(x^2+x+1)^2+(2x-2)(x^2+x+1)+ax+b+1. \end{align} $$
Since
$\min \{v_2(a),v_2(b+1)\}=1$
, the
$\phi _1$
-Newton polygon of
$f(x)$
with respect to prime
$2$
has a single edge of positive slope, say S joining the point
$(1, 0)$
with
$(3, 1)$
. The polynomial associated to
$f(x)$
with respect to
$(\phi _1,S)$
is linear.
Since
$a \equiv 2 \mod 4,~b\equiv 1 \mod 4$
, we have
$v_2(D)\geq 8$
. Since
$v_2(D)$
is even, denote
$\frac {v_2(D)-6}{2}$
by u. Consider a rational number
$\delta = \frac {2^u-3b}{5a_2}$
with
$a_2 = \frac {a}{2}.$
Note that
$v_2(\delta ) = 0$
. Now set
$\phi _2(x) = x-\delta $
. The
$\phi _2$
-expansion of
$f(x)$
is given by
$$ \begin{align} f(x)&=(x-\delta)^6+6\delta(x-\delta)^5+15\delta^2(x-\delta)^4+20\delta^3(x-\delta)^3+15\delta^4(x-\delta)^2\nonumber\\ &\quad +f'(\delta)(x-\delta)+f(\delta). \end{align} $$
We claim that
$$ \begin{align} v_2(f(\delta)) = 2u+2,~v_2(f'(\delta))=u+1. \end{align} $$
Substituting
$\delta =\frac {2^u-3b}{5a_2}$
in
$f(\delta )=\delta ^6+a\delta +b$
, we have
$$\begin{align*}5^6a_2^6f(\delta)=(2^u-3b)^6+a(2^u-3b)(5a_2)^5+b(5a_2)^6;\end{align*}$$
the above equation on applying binomial theorem and rearranging terms can be rewritten as
$$ \begin{align*} 5^6a_2^6f(\delta)&=2^{6u}-9\cdot2^{5u+1}b+135b^22^{4u}-(3b)^3\cdot5\cdot2^{3u+2}+15(3b)^42^{2u}\\ &\quad +(b-2^{u+1})(3^6b^5-5^5a_2^6). \end{align*} $$
Dividing the above equation by
$2^{2u}$
and taking congruence modulo
$8$
, we see that
$$ \begin{align} \frac{5^6a_2^6f(\delta)}{2^{2u}}\equiv -bD_2-1 \mod 8. \end{align} $$
By hypothesis we have
$a\equiv 2 \mod 4, b\equiv 1 \mod 4$
,
$D_2 \equiv 3 \mod 4$
and
$bD_2 \not \equiv 7 \mod 8$
. So by (3.4), we have
$v_2(f(\delta )) = 2u+2$
. Now substituting
$x=\delta $
in the relation
$6f(x)-xf'(x)=5ax+6b$
and keeping in mind that
$5a\delta +6b=2^{u+1}$
together with the fact
$v_2(f(\delta )) = 2u+2$
, we see that
$v_2(f'(\delta ))=u+1$
. This proves our claim.
Using (3.2) and (3.3), one can see that the
$\phi _2 $
-Newton polygon of f has a single edge of positive slope, say
$S' $
joining the points
$(4, 0)$
and
$(6, 2u+2) $
with the lattice point
$(5, u+1)$
lying on it. The polynomial associated to
$f(x)$
with respect to
$(\phi _2,S')$
is
$Y^2+Y+\overline {1}$
which has no repeated roots. Therefore,
$f(x)$
is 2-regular with respect to
$\phi _1,~\phi _2$
. Applying Theorem 2.4, we see that there are two distinct prime ideals of
$\mathbb Z_K$
lying above
$2$
having residual degree two each. Since there is only one irreducible polynomial over
$\mathbb F_2$
of degree two, by Lemma 2.1, K is not monogenic.▪
Acknowledgment
The second author is thankful to his Ph.D. fellowship for the financial assistance.
