We develop a generalisation of the square sieve of Heath-Brown and use it to give an alternate proof of one of the large sieve inequalities in our previous paper [‘A large sieve inequality for characters to quadratic moduli’, Preprint, https://web.maths.unsw.edu.au/~ccorrigan/preprint6.pdf].

We prove that any positive rational number is the sum of distinct unit fractions with denominators in $\{p-1 : p\textrm { prime}\}$. The same conclusion holds for the set $\{p-h : p\textrm { prime}\}$ for any $h\in \mathbb {Z}\backslash \{0\}$, provided a necessary congruence condition is satisfied. We also prove that this is true for any subset of the primes of relative positive density, provided a necessary congruence condition is satisfied.

We study bracket words, which are a far-reaching generalization of Sturmian words, along Hardy field sequences, which are a far-reaching generalization of Piatetski-Shapiro sequences $\lfloor n^c \rfloor $. We show that sequences thus obtained are deterministic (that is, they have subexponential subword complexity) and satisfy Sarnak’s conjecture.

There has been recent interest in a hybrid form of the celebrated conjectures of Hardy–Littlewood and of Chowla. We prove that for any $k,\ell \ge 1$ and distinct integers $h_2,\ldots ,h_k,a_1,\ldots ,a_\ell $, we have:

$$ \begin{align*}\sum_{n\leq X}\mu(n+h_1)\cdots \mu(n+h_k)\Lambda(n+a_1)\cdots\Lambda(n+a_{\ell})=o(X)\end{align*} $$

for all except $o(H)$ values of $h_1\leq H$, so long as $H\geq (\log X)^{\ell +\varepsilon }$. This improves on the range $H\ge (\log X)^{\psi (X)}$, $\psi (X)\to \infty $, obtained in previous work of the first author. Our results also generalise from the Möbius function $\mu $ to arbitrary (non-pretentious) multiplicative functions.

We obtain some improved results for the exponential sum $\sum _{x<n\leq 2x}\Lambda (n)e(\alpha k n^{\theta })$ with $\theta \in (0,5/12),$ where $\Lambda (n)$ is the von Mangoldt function. Such exponential sums have relations with the so-called quasi-Riemann hypothesis and were considered by Murty and Srinivas [‘On the uniform distribution of certain sequences’, Ramanujan J. 7 (2003), 185–192].

We consider sums involving the divisor function over nonhomogeneous ( $\beta \neq 0$ ) Beatty sequences $ \mathcal {B}_{\alpha ,\beta }:=\{[\alpha n+\beta ]\}_{n=1}^{\infty } $ and show that

$$ \begin{align*} \sum_{n\leq N,\ n\in\mathcal{B}_{\alpha,\beta}}d(n) =\alpha^{-1}\sum_{m\leq N}d(m) +O(N^{1-1/(\tau+1)+\varepsilon}), \end{align*} $$

where N is a sufficiently large integer, $\alpha $ is of finite type $\tau $ and $\beta \neq 0$ . Previously, such estimates were only obtained for homogeneous Beatty sequences or for almost all $\alpha $ .

We prove a new generalization of Davenport's Fourier expansion of the infinite series involving the fractional part function over arithmetic functions. A new Mellin transform related to the Riemann zeta function is also established.

We study the analogue of the Bombieri–Vinogradov theorem for $\operatorname{SL}_{m}(\mathbb{Z})$ Hecke–Maass form $F(z)$. In particular, for $\operatorname{SL}_{2}(\mathbb{Z})$ holomorphic or Maass Hecke eigenforms, symmetric-square lifts of holomorphic Hecke eigenforms on $\operatorname{SL}_{2}(\mathbb{Z})$, and $\operatorname{SL}_{3}(\mathbb{Z})$ Maass Hecke eigenforms under the Ramanujan conjecture, the levels of distribution are all equal to $1/2,$ which is as strong as the Bombieri–Vinogradov theorem. As an application, we study an automorphic version of Titchmarch’s divisor problem; namely for $a\neq 0,$

$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D70C}(n)d(n-a)\ll x\log \log x,\end{eqnarray}$$

$\unicode[STIX]{x1D70C}(n)$

$\unicode[STIX]{x1D706}_{f}(n)$

$f$

$\operatorname{SL}_{2}(\mathbb{Z})$

$A_{F}(n,1)$

$F$

$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}\unicode[STIX]{x1D6EC}(n)\unicode[STIX]{x1D706}_{f}^{2}(n)d(n-a)=E_{1}(a)x\log x+O(x\log \log x),\end{eqnarray}$$

$E_{1}(a)$

$a$

$\unicode[STIX]{x1D70C}(n)d(n-a)$

Let $\Vert \cdots \Vert$ denote distance from the integers. Let $\unicode[STIX]{x1D6FC}$, $\unicode[STIX]{x1D6FD}$, $\unicode[STIX]{x1D6FE}$ be real numbers with $\unicode[STIX]{x1D6FC}$ irrational. We show that the inequality

$$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FC}p^{2}+\unicode[STIX]{x1D6FD}p+\unicode[STIX]{x1D6FE}\Vert <p^{-3/17+\unicode[STIX]{x1D700}}\end{eqnarray}$$

$p$

$\unicode[STIX]{x1D6FC}p$

$\unicode[STIX]{x1D6FD}=0$

Let $b$ be an integer larger than 1. We give an asymptotic formula for the exponential sum

$$\begin{eqnarray}\mathop{\sum }_{\substack{ p\leqslant x \\ g(p)=k}}\exp \big(2\text{i}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}p\big),\end{eqnarray}$$

$p$

$\unicode[STIX]{x1D6FD}\in \mathbb{R}$

$k\in \mathbb{Z}$

$g:\mathbb{N}\rightarrow \mathbb{Z}$

$b$

$\operatorname{pgcd}(g(1),\ldots ,g(b-1))=1$

Let $f$ be a polynomial of degree $k>1$ with irrational leading coefficient. We obtain results of the form

$$\begin{eqnarray}\Vert f(p)\Vert <p^{-\unicode[STIX]{x1D70E}}\end{eqnarray}$$

$p$

$\unicode[STIX]{x1D6FC}p^{k}$

Let $E(N)$ denote the number of positive integers $n\leqslant N$, with $n\equiv 4\;(\text{mod}\;24)$, which cannot be represented as the sum of four squares of primes. We establish that $E(N)\ll N^{11/32}$, thus improving on an earlier result of Harman and the first author, where the exponent $7/20$ appears in place of $11/32$.

We show that substantially more than a quarter of the odd integers of the form $pq$ up to $x$, with $p,q$ both prime, satisfy $p\equiv q\equiv 3~(\text{mod}\,4)$.

The main goal of this paper is to provide asymptotic expansions for the numbers #{p≤x:p prime,sq(p)=k} for k close to ((q−1)/2)log qx, where sq(n) denotes the q-ary sum-of-digits function. The proof is based on a thorough analysis of exponential sums of the form (where the sum is restricted to p prime), for which we have to extend a recent result by the second two authors.

We investigate exceptional sets in the Waring–Goldbach problem. For example, in the cubic case, we show that all but $O\left( {{N}^{79/84+\in }} \right)$ integers subject to the necessary local conditions can be represented as the sum of five cubes of primes. Furthermore, we develop a new device that leads easily to similar estimates for exceptional sets for sums of fourth and higher powers of primes.

We give estimates for exponential sums of the form $\sum_{n \leq N}\Lambda(n)\exp(2 \pi i a g^n/m)$, where m is a positive integer, a and g are integers relatively prime to m, and $\Lambda$ is the von Mangoldt function. In particular, our results yield bounds for exponential sums of the form $\sum_{p \leq N}\exp(2 \pi i a M_p/m)$, where Mp is the Mersenne number; $M_p=2^p-1$ for any prime p. We also estimate some closely related sums, including $\sum_{n \leq N}\mu(n)\exp(2 \pi i a g^n/m)$ and $\sum_{n \leq N}\mu^2(n)\exp(2 \pi i a g^n/m)$, where $\mu$ is the Möbius function.

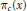For $c\,>\,1$ we denote by ${{\pi }_{c}}\left( x \right)$ the number of integers $n\,\le \,x$ such that 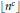$\left\lfloor {{n}^{c}} \right\rfloor $ is prime. In 1953, Piatetski-Shapiro has proved that 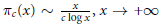${{\pi }_{c}}\left( x \right)\,\sim \,\frac{x}{c\,\log \,x},\,x\to \,+\infty $ holds for 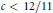$c\,<\,12/11$. Many authors have extended this range, which measures our progress in exponential sums techniques. In this article we obtain 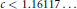$c\,<\,1.16117\ldots $.