Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T08:02:09.798Z Has data issue: false hasContentIssue false
  • English
  • Français

PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS

Part of: Diophantine approximation, transcendental number theory Elementary number theory Exponential sums and character sums Probabilistic theory: distribution modulo $1$; metric theory of algorithms Multiplicative number theory

Published online by Cambridge University Press:  04 April 2017

Bruno Martin ,
Christian Mauduit  and
Joël Rivat
Bruno Martin
Affiliation:
Univ. du Littoral-Côte-d’Opale, EA 2797 – LMPA – Laboratoire de mathématiques pures et appliquées Joseph-Liouville, 62228 Calais, France (martin@lmpa.univ-littoral.fr)
Christian Mauduit
Affiliation:
Université d’Aix-Marseille et Institut Universitaire de France, Institut de mathématiques de Marseille CNRS UMR 7373, 163 avenue de Luminy, Case 907, 13288 Marseille Cedex 9, France (mauduit@iml.univ-mrs.fr)
Joël Rivat
Affiliation:
Université d’Aix-Marseille, Institut de mathématiques de Marseille CNRS UMR 7373, 163 avenue de Luminy, Case 907, 13288 Marseille Cedex 9, France (rivat@iml.univ-mrs.fr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 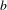$b$ be an integer larger than 1. We give an asymptotic formula for the exponential sum

$$\begin{eqnarray}\mathop{\sum }_{\substack{ p\leqslant x \\ g(p)=k}}\exp \big(2\text{i}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}p\big),\end{eqnarray}$$
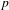where the summation runs over prime numbers $p$ and where 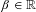$\unicode[STIX]{x1D6FD}\in \mathbb{R}$, 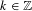$k\in \mathbb{Z}$, and 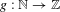$g:\mathbb{N}\rightarrow \mathbb{Z}$ is a strongly 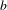$b$-additive function such that 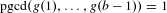$\operatorname{pgcd}(g(1),\ldots ,g(b-1))=1$.

Soit 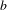$b$ un nombre entier supérieur ou égal à 2. Nous donnons une formule asymptotique pour la somme d’exponentielles

$$\begin{eqnarray}\mathop{\sum }_{\substack{ p\leqslant x \\ g(p)=k}}\exp \big(2\text{i}\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FD}p\big),\end{eqnarray}$$
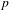où la sommation est effectuée sur les nombres premiers $p$, et où $\unicode[STIX]{x1D6FD}$ est un nombre réel, $k$ un nombre entier et $g:\mathbb{N}\rightarrow \mathbb{Z}$ une fonction fortement $b$-additive telle que $\operatorname{pgcd}(g(1),\ldots ,g(b-1))=1$.

Keywords

prime numbersexponential sumsb-additive functionsuniform distribution modulo 1

MSC classification

Primary: 11A63: Radix representation; digital problems 11J71: Distribution modulo one 11K65: Arithmetic functions 11L20: Sums over primes 11N05: Distribution of primes
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 1 , January 2019 , pp. 189 - 224
Copyright
© Cambridge University Press 2017 

Footnotes

Ce travail a bénéficié des aides de l’Agence nationale de la recherche portant les références « ANR-14-CE34-0009 » MUDERA, de Ciência sem Fronteiras, projet PVE 407308/2013-0, et du projet d’échange DynEurBraz (FP7 Irses 230844).

References

Références

Bassily, N. L. et Kátai, I., Distribution of the values of q-additive functions on polynomial sequences, Acta Math. Hungar. 68(4) (1995), 353–361.Google Scholar
Billingsley, P., Probability and measure, éd. third, Wiley Series in Probability and Mathematical Statistics, (John Wiley & Sons, Inc., New York, 1995). A Wiley-Interscience Publication.Google Scholar
Bourgain, J., Prescribing the binary digits of primes, Israel J. Math. 194(2) (2013), 935–955.Google Scholar
Bourgain, J., Prescribing the binary digits of primes, II, Israel J. Math. 206(1) (2015), 165–182.Google Scholar
Drmota, M. et Grabner, P. J., Analysis of digital functions and applications, in Combinatorics, automata and number theory, Encyclopedia of Mathematics and its Applications, Volume 135, pp. 452–504 (Cambridge University Press, Cambridge, 2010).Google Scholar
Drmota, M. et Mauduit, C., Weyl sums over integers with affine digit restrictions, J. Number Theory 130(11) (2010), 2404–2427.Google Scholar
Drmota, M., Mauduit, C. et Rivat, J., Primes with an Average Sum of Digits, Compositio 145(2) (2009), 271–292.Google Scholar
Fouvry, E. et Mauduit, C., Sur les entiers dont la somme des chiffres est moyenne, J. Number Theory 114(1) (2005), 135–152.Google Scholar
Harman, G., Primes with preassigned digits, Acta Arith. 125(2) (2006), 179–185.Google Scholar
Harman, G. et Kátai, I., Primes with preassigned digits. II, Acta Arith. 133(2) (2008), 171–184.Google Scholar
Iwaniec, H. et Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, Volume 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Kàtai, I., On the sum of digits of primes, Acta Math. Acad. Sci. Hungar. 30(1–2) (1977), 169–173.Google Scholar
Kàtai, I., Distribution of digits of primes in q-ary canonical form, Acta Math. Hungar. 47(3–4) (1986), 341–359.Google Scholar
Kuipers, L. et Niederreiter, H., Uniform distribution of sequences, Pure and Applied Mathematics (Wiley-Interscience John Wiley & Sons, New York, 1974), 390 pp.Google Scholar
Martin, B., Mauduit, C. et Rivat, J., Théorème des nombres premiers pour les fonctions digitales, Acta Arith. 165(1) (2014), 11–45.Google Scholar
Martin, B., Mauduit, C. et Rivat, J., Fonctions digitales le long des nombres premiers, Acta Arith. 170(2) (2015), 175–197.Google Scholar
Mauduit, C., Propriétés arithmétiques des substitutions et automates infinis, Ann. Inst. Fourier (Grenoble) 56(7) (2006), 2525–2549.Google Scholar
Mauduit, C. et Rivat, J., Sur un problème de Gelfond : la somme des chiffres des nombres premiers, Ann. of Math. (2) 171(3) (2010), 1591–1646.Google Scholar
Mauduit, C. et Sárközy, A., On the arithmetic structure of the integers whose sum of digits is fixed, Acta Arith. 81 (1997), 145–173.Google Scholar
Pólya, G. et Szegö, G., Problems and theorems in analysis. I, Classics in Mathematics (Springer, Berlin, 1998). Series, integral calculus, theory of functions, Translated from the German by Dorothee Aeppli, Reprint of the 1978 English translation.Google Scholar
Vinogradov, I., The method of trigonometrical sums in the theory of numbers, Tr. Mat. Inst. Steklova 23(1947) (1947), 110 pp.Google Scholar
Vinogradov, I., The method of Trigonometrical Sums in the Theory of Numbers, translated from the Russian, revised and annotated by K. F. Roth and A. Davenport (Interscience, London, 1954).Google Scholar
Wolke, D., Primes with preassigned digits, Acta Arith. 119(2) (2005), 201–209.Google Scholar