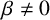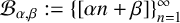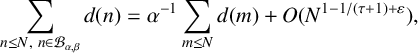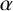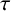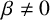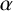1 Introduction
We investigate sums involving the divisor function over nonhomogeneous Beatty sequences. The nonhomogeneous Beatty sequences of integers are defined by
where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are fixed real numbers and
$\beta $
are fixed real numbers and
![]() $\beta \neq 0$
. Here,
$\beta \neq 0$
. Here,
![]() $[x]$
denotes the greatest integer not larger than x. The distribution properties of such sequences are related to the type of
$[x]$
denotes the greatest integer not larger than x. The distribution properties of such sequences are related to the type of
![]() $\alpha .$
For an irrational number
$\alpha .$
For an irrational number
![]() $\alpha ,$
we define its type
$\alpha ,$
we define its type
![]() $\tau $
by the relation
$\tau $
by the relation
where
![]() $\lVert u\rVert $
denotes the distance of u from the nearest integer. Thus, an irrational number
$\lVert u\rVert $
denotes the distance of u from the nearest integer. Thus, an irrational number
![]() $\alpha $
is of type
$\alpha $
is of type
![]() $\tau $
if and only if for every
$\tau $
if and only if for every
![]() $\epsilon>0$
, there is a constant
$\epsilon>0$
, there is a constant
![]() $c(\tau ,\alpha )$
such that
$c(\tau ,\alpha )$
such that
For properties and extensions of the type, see [Reference Abercrombie, Banks and Shparlinski2, Reference Banks and Shparlinski3].
Let
![]() $\alpha>1$
and
$\alpha>1$
and
![]() $\beta $
be fixed real numbers with
$\beta $
be fixed real numbers with
![]() $\alpha $
positive, irrational and of finite type
$\alpha $
positive, irrational and of finite type
![]() $\tau =\tau (\alpha )$
. The classical divisor function
$\tau =\tau (\alpha )$
. The classical divisor function
![]() $d(n)$
denotes the number of divisors of the integer n. There are precise estimates for sums of the divisor function over homogeneous Beatty sequences. Abercrombie proved in [Reference Abercrombie1] that for almost all
$d(n)$
denotes the number of divisors of the integer n. There are precise estimates for sums of the divisor function over homogeneous Beatty sequences. Abercrombie proved in [Reference Abercrombie1] that for almost all
![]() $\alpha>1$
with respect to the Lebesgue measure,
$\alpha>1$
with respect to the Lebesgue measure,
 $$ \begin{align*} \sum_{n\leq x, \, n\in \mathcal{B}_{\alpha,0}}d(n)=\alpha^{-1}\sum_{n\leq x}d(n)+O(x^{5/7+\varepsilon}), \end{align*} $$
$$ \begin{align*} \sum_{n\leq x, \, n\in \mathcal{B}_{\alpha,0}}d(n)=\alpha^{-1}\sum_{n\leq x}d(n)+O(x^{5/7+\varepsilon}), \end{align*} $$
where the implied constant may depend on
![]() $\alpha $
and
$\alpha $
and
![]() $\varepsilon .$
This result was subsequently improved and extended in various ways (see [Reference Abercrombie, Banks and Shparlinski2, Reference Lü and Zhai9, Reference Technau and Zafeiropoulos11, Reference Zhai14]). Zhai [Reference Zhai14] proved that for almost all
$\varepsilon .$
This result was subsequently improved and extended in various ways (see [Reference Abercrombie, Banks and Shparlinski2, Reference Lü and Zhai9, Reference Technau and Zafeiropoulos11, Reference Zhai14]). Zhai [Reference Zhai14] proved that for almost all
![]() $\alpha>1$
with respect to the Lebesgue measure,
$\alpha>1$
with respect to the Lebesgue measure,
 $$ \begin{align*} \sum_{n\leq x, \, n\in \mathcal{B}_{\alpha,0}}d(n)=\alpha^{-1}\sum_{n\leq x}d(n)+O(x^{1/2+\varepsilon}), \end{align*} $$
$$ \begin{align*} \sum_{n\leq x, \, n\in \mathcal{B}_{\alpha,0}}d(n)=\alpha^{-1}\sum_{n\leq x}d(n)+O(x^{1/2+\varepsilon}), \end{align*} $$
where the implied constant may depend on
![]() $\alpha $
and
$\alpha $
and
![]() $\varepsilon .$
In fact, this result can be modified to apply to an individual
$\varepsilon .$
In fact, this result can be modified to apply to an individual
![]() $\alpha .$
$\alpha .$
The main aim of this paper is to generalise such sums to nonhomogeneous Beatty sequences and an individual number
![]() $\alpha $
with an error term as strong as previous results (obtained for almost all numbers). By the method of [Reference Abercrombie, Banks and Shparlinski2] or [Reference Zhai14], it is not easy to obtain such results for nonhomogeneous Beatty sequences and an individual
$\alpha $
with an error term as strong as previous results (obtained for almost all numbers). By the method of [Reference Abercrombie, Banks and Shparlinski2] or [Reference Zhai14], it is not easy to obtain such results for nonhomogeneous Beatty sequences and an individual
![]() $\alpha $
, and we borrow some ideas from [Reference Banks and Shparlinski3].
$\alpha $
, and we borrow some ideas from [Reference Banks and Shparlinski3].
Before we focus on sums of the divisor function over Beatty sequences, we investigate a related double exponential sum, analogous to a result of Vaughan [Reference Vaughan12].
Theorem 1.1. Let
![]() $\alpha>1$
be a real number. Suppose that
$\alpha>1$
be a real number. Suppose that
![]() $a,q,h\in \mathbb {N}^{+}$
and
$a,q,h\in \mathbb {N}^{+}$
and
![]() $H,x\geq 1$
with
$H,x\geq 1$
with
![]() $H\ll x.$
If
$H\ll x.$
If
then
 $$ \begin{align*} \sum_{h\leq H}\bigg|\sum_{n\leq x}d(n)e(\alpha hn) \bigg|\ll\big(Hx^{1/2}+q+Hxq^{-1}\big)x^{\varepsilon}. \end{align*} $$
$$ \begin{align*} \sum_{h\leq H}\bigg|\sum_{n\leq x}d(n)e(\alpha hn) \bigg|\ll\big(Hx^{1/2}+q+Hxq^{-1}\big)x^{\varepsilon}. \end{align*} $$
Estimates for exponential functions twisted with divisor functions are classical problems in analytic number theory. For example, Chowla [Reference Chowla4] proved that for almost all irrational
![]() $\alpha ,$
$\alpha ,$
as
![]() $x\rightarrow \infty .$
Erdös [Reference Erdős5] improved the error term in this result to
$x\rightarrow \infty .$
Erdös [Reference Erdős5] improved the error term in this result to
for almost all
![]() $\alpha .$
However, such estimates give no idea about the numbers
$\alpha .$
However, such estimates give no idea about the numbers
![]() $\alpha $
to which the result applies. The estimates we obtain for such sums depend on the type of
$\alpha $
to which the result applies. The estimates we obtain for such sums depend on the type of
![]() $\alpha $
and we show that the estimate applies to any individual
$\alpha $
and we show that the estimate applies to any individual
![]() $\alpha $
whose rational approximations satisfy certain hypotheses. In this way, we can derive estimates for specific values of
$\alpha $
whose rational approximations satisfy certain hypotheses. In this way, we can derive estimates for specific values of
![]() $\alpha $
(or over interesting classes of
$\alpha $
(or over interesting classes of
![]() $\alpha $
such as the class of algebraic numbers). For example, we give the following consequence of Theorem 1.1.
$\alpha $
such as the class of algebraic numbers). For example, we give the following consequence of Theorem 1.1.
Corollary 1.2. For all irrational
![]() $\alpha>1$
of finite type
$\alpha>1$
of finite type
![]() $\tau <\infty , h\in \mathbb {N}^{+}$
and
$\tau <\infty , h\in \mathbb {N}^{+}$
and
![]() $H,x\geq 1$
with
$H,x\geq 1$
with
![]() $H\ll x,$
$H\ll x,$
 $$ \begin{align*} \sum_{h\leq H}\bigg|\sum_{n\leq x}d(n)e(\alpha hn)\bigg| \ll Hx^{1/2+\varepsilon}+(Hx)^{1-1/(\tau+1)+\varepsilon}, \end{align*} $$
$$ \begin{align*} \sum_{h\leq H}\bigg|\sum_{n\leq x}d(n)e(\alpha hn)\bigg| \ll Hx^{1/2+\varepsilon}+(Hx)^{1-1/(\tau+1)+\varepsilon}, \end{align*} $$
where the implied constant may depend on
![]() $\alpha $
and
$\alpha $
and
![]() $\varepsilon .$
$\varepsilon .$
Remark 1.3. Taking
![]() $\tau =1$
and
$\tau =1$
and
![]() $H=1$
gives a similar upper bound for the sum
$H=1$
gives a similar upper bound for the sum
for individual numbers
![]() $\alpha $
of finite type
$\alpha $
of finite type
![]() $\tau <\infty $
.
$\tau <\infty $
.
By adapting the method of proving Theorem 1.1, we can obtain the following result for inhomogeneous Beatty sequences.
Theorem 1.4. Let
![]() $\alpha>1$
be a fixed irrational number of finite type
$\alpha>1$
be a fixed irrational number of finite type
![]() $\tau <\infty $
and
$\tau <\infty $
and
![]() $\beta \in \mathbb {R}$
be fixed. Then there is a constant
$\beta \in \mathbb {R}$
be fixed. Then there is a constant
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
 $$ \begin{align*} \sum_{n\leq N,\ n\in\mathcal{B}_{\alpha,\beta}}d(n) =\alpha^{-1}\sum_{m\leq N}d(m) +O(N^{1-1/(\tau+1)+\varepsilon}), \end{align*} $$
$$ \begin{align*} \sum_{n\leq N,\ n\in\mathcal{B}_{\alpha,\beta}}d(n) =\alpha^{-1}\sum_{m\leq N}d(m) +O(N^{1-1/(\tau+1)+\varepsilon}), \end{align*} $$
where N is a sufficiently large integer and the implied constant depends only on
![]() $\alpha , \beta $
and
$\alpha , \beta $
and
![]() $\varepsilon $
.
$\varepsilon $
.
Remark 1.5. Previously, such estimates were proved only for almost all
![]() $\alpha>1$
(not for an individual
$\alpha>1$
(not for an individual
![]() $\alpha $
) and for homogeneous Beatty sequences. Our result also gives almost all results for nonhomogeneous Beatty sequences because, by the theorems of Khinchin [Reference Khinchin7] and of Roth [Reference Roth10], almost all real numbers and all irrational algebraic numbers are of type
$\alpha $
) and for homogeneous Beatty sequences. Our result also gives almost all results for nonhomogeneous Beatty sequences because, by the theorems of Khinchin [Reference Khinchin7] and of Roth [Reference Roth10], almost all real numbers and all irrational algebraic numbers are of type
![]() $\tau =1$
. One can also consider generalised divisor functions, which were studied in [Reference Lü and Zhai9, Reference Zhai14] only for the case of homogeneous Beatty sequences.
$\tau =1$
. One can also consider generalised divisor functions, which were studied in [Reference Lü and Zhai9, Reference Zhai14] only for the case of homogeneous Beatty sequences.
2 Proof of Theorem 1.1
To prove the theorem, we need the concept of discrepancy. For a sequence
![]() $u_{m}, m=1,2,\ldots\, $
, M, of points of
$u_{m}, m=1,2,\ldots\, $
, M, of points of
![]() $\mathbb {R}/\mathbb {Z}$
, the discrepancy
$\mathbb {R}/\mathbb {Z}$
, the discrepancy
![]() $D(M)$
of the sequence is
$D(M)$
of the sequence is
 $$ \begin{align} D(M)=\sup_{\mathcal{I}\in[0,1)} \bigg|\frac{\mathcal{V}(\mathcal{I},M)}{M} -|\mathcal{I}|\bigg|, \end{align} $$
$$ \begin{align} D(M)=\sup_{\mathcal{I}\in[0,1)} \bigg|\frac{\mathcal{V}(\mathcal{I},M)}{M} -|\mathcal{I}|\bigg|, \end{align} $$
where the supremum is taken over all subintervals
![]() $\mathcal {I}=(c, d)$
of the interval
$\mathcal {I}=(c, d)$
of the interval
![]() $[0, 1), \mathcal {V} (\mathcal {I}, M)$
is the number of positive integers
$[0, 1), \mathcal {V} (\mathcal {I}, M)$
is the number of positive integers
![]() $m\leq M$
such that
$m\leq M$
such that
![]() $u_{m}\in \mathcal {I}$
, and
$u_{m}\in \mathcal {I}$
, and
![]() $|\mathcal {I}| = d-c$
is the length of
$|\mathcal {I}| = d-c$
is the length of
![]() $|\mathcal {I}|.$
$|\mathcal {I}|.$
Let
![]() $D_{\alpha ,\beta }(M)$
denote the discrepancy of the sequence
$D_{\alpha ,\beta }(M)$
denote the discrepancy of the sequence
![]() $\{\alpha m+\beta \}, m=1,2,\ldots , M$
, where
$\{\alpha m+\beta \}, m=1,2,\ldots , M$
, where
![]() $\{x\}=x-[x].$
We introduce several auxiliary lemmas.
$\{x\}=x-[x].$
We introduce several auxiliary lemmas.
Lemma 2.1 [Reference Banks and Shparlinski3].
Let
![]() $\alpha>1.$
An integer m has the form
$\alpha>1.$
An integer m has the form
![]() $m=[\alpha n+\beta ]$
for some integer n if and only if
$m=[\alpha n+\beta ]$
for some integer n if and only if
The value of n is determined uniquely by
![]() $m.$
$m.$
Lemma 2.2 [Reference Kuipers and Niederreiter8, Ch. 2, Theorem 3.2].
Let
![]() $\alpha $
be a fixed irrational number of finite type
$\alpha $
be a fixed irrational number of finite type
![]() $\tau <\infty .$
Then, for all
$\tau <\infty .$
Then, for all
![]() $\beta \in \mathbb {R},$
we have
$\beta \in \mathbb {R},$
we have
as
![]() $M\rightarrow \infty $
, where the function implied by
$M\rightarrow \infty $
, where the function implied by
![]() $o(1)$
depends only on
$o(1)$
depends only on
![]() $\alpha .$
$\alpha .$
Lemma 2.3 [Reference Vinogradov13, page 32].
For any
![]() $\Delta \in \mathbb {R}$
such that
$\Delta \in \mathbb {R}$
such that
![]() $0<\Delta <1/8$
and
$0<\Delta <1/8$
and
![]() $\Delta \leq 1/2\min \{\gamma ,1-\gamma \},$
there exists a periodic function
$\Delta \leq 1/2\min \{\gamma ,1-\gamma \},$
there exists a periodic function
![]() $\Psi _{\Delta }(x)$
of period 1 such that:
$\Psi _{\Delta }(x)$
of period 1 such that:
-
(1)
 $0\leq \Psi _{\Delta }(x) \leq 1 \mbox { for all } x\in \mathbb {R};$
$0\leq \Psi _{\Delta }(x) \leq 1 \mbox { for all } x\in \mathbb {R};$
-
(2)
 $\Psi _{\Delta }(x)=\Psi (x) \mbox { if } \Delta \leq x\leq \gamma -\Delta \mbox { or } \gamma +\Delta \leq x\leq 1-\Delta $
where
$\Psi _{\Delta }(x)=\Psi (x) \mbox { if } \Delta \leq x\leq \gamma -\Delta \mbox { or } \gamma +\Delta \leq x\leq 1-\Delta $
where  $$ \begin{align*} \Psi(x)= \begin{cases} 1\ \ &\mbox{if}\ \,0<x\leq \gamma,\\ 0\ \ &\mbox{if}\ \,\gamma<x\leq 1; \end{cases} \end{align*} $$
$$ \begin{align*} \Psi(x)= \begin{cases} 1\ \ &\mbox{if}\ \,0<x\leq \gamma,\\ 0\ \ &\mbox{if}\ \,\gamma<x\leq 1; \end{cases} \end{align*} $$
-
(3)
 $\Psi _{\Delta }(x)$
can be represented as a Fourier series (2.2)where the coefficients
$\Psi _{\Delta }(x)$
can be represented as a Fourier series (2.2)where the coefficients $$ \begin{align} \Psi_{\Delta}(x)=\gamma+\sum_{j=1}^{\infty} g_{j}e({\kern1.5pt}jx)+h_{j}e(-jx), \end{align} $$
$$ \begin{align} \Psi_{\Delta}(x)=\gamma+\sum_{j=1}^{\infty} g_{j}e({\kern1.5pt}jx)+h_{j}e(-jx), \end{align} $$
 $g_{j}$
and
$g_{j}$
and
 $h_{j}$
satisfy
$h_{j}$
satisfy
 $\max \{|g_{j}|, |h_{j}|\}\ll \min \{{\kern1.5pt}j^{-1},j^{-2}\Delta ^{-1}\}$
for
$\max \{|g_{j}|, |h_{j}|\}\ll \min \{{\kern1.5pt}j^{-1},j^{-2}\Delta ^{-1}\}$
for
 $j\geq 1$
.
$j\geq 1$
.
Lemma 2.4. Let
![]() $\alpha $
be of finite type
$\alpha $
be of finite type
![]() $\tau <\infty $
and let K be sufficiently large. For an integer
$\tau <\infty $
and let K be sufficiently large. For an integer
![]() $w\geq 1,$
there exist
$w\geq 1,$
there exist
![]() $a,q\in \mathbb {Z}, a/q\in \mathbb {Q}$
with
$a,q\in \mathbb {Z}, a/q\in \mathbb {Q}$
with
![]() $(a,q)=1$
and
$(a,q)=1$
and
![]() $K^{1/\tau -\varepsilon }w^{-1}<q\leq K$
such that
$K^{1/\tau -\varepsilon }w^{-1}<q\leq K$
such that
 $$ \begin{align*} \bigg|\alpha w-\frac{a}{q}\bigg|\leq \frac{1}{qK}. \end{align*} $$
$$ \begin{align*} \bigg|\alpha w-\frac{a}{q}\bigg|\leq \frac{1}{qK}. \end{align*} $$
Proof. By the Dirichlet approximation theorem, there is a rational number
![]() $a/q$
with
$a/q$
with
![]() $(a,q)=1$
and
$(a,q)=1$
and
![]() $q\leq K$
such that
$q\leq K$
such that
 $$ \begin{align*} \bigg|\alpha w-\frac{a}{q}\bigg|<\frac{1}{qK}, \end{align*} $$
$$ \begin{align*} \bigg|\alpha w-\frac{a}{q}\bigg|<\frac{1}{qK}, \end{align*} $$
that is,
![]() $ \lVert qw\alpha \rVert \,\leq 1/K. $
Since
$ \lVert qw\alpha \rVert \,\leq 1/K. $
Since
![]() $\alpha $
is of type
$\alpha $
is of type
![]() $\tau <\infty ,$
for sufficiently large
$\tau <\infty ,$
for sufficiently large
![]() $K,$
we have
$K,$
we have
Thus
which gives
Lemma 2.5 [Reference Iwaniec and Kowalski6, Section 13.5].
If
![]() $\vert \alpha -a/q\vert \leq q^{-2}, a,q\in \mathbb {N}$
and
$\vert \alpha -a/q\vert \leq q^{-2}, a,q\in \mathbb {N}$
and
![]() $(a,q)=1,$
then
$(a,q)=1,$
then
 $$ \begin{align*} \sum_{1\leq n \leq M}\min\bigg\{\frac{x}{n},\frac{1}{2\lVert n\alpha\rVert}\bigg\}\ll (M+q+xq^{-1})\log 2qx. \end{align*} $$
$$ \begin{align*} \sum_{1\leq n \leq M}\min\bigg\{\frac{x}{n},\frac{1}{2\lVert n\alpha\rVert}\bigg\}\ll (M+q+xq^{-1})\log 2qx. \end{align*} $$
Proof of Theorem 1.1.
By the Dirichlet hyperbolic method,
 $$ \begin{align} \sum_{h\leq H}\bigg|\sum_{1\leq n\leq x}d(n) e(\alpha h n)\bigg|=\sum_{h\leq H} \bigg|\sum_{n_{1}n_{2}\leq x}e(\alpha hn_{1}n_{2}) \bigg| \leq \sum_{h\leq H} 2\bigg|\sum_{\substack{n_{1}n_{2}\leq x \\ n_{1}\leq n_{2}}}e(\alpha hn_{1}n_{2})\bigg|. \end{align} $$
$$ \begin{align} \sum_{h\leq H}\bigg|\sum_{1\leq n\leq x}d(n) e(\alpha h n)\bigg|=\sum_{h\leq H} \bigg|\sum_{n_{1}n_{2}\leq x}e(\alpha hn_{1}n_{2}) \bigg| \leq \sum_{h\leq H} 2\bigg|\sum_{\substack{n_{1}n_{2}\leq x \\ n_{1}\leq n_{2}}}e(\alpha hn_{1}n_{2})\bigg|. \end{align} $$
However,
 $$ \begin{align*} \bigg|\sum_{\substack{n_{1}n_{2}\leq x \\ n_{1}\leq n_{2}}}e(\alpha hn_{1}n_{2})\bigg|\ll \sum_{n_{1}\leq x^{1/2}}\bigg|\sum_{n_{2}\leq x/n_{1}}e(\alpha hn_{1}n_{2})\bigg|. \end{align*} $$
$$ \begin{align*} \bigg|\sum_{\substack{n_{1}n_{2}\leq x \\ n_{1}\leq n_{2}}}e(\alpha hn_{1}n_{2})\bigg|\ll \sum_{n_{1}\leq x^{1/2}}\bigg|\sum_{n_{2}\leq x/n_{1}}e(\alpha hn_{1}n_{2})\bigg|. \end{align*} $$
By the well-known estimate
 $$ \begin{align*} \sum_{1\leq n\leq x}e(\alpha n)\leq \min\bigg(x,\frac{1}{2\lVert\alpha\rVert} \bigg) ,\end{align*} $$
$$ \begin{align*} \sum_{1\leq n\leq x}e(\alpha n)\leq \min\bigg(x,\frac{1}{2\lVert\alpha\rVert} \bigg) ,\end{align*} $$
we have
 $$ \begin{align*} \bigg|\sum_{n_{2}\leq x/n_{1}}e(\alpha hn_{1}n_{2})\bigg| \leq \min\bigg(\frac{x}{n_{1}},\frac{1}{2\lVert\alpha hn_{1}\rVert} \bigg). \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n_{2}\leq x/n_{1}}e(\alpha hn_{1}n_{2})\bigg| \leq \min\bigg(\frac{x}{n_{1}},\frac{1}{2\lVert\alpha hn_{1}\rVert} \bigg). \end{align*} $$
Hence by Lemma 2.5,
 $$ \begin{align} \sum_{h\leq H}\bigg|\sum_{\substack{n_{1}n_{2}\leq x \\ n_{1}\leq n_{2}}}e(\alpha hn_{1}n_{2})\bigg|&\ll \sum_{h\leq H}\sum_{n_{1}\leq x^{1/2}} \min\bigg(\frac{x}{n_{1}},\frac{1}{2\lVert\alpha hn_{1}\rVert} \bigg) \nonumber\\[3pt] &\ll x^{\varepsilon}\sum_{n\leq Hx^{1/2}} \min\bigg(\frac{Hx}{n},\frac{1}{2\lVert\alpha n\rVert} \bigg) \nonumber\\[3pt] &\ll x^{\varepsilon}(Hx^{1/2}+q+Hxq^{-1})\log 2qx. \end{align} $$
$$ \begin{align} \sum_{h\leq H}\bigg|\sum_{\substack{n_{1}n_{2}\leq x \\ n_{1}\leq n_{2}}}e(\alpha hn_{1}n_{2})\bigg|&\ll \sum_{h\leq H}\sum_{n_{1}\leq x^{1/2}} \min\bigg(\frac{x}{n_{1}},\frac{1}{2\lVert\alpha hn_{1}\rVert} \bigg) \nonumber\\[3pt] &\ll x^{\varepsilon}\sum_{n\leq Hx^{1/2}} \min\bigg(\frac{Hx}{n},\frac{1}{2\lVert\alpha n\rVert} \bigg) \nonumber\\[3pt] &\ll x^{\varepsilon}(Hx^{1/2}+q+Hxq^{-1})\log 2qx. \end{align} $$
Hence, by Lemma 2.4, (2.3) and (2.4), for all irrational
![]() $\alpha $
of finite type
$\alpha $
of finite type
![]() $\tau <\infty $
,
$\tau <\infty $
,
3 Proof of Theorem 1.4
It is easy to see that
 $$ \begin{align*} \sum_{n\leq x,\ n\in\mathcal{B}_{\alpha,\beta}}d(n) = \sum_{n\leq (x-\beta)/\alpha} d([\alpha n+\beta]). \end{align*} $$
$$ \begin{align*} \sum_{n\leq x,\ n\in\mathcal{B}_{\alpha,\beta}}d(n) = \sum_{n\leq (x-\beta)/\alpha} d([\alpha n+\beta]). \end{align*} $$
Hence, we can focus on the right-hand sum. The proof is similar to the argument of Theorem 1.1. Let
![]() $\delta =\alpha ^{-1}(1-\beta )$
and
$\delta =\alpha ^{-1}(1-\beta )$
and
![]() $M=[\alpha N+\beta ].$
Then by Lemma 2.1,
$M=[\alpha N+\beta ].$
Then by Lemma 2.1,
 $$ \begin{align} \sum_{n\leq N}d([\alpha n+\beta])=\sum_{\substack{m\leq M \\[3pt] 0<\{\gamma m+\delta\}\leq \gamma}}d(m)+O(1) =\sum_{m\leq M}d(m)\Psi(\gamma m+\delta)+O(1), \end{align} $$
$$ \begin{align} \sum_{n\leq N}d([\alpha n+\beta])=\sum_{\substack{m\leq M \\[3pt] 0<\{\gamma m+\delta\}\leq \gamma}}d(m)+O(1) =\sum_{m\leq M}d(m)\Psi(\gamma m+\delta)+O(1), \end{align} $$
where
![]() $\Psi (x)$
is the periodic function with period one for which
$\Psi (x)$
is the periodic function with period one for which
 $$ \begin{align*} \Psi(x)= \begin{cases} 1\ \ &\textup{if}\ 0<x\leq \gamma,\\ 0\ \ &\textup{if}\ \gamma<x\leq 1. \end{cases} \end{align*} $$
$$ \begin{align*} \Psi(x)= \begin{cases} 1\ \ &\textup{if}\ 0<x\leq \gamma,\\ 0\ \ &\textup{if}\ \gamma<x\leq 1. \end{cases} \end{align*} $$
Let
![]() $\Delta $
and
$\Delta $
and
![]() $\Psi _{\Delta }(x)$
satisfy the conditions of Lemma 2.3 with
$\Psi _{\Delta }(x)$
satisfy the conditions of Lemma 2.3 with
From (3.1),
 $$ \begin{align} \sum_{n\leq N}d([\alpha n+\beta]) &=\sum_{m\leq M}d(m)\Psi(\gamma m+\delta)+O(1)\nonumber\\[3pt] &=\sum_{m\leq M}d(m)\Psi_{\Delta}(\gamma m+\delta) +O(1+\mathcal{V}(I,M)\log N), \end{align} $$
$$ \begin{align} \sum_{n\leq N}d([\alpha n+\beta]) &=\sum_{m\leq M}d(m)\Psi(\gamma m+\delta)+O(1)\nonumber\\[3pt] &=\sum_{m\leq M}d(m)\Psi_{\Delta}(\gamma m+\delta) +O(1+\mathcal{V}(I,M)\log N), \end{align} $$
where
![]() $\mathcal {V}(I,M)$
denotes the number of positive integers
$\mathcal {V}(I,M)$
denotes the number of positive integers
![]() $m\leq M$
such that
$m\leq M$
such that
Since
![]() $|I|\ll \Delta ,$
it follows from the definition (2.1) and Lemma 2.2 that
$|I|\ll \Delta ,$
it follows from the definition (2.1) and Lemma 2.2 that
where the implied constant depends only on
![]() $\alpha .$
By (2.2),
$\alpha .$
By (2.2),
 $$ \begin{align} \sum_{m\leq M} & d(m) \Psi_{\Delta}(\gamma m+\delta) \nonumber \\[3pt] &=\gamma\sum_{m\leq M}d(m)+\sum_{k=1}^{\infty}g_{k}e(\delta k)\sum_{m\leq M}d(m)e(\gamma km) +\sum_{k=1}^{\infty}h_{k}e(-\delta k) \sum_{m\leq M}d(m)e(-\gamma km). \end{align} $$
$$ \begin{align} \sum_{m\leq M} & d(m) \Psi_{\Delta}(\gamma m+\delta) \nonumber \\[3pt] &=\gamma\sum_{m\leq M}d(m)+\sum_{k=1}^{\infty}g_{k}e(\delta k)\sum_{m\leq M}d(m)e(\gamma km) +\sum_{k=1}^{\infty}h_{k}e(-\delta k) \sum_{m\leq M}d(m)e(-\gamma km). \end{align} $$
By Lemma 2.3, for
we have
Then by Theorem 1.1, (3.5) and (3.6),
 $$ \begin{align} \sum_{k\leq N^{2/(\tau+1)}}g_{k}e(\delta k)\sum_{m\leq M}d(m)e(\gamma km) &\ll N^{\varepsilon}\sum_{k \sim H}g_{k}e(\delta k)\sum_{m\leq M}d(m)e(\gamma km) \nonumber \\[3pt] &\ll N^{\varepsilon}(N^{1/2} +q+ N/q) \nonumber \\[3pt] &\ll N^{1-1/(\tau+1)+\varepsilon}, \end{align} $$
$$ \begin{align} \sum_{k\leq N^{2/(\tau+1)}}g_{k}e(\delta k)\sum_{m\leq M}d(m)e(\gamma km) &\ll N^{\varepsilon}\sum_{k \sim H}g_{k}e(\delta k)\sum_{m\leq M}d(m)e(\gamma km) \nonumber \\[3pt] &\ll N^{\varepsilon}(N^{1/2} +q+ N/q) \nonumber \\[3pt] &\ll N^{1-1/(\tau+1)+\varepsilon}, \end{align} $$
where
![]() $1\leq H\leq N^{2/(\tau +1)}$
and q is determined by (3.5) and (3.6) with
$1\leq H\leq N^{2/(\tau +1)}$
and q is determined by (3.5) and (3.6) with
![]() $K=N^{\tau /(\tau +1)}$
. Similarly,
$K=N^{\tau /(\tau +1)}$
. Similarly,
 $$ \begin{align} \begin{split} \sum_{k\leq N^{2/(\tau+1)}}g_{k}e(-\delta k)\sum_{m\leq M}d(dm+c)e(-\gamma km) &\ll N^{1-1/(\tau+1)+\varepsilon}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sum_{k\leq N^{2/(\tau+1)}}g_{k}e(-\delta k)\sum_{m\leq M}d(dm+c)e(-\gamma km) &\ll N^{1-1/(\tau+1)+\varepsilon}. \end{split} \end{align} $$
However, the well-known bound
implies that
 $$ \begin{align} \sum_{k\geq N^{2/(\tau+1)}}g_{k}e(\delta k)\sum_{m\leq M}d(dm+c)e(\gamma km)\ll N^{1+\varepsilon}\sum_{k\geq N^{2/(\tau+1)}}k^{-2}\Delta^{-1} \ll N^{1-1/(\tau+1)+\varepsilon} \end{align} $$
$$ \begin{align} \sum_{k\geq N^{2/(\tau+1)}}g_{k}e(\delta k)\sum_{m\leq M}d(dm+c)e(\gamma km)\ll N^{1+\varepsilon}\sum_{k\geq N^{2/(\tau+1)}}k^{-2}\Delta^{-1} \ll N^{1-1/(\tau+1)+\varepsilon} \end{align} $$
and
 $$ \begin{align} \sum_{k\geq N^{2/(\tau+1)}}g_{k}e(-\delta k)\sum_{m\leq M}d(m)e(-\gamma km)\ll N^{1+\varepsilon}\sum_{k\geq N^{2/(\tau+1)}}k^{-2}\Delta^{-1} \ll N^{1-1/(\tau+1)+\varepsilon}, \end{align} $$
$$ \begin{align} \sum_{k\geq N^{2/(\tau+1)}}g_{k}e(-\delta k)\sum_{m\leq M}d(m)e(-\gamma km)\ll N^{1+\varepsilon}\sum_{k\geq N^{2/(\tau+1)}}k^{-2}\Delta^{-1} \ll N^{1-1/(\tau+1)+\varepsilon}, \end{align} $$
where
![]() $\Delta =N^{-1/(\tau +1)}.$
Inserting the bounds (3.7)–(3.10) into (3.4),
$\Delta =N^{-1/(\tau +1)}.$
Inserting the bounds (3.7)–(3.10) into (3.4),
where the implied constant depends on
![]() $\alpha , \beta $
and
$\alpha , \beta $
and
![]() $\varepsilon .$
Substituting this bound and (3.3) into (3.2) and recalling the choice of
$\varepsilon .$
Substituting this bound and (3.3) into (3.2) and recalling the choice of
![]() $\Delta =N^{-1/(\tau +1)}$
completes the proof of Theorem 1.4.
$\Delta =N^{-1/(\tau +1)}$
completes the proof of Theorem 1.4.
Acknowledgement
I am deeply grateful to the referee(s) for carefully reading the manuscript and making useful suggestions.