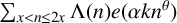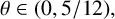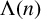1 Introduction
We are interested in the exponential sum
$$ \begin{align*} S(k,x,\theta):=\sum_{x<n\leq 2x}\Lambda(n)e(k\alpha n^{\theta}), \end{align*} $$
where
$x\geq 2$
and
$k\in \mathbb {Z}^{+}$
are the main parameters,
$\alpha \neq 0$
and
$0<\theta <1$
are fixed,
$\Lambda (n)$
is the von Mangoldt function and
$e(z) = e^{2\pi iz}.$
In [Reference Iwaniec, Luo and Sarnak4], Iwaniec et al. showed that such exponential sums are connected to the quasi-Riemann hypothesis (or the existence of a zero-free region) for
$L(s,f)$
, where f is any holomorphic cusp form of integral weight for
$\mbox {SL}(2,\mathbb {Z})$
.
We refer to
$S(k, x,\theta )$
as Vinogradov’s exponential sum, since it was first considered by Vinogradov [Reference Vinogradov8] in the special case
$\theta = 1/2$
. He proved in [Reference Vinogradov8] that, for
$k \leq x^{1/10},$
$$ \begin{align*} S(k, x, 1/2) \ll k^{1/4}x^{7/8+\varepsilon}, \end{align*} $$
where
$\varepsilon>0$
, and the implied constant may depend on
$\alpha $
and
$\varepsilon $
. Iwaniec and Kowalski (see [Reference Iwaniec and Kowalski3, formula (13.55)]) remarked that the stronger inequality
$$ \begin{align*}S(1,x,1/2) \ll x^{5/6}\log^{4} x \end{align*} $$
follows from an application of Vaughan’s identity. For general
$\theta $
and k, Murty and Srinivas [Reference Murty and Srinivas5] proved that
$$ \begin{align*}S(k, x,\theta) \ll k^{1/8}x {}^{(7+\theta)/8}\log (xk^{3}),\end{align*} $$
where the implied constant may depend on
$\alpha $
and
$\theta $
. In 2006, Ren [Reference Ren6] proved that
$$ \begin{align*} S(k, x,\theta)\ll (k^{1/2}x^{(1+\theta)/2}+ x^{4/5}+k^{-1/2}x^{1-\theta/2}){\log}^{\kern1ptA}x, \end{align*} $$
for arbitrary
$A>0$
, and that for
$\theta \leq 1/2$
and
$k<x^{1/2-\theta },$
$$ \begin{align} S(k, x,\theta)\ll( k^{1/10}x^{3/4+\theta/10} +k^{-1/2}x^{1-\theta/2})\log^{\kern1pt11}x. \end{align} $$
We prove the following result, which is new for
$\theta \in (0,5/12).$
Theorem 1.1. For
$0<\theta <5/12$
,
$\varepsilon>0$
and
$1\leq k<x^{5/12-\theta -\varepsilon },$
there exists an absolute constant
$c_{0}>0$
such that
$$ \begin{align*} S(k, x,\theta)\ll k^{-1/2}x^{1-\theta/2}\exp(-c_{0}(\log x)^{1/3-\varepsilon}), \end{align*} $$
where the implied constant may depend on
$\alpha , \theta $
and
$\varepsilon $
.
Obviously, when
$\theta <5/12$
and
$k<x^{5/12-\theta -\varepsilon },$
Theorem 1.1 improves (1.1). Some much sharper estimates can be obtained if one assumes the zero-density hypothesis,
$$ \begin{align} N(\sigma,T)\ll T^{2(1-\sigma)}\log^{\kern1ptB} T, \quad\mbox{for all } \sigma\geq1/2, \end{align} $$
where
$N(\sigma , T)$
is the number of zeros of
$\zeta (s)$
in the region
$\{\sigma \leq \Re s\leq 1, |t|\leq T\}$
and B is some positive constant. Under (1.2), it is proved in [Reference Ren6] that
$$ \begin{align} S(k, x,\theta)\ll (k^{1/2}x^{(1+\theta)/2}+ k^{-1/2}x^{1-\theta/2})\log^{\kern1ptB+2}x, \end{align} $$
where the implied constant may depend on
$\alpha $
,
$\theta $
and B. Our idea can also be used to improve (1.3).
Theorem 1.2. Under (1.2), for
$0<\theta <1/2$
,
$\varepsilon>0$
and
$1\leq k<x^{1/2-\theta -\varepsilon },$
there exists an absolute constant
$c_{0}$
such that
$$ \begin{align*} S(k, x,\theta)\ll k^{-1/2}x^{1-\theta/2}\exp(-c_{0}(\log x)^{1/3-\varepsilon}), \end{align*} $$
where the implied constant may depend on
$\alpha , \varepsilon $
and
$\theta $
.
It is worth pointing out that, compared with Theorem 1.1, the ranges of
$\theta $
and k have been extended in Theorem 1.2.
2 Proof of Theorem 1.1
To prove Theorem 1.1, we will borrow the idea in [Reference Ren6] and use results related to zeros of the Riemann zeta function. The following lemma will be used in the proofs of Theorems 1.1 and 1.2.
Lemma 2.1 [Reference Titchmarsh7, page 71].
Let
$F(u)$
and
$G(u)$
be real functions on
$[a,b],$
such that
$G(u)$
and
$1/F^{\prime }(u)$
are monotone and
$|G(u)|\leq M$
.
-
(1) If
$F^{\prime }(u)\geq m>0$
or
$F^{\prime }(u)\leq -m<0,$
then
$$ \begin{align*} \int_{a}^{b}G(u)e(F(u))\,du\ll \frac{M}{m}. \end{align*} $$
-
(2) If
$F^{\prime \prime }(u)\geq r>0$
or
$F^{\prime \prime }(u)\leq -r<0,$
then
$$ \begin{align*} \int_{a}^{b}G(u)e(F(u))\,du\ll \frac{M}{\sqrt{r}}. \end{align*} $$
Proof of Theorem 1.1.
Denote the zeros of
$\zeta (s)$
in the critical strip by
$\rho =\beta +i\gamma $
, where
$0<\beta <1$
,
$|\gamma |\leq T$
. Using partial summation and the explicit formula in [Reference Iwaniec and Kowalski3, formula (5.53)],
$$ \begin{align*} \sum_{n\leq x}\Lambda(n)=x-\sum_{|\gamma|\leq T}\frac{x^{\rho}}{\rho}+O\bigg(\frac{x}{T}(\log xT)^{2} \bigg), \quad\mbox{for } 1\leq T\leq x. \end{align*} $$
From this formula,
$$ \begin{align} \sum_{x<n\leq2x}\Lambda(n)e( k\alpha n^{\theta}) &=\int_{x}^{2x}e(k\alpha u^{\theta})\,d\sum_{n\leq u}\Lambda(n)\nonumber\\ &=\int_{x}^{2x}e(k\alpha u^{\theta})\,du-\sum_{|\gamma|\leq T}\int_{x}^{2x}u^{\rho-1}e(k\alpha u^{\theta})\,du \nonumber\\ & \kern-7pt\qquad\qquad\qquad\qquad +O\bigg((1+ k|\alpha| x^{\theta})\frac{x \log^{2}x}{T} \bigg). \end{align} $$
Setting
$$ \begin{align*} T=T_{0}=x, \end{align*} $$
the error-term is
$O((1+k|\alpha |x^{\theta })\log^{2}x) =O_{\alpha }(kx^{\theta }\log^{2}x)$
. Moreover,
$$ \begin{align} \int_{x}^{2x}e(k\alpha u^{\theta})\,du= \frac1\theta \int_{x^{\theta}}^{(2x)^{\theta}}u^{1/\theta-1}e(k\alpha u)\,du \ll_{\alpha,\theta} k^{-1}x^{1-\theta}. \end{align} $$
Making the change of variable
$u^{\theta }=v,$
$$ \begin{align*} \int_{x}^{2x}u^{\rho-1}e(k\alpha u^{\theta})\,du=\frac1{\theta}\int_{x^{\theta}}^{(2x)^{\theta}}v^{\,\beta/\theta-1}e(f(v))\,dv, \end{align*} $$
where
$$ \begin{align*} f(v)= k\alpha v +\frac{\gamma}{2\pi\theta}\log v. \end{align*} $$
Trivially,
$$ \begin{align} \int_{x}^{2x}u^{\rho-1}e(k\alpha u^{\theta})\,du \ll x^{\beta}. \end{align} $$
However,
$$ \begin{align*} &|f^{\prime}(v)|=\bigg|k\alpha+\frac{\gamma}{2\pi\theta v}\bigg|\geq \frac{\min_{v\in[x^{\theta},(2x)^{\theta}]}|\gamma +2\theta\pi k\alpha v|}{2\pi\theta |v|},\\ &|f^{\prime\prime}(v)|=\frac{|\gamma|}{2\pi\theta v^{2}}. \end{align*} $$
$$ \begin{align*} \int_{x^{\theta}}^{(2x)^{\theta}}v^{\,\beta/\theta-1}e(f(v))\,dv\ll\begin{cases} \dfrac{x^{\,\beta}}{\sqrt{1+\theta k|\alpha| x^{\theta}}} &\textrm{for } |\gamma| \leq 4(1+\theta\pi k|\alpha|(2x)^{\theta}), \\ \dfrac{x^{\,\beta}}{ 1+|\gamma|} &\textrm{for } 4(1+\theta\pi k|\alpha|(2x)^{\theta}) <|\gamma| \leq T_{0}. \end{cases} \end{align*} $$
Therefore,
$$ \begin{align*} &\sum_{|\gamma|\leq T} \int_{x}^{2x}u^{\rho-1}e(k\alpha u^{\theta})\,du\\ &\quad\ll\frac{1}{\sqrt{1+\theta k|\alpha|x^{\theta}}}\sum_{|\gamma| \leq 4(1+\theta\pi k|\alpha|(2x)^{\theta})}x^{\,\beta}+ \sum_{4(1+\theta\pi k|\alpha|(2x)^{\theta}) < |\gamma| \leq T_{0}}\frac{x^{\,\beta}}{1+|\gamma|}. \end{align*} $$
Assume that, for some positive constant C,
$$ \begin{align*} N(\sigma,T)\ll T^{A(\sigma)(1-\sigma)}\log^{\kern1ptC} T. \end{align*} $$
Then by the Riemann–von Mangoldt formula, for
$2\leq U\leq T_{0}$
,
$$ \begin{align*} \sum_{|\gamma|\leq U}x^{\,\beta}&=-\int^{1}_{0}x^{\sigma}\,dN(\sigma,U)\nonumber\\ &\ll x^{1/2}U\log U+(\log U)^{C}\log x\max_{1/2\leq\sigma\leq\sigma_{0}}U^{A(\sigma)(1-\sigma)}x^{\sigma}, \end{align*} $$
where
$$ \begin{align*} \sigma_{0}=1-c_{0}(\log T )^{-2/3}(\log \log T )^{-1/3} \end{align*} $$
with
$c_{0}$
an absolute positive constant. Here we have used the well-known zero-free region results (for example, see [Reference Iwaniec and Kowalski3, Reference Titchmarsh7]) which state that
$\zeta (s)\not =0$
for
$ \sigma>\sigma _{0}. $
Let x be sufficiently large such that
$\theta \pi k|\alpha | (2x)^{\theta }\gg 1$
. Then
$$ \begin{align*} &\frac{1}{\sqrt{1+\theta k|\alpha| x^{\theta}}} \sum_{|\gamma| \leq 4(1+\theta\pi k|\alpha|(2x)^{\theta})}x^{\,\beta}\nonumber\\ &\quad\ll (\log x)^{C+1}(k^{1/2}x^{(1+\theta)/2} +\max_{1/2\leq\sigma\leq\sigma_{0}}k^{A(\sigma)(1-\sigma) -1/2}x^{\sigma+\theta A(\sigma)(1-\sigma)-\theta/2}), \end{align*} $$
and
$$ \begin{align*} \sum_{4(1+\theta\pi k|\alpha|(2x)^{\theta})\leq|\gamma| \leq T_{0}} \frac{x^{\,\beta}}{1+|\gamma|} & \ll (\log x)\max_{4(1+\theta\pi k|\alpha|(2x)^{\theta})<T_{1}\leq T}T_{1}^{-1} \sum_{T_{1}\leq|\gamma|\leq2T_{1}}x^{\,\beta}\\ &\ll (\log x)^{C+2}(x^{1/2}+\max_{1/2\leq\sigma\leq\sigma_{0}} k^{A(\sigma)(1-\sigma)-1}x^{\sigma+\theta A(\sigma)(1-\sigma)-\theta}). \end{align*} $$
Writing
$$ \begin{align*} g(\sigma)=\sigma+\theta A(\sigma)(1-\sigma)-\frac{\theta}{2} \end{align*} $$
and collecting the above estimates,
$$ \begin{align*} \sum_{|\gamma|\leq T}\int_{x}^{2x}u^{\rho-1}e(k\alpha u^{\theta})\,du \ll (\log x)^{C+2}( k^{1/2}x^{(1+\theta)/2} +\max_{1/2\leq\sigma\leq\sigma_{0}}k^{A(\sigma)(1-\sigma) -1/2} x^{g(\sigma)}). \end{align*} $$
By the well-known result of Ingham [Reference Ingham2] and Huxley [Reference Huxley1], we can choose
$A(\sigma )=12/5.$
Thus we have
$$ \begin{align*} \max\limits_{1/2\leq\sigma\leq \sigma_{0}} k^{A(\sigma)(1-\sigma)-1/2}x^{g(\sigma)} &\ll (\log x)^{C_{1}} \sup_{1/2\leq \sigma\leq\sigma_{0}}k^{A(\sigma)(1-\sigma)-1/2} x^{\sigma+12\theta (1-\sigma)/5-\theta/2}\\ &\ll k^{-1/2}x^{1-\theta/2}(\log x)^{C_{1}}\sup\limits_{1/2\leq \sigma\leq\sigma_{0}}(k^{12/5}x^{12\theta/5-1})^{1-\sigma}. \end{align*} $$
Thus for
$\theta <5/12$
and
$k<x^{5/12-\theta -\varepsilon },$
$$ \begin{align*} \max\limits_{1/2\leq\sigma\leq \sigma_{0}} k^{A(\sigma)(1-\sigma)-1/2}x^{g(\sigma)} &\ll k^{-1/2}x^{1-\theta/2}(\log x)^{C_{1}}\sup_{1/2\leq \sigma\leq\sigma_{0}}x^{-c_{0}(\log x)^{-2/3}(\log \log x)^{-1/3}} \\ &\ll k^{-1/2}x^{1-\theta/2}\exp(-c_{0}(\log x)^{1/3} (\log x\log x)^{-1/3})\\ &\ll k^{-1/2}x^{1-\theta/2}\exp(-c_{0}(\log x)^{1/3-\varepsilon}). \end{align*} $$
This together with (2.1) and (2.2) shows that, for
$\theta \in (0,5/12)$
and
$1\leq k<x^{5/12-\theta -\varepsilon }$
,
$$ \begin{align*} \sum_{x<n\leq2x} & \Lambda(n)e( \alpha n^{\theta})\\ &\ll k^{1/2}x^{(1+\theta)/2}(\log x)^{C} +k^{-1/2}x^{1-\theta/2}\exp(-c_{0}(\log x)^{1/3-\varepsilon})+k^{-1}x^{1-\theta}+kx^{\theta}\\ &\ll k^{-1/2}x^{1-\theta/2}\exp(-c_{0}(\log x)^{1/3-\varepsilon}). \end{align*} $$
This finishes the proof of Theorem 1.1.
