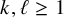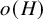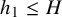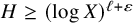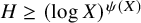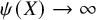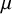1 Introduction
Let ![]() $\mu $ and
$\mu $ and ![]() $\Lambda $ denote the Möbius and von Mangoldt functions, respectively, defined by
$\Lambda $ denote the Möbius and von Mangoldt functions, respectively, defined by
 $$\begin{align*}\mu(n) = \begin{cases} (-1)^r & n=p_1\cdots p_r,\; p_i \text{ distinct,}\\ 0 & \ \text{else.} \end{cases}\quad\text{and} \quad \Lambda(n) = \begin{cases} \log p & n=p^e,\;e\ge1,\\ 0 & \ \text{else.} \end{cases} \end{align*}$$
$$\begin{align*}\mu(n) = \begin{cases} (-1)^r & n=p_1\cdots p_r,\; p_i \text{ distinct,}\\ 0 & \ \text{else.} \end{cases}\quad\text{and} \quad \Lambda(n) = \begin{cases} \log p & n=p^e,\;e\ge1,\\ 0 & \ \text{else.} \end{cases} \end{align*}$$Also, let ![]() $\lambda $ be the Liouville function given by
$\lambda $ be the Liouville function given by ![]() $\lambda (n)=(-1)^{\Omega (n)}$, where
$\lambda (n)=(-1)^{\Omega (n)}$, where ![]() $\Omega (n)$ is the total number of prime factors of n with multiplicities. For technical convenience, we extend these functions to the non-positive integers as zero (the choice of the extension makes no difference). Recall that the prime number theorem is equivalent to the average bounds
$\Omega (n)$ is the total number of prime factors of n with multiplicities. For technical convenience, we extend these functions to the non-positive integers as zero (the choice of the extension makes no difference). Recall that the prime number theorem is equivalent to the average bounds ![]() $\sum _{n\le X}\mu (n) = o(X)$ and
$\sum _{n\le X}\mu (n) = o(X)$ and ![]() $\sum _{n\le X}\Lambda (n) = (1+o(1))X$. The influential conjectures of Chowla [Reference Chowla2] and Hardy–Littlewood [Reference Hardy and Littlewood6] assert that for any fixed tuple of distinct integers
$\sum _{n\le X}\Lambda (n) = (1+o(1))X$. The influential conjectures of Chowla [Reference Chowla2] and Hardy–Littlewood [Reference Hardy and Littlewood6] assert that for any fixed tuple of distinct integers ![]() $h_1,\ldots ,h_k$,
$h_1,\ldots ,h_k$,
 $$ \begin{align*} \sum_{n\le X}\mu(n+h_1)\cdots\mu(n+h_k) \ &= \ o(X),\\ \sum_{n\le X}\Lambda(n+h_1)\cdots\Lambda(n+h_k) \ & = \ (\mathfrak{S}(\mathcal{H}) + o(1))X, \end{align*} $$
$$ \begin{align*} \sum_{n\le X}\mu(n+h_1)\cdots\mu(n+h_k) \ &= \ o(X),\\ \sum_{n\le X}\Lambda(n+h_1)\cdots\Lambda(n+h_k) \ & = \ (\mathfrak{S}(\mathcal{H}) + o(1))X, \end{align*} $$where ![]() $\mathcal {H}=\{h_1,\ldots , h_k\}$ and the singular series is given by
$\mathcal {H}=\{h_1,\ldots , h_k\}$ and the singular series is given by
 $$ \begin{align}\mathfrak{S}(\mathcal{H}) = \prod_{p}\frac{1-\nu_p(\mathcal{H})/p}{(1-1/p)^k}, \end{align} $$
$$ \begin{align}\mathfrak{S}(\mathcal{H}) = \prod_{p}\frac{1-\nu_p(\mathcal{H})/p}{(1-1/p)^k}, \end{align} $$where ![]() $\nu _p(\mathcal {H}) = |\{h\;(\text {mod }p) : h\in \mathcal {H}\}|$. Both conjectures remain open for any
$\nu _p(\mathcal {H}) = |\{h\;(\text {mod }p) : h\in \mathcal {H}\}|$. Both conjectures remain open for any ![]() $k\ge 2$.
$k\ge 2$.
It is natural to consider the following hybrid conjecture, which, following [Reference Lichtman10] and [Reference Tao and Teräväinen20], we call the Hardy–Littlewood–Chowla conjecture.
Conjecture 1.1 (Hardy–Littlewood–Chowla).
Let ![]() $k,\ell \geq 0$, and let
$k,\ell \geq 0$, and let ![]() $h_1,\ldots ,h_k$,
$h_1,\ldots ,h_k$, ![]() $a_1,\ldots , a_\ell $ be distinct integers. Then we haveFootnote 1
$a_1,\ldots , a_\ell $ be distinct integers. Then we haveFootnote 1
Here, ![]() $\mathfrak {S}=\mathfrak {S}(\{a_1,\ldots , a_\ell \})$ as in (1.1) if
$\mathfrak {S}=\mathfrak {S}(\{a_1,\ldots , a_\ell \})$ as in (1.1) if ![]() $k=0$, and
$k=0$, and ![]() $\mathfrak {S}=0$ if
$\mathfrak {S}=0$ if ![]() $k>0$.
$k>0$.
The ‘pure’ cases ![]() $k=0$ and
$k=0$ and ![]() $\ell =0$ specialise to the original conjectures of Hardy–Littlewood and of Chowla, respectively. We remark that under the hypothetical assumption of infinitely many Siegel zeros, Conjecture 1.1 was recently verified for
$\ell =0$ specialise to the original conjectures of Hardy–Littlewood and of Chowla, respectively. We remark that under the hypothetical assumption of infinitely many Siegel zeros, Conjecture 1.1 was recently verified for ![]() $\ell \leq 2$ by Tao and the second author [Reference Tao and Teräväinen20] (generalising works of Heath-Brown [Reference Heath-Brown7] and Chinis [Reference Chinis1]). In the current paper, we will be concerned with unconditional results.
$\ell \leq 2$ by Tao and the second author [Reference Tao and Teräväinen20] (generalising works of Heath-Brown [Reference Heath-Brown7] and Chinis [Reference Chinis1]). In the current paper, we will be concerned with unconditional results.
Our main result is an averaged form of Conjecture 1.1 for the genuinely ‘hybrid’ cases ![]() $k,\ell \ge 1$.
$k,\ell \ge 1$.
Theorem 1.2 (Hardy–Littlewood–Chowla on average).
Let ![]() $\varepsilon>0$ and
$\varepsilon>0$ and ![]() $k,\ell \geq 1$ be fixed, and let
$k,\ell \geq 1$ be fixed, and let ![]() $h_2,\ldots ,h_{k}$,
$h_2,\ldots ,h_{k}$, ![]() $a_1,\ldots ,a_{\ell }$ be fixed and distinct positive integers.
$a_1,\ldots ,a_{\ell }$ be fixed and distinct positive integers.
(i) Let
 $(\log X)^{\ell +\varepsilon }\leq H\leq \exp ((\log X)^{a})$ with
$(\log X)^{\ell +\varepsilon }\leq H\leq \exp ((\log X)^{a})$ with  $a=a(\varepsilon ,\ell )>0$ small enough. Then (1.3)
$a=a(\varepsilon ,\ell )>0$ small enough. Then (1.3) $$ \begin{align} \sum_{h_1\le H}\bigg|\sum_{n\leq X}\mu(n+h_1)\cdots \mu(n+h_k)\Lambda(n+a_1)\cdots\Lambda(n+a_{\ell})\bigg| \ \ll \ HX\,\frac{\log \log H}{\log H}. \end{align} $$
$$ \begin{align} \sum_{h_1\le H}\bigg|\sum_{n\leq X}\mu(n+h_1)\cdots \mu(n+h_k)\Lambda(n+a_1)\cdots\Lambda(n+a_{\ell})\bigg| \ \ll \ HX\,\frac{\log \log H}{\log H}. \end{align} $$(ii) Let
 $C\geq 1$ be fixed, and let
$C\geq 1$ be fixed, and let  $(\log X)^{\ell +\varepsilon }\leq H\leq (\log X)^{C}$. There exists an absolute constant
$(\log X)^{\ell +\varepsilon }\leq H\leq (\log X)^{C}$. There exists an absolute constant  $c>0$, such that for any
$c>0$, such that for any  $10^4\ell \varepsilon ^{-1}(\log \log H)/(\log H)\leq \delta \leq c/C$, we have for all except
$10^4\ell \varepsilon ^{-1}(\log \log H)/(\log H)\leq \delta \leq c/C$, we have for all except $$ \begin{align*} \bigg|\sum_{n\leq X}\mu(n+h_1)\cdots \mu(n+h_k)\Lambda(n+a_1)\cdots\Lambda(n+a_{\ell})\bigg|\leq \delta X \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n\leq X}\mu(n+h_1)\cdots \mu(n+h_k)\Lambda(n+a_1)\cdots\Lambda(n+a_{\ell})\bigg|\leq \delta X \end{align*} $$ $\ll H^{1-c\delta \varepsilon /\ell }$ values of
$\ll H^{1-c\delta \varepsilon /\ell }$ values of  $h_1\leq H$.
$h_1\leq H$.
In particular, (1.2) holds for all but ![]() $o(H)$ values of
$o(H)$ values of ![]() $h_1\leq H$ (and the exceptional set can be taken to be nearly power saving).
$h_1\leq H$ (and the exceptional set can be taken to be nearly power saving).
As is clear from the proof, Theorem 1.2 holds equally well with the Liouville function in place of the Möbius function.
Remark 1.3. It is likely that with some extra effort (in particular, refining Proposition 2.1 for ![]() $\mu $ in the spirit of [Reference Lichtman10, Theorem 2.2]), Theorem 1.2(ii) could be extended to the regime
$\mu $ in the spirit of [Reference Lichtman10, Theorem 2.2]), Theorem 1.2(ii) could be extended to the regime ![]() $(\log X)^{\ell +\varepsilon }\leq H\leq X$. However, our main interest here is in taking H as small as possible.
$(\log X)^{\ell +\varepsilon }\leq H\leq X$. However, our main interest here is in taking H as small as possible.
Earlier, Matomäki, Radziwiłł and Tao [Reference Matomäki, Radziwiłł and Tao12] proved the case ![]() $\ell =0$ of Conjecture 1.1 for almost all
$\ell =0$ of Conjecture 1.1 for almost all ![]() $h_1\leq H$, with
$h_1\leq H$, with ![]() $H=\psi (X)$ tending to infinity arbitrarily slowly. In [Reference Matomäki, Radziwiłł and Tao13], they considered the case
$H=\psi (X)$ tending to infinity arbitrarily slowly. In [Reference Matomäki, Radziwiłł and Tao13], they considered the case ![]() $k=0$,
$k=0$, ![]() $\ell =2$ and proved the conjecture for almost all
$\ell =2$ and proved the conjecture for almost all ![]() $h_1\leq H$, with
$h_1\leq H$, with ![]() $H\geq X^{8/33+\varepsilon }$. The first author [Reference Lichtman10] obtained cancellation in the range
$H\geq X^{8/33+\varepsilon }$. The first author [Reference Lichtman10] obtained cancellation in the range ![]() $H\geq (\log X)^{\psi (X)}$, implied by the stronger quantitative bound
$H\geq (\log X)^{\psi (X)}$, implied by the stronger quantitative bound
 $$ \begin{align*} \sum_{h_1,\ldots, h_k\leq H}\bigg|\sum_{n\leq X} \mu(n+h_1)\cdots \mu(n+h_k) & \Lambda(n+a_1)\cdots \Lambda(n+a_{\ell}) \bigg| \\ &\ll \ \frac{H^kX}{\min\big\{\psi(X)^k,(\log X)^{k/3-o(1)}\big\}}. \end{align*} $$
$$ \begin{align*} \sum_{h_1,\ldots, h_k\leq H}\bigg|\sum_{n\leq X} \mu(n+h_1)\cdots \mu(n+h_k) & \Lambda(n+a_1)\cdots \Lambda(n+a_{\ell}) \bigg| \\ &\ll \ \frac{H^kX}{\min\big\{\psi(X)^k,(\log X)^{k/3-o(1)}\big\}}. \end{align*} $$ The simplest hybrid case ![]() $k=\ell =1$ reduces to the Möbius function on shifted primes. It is a folklore conjecture and a well-known model case for the parity problem in sieve theory that
$k=\ell =1$ reduces to the Möbius function on shifted primes. It is a folklore conjecture and a well-known model case for the parity problem in sieve theory that
for any fixed shift ![]() $h\neq 0$. This has appeared in print (for
$h\neq 0$. This has appeared in print (for ![]() $h=1$) at least since Hildebrand [Reference Hildebrand9] (see also Pintz [Reference Pintz18] and Murty–Vatwani [Reference R. Murty and Vatwani16, Equation (1.2)]). Theorem 1.2 directly implies an averaged form of this conjecture for
$h=1$) at least since Hildebrand [Reference Hildebrand9] (see also Pintz [Reference Pintz18] and Murty–Vatwani [Reference R. Murty and Vatwani16, Equation (1.2)]). Theorem 1.2 directly implies an averaged form of this conjecture for ![]() $H\ge (\log X)^{1+\varepsilon }$.
$H\ge (\log X)^{1+\varepsilon }$.
Corollary 1.4. Let ![]() $\varepsilon>0$. Then, for
$\varepsilon>0$. Then, for ![]() $X\geq H\geq (\log X)^{1+\varepsilon }$, we have
$X\geq H\geq (\log X)^{1+\varepsilon }$, we have
for all except ![]() $o(H)$ values of
$o(H)$ values of ![]() $h\leq H$.
$h\leq H$.
This improves on work of the first author [Reference Lichtman10] that established Corollary 1.4 when ![]() $H\geq (\log X)^{\psi (X)}$ for any function
$H\geq (\log X)^{\psi (X)}$ for any function ![]() $\psi (X)$ tending to infinity with X.
$\psi (X)$ tending to infinity with X.
1.1 Other multiplicative functions
We also consider a variant of Conjecture 1.1, where the occurrences of the Möbius function are replaced with other 1-bounded multiplicative functions ![]() $f_i:\mathbb {N}\to \mathbb {C}$, with
$f_i:\mathbb {N}\to \mathbb {C}$, with ![]() $f_1$ not pretending to be a twisted character
$f_1$ not pretending to be a twisted character ![]() $\chi (n)n^{it}$ for any
$\chi (n)n^{it}$ for any ![]() $\chi\ \pmod q$ and
$\chi\ \pmod q$ and ![]() $t\in \mathbb {R}$. Here, following Granville and Soundararajan [Reference Granville and Soundararajan5], pretentiousness is measured by the pretentious distance
$t\in \mathbb {R}$. Here, following Granville and Soundararajan [Reference Granville and Soundararajan5], pretentiousness is measured by the pretentious distance
 $$ \begin{align*} \mathbb{D}(f,g;X) = \bigg(\sum_{p\le X}\frac{1-\text{Re}(f(p)\overline{g(p)})}{p}\bigg)^{1/2} \end{align*} $$
$$ \begin{align*} \mathbb{D}(f,g;X) = \bigg(\sum_{p\le X}\frac{1-\text{Re}(f(p)\overline{g(p)})}{p}\bigg)^{1/2} \end{align*} $$and the related quantity
 $$ \begin{align} M(f;X,Q) = \inf_{\substack{|t|\le X\\\chi\,(q), \, q\le Q}} \mathbb{D}\big(f,\, n\mapsto n^{it}\chi(n); X\big)^2. \end{align} $$
$$ \begin{align} M(f;X,Q) = \inf_{\substack{|t|\le X\\\chi\,(q), \, q\le Q}} \mathbb{D}\big(f,\, n\mapsto n^{it}\chi(n); X\big)^2. \end{align} $$The following generalisation of Conjecture 1.1 is closely related to Elliott’s conjecture [Reference Elliott3] on correlations of multiplicative functions (in fact, the case ![]() $\ell =0$ is precisely Elliott’s conjecture), so we shall call it the Hardy–Littlewood–Elliott conjecture.
$\ell =0$ is precisely Elliott’s conjecture), so we shall call it the Hardy–Littlewood–Elliott conjecture.
Conjecture 1.5 (Hardy–Littlewood–Elliott).
Let ![]() $h_1,\ldots , h_k,a_1,\ldots , a_{\ell }$ be distinct integers. Fix 1-bounded multiplicative functions
$h_1,\ldots , h_k,a_1,\ldots , a_{\ell }$ be distinct integers. Fix 1-bounded multiplicative functions ![]() $f_1,\ldots , f_k$. Suppose that
$f_1,\ldots , f_k$. Suppose that ![]() $f_1$ is non-pretentious in the sense that
$f_1$ is non-pretentious in the sense that
for any ![]() $Q\geq 1$. Then we have
$Q\geq 1$. Then we have
The case ![]() $\ell =0$ of this is Elliott’s conjecture (in the slightly corrected formulation of [Reference Tao and Teräväinen19, Conjecture 1.3]).
$\ell =0$ of this is Elliott’s conjecture (in the slightly corrected formulation of [Reference Tao and Teräväinen19, Conjecture 1.3]).
We extend our results to non-pretentious multiplicative functions in the regime ![]() $H\ge (\log X)^{\ell +\varepsilon }$.
$H\ge (\log X)^{\ell +\varepsilon }$.
Theorem 1.6 (Hardy–Littlewood–Elliott on average).
Let ![]() $\varepsilon>0$,
$\varepsilon>0$, ![]() $k,\ell \geq 1$ be fixed, and let
$k,\ell \geq 1$ be fixed, and let ![]() $h_2,\ldots , h_k,a_1,\ldots , a_{\ell }$ be fixed and distinct positive integers. Let
$h_2,\ldots , h_k,a_1,\ldots , a_{\ell }$ be fixed and distinct positive integers. Let ![]() $(\log X)^{\ell +\varepsilon }\leq H\leq \exp ((\log X)^{1/1000})$. Let
$(\log X)^{\ell +\varepsilon }\leq H\leq \exp ((\log X)^{1/1000})$. Let ![]() $f_1,\ldots , f_k$ be 1-bounded multiplicative functions. Then we have
$f_1,\ldots , f_k$ be 1-bounded multiplicative functions. Then we have
 $$ \begin{align*} \sum_{h_1\leq H} &\bigg|\sum_{n\leq X}f_1(n+h_1)\cdots f_k(n+h_k)\Lambda(n+a_1)\cdots \Lambda(n+a_{\ell})\bigg|\\ &\ll HX\left(\exp\big({-M(f_1;X,\min\{(\log X)^{1/125},(\log H)^5\}\big)}/(10\, 000\ell\varepsilon^{-1})+\frac{\log \log H}{\log H}\right). \end{align*} $$
$$ \begin{align*} \sum_{h_1\leq H} &\bigg|\sum_{n\leq X}f_1(n+h_1)\cdots f_k(n+h_k)\Lambda(n+a_1)\cdots \Lambda(n+a_{\ell})\bigg|\\ &\ll HX\left(\exp\big({-M(f_1;X,\min\{(\log X)^{1/125},(\log H)^5\}\big)}/(10\, 000\ell\varepsilon^{-1})+\frac{\log \log H}{\log H}\right). \end{align*} $$In particular, if ![]() $(\log X)^{\ell +\varepsilon } \leq H\leq \exp ((\log X)^{1/1000})$ and
$(\log X)^{\ell +\varepsilon } \leq H\leq \exp ((\log X)^{1/1000})$ and
then (1.6) holds for all except ![]() $o(H)$ values of
$o(H)$ values of ![]() $h_1\leq H$.
$h_1\leq H$.
Remark 1.7. As a well-known consequence of the Vinogradov–Korobov zero-free region for L-functions, for any fixed ![]() $\epsilon>0$,
$\epsilon>0$, ![]() $A\geq 1$ we have
$A\geq 1$ we have
 $$ \begin{align}\begin{split} M(\mu; X,(\log X)^{A}) \ &\ge \ \inf_{\substack{|t|\le X\\\chi\,(q), \, q\le Q}}\,\, \sum_{\exp((\log X)^{2/3+\epsilon})\le p\le X}\frac{1+\text{Re}(\chi(p)p^{it})}{p}\\ \ &\ge \ \Big(\frac{1}{3}-\epsilon\Big)\log\log X + O(1).\end{split} \end{align} $$
$$ \begin{align}\begin{split} M(\mu; X,(\log X)^{A}) \ &\ge \ \inf_{\substack{|t|\le X\\\chi\,(q), \, q\le Q}}\,\, \sum_{\exp((\log X)^{2/3+\epsilon})\le p\le X}\frac{1+\text{Re}(\chi(p)p^{it})}{p}\\ \ &\ge \ \Big(\frac{1}{3}-\epsilon\Big)\log\log X + O(1).\end{split} \end{align} $$Hence, the bound of Theorem 1.6 in the case of ![]() $f_1=\mu $ simplifies to
$f_1=\mu $ simplifies to
 $$ \begin{align*} \sum_{h_1\leq H}\bigg|\sum_{n\leq X}\mu(n+h_1)\cdots f_k(n+h_k)&\Lambda(n+a_1)\cdots \Lambda(n+a_{\ell})\bigg|\\ &\ll HX\left(\frac{\log \log H}{\log H}+(\log X)^{-a}\right) \end{align*} $$
$$ \begin{align*} \sum_{h_1\leq H}\bigg|\sum_{n\leq X}\mu(n+h_1)\cdots f_k(n+h_k)&\Lambda(n+a_1)\cdots \Lambda(n+a_{\ell})\bigg|\\ &\ll HX\left(\frac{\log \log H}{\log H}+(\log X)^{-a}\right) \end{align*} $$for some constant ![]() $a=a(\varepsilon ,\ell )>0$. The same holds with
$a=a(\varepsilon ,\ell )>0$. The same holds with ![]() $\lambda $ in place of
$\lambda $ in place of ![]() $\mu $, since (1.7) holds equally well for
$\mu $, since (1.7) holds equally well for ![]() $\lambda $. Restricting to
$\lambda $. Restricting to ![]() $\exp ((\log X)^{a})\geq H\geq (\log X)^{\ell +\varepsilon }$, the bound simplifies to
$\exp ((\log X)^{a})\geq H\geq (\log X)^{\ell +\varepsilon }$, the bound simplifies to ![]() $\ll HX(\log \log H)/\log H$. Hence, Theorem 1.2(i) is a special case of Theorem 1.6. The rest of the paper is therefore devoted to the proofs of Theorems 1.2(ii) and 1.6.
$\ll HX(\log \log H)/\log H$. Hence, Theorem 1.2(i) is a special case of Theorem 1.6. The rest of the paper is therefore devoted to the proofs of Theorems 1.2(ii) and 1.6.
Theorem 1.6 improves on the range ![]() $H\geq \exp ((\log X)^{5/8+\varepsilon })$, which follows (under a slightly different pretentiousness hypothesis) from Fourier uniformity bounds of Matomäki, Radziwiłł, Tao, Ziegler and the second author [Reference Matomäki, Radziwiłł, Tao, Teräväinen and Ziegler15, Theorem 1.8] (see [Reference Lichtman10, Theorem 1.8] for the details of this implication).Footnote 2 We also note that the case
$H\geq \exp ((\log X)^{5/8+\varepsilon })$, which follows (under a slightly different pretentiousness hypothesis) from Fourier uniformity bounds of Matomäki, Radziwiłł, Tao, Ziegler and the second author [Reference Matomäki, Radziwiłł, Tao, Teräväinen and Ziegler15, Theorem 1.8] (see [Reference Lichtman10, Theorem 1.8] for the details of this implication).Footnote 2 We also note that the case ![]() $\ell =0$ of Conjecture 1.5 was proven on average by Matomäki–Radziwiłł–Tao [Reference Matomäki, Radziwiłł and Tao12] in the regime
$\ell =0$ of Conjecture 1.5 was proven on average by Matomäki–Radziwiłł–Tao [Reference Matomäki, Radziwiłł and Tao12] in the regime ![]() $H=\psi (X)\to \infty $.
$H=\psi (X)\to \infty $.
1.2 Outline of the proof
The proof method of Theorem 1.2 (and Theorem 1.6) is somewhat different from that of [Reference Lichtman10] (or [Reference Matomäki, Radziwiłł and Tao12]). Both proofs begin with Fourier-analytic identities, namely, [Reference Lichtman10, Lemma 2.1] and Proposition 3.2 below. The latter allows one to study mixed 2-point correlations on average, for some functions f and g which satisfy certain technical hypotheses. Crucially, in Proposition 3.2, having qualitative cancellation for the exponential sum of f on average over short intervals ![]() $[x,x+H]$ suffices, whereas in [Reference Lichtman10, Lemma 2.1], one needs to save a factor comparable to
$[x,x+H]$ suffices, whereas in [Reference Lichtman10, Lemma 2.1], one needs to save a factor comparable to ![]() $((1/X)\sum _{n\leq X}|g(n)|^2)^{-1/2}$ (but no additional hypotheses were required of
$((1/X)\sum _{n\leq X}|g(n)|^2)^{-1/2}$ (but no additional hypotheses were required of ![]() $f, g$). For intervals of length
$f, g$). For intervals of length ![]() $H=(\log X)^{O(1)}$, the bound in [Reference Matomäki, Radziwiłł and Tao12] for the exponential sum of a multiplicative f on average over short intervals
$H=(\log X)^{O(1)}$, the bound in [Reference Matomäki, Radziwiłł and Tao12] for the exponential sum of a multiplicative f on average over short intervals ![]() $[x,x+H]$ saves less than
$[x,x+H]$ saves less than ![]() $(\log X)^{-o(1)}$, which is problematic if the mean value of
$(\log X)^{-o(1)}$, which is problematic if the mean value of ![]() $|g|^2$ is a power of
$|g|^2$ is a power of ![]() $\log X$, so the weakening of the Fourier assumption on f in Proposition 3.2 is important for us.
$\log X$, so the weakening of the Fourier assumption on f in Proposition 3.2 is important for us.
One ultimately applies Proposition 3.2 for the choices ![]() $f = \mu $ (say) and
$f = \mu $ (say) and ![]() $g(n) = \mu (n + h_2)\cdots \mu (n+h_k)\Lambda (n+a_1)\cdots \Lambda (n+a_\ell )$, in which case, verifying the technical hypotheses may be reduced to the following problems:
$g(n) = \mu (n + h_2)\cdots \mu (n+h_k)\Lambda (n+a_1)\cdots \Lambda (n+a_\ell )$, in which case, verifying the technical hypotheses may be reduced to the following problems:
(I) cancellation in short exponential sums of
 $\mu $ on average,
$\mu $ on average,(II) moment estimates for short exponential sums over primes, that is, for ‘typical’ x,
 $$ \begin{align*} \int_{0}^1\bigg|\sum_{x\leq n\leq x+H}\Lambda(n)e(\alpha n)\bigg|^{2m}{\textrm{d}}{\alpha} \ \ll \ H^{2m-1}. \end{align*} $$
$$ \begin{align*} \int_{0}^1\bigg|\sum_{x\leq n\leq x+H}\Lambda(n)e(\alpha n)\bigg|^{2m}{\textrm{d}}{\alpha} \ \ll \ H^{2m-1}. \end{align*} $$
Here, (I) is deduced from the work of Matomäki–Radziwiłł–Tao [Reference Matomäki, Radziwiłł and Tao12], with special care paid to the shape of the error terms in order to obtain a power-saving error term in Theorem 1.2(ii). This is carried out in Proposition 2.1.
For (II), the intervals involved are too short for sieve methods to provide us with a strong enough pointwise bound on these moments. However, on average over x, in Proposition 2.7, we show that the moments above are of the expected order of magnitude by applying upper bounds for prime tuples coming from Selberg’s sieve, and by performing an analysis of the resulting singular series.
The method presented is rather flexible and could be applied (with some additional effort) to other correlation problems as well, such as the sums
on average over h (with ![]() $P(Y)\in \mathbb {Z}[Y]$). We leave the details of such generalisations to the interested reader.
$P(Y)\in \mathbb {Z}[Y]$). We leave the details of such generalisations to the interested reader.
2 Auxiliary results
2.1 A short exponential sum estimate
As in [Reference Matomäki, Radziwiłł and Tao12], we introduce a set ![]() $\mathcal {S}_{P_1,Q_1,X}$ (depending on parameters
$\mathcal {S}_{P_1,Q_1,X}$ (depending on parameters ![]() $10<P_1<Q_1\leq X$) consisting of the ‘typical’ numbers having prime factors from certain long ranges. More precisely,
$10<P_1<Q_1\leq X$) consisting of the ‘typical’ numbers having prime factors from certain long ranges. More precisely, ![]() $\mathcal {S}_{P_1,Q_1,X}$ is the set of positive integers having a prime factor in each of the ranges
$\mathcal {S}_{P_1,Q_1,X}$ is the set of positive integers having a prime factor in each of the ranges ![]() $[P_j,Q_j]$,
$[P_j,Q_j]$, ![]() $j=1,\ldots , J$, where for
$j=1,\ldots , J$, where for ![]() $j>1$, we define:
$j>1$, we define:
 $$ \begin{align*} P_j &=\exp(j^{4j}(\log Q_1)^{j-1}(\log P_1)),\\ Q_j &=\exp(j^{4j+2}(\log Q_1)^j) \end{align*} $$
$$ \begin{align*} P_j &=\exp(j^{4j}(\log Q_1)^{j-1}(\log P_1)),\\ Q_j &=\exp(j^{4j+2}(\log Q_1)^j) \end{align*} $$and J is the largest index, such that ![]() $Q_J\leq \exp (\sqrt {\frac {1}{2}\log X})$. If
$Q_J\leq \exp (\sqrt {\frac {1}{2}\log X})$. If ![]() $\mathcal {S}_{P_1,Q_1,X}^{c}$ denotes the complement of
$\mathcal {S}_{P_1,Q_1,X}^{c}$ denotes the complement of ![]() $\mathcal {S}_{P_1,Q_1,X}$ in
$\mathcal {S}_{P_1,Q_1,X}$ in ![]() $\mathbb {N}\cap [1,X]$, then the fundamental lemma of sieve theory [Reference Friedlander and Iwaniec4, Lemma 6.17] tells us that
$\mathbb {N}\cap [1,X]$, then the fundamental lemma of sieve theory [Reference Friedlander and Iwaniec4, Lemma 6.17] tells us that
 $$ \begin{align} \big|\mathcal{S}_{P_1,Q_1,X}^{c}\big|\ll \sum_{j\leq J}\frac{\log P_j}{\log Q_j}X\ll \frac{\log P_1}{\log Q_1}X. \end{align} $$
$$ \begin{align} \big|\mathcal{S}_{P_1,Q_1,X}^{c}\big|\ll \sum_{j\leq J}\frac{\log P_j}{\log Q_j}X\ll \frac{\log P_1}{\log Q_1}X. \end{align} $$We then have the following exponential sum estimate (with the supremum outside) for short sums of multiplicative functions, which follows from [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3].
Proposition 2.1. Let ![]() $3\leq H\leq \exp ((\log X)^{1/1000})$ and
$3\leq H\leq \exp ((\log X)^{1/1000})$ and
Let f be a 1-bounded multiplicative function. Then there exist ![]() $10<P_1<Q_1\leq X$, such that
$10<P_1<Q_1\leq X$, such that
and, such that for ![]() $\mathcal {S}=\mathcal {S}_{P_1,Q_1,X}$, we have
$\mathcal {S}=\mathcal {S}_{P_1,Q_1,X}$, we have
 $$ \begin{align} \sup_{\alpha}\int_0^X & \bigg|\sum_{x\le n\le x+H}f(n){\mathbf 1}_{\mathcal{S}}(n) e(n\alpha)\bigg|{\textrm{d}}{x}\ll \bigg(\exp(-M(f;X,Q)/2000)+H^{-\delta}\bigg)HX, \end{align} $$
$$ \begin{align} \sup_{\alpha}\int_0^X & \bigg|\sum_{x\le n\le x+H}f(n){\mathbf 1}_{\mathcal{S}}(n) e(n\alpha)\bigg|{\textrm{d}}{x}\ll \bigg(\exp(-M(f;X,Q)/2000)+H^{-\delta}\bigg)HX, \end{align} $$where ![]() $Q= \min \{(\log X)^{1/125}, (\log H)^5\}$.
$Q= \min \{(\log X)^{1/125}, (\log H)^5\}$.
Remark 2.2. Applying (1.7), and assuming that ![]() $H\leq (\log X)^C$, the bound (2.3) in the case of
$H\leq (\log X)^C$, the bound (2.3) in the case of ![]() $f=\mu $ simplifies to
$f=\mu $ simplifies to
 $$ \begin{align} \sup_{\alpha}\int_0^X & \bigg|\sum_{x\le n\le x+H}\mu(n){\mathbf 1}_{\mathcal{S}}(n) e(n\alpha)\bigg|{\textrm{d}}{x}\ll H^{1-\delta}X \end{align} $$
$$ \begin{align} \sup_{\alpha}\int_0^X & \bigg|\sum_{x\le n\le x+H}\mu(n){\mathbf 1}_{\mathcal{S}}(n) e(n\alpha)\bigg|{\textrm{d}}{x}\ll H^{1-\delta}X \end{align} $$for some ![]() $\delta =\delta (C)>0$, and the same holds with
$\delta =\delta (C)>0$, and the same holds with ![]() $\lambda $ in place of
$\lambda $ in place of ![]() $\mu $. Moreover, (2.2) then simplifies to
$\mu $. Moreover, (2.2) then simplifies to ![]() $(\log P_1)/(\log Q_1)\ll \delta $.
$(\log P_1)/(\log Q_1)\ll \delta $.
Proof. Without loss of generality, we may assume that ![]() $H\geq H_0$ for a large enough constant
$H\geq H_0$ for a large enough constant ![]() $H_0$. Denote the integral in (2.3) by
$H_0$. Denote the integral in (2.3) by ![]() $J_f$. Suppose first that
$J_f$. Suppose first that
Let
and let ![]() $P_1=W^{200}$,
$P_1=W^{200}$, ![]() $Q_1=H/W^{3}$ be as in [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3]. Note that
$Q_1=H/W^{3}$ be as in [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3]. Note that ![]() $W\ll (\log X)^{1/150}$ by the fact that
$W\ll (\log X)^{1/150}$ by the fact that ![]() $M(f;X,Q)\leq 2\log \log X+O(1)$. Note also that
$M(f;X,Q)\leq 2\log \log X+O(1)$. Note also that ![]() $\frac {\log P_1}{\log Q_1}\ll \frac {\log W}{\log H}\ll \delta $ and that all the conditions for W in [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3] are satisfied (that is,
$\frac {\log P_1}{\log Q_1}\ll \frac {\log W}{\log H}\ll \delta $ and that all the conditions for W in [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3] are satisfied (that is, ![]() $W\geq (\log H)^5$ and
$W\geq (\log H)^5$ and ![]() $W\leq \min \{H^{1/250},(\log X)^{1/125}\}$ and
$W\leq \min \{H^{1/250},(\log X)^{1/125}\}$ and ![]() $W\leq \exp (M(f;X,Q)/3)$), so we obtain
$W\leq \exp (M(f;X,Q)/3)$), so we obtain
Suppose then that
Let
and let ![]() $P_1=W^{200}$,
$P_1=W^{200}$, ![]() $Q_1=H/W^3$ as before. We may assume
$Q_1=H/W^3$ as before. We may assume ![]() $H_1\geq 1000$, since otherwise, the claim is trivial. Now, by noting that
$H_1\geq 1000$, since otherwise, the claim is trivial. Now, by noting that ![]() $\frac {\log P_1}{\log Q_1}\ll \exp (-M(f;X,Q)/2000)$ and splitting the sum on H in (2.3) into shorter sums of length in
$\frac {\log P_1}{\log Q_1}\ll \exp (-M(f;X,Q)/2000)$ and splitting the sum on H in (2.3) into shorter sums of length in ![]() $[H_1/4,H_1/2]$, it suffices to prove that
$[H_1/4,H_1/2]$, it suffices to prove that
 $$ \begin{align*} \sup_{\alpha}\int_0^X & \bigg|\sum_{x\le n\le x+H'}f(n){\mathbf 1}_{\mathcal{S}}(n) e(n\alpha)\bigg|{\textrm{d}}{x}\ll \exp(-M(f;X,Q)/2000)H'X, \end{align*} $$
$$ \begin{align*} \sup_{\alpha}\int_0^X & \bigg|\sum_{x\le n\le x+H'}f(n){\mathbf 1}_{\mathcal{S}}(n) e(n\alpha)\bigg|{\textrm{d}}{x}\ll \exp(-M(f;X,Q)/2000)H'X, \end{align*} $$uniformly for ![]() $H'\in [H_1/4,H_1/2]$. Since the conditions for W in [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3] are satisfied, we can again apply that theorem to obtain the desired bound (noting that
$H'\in [H_1/4,H_1/2]$. Since the conditions for W in [Reference Matomäki, Radziwiłł and Tao12, Theorem 2.3] are satisfied, we can again apply that theorem to obtain the desired bound (noting that ![]() $\frac {(\log H_1)^{1/4}(\log \log H_1)}{W^{1/4}}\ll \exp (-M(f;X,Q)/2000)$ in this situation). This completes the proof.
$\frac {(\log H_1)^{1/4}(\log \log H_1)}{W^{1/4}}\ll \exp (-M(f;X,Q)/2000)$ in this situation). This completes the proof.
2.2 Upper-bounding correlations of primes
The goal of this subsection is to prove Proposition 2.7 below, which gives optimal bounds for even moments of the short exponential sums associated with correlations of the von Mangoldt function. We first need a few lemmas on tuples of primes and averages of singular series.
Recall for a tuple ![]() $\mathcal H$ of integers,
$\mathcal H$ of integers, ![]() $\nu _{p}(\mathcal {H}) = |\{h\pmod {p} : h\in \mathcal H\}|$. A well-known application of Selberg’s sieve upper bounds the number of k-tuples of primes, for fixed k.
$\nu _{p}(\mathcal {H}) = |\{h\pmod {p} : h\in \mathcal H\}|$. A well-known application of Selberg’s sieve upper bounds the number of k-tuples of primes, for fixed k.
Lemma 2.3. Let ![]() $k\geq 1$ be fixed, let
$k\geq 1$ be fixed, let ![]() $X\geq X_0(k)$ and suppose that
$X\geq X_0(k)$ and suppose that ![]() $h_1,\ldots , h_k\in [-X,X]$ are distinct integers. Denote
$h_1,\ldots , h_k\in [-X,X]$ are distinct integers. Denote ![]() $\mathcal H = \{h_1,\ldots ,h_k\}$. Then we have
$\mathcal H = \{h_1,\ldots ,h_k\}$. Then we have
where the singular series is given by
 $$ \begin{align*} \mathfrak{S}(\mathcal H) := \prod_p \Big(1-\frac{\nu_{p}(\mathcal{H})}{p}\Big)\Big(1-\frac{1}{p}\Big)^{-k}. \end{align*} $$
$$ \begin{align*} \mathfrak{S}(\mathcal H) := \prod_p \Big(1-\frac{\nu_{p}(\mathcal{H})}{p}\Big)\Big(1-\frac{1}{p}\Big)^{-k}. \end{align*} $$Proof. This is [Reference Friedlander and Iwaniec4, Theorem 7.16].
We have a trivial upper bound for the values of the singular series, which we will need in what follows.
Lemma 2.4. Let ![]() $k\geq 1$, and let
$k\geq 1$, and let ![]() $\mathcal {H}=\{h_1,\ldots , h_k\}$ be a tuple of distinct integers. Then
$\mathcal {H}=\{h_1,\ldots , h_k\}$ be a tuple of distinct integers. Then
 $$ \begin{align*} \mathfrak{S}(\mathcal{H})\ll_k \prod_{1\leq i<j\leq k}\Big(\frac{|h_i-h_j|}{\varphi(|h_i-h_j|)}\Big)^k. \end{align*} $$
$$ \begin{align*} \mathfrak{S}(\mathcal{H})\ll_k \prod_{1\leq i<j\leq k}\Big(\frac{|h_i-h_j|}{\varphi(|h_i-h_j|)}\Big)^k. \end{align*} $$Proof. Note that ![]() $\nu _{p}(\mathcal {H})\le k$, and that if
$\nu _{p}(\mathcal {H})\le k$, and that if ![]() $\nu _{p}(\mathcal {H})<k$, then p must divide
$\nu _{p}(\mathcal {H})<k$, then p must divide ![]() $h_i-h_j$ for some
$h_i-h_j$ for some ![]() $i<j$. Hence
$i<j$. Hence
 $$ \begin{align*} \mathfrak{S}(\mathcal{H}) &\le \prod_{\nu_{p}(\mathcal{H})=k} \left(1-\frac{k}{p}\right)\left(1-\frac{1}{p}\right)^{-k}\prod_{\nu_{p}(\mathcal{H})<k}\left(1-\frac{1}{p}\right)^{-k}\\ &\le \prod_{p>k}\left(1-\frac{k}{p}\right)\left(1-\frac{1}{p}\right)^{-k}\prod_{1\leq i<j\leq k}\prod_{p\mid h_i-h_j}\left(1-\frac{1}{p}\right)^{-k}\ll_k \prod_{1\leq i<j\leq k}\Big(\frac{|h_i-h_j|}{\varphi(|h_i-h_j|)}\Big)^k, \end{align*} $$
$$ \begin{align*} \mathfrak{S}(\mathcal{H}) &\le \prod_{\nu_{p}(\mathcal{H})=k} \left(1-\frac{k}{p}\right)\left(1-\frac{1}{p}\right)^{-k}\prod_{\nu_{p}(\mathcal{H})<k}\left(1-\frac{1}{p}\right)^{-k}\\ &\le \prod_{p>k}\left(1-\frac{k}{p}\right)\left(1-\frac{1}{p}\right)^{-k}\prod_{1\leq i<j\leq k}\prod_{p\mid h_i-h_j}\left(1-\frac{1}{p}\right)^{-k}\ll_k \prod_{1\leq i<j\leq k}\Big(\frac{|h_i-h_j|}{\varphi(|h_i-h_j|)}\Big)^k, \end{align*} $$as claimed.
We will also need an upper bound for the autocorrelations of ![]() $h/\varphi (h)$.
$h/\varphi (h)$.
Lemma 2.5. Let ![]() $H\geq 1$, and let
$H\geq 1$, and let ![]() $C,k,r\geq 1$ be fixed. Then we haveFootnote 3
$C,k,r\geq 1$ be fixed. Then we haveFootnote 3
 $$ \begin{align*} \sum_{h\leq H}\prod_{i=1}^r\left(\frac{|L_i(h)|}{\varphi(|L_i(h)|)}\right)^k \ll_{r,k,C} H \end{align*} $$
$$ \begin{align*} \sum_{h\leq H}\prod_{i=1}^r\left(\frac{|L_i(h)|}{\varphi(|L_i(h)|)}\right)^k \ll_{r,k,C} H \end{align*} $$uniformly for any linear functions ![]() $L_i(h)=a_ih+b_i$ with
$L_i(h)=a_ih+b_i$ with ![]() $a_i,b_i\in [-C,C]\cap \mathbb {Z}$.
$a_i,b_i\in [-C,C]\cap \mathbb {Z}$.
Proof. First note that for ![]() $H'\geq 1$ and any integer
$H'\geq 1$ and any integer ![]() $m\geq 1$, we have
$m\geq 1$, we have
 $$ \begin{align} \sum_{h\leq H'}\left(\frac{h}{\varphi(h)}\right)^{m} \ &= \ \sum_{h\leq H'} \bigg(\sum_{d\mid h}\frac{1}{d}\bigg)^{m} =\sum_{d_1,\ldots, d_m\geq 1} \frac{1}{d_1\cdots d_m}\sum_{\substack{h\leq H'\\d_i\mid h\;\forall i\le m}}1 \nonumber\\ &\ll H'\sum_{d_1,\ldots, d_m\geq 1}\frac{1}{d_1\cdots d_m[d_1,\ldots, d_m]} \nonumber\\ &\ll H'\prod_{p_1,\ldots, p_m}\left(1+\sum_{\substack{j_1,\ldots, j_m\geq 0\\ (j_1,\ldots, j_m)\neq (0,\ldots, 0)}}\frac{1}{p_1^{j_1}\cdots p_m^{j_m}[p_1^{j_1},\ldots, p_m^{j_m}]}\right) \ \ll_m \ H'. \end{align} $$
$$ \begin{align} \sum_{h\leq H'}\left(\frac{h}{\varphi(h)}\right)^{m} \ &= \ \sum_{h\leq H'} \bigg(\sum_{d\mid h}\frac{1}{d}\bigg)^{m} =\sum_{d_1,\ldots, d_m\geq 1} \frac{1}{d_1\cdots d_m}\sum_{\substack{h\leq H'\\d_i\mid h\;\forall i\le m}}1 \nonumber\\ &\ll H'\sum_{d_1,\ldots, d_m\geq 1}\frac{1}{d_1\cdots d_m[d_1,\ldots, d_m]} \nonumber\\ &\ll H'\prod_{p_1,\ldots, p_m}\left(1+\sum_{\substack{j_1,\ldots, j_m\geq 0\\ (j_1,\ldots, j_m)\neq (0,\ldots, 0)}}\frac{1}{p_1^{j_1}\cdots p_m^{j_m}[p_1^{j_1},\ldots, p_m^{j_m}]}\right) \ \ll_m \ H'. \end{align} $$Then, by Hölder’s inequality and (2.6) with ![]() $H'=(C+1)H$, we have
$H'=(C+1)H$, we have
 $$ \begin{align*} \sum_{h\leq H}\prod_{i\le r}\left(\frac{|L_i(h)|}{\varphi(|L_i(h)|)}\right)^k &\leq \prod_{i\le r} \left(\sum_{h\leq H} \left(\frac{|L_i(h)|}{\varphi(|L_i(h)|)}\right)^{rk}\right)^{1/r}\\ &\leq \prod_{i\le r} \left(\sum_{h\leq (C+1)H} \left(\frac{h}{\varphi(h)}\right)^{rk}\right)^{1/r} \ \ll_{r,k,C} \ H, \end{align*} $$
$$ \begin{align*} \sum_{h\leq H}\prod_{i\le r}\left(\frac{|L_i(h)|}{\varphi(|L_i(h)|)}\right)^k &\leq \prod_{i\le r} \left(\sum_{h\leq H} \left(\frac{|L_i(h)|}{\varphi(|L_i(h)|)}\right)^{rk}\right)^{1/r}\\ &\leq \prod_{i\le r} \left(\sum_{h\leq (C+1)H} \left(\frac{h}{\varphi(h)}\right)^{rk}\right)^{1/r} \ \ll_{r,k,C} \ H, \end{align*} $$using the fact that ![]() $L_i(\cdot )$ takes any integer value at most once.
$L_i(\cdot )$ takes any integer value at most once.
The previous lemmas lead to the following corollary.
Corollary 2.6. Let ![]() $k\geq m\geq 1$ be fixed. Then
$k\geq m\geq 1$ be fixed. Then
where the supremum ranges over affine-linear forms ![]() $L_j(h_1,\ldots ,h_m) = a_j+\sum _{i=1}^ma_{i,j}h_i$ with integer coefficients and with
$L_j(h_1,\ldots ,h_m) = a_j+\sum _{i=1}^ma_{i,j}h_i$ with integer coefficients and with ![]() $|a_{i,j}|,|a_j|\le A$.
$|a_{i,j}|,|a_j|\le A$.
Proof. Denote by ![]() $\Sigma $ the sum of interest on the left-hand side. Since there are
$\Sigma $ the sum of interest on the left-hand side. Since there are ![]() $O_{k,A}(1)$ many choices of affine-linear forms
$O_{k,A}(1)$ many choices of affine-linear forms ![]() $L_1,\ldots ,L_k$ with A-bounded coefficients, it suffices to take the supremum outside the sum in
$L_1,\ldots ,L_k$ with A-bounded coefficients, it suffices to take the supremum outside the sum in ![]() $\Sigma $. Then for each
$\Sigma $. Then for each ![]() $L_1,\ldots ,L_k$, by Lemma 2.4, we bound
$L_1,\ldots ,L_k$, by Lemma 2.4, we bound ![]() $\Sigma $ as
$\Sigma $ as
 $$ \begin{align*} \Sigma \ &\ll_k \ \sum_{\mathbf{h}\in [0,H]^m}\prod_{1\le j<j'\le k}\left(\frac{|L_j(\mathbf{h})-L_{j'}(\mathbf{h}) |}{\varphi(|L_j(\mathbf{h})-L_{j'}(\mathbf{h})|)}\right)^k\\ &= \sum_{\mathbf{h}\in [0,H]^{m-1}}\sum_{h\le H}\prod_{1\le j<j'\le k}\left(\frac{|L_{j,j',\mathbf{h}}(h)|}{\varphi(|L_{j,j',\mathbf{h}}(h))|}\right)^k \ \ll \ \sum_{\mathbf{h}\in [0,H]^{m-1}}H \ll H^m, \end{align*} $$
$$ \begin{align*} \Sigma \ &\ll_k \ \sum_{\mathbf{h}\in [0,H]^m}\prod_{1\le j<j'\le k}\left(\frac{|L_j(\mathbf{h})-L_{j'}(\mathbf{h}) |}{\varphi(|L_j(\mathbf{h})-L_{j'}(\mathbf{h})|)}\right)^k\\ &= \sum_{\mathbf{h}\in [0,H]^{m-1}}\sum_{h\le H}\prod_{1\le j<j'\le k}\left(\frac{|L_{j,j',\mathbf{h}}(h)|}{\varphi(|L_{j,j',\mathbf{h}}(h))|}\right)^k \ \ll \ \sum_{\mathbf{h}\in [0,H]^{m-1}}H \ll H^m, \end{align*} $$since to each ![]() $\mathbf {h}\in [0,H]^{m-1}$ we can apply Lemma 2.5 with
$\mathbf {h}\in [0,H]^{m-1}$ we can apply Lemma 2.5 with ![]() $r=\binom {k}{2}$,
$r=\binom {k}{2}$, ![]() $C = mA$ and linear functions
$C = mA$ and linear functions ![]() $L_{j,j',\mathbf {h}}(h) := L_j(\mathbf {h},h)-L_{j'}(\mathbf {h},h)$.
$L_{j,j',\mathbf {h}}(h) := L_j(\mathbf {h},h)-L_{j'}(\mathbf {h},h)$.
Using Corollary 2.6, we can prove the following bound for high moments of short exponential sums associated with the correlations of the von Mangoldt function. This estimate will be needed in Section 4.
Proposition 2.7. Let ![]() $\ell \geq 1$,
$\ell \geq 1$, ![]() $k\geq 2$ be fixed, and let
$k\geq 2$ be fixed, and let ![]() $a_1,\ldots ,a_{\ell }$ be distinct fixed integers. For
$a_1,\ldots ,a_{\ell }$ be distinct fixed integers. For ![]() $X\geq H\geq 2$ and
$X\geq H\geq 2$ and ![]() $|g(n)|\leq 1$, we have
$|g(n)|\leq 1$, we have
 $$ \begin{align*} M_{2k}:= &\int_{0}^X \int_{0}^{1}\bigg|\sum_{x\leq n\leq x+H} g(n) e(\alpha n)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|^{2k}{\textrm{d}}\alpha {\textrm{d}} x \\ & \ll \ X(H^{2k-1}+H^{k}(\log X)^{k\ell}+H(\log X)^{(2k-1)\ell}). \end{align*} $$
$$ \begin{align*} M_{2k}:= &\int_{0}^X \int_{0}^{1}\bigg|\sum_{x\leq n\leq x+H} g(n) e(\alpha n)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|^{2k}{\textrm{d}}\alpha {\textrm{d}} x \\ & \ll \ X(H^{2k-1}+H^{k}(\log X)^{k\ell}+H(\log X)^{(2k-1)\ell}). \end{align*} $$In particular, if ![]() $H\geq (\log X)^{\ell k/(k-1)}$, then
$H\geq (\log X)^{\ell k/(k-1)}$, then
Remark 2.8. The bound above for ![]() $M_{2k}$ is optimal up to a constant factor, assuming the Hardy–Littlewood prime tuples conjecture. Indeed, one can show that
$M_{2k}$ is optimal up to a constant factor, assuming the Hardy–Littlewood prime tuples conjecture. Indeed, one can show that ![]() $M_{2k}\gg X H^{2k-1}$ in the case
$M_{2k}\gg X H^{2k-1}$ in the case ![]() $g(n)\equiv 1$, assuming the Hardy–Littlewood conjecture (this is done by considering the contribution to (2.8) below coming from those
$g(n)\equiv 1$, assuming the Hardy–Littlewood conjecture (this is done by considering the contribution to (2.8) below coming from those ![]() $(n_1,\ldots , n_{2k})$ with
$(n_1,\ldots , n_{2k})$ with ![]() $H>|n_i-n_j|>\max _{i}|a_i|$ for all
$H>|n_i-n_j|>\max _{i}|a_i|$ for all ![]() $i\neq j$). Similarly, one can show
$i\neq j$). Similarly, one can show ![]() $M_{2k}\gg XH^{k}(\log X)^{k\ell }$ (by considering the contribution to (2.8) below coming from those
$M_{2k}\gg XH^{k}(\log X)^{k\ell }$ (by considering the contribution to (2.8) below coming from those ![]() $(n_1,\ldots , n_{2k})$ with
$(n_1,\ldots , n_{2k})$ with ![]() $n_{k+i}=n_i$ for all
$n_{k+i}=n_i$ for all ![]() $i\le k$ and
$i\le k$ and ![]() $H>|n_i-n_j|>\max _{i}|a_i|$). Last, one can show
$H>|n_i-n_j|>\max _{i}|a_i|$). Last, one can show ![]() $M_{2k}\gg XH(\log X)^{(2k-1)\ell }$ (by considering the contribution to (2.8) below coming from those
$M_{2k}\gg XH(\log X)^{(2k-1)\ell }$ (by considering the contribution to (2.8) below coming from those ![]() $(n_1,\ldots , n_{2k})$ with
$(n_1,\ldots , n_{2k})$ with ![]() $n_1=\cdots =n_{2k}$).
$n_1=\cdots =n_{2k}$).
Proof. Expanding out the definition of ![]() $M_{2k}$ using orthogonality, we obtain
$M_{2k}$ using orthogonality, we obtain
 $$ \begin{align} M_{2k} &= \int_{0}^X\sum_{\substack{x\leq n_1,\ldots, n_{2k}\leq x+H\\n_1+\cdots +n_k=n_{k+1}+\cdots +n_{2k}}}g(n_1)\cdots g(n_k)\overline{g(n_{k+1})\cdots g(n_{2k})}\prod_{\substack{j\le \ell\\i\le 2k}} \Lambda(n_i+a_j) {\textrm{d}} x, \end{align} $$
$$ \begin{align} M_{2k} &= \int_{0}^X\sum_{\substack{x\leq n_1,\ldots, n_{2k}\leq x+H\\n_1+\cdots +n_k=n_{k+1}+\cdots +n_{2k}}}g(n_1)\cdots g(n_k)\overline{g(n_{k+1})\cdots g(n_{2k})}\prod_{\substack{j\le \ell\\i\le 2k}} \Lambda(n_i+a_j) {\textrm{d}} x, \end{align} $$and so ![]() $|g(n)|\le 1$ implies
$|g(n)|\le 1$ implies
 $$ \begin{align} M_{2k} &\le \sum_{\substack{n_1,\ldots, n_{2k}\leq X+H\\n_1+\cdots +n_k=n_{k+1}+\cdots +n_{2k}}}\prod_{\substack{j\le \ell\\i\le 2k}} \Lambda(n_i+a_j)\cdot \int_{0}^X {\mathbf 1}_{x\leq n_1\leq x+H}\cdots {\mathbf 1}_{x\leq n_{2k}\leq x+H}{\textrm{d}} x. \end{align} $$
$$ \begin{align} M_{2k} &\le \sum_{\substack{n_1,\ldots, n_{2k}\leq X+H\\n_1+\cdots +n_k=n_{k+1}+\cdots +n_{2k}}}\prod_{\substack{j\le \ell\\i\le 2k}} \Lambda(n_i+a_j)\cdot \int_{0}^X {\mathbf 1}_{x\leq n_1\leq x+H}\cdots {\mathbf 1}_{x\leq n_{2k}\leq x+H}{\textrm{d}} x. \end{align} $$For each ![]() $n_1,\ldots , n_{2k}\leq X+H$, denote
$n_1,\ldots , n_{2k}\leq X+H$, denote ![]() $M=\max _{1\le i,j\le 2k} |n_i-n_j|$, so that
$M=\max _{1\le i,j\le 2k} |n_i-n_j|$, so that
 $$ \begin{align*} \int_{0}^X {\mathbf 1}_{x\leq n_1\leq x+H}\cdots {\mathbf 1}_{x\leq n_{2k}\leq x+H}{\textrm{d}}{x}&=(H-M){\mathbf 1}_{0\leq M\leq H} \ \leq \ H {\mathbf 1}_{0\leq M< H}, \end{align*} $$
$$ \begin{align*} \int_{0}^X {\mathbf 1}_{x\leq n_1\leq x+H}\cdots {\mathbf 1}_{x\leq n_{2k}\leq x+H}{\textrm{d}}{x}&=(H-M){\mathbf 1}_{0\leq M\leq H} \ \leq \ H {\mathbf 1}_{0\leq M< H}, \end{align*} $$and if we let ![]() $n=n_{2k}$,
$n=n_{2k}$, ![]() $h_i = n_i-n$ (so
$h_i = n_i-n$ (so ![]() $h_{2k}=0$), then (2.9) becomes
$h_{2k}=0$), then (2.9) becomes
 $$ \begin{align*} M_{2k} &\le \ H\sum_{\substack{n_1,\ldots, n_{2k}\leq X+H\\n_1+\cdots +n_k=n_{k+1}+\cdots +n_{2k}\\\max_{i,j}|n_i-n_j|< H}}\prod_{\substack{j\le \ell\\i\le 2k}} \Lambda(n_i+a_j)\\ &\leq \ H\sum_{\substack{-H\leq h_1,\ldots, h_{2k-1}\leq H\\h_1+\cdots+h_k=h_{k+1}+\cdots +h_{2k-1}}}\sum_{n\leq X+H}\prod_{\substack{1\le j\le \ell\\0\le i\le 2k-1}} \Lambda(n+h_i+a_j). \end{align*} $$
$$ \begin{align*} M_{2k} &\le \ H\sum_{\substack{n_1,\ldots, n_{2k}\leq X+H\\n_1+\cdots +n_k=n_{k+1}+\cdots +n_{2k}\\\max_{i,j}|n_i-n_j|< H}}\prod_{\substack{j\le \ell\\i\le 2k}} \Lambda(n_i+a_j)\\ &\leq \ H\sum_{\substack{-H\leq h_1,\ldots, h_{2k-1}\leq H\\h_1+\cdots+h_k=h_{k+1}+\cdots +h_{2k-1}}}\sum_{n\leq X+H}\prod_{\substack{1\le j\le \ell\\0\le i\le 2k-1}} \Lambda(n+h_i+a_j). \end{align*} $$Write ![]() $\mathcal {A}=\{a_1,\ldots , a_{\ell }\}$ and
$\mathcal {A}=\{a_1,\ldots , a_{\ell }\}$ and ![]() $\mathcal H=\{0,h_1,\ldots , h_{2k-1}\}$ (note
$\mathcal H=\{0,h_1,\ldots , h_{2k-1}\}$ (note ![]() $h_{2k-1}=h_1+\cdots +h_{k-1}-h_{k}-\cdots -h_{2k-2}$). Let
$h_{2k-1}=h_1+\cdots +h_{k-1}-h_{k}-\cdots -h_{2k-2}$). Let ![]() $\mathcal {A}+\mathcal {H}$ denote the sumset, and observe that
$\mathcal {A}+\mathcal {H}$ denote the sumset, and observe that ![]() $|\mathcal {A}+\mathcal {H}|\in [\ell ,2k\ell ]$. In what follows, for convenience of notation, we denote
$|\mathcal {A}+\mathcal {H}|\in [\ell ,2k\ell ]$. In what follows, for convenience of notation, we denote ![]() $h_0=0$.
$h_0=0$.
Now, we partition the tuples ![]() $\mathcal H$ according to
$\mathcal H$ according to ![]() $|\mathcal {A}+\mathcal {H}|$, namely, for
$|\mathcal {A}+\mathcal {H}|$, namely, for ![]() $m\in [0,(2k-1)\ell ]$, denote
$m\in [0,(2k-1)\ell ]$, denote
so that by Lemma 2.3,
 $$ \begin{align} M_{2k} &\ll XH\sum_{m=0}^{(2k-1)\ell}(\log X)^{m}\sum_{(h_1,\ldots,h_{2k-2})\in {\textrm{H}}_m}\,\mathfrak{S}\big(\mathcal{A}+\mathcal{H}\big). \end{align} $$
$$ \begin{align} M_{2k} &\ll XH\sum_{m=0}^{(2k-1)\ell}(\log X)^{m}\sum_{(h_1,\ldots,h_{2k-2})\in {\textrm{H}}_m}\,\mathfrak{S}\big(\mathcal{A}+\mathcal{H}\big). \end{align} $$Let ![]() $A=\max _{a\in \mathcal A}|a|$. We claim that
$A=\max _{a\in \mathcal A}|a|$. We claim that
To show this, first note that all the sums ![]() $a_j+h_i$,
$a_j+h_i$, ![]() $j\leq \ell $,
$j\leq \ell $, ![]() $i\not \in \mathcal {I}$ are distinct, since if there was a coincidence
$i\not \in \mathcal {I}$ are distinct, since if there was a coincidence ![]() $a+h_i=a'+h_{i'}$ for some
$a+h_i=a'+h_{i'}$ for some ![]() $a,a'\in \mathcal A$,
$a,a'\in \mathcal A$, ![]() $i'>i$, then
$i'>i$, then ![]() $h_i-h_{i'}=a'-a\in [-A,A]$ and so
$h_i-h_{i'}=a'-a\in [-A,A]$ and so ![]() $i\in \mathcal {I}$. Thus, we must have
$i\in \mathcal {I}$. Thus, we must have
so ![]() $|\mathcal {I}|\geq m/\ell $, as claimed. Now, for
$|\mathcal {I}|\geq m/\ell $, as claimed. Now, for ![]() $I:=|\mathcal {I}|$, we have a system of
$I:=|\mathcal {I}|$, we have a system of ![]() $I+1$ linear inequalities constraining the vector
$I+1$ linear inequalities constraining the vector ![]() $(h_1,\ldots , h_{2k-1})\in [-H,H]^{2k-1}$
$(h_1,\ldots , h_{2k-1})\in [-H,H]^{2k-1}$
 $$ \begin{align*} \begin{cases} h_1+\cdots+h_{k-1}-h_k-\cdots-h_{2k-2}-h_{2k-1}=0\\ |h_i-h_{\sigma(i)}|\leq A,\quad i\in \mathcal{I}, \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} h_1+\cdots+h_{k-1}-h_k-\cdots-h_{2k-2}-h_{2k-1}=0\\ |h_i-h_{\sigma(i)}|\leq A,\quad i\in \mathcal{I}, \end{cases} \end{align*} $$where ![]() $h_0=0$, and
$h_0=0$, and ![]() $\sigma (i)\in [i+1,2k-1]$ are some integers.
$\sigma (i)\in [i+1,2k-1]$ are some integers.
Let ![]() $I'=I+1$ if
$I'=I+1$ if ![]() $I\leq k-1$, and let
$I\leq k-1$, and let ![]() $I'=I$ if
$I'=I$ if ![]() $I\geq k$. Then, by basic linear algebra, the set of
$I\geq k$. Then, by basic linear algebra, the set of ![]() $I+1$ linear forms above contains a subset of
$I+1$ linear forms above contains a subset of ![]() $I'$ linearly independent forms, so there exists a vector
$I'$ linearly independent forms, so there exists a vector ![]() ${\textbf {u}}=(u_1,\ldots , u_{2k-1-I'})\in [-H,H]^{2k-1-I'}$ (depending on
${\textbf {u}}=(u_1,\ldots , u_{2k-1-I'})\in [-H,H]^{2k-1-I'}$ (depending on ![]() $h_i$) and linear forms
$h_i$) and linear forms ![]() $L_i:\mathbb {Z}^{2k-2-I'}\to \mathbb {Z}$ with bounded coefficients (and with
$L_i:\mathbb {Z}^{2k-2-I'}\to \mathbb {Z}$ with bounded coefficients (and with ![]() $L_{0}\equiv 0$), such that by denoting
$L_{0}\equiv 0$), such that by denoting ![]() $L_{i,j}({\textbf {u}}) = a_j + L_i({\textbf {u}})$, we have
$L_{i,j}({\textbf {u}}) = a_j + L_i({\textbf {u}})$, we have
 $$ \begin{align} \mathcal{H}&=\{L_0({\textbf{u}})+O(1),\ldots, L_{2k-1}({\textbf{u}})+O(1)\} \nonumber\\ \mathcal{A}+\mathcal{H}&= \{L_{i,j}({\textbf{u}})+O(1): 0\leq i\le 2k-1, j\le \ell\}. \end{align} $$
$$ \begin{align} \mathcal{H}&=\{L_0({\textbf{u}})+O(1),\ldots, L_{2k-1}({\textbf{u}})+O(1)\} \nonumber\\ \mathcal{A}+\mathcal{H}&= \{L_{i,j}({\textbf{u}})+O(1): 0\leq i\le 2k-1, j\le \ell\}. \end{align} $$Thus, by Corollary 2.6 and the fact that ![]() $I'\geq \lceil m/\ell \rceil +1_{m\leq (k-1)\ell }$, for each m, we have
$I'\geq \lceil m/\ell \rceil +1_{m\leq (k-1)\ell }$, for each m, we have
 $$ \begin{align}\begin{split} \sum_{(h_1,\ldots,h_{2k-2})\in {\textrm{H}}_m}\,\mathfrak{S}\big(\mathcal{A}+\mathcal{H}\big) &\le \sum_{{\textbf{u}}\in[-H,H]^{2k-2-\lceil m/\ell\rceil+{\mathbf 1}_{m> (k-1)\ell}}}\mathfrak{S}\big(\big(L_{i,j}({\textbf{u}})+r\big)_{0\leq i\leq 2k-1, j\leq \ell,r=O(1)}\big)\\ &\ll H^{2k-2-\lceil m/\ell\rceil+{\mathbf 1}_{m> (k-1)\ell}}. \end{split} \end{align} $$
$$ \begin{align}\begin{split} \sum_{(h_1,\ldots,h_{2k-2})\in {\textrm{H}}_m}\,\mathfrak{S}\big(\mathcal{A}+\mathcal{H}\big) &\le \sum_{{\textbf{u}}\in[-H,H]^{2k-2-\lceil m/\ell\rceil+{\mathbf 1}_{m> (k-1)\ell}}}\mathfrak{S}\big(\big(L_{i,j}({\textbf{u}})+r\big)_{0\leq i\leq 2k-1, j\leq \ell,r=O(1)}\big)\\ &\ll H^{2k-2-\lceil m/\ell\rceil+{\mathbf 1}_{m> (k-1)\ell}}. \end{split} \end{align} $$Hence, the bound in (2.10) becomes
 $$ \begin{align*} M_{2k} &\ll XH\sum_{m=0}^{(2k-1)\ell}(\log X)^mH^{2k-2-\lceil m/\ell\rceil+{\mathbf 1}_{m> (k-1)\ell}}\\ &\ll X(H^{2k-1}+H^{k}(\log X)^{k\ell}+H(\log X)^{(2k-1)\ell}). \end{align*} $$
$$ \begin{align*} M_{2k} &\ll XH\sum_{m=0}^{(2k-1)\ell}(\log X)^mH^{2k-2-\lceil m/\ell\rceil+{\mathbf 1}_{m> (k-1)\ell}}\\ &\ll X(H^{2k-1}+H^{k}(\log X)^{k\ell}+H(\log X)^{(2k-1)\ell}). \end{align*} $$Finally, the assumption ![]() $H \ge (\log X)^{\ell k/(k-1)}$ implies
$H \ge (\log X)^{\ell k/(k-1)}$ implies ![]() $M_{2k} \ll XH^{2k-1}$ as claimed.
$M_{2k} \ll XH^{2k-1}$ as claimed.
2.3 Correlations of primes and integers having typical factorisation
In this subsection, we will prove Lemma 2.11, which upper bounds the correlations of the von Mangoldt function and the indicator of numbers having prime factors in prescribed intervals.
We first consider a class of multiplicative functions with ‘moderate growth’.
Definition 2.9. Denote the set ![]() $\mathcal M$ of multiplicative
$\mathcal M$ of multiplicative ![]() $f:\mathbb {N}\to \mathbb {R}_{\ge 0}$ with
$f:\mathbb {N}\to \mathbb {R}_{\ge 0}$ with
(i)
 $f(p^\nu ) \le 2^\nu $ for all primes p,
$f(p^\nu ) \le 2^\nu $ for all primes p,  $\nu \ge 1$;
$\nu \ge 1$;(ii) for all
 $\varepsilon>0$, there exists
$\varepsilon>0$, there exists  $B=B(\varepsilon )$, such that
$B=B(\varepsilon )$, such that  $f(n) \le Bn^{\varepsilon }$ for all
$f(n) \le Bn^{\varepsilon }$ for all  $n\ge 1$.
$n\ge 1$.
Now, we give a special case of a general bound of Henriot [Reference Henriot8] for the class ![]() $\mathcal M$. Henriot’s result refines earlier work of Nair–Tenenbaum [Reference Nair and Tenenbaum17], and importantly, it is uniform in the discriminant.
$\mathcal M$. Henriot’s result refines earlier work of Nair–Tenenbaum [Reference Nair and Tenenbaum17], and importantly, it is uniform in the discriminant.
Lemma 2.10. Given ![]() $k\ge 1$ and a tuple
$k\ge 1$ and a tuple ![]() $\mathcal H=\{h_1,\ldots ,h_k\}\subset [1,X]$, denote
$\mathcal H=\{h_1,\ldots ,h_k\}\subset [1,X]$, denote ![]() $\nu _p(\mathcal {H}) = |\{h\,(\text {mod }p) : h\in \mathcal H\}|$. Then for any multiplicative functions
$\nu _p(\mathcal {H}) = |\{h\,(\text {mod }p) : h\in \mathcal H\}|$. Then for any multiplicative functions ![]() $f_j\in \mathcal M$,
$f_j\in \mathcal M$,
 $$ \begin{align} \sum_{\sqrt{X} \le n\le X}\prod_{j=1}^k f_j(n+h_j) \ \ll_{k} \Delta_D\,X\prod_{p\le \sqrt{X}}\Big(1-\frac{\nu_p(\mathcal{H})}{p}\Big)\prod_{j=1}^k\sum_{n\le \sqrt{X}}\frac{f_j(n)}{n} ,\end{align} $$
$$ \begin{align} \sum_{\sqrt{X} \le n\le X}\prod_{j=1}^k f_j(n+h_j) \ \ll_{k} \Delta_D\,X\prod_{p\le \sqrt{X}}\Big(1-\frac{\nu_p(\mathcal{H})}{p}\Big)\prod_{j=1}^k\sum_{n\le \sqrt{X}}\frac{f_j(n)}{n} ,\end{align} $$where ![]() $D=D(\mathcal H)=\prod _{i<j}(h_j-h_i)^2$, and
$D=D(\mathcal H)=\prod _{i<j}(h_j-h_i)^2$, and
 $$ \begin{align*} \Delta_D = \prod_{p\mid D}\bigg(1\ + \sum_{\substack{0\leq \nu_1,\ldots, \nu_k\leq 1\\ (\nu_1,\ldots, \nu_k)\neq (0,\ldots, 0)}} \frac{|\{n\, (\text{mod }p^{2})\,:\, p^{\nu_j}\mid\mid n+h_j\, \forall j \}|}{p^2}\prod_{j=1}^k f_j(p)\bigg) .\end{align*} $$
$$ \begin{align*} \Delta_D = \prod_{p\mid D}\bigg(1\ + \sum_{\substack{0\leq \nu_1,\ldots, \nu_k\leq 1\\ (\nu_1,\ldots, \nu_k)\neq (0,\ldots, 0)}} \frac{|\{n\, (\text{mod }p^{2})\,:\, p^{\nu_j}\mid\mid n+h_j\, \forall j \}|}{p^2}\prod_{j=1}^k f_j(p)\bigg) .\end{align*} $$In particular, if ![]() $|f(p)|\leq 1$ for all p, we have
$|f(p)|\leq 1$ for all p, we have ![]() $\Delta _D \le \prod _{p\mid D}(1+ 2^k/p)$.
$\Delta _D \le \prod _{p\mid D}(1+ 2^k/p)$.
Proof. This is [Reference Henriot8, Theorem 3] in the special case of ![]() $x=\sqrt {X}$,
$x=\sqrt {X}$, ![]() $y=X$,
$y=X$, ![]() $\delta = 1/(2k)$, with linear polynomials
$\delta = 1/(2k)$, with linear polynomials ![]() $Q_j(n)=n+h_j$,
$Q_j(n)=n+h_j$, ![]() $Q(n) = \prod _{j=1}^k Q_j(n)$, and the multiplicative function
$Q(n) = \prod _{j=1}^k Q_j(n)$, and the multiplicative function ![]() $F(n_1,\ldots ,n_k)=\prod _{j=1}^k f_j(n_j)$. Note, that the discriminant of the polynomial Q is
$F(n_1,\ldots ,n_k)=\prod _{j=1}^k f_j(n_j)$. Note, that the discriminant of the polynomial Q is ![]() $\prod _{i<j}(h_i-h_j)^2=D$ and the sum of coefficients is
$\prod _{i<j}(h_i-h_j)^2=D$ and the sum of coefficients is ![]() $\|Q\| \ll \prod _{j=1}^k h_j \ll X^{k}$.
$\|Q\| \ll \prod _{j=1}^k h_j \ll X^{k}$.
We remark that the bound (2.13) is of the correct order of magnitude when the functions ![]() $f_j$ are not too small, for example,
$f_j$ are not too small, for example, ![]() $f_j(n) \ge \eta ^{\Omega (n)}$ for some
$f_j(n) \ge \eta ^{\Omega (n)}$ for some ![]() $\eta>0$ (see [Reference Henriot8, Theorem 6].
$\eta>0$ (see [Reference Henriot8, Theorem 6].
As mentioned, we will need in Section 4 a simple upper bound for the correlations of the primes and integers with prescribed factorisation patterns.
Lemma 2.11. Let ![]() $\ell \geq 1$ be fixed, and let
$\ell \geq 1$ be fixed, and let ![]() $a_1,\ldots , a_{\ell }$ be fixed and distinct. Let
$a_1,\ldots , a_{\ell }$ be fixed and distinct. Let ![]() $X\geq 2$ and
$X\geq 2$ and ![]() $1\leq h\leq X$ with
$1\leq h\leq X$ with ![]() $h\neq a_j$ for all
$h\neq a_j$ for all ![]() $1\leq j\leq \ell $. Let
$1\leq j\leq \ell $. Let ![]() $\mathcal {I}\subset [1,X]$, and let
$\mathcal {I}\subset [1,X]$, and let ![]() $\mathcal {N}$ be the set of positive integers having no prime factors from
$\mathcal {N}$ be the set of positive integers having no prime factors from ![]() $\mathcal {I}$. Then we have
$\mathcal {I}$. Then we have
 $$ \begin{align} \sum_{n\leq X}{\mathbf 1}_{\mathcal{N}}(n+h)\Lambda(n+a_1)\cdots \Lambda(n+a_{\ell})\ll X\prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)} \right)^{2^{\ell+1}}\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right). \end{align} $$
$$ \begin{align} \sum_{n\leq X}{\mathbf 1}_{\mathcal{N}}(n+h)\Lambda(n+a_1)\cdots \Lambda(n+a_{\ell})\ll X\prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)} \right)^{2^{\ell+1}}\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right). \end{align} $$Proof. Let ![]() $P(z)=\prod _{p< z} p$. We may assume that the summation in (2.14) runs over
$P(z)=\prod _{p< z} p$. We may assume that the summation in (2.14) runs over ![]() $(2X)^{1/2}\leq n\leq X$, since the contribution of
$(2X)^{1/2}\leq n\leq X$, since the contribution of ![]() $n<(2X)^{1/2}$ is negligible. Therefore, the proof of (2.14) has been reduced to showing:
$n<(2X)^{1/2}$ is negligible. Therefore, the proof of (2.14) has been reduced to showing:
 $$ \begin{align} \sum_{n\leq X}{\mathbf 1}_{\mathcal{N}}(n+h)\prod_{j=1}^{\ell}{\mathbf 1}_{(n+a_j,P((2X)^{1/2}))=1}\ll X(\log X)^{-\ell}\prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)} \right)^{2^{\ell+1}}\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right). \end{align} $$
$$ \begin{align} \sum_{n\leq X}{\mathbf 1}_{\mathcal{N}}(n+h)\prod_{j=1}^{\ell}{\mathbf 1}_{(n+a_j,P((2X)^{1/2}))=1}\ll X(\log X)^{-\ell}\prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)} \right)^{2^{\ell+1}}\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right). \end{align} $$Note that all the indicator functions above are multiplicative. Denote ![]() $D=\prod _{1\le i<j\le \ell }(a_i-a_j)\prod _{j\leq \ell } (h-a_j)$. Now, by Lemma 2.10, we have
$D=\prod _{1\le i<j\le \ell }(a_i-a_j)\prod _{j\leq \ell } (h-a_j)$. Now, by Lemma 2.10, we have
 $$ \begin{align} \sum_{n\leq X}{\mathbf 1}_{\mathcal{N}}(n+h)\prod_{j=1}^{\ell} & {\mathbf 1}_{(n+a_j,P((2X)^{1/2}))=1} \nonumber\\ &\ll \ \Delta_D X\prod_{p\leq X}\left(1-\frac{\ell+1}{p}\right) \sum_{n_0,n_1,\ldots, n_{\ell}\leq X}\frac{{\mathbf 1}_{\mathcal{N}}(n_0)\prod_{j=1}^{\ell}{\mathbf 1}_{(n_j,P((2X)^{1/2}))=1}}{n_0n_1\cdots n_{\ell}}, \end{align} $$
$$ \begin{align} \sum_{n\leq X}{\mathbf 1}_{\mathcal{N}}(n+h)\prod_{j=1}^{\ell} & {\mathbf 1}_{(n+a_j,P((2X)^{1/2}))=1} \nonumber\\ &\ll \ \Delta_D X\prod_{p\leq X}\left(1-\frac{\ell+1}{p}\right) \sum_{n_0,n_1,\ldots, n_{\ell}\leq X}\frac{{\mathbf 1}_{\mathcal{N}}(n_0)\prod_{j=1}^{\ell}{\mathbf 1}_{(n_j,P((2X)^{1/2}))=1}}{n_0n_1\cdots n_{\ell}}, \end{align} $$where ![]() $\Delta _D$ is crudely bounded as
$\Delta _D$ is crudely bounded as
 $$ \begin{align*} \Delta_D\le \prod_{p\mid D}\left(1+\frac{2^{\ell+1}}{p}\right)\ll \prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)} \right)^{2^{\ell+1}}. \end{align*} $$
$$ \begin{align*} \Delta_D\le \prod_{p\mid D}\left(1+\frac{2^{\ell+1}}{p}\right)\ll \prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)} \right)^{2^{\ell+1}}. \end{align*} $$Now, (2.15) follows by noting that by Euler products and Mertens’s theorem
 $$ \begin{align*} \sum_{n\leq X}\frac{{\mathbf 1}_{\mathcal{N}}(n)}{n}\leq \prod_{\substack{p\leq X\\p\not \in \mathcal{I}}}\left(1+\frac{1}{p}+\frac{1}{p^2}+\cdots\right)&= \prod_{p\leq X}\left(1+\frac{1}{p}+\frac{1}{p^2}+\cdots\right)\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right)\\ &\ll (\log X)^{-\ell} \prod_{p\leq X}\left(1-\frac{\ell+1}{p}\right)^{-1}\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right), \end{align*} $$
$$ \begin{align*} \sum_{n\leq X}\frac{{\mathbf 1}_{\mathcal{N}}(n)}{n}\leq \prod_{\substack{p\leq X\\p\not \in \mathcal{I}}}\left(1+\frac{1}{p}+\frac{1}{p^2}+\cdots\right)&= \prod_{p\leq X}\left(1+\frac{1}{p}+\frac{1}{p^2}+\cdots\right)\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right)\\ &\ll (\log X)^{-\ell} \prod_{p\leq X}\left(1-\frac{\ell+1}{p}\right)^{-1}\prod_{p\in \mathcal{I}}\left(1-\frac{1}{p}\right), \end{align*} $$and also by Mertens’s theorem
 $$ \begin{align*} \sum_{n\leq X}\frac{{\mathbf 1}_{(n,P((2X)^{1/2}))=1}}{n}=1+\sum_{(2X)^{1/2}\leq p\leq X} \frac{1}{p}\asymp 1.\\[-4.4pc] \end{align*} $$
$$ \begin{align*} \sum_{n\leq X}\frac{{\mathbf 1}_{(n,P((2X)^{1/2}))=1}}{n}=1+\sum_{(2X)^{1/2}\leq p\leq X} \frac{1}{p}\asymp 1.\\[-4.4pc] \end{align*} $$3 A Fourier-analytic argument
Our main theorems will be a consequence of the propositions in the previous section and Proposition 3.2 below on correlations on average under suitable hypotheses. We begin by formulating the necessary hypotheses.
In the rest of the paper, given a function ![]() $f:\mathbb {N}\to \mathbb {C}$, let
$f:\mathbb {N}\to \mathbb {C}$, let ![]() $E_f$ be a convenient upper bound for the average of f, so that
$E_f$ be a convenient upper bound for the average of f, so that
 $$ \begin{align*} \frac{1}{X}\sum_{n\leq X}|f(n)| \le E_f(X). \end{align*} $$
$$ \begin{align*} \frac{1}{X}\sum_{n\leq X}|f(n)| \le E_f(X). \end{align*} $$For example, we may simply take ![]() $E_f=O(1)$ if f is bounded, or if
$E_f=O(1)$ if f is bounded, or if ![]() $f=\Lambda $.
$f=\Lambda $.
Definition 3.1. Let ![]() $X,H,C,p>1$ and
$X,H,C,p>1$ and ![]() $\eta>0$, and let
$\eta>0$, and let ![]() $f:\mathbb {N}\to \mathbb {C}$. We say that f satisfies hypothesis
$f:\mathbb {N}\to \mathbb {C}$. We say that f satisfies hypothesis ![]() $\mathsf {H}_1(X,H,C,p)$ if
$\mathsf {H}_1(X,H,C,p)$ if
 $$ \begin{align*} \int_{0}^{X}\int_{0}^{1}\bigg|\sum_{x\leq n\leq x+2H}f(n)e(\alpha n)\bigg|^p\, {\textrm{d}}{\alpha} \,{\textrm{d}}{x}\leq C H^{p-1}XE_f(X)^p. \end{align*} $$
$$ \begin{align*} \int_{0}^{X}\int_{0}^{1}\bigg|\sum_{x\leq n\leq x+2H}f(n)e(\alpha n)\bigg|^p\, {\textrm{d}}{\alpha} \,{\textrm{d}}{x}\leq C H^{p-1}XE_f(X)^p. \end{align*} $$ We say that f satisfies hypothesis ![]() $\mathsf {H}_2(X,H,\eta )$ if
$\mathsf {H}_2(X,H,\eta )$ if
 $$ \begin{align*} \sup_{\alpha}\int_{0}^{X}\bigg|\sum_{x\leq n\leq x+2H}f(n)e(\alpha n)\bigg|^2\, {\textrm{d}}{x}\leq \eta H^2XE_f(X)^2. \end{align*} $$
$$ \begin{align*} \sup_{\alpha}\int_{0}^{X}\bigg|\sum_{x\leq n\leq x+2H}f(n)e(\alpha n)\bigg|^2\, {\textrm{d}}{x}\leq \eta H^2XE_f(X)^2. \end{align*} $$Proposition 3.2. Let ![]() $X\geq H\geq 2$. Let
$X\geq H\geq 2$. Let ![]() $C\geq 1$,
$C\geq 1$, ![]() $p\geq 2$ and
$p\geq 2$ and ![]() $\eta>0$. Let
$\eta>0$. Let ![]() $f:\mathbb {N}\to \mathbb {C}$ be any function supported on
$f:\mathbb {N}\to \mathbb {C}$ be any function supported on ![]() $[0,X]$ and satisfying
$[0,X]$ and satisfying ![]() $\mathsf {H}_2(X,H,\eta )$, and let
$\mathsf {H}_2(X,H,\eta )$, and let ![]() $g:\mathbb {N}\to \mathbb {C}$ be any function satisfying
$g:\mathbb {N}\to \mathbb {C}$ be any function satisfying ![]() $\mathsf {H}_1(X,H,C,p)$. Then we have
$\mathsf {H}_1(X,H,C,p)$. Then we have
 $$ \begin{align*} \sum_{h\leq H}\bigg|\sum_{n\leq X}f(n+h)g(n)\bigg|\ll (\eta C)^{1/p}HX E_{|f|+|f|^2}(X)E_{g}(X). \end{align*} $$
$$ \begin{align*} \sum_{h\leq H}\bigg|\sum_{n\leq X}f(n+h)g(n)\bigg|\ll (\eta C)^{1/p}HX E_{|f|+|f|^2}(X)E_{g}(X). \end{align*} $$ Note that if ![]() $|f(n)|\leq 1$, we can simply take
$|f(n)|\leq 1$, we can simply take ![]() $E_{|f|+|f|^2}(X)=O(E_{|f|}(X))$.
$E_{|f|+|f|^2}(X)=O(E_{|f|}(X))$.
Proof. Let us denote
 $$ \begin{align*} S_{f,g} := \sum_{h\le H}\Big|\sum_{n\le X}f(n+h)g(n)\Big|. \end{align*} $$
$$ \begin{align*} S_{f,g} := \sum_{h\le H}\Big|\sum_{n\le X}f(n+h)g(n)\Big|. \end{align*} $$Then the task is to show that if f satisfies ![]() $\mathsf {H}_2(X,H,\eta )$ and g satisfies
$\mathsf {H}_2(X,H,\eta )$ and g satisfies ![]() $\mathsf {H}_1(X,H,C,p)$, then
$\mathsf {H}_1(X,H,C,p)$, then
For proving this, we first note that
 $$ \begin{align*} S_{f,g}\leq \frac{1}{H}\sum_{h\le 2H}(2H-h)\Big|\sum_{n\le X}f(n+h)g(n)\Big|. \end{align*} $$
$$ \begin{align*} S_{f,g}\leq \frac{1}{H}\sum_{h\le 2H}(2H-h)\Big|\sum_{n\le X}f(n+h)g(n)\Big|. \end{align*} $$We introduce unimodular coefficients ![]() $c(h)$ to denote the phase of
$c(h)$ to denote the phase of ![]() $\sum _{n\le X}f(n+h)g(n)$, so that
$\sum _{n\le X}f(n+h)g(n)$, so that
 $$ \begin{align*} |S_{f,g}| & \le \frac{1}{H}\sum_{h\le 2H}(2H-h)c(h)\sum_{n\le X}f(n+h)g(n)\\ & = \frac{1}{H}\sum_{h\le 2H}c(h)\sum_{n\le X+2H} f(n) \sum_{m\le X}g(m){\mathbf 1}_{n=m+h}\cdot\int_0^X {\mathbf 1}_{x\le n,m\le x+2H}{\textrm{d}}{x}\\ & = \frac{1}{H}\int_0^X\int_0^1\sum_{h\le 2H}c(h)e(h\alpha) \sum_{x\le n,m\le x+2H}f(n)g(m)e\big((m-n)\alpha\big){\textrm{d}}{\alpha}{\textrm{d}}{x}, \end{align*} $$
$$ \begin{align*} |S_{f,g}| & \le \frac{1}{H}\sum_{h\le 2H}(2H-h)c(h)\sum_{n\le X}f(n+h)g(n)\\ & = \frac{1}{H}\sum_{h\le 2H}c(h)\sum_{n\le X+2H} f(n) \sum_{m\le X}g(m){\mathbf 1}_{n=m+h}\cdot\int_0^X {\mathbf 1}_{x\le n,m\le x+2H}{\textrm{d}}{x}\\ & = \frac{1}{H}\int_0^X\int_0^1\sum_{h\le 2H}c(h)e(h\alpha) \sum_{x\le n,m\le x+2H}f(n)g(m)e\big((m-n)\alpha\big){\textrm{d}}{\alpha}{\textrm{d}}{x}, \end{align*} $$where we used the orthogonality relation ![]() ${\mathbf 1}_{n=0}=\int _0^1 e(n\alpha ){\textrm {d}}{\alpha }$. Therefore, we have the upper bound
${\mathbf 1}_{n=0}=\int _0^1 e(n\alpha ){\textrm {d}}{\alpha }$. Therefore, we have the upper bound
 $$ \begin{align} |S_{f,g}| \ \leq \frac{1}{H}\left|\int_0^X\int_0^1 C_0(\alpha) F_x(-\alpha) G_x(\alpha){\textrm{d}}{\alpha}{\textrm{d}}{x}\right|, \end{align} $$
$$ \begin{align} |S_{f,g}| \ \leq \frac{1}{H}\left|\int_0^X\int_0^1 C_0(\alpha) F_x(-\alpha) G_x(\alpha){\textrm{d}}{\alpha}{\textrm{d}}{x}\right|, \end{align} $$where in the triple convolution integral, the three exponential sums are
 $$ \begin{align*} C_0(\alpha) &:= \sum_{h\le 2H}c(h)e(h\alpha),\\ F_x(\alpha) &:=\sum_{x\le n\le x+2H}f(n)e(n\alpha),\\ G_x(\alpha) &:=\sum_{x\le m\le x+2H}g(m)e(m\alpha). \end{align*} $$
$$ \begin{align*} C_0(\alpha) &:= \sum_{h\le 2H}c(h)e(h\alpha),\\ F_x(\alpha) &:=\sum_{x\le n\le x+2H}f(n)e(n\alpha),\\ G_x(\alpha) &:=\sum_{x\le m\le x+2H}g(m)e(m\alpha). \end{align*} $$By Fubini’s theorem, the triangle inequality and Cauchy–Schwarz, from (3.1), we deduce that
 $$ \begin{align*} |S_{f,g}|\leq \frac{1}{H}\int_{0}^{1}|C_0(\alpha)|\left(\int_{0}^{X}|F_x(-\alpha)|^2{\textrm{d}}{x}\right)^{\frac{1}{2}} \left(\int_{0}^{X}|G_x(\alpha)|^2{\textrm{d}}{x}\right)^{\frac{1}{2}} {\textrm{d}}{\alpha}. \end{align*} $$
$$ \begin{align*} |S_{f,g}|\leq \frac{1}{H}\int_{0}^{1}|C_0(\alpha)|\left(\int_{0}^{X}|F_x(-\alpha)|^2{\textrm{d}}{x}\right)^{\frac{1}{2}} \left(\int_{0}^{X}|G_x(\alpha)|^2{\textrm{d}}{x}\right)^{\frac{1}{2}} {\textrm{d}}{\alpha}. \end{align*} $$Let q satisfy ![]() $1/p+1/q=1/2$. By taking the supremum of the integral with
$1/p+1/q=1/2$. By taking the supremum of the integral with ![]() $F_x(-\alpha )$ to the power
$F_x(-\alpha )$ to the power ![]() $1/p$ and applying Hölder’s inequality with exponents
$1/p$ and applying Hölder’s inequality with exponents ![]() $(2,q,p)$, we obtain
$(2,q,p)$, we obtain
 $$ \begin{align*} |S_{f,g}|&\leq \frac{1}{H}\sup_{\alpha}\left(\int_{0}^{X}|F_x(-\alpha)|^2{\textrm{d}}{x}\right)^{\frac{1}{p}} \left(\int_{0}^{1}|C_0(\alpha)|^2{\textrm{d}}{\alpha}\right)^{\frac{1}{2}}\\ & \ \cdot\left(\int_{0}^1\int_{0}^{X}|F_x(-\alpha)|^2{\textrm{d}}{x}{\textrm{d}}{\alpha}\right)^{\frac{1}{q}}\left(\int_{0}^1\left(\int_{0}^{X}|G_x(\alpha)|^2{\textrm{d}}{x}\right)^{\frac{p}{2}}{\textrm{d}}{\alpha}\right)^{\frac{1}{p}} =:\frac{1}{H}I_0^{1/p}I_1^{1/2}I_2^{1/q}I_3^{1/p}, \end{align*} $$
$$ \begin{align*} |S_{f,g}|&\leq \frac{1}{H}\sup_{\alpha}\left(\int_{0}^{X}|F_x(-\alpha)|^2{\textrm{d}}{x}\right)^{\frac{1}{p}} \left(\int_{0}^{1}|C_0(\alpha)|^2{\textrm{d}}{\alpha}\right)^{\frac{1}{2}}\\ & \ \cdot\left(\int_{0}^1\int_{0}^{X}|F_x(-\alpha)|^2{\textrm{d}}{x}{\textrm{d}}{\alpha}\right)^{\frac{1}{q}}\left(\int_{0}^1\left(\int_{0}^{X}|G_x(\alpha)|^2{\textrm{d}}{x}\right)^{\frac{p}{2}}{\textrm{d}}{\alpha}\right)^{\frac{1}{p}} =:\frac{1}{H}I_0^{1/p}I_1^{1/2}I_2^{1/q}I_3^{1/p}, \end{align*} $$say. Since f satisfies ![]() $\mathsf {H}_2(X,H,\eta )$, we have
$\mathsf {H}_2(X,H,\eta )$, we have
By Parseval, we have
Last, using Hölder’s inequality and the fact that g satisfies ![]() $\mathsf {H}_1(X,H,C,p)$, we have
$\mathsf {H}_1(X,H,C,p)$, we have
 $$ \begin{align*} I_3\leq X^{p/2-1} \int_{0}^1\int_{0}^{X}|G_x(\alpha)|^p{\textrm{d}}{x}{\textrm{d}}{\alpha} \leq CH^{p-1}X^{p/2}E_g(X)^p. \end{align*} $$
$$ \begin{align*} I_3\leq X^{p/2-1} \int_{0}^1\int_{0}^{X}|G_x(\alpha)|^p{\textrm{d}}{x}{\textrm{d}}{\alpha} \leq CH^{p-1}X^{p/2}E_g(X)^p. \end{align*} $$Combining the bounds, we see that
 $$ \begin{align*} |S_{f,g}|&\ll H^{-1}\big(\eta H^2XE_f(X)^2\big)^{1/p}H^{1/2} \big(HXE_{|f|^2}(X)^2\big)^{1/q} \big(CH^{p-1}X^{p/2}E_g(X)^p\big)^{1/p}\\ &\ll (\eta C)^{1/p}HXE_{|f|+|f|^2}(X)E_g(X), \end{align*} $$
$$ \begin{align*} |S_{f,g}|&\ll H^{-1}\big(\eta H^2XE_f(X)^2\big)^{1/p}H^{1/2} \big(HXE_{|f|^2}(X)^2\big)^{1/q} \big(CH^{p-1}X^{p/2}E_g(X)^p\big)^{1/p}\\ &\ll (\eta C)^{1/p}HXE_{|f|+|f|^2}(X)E_g(X), \end{align*} $$as desired.
4 Proofs of the main theorems
We are now ready to prove Theorem 1.6. As already discussed in Remark 1.7, Theorem 1.2(i) concerning the Möbius case follows immediately as a special case. As we shall see, Theorem 1.2(ii) also follows with essentially the same proof.
Proof of Theorem 1.6.
Fix ![]() $\varepsilon \in (0,1)$ and
$\varepsilon \in (0,1)$ and ![]() $k,\ell \geq 1$, and let
$k,\ell \geq 1$, and let ![]() $2\leq (\log X)^{\ell +\varepsilon }\leq H\leq \exp ((\log X)^{1/1000})$. Let:
$2\leq (\log X)^{\ell +\varepsilon }\leq H\leq \exp ((\log X)^{1/1000})$. Let:
Set:
 $$ \begin{align*} f(n)=f_1(n) {\mathbf 1}_{\mathcal{S}}(n){\mathbf 1}_{[0,X]}(n),\quad\text{and}\quad g(n)=\prod_{i=2}^kf_i(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j), \end{align*} $$
$$ \begin{align*} f(n)=f_1(n) {\mathbf 1}_{\mathcal{S}}(n){\mathbf 1}_{[0,X]}(n),\quad\text{and}\quad g(n)=\prod_{i=2}^kf_i(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j), \end{align*} $$where ![]() $\mathcal {S}$ is the set of positive integers having a prime factor in each of the intervals
$\mathcal {S}$ is the set of positive integers having a prime factor in each of the intervals ![]() $[P_i, Q_i]$, with
$[P_i, Q_i]$, with ![]() $P_i,Q_i$ as in Proposition 2.1 and
$P_i,Q_i$ as in Proposition 2.1 and ![]() $\delta $ as above. Then, by Lemma 2.11 (and the fact that
$\delta $ as above. Then, by Lemma 2.11 (and the fact that ![]() $\mathcal {S}^c\subset \bigcup _{j\leq J}\mathcal {S}_j^c$, where
$\mathcal {S}^c\subset \bigcup _{j\leq J}\mathcal {S}_j^c$, where ![]() $\mathcal {S}_j^c$ is the set of integers having no prime factors in
$\mathcal {S}_j^c$ is the set of integers having no prime factors in ![]() $[P_j,Q_j]$), for all
$[P_j,Q_j]$), for all ![]() $X\geq 2$, we have
$X\geq 2$, we have
 $$ \begin{align} \bigg|\sum_{\substack{n\leq X\\n+h\notin \mathcal{S}}} f_1(n+h) g(n)\bigg| &\le \sum_{n\le X}{\mathbf 1}_{\mathcal S^c}(n+h) \prod_{j=1}^{\ell}\Lambda(n+a_j) \nonumber\\ &\ll \sum_{j\leq J}X\prod_{p\in [P_j,Q_j]}\left(1-\frac{1}{p}\right) \prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)}\right)^{2^{\ell+1}}. \end{align} $$
$$ \begin{align} \bigg|\sum_{\substack{n\leq X\\n+h\notin \mathcal{S}}} f_1(n+h) g(n)\bigg| &\le \sum_{n\le X}{\mathbf 1}_{\mathcal S^c}(n+h) \prod_{j=1}^{\ell}\Lambda(n+a_j) \nonumber\\ &\ll \sum_{j\leq J}X\prod_{p\in [P_j,Q_j]}\left(1-\frac{1}{p}\right) \prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)}\right)^{2^{\ell+1}}. \end{align} $$By (2.1), we have
 $$ \begin{align*} \sum_{j\leq J}\prod_{p\in [P_j,Q_j]}\left(1-\frac{1}{p}\right) \ll \sum_{j\leq J} \frac{\log P_j}{\log Q_j}\ll\frac{\log P_1}{\log Q_1}\ll \delta+\exp(-M(f;X,Q)/2000) =: \delta'. \end{align*} $$
$$ \begin{align*} \sum_{j\leq J}\prod_{p\in [P_j,Q_j]}\left(1-\frac{1}{p}\right) \ll \sum_{j\leq J} \frac{\log P_j}{\log Q_j}\ll\frac{\log P_1}{\log Q_1}\ll \delta+\exp(-M(f;X,Q)/2000) =: \delta'. \end{align*} $$Also, by Lemma 2.5, we have
 $$ \begin{align*} \sum_{h\leq H}\prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)}\right)^{2^{\ell+1}}\ll H, \end{align*} $$
$$ \begin{align*} \sum_{h\leq H}\prod_{j=1}^{\ell}\left(\frac{|h-a_j|}{\varphi(|h-a_j|)}\right)^{2^{\ell+1}}\ll H, \end{align*} $$and so plugging back into (4.1) gives
 $$ \begin{align} \sum_{h\leq H}\bigg|\sum_{\substack{n\leq X\\n+h\notin \mathcal{S}}} f_1(n+h)g(n)\bigg| \ \ll \ \delta' \,XH. \end{align} $$
$$ \begin{align} \sum_{h\leq H}\bigg|\sum_{\substack{n\leq X\\n+h\notin \mathcal{S}}} f_1(n+h)g(n)\bigg| \ \ll \ \delta' \,XH. \end{align} $$Let
In view of (4.2), to prove Theorem 1.6, it suffices to show that
 $$ \begin{align} \sum_{h\leq H}\bigg|\sum_{n\leq X}f(n+h)g(n)\bigg|\ll \left(\frac{\log \log H}{\log H}+\exp(-M(f;X,Q)/(2000p))\right)HX, \end{align} $$
$$ \begin{align} \sum_{h\leq H}\bigg|\sum_{n\leq X}f(n+h)g(n)\bigg|\ll \left(\frac{\log \log H}{\log H}+\exp(-M(f;X,Q)/(2000p))\right)HX, \end{align} $$since we can crudely estimate ![]() $2000p<10\, 000\ell /\varepsilon $. Note that by Lemma 2.3, we can take
$2000p<10\, 000\ell /\varepsilon $. Note that by Lemma 2.3, we can take
and we can trivially take ![]() $E_{f}(X), E_{|f|+|f|^2}(X)\asymp 1$, so it suffices to prove (4.3) with an extra factor of
$E_{f}(X), E_{|f|+|f|^2}(X)\asymp 1$, so it suffices to prove (4.3) with an extra factor of ![]() $E_{|f|+|f|^2}(X)E_{g}(X)$ on the right-hand side.
$E_{|f|+|f|^2}(X)E_{g}(X)$ on the right-hand side.
By Proposition 2.7 (and the fact that p is even and satisfies ![]() $\ell +\varepsilon> \ell p/(p-2)$), there exists a constant
$\ell +\varepsilon> \ell p/(p-2)$), there exists a constant ![]() $B=B_{\ell ,\varepsilon }>0$, for which
$B=B_{\ell ,\varepsilon }>0$, for which
 $$ \begin{align*} \int_{0}^{1}\int_{0}^X\bigg|\sum_{x\leq n\leq x+2H}e(\alpha n)\prod_{i=2}^kf_i(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|^p {\textrm{d}} x{\textrm{d}}\alpha \ \le \ BXH^{p-1}. \end{align*} $$
$$ \begin{align*} \int_{0}^{1}\int_{0}^X\bigg|\sum_{x\leq n\leq x+2H}e(\alpha n)\prod_{i=2}^kf_i(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|^p {\textrm{d}} x{\textrm{d}}\alpha \ \le \ BXH^{p-1}. \end{align*} $$Therefore, g satisfies hypothesis ![]() $\mathsf {H}_1(X,H,B',p)$ for some
$\mathsf {H}_1(X,H,B',p)$ for some ![]() $B'\ll 1$.
$B'\ll 1$.
We also note that by Proposition 2.1, f satisfies ![]() $\mathsf {H}_2(X,H,\eta )$ with
$\mathsf {H}_2(X,H,\eta )$ with
Now, applying Proposition 3.2 with the choices of ![]() $f,g$ above, we obtain
$f,g$ above, we obtain
 $$ \begin{align}\begin{split} \sum_{h\leq H}\bigg|\sum_{n\leq X}f_1{\mathbf 1}_{\mathcal{S}}(n+h) &\prod_{i=2}^kf_i(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|\\ &\ll \eta^{1/p}HX \ \ll \ (H^{-\delta/p}+\exp(-M(f;X,Q)/(2000p)))HX. \end{split} \end{align} $$
$$ \begin{align}\begin{split} \sum_{h\leq H}\bigg|\sum_{n\leq X}f_1{\mathbf 1}_{\mathcal{S}}(n+h) &\prod_{i=2}^kf_i(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|\\ &\ll \eta^{1/p}HX \ \ll \ (H^{-\delta/p}+\exp(-M(f;X,Q)/(2000p)))HX. \end{split} \end{align} $$Thus, since ![]() $\delta = 10^4\ell \varepsilon ^{-1}(\log \log H)/(\log H)$, this gives (4.3), as desired. The proof of Theorem 1.6 (and, hence, of Theorem 1.2(i)) is now complete.
$\delta = 10^4\ell \varepsilon ^{-1}(\log \log H)/(\log H)$, this gives (4.3), as desired. The proof of Theorem 1.6 (and, hence, of Theorem 1.2(i)) is now complete.
Proof of Theorem 1.2(ii).
Let ![]() $\delta $ be as in the theorem, so that, in particular,
$\delta $ be as in the theorem, so that, in particular, ![]() $\delta \leq c/C$ with
$\delta \leq c/C$ with ![]() $c>0$ be small enough. Take
$c>0$ be small enough. Take ![]() $c=1/10\, 000$. Applying (4.4) and Markov’s inequality, we see that
$c=1/10\, 000$. Applying (4.4) and Markov’s inequality, we see that
 $$ \begin{align*} \bigg|\sum_{n\leq X}\mu{\mathbf 1}_{\mathcal{S}}(n+h) &\prod_{i=2}^k\mu(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|\\ &\ll (H^{-\delta/(2p)}+H^{\delta/(2p)}\exp(-M(\mu;X,Q)/(2000p)))HX \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n\leq X}\mu{\mathbf 1}_{\mathcal{S}}(n+h) &\prod_{i=2}^k\mu(n+h_i)\prod_{j=1}^{\ell}\Lambda(n+a_j)\bigg|\\ &\ll (H^{-\delta/(2p)}+H^{\delta/(2p)}\exp(-M(\mu;X,Q)/(2000p)))HX \end{align*} $$for all but ![]() $\ll H^{1-\delta /(2p)}$ integers
$\ll H^{1-\delta /(2p)}$ integers ![]() $h\leq H$. By (1.7), we have
$h\leq H$. By (1.7), we have ![]() $M(\mu ;X,Q)\geq \frac {1}{4}\log \log X+O(1)$, so we see that
$M(\mu ;X,Q)\geq \frac {1}{4}\log \log X+O(1)$, so we see that
and the claim follows.
Acknowledgements
The first author was supported by a Clarendon Scholarship. The second author was supported by a Titchmarsh Fellowship and Academy of Finland grant no. 340098. The authors would like to thank the anonymous referee for detailed feedback and corrections.
Conflict of Interest
The authors have no conflicts of interest to declare.