Let f(x) and g(x) be polynomials in $\mathbb F_{2}[x]$ with ${\rm deg}\text{ } f=n$. It is shown that for $n\gg 1$, there is an $g_{1}(x)\in \mathbb F_{2}[x]$ with ${\rm deg}\text{ } g_{1}\leqslant \max\{{\rm deg}\text{ } g, 6.7\log n\}$ and $g(x)-g_{1}(x)$ having $ \lt 6.7\log n$ terms such that $\gcd(f(x), g_{1}(x))=1$. As an application, it is established using a result of Dubickas and Sha that given $f(x)\in \mathbb F_{2}[x]$ of degree $n\geqslant 1$, there is a separable $g(x)\in 2[x]$ with ${\rm deg}\text{ } g= {\rm deg}\text{ } f$ and satisfying that $f(x)-g(x)$ has $\leqslant 6.7\log n$ terms. As a simple consequence, the latter result holds in $\mathbb Z[x]$ after replacing ‘number of terms’ by the L1-norm of a polynomial and $6.7\log n$ by $6.8\log n$. This improves the bound $(\log n)^{\log 4 +\operatorname{\varepsilon}}$ obtained by Filaseta and Moy.

Niven’s theorem asserts that $\{\cos (r\pi ) \mid r\in \mathbb {Q}\}\cap \mathbb {Q}=\{0,\pm 1,\pm 1/2\}.$ In this paper, we use elementary techniques and results from arithmetic dynamics to obtain an algorithm for classifying all values in the set $\{\cos (r\pi ) \mid r\in \mathbb {Q}\}\cap K$, where K is an arbitrary number field.

Granville recently asked how the Mahler measure behaves in the context of polynomial dynamics. For a polynomial $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$ we show that the Mahler measure of the iterates $f^n$ grows geometrically fast with the degree $d^n,$ and find the exact base of that exponential growth. This base is expressed via an integral of $\log ^+|z|$ with respect to the invariant measure of the Julia set for the polynomial $f.$ Moreover, we give sharp estimates for such an integral when the Julia set is connected.

By analogy with the trace of an algebraic integer $\alpha $ with conjugates $\alpha _1=\alpha , \ldots , \alpha _d$ , we define the G-measure $ {\mathrm {G}} (\alpha )= \sum _{i=1}^d ( |\alpha _i| + 1/ | \alpha _i | )$ and the absolute ${\mathrm G}$ -measure ${\mathrm {g}}(\alpha )={\mathrm {G}}(\alpha )/d$ . We establish an analogue of the Schur–Siegel–Smyth trace problem for totally positive algebraic integers. Then we consider the case where $\alpha $ has all its conjugates in a sector $| \arg z | \leq \theta $ , $0 < \theta < 90^{\circ }$ . We compute the greatest lower bound $c(\theta )$ of the absolute G-measure of $\alpha $ , for $\alpha $ belonging to $11$ consecutive subintervals of $]0, 90 [$ . This phenomenon appears here for the first time, conforming to a conjecture of Rhin and Smyth on the nature of the function $c(\theta )$ . All computations are done by the method of explicit auxiliary functions.

Let $\alpha $ be a totally positive algebraic integer of degree d, with conjugates $\alpha _1=\alpha , \alpha _2, \ldots , \alpha _d$ . The absolute $S_k$ -measure of $\alpha $ is defined by $s_k(\alpha )= d^{-1} \sum _{i=1}^{d}\alpha _i^k$ . We compute the lower bounds $\upsilon _k$ of $s_k(\alpha )$ for each integer in the range $2\leq k \leq 15$ and give a conjecture on the results for integers $k>15$ . Then we derive the lower bounds of $s_k(\alpha )$ for all real numbers $k>2$ . Our computation is based on an improvement in the application of the LLL algorithm and analysis of the polynomials in the explicit auxiliary functions.

A finite set of integers A tiles the integers by translations if $\mathbb {Z}$ can be covered by pairwise disjoint translated copies of A. Restricting attention to one tiling period, we have $A\oplus B=\mathbb {Z}_M$ for some $M\in \mathbb {N}$ and $B\subset \mathbb {Z}$. This can also be stated in terms of cyclotomic divisibility of the mask polynomials $A(X)$ and $B(X)$ associated with A and B.

In this article, we introduce a new approach to a systematic study of such tilings. Our main new tools are the box product, multiscale cuboids and saturating sets, developed through a combination of harmonic-analytic and combinatorial methods. We provide new criteria for tiling and cyclotomic divisibility in terms of these concepts. As an application, we can determine whether a set A containing certain configurations can tile a cyclic group $\mathbb {Z}_M$, or recover a tiling set based on partial information about it. We also develop tiling reductions where a given tiling can be replaced by one or more tilings with a simpler structure. The tools introduced here are crucial in our proof in [24] that all tilings of period $(pqr)^2$, where $p,q,r$ are distinct odd primes, satisfy a tiling condition proposed by Coven and Meyerowitz [2].

In this paper, we prove the assertion that the number of monic cubic polynomials $F(x) = x^3 + a_2 x^2 + a_1 x + a_0$ with integer coefficients and irreducible, Galois over ${\mathbb {Q}}$ satisfying $\max \{|a_2|, |a_1|, |a_0|\} \leq X$ is bounded from above by $O(X (\log X)^2)$. We also count the number of abelian monic binary cubic forms with integer coefficients up to a natural equivalence relation ordered by the so-called Bhargava–Shankar height. Finally, we prove an assertion characterizing the splitting field of 2-torsion points of semi-stable abelian elliptic curves.

We obtain an effective analytic formula, with explicit constants, for the number of distinct irreducible factors of a polynomial $f \in \mathbb {Z}[x]$ . We use an explicit version of Mertens’ theorem for number fields to estimate a related sum over rational primes. For a given $f \in \mathbb {Z}[x]$ , our result yields a finite list of primes that certifies the number of distinct irreducible factors of f.

Girstmair [‘On an irreducibility criterion of M. Ram Murty’, Amer. Math. Monthly 112(3) (2005), 269–270] gave a generalisation of Ram Murty’s irreducibility criterion. We further generalise these criteria.

We study a class of two-variable polynomials called exact polynomials which contains $A$-polynomials of knot complements. The Mahler measure of these polynomials can be computed in terms of a volume function defined on the vanishing set of the polynomial. We prove that the local extrema of the volume function are on the two-dimensional torus and give a closed formula for the Mahler measure in terms of these extremal values. This formula shows that the Mahler measure of an irreducible and exact polynomial divided by $\pi$ is greater than the amplitude of the volume function. We also prove a K-theoretic criterion for a polynomial to be a factor of an $A$-polynomial and give a topological interpretation of its Mahler measure.

We study intersections of orbits in polynomial semigroup dynamics with lines on the affine plane over a number field, extending previous work of D. Ghioca, T. Tucker, and M. Zieve (2008).

We prove that for every sufficiently large integer $n$, the polynomial $1+x+x^{2}/11+x^{3}/111+\cdots +x^{n}/111\ldots 1$ is irreducible over the rationals, where the coefficient of $x^{k}$ for $1\leqslant k\leqslant n$ is the reciprocal of the decimal number consisting of $k$ digits which are each $1$. Similar results following from the same techniques are discussed.

For a finite field of odd cardinality $q$, we show that the sequence of iterates of $aX^{2}+c$, starting at $0$, always recurs after $O(q/\text{log}\log q)$ steps. For $X^{2}+1$, the same is true for any starting value. We suggest that the traditional “birthday paradox” model is inappropriate for iterates of $X^{3}+c$, when $q$ is 2 mod 3.

In this paper we give an extension of the results of the generalized waiting time problem given by El-Desouky and Hussen (1990). An urn contains m types of balls of unequal numbers, and balls are drawn with replacement until first duplication. In the case of finite memory of order k, let ni be the number of type i, i = 1, 2, …, m. The probability of success pi = ni/N, i = 1, 2, …, m, where ni is a positive integer and Let Ym,k be the number of drawings required until first duplication. We obtain some new expressions of the probability function, in terms of Stirling numbers, symmetric polynomials, and generalized harmonic numbers. Moreover, some special cases are investigated. Finally, some important new combinatorial identities are obtained.

We investigate the numbers of complex zeros of Littlewood polynomials $p\left( z \right)$ (polynomials with coefficients {−1, 1}) inside or on the unit circle 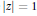$\left| z \right|\,=\,1$, denoted by 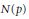$N\left( p \right)$ and 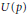$U\left( p \right)$, respectively. Two types of Littlewood polynomials are considered: Littlewood polynomials with one sign change in the sequence of coefficients and Littlewood polynomials with one negative coefficient. We obtain explicit formulas for 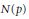$N\left( p \right)$, 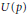$U\left( p \right)$ for polynomials $p\left( z \right)$ of these types. We show that if $n\,+\,1$ is a prime number, then for each integer 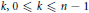$k,\,0\,⩽\,k\,⩽\,n-1$, there exists a Littlewood polynomial $p\left( z \right)$ of degree 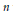$n$ with 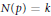$N\left( p \right)\,=\,k$ and 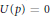$U\left( p \right)\,=\,0$. 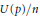Furthermore, we describe some cases where the ratios $N\left( p \right)/n$ and $U\left( p \right)/n$ have limits as $n\,\to \,\infty $ and find the corresponding limit values.

We give a short and elementary proof of an inverse Bernstein-type inequality found by S. Khrushchev for the derivative of a polynomial having all its zeros on the unit circle. The inequality is used to show that equally-spaced points solve a min–max–min problem for the logarithmic potential of such polynomials. Using techniques recently developed for polarization (Chebyshev-type) problems, we show that this optimality also holds for a large class of potentials, including the Riesz potentials $1/r^{s}$ with $s>0.$

We prove a necessary and sufficient condition on the list of nonzero integers ${{u}_{1}},...,{{u}_{k}}$, $k\,\ge \,2$, under which a monic polynomial $f\,\in \,\mathbb{Z}\left| x \right|$ is expressible by a linear form ${{u}_{1}}\,{{f}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{u}_{k}}\,{{f}_{k}}$ in monic polynomials ${{f}_{1}},...,\,{{f}_{k}}\,\in \,\mathbb{Z}\left| x \right|$. This condition is independent of $f$. We also show that if this condition holds, then the monic polynomials ${{f}_{1}},...,\,{{f}_{k}}$ can be chosen to be irreducible in $\mathbb{Z}\left[ x \right]$.

We recall that a polynomial f(X) ∈ K[X] over a field K is called stable if all its iterates are irreducible over K. We show that almost all monic quadratic polynomials f(X) ∈ ℤ[X] are stable over ℚ. We also show that the presence of squares in so-called critical orbits of a quadratic polynomial f(X) ∈ ℤ[X] can be detected by a finite algorithm; this property is closely related to the stability of f(X). We also prove there are no stable quadratic polynomials over finite fields of characteristic 2 but they exist over some infinite fields of characteristic 2.

Let G be a subgroup of the symmetric group Sn, and let δG=∣Sn/G∣−1 where ∣Sn/G∣ is the index of G in Sn. Then there are at most On,ϵ(Hn−1+δG+ϵ) monic integer polynomials of degree n that have Galois group G and height not exceeding H, so there are only a “few” polynomials having a “small” Galois group.

A Pisot number is a real algebraic integer greater than 1, all of whose conjugates lie strictly inside the open unit disk; a Salem number is a real algebraic integer greater than 1, all of whose conjugate roots are inside the closed unit disk, with at least one of them of modulus exactly 1. Pisot numbers have been studied extensively, and an algorithm to generate them is well known. Our main result characterises all Pisot numbers whose minimal polynomial is derived from a Newman polynomial — one with $\{0,\,1\}$-coefficients — and shows that they form a strictly increasing sequence with limit $\left( 1\,+\,\sqrt{5} \right)/2$. It has long been known that every Pisot number is a limit point, from both sides, of sequences of Salem numbers. We show that this remains true, from at least one side, for the restricted sets of Pisot and Salem numbers that are generated by Newman polynomials.