No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We prove a necessary and sufficient condition on the list of nonzero integers  ${{u}_{1}},...,{{u}_{k}}$,
${{u}_{1}},...,{{u}_{k}}$, 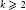 $k\,\ge \,2$, under which a monic polynomial
$k\,\ge \,2$, under which a monic polynomial  $f\,\in \,\mathbb{Z}\left| x \right|$ is expressible by a linear form
$f\,\in \,\mathbb{Z}\left| x \right|$ is expressible by a linear form  ${{u}_{1}}\,{{f}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{u}_{k}}\,{{f}_{k}}$ in monic polynomials
${{u}_{1}}\,{{f}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{u}_{k}}\,{{f}_{k}}$ in monic polynomials 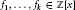 ${{f}_{1}},...,\,{{f}_{k}}\,\in \,\mathbb{Z}\left| x \right|$. This condition is independent of
${{f}_{1}},...,\,{{f}_{k}}\,\in \,\mathbb{Z}\left| x \right|$. This condition is independent of  $f$. We also show that if this condition holds, then the monic polynomials
$f$. We also show that if this condition holds, then the monic polynomials  ${{f}_{1}},...,\,{{f}_{k}}$ can be chosen to be irreducible in
${{f}_{1}},...,\,{{f}_{k}}$ can be chosen to be irreducible in 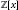 $\mathbb{Z}\left[ x \right]$.
$\mathbb{Z}\left[ x \right]$.