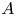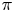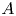Introduction
A polynomial 
$P\in \mathbb {C}[X^{\pm 1}, Y^{\pm 1}]$ vanishing on a curve 
$C\subset (\mathbb {C}^{*})^{2}$ is said to be exact if there exists a function 
$V:C\to \mathbb {R}$ (called a volume function) satisfying
\[ dV=\log\! |y| d\arg x-\log\! |x| d\arg y. \]
In this paper we study the properties of volume functions 
$V$. For instance, we show that the volume function extends continuously to the smooth projective model 
$\hat {C}$ of 
$C$ and study its local extrema. Our main result concerning 
$V$, proved in § 2, is that the extrema of a volume function are only attained at so-called toric points.
Theorem The local extrema of 
$V$ are necessarily finite points of 
$\hat {C}$ projecting to pairs 
$(x,y)\in (\mathbb {C}^{*})^{2}$ satisfying 
$|x|=|y|=1$.
The proof is rather elementary and can be visualized with the help of two notions from real algebraic geometry: the logarithmic Gauss map and amoebas.
Our motivation comes from topology. Let 
$M$ be a 3-manifold with toric boundary. We denote by 
$X(M)$ its character variety, that is, the algebraic quotient 
$\operatorname {Hom}(\pi _1(M),\mathrm {SL}_2(\mathbb {C}))//\mathrm {SL}_2(\mathbb {C})$. The character variety of the boundary 
$X(\partial M)$ is the quotient of 
$(\mathbb {C}^{*})^{2}$ by the involution 
$(x,y)\sim (x^{-1},y^{-1})$: we denote by 
$\pi :(\mathbb {C}^{*})^{2}\to X(\partial M)$ the quotient map. The inclusion 
$i:\partial M\to M$ induces a restriction map 
$r:X(M)\to X(\partial M)$ by 
$r([\rho ])=[\rho \circ i_*]$. It has the property that 
$\pi ^{-1}\overline {r(X(M))}$ is the vanishing set of some polynomial 
$A_M\in \mathbb {Z}[X^{\pm 1},Y^{\pm 1}]$. This polynomial – called the 
$A$-polynomial of 
$M$ – was introduced by [Reference Cooper, Culler, Gillet, Long and ShalenCCGLS94] and is known to be exact.
Indeed, given a representation 
$\rho :\pi _1(M)\to \mathrm {SL}_2(\mathbb {C})$, 
$V(r([\rho ]))$ is the volume of the representation 
$\rho$, for which we refer to [Reference FrancavigliaFra04]. Hence our first theorem partially recovers a recent result of Francaviglia and Savini [Reference Francaviglia and SaviniFS20]. They prove that the volume function 
$V:X(M)\to \mathbb {R}$ cannot reach its maximum at ideal points. However, our simpler proof works only under the assumption that the restriction map 
$r:X(M)\to X(\partial M)$ is proper. This assumption holds, for instance, if 
$M$ does not contain any closed incompressible surface. These considerations were a starting point for this work, but we will not go further in this direction.
Instead, we investigate in § 3 the computation of the Mahler measure of an exact polynomial. Given a two-variable Laurent polynomial 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$, the problem of computing explicitly its logarithmic Mahler measure
\[ m(P)=\frac{1}{(2\pi)^{2}}\int_0^{2\pi}\int_0^{2\pi}\log\! |P(e^{i\theta},e^{i\phi})|\,d\theta\,d\phi \]
looked intractable before the remarkable computation by Smyth of the Mahler measure of the two-variable polynomial 
$X+Y-1$ [Reference SmythSmy81]. Since then, many new examples have been found. For instance, in the article [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05] building on [Reference Boyd and Rodriguez-VillegasBR02, Reference BoydBoy02], the authors used K-theoretic tools to exhibit a class of two-variables polynomials with the property that their Mahler measure multiplied by 
$\pi$ is a rational linear combination of evaluations of the Bloch–Wigner dilogarithm at algebraic arguments. They proceed to give a number-theoretic interpretation of this sum of dilogarithms. They give a lot of examples, among them all 
$A$-polynomials of 
$3$-manifolds 
$M$ with toric boundary. Finally, they observed that the Mahler measure multiplied by 
$\pi$ is often – but not always – equal to the hyperbolic volume of 
$M$. Other techniques, which seem unrelated to our work, allow the computation of the Mahler measure for non-exact polynomials (e.g. [Reference LalínLal03, Reference Brunault and NeururerBN19, Reference MaillotMai00]). We refer to the survey [Reference Bertin and LalínBL13] for a description of these works.
Starting from the computation of the Mahler measure of an exact polynomial (borrowed from [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05]), it is known that the formula only involves the values of 
$V$ at critical points which sit inside the torus. What was not known is that the contribution of each critical point can be computed directly. Here is a simple version with strong assumptions granting that only the local extrema appear.
Theorem Let 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ be an irreducible exact polynomial vanishing on 
$C$ with volume function 
$V$. Suppose that the curve 
$C$ is transversal to the torus 
$S^{1}\times S^{1}$ in 
$(\mathbb {C}^{*})^{2}$. Then, up to normalizing 
$P$, one has
\[ 2\pi m(P)=\sum_i V(M_i)-\sum_j V(m_j), \]
where the 
$M_i$ and the 
$m_j$ are respectively the local maxima and minima of 
$V$.
These assumptions generally do not hold for 
$A$-polynomials, hence we provide a version with weaker transversality assumptions (Theorem 3.5) and a general formula (Theorem 3.14). This proves that the Mahler measure is greater than the amplitude of the volume function (see Theorems 3.6 and 3.15).
Theorem Let 
$P$ be a (suitably normalized) irreducible exact polynomial and 
$V$ be a volume function. Then
\[ 2\pi m(P)\ge \max V- \min V. \] This inequality is particularly nice in the context of hyperbolic manifolds as the maximum of our volume function on 
$X(M)$ is the hyperbolic volume of the 3-manifold 
$M$ denoted by vol
$(M)$. When 
$A_M$ is irreducible over 
$\mathbb {C}$, we get the inequality
\[ \pi m(A_M)\ge \textrm{vol}(M). \]This sheds some light on the cases were equality were observed; manifolds with increasing complexity satisfy a strict inequality and we will give an example of this phenomenon.
Although it is easy to understand which polynomials are exact in genus 0, the problem looks intractable for higher-genus cases. For example, the question found in the fourth final remark in [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05, § 8] reads: no continuous family of exact polynomials exists. In § 4, we obtain for genus 1 polynomials the following finiteness result which we expect to be true without assumptions on the genus.
Theorem Up to monomial transformations, there are a finite number of exact polynomials 
$P\in \bar {\mathbb {Q}}[X^{\pm 1},Y^{\pm 1}]$ of genus 
$g\le 1$ with Newton polygon of bounded area.
The last part of the paper contains some 
$K$-theoretic arguments. We prove the following theorem.
Theorem Let 
$P\in \bar {\mathbb {Q}}[X^{{\pm }1},Y^{{\pm }1}]$ be an irreducible polynomial. It satisfies the condition
\[ \{X,Y\}=0\in K_2(K_P)\otimes \mathbb{Q}\quad \text{where}\ K_P=\operatorname{Frac}\bigl( \bar{\mathbb{Q}}[X^{{\pm} 1},Y^{{\pm} 1}]/P\bigr) \]
if and only if 
$P$ is a factor of the 
$A$-polynomial of some 
$3$-manifold with boundary.
The 
$K$-theoretic condition above is the same as in [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05]. The proof given in § 5.1 borrows arguments from Ghys (private communication). Hence, at least theoretically, one can recognize which polynomials are 
$A$-polynomials of 3-manifolds, although the criterion is effective only for polynomials defining a curve of genus 0. We then describe the computation of Mahler measures of a few 
$A$-polynomials, recovering in part known results.
We end the section and the paper by proving a formula which gives a topological interpretation of 
$m(A_M)$ where 
$A_M$ is the 
$A$-polynomial of 
$M$. Consider a closed manifold 
$M$ with a knot 
$K$ inside. Assuming that 
$X(M)$ is a finite set as we expect for a ‘generic’ 3-manifold, we define
\[ m(M,K)=\sum_{[\rho]\in X(M)}\log\! \|\rho(K)\| \]
where 
$\|A\|$ is the spectral radius of 
$A$. If 
$\rho$ is the hyperbolic representation, 
$\log\! \|\rho (K)\|$ is the length of the geodesic represented by 
$K$. Hence 
$m(M,K)$ is the sum of all ‘lengths’ of 
$K$ over all possible (non necessarily geometric) representations. Our result is as follows.
Theorem Let 
$M$ be a manifold with toric boundary satisfying the hypotheses of Proposition 5.5. We have
\[ \lim_{p^{2}+q^{2}\to \infty} m(M_{p/q},K_{p/q})=m(A_M), \]
where 
$M_{p/q}$ denotes the Dehn filling of 
$M$ with parameters 
$p/q$ and 
$K_{p/q}$ is the core of the surgery.
1. Exact polynomials, volume function
Consider a Laurent polynomial 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ with two variables and let 
$C$ be the set of its complex smooth points, that is,
\[ C=\{(x,y)\in\mathbb{C}^{*}, P(x,y)=0, dP(x,y)\ne 0\} \]
Here and below, we denote by 
$X,Y$ the formal variables and by 
$x,y$ the corresponding coordinate functions. Define the 1-form 
$\eta$ on 
$(\mathbb {C}^{*})^{2}$ by the formula
\[ \eta= \log\! |y| d \arg(x)-\log\! |x| d\arg(y). \]
This form restricted to 
$C$ is closed as one has 
$d\eta =-\operatorname {Im} ({{d} x}/{x}\wedge {{d} y}/{y})$. Note that, comparing with [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05], their 
$\eta$ is minus ours. This different normalization is mainly due to simplifications of notation.
Definition 1.1 We will say that 
$P\in \mathbb {C}[X^{\pm 1},Y^{\pm 1}]$ is exact if the form 
$\eta$ restricted to 
$C$ is exact.
Definition 1.2 A volume function associated to an exact polynomial 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ is any function 
$V:C\to \mathbb {R}$ satisfying 
$dV=\eta |_C$.
Remark 1.3 (Case of real polynomials) Suppose that 
$P$ is real and irreducible over 
$\mathbb {C}$. The following argument shows that in this case there is a preferred choice for a volume function.
We define the complex conjugation on 
$(\mathbb {C}^{*})^{2}$ by 
$\sigma (x,y)=(\bar {x},\bar {y})$. As the coefficients of 
$P$ are real, this conjugation preserves the curve 
$C$ and satisfies 
$\sigma ^{*}\eta =-\eta$. Given a volume function 
$V_0:C\to \mathbb {R}$ such that 
$dV_0=\eta |_C$, the function 
$V=\frac {1}{2}(V_0-V_0\circ \sigma )$ is the unique volume function that is odd with respect to conjugation: 
$V \circ \sigma = -V$.
Example 1.4 We give some examples of exact polynomials.
(i) Any
$A$-polynomial of a knot is exact. This can be proved by defining directly the volume function which comes from volumes of representations of cusped 3-manifolds. There is an alternative proof using $K$-theoretic tools. In any case, we refer to [Reference Cooper, Culler, Gillet, Long and ShalenCCGLS94].(ii)
$P(X,Y) = X+Y-1$. The volume function (in the sense of the previous remark) is $V(x,y) = -D(x)$ where $D$ is the Bloch–Wigner dilogarithm.(iii) If
$\phi _5$ is the fifth cyclotomic polynomial, $P(X,Y) = Y-\phi _5(X)$ is exact. The volume function is $V(x,y) = D(x) -\frac {1}{5} D(x^{5})$.(iv)
$P(X,Y) = 1 + X + Y + XY + X^{2} + Y^{2}$.(v)
$P(X,Y) = 1 + iX + iY + XY$.
Example (ii) and various others are treated in [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05]. In fact, we will show later on (see § 5.1) that each of these polynomials is a factor of the 
$A$-polynomial of some 
$3$-manifold; which 
$3$-manifold is unknown, apart from the last case (see [Reference DunfieldDun99b] and § 5.2).
Any volume function is clearly analytical on 
$C$ and extends to the completion of 
$C$ thanks to the following proposition.
Proposition 1.5 Let 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ be an exact polynomial and 
$V:C\to \mathbb {R}$ be a volume function. Then 
$V$ extends continuously to any projective model 
$\hat {C}$ of 
$C$.
Proof. Let 
$z$ be a point of 
$\hat {C}\setminus C$. There exists a local coordinate 
$t$ around 
$z$ such that 
$x=t^{p}$ and 
$y=t^{q}F(t)$ where 
$p$ and 
$q$ are coprime integers and 
$F$ is a convergent series with 
$F(0)\ne 0$. We compute that in the coordinate 
$t=\rho e^{i\theta }$ one has
\[ \eta=p\log\! |F(\rho e^{i\theta})|\,d\theta-p \log(\rho)d \arg F(\rho e^{i\theta}). \]
By integrating this form over a circle of radius 
$\rho$ and letting 
$\rho$ go to 
$0$, we find 
$\int _{C_z}\eta =2\pi p \log\! |F(0)|$. Hence the exactness of 
$\eta$ implies 
$\log\! |F(0)|=0$. This proves that we can factorize 
$\log (\rho )$ from the right-hand side and conclude that 
$\eta$ is integrable at 
$0$, showing that its integral, 
$V$, extends continuously at 
$0$.
The previous proposition also gives the condition for 
$\eta$ to be exact in the neighborhood of an ideal point. This condition can be interpreted in terms of the tame symbol 
$\{x,y\}_z$ as already fully explained in [Reference Rodriguez-VillegasRod99] and [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05]. We recall these facts in the next two propositions for the sake of completeness.
Recall the notion of tame symbol. Let 
$f,g$ be two meromorphic functions on a Riemann surface 
$X$ and 
$z$ be a point of 
$X$. Denoting by 
$v_z(f),v_z(g)$ the valuation of 
$f$ and 
$g$ at 
$z$ and by ev
$_z$ the evaluation at 
$z$, we set
\[ \{f,g\}_z=({-}1)^{v_z(f)v_z(g)}\textrm{ev}_z\bigg(\frac{f^{v_z(g)}}{g^{v_z(f)}}\bigg)\in \mathbb{C}^{*}. \]Proposition 1.6 The form 
$\eta$ is exact in a neighborhood of 
$z\in \hat {C}$ if and only if 
$|\{x,y\}_z|=1$.
Proof. We compute the tame symbol 
$\{x,y\}_z$ using Puiseux coordinates: this gives 
$(-1)^{pq}F(0)^{-p}$. Hence, given a small circle 
$C_z$ around 
$z$, we get
\[ \int_{C_z}\eta=2\pi p \log\! |F(0)|={-}2\pi \log\! |\{x,y\}_z|. \] The exactness of 
$\eta$ around 
$z$ is equivalent to the vanishing of its integral around 
$z$. The previous equation proves it is equivalent to 
$|\{x,y\}_z|=1$.
We give a name to polynomials satisfying the condition in the proposition.
Definition 1.7 A polynomial 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ is said to be tempered if 
$|\{x,y\}_z|=1$ for all 
$z\in \hat {C}$.
We see from Proposition 1.6 that an exact polynomial is tempered. Let us leverage the proposition to describe better the set of tempered polynomials. Write 
$P=\sum _{(i,j)\in \mathbb {Z}^{2}} c_{i,j}X^{i}Y^{j}$ and let 
$\Delta$ be the Newton polygon of 
$P$, that is, the convex hull in 
$\mathbb {R}^{2}$ of the set of indices 
$(i,j)\in \mathbb {Z}^{2}$ such that 
$c_{i,j}\ne 0$. The group 
$\mathrm {SL}_2(\mathbb {Z})$ acts on 
$(\mathbb {C}^{*})^{2}$ by the following monomial transformation:
\[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} .(X,Y)=(X^{a}Y^{b},X^{c} Y^{d}). \]
This action preserves the form 
$\eta$. It follows that the induced action on polynomials preserves the family of exact ones.
Given a polynomial 
$P$ with polygon 
$\Delta$, each side 
$s$ of the Newton polygon can be identified with the line 
$j=0$ with a monomial transformation. Collecting the monomials appearing along this line, we get a polynomial that we call the side polynomial 
$P_s\in \mathbb {C}[X^{{\pm }1}]$.
Proposition 1.8 Let 
$P\in \mathbb {C}[X^{\pm 1},Y^{\pm 1}]$ be a polynomial with Newton polygon 
$\Delta$. The following assertions are equivalent.
(i)
$P$ is tempered.(ii) For all sides
$s$ of $\Delta$, the roots of the polynomial $P_s$ have modulus $1$.(iii) The form
$\eta |_C$ defines a cohomology class in $H^{1}(\hat {C},\mathbb {R})$.
Proof. The equivalence of (i) and (iii) is clear from Proposition 1.6.
Write 
$P=\sum _{i,j\in \mathbb {Z}}c_{ij}X^{i}Y^{j}$ and let 
$z$ be an ideal point of 
$\hat {C}$. We consider a Newton–Puiseux coordinate as before, that is, 
$x=t^{p},y=t^{q}F(t)$. Then expanding 
$P(t^{p},t^{q}F(t))$ into powers of 
$t$, we get a lower-order term of the form
\[ \sum_{pi+qj=N}c_{i,j}F(0)^{j}t^{N}+o(t^{N}) \]
where the line 
$pi+qj=N$ is a side of 
$\Delta$. We get that 
$F(0)$ is a zero of the side polynomial 
$P_s=\sum _{pi+qj=N}c_{ij}X^{j}$. If 
$P$ is tempered, then 
$F(0)$ has modulus 1. Moreover, any root of any side polynomial gives rise to at least one Newton–Puiseux expansion and hence to one ideal point. This proves the equivalence of (i) and (ii).
Remark 1.9 (Case of real polynomials) Suppose that 
$P$ is a real polynomial, tempered and irreducible over 
$\mathbb {C}$. As 
$\eta$ satisfies 
$\sigma ^{*}\eta =-\eta$, its cohomology class belongs to the space 
$H^{1}(\hat {C},\mathbb {R})^{-}$ of odd cohomology classes with respect to the involution 
$\sigma ^{*}$, whose dimension is the genus of 
$\hat {C}$.
2. Extrema of the volume function
Let 
$P$ be an exact polynomial and 
$C$ be the smooth part of the zero set of 
$P$ in 
$(\mathbb {C}^{*})^{2}$. We denote by 
$\bar {C}$ the normalization of the zero set of 
$P$ in 
$(\mathbb {C}^{*})^{2}$. It is also the set of finite points of 
$\hat {C}$, where neither 
$x$ nor 
$y$ has a zero or a pole. For this whole section, we choose a volume function on 
$C$.
We are interested in this section in the extrema of a volume function 
$V$, as it will turn out in the next section that these extrema are the key input in a formula for the Mahler measure of exact polynomials. We will first describe two geometric tools to understand the variations of the volume, then continue with a study of critical points for the volume before describing the extrema. At the end of this section, we are able to prove a first theorem on exact polynomials: they should have a zero in the torus 
$|x| = |y|=1$.
2.1 Amoeba and Gauss logarithmic map
Definition 2.1 The amoeba of 
$C$ is the image of the map 
$\mu :\bar {C}\to \mathbb {R}^{2}$ defined by 
$\mu (x,y)=(\log\! |x|,\log\! |y|)$.
Definition 2.2 The logarithmic Gauss map is the map 
$\gamma :C\to \mathbb {P}^{1}(\mathbb {C})$ defined by 
$\gamma (x,y)=[x\partial _xP,y\partial _yP]$.
Being algebraic, 
$\gamma$ automatically extends to 
$\hat {C}$ as a holomorphic function: we will make this extension explicit in Proposition 2.8. There is a relation between these two notions as shown in the following proposition, taken from [Reference MikhalkinMik00].
Proposition 2.3 Let 
$C\subset (\mathbb {C}^{*})^{2}$ be the smooth part of the curve defined by 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$. Then
\[ \{(x,y)\in C, d\mu \text{ is not invertible}\}=\gamma^{{-}1}(\mathbb{P}^{1}(\mathbb{R})). \]Proof. Let 
$z=(x,y)$ be a point of 
$C$ and consider the zero set of the function 
$(u,v)\mapsto P(xe^{u},ye^{v})$ for 
$u$ and 
$v$ small. It defines a smooth submanifold around 
$0$ whose tangent space is given by 
$x\partial _x P(x,y) u+y\partial _y P(x,y) v=0$. In these coordinates, the derivative of 
$\mu$ is simply the map 
$(u,v)\mapsto (\operatorname {Re}(u),\operatorname {Re}(v))$. This map is non-invertible if and only if there exists 
$(u,v)\in \mathbb {R}^{2}\setminus \{(0,0)\}$ such that 
$x\partial _x P(x,y) u+y\partial _y P(x,y) v=0$. This is equivalent to 
$\gamma (x,y)$ being in 
$\mathbb {P}^{1}(\mathbb {R})$.
We can even specify where 
$\mu$ preserves orientation, recalling that 
$C$ is naturally oriented, being a complex curve. Here comes a convention.
Definition 2.4 We will say that 
$[z_1,z_2]\in \mathbb {P}^{1}(\mathbb {C})\setminus \mathbb {P}^{1}(\mathbb {R})$ lies in 
$\mathbb {P}^{1}_{+}(\mathbb {C})$ if 
$z_1/z_2$ has positive imaginary part and in 
$\mathbb {P}^{1}_-(\mathbb {C})$ if 
$z_1/z_2$ has negative imaginary part. More invariantly, a non-zero vector in 
$\mathbb {C}^{2}$ may be written 
$w=u+iv$ for 
$u,v\in \mathbb {R}^{2}$. We will say that 
$[w]\in \mathbb {P}^{1}_{\pm }(\mathbb {C})$ if 
$\mp \det (u,v)>0$.
Proposition 2.5 (Sequel of Proposition 2.3) In the same settings, for any 
$(x,y)\in C$ and 
$\varepsilon \in \{\pm 1\}$ such that 
$\gamma (x,y)\in \mathbb {P}^{1}_{\varepsilon }(\mathbb {C})$, the differential 
$d_{(x,y)}\mu$ preserves the orientation if 
$\varepsilon =1$ and reverses it if 
$\varepsilon =-1$.
Proof. Take a non-zero solution 
$(u,v)$ of the equation
\[ x\partial_x P(x,y) u+y\partial_y P(x,y) v=0. \]
Then an oriented basis of 
$T_zC$ is given by 
$(u,v), (iu,iv)$. The Jacobian of 
$\mu$ at 
$z$ in this basis is 
$\operatorname {Re}(v)\operatorname {Im}(u)-\operatorname {Re}(u)\operatorname {Im}(v)=\operatorname {Im}(u\bar {v})$. This number has the same sign as 
$\operatorname {Im} ({x\partial _xP}/{y\partial _yP})$.
With these two concepts at hand, we proceed with the study of the critical points of the volume.
2.2 Critical points of the volume function
We now look at the volume function 
$V$ on 
$C$ and spot its critical points.
Proposition 2.6 A point 
$(x,y)\in C$ is a critical point of 
$V$ if and only if the equation
\begin{equation} \log\! |x| x\partial_xP(x,y)+\log\! |y|y\partial_y P(x,y)=0 \end{equation}
holds. In particular, 
$(x,y)$ is critical if and only if either 
$\mu (x,y)=(0,0)$ or 
$\gamma (x,y)=[-\log\! |y|,\log\! |x|]\in \mathbb {P}^{1}(\mathbb {R})$.
Proof. We consider as before a point of the form 
$(xe^{u},ye^{v})$ belonging to 
$C$. Then at first order we have 
$u x\partial _xP(x,y)+v y\partial _y P(x,y)=0$ but 
$\eta _{(x,y)}(u,v)=-\log\! |x|\operatorname {Im} v +\log\! |y| \operatorname {Im} u$. A real basis of the tangent space in these coordinates is given by 
$(-y\partial _yP,x\partial _xP)$ and 
$(-iy\partial _yP,ix\partial _xP)$: the linear form 
$\eta _{(x,y)}$ vanishes on these vectors if and only if (1) holds. The conclusion follows.
One may connect Propositions 2.3 and 2.6 by noticing that critical points of 
$V$ are located inside the critical locus of 
$\mu$, precisely on points where 
$\gamma (x,y)=[-\log\! |y|,\log\! |x|]$ except for those satisfying 
$\mu =0$.
In order to describe the behavior of 
$V$ at ideal points, we introduce a topological notion to describe the volume function at ideal or ramification points:
Definition 2.7 We will say that a continuous real function 
$f$ on a Riemann surface 
$X$ has a saddle of order 
$k$ at 
$x$ if there is a local coordinate 
$z=\rho e^{i\theta }$ centered at 
$x$ and a continuous and strictly increasing function 
$h:\mathbb {R}\to \mathbb {R}$ such that 
$h(0)=0$ and 
$f(z)=f(x)+h(\rho )\cos (k\theta )+o(h(\rho ))$. In particular, 
$x$ is not an extremum of 
$f$ if 
$k>0$.
Notice that if 
$f$ is smooth and 
$df(x)\ne 0$, then 
$f$ has a saddle of order 
$1$ at 
$x$. If 
$f$ has a Morse critical point of index 
$1$ at 
$x$, then it has a saddle of order 
$2$. Also notice than one can replace 
$\cos$ with 
$\sin$ in Definition 2.7.
The next proposition shows that the behavior of 
$V$ at an ideal point is quite simple.
Proposition 2.8 Let 
$z$ be a point of 
$\hat {C}\setminus \bar {C}$ and denote by 
$k$ the order of ramification of 
$\gamma$ at 
$z$. If 
$\gamma$ is not constant around 
$z$, 
$V$ has a saddle point of order 
$k$ at 
$z$.
Proof. Up to exchanging 
$x$ and 
$y$, we can choose Newton–Puiseux coordinates around 
$z\in \hat {C}\setminus \bar {C}$ of the form 
$x=t^{p},y=t^{q}F(t)$ with 
$p\ne 0$ and 
$|F(0)|=1$.
Differentiating the equality 
$P(t^{p},t^{q}F(t))=0$ and writing 
$\gamma ={x\partial _xP}/{y\partial _yP}$, we get
\begin{equation} {-}\gamma(t)=\frac{q}{p}+\frac{tF'(t)}{pF(t)}. \end{equation} If 
$\gamma$ is non-constant, then neither is 
$F$ and we may write 
$F(t)=e^{i\phi +a_K t^{K}+O(t^{K+1})}$ with 
$\phi \in \mathbb {R}$, 
$K>0$ and 
$a_K\ne 0$. Comparing with (2), we find that 
$K$ is equal to the ramification order of 
$\gamma$ denoted by 
$k$.
Plugging the formulas for 
$x$ and 
$y$ into the differential of 
$V$, we get
\[ \eta=p\log\! |F(t)| d\arg(t)-p\log\! |t| d\arg F(t). \]
Integrating along the ray 
$[0,t]$, the form 
$d\arg t$ vanishes, giving
\[ V(t)-V(z)={-}p\int_{[0,t]}\log\! |t|d\arg F(t). \]An integration by parts yields
\[ V(t)-V(z)={-}p \log\! |t|\arg F(t)+p\int_{[0,t]} \arg F(t) d\log\! |t|. \]
Writing 
$F(t)=e^{i\phi +a_k t^{k}+O(t^{k+1})}$, we get the expression
\[ V(t)=V(z)-p\log\! |t|\operatorname{Im} (a_kt^{k})+O( t^{k}). \]
This shows that 
$V$ has a saddle of order 
$k$ if one sets 
$h(\rho )=-\log\! |\rho |\rho ^{k}$.
Note, in particular, that 
$V$ cannot have an extremum at an ideal point of 
$\hat C$, unless it is constant. Let us consider when this happens.
Corollary 2.9 If 
$P$ is irreducible and 
$V$ is constant on 
$C$, then 
$P=X^{p}Y^{q}-\lambda$ for some coprime integers 
$p,q$ and 
$\lambda \in \mathbb {C}$.
2.3 Extrema of the volume
We now leverage the study of critical points to see that the extrema of the volume only happen above the torus 
$|x|=|y|=1$ in 
$\bar {C}$.
Proposition 2.10 Let 
$z$ be a point of 
$\bar {C}$ mapping to 
$(x_0,y_0)$. We denote by 
$k$ the order of ramification at 
$z$ of the map 
$(x,y):\bar {C}\to (\mathbb {C}^{*})^{2}$. Denote by 
$\gamma :\bar {C}\to \mathbb {P}^{1}(\mathbb {C})=\mathbb {C}\cup \{\infty \}$ the logarithmic Gauss map, identifying 
$z$ with 
$[z,1]$, and suppose that 
$\gamma (z)\ne \infty$. We denote by 
$l$ the order of ramification of 
$\gamma$ at 
$z$.
(i) If
$\log\! |x_0|\gamma (z)+\log\! |y_0|\ne 0$ then $V$ has a saddle of order $k$ at $z$.(ii) If
$\log\! |x_0|\gamma (z)+\log\! |y_0|= 0$ and $\mu (z)\ne 0$ then $V$ has a saddle of order $k+l$ at $z$.(iii) If
$\mu (z)=0$ and $\gamma (z)\notin \mathbb {R}$ then $V$ has a local maximum at $z$ if $\operatorname {Im} \gamma (z)<0$ and a local minimum if $\operatorname {Im}\gamma (z)>0$.(iv) If
$\mu (z)=0$ and $\gamma (z) \in \mathbb {R}$ then $V$ does not have a local extremum at $z$.
Proof. Up to a monomial transformation, we can find a local coordinate around 
$z$ such that 
$x=x_0e^{t^{k}}$ and 
$y=y_0e^{t^{k}F(t)}$ where 
$F(t)=F_0+F_lt^{l}+O(t^{l+1})$. Again, differentiating the equation 
$P(x,y)=0$ gives
\[ -\gamma(t)=F(t)+\frac{t}{k}F'(t)=F_0+F_l(1+l/k)t^{l}+O(t^{l+1}). \]
Plugging the formulas of 
$x$ and 
$y$ in the derivative of 
$V$ one gets
\begin{align} V(t)&=V(z)+\operatorname{Im}(\log\! |y_0|t^{k}-\log\! |x_0| t^{k} F(t)) \nonumber\\ &\quad +\int_0^{t} (\operatorname{Re}(t^{k}F(t))d\operatorname{Im} t^{k}-\operatorname{Re} t^{k} d\operatorname{Im}(t^{k}F(t))). \end{align}
If 
$\log\! |y_0|-\log\! |x_0|F_0\ne 0$ then 
$V$ has a saddle of order 
$k$ as before and the first item of the proposition is proved.
Suppose from now that one has
\begin{equation} \log\! |x_0|\gamma(z)+\log\! |y_0|=0. \end{equation}
If 
$\mu (z)\ne 0$, we conclude from (4) that 
$\log\! |x_0|\ne 0$ and that 
$F_0$ is real. The first-order term on the first line of (3) becomes 
$-\operatorname {Im}(\log\! |x_0|F_lt^{k+l})$, whereas a computation shows that the first-order term on the second line has the order of 
$t^{2k+l}$. Hence, in that case, 
$V$ has a saddle of order 
$k+l$.
Suppose now that 
$\log\! |x_0|=\log\! |y_0|=0$. Then the first expression vanishes identically. If 
$F_0$ is not real, the first order in the integral is equal to 
$-\frac {1}{2}|t|^{2k}\operatorname {Im} F_0$. In that case, 
$V$ has a maximum if 
$\operatorname {Im} F_0>0$ and a minimum if 
$\operatorname {Im} F_0<0$.
Suppose now that 
$F_0$ is real so that this term vanishes. Writing 
$t=\rho e^{i\theta }$ and 
$F_l=r_le^{i\phi _l}$, we compute
\begin{align*} V(t)-V(z)&={-}\frac{\rho^{2k+l}r_l}{2k+l}\big(l\cos(k\theta)\sin(\phi_l+(k+l)\theta)+k\sin(\phi_l+l\theta) \big)\\ &={-}\frac{\rho^{2k+l}r_l}{2k+l} \bigg(\frac{l}{2}\sin(\phi_l+(2k+l)\theta)+\bigg(\frac{l}{2}+k\bigg)\sin(\phi_l+l\theta)\bigg) \end{align*}
This expression cannot vanish and its integral over 
$\theta$ vanishes. This proves that 
$V$ does not have an extremum at 
$z_0$.
The fourth case will be explored and described more precisely in § 3.3.1.
There is a nice way to understand the properties of 
$V$ by looking at the amoeba of 
$C$. One can define gradient lines of 
$V$ as integral lines of the distribution 
$\star \eta$ where 
$\star$ denotes the Hodge star on 
$C$. A direct computation shows that
\[{\star} \eta=\log\! |y|d\log\! |x|-\log\! |x|d\log\! |y|=\mu^{*} (v\,du-u\,dv) \]
where 
$u$ and 
$v$ are the coordinates in the image of 
$\mu$. This shows that gradient lines of 
$V$ project to half-lines in the amoeba of 
$C$. Moreover, flowing from the origin on the half-line, the volume is increasing if 
$\operatorname {Im} \gamma >0$ or if 
$\mu$ preserves the orientation, and is decreasing if 
$\operatorname {Im} \gamma <0$ or if 
$\mu$ reverses the orientation.
To prove this last assertion, it is sufficient up to monomial transformations to prove it for the half-line 
$u=0,v>0$. We may parametrize the gradient line by setting 
$x(t)=e^{i\alpha (t)},y(t)=e^{t+i\beta (t)}$ so that we have 
$V'(t)=t\alpha '(t)$. Differentiating the equation 
$P(e^{i\alpha (t)},e^{t+i\beta (t)})=0$, we get 
$x\partial _x P i\alpha '+y\partial _y P(1+i\beta ')=0$. Dividing by 
$y\partial _y P$ and taking the real part gives the equation 
$\alpha ' \operatorname {Im} \gamma =1$. This implies that 
$V'(t)=t/\operatorname {Im} \gamma (t)$, proving the claim.
Here is the example of the polynomial 
$P=X+Y-1$. The volume function is 
$V(x,y)=-D(x)$ where 
$D$ is the Bloch–Wigner dilogarithm. Clearly, there are two points in 
$\mu ^{-1}(0,0)$, which are 
$(e^{i\pi /3},e^{-i\pi /3})$ and its conjugate. They correspond to the extrema of the function 
$D$, that is, the maximal volume of a hyperbolic tetrahedron.
From Propositions 2.8 and 2.10, we see that the extrema of 
$V$ can only occur in 
$\mu ^{-1}(0,0)$. They will play a crucial role, so we call them toric points, as they project to the torus 
$|x|=|y|=1$.
Definition 2.11 A point 
$z$ in 
$\bar {C}$ such that 
$\mu (z) = (0,0)$ is called a toric point.
If the volume function 
$V$ is non-constant, it has extrema, hence 
$\bar C$ has toric points. This gives us the following result.
Theorem 2.12 Let 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ be an exact irreducible polynomial such that the corresponding volume function is not constant. Then there exists 
$(x,y)\in (\mathbb {C}^{*})^{2}$ such that 
$|x|=|y|=1$ and 
$P(x,y)=0$.
We will build upon this theorem in § 4.
3. Mahler measure of exact polynomials
We describe in this section the Mahler measure of exact polynomials, in a spirit similar to [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05] but focusing on extrema and, more broadly, critical points of the volume function.
3.1 Mahler measure and the volume function
Following an idea used by several authors [Reference DeningerDen97, Reference Rodriguez-VillegasRod99, Reference Boyd, Rodriguez-Villegas and DunfieldBRD05], the Mahler measure of a polynomial is computed by integrating the form 
$\eta$ on a collection of arcs inside 
$\hat {C}$ that we now define. This formulation will give further information when 
$\eta$ is exact.
Lemma 3.1 Let 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ be an exact irreducible polynomial whose Newton polygon has non-empty interior. Let 
$\bar {C}$ be the normalization of the zero set of 
$P$ in 
$(\mathbb {C}^{*})^{2}$ and consider the natural coordinate map 
$(x,y):\bar {C}\to (\mathbb {C}^{*})^{2}$. Then, for all but a finite number of monomial transformations applied to 
$P$, the subset
\[ \Gamma=\{z\in \bar{C}, |x(z)|=1,|y(z)|>1\} \]
is a finite collection of arcs such that the volume function 
$V:\Gamma \to \mathbb {R}$ is monotonic on each interval, increasing in the direction of increasing 
$\arg (x)$.
Proof. The proposition contains two parts: 
$\Gamma$ is a union of arcs (without crossings) and 
$V$ is monotonic on each component. First, one may visualize 
$\Gamma$ as the preimage of the half-line 
$u=0,v>0$ by the map 
$\mu$. Applying a monomial transformation amounts to taking instead the preimage of any rational half-line. As a consequence, only a finite number of these lines meet a finite subset of 
$\mathbb {R}^{2}\setminus \{(0,0)\}$. We take as a finite set the image by 
$\mu$ of the union of the singularities of 
$C$ and the critical points of 
$V$.
Notice that the set of critical points is finite. Indeed, we assumed that the Newton polygon has non-empty interior, and from Corollary 2.9 and its proof, the volume function 
$V$ is non-constant on the connected surface 
$\bar {C}$. Proposition 2.10 then shows that critical points are isolated.
Hence we suppose that the half-line 
$u=0,v>0$ avoids all singularities of 
$C$ and critical points of 
$V$ except those with 
$\mu =0$.
For all 
$z\in \Gamma$ with 
$\mu (z)\ne (0,0)$, the map 
$z\mapsto x(z)$ is not ramified. Indeed, if it were so, then we would have 
$\partial _y P(x,y)=0$ and 
$\gamma (z)=\infty$. As 
$\log\! |x|=0$, Proposition 2.6 implies that 
$z$ is a critical point of 
$V$, which we excluded. It follows that 
$\Gamma$ is smooth at these points. Let us show that 
$V|_\Gamma$ is not critical either. Indeed, on 
$\Gamma$ we have 
$|x|=1$, hence 
$\ln |x|=0$. That gives 
$dV=\eta =\log\! |y|d\arg (x)$ on 
$\Gamma$. Moreover, we have both 
$\log\! |y|\ne 0$ and 
$|x|=1$ on 
$\Gamma$. So the form 
$dV$ does not vanish.
Let us compute the Mahler measure of 
$P$ given by
\[ m(P)=\frac{1}{(2\pi)^{2}}\int_0^{2\pi}\int_0^{2\pi}\log\! |P(e^{i\theta},e^{i\phi})|\,d\theta\,d\phi. \]
By Fubini's theorem, setting 
$P_\theta (y)=P(e^{i\theta },y)$ we get
\[ m(P)=\frac{1}{2\pi}\int_0^{2\pi}m(P_\theta)\,d\theta. \]
Here 
$m(P_\theta )$ is the one-dimensional Mahler measure which can be computed thanks to Jensen's formula:
\[ m(P_\theta)=\log\! |a(\theta)|+\sum_{j}\log^{+}\!|y_j(\theta)|. \]
In this formula we wrote 
$P_\theta (y)=a(\theta )\prod _i(y-y_j(\theta ))$ and as usual 
$\log ^{+}\!|y|=\max (0,\log\!|y|)$.
As the Mahler measure of 
$P$ is obviously invariant by monomial transformations, we can suppose that 
$a(\theta )=ae^{in\theta }$ for some 
$n\in \mathbb {Z}$: this is equivalent to saying that the Newton polygon 
$\Delta$ does not have a top horizontal slope. We also observe that the subset 
$\Gamma$ of Lemma 3.1 is exactly the set of pairs 
$(e^{i\theta },y_j(\theta ))$ where 
$|y_j(\theta )|>1$. Denote by 
$\bar {\Gamma }$ the abstract completion of 
$\Gamma$: it is a union of closed intervals. As 
$\Gamma$ belongs to a compact subset of 
$\bar {C}$, the inclusion 
$\Gamma \subset C$ extends to a map 
$\bar {\Gamma }\to \bar {C}$ which is no longer injective. Nevertheless, we can suppose that the integration goes along the completion 
$\bar {\Gamma }$ of 
$\Gamma$ that we orient in the direction of increasing 
$V$. We find
\[ m(P)=\log\! |a|+\frac{1}{2\pi}\int_{\bar{\Gamma}}\eta=\log\! |a|+\frac{1}{2\pi}V(\partial\bar{\Gamma}). \]
Notice that 
$\partial \bar {\Gamma }$ is included in the set of toric points.
Remark 3.2 As noted above, the Mahler measure may be computed by integration along the preimage of any rational half-line. For instance, applying the monomial transformation 
$(x,y)\mapsto ({1}/{x},{1}/{y})$ and assuming we avoid the singularities, one may integrate along the preimage of 
$\mathbb {R}_{<0}\times \{0\}$, that is, the collection of arcs
\[ \Gamma_{{<}0}=\{z\in \bar{C}, |x(z)|=1,|y(z)|<1\}. \]This will be useful later on (see the proof of Theorem 3.14).
Remark 3.3 We observe that, given an exact polynomial 
$P$, all its coefficients in the corners of the Newton polygon are equal in absolute value. This is simply because the slope polynomial having roots of modulus one, their product also has modulus one. Hence, the extremal coefficients of these polynomial are equal in modulus. We will denote by 
$c(P)\in (0,+\infty )$ the absolute value of these corner coefficients and say that 
$P$ is normalized if 
$c(P)=1$.
3.2 A formula for the Mahler measure: the generic case
In this section we give a first formula for the Mahler measure of an exact polynomial under some hypotheses on the polynomial. Generically these hypotheses are fulfilled. Unfortunately, 
$A$-polynomials of hyperbolic cusped manifolds do not satisfy it in general due to extra symmetries. We will explain later on how to compute the Mahler measure in general. Recall from Definition 2.11 that a point 
$z$ in 
$\bar {C}$ is a toric point if 
$\mu (z)=(0,0)$.
Definition 3.4 We will say that an exact polynomial 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ is regular if, for every toric point 
$z$ in 
$\bar {C}$, we have 
$\gamma (z)\notin \mathbb {P}^{1}(\mathbb {R})$.
Hence any such toric point 
$z$ is either a local maximum or minimum of the volume function 
$V$. We will denote by 
$\varepsilon (z)$ minus the sign of the imaginary part of 
$\gamma (z)$ and by 
$k(z)$ the ramification at 
$z$ of the map 
$(x,y):\bar {C}\to (\mathbb {C}^{*})^{2}$
The following theorem expresses the Mahler measure (up to a factor 
$2\pi$) as a sum of values of the volume function at toric points.
Theorem 3.5 Let 
$P\in \mathbb {C}[X^{\pm 1},Y^{\pm 1}]$ be irreducible, normalized, exact and regular. We have the formula
\[ m(P)=\frac{1}{2\pi}\sum_{z\in \mu^{{-}1}(0,0)} k(z)\varepsilon(z)V(z). \]Proof. We analyze for each toric point 
$z=(x_0,y_0)\in \mu ^{-1}(0,0)$ how many branches of 
$\bar {\Gamma }$ end at 
$z$. Take logarithmic Newton–Puiseux coordinates 
$x=x_0e^{t^{k}},y=y_0e^{t^{k}F(t)}$ with 
$\operatorname {Im} F(0)\ne 0$; indeed, 
$F(0)$ is the slope 
$\gamma (z)$ (see the proof of Proposition 2.10).
The manifold 
$\Gamma$ is defined by 
$|x(t)|=1$ and 
$|y(t)|>1$. In coordinates, this means:
•
$|x(t)| = 1$ is equivalent to $\operatorname {Re} t^{k} = 0$, which gives $\operatorname {Im} t^{k} = {\pm }|t^{k}|$;•
$|y(t)| > 1$ is equivalent to $\operatorname {Re} (t^{k}F(t)) > 0$.
Using 
$\operatorname {Re} t^{k} = 0$, we get
\begin{align*} 0<\operatorname{Re} t^{k} F(t)&=\operatorname{Re} t^{k} F(0)+O(t^{k+1})={-}\operatorname{Im} t^{k}\operatorname{Im} F(0)+O(\rho^{k+1})\\ & ={-}\operatorname{Im} t^{k}\operatorname{Im} \gamma(z)+O(\rho^{k+1}). \end{align*}
So we have the additional condition that 
$\operatorname {Im} t^{k}$ has minus the sign of 
$\operatorname {Im} \gamma (z)$. In any case, among the 
$2k$ half-lines defined by 
$\operatorname {Re} t^{k} =0$, we select exactly 
$k$ branches of 
$\Gamma$ adjacent to 
$z$. By item (iii) of Proposition 2.10, if 
$\operatorname {Im} \gamma (z)>0$, 
$V$ has a minimum and the branches of 
$\Gamma$ start from 
$z$, justifying 
$\varepsilon (z)=-1$. This explains the sign and ends the proof of the theorem.
We get a lower bound on the Mahler measure in the irreducible case.
Theorem 3.6 Let 
$P\in \mathbb {C}[X^{\pm 1},Y^{\pm 1}]$ be a regular exact normalized polynomial irreducible over 
$\mathbb {C}$. Then we have the inequality
\[ 2\pi m(P)\ge \max V-\min V. \]Proof. Let 
$z_1,\ldots , z_n$ be the local maxima of 
$V$ ordered so that we have 
$V(z_1)\le \cdots \le V(z_n)$ and denote by 
$k_1,\ldots ,k_n$ the corresponding ramifications orders. We also denote by 
$t_1,\ldots ,t_m$ and 
$l_1,\ldots ,l_m$ the similar data corresponding to the local minima of 
$V$. Lemma 3.1 provides a collection of arcs 
$\bar {\Gamma }$ as the completion of 
$\mu ^{-1}(\{0\}\times (0,+\infty ))$ and the proof shows that we could have taken instead of 
$\{0\}\times (0,+\infty )$ any rational half-line except for a finite number of them. Denote by 
$0<\theta _1<\cdots <\theta _m<2\pi$ the arguments of these forbidden half-lines. For any 
$\alpha /2\pi \in \mathbb {Q}/\mathbb {Z}$ such that 
$2\pi \alpha$ is distinct from these arguments, we denote by 
$\bar {\Gamma }_\alpha$ the completion of the preimage of the half-line with argument 
$2\pi \alpha$. We always have
\[ 2\pi m(P)= V(\partial \bar{\Gamma}_\alpha)=\sum_{i=1}^{n} k_i V(z_i)-\sum_{i=1}^{m} l_i V(t_i), \]
Set 
$I_\alpha =V(\bar {\Gamma }_\alpha )\subset [\min V,\max V]$. As 
$V$ is increasing along the components of 
$\bar {\Gamma }_\alpha$ we have 
$2\pi m(P)\ge \lambda (I_\alpha )$ where 
$\lambda$ denotes the Lebesgue measure. Suppose by contradiction that we have 
$2\pi m(P)<\max V-\min V$. Observing that all local extrema of 
$V$ belong to 
$I_\alpha$, we see that 
$I_\alpha$ has a ‘hole’, meaning that there exists 
$x\in (\min V,\max V)$ such that 
$x\notin I_\alpha$.
Hence 
$\Gamma _\alpha$ splits into two parts, mapped by 
$V$ to 
$(\min V,x)$ and 
$(x,\max V)$, respectively. We should have as many maxima as minima above 
$x$: formally this implies that 
$\sum _{i, V(z_i)>x}k_i=\sum _{i, V(t_i)>x}l_i$. Taking any other collection 
$\bar {\Gamma }_\beta$, the number 
$\sum _{i, V(t_i)>x}l_i$ also corresponds to the number of increasing branches of 
$\bar {\Gamma }_\beta$ starting from a point above 
$x$. As there are as many arriving points above 
$x$, this implies that no other branch of 
$\bar {\Gamma }_\beta$ can come from below 
$x$. We conclude that 
$x\notin I_\beta$ for all 
$\beta \notin \{\theta _1,\ldots ,\theta _m\}$.
As the extremal points of 
$I_\beta$ are one of the local extrema of 
$V$, there exists 
$\varepsilon >0$ such that 
$(x-\varepsilon ,x+\varepsilon )\cap I_\beta =\emptyset$. However, it is clear that 
${\bigcup} _{\beta \in 2\pi \mathbb {Q}/2\pi \mathbb {Z}\setminus \{\theta _1,\ldots ,\theta _m\}} \bar {\Gamma }_\beta$ is dense in 
$\hat {C}$, hence we conclude that
\[ V(\hat{C})\cap (x-\varepsilon,x+\varepsilon)=\emptyset. \]
As 
$P$ is irreducible, 
$\hat {C}$ is connected and this contradicts the continuity of 
$V$.
We remark that if we have the equality 
$2\pi m(P)=\max V-\min V$, this means that the map 
$V:\bar {\Gamma }_\alpha \to [\min V,\max V]$ does not have overlaps except at 
$\partial \bar {\Gamma }$ and is surjective. This is possible only if 
$k_i=l_i=1$ for all 
$i$ and 
$V(t_1) < V(z_1)=V(t_2) < \cdots V(z_{n-1})=V(t_n) < V(z_n)$.
3.3 A formula for the Mahler measure: the general case
We now extend our previous formula to the more complicated case of a general exact polynomial. We shall define an index 
$\textrm {Ind}(z)$ of a toric point 
$z$ which will play the role of the numbers 
$k(z) \varepsilon (z)$ in the previous version. The general formula will involve values of the volume function at toric points.
3.3.1 Maximally tangent curves
Let 
$z \in \hat C$ be a toric point, that is such that 
$\mu (z) = (0,0)$. Let 
$k$ be the ramification order at 
$z$ of the map 
$\hat C \to (\mathbb {C}^{*})^{2}$.
In the case 
$\operatorname {Im}(\gamma (z))\neq 0$, we call the number 
$k(z)\varepsilon (z)$ which appears in the formula in the previous subsection the index of 
$z$. From now on, we suppose that 
$\gamma (z)\in \mathbb {R}\setminus \{0\}$.
Let 
$\xi$ be an element of 
$\mathbb {P}(T_z \hat C)$, that is, a real line in 
$T_z \hat C$. We define below its order of tangency to the torus as the maximal order of tangency with the torus of a curve in 
$\hat C$ tangent to 
$\xi$. Recall that the points in 
$\hat C$ which project to the torus are exactly those satisfying 
$\mu (z)=(0,0)$.
Definition 3.7 For 
$\xi \in \mathbb {P}(T_z \hat C)$, the order of 
$\xi$ is the number 
$\operatorname {ord}(\xi ) \in \mathbb {N} \cup {+\infty }$ defined by
\[ {\rm ord}(\xi) = \sup\biggl\{ l \in \mathbb N \biggm|\begin{matrix}\exists\alpha :\ ]-\epsilon,\epsilon[\to \hat C \text{ smooth curve satisfying }\\ \alpha_0 = z,\alpha'_0 \in \xi\setminus\{0\} \text{ and }\mu(\alpha_s)=O(s^l)\end{matrix}\!\!\biggr\}. \]
Moreover, a smooth curve with maximal 
$l$ above is said to be maximally tangent to the torus in the direction 
$\xi$.
The following proposition shows that there is a relation between the ramification index 
$k$ and the various orders of tangency at 
$z$.
Proposition 3.8 Let 
$z\in \hat C$ satisfy 
$\mu (z)=(0,0)$ and set 
$k=k(z)$. For every direction 
$\xi$ but exactly 
$k$, we have 
$\operatorname {ord}(\xi ) = k$. For the 
$k$ remaining directions 
$\xi _1, \ldots , \xi _k$, the order is 
$\geq k+1$.
Proof. Take a local coordinate 
$t$ such as 
$(x = x_0 e^{it^{k}}, y = y_0 e^{i t^{k}F(t)})$. Consider a smooth curve 
$\alpha :(-\varepsilon ,\varepsilon )\to \hat {C}$ with 
$\alpha _0 = z$. At the coordinate 
$t$ we have 
$\alpha _0=0$ and 
$\alpha '_0\in \xi \setminus \{0\}$. Recall that as 
$\gamma (z)$ is real, we have 
$F(0)\in \mathbb {R}$. Using 
$\alpha _s=s\alpha '_0+O(s^{2})$ yields
\[ \mu(\alpha_s) = (\ln|x(\alpha_s)|,\ln|y(\alpha_s)|) ={-}s^{k}(\operatorname{Im}({\alpha'_0}^{k}), F(0) \operatorname{Im}({\alpha'_0}^{k})) + O(s^{k+1}). \]
We see that 
$\mu (\alpha _s)=O(s^{k+1})$ if and only if 
$\operatorname {Im}({\alpha _0'}^{k}) = 0$, defining the 
$k$ particular directions of 
$\alpha '_0\in \xi$. In the coordinate 
$t$, these directions are the 
$k$ lines of angle 
$\theta _j$ with 
$k \theta _j \equiv 0 [\pi ]$.
3.3.2 Variation of the volume
We show here that the variation of the volume on maximally tangent curves in the directions 
$\xi _j$ only depends on the direction. We shall use again a local coordinate 
$t$ such that 
$(x= x_0e^{it^{k}}, y=y_0 e^{it^{k} F(t)})$, where 
$F(t) = \sum _{i\ge 0} F_it^{i}$. Fix the direction 
$\xi _j$, corresponding at this coordinate to the angle 
$\theta _j$. Let 
$\alpha _s$ be a tangent curve in the direction 
$\xi _j$, written in coordinates in the form
\[ \alpha_s = e^{i\theta_j}s\bigg(1 + \sum_{i\geq 1} a_i s^{i}\bigg). \]Let us begin with a characterization in the chosen coordinate of maximally tangent curves.
Lemma 3.9 The order of tangency of 
$\xi _j$ is 
$\operatorname {ord}(\xi _j)=k+l$ where 
$l$ is the first integer such that 
$F_le^{il\theta _j}$ is not real.
Moreover the curve 
$\alpha _s = e^{i\theta _j}s(1 + a_1 s +\cdots )$ is maximally tangent to the torus if and only if the coefficients 
$a_1, \ldots , a_{\operatorname {ord}(\xi _j) - k}$ are real.
Proof. Let 
$l$ be the first integer such that 
$F_{l}e^{(k+l)i\theta _j}$ is not real. We have to prove that 
$k+l$ is the order of 
$\xi _j$.
First, consider the curve 
$\alpha _s=s e^{i\theta _j}$. Applying the map 
$\mu$, we compute
\[ \mu(\alpha_s) ={-}s^{k+l}\big(0,\operatorname{Im}(F_le^{(k+l)i\theta_j})\big) + o(s^{k+l}). \]
Hence 
$\operatorname {ord}(\xi _j) \geq k+l$.
Second, consider a curve 
$\alpha _s$, written 
$\alpha _s = e^{i\theta _j}s(1 + a_1 s +\cdots )$ as above, whose order of tangency to the torus is 
$\geq k+l$. Let 
$r$ be the smallest integer (if it exists) such that 
$a_r$ is non-real. The first non-vanishing term of 
$\ln |x(\alpha _s)|$ (if it exists) is 
$- ks^{r+k}\operatorname {Im}(e^{ik\theta _j}a_r)+\cdots .$ Recalling that 
$e^{ik\theta _j}=\pm 1$ and using the assumption on the order of tangency, we get 
$r \geq l$.
If we have 
$r = l$, we may compute the term of order 
$k+l$ in 
$\mu (\alpha _s)$: it is equal to
\[ s^{k+l} \big({-}k\operatorname{Im}(e^{ik\theta_j}a_r\big), -\operatorname{Im}\big(ke^{i\theta_j}a_rF_0+F_le^{(l+k)i\theta_j})\big). \]
On the other hand, if we have 
$r>l$, this term equals 
$s^{k+l} (0, -\operatorname {Im}(F_le^{(l+k)i\theta _j}))$. In any case, 
$\mu (\alpha _s)$ has order 
$k+l$. This proves the lemma.
In other terms, up to a real reparametrization of the variable 
$s$, we may write any maximally tangent curve in the direction 
$\xi _j$ in the form 
$\alpha _s = se^{i\theta _j}(1 + a_ls^{l} + \cdots )$. Note that any curve satisfying 
$|x|=1$ along the curve is maximally tangent: for a curve 
$\alpha _s = e^{i\theta }s(1 + a_1 s +\cdots )$ to satisfy 
$|x(\alpha _s)| = 1$, we must have 
$\theta = \theta _j$ for some 
$j$ and every coefficient 
$a_m$ real, as shown by a computation similar to the proof of Lemma 3.9.
Remark 3.10 From the above discussion, any arc 
$\delta$ in 
$\mu ^{-1}(\{ 0 \}\times \mathbb {R})$ is maximally tangent to the torus at any point of 
$\delta \cap \mu ^{-1}(\{(0,0)\})$. Moreover, at such a point, 
$\mu ^{-1}(\{ 0 \}\times \mathbb {R})$ contains 
$k$ maximally tangent curves, one for each direction described in Proposition 3.8.
As the definition of maximally tangent curves is invariant under monomial transformation, we see that this is true for any 
$\mu ^{-1}(d)$ where 
$d$ is a line of rational slope through 
$0$ in 
$\mathbb {R}^{2}$.
The behavior of the volume function along a maximally tangent curve 
$\alpha$ only depends on the order 
$\operatorname {ord}(\xi _j)$ and the sign 
$\varepsilon _j$ of 
$\operatorname {Im}(F_{l}e^{il\theta _j})$ where 
$\operatorname {ord}(\xi _j)=k+l$, called the sign of the direction. At this point, it seems to depend on the local coordinate chosen. However, the following lemma shows that it does not.
Proposition 3.11 Let 
$\alpha$ be a maximal tangent curve in the direction 
$\xi _j$ of order 
$\operatorname {ord}(\xi _j)$ and sign 
$\varepsilon _j$. Then:
(i) if
$k+\operatorname {ord}(\xi _j)= +\infty$, then $s\mapsto V(\alpha _s)$ is constant;(ii) if
$k+\operatorname {ord}(\xi _j)$ is even, and $\varepsilon _j >0$, then $s\mapsto V(\alpha _s)$ has a strict local maximum at $0$;(iii) if
$k+\operatorname {ord}(\xi _j)$ is even, and $\varepsilon _j <0$, then $s\mapsto V(\alpha _s)$ has a strict local minimum at $0$;(iv) if
$k+\operatorname {ord}(\xi _j)$ is odd, then $s\mapsto V(\alpha _s)$ is strictly monotonic.
Proof. If 
$\operatorname {ord}(\xi _j)=+\infty$ then Lemma 3.9 implies that 
$F_le^{il\theta _j}$ and 
$a_l$ are real for all 
$l\in \mathbb {N}$. This implies that one can write 
$t=e^{i\theta _j}f(s)$ and 
$F(t)=g(s)$ where 
$f$ and 
$g$ are two real functions. Hence 
$x=x_0e^{it^{k}}$ and 
$y=y_0e^{it^{k} F(t)}$ have modulus 1 for small 
$s$. Hence 
$\alpha _s$ belong to the torus 
$\mu =0$ and the volume is constant.
In the other case, set 
$l = \operatorname {ord}(\xi _j)-k$ and 
$\theta = \theta _j$. The statement does not depend on a real reparametrization of the variable 
$s$, so we assume that we can write in the local coordinate 
$\alpha _s = se^{i\theta }(1 + \alpha _ls^{l} + \cdots )$.
Using the formula for 
$dV$, this parametrization and computations similar to those of the previous lemma, we get that the first non vanishing term in 
$({d}/{ds})V(\alpha _s)$ is of order 
$2k+l-1$. Indeed, this first non-vanishing term is obtained by looking at the terms of order 
$k+l$ of 
$\ln |x|$ and 
$\ln |y|$ and 
$k-1$ of 
$d\arg (x)$ and 
$d\arg (y)$. There may be some vanishing terms in the following expressions but we may anyway write (recall that 
$e^{ik\theta }$ and 
$F_0$ are real):
(i)
$\ln |x| = s^{k+l} (-k\operatorname {Im}(e^{ik\theta } \alpha _l))+\cdots$;(ii)
$d\arg (x) = ke^{ik\theta } s^{k-1}ds+\cdots$;(iii)
$\ln |y| = s^{k+l} (-\operatorname {Im}(e^{i(k+l)\theta } F_l)- \operatorname {Im}(F_0 ke^{ik\theta }\alpha _l))+\cdots$;(iv)
$d\arg (y) = ke^{ik\theta } F_0 s^{k-1}ds+\cdots$.
We deduce that
\begin{align*} \frac{d}{ds}V(\alpha_s) &= \ln|y|d\arg(x) - \ln|x|d\arg(y) \\ &= k^{2}s^{2k+l-1}\big(-\operatorname{Im}(F_{l} e^{il\theta})\big)+ \cdots. \end{align*} So the sign of this derivative is 
$-\varepsilon$ times the sign of 
$s^{2k+l-1}$. This proves the proposition.
In cases (ii), (iii) and (iv) we call the direction 
$\xi _j$ respectively maximizing, minimizing, or monotonic. We are ready to define the index of the point 
$z \in \hat C$, which extends the regular case.
Definition 3.12 Let 
$z$ be a point in 
$\hat C$ with 
$\mu (z)=(0,0)$.
If 
$\gamma (z)$ is not real, then let 
$k$ be the ramification at 
$z$ of 
$z\to (x,y)$ and 
$\varepsilon$ be minus the sign of 
$\operatorname {Im}(\gamma (z))$. Then the index of 
$z$, denoted by 
$\text {Ind}(z)$, is 
$k\varepsilon$.
If 
$\gamma (z)$ is real, the index of 
$z$, denoted by 
$\text {Ind}(z)$, is the number of maximizing directions minus the number of minimizing directions.
Remark 3.13 As discussed in the Remark 3.10, the index of a point 
$z$ is invariant under monomial transformations: such a transformation sends minimizing (respectively, maximizing) curves to minimizing (respectively, maximizing) curves.
Note that only a finite number of points 
$z\in \mu ^{-1}(0,0)$ have a non-trivial index. In particular, any non-singular point of a curve in the intersection of 
$C$ and the torus has index 
$0$: at such a point, there is only one maximally tangent curve to the torus, which is included in the torus. Along this curve, the volume is constant.
3.3.3 Mahler measure of exact polynomial, general case
The index we defined above also describes the contributions of points in the torus to the Mahler measure as shown by the following theorem.
Theorem 3.14 Let 
$P\in \mathbb {C}[X^{{\pm }1},Y^{{\pm }1}]$ be an exact, irreducible and normalized polynomial. We have the formula
\[ m(P)=\frac{1}{2\pi}\sum_{z\in \mu^{{-}1}(0,0)} \mathrm{Ind}(z)V(z). \]Proof. This time we will use two different set of arcs: apply Lemma 3.1 so that both 
$\Gamma _{>0}=\mu ^{-1}(\{0\}\times \mathbb {R}_{>0})$ and 
$\Gamma _{<0}=\mu ^{-1}(\{0\}\times \mathbb {R}_{<0})$ are a smooth collection of arcs with monotonic volume on each component. Denote their union by 
$\Gamma$.
Up to applying yet another monomial transformation, we may assume that the slope 
$\gamma$ is never 
$0$ for an isolated or singular point 
$z$ in 
$\mu ^{-1}(0,0)$. Let 
$k$ be the ramification order at 
$z$ of 
$z \mapsto (x,y)$. If 
$\gamma (z)$ is not real, then its contribution to the Mahler measure has already been understood in the proof of Theorem 3.5: it is 
$k\varepsilon V(z) = \text {Ind}(z) V(z)$. The strategy for dealing with the case of 
$\gamma (z)$ real will recover this contribution.
So consider such an isolated or singular point 
$z$ in 
$\mu ^{-1}(0,0)$. Let 
$D_\textrm {real}(z)$ be the number of directions included in the torus, 
$D_{\min }(z)$ the number of minimizing directions, 
$D_{\max }(z)$ the number of maximizing directions, and 
$D_\textrm {mon}(z)$ the number of monotonic directions. Note that the sum of these four numbers is 
$k$ and that if the slope 
$\gamma (z)$ is not real, we have 
$D_{\min }(z) = k$ or 
$D_{\max }(z)=k$ depending on the sign of its imaginary part.
Around the point 
$z$, the set 
$\bar {\Gamma }$ is the union of 
$k-D_\textrm {real}$ curves which split into twice this number of arcs. Indeed, the direction included in the torus is not seen by 
$\Gamma$. Recall that each of these arcs is oriented so that the volume is increasing. Hence, for each minimizing direction, there are two arcs in 
$\Gamma$ leaving 
$z$. Likewise, for each maximizing direction there are two arcs incoming and for each monotonic direction one arc is incoming and the other one leaving. We thus get 
$2D_{\max }+D_\textrm {mon}$ incoming and 
$2D_{\min } + D_\textrm {mon}$ leaving arcs. One may compute which arcs belong to 
$\Gamma _{>0}$ or to 
$\Gamma _{<0}$, but the description becomes intricate and we do not need this additional information.
Indeed, both 
$\Gamma _{>0}$ and 
$\Gamma _{<0}$ may be used to compute the Mahler measure of 
$P$. So we can take into account both computations:
\[ 2\pi m(P) = \frac{1}{2}\Big[V(\partial \overline{\Gamma_{{>}0}})+ V\big(\partial \overline{\Gamma_{{<}0}}\big)\Big]. \]
The contribution of the point 
$z$ to the Mahler measure computed with 
$\Gamma$ is 
${V(z)}/{2}$ times the number of incoming arcs minus the number of leaving arcs. From the previous discussion, this amounts to
\begin{align*} \frac{V(z)}{2} \big( \big(2D_{\max}+D_\textrm{mon}\big) - \big(2D_{\min}+D_\textrm{mon}\big)\big) &= (D_{\max} -D_{\min})V(z)\\ &= \text{Ind}(z)V(z). \end{align*}
Summing over all 
$z$, we get the formula of the theorem.
Arguing as in the regular case, we get the following result.
Theorem 3.15 Let 
$P\in \mathbb {C}[X^{\pm 1},Y^{\pm 1}]$ be an exact polynomial irreducible over 
$\mathbb {C}$ and normalized. Then we have the inequality
\[ 2\pi m(P)\ge \max V-\min V. \]4. Finding exact polynomials
In the previous section we proved a closed formula for the Mahler measure of exact polynomials. We now study more precisely the notion of exact polynomials, proving a finiteness result once the sides of the Newton polygon are fixed.
Choose a polygon 
$\Delta \in \mathbb {R}^{2}$ with integral corners and coefficients 
$c_{i,j}\in \mathbb {C}$ for 
$(i,j)\in \partial \Delta \cap \mathbb {Z}^{2}$ such that the side polynomials constructed from these coefficients have all their roots of modulus 1. Then any choice of coefficients 
$c=(c_{i,j})$ for 
$(i,j)\in \operatorname {Int}{\Delta }\cap \mathbb {Z}^{2}$ gives rise to a tempered polynomial 
$P_c$. The question we address in this section is: for which coefficients is 
$P_c$ exact?
It is well known that generically, the curve 
$\hat {C}_c$ associated to 
$P_c$ is smooth and has genus 
$N=\operatorname {Card} (\operatorname {Int}{\Delta }\cap \mathbb {Z}^{2})$. Hence, the cohomology class of 
$\eta |_{\hat {C}_c}$ belongs to the 
$N$-dimensional space 
$H^{1}(\hat {C}_c)$. Moreover, the period map being analytical, we expect that the 
$N$-dimensional family 
$(P_c)$ is exact only for a finite number of 
$c$.
This is trivial for polygons which have no interior point. In this section we prove it for tempered families of elliptic curves, that is, for polygons with one interior integral point.
Theorem 4.1 Let 
$\Delta$ be a Newton polygon with 
$(0,0)$ as the unique integral interior point and let 
$(c_{i,j})_{(i,j)\in \partial \Delta \cap \mathbb {Z}^{2}}$ be a system of coefficients such that all side polynomials have roots which are simple and of modulus 1. Then, for all but a finite number of values of 
$c\in \mathbb {C}$, the polynomial
\[ P_c=\sum_{(i,j)\in\partial \Delta\cap\mathbb{Z}^{2}}c_{i,j}X^{i}Y^{j} -c \]is exact.
Proof. By Theorem 2.12, if 
$P_c$ is exact, there exist 
$x,y\in \mathbb {C}$ with 
$|x|=|y|=1$ and 
$P(x,y)=0$. As the coefficients 
$c_{i,j}$ are fixed, this implies that 
$c$ lives in a compact set. Let 
$c$ be a regular value of the map 
$P:(\mathbb {C}^{*})^{2}\to \mathbb {C}$ defined by 
$P=\sum _{(i,j)\in \partial \Delta \cap \mathbb {Z}^{2}}c_{i,j}X^{i}Y^{j}$ and 
$C_c$ be its level set 
$\{(x,y) \in (\mathbb {C}^{*})^{2} | P(x,y)=c\}$.
Let 
$[\eta _c]\in H^{1}(\hat {C}_c,\mathbb {R})$ be the cohomology class of the restriction of 
$\eta$ to 
$\hat {C}_c$. There is a neighborhood 
$U$ of 
$c$ such that 
$P$ corestricted to 
$U$ is a trivial fibration. This allows us to define the period map 
$\mathcal {P}:U\to H^{1}(\hat {C}_c,\mathbb {R})$ defined by 
$\mathcal {P}(x)=[\eta _x]\in H^{1}(\hat {C}_x,\mathbb {R})\simeq H^{1}(\hat {C}_c,\mathbb {R})$. The polynomial 
$P_x$ is exact if and only if 
$\mathcal {P}(x)=0$. Hence, if we show that the differential of the period map is invertible at 
$c$, we will conclude that the set of values of 
$c$ for which 
$P_c$ is exact is discrete and hence conclude the proof of the theorem.
We define 
$\omega ={{d} x}/{x}\wedge {{d} y}/{y}$ and 
$X_P$ the Hamiltonian vector field satisfying 
$i_{X_P}\omega =dP$. In coordinates, 
$X_P=xy(\partial _yP\partial _x-\partial _xP\partial _y)$. This vector field is tangent to 
$C_c$ and does not vanish. We denote by 
$\alpha _P$ the holomorphic form satisfying 
$\alpha _P(X_P)=1$. By Lemma 4.2 below, this form is indeed holomorphic on the smooth projective model 
$\hat {C}_c$ which has genus 1 and hence does not vanish. Hence the flow of 
$X_P$ gives the uniformization of 
$\hat {C}_c$.
Consider a smooth family of cycles 
$\delta _t:S^{1}\to C_{c(t)}$ where 
$c(0)=c$ and 
$c'(0)=\lambda$. As 
$d\eta =-\operatorname {Im} \omega$ we have by Stokes's formula 
$\int _{\delta _1}\eta -\int _{\delta _0}\eta =-\int _{S^{1}\times [0,1]}\operatorname {Im}(\delta ^{*}\omega )$. Letting 
$t$ go to 
$0$, we find that
\[ \mathcal{P}'(c)(\delta_0)=\frac{d}{dt}\bigg|_{t=0}\int_{\delta_t}\eta=\int_{\delta_0}\operatorname{Im} (\lambda i_\xi\omega), \]
where 
$\xi$ is a vector field defined on 
$C_c$ such that 
$dP(\xi )=1$.
Take as 
$\delta _0$ a periodic orbit of the flow of 
$X_P$ of period 
$T$. As periods form a lattice in 
$\mathbb {C}$, one can assume that 
$\lambda T$ is not real. We compute 
$\int _{\delta _0} i_\xi \omega =\int \omega (\xi ,X_P)\,dt=\int \,dP(\xi )\,dt=T$. This proves that 
$\mathcal {P}'(c)\ne 0$ and hence the theorem.
Lemma 4.2 Let 
$P\in \mathbb {C}[X^{\pm 1},Y^{\pm 1}]$ be a polynomial with Newton polygon having one integral interior point and whose side polynomials have only simple roots of modulus 
$1$. Suppose that the vanishing locus 
$C$ of 
$P$ on 
$(\mathbb {C}^{*})^{2}$ is smooth and denote by 
$\hat {C}$ its projective model. Then the form 
$\alpha _P$ dual to the Hamiltonian vector field 
$X_P$ of 
$P$ relative to the symplectic form 
$\omega ={{d} x}/{x}\wedge {{d} y}/{y}$ has no pole nor zero on 
$\hat {C}$.
Proof. As 
$dP$ does not vanish on 
$C$, neither does the vector field 
$X_P$. Hence, it is sufficient to show that 
$\alpha _P$ is holomorphic at each ideal point. Up to translations and monomial transformations, one can suppose that the interior point is the origin and the side of 
$\Delta$ we are looking at is 
$i=1$. Hence, we have Newton–Puiseux coordinates 
$x=t^{-1}, y=F(t)$ where 
$\sum _{i=1,j}c_{i,j}F(0)^{j}=0$. One can write 
$\alpha _P={{d}x}/({xy\partial _yP})$. As 
$y\partial _yP=t^{-1}\sum _{i=1,j}c_{i,j}jF(0)^{j}+o(t)$, we get 
$y\partial _yP\sim \beta t^{-1}$ and 
$\alpha _P\sim -dt\beta ^{-1}$ where 
$\beta$ is non-zero, being the derivative of a side polynomial at a simple zero. This proves that 
$\alpha _P$ is regular at the corresponding ideal point.
5. $A$-polynomials
We focus in this section on 
$A$-polynomials as a particular class of exact polynomials. We gather different observations and examples. We first explain that there is an algebraic criterion for being an 
$A$-polynomial which is effective in genus 0. Then we return to the examples given in § 1 (Example 1.4), proving they are 
$A$-polynomials and computing their Mahler measure. We add a few examples of 
$A$-polynomials of cusped hyperbolic 
$3$-manifolds to exhibit different possible behaviors. We then move on to give an interpretation of the Mahler measure of some knot exteriors 
$M$ in terms of ‘lengths’ of the filling geodesic in long Dehn surgeries of 
$M$.
From now on, 
$P$ will be a polynomial over 
$\bar {\mathbb {Q}}$ and often over 
$\mathbb {Z}$.
5.1 A K-theoretic criterion for being an $A$-polynomial
Recall the construction from the introduction: for a 
$3$-manifold 
$M$ with toric boundary, we defined a restriction map 
$r:X(M)\to X(\partial M)$ and a projection 
$\pi : (\mathbb {C}^{*})^{2} \to X(\partial M)$. The 
$A$-polynomial 
$A_M$ is the polynomial whose vanishing locus is 
$\pi ^{-1}\overline {r(X(M))}$.
Definition 5.1 We say that an irreducible polynomial 
$P\in \bar {\mathbb {Q}}[X^{\pm },Y^{\pm }]$ is an 
$A$-factor if there exists a 3-manifold 
$M$ with toric boundary such that 
$P$ is a factor of 
$A_M$.
In the sequel, we will write 
$F_P=\textrm {Frac }\,\bar {\mathbb {Q}}[X^{\pm },Y^{\pm }]/(P)$.
Proposition 5.2 The polynomial 
$P\in \bar {\mathbb {Q}}[X^{\pm },Y^{\pm }]$ is an 
$A$-factor if and only if the Steinberg symbol 
$\{X,Y\}$ vanishes in 
$K_2(F_P)\otimes \mathbb {Q}$.
Proof. Suppose that 
$P$ is a factor of the 
$A$-polynomial of a manifold 
$M$. As the vanishing set of 
$P$ describes a component of 
$\pi ^{-1}\overline {r(X(M))}$, there exists a curve 
$C$ in the representation variety 
$\operatorname {Hom}(\pi _1(M),\mathrm {SL}_2(\bar {\mathbb {Q}}))$ such that 
$\pi ^{-1}r(C)$ is dense in the zero set of 
$P$. Consider 
$E$ the function field of 
$C$: it is a finite extension of 
$F_P$ and there is a tautological representation 
$\rho :\pi _1(M)\to \mathrm {SL}_2(E)$ (see [Reference Cooper, Culler, Gillet, Long and ShalenCCGLS94, Proposition 2.3]). In light of the argument of [Reference Cooper, Culler, Gillet, Long and ShalenCCGLS94, p. 59], it follows that 
$2\{X,Y\}=0$ in 
$K_2(E)$. As the map 
$K_2(F_P)\to K_2(E)$ is injective modulo torsion thanks to the transfer map [Reference WeibelWei13, Corollary 5.6.3], we conclude that 
$\{x,y\}=0\in K_2(F_P)\otimes \mathbb {Q}$.
Reciprocally, suppose that 
$\{X,Y\}=0\in K_2(F_P)\otimes \mathbb {Q}$. Then Matsumoto's theorem [Reference WeibelWei13, Theorem 6.1] shows that 
$K_2(\overline {F_P})=\lim _{\to }K_2(E)$ where 
$E$ ranges over the finite extensions of 
$F_P$. Due to the Bass–Tate theorem [Reference WeibelWei13, Theorem 6.r], this group is divisible, hence 
$2\{X,Y\}=0\in K_2(\overline {F_P})$.
Let 
$\rho :\pi _1(S^{1}\times S^{1})\to \mathrm {SL}_2(\overline {F_P})$ be the representation that sends 
$l$ to the diagonal matrix with entries 
$X,X^{-1}$ and 
$m$ to the diagonal matrix with entries 
$Y,Y^{-1}$. Then 
$\rho _*([S^{1}\times S^{1}])\in H_2(\mathrm {SL}(\overline {F_P}))$ is mapped to 
$2\{X,Y\}=0\in K_2(\overline {F_P})$.
Let us next recall Suslin's stability theorem as explained in [Reference HutchinsonHut16, § 3]. For an infinite field 
$F$, there is a sequence of isomorphisms
\[ H_0(F^{*},H_2(\mathrm{SL}_2(F)))\simeq H_2(\mathrm{SL}_3(F))\simeq \cdots \simeq H_2(\mathrm{SL}(F))=K_2(F). \]
In the first group, the action of 
$\lambda \in F^{*}$ on 
$\mathrm {SL}_2(F)$ is by conjugation with the diagonal matrix with entries 
$(\lambda ,1)$. If 
$F$ is algebraically closed, this action is by interior conjugation, hence trivial on 
$H_2(\mathrm {SL}_2(F))$ and the natural map 
$H_2(\mathrm {SL}_2(F))\to K_2(F)$ is an isomorphism.
It follows that 
$\rho _*([S^{1}\times S^{1}])=0\in H_2(\mathrm {SL}_2(\overline {F_P}))$. Denote by 
$Z$ the classifying space of the (discrete) group 
$\mathrm {SL}_2(\overline {F_P})$. There is a continuous map 
$f:S^{1}\times S^{1}\to Z$ inducing 
$\rho$ on fundamental groups: this map defines a class 
$[S^{1}\times S^{1},f]$ in the bordism group 
$\Omega _2(Z)$. This class vanishes if and only if there exist a 3-manifold 
$M$ with boundary 
$S^{1}\times S^{1}$ and a map 
$F:M\to Z$ extending 
$f$. The map 
$F$ induces on fundamental groups a representation 
$\tilde {\rho }:\pi _1(M)\to \mathrm {SL}_2(\bar {F}_P)$ extending 
$\rho$. As 
$\pi _1(M)$ is finitely generated, this representation actually takes values in 
$\mathrm {SL}_2(E)$ for some finite extension of 
$F_P$. This field is the function field of a curve inside the representation variety of 
$M$ which restricts to the zero set of 
$P$. Hence we are done if we can prove that 
$[S^{1}\times S^{1},f]=0\in \Omega _2(Z)$.
At this point we only know that 
$f_*[S^{1}\times S^{1}]=0\in H_2(Z)$. It is known, however, that there is a spectral sequence (due to Atiyah and Hirzebruch) whose second page is 
$H_p(Z,\Omega _q)$ converging to 
$\Omega _{p+q}(Z)$. As 
$\Omega _{0}=\mathbb {Z}$ and 
$\Omega _n=0$ for 
$n=1,2,3$, it implies that the natural map 
$\Omega _2(Z)\to H_2(Z)$ is an isomorphism, finally proving the claim. We refer to [Reference Liechti and MarchéLM19] for a more elementary and explicit proof.
Hence, it is easy to recognize 
$A$-factors of genus 0 because by the localization formula for 
$K_2$ (see [Reference WeibelWei13, p. 257]), the criterion for being an 
$A$-factor reduces to the condition that all tame symbols 
$\{X,Y\}_z$ are torsion. Thus we get the following corollary.
Corollary 5.3 An irreducible polynomial 
$P\in \bar {\mathbb {Q}}[X^{\pm },Y^{\pm }]$ of genus 
$0$ is an 
$A$-factor if and only if the roots of its side polynomials are roots of unity.
It follows that the polynomials 
$X+Y-1$ and 
$1+X+Y+XY+X^{2}+Y^{2}$ are 
$A$-factors but we do not know to which 3-manifolds they correspond. Indeed, the simplest non-trivial genus 0 
$A$-factor we know is 
$1+iX+iY+XY$ which corresponds to the suspension of a punctured torus over the circle with monodromy 
$\big (\begin {smallmatrix}-1 & -2 \\ -2 & -5\end {smallmatrix}\big )$; see [Reference DunfieldDun99b].
5.2 Examples
We review here some examples of exact polynomials given in § 1 (Example 1.4) and prove that they are indeed 
$A$-polynomials. We then proceed with the computations of their Mahler measure.
5.2.1 $P_1 = X+Y-1$
This example is directly related to the original one of Smyth [Reference SmythSmy81]. On the curve defined by 
$P_1$ we have 
$\{x,y\} = \{x,1-x\} = 0$ in 
$K_2(F_{P_1})$, and the previous proposition shows 
$P_1$ is an 
$A$-factor.
It is easy to see that the volume function on the curve is given by 
$-D(x)$. Indeed, we recognize its differential in the expression
\[ \eta(x,1-x)= \log\! |1-x|d\arg(x) - \log\! |x|d\arg(1-x). \]
Moreover, the only two points of the curve on the torus are given by 
$x = e^{{\pm }{i\pi }/{3}}$. They are the maximum and minimum points of the volume, with the value being plus or minus the volume 
$v_3$ of the regular ideal hyperbolic tetrahedron. This whole discussion is given in [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05] and builds upon a computation by Smyth [Reference SmythSmy81]. In these references, a further number-theoretic description of the Mahler measure is also given.
It is easy to see that the volume above the circle 
$|x|=1$ has no critical points. The Mahler measure is then computed using § 3:
\[ m(P_1) = \frac{v_3}{\pi}. \]5.2.2 $P_2(X,Y) = Y-\phi _5(X)$
This is an instance of examples treated by Boyd and Rodriguez-Villegas [Reference Boyd and Rodriguez-VillegasBR02]. On the curve 
$C_2$ defined by 
$P_2$, we have 
$\{x,y\} = \frac {1}{5}\{x^{5},1-x^{5}\} - \{x,1-x\} = 0$ in 
$K_2(F_{P_2})$ and the previous proposition shows 
$P_2$ is a (factor of) an 
$A$-polynomial.
As before, we see that the function 
$x \to V_2(x) = D(x)-\frac {1}{5} D(x^{5})$ is the volume function. We plot this function above the circle 
$|x|=1$ in Figure 1.
Figure 1. Volume function for 
$P_2(x,y)$ above the circle 
$|x|=1$.
The intersection of 
$C_2$ with the torus 
$|x|=|y|=1$ consists of seven points, corresponding to 
$x=- 1, \pm i, \omega = ({1+i\sqrt {3}})/{2},\omega ^{2},\omega ^{4},\omega ^{5}$. These points are easily spotted on the figure as they correspond to critical points of the volume function. From the figure, it is quite clear that
\[ 2\pi m(P_2) = V_2(\omega) - V_2(i) + V_2(\omega^{2}) - V_2(\omega^{4}) +V_2({-}i) -V_2(\omega^{5}). \]Let us prove this from formula (3.14). The logarithmic Gauss map at these points may be computed:
\[ X\partial_X P_2 ={-}(X+2X^{2}+3X^{3}+4X^{4})\quad \text{and}\quad Y\partial_YP_2 = Y=1+X+X^{2}+X^{3}+X^{4}. \]
We then decide if the point is in 
$\mathbb {P}^{1}_+(\mathbb {C})$, 
$\mathbb {P}^{1}(\mathbb {R})$ or 
$\mathbb {P}^{1}_-(\mathbb {C})$. Table 1 displays the computation of this sign for 
$\omega$, 
$i$, 
$\omega ^{2}$, 
$-1$. The three remaining points 
$\omega ^{4}$, 
$-i$, 
$\omega ^{5}$ are the complex conjugates of 
$\omega$, 
$i$, 
$\omega ^{2}$, so the table is easily filled.
Table 1. Slope of points in the torus.
The sign is in accordance with what is shown on the figure: at a point in 
$\mathbb {P}^{1}_+(\mathbb {C})$, the volume exhibits a local minimum. The point 
$-1$ of real slope is easily discarded in the formula: whatever its index is, its volume vanishes, so it does not contribute to the Mahler measure. Its index is indeed 
$0$: at this point, there is only one maximally tangent curve, which is monotonic.
Using the explicit formula for 
$V_2$, we get
\[ m(P_2) = \frac{2}{5\pi} \big(3D(\omega) +3D(\omega^{2}) - 2D(i)\big). \]5.2.3 $P_3(X,Y) = 1 + X + Y + XY + X^{2} + Y^{2}$
In this example, the curve 
$C_3$ has no real points. However, we know that it must have points on the torus, as 
$P_3$ is exact. Indeed, we find eight such points: 
$(-1,i)$, 
$(-1,-i)$, 
$(i,-1)$, 
$(-i,-1)$, 
$(i,-i)$, 
$(-i,i)$, 
$(\omega ^{2},\omega ^{4})$, 
$(\omega ^{4},\omega ^{2})$. All these points have non-real slope and no ramification, hence, using symmetries and denoting by 
$V_3$ the volume function (which is well defined; see Remark 1.3), we get
\[ 2\pi m(P_3)=4V_3({-}1,-i)+2V_3(i,-i)+2V_3(\omega^{4},\omega^{2}). \]This time, we do not provide an explicit computation using the Bloch–Wigner dilogarithm, although such an expression should exist.
5.2.4 $P_4(X,Y) = 1 + iX + iY + XY$
This example is (almost) already computed in [Reference Boyd, Rodriguez-Villegas and DunfieldBRD05, Example 9]. Here, using the same techniques as described above, we get that 
$\{x,y\} =\{-ix,1+ix\}-\{ix,1-ix\}$ vanishes modulo torsion on the curve defined by 
$P_4$. Moreover, it follows that the volume function is 
$D(ix)-D(-ix)$ for any point 
$(x,y)$ in the curve.
The intersection between the torus and the curve has two points, corresponding to 
$x = {\pm }1$. It is quite straightforward that 
$\pi m(P_4) = 2D(i)$.
5.2.5 A-polynomial of m337
Using Culler's PE [Reference Culler and DunfieldCD17], based on SageMath [Sag17], SnapPy [Reference Culler, Dunfield, Goerner and WeeksCDGW17] and PHCPack [Reference VerscheldeVer99], one can compute the 
$A$-polynomial for the manifold 
$m337$ in SnapPy. It factorizes into two (almost identical) factors, each of bidegree 
$(20,13)$. Note that the curve 
$C$ defined by this 
$A$-polynomial is invariant by change of sign of any variable, by 
$(x,y)\to (1/x,1/y)$ and 
$(x,y)\to (\bar x,\bar y)$, so we prefer to work with the polynomial whose zero set consists of the points 
$(x^{2},y^{2})$, hereafter denoted by 
$P$. The multi-graph of the volume above 
$|x|=1$ (here 
$x$ is the eigenvalue of the meridian for SnapPy) is given by PE and we display it in Figure 2.
Figure 2. Volume function for the 
$A$-polynomial of 
$m337$ above the circle 
$|x|=1$. The horizontal axis is 
$\arg (x)$.
As is quite clear from the figure, the Mahler measure of this polynomial is (up to a factor 
$\pi$) of the form 
$v_1 + v_2 + 2v_3$ where 
$v_1$ and 
$v_2$ are the two positive volumes above 
$x=1$ (i.e. the intersection with the vertical axis in the picture) and 
$v_3$ is the common value of the two local maxima.
The local maximum 
$v_3$ corresponds to an intersection between the curve 
$P=0$ and the torus, which does not lie above 
$x=1$. One can plot this intersection: it has a one-dimensional part and a zero-dimensional part corresponding to the set of singular points of the algebraic curve that sit inside the torus; see Figure 3.
Figure 3. Points on the torus (axes are the arguments of 
$x$ and 
$y$). The singular points, represented by a small disc, are all intersections of one-dimensional branches, but two are isolated.
We then find two singular points outside of the one-dimensional part, of coordinates 
$(x,y)$ where 
$x$ and 
$y$ are both algebraic numbers of degree 
$12$ in the same number field. They are not roots of unity and the number field has five complex places. Note that the two values of 
$x$ are the points where the local maxima in Figure 2 are attained. These two singular points are complex conjugates, so we may just study one of them. We can check, using for example SageMath, that two branches of 
$C$ go through these points: they correspond to two distinct points in 
$\hat C$. We then check that the two slopes are not real and are complex conjugates: this explains the local maximum and the local minimum for the volume above this value of 
$x$. The other singular points inside the torus are easily seen not to contribute to the Mahler measure: at each of these points, there are two maximally tangent directions which are clearly real.
It is possible to express 
$v_1$, 
$v_2$ and 
$v_3$ as sums of dilogarithms of algebraic numbers, solving the gluing equations for 
$m337$. We do not give explicit details here. An approximate value is
\[ \pi m(P) = v_1 + v_2 + 2v_3 = 8.1594511763 \pm 10^{{-}10}. \]5.3 An interpretation of the Mahler measure of the $A$-polynomial
For 
$A\in \mathrm {SL}_2(\mathbb {C})$ we denote by 
$\|A\|$ its spectral radius, that is, the maximal modulus of an eigenvalue of 
$A$.
Definition 5.4 Let 
$M$ be a closed oriented 
$3$-manifold and 
$K$ be a knot in 
$M$. Suppose that the character variety 
$X(M)$ is reduced of dimension 0. Then we set
\[ m(M,K)=\sum_{[\rho]\in X(M)} \log\! \|\rho(K)\|. \] Given an oriented manifold 
$M$ with toric boundary 
$S^{1}\times S^{1}$, we denote by 
$M_{p/q}$ the Dehn surgery with slope 
$p/q$, that is, 
$M_{p/q}=M\cup _\phi D^{2}\times S^{1}$ where 
$\phi :\partial D^{2}\times S^{1}\to \partial M$ is given by 
$\phi (z,1)=(z^{p},z^{q})$. We denote by 
$K_{p/q}$ the knot 
$\{0\}\times S^{1}$ viewed in 
$M_{p/q}$.
Proposition 5.5 Suppose that 
$M$ is a manifold with 
$\partial M=S^{1}\times S^{1}$ and 
$A$-polynomial 
$A_M$ satisfying the following hypotheses.
(i) The restriction map
$r:X(M)\to X(\partial M)$ is birational on its image.(ii) The singular points of
$X(M)$ do not restrict to torsion points in $X(\partial M)$ (i.e. images by $\pi$ of pairs of roots of unity).
Then we have
\[ \lim_{p^{2}+q^{2}\to\infty}m(M_{p/q},K_{p/q})=m(A). \] A theorem of Dunfield states that the first assumption holds for any component of the character variety which contains a lift of a discrete and faithful representation (see [Reference DunfieldDun99a]); notice that we assume implicitly that 
$X(M)$ is irreducible and reduced. This can be weakened as in [Reference Lê and ZhangLZ17]. The roots of the Alexander polynomial of 
$M$ correspond to singular points of 
$X(M)$, hence we assume that this polynomial does not vanish at roots of unity. These hypotheses are already present in [Reference Marché and MaurinMM14] where they serve similar purposes.
Proof. Let 
$p$ and 
$q$ be two relatively prime integers and let 
$\gamma _{p/q}\subset \partial M$ be the curve parametrized by 
$\gamma _{p/q}(z)=(z^{p},z^{q})$. As 
$\pi _1(M_{p/q})=\pi _1(M)/\langle \gamma _{p,q}\rangle$, a representation 
$\rho :\pi _1(M_{p/q})\to \mathrm {SL}_2(\mathbb {C})$ corresponds to a representation 
$\rho :\pi _1(M)\to \mathrm {SL}_2(\mathbb {C})$ such that 
$\rho (\gamma _{p/q})=1$. Denoting by 
$l,m$ the homotopy classes of 
$S^{1}\times \{1\}$ and 
$\{1\}\times S^{1}$ respectively, one can suppose that
\[ \rho(l)=\begin{pmatrix} x & * \\ 0 & x^{{-}1}\end{pmatrix},\quad \rho(m)=\begin{pmatrix} y & * \\ 0 & y^{{-}1}\end{pmatrix} \]
with 
$A(x,y)=0$ and 
$x^{p} y^{q}=1$. If 
$x\ne {\pm }1$ or 
$y\ne {\pm }1$, the pair 
$(x^{-1},y^{-1})$ satisfies the same equation and corresponds to the same representation up to conjugation. Hence we will sum over all solutions of the system 
$A(x,y)=0,x^{p}y^{q}=1$ and divide by 2 afterwards. Reciprocally, to a solution 
$(x,y)$ of this system corresponds generically one representation by the birational assumption. By the second assumption, points where there are more solutions map to non-torsion points, and hence satisfy at most one equation of the form 
$x^{p}y^{q}=1$. Hence, we can neglect them in the limit. We will see that the case where 
$x={\pm }1$ and 
$y={\pm }1$ does not contribute to the result, hence we discard them also.
Now, the core of the torus 
$D^{2}\times S^{1}$ is mapped through 
$\phi$ to a curve of the form 
$K(t)=(t^{r},t^{s})$ where 
$ps-qr=1$. Parametrizing the solutions of 
$x^{p}y^{q}=1$ by setting 
$x=t^{-q},y=t^{p}$, we find that the eigenvalue of 
$\rho (K_{p,q})$ is 
$t$. Hence
\[ m(M_{p/q},K_{p/q})=\frac{1}{2}\sum_{t\ne 0,A(t^{{-}q},t^{p})=0} |\!\log\! |t\|=m(A(t^{{-}q},t^{p})), \]
where 
$m$ denotes the usual Mahler measure. Notice that we packed 
$t$ with 
$t^{-1}$ and used the formula 
$\frac {1}{2}|\!\log\! |t\|+\frac {1}{2}|\!\log\! |t^{-1}\|=\log ^{+}\!|t|+\log ^{+}\!|t^{-1}|$. As 
$p^{2}+q^{2}$ goes to infinity, the integral formula for the Mahler measure shows that this quantity converges to 
$m(A)$ and the conclusion follows.
Acknowledgements
We would like to thank N. Bergeron, G. Calsamiglia, G. Courtois, M. Culler, B. Deroin, E. Falbel, E. Ghys and J. Josi for valuable discussions around this paper. We also thank the anonymous referee for the very careful reading.
