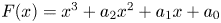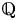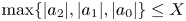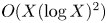1. Introduction
In the 19th century, Hilbert established the so-called Hilbert irreducibility theorem. One version of it can be stated as follows: when ordering degree-
$n$ monic polynomials
\[ f(x) = x^n + a_{1} x^{n-1} + \cdots + a_n, a_i \in {\mathbb{Z}} \quad \text{for } i = 1, \ldots, n \]with the box height
\begin{equation} H(f) = \max\{|a_1|, \ldots, |a_n|\} \end{equation}
a proportion tending to 100 % of such polynomials will be irreducible and have Galois group isomorphic to the symmetric group 
$S_n$.
Hilbert's original proof of his theorem is not quantitative in the sense that it does not give a way to quantify how many degree-
$n$ polynomials of bounded box height fail to have 
$S_n$ as their Galois group. For any transitive subgroup 
$G \leq S_n$ and positive number 
$X \geq 1$, we write
\begin{equation} {\mathcal{N}}_G^{(n)}(X) = \# \{f(x) = x^n + a_1 x^{n-1} + \cdots + a_n \in {\mathbb{Z}}[x], H(f) \leq X, \operatorname{Gal}(f) \cong G\}. \end{equation}Van der Waerden [Reference van der WaerdenvdW36] proved that
\begin{equation} {\mathcal{N}}_{S_n}^{(n)}(X) = (2X)^n + O_n (X^{n - {6}/{((n-2) \log \log n)}}) \end{equation}
for 
$n \geq 3$. He conjectured that one should be able to replace the error term by 
$O_n(X^{n-1})$, which is best possible because the subset of monic polynomials where the constant coefficient vanishes, all of which are reducible, already gives this order of magnitude.
A more precise formulation of van der Waerden's question is to ask whether one can obtain a sharper error term once the obvious reducible polynomials are removed and, indeed, to ask for asymptotic estimates for 
${\mathcal {N}}_G^{(n)}(X)$ when 
$G \ne S_n$.
The simplest case of this question corresponds to 
$n = 3$ and 
$G = C_3$. Such polynomials are called abelian cubics. It is well known that an irreducible cubic polynomial with integer coefficients is abelian if and only if its discriminant is a square integer.
In this paper, we give an estimate for 
${\mathcal {N}}_{C_3}^{(3)}(X)$. We prove the following result.
Theorem 1.1 Let 
$C_3$ be the cyclic group of order three and 
${\mathcal {N}}_{C_3}^{(3)}(X)$ given as in (1.2). Then there exist positive numbers 
$k_1, k_2$ such that for all 
$X > k_2$ we have
\begin{equation} 2X \leq {\mathcal{N}}_{C_3}^{(3)}(X) < k_1 X (\log X)^2. \end{equation} One should compare Theorem 1.1 with the results regarding monic quartic polynomials obtained by Chow and Dietmann [Reference Chow and DietmannCD20]. They proved that 
${\mathcal {N}}_{G}^{(4)}(X) = o(X^{3 - \delta _G} )$ for all transitive proper subgroups 
$G$ of 
$S_4$, where 
$\delta _G$ is a positive number which depends on 
$G$. Most notably they obtained the exact asymptotic order of magnitude (but not an asymptotic formula) for 
${\mathcal {N}}_{D_4}^{(4)}(X)$, namely that
\[ {\mathcal{N}}_{D_4}^{(4)}(X) \asymp X (\log X)^2. \]
They also proved that 
${\mathcal {N}}_{C_3}^{(3)}(X) = O_\varepsilon (X^{3/2 + \varepsilon })$ for any 
$\varepsilon > 0$. Lefton [Reference LeftonLef79] obtained the bound 
$O_\varepsilon (X^{2 + \varepsilon } )$, which narrowly misses the mark when it comes to van der Waerden's conjecture. Two recent results, due to Chow and Dietmann [Reference Chow and DietmannCD21] and Bhargava [Reference BhargavaBha21], are of note. In [Reference Chow and DietmannCD21], the authors gave power-saving bounds for 
$N_G^{(n)}(X)$ for all 
$n \geq 4$, and in [Reference BhargavaBha21] Bhargava resolved van der Waerden's original conjecture by showing that the error term in (1.3) can indeed be taken to be 
$O_n(X^{n-1})$.
Our Theorem 1.1 and Chow and Dietmann's theorem are the only results we are aware of that establishes the exact exponent when counting monic polynomials of degree 
$n \geq 3$ having Galois isomorphic to 
$G$ a proper subgroup of 
$S_n$ with respect to box height.
The upper bound in Theorem 1.1 should be considered the main contribution of this paper. The lower bound is given by a simple and classical construction (see, for example, [Reference StewartSte91]). In view of the upper bound one should ask whether the lower bound or the upper bound is closer to the truth. We note that if we count monic totally reducible cubic polynomials instead, then we achieve the upper bound exactly. Indeed, such polynomials are characterized by triples of integers 
$r_1, r_2, r_3$ by
\[ f(x) = (x - r_1)(x - r_2)(x - r_3) = x - (r_1 + r_2 + r_3)x^2 + (r_1 r_2 + r_1 r_3 + r_2 r_3)x - r_1 r_2 r_3. \]
It is clear that there are 
$O(X)$ such polynomials with at least two of 
$r_1, r_2, r_3 = 0$ and box height at most 
$X$, and 
$O(X \log X)$ such polynomials if exactly one of 
$r_1, r_2, r_3$ is zero. If 
$r_1, r_2, r_3 \ne 0$, then the condition 
$|r_1 r_2 r_3| \leq X$ implies that 
$|r_1 + r_2 + r_3|, |r_1 r_2 + r_1 r_3 + r_2 r_3| \ll X$, so there are 
$O(X (\log X)^2)$ such polynomials. Moreover, it is easy to choose 
$\gg X (\log X)^2$ triples 
$(r_1, r_2, r_3)$ such that 
$f(x)$ has height 
$H(f) \leq X$. If one considers abelian cubics to be comparable to totally reducible cubics, then the upper bound in Theorem 1.1 can be seen as best possible, and quite possibly the exact order of magnitude.
To prove Theorem 1.1 we first need to parametrize monic abelian cubic polynomials. Note that the set of monic cubic polynomials is invariant under translations. The action which sends 
$x \mapsto x + u$ has two basic polynomial invariants, which we denote by 
$I$ and 
$J$, given by
\begin{equation} I(F) = a_2^2 - 3a_1, \quad J(F) = -2a_2^3 + 9a_2 a_1 - 27 a_0, \end{equation}
where 
$F(x) = x^3 + a_2 x^2 + a_1 x + a_0$. It follows that 
$F$ has a unique representation as
\begin{equation} F\biggl(x - \frac{a_2}{3}\biggr) = x^3 - \frac{I(F)}{3} x - \frac{J(F)}{27}. \end{equation} One can interpret this as an action of a subgroup of 
$\operatorname {GL}_2({\mathbb {Z}})$ on the lattice of integral binary cubic forms. For the set of monic binary cubic forms, the natural action given above is realized by the upper triangular subgroup of 
$\operatorname {GL}_2({\mathbb {Z}})$, namely
\[ U({\mathbb{Z}}) = \biggl\{ \begin{pmatrix} 1 & n \\ 0 & 1 \end{pmatrix} : n \in {\mathbb{Z}} \biggr\}. \]
The quantities 
$I(F), J(F)$ given in (1.5) are then invariants with respect to this action. In fact, all polynomial invariants of this action are generated by 
$I,J$.
To prove Theorem 1.1, it is convenient to consider binary cubic forms rather than cubic polynomials. We thus need to parametrize monic binary cubic forms. It is well known that for any monic cubic form that
\begin{equation} \frac{4I(F)^3 - J(F)^2}{27} = \Delta(F). \end{equation}
As an irreducible cubic form 
$F$ is abelian if and only if 
$\Delta (F)$ is a square, it follows that we are required to study integer solutions to the equation
\[ 4z^3 = x^2 + 3y^2. \]
If 
$\gcd (x,y,z) = 1$, then the parametrization is provided in full by Cohen [Reference CohenCoh07]. However, it is not always the case that 
$\gcd (x,y,z) = 1$. We show in § 3 that it suffices to study the equation
\begin{equation} cx^3 = u^2 - uv + v^2,\quad \gcd(x,u) = 1, \end{equation}
where 
$c = c_1^2 - c_1 c_2 + c_2^2$ for 
$c_1, c_2 \in {\mathbb {Z}}$; see Proposition 2.1.
Of course, given the symmetry of (1.8), the roles of 
$u,v$ may be swapped in Proposition 2.1.
Using Proposition 2.1 we obtain the following parametrization of monic abelian cubics given by the shape (1.6).
Theorem 1.2 Let 
$F(x,y) = x^3 + a_2 x^2 y + a_1 xy^2 + a_0 y^3 \in {\mathbb {Z}}[x,y]$ be an irreducible cubic form such that 
$\operatorname {Gal}(F) \cong A_3$. Then 
$(I(F), J(F))$ is given by one of the following three possibilities:
\begin{align} \begin{pmatrix} I(F) \\ J(F) \end{pmatrix} = \begin{pmatrix} 9c(s^2 - st + t^2) \\ 27c((2 c_1 - c_2)s^3 - 3(c_1 + c_2)s^2 t + 3(2c_2 - c_1) st^2 + (2 c_1 - c_2)t^3 ) \end{pmatrix}, \quad \gcd(s,t) = 1, \end{align}
where 
$c = c_1^2 - c_1 c_2 + c_2^2$ and 
$3 \nmid s^2 - st + t^2$,
\begin{equation} \begin{pmatrix} I(F) \\ J(F) \end{pmatrix} = \begin{pmatrix} 3c(s^2 - st + t^2) \\ 27c (c_2 s^3 + (c_1 - 3c_2)s^2 t - c_1 st^2 + c_2 t^3 ) \end{pmatrix}, \quad \gcd(s,t) = 1, \end{equation}
with 
$c = c_1^2 - 3c_1 c_2 + 9c_2^2, 3 \nmid c_1, s^2 - st + t^2$, and
\begin{align} \begin{pmatrix} I(F) \\ J(F) \end{pmatrix} = \begin{pmatrix} c(s^2 - st + t^2) \\ c((2c_1 - 3c_2)s^3 - 3(c_1 + 3c_2)s^2 t + 3(6c_2 - c_1)st^2 + (2c_1 - 3c_2)t^3) \end{pmatrix}, \quad \gcd(s,t) = 1 \end{align}
with 
$c = c_1^2 - 3c_1 c_2 + 9c_2^2, 3 \nmid c_1, s^2 - st + t^2$.
It turns out that a rather convenient way to establish Theorem 1.2 from Proposition 2.1 is to first parametrize binary cubic forms (not necessarily monic) by their Hessian covariants, or in the parlance of [Reference Bhargava and ShnidmanBS14], by their shape; see Proposition 3.1.
A consequence of Proposition 3.1 is that we are able to recover a classical theorem in composition laws of rings and ideals of low rank, namely the correspondence between 
$3$-torsion of class groups of quadratic fields and cubic fields which are nowhere totally ramified (see [Reference BhargavaBha04] for a modern view of this phenomenon through composition laws). Our proof perhaps highlights the phenomenon that the shape (Hessian covariant) of a cubic ring is able to identify certain arithmetic properties. In essence, we replace an explicit algebraic characterization of the map between nowhere totally ramified cubic rings and certain ideal classes of the corresponding quadratic field by identifying a cubic ring with certain integers representable by its Hessian covariant.
The 
$I,J$-invariants can be used to define a height for monic binary cubic forms, which is perhaps more natural than the box height. In [Reference Bhargava and ShankarBS15], Bhargava and Shankar used analogous invariants to define a height on the space of binary quartic forms, which descends to a height on the space of monic binary cubic forms. We denote this height by the Bhargava–Shankar height, given by
\begin{equation} H_{\text{BS}}(F) = \max\{I(F)|^3, J(F)^2/4\}. \end{equation}
Observe that 
$H_{\text {BS}}$ is only well defined for monic binary cubic forms.
When restricted to abelian cubics, and the observation that 
$\Delta (F) = (4I(F)^3 - J(F)^2)/27$, it follows that 
$H_{\text {BS}}(F) = I(F)^3$ for all 
$F$ abelian (because necessarily 
$\Delta (F) > 0$ in this case). We then have the following theorem.
Theorem 1.3 Let 
${\mathcal {M}}_{\text {BS}}(X)$ denote the number of 
$U({\mathbb {Z}})$-equivalence classes of irreducible binary cubic forms with integer coefficients and Galois over 
${\mathbb {Q}}$ with Bhargava–Shankar height bounded by 
$X$. Then
\[ {\mathcal{M}}_{\text{BS}}(X) = \tfrac{3}{2} X^{1/3} \log X + O(X^{1/3}). \] One should compare Theorem 1.3 with the following statement enumerating monic binary cubic forms which are totally reducible over 
${\mathbb {Q}}$. Let 
${\mathcal {M}}_{\text {BS}}^{{\dagger}} (X)$ denote the number of 
$U({\mathbb {Z}})$-equivalence classes of totally reducible binary cubic forms with integer coefficients, ordered by Bhargava–Shankar height. Then we have
\begin{equation} {\mathcal{M}}_{\text{BS}}^{{\dagger}}(X) = c_0 X^{1/3} + O (X^{1/6}) \end{equation}
for some positive number 
$c_0$. We remark that there is a result of Yu [Reference YuYu06] which suggests that there ought to be 
$O_\varepsilon (X^{1/3 + \varepsilon })$ 
$\operatorname {GL}_2({\mathbb {Z}})$-equivalence classes of quartic forms with Galois group 
$V_4$ with Bhargava–Shankar height up to 
$X$. The consequence of Theorem 1.3 suggests that the same should be expected for 
$A_4$-quartic forms.
Another curiosity about elliptic curves that arises from Theorem 1.2 is the following. It is well known that all elliptic curves 
$E/{\mathbb {Q}}$ have a unique minimal Weierstrass model of the shape
\begin{equation} E: y^2 = x^3 - \frac{I}{3}x - \frac{J}{27}, \end{equation}
where 
$(I,J)$ has to satisfy some congruence condition modulo 
$27$. In view of (1.6), it follows that an abelian elliptic curve, or an elliptic curve where the corresponding cubic polynomial is abelian, has 
$(I,J)$ given by Theorem 1.2. Note that an elliptic curve 
$E$ can be semi-stable only if for all primes 
$p$, the corresponding cubic polynomial does not totally ramify. This implies that 
$\gcd (I,J) = 1$. This leads to the following conclusion.
Theorem 1.4 Let 
$E/{\mathbb {Q}}$ be a semi-stable elliptic curve given by the Weierstrass model (1.14). Suppose that the attached cubic polynomial 
$f(x) = x^3 - Ix/3 - J/27$ is an abelian cubic polynomial. Then the splitting field of 
$f$ is 
${\mathbb {Q}}(\zeta _9 + \zeta _9^{-1})$, where 
$\zeta _9$ is a primitive ninth root of unity.
The outline of this paper is as follows. We first prove Proposition 2.1, which is necessary to parametrize our abelian cubic forms. Next, in § 3 we use the Hessian covariant of binary cubic forms to parametrize monic binary cubic forms. Then, using Proposition 2.1, we obtain a parametrization of monic abelian cubic forms. Section 4 contains the proof of Theorem 1.1. Finally, auxiliary algebraic consequences, namely Theorems 6.1 and 1.4, are contained in § 6.
2. Parametrizing points on a family of genus-0 curves
In this section, we solve (1.8) in the following sense.
Proposition 2.1 The integer solutions to (1.8) are parametrized by
\begin{align} x(s,t) &= s^2 - st + t^2,\quad u(s,t) = c_1 s^3 - 3 c_2 s^2 t + 3 (c_2 - c_1)st^2 + c_1 t^3 ,\nonumber\end{align}
\begin{align} v(s,t) &= c_2 s^3 + 3(c_1 - c_2) s^2 t - 3c_1 st^2 + c_2 t^3,\quad s, t \in {\mathbb{Z}},\ \gcd(s,t) = 1\nonumber \end{align}
and ranging over all pairs 
$c_1, c_2 \in {\mathbb {Z}}$ such that 
$c = c_1^2 - c_1 c_2 + c_2^2$.
Proposition 2.1 is a simple consequence of the fact that the ring of Eisenstein integers is a unique factorization domain. This type of structure has been exploited before in similar counting problems; see, for example, [Reference Heath-BrownHea12].
We treat (1.8) as an equation over the Eisenstein integers 
${\mathbb {Z}}[\zeta _3]$, where 
$\zeta _3 = (-1 + \sqrt {-3})/2$. We further factor (1.8) as
\[ (u + \zeta_3 v)(u + \zeta_3^2 v) = (c_1 + \zeta_3 c_2)(c_1 + \zeta_3^2 c_2)(x_1 + \zeta_3 x_2)^3 (x_1 + \zeta_3^2 x_2)^3, \]
where 
$c = c_1^2 - c_1 c_2 + c_2^2$, 
$a = s^2 - st + t^2$. The co-primality of 
$x$ with 
$u,v$ implies that 
$(x_1 + \zeta _3 x_2)^3$ must divide one of 
$u + \zeta _3 v, u + \zeta _3^2 v$. Without loss of generality, we assume that 
$(x_1 + \zeta _3 x_2)^3 | u + \zeta _3 v$ over 
${\mathbb {Z}}[\zeta _3]$. This implies that
\[ u + \zeta_3 v = \zeta_3^k(c_1 + \zeta_3 c_2)(x_1 + \zeta_3 x_2)^3,\quad k \in \{0,1,2\}. \]
We can absorb the 
$\zeta _3^k$ term into 
$c_1 + \zeta _3 c_2$, so it suffices to fix a value of 
$k$. For 
$k = 0$, we obtain the parametrization
\begin{align*} u + \zeta_3 v & = (c_1 + \zeta_3 c_2)(x_1^3 + 3 \zeta_3 x_1^2 x_2 + 3 \zeta_3^2 x_1 x_2^2 + x_2^3) \\ & = (c_1 + \zeta_3 c_2)(x_1^3 + x_2^3 - 3x_1 x_2^2 + 3\zeta_3 x_1 x_2(x_1 -x_2) ) \\ & = (c_1(x_1^3 + x_2^3 - 3x_1 x_2^2) -3 c_2 x_1 x_2 (x_1 - x_2) + \zeta_3(c_2(x_1^3 + x_2^3 - 3x_1^2 x_2 )\\ &\quad + 3c_1x_1 x_2 (x_1 - x_2))). \end{align*}Comparing coefficients we obtain that
\[ v = c_2 x_1^3 + 3 (c_1 - c_2) x_1^2 x_2 - 3c_1 x_1 x_2^2 + c_2 x_2^3 \]and
\[ u = c_1 x_1^3 - 3c_2 x_1^2 x_2 + 3(c_2 - c_1)x_1 x_2^2 + c_1 x_2^3. \]
The co-primality of 
$x$ and 
$u,v$ implies that 
$\gcd (x_1, x_2) = 1$. This completes the proof of the proposition.
3. Standard form of monic binary cubic forms and Hessian covariants
For a given binary cubic form
\[ F(x,y) = a_3 x^3 + a_2 x^2y + a_1 xy^2 + a_0 y^3, \]
define the Hessian covariant of 
$F$ to be
\[ H_F(x,y) = \frac{1}{4} \det \begin{pmatrix} \dfrac{\partial^2 F}{\partial x^2} & \dfrac{\partial^2 F}{\partial x \partial y}\\ \dfrac{\partial^2 F}{\partial x \partial y} & \dfrac{\partial^2 F}{\partial y^2} \end{pmatrix}. \]Explicitly, we have
\begin{equation} H_F(x,y) = (a_2^2 - 3 a_3 a_1)x^2 + (a_2 a_1 - 9 a_3 a_0)xy + (a_1^2 - 3 a_2 a_0)y^2 = Ax^2 + Bxy + Cy^2. \end{equation}
For a binary quadratic form 
$g(x,y) = ax^2 + bxy + cy^2$, we define
\[ V_g({\mathbb{C}}) = \{F(x,y) = a_3 x^3 + a_2 x^2 y + a_1 xy^2 + a_0 y^3 : H_F(x,y)\ \text{is proportional to } g(x,y)\}. \]We have the following result.
Proposition 3.1 Let 
$g(x,y) = ax^2 + bxy + cy^2 \in {\mathbb {C}}[x,y]$ be a non-singular binary quadratic form with 
$a \ne 0$. Then
\begin{equation} V_g({\mathbb{C}}) = \biggl\{a_3 x^3 + a_2 x^2 y + \frac{ba_2 - 3ca_3}{a} xy^2 + \frac{(b^2 - ac)a_2 - 3bc a_3}{3a^2} y^3 : a_3, a_2 \in {\mathbb{C}} \biggr\}.\end{equation}This fact appears well known; see, for example, [Reference Bhargava and ShnidmanBS14]. Nevertheless we give a proof of it for completeness.
Proof. We recall notation from [Reference XiaoXia19], where we dealt with the so-called Hooley matrix:
\[ \mathcal{H}_F = \frac{1}{2 \Delta(H_F)} \begin{pmatrix} B \sqrt{-3\Delta(H_F)} - \Delta(H_F) & 2 C \sqrt{-3\Delta(H_F)} \\ -2A \sqrt{-3\Delta(H_F)} & -B \sqrt{-3\Delta(H_F)} - \Delta(H_F) \end{pmatrix}, \]
where 
$A,B,C$ are as in (3.1). It was shown by Hooley in [Reference HooleyHoo00] that 
$\mathcal {H}_F$ is a stabilizer of 
$F$ with respect to the substitution action of 
$\operatorname {GL}_2$. Moreover, it was shown in [Reference XiaoXia19] that for a given binary quadratic form 
$g(x,y) = ax^2 + bxy + cy^2$ with real coefficients and non-zero discriminant and associated matrix
\[ \mathcal{H}_g = \frac{1}{2 \Delta(g)} \begin{pmatrix} b \sqrt{-3\Delta(g)} - \Delta(g) & 2 c \sqrt{-3\Delta(g)} \\ -2a \sqrt{-3\Delta(g)} & -b \sqrt{-3\Delta(g)} - \Delta(g) \end{pmatrix}, \]
that 
$\mathcal {H}_g \in \operatorname {Aut}_{\mathbb {R}} (F)$ if and only if 
$g$ is proportional to 
$H_F$. Here 
$\operatorname {Aut}_{\mathbb {R}}(F)$ refers to the stabilizer subgroup of 
$F$ in 
$\operatorname {GL}_2({\mathbb {R}})$ corresponding to the substitution action. Using this, one checks through explicit calculation that 
$H_F$ is proportional to 
$g$ if and only if 
$F$ is given as in (3.2). Similarly, that any element 
$F \in V_g({\mathbb {C}})$ does indeed have Hessian covariant proportional to 
$g$ is easily checked.
Remark 3.2 One can also prove Proposition 3.1 by observing that every binary cubic form 
$F$ with non-zero discriminant is 
$\operatorname {GL}_2({\mathbb {C}})$-equivalent to 
$xy(x+y)$.
Remark 3.3 Bhargava and Shnidman gave a slightly different form of the set 
$V_g({\mathbb {C}})$ given in (3.2). Indeed, 
$V_g({\mathbb {C}})$ corresponds to cubic forms of a given shape 
$g$.
We now focus on monic binary cubic forms. Let 
$g(x,y)$ be the primitive integral binary quadratic form proportional to 
$H_F$. As 
$\Delta (H_F) = -3 \Delta (F)$, it follows that 
$3 | \Delta (g)$ whenever 
$\Delta (F)$ is a square. As 
$H_F$ is a covariant of 
$F$, it follows that 
$g$ is also a covariant of 
$F$. Applying the transformation in the lemma to 
$g$ shows that 
$9g(x+vy, y) \in {\mathbb {Z}}[x,y]$.
Without loss of generality, we first translate 
$F$ by an integer, which enables us to assume that 
$a_2 \in \{-1,0,1\}$. We then further translate so that 
$F$ is of the form (1.6). Let 
$g(x,y) = ax^2 + bxy + cy^2$ be a primitive, integral binary quadratic form such that 
$H_F$ is proportional to 
$g$. It then follows from Proposition 3.1 that
\begin{equation} F(x,y) = x^3 - \frac{3c}{a}xy^2 - \frac{bc}{a^2} y^3. \end{equation}
Comparing (1.6) and (3.3), we see that if 
$F \in {\mathbb {Z}}[x,y]$, then 
$I(F), J(F) \in {\mathbb {Z}}$, and either 
$a_2 \equiv 0 \pmod {3}$ so 
$I(F) \equiv 0 \pmod {3}, J(F) \equiv 0 \pmod {27}$ or
\[ I(F) \equiv 1 \pmod{3}, \quad J(F) \equiv (\pm 1)(2 - 9a_1) \pmod{27}. \]
Observe that 
$9a_1 \equiv 0, 9, 18 \pmod {27}$, so 
$(\pm 1)(9 a_1 - 2) \equiv \pm 2, \pm 7, \pm 16 \pmod {27}$. Next we see that
\[ \frac{9c}{a}, \frac{27bc}{a^2} \in {\mathbb{Z}}. \]
Put 
$a = 3^k \alpha$, with 
$\gcd (\alpha, 3) = 1$. We then see that 
$\alpha | c$. As 
$g$ is assumed to be primitive, it follows that 
$\gcd (\alpha, b) = 1$. It thus follows that 
$\alpha ^2 | c$. As observed earlier, we have that 
$3 | \Delta (g)$. Thus, if 
$k \geq 1$, then 
$3 | b$ and, hence, 
$3 \nmid c$. It follows that 
$k \leq 2$.
We first treat the case when 
$k = 0$. Then we have 
$c = a^2 c^\prime$ for 
$c^\prime \in {\mathbb {Z}}$. It then follows that
\begin{equation} F(x,y) = x^3 - 3a c xy^2 - b c y^3, \quad \gcd(a,b) = 1. \end{equation}
We then see that 
$9c^\prime =\ \gcd (I(F), J(F))$. If 
$k = 1$, then we rewrite 
$(a,b,c)$ as 
$(3\alpha, 3 \beta, \alpha ^2 \gamma )$, with 
$3 \nmid \alpha$. Then we see
\[ F(x,y) = x^3 - \alpha \gamma xy^2 - \frac{\beta \gamma}{3} y^3,\quad \gcd(\alpha,\beta) = 1. \]
In this case we have 
$J(F) = 9\beta \gamma$, so, in fact, 
$J(F) \equiv 0 \pmod {27}$. As 
$3 \nmid \gamma$ it follows that 
$3 | \beta$, whence 
$9 | b$. We thus obtain the shape
\begin{equation} F(x,y) = x^3 - ac xy^2 - bc y^3,\quad \gcd(a,b) = 1. \end{equation}
Finally, if 
$k = 2$, then we obtain
\begin{equation} F(x,y) = x^3 - \frac{ac}{3} xy^2 - \frac{bc}{27}y^3, \quad \gcd(a,b) = 1. \end{equation}Comparing (3.4), (3.5), and (3.6) with (1.6) gives
\begin{equation} (I,J) = \begin{cases} (9ac, 27bc), 3 \nmid a, \quad & \gcd(a,b) = 1 \\ (3ac, 9bc), 3 \nmid a, \quad & \gcd(a,b) = 1 \\ (ac, bc), 3 \nmid a, \quad & \gcd(a,b) = 1. \end{cases} \end{equation}
Then it is easy to see that 
$\Delta (F)$ for 
$F$ given as in (3.4), (3.5), and (3.6) is given by
\begin{equation} \Delta(F) = \begin{cases} 27c^2(4ca^3 - b^2) & \text{if } F \text{ is given by (3.4)} \\ c^2(4ca^3 - 27b^2) & \text{if } F \text{ is given by (3.5)} \\ \dfrac{c^2(4ca^3 - b^2)}{27} & \text{if } F \text{ is given by (3.6)}.\end{cases} \end{equation}Using (3.8), we can write out all abelian cubic forms of the shape (1.6) which is a translate of an integral form. In each of the cases in (3.8) we have an equation of the form
\begin{equation} 4ca^3 = u^2 + 3v^2,\quad u,v \in {\mathbb{Z}},\ \gcd(a,u) = \gcd(a,v) = 1. \end{equation}
Note that the right-hand side is a norm in 
${\mathbb {Z}}[\zeta _3]$, hence the left-hand side must be as well. If 
$c$ is a norm in 
${\mathbb {Z}}[\zeta _3]$, then we are done. Otherwise, there must exist a prime 
$p$ which is not a norm in 
${\mathbb {Z}}[\zeta _3]$ and which divides 
$c$ with odd multiplicity. It follows that 
$p$ also divides 
$a$, and 
$p | u,v$. However, then 
$a$ is not co-prime to 
$u,v$, contradicting our assumption. Thus, 
$c$ must be a norm in 
${\mathbb {Z}}[\zeta _3]$.
We aim to obtain a parametrized set of solutions for this equation, following [Reference CohenCoh07]. First we massage (3.9). Note that 
$u^2 + 3v^2 = (u - v)^2 - (u - v)(-2v) + (2v)^2$. Put 
$u_1 = u - v, v_1 = -2v$, so that (3.9) becomes 
$4ca^3 = u_1^2 - u_1 v_1 + v_1^2$. Observe that, by definition, 
$v_1$ is even, thus the right-hand side can be even if and only if 
$u_1$ is even. Now put 
$u_1 = 2x$ and 
$y = -v$, to obtain 
$ca^3 = x^2 - xy + y^2$, which is equivalent to (1.8). We may then proceed with the proof of Theorem 1.2.
3.1 Proof of Theorem 1.2
We unwrap (3.8) and Proposition 2.1 to obtain the desired parametrization. In the first case, we have
\begin{equation} 4ca^3 = b^2 + 3n^2,\quad n \in {\mathbb{Z}}. \end{equation}We then see that
\begin{align*} b(s,t) & = 2(c_1 s^3 - 3 c_2 s^2 t + 3 (c_2 - c_1)st^2 + c_1 t^3 ) - c_2 s^3 - 3(c_1 - c_2) s^2 t + 3c_1 st^2 - c_2 t^3 \\ & = (2 c_1 - c_2)s^3 - 3(c_1 + c_2)s^2 t + 3(2c_2 - c_1) st^2 + (2 c_1 - c_2)t^3 \end{align*}
for some 
$c_1, c_2$ such that 
$c = c_1^2 - c_1 c_2 + c_2^2$. In the second case, we have
\[ 4ca^3 = 3b^2 + n^2,\quad n \in {\mathbb{Z}}, \]whence
\[ b(s,t) = c_2 s^3 + 3(c_1 - c_2)s^2 t - 3c_1 st^2 + c_2 t^3, \quad c = c_1^2 - c_1 c_2 + c_2^2. \]
However, in this case more needs to be said. As 
$I(F) \equiv 0 \pmod {3}$, it follows that 
$J(F) \equiv 0 \pmod {27}$. However, this implies that 
$bc \equiv 0 \pmod {3}$. We had already deduced that 
$3 \nmid c$ in this case, so we must have 
$b \equiv 0 \pmod {3}$. Note that 
$b(s,t) \equiv c_2(s^3 + t^3) \pmod {3}$. If 
$c_2 \not \equiv 0 \pmod {3}$, then 
$s^3 + t^3 \equiv 0 \pmod {3}$. This implies that 
$n \equiv 0 \pmod {3}$, and because 
$3 \nmid c$, that 
$a \equiv 0 \pmod {3}$. This violates the fact that 
$\gcd (a,b) = 1$, whence 
$c_2 \equiv 0 \pmod {3}$.
Finally, suppose that the third case in (3.8) occurs. Then once again we have
\begin{align*} a(s,t) &= s^2 - st + t^2, b(s,t) = (2 c_1 - c_2)s^3 - 3(c_1 + c_2)s^2 t \\ &\quad +3(2c_2 - c_1) st^2 + (2 c_1 - c_2)t^3, \quad s, t \in {\mathbb{Z}},\ \gcd(s,t) = 1. \end{align*}However, now we need to impose an additional congruence relation, on
\[ n(s,t) = c_2 s^3 + 3(c_1 - c_2)s^2 t - 3c_1 st^2 + c_2 t^3. \]
Indeed, we must have 
$n(s,t) \equiv 0 \pmod {3}$. For the same reasons as in the previous case, we conclude that 
$c_2 \equiv 0 \pmod {3}$.
4. Counting monic abelian cubics by box height
In this section, we count monic, abelian cubics by the naive box height. Although the arguments given in this section are elementary, it is worthwhile to give a short description of the strategy to be carried out.
By Theorem 1.2, each monic abelian cubic form can be put into a standard form with vanishing 
$x^2y$-coefficient. Our strategy is to first count monic forms of this shape, and then see which admit at least one translation 
$x \mapsto x + u/3$ with the property that the translated form has box height bounded by 
$X$.
It turns out when we fix 
$\gcd (I,J)$, the above condition turns into a question of counting integer solutions to
\[ N(x_1, x_2, x_3) \leq X, \]
where 
$N$ is a cubic decomposable form. This immediately shows that for a fixed value of 
$c = \gcd (I,J)$ the corresponding number of cubics is 
$O_c(X (\log X)^2)$.
To deal with varying (and possibly very large) values of 
$c$, we consider ranges of 
$a,c$ separately; that is, we restrict 
$a,c$ to distinct dyadic ranges, say
\[ T_1 < a \leq 2T_1, \quad T_2 < c \leq 2 T_2. \]
Our box height condition implies that 
$ac \ll X^2$, so naturally 
$T_1 T_2 \ll X^2$. We then devise arguments to deal with each relevant range of 
$T_1, T_2$.
We consider the first case of (3.8); the other two cases being similar. We look for the number of 
$u \in {\mathbb {Q}}$ with 
$3u \in {\mathbb {Z}}$ such that the translated polynomial
\[ F_u(x) = (x - u)^3 - 3ac(x-u) - bc = x^3 - 3ux^2 + 3(u^2 - ac)x - (u^3 - 3acu + bc) \]
satisfies 
$H(F_u) \leq X$. Suppose that 
$c = c_1^2 - c_1 c_2 + c_2^2$. By Theorem 1.2, we have
$$\begin{gather} a = s^2 - st + t^2,\quad b = (2c_1 - c_2)s^3 - 3(c_1 + c_2)s^2 t + 3 (2c_2 - c_1)st^2 + (2c_1 - c_2)t^3, \end{gather}$$
\begin{gather}n = - c_2 s^3 - 3(c_1 - c_2)s^2 t + 3c_1 st^2 - c_2 t^3.\nonumber\end{gather}
It follows that the constant coefficient of 
$F_u(x)$ is given by
\begin{align} {\mathcal{G}}_{c_1,c_2}(u,s,t) &= -u^3 + 3c(s^2 - st + t^2)u + c((2c_1 - c_2)s^3 - 3(c_1 + c_2)s^2 t \nonumber\\ &\quad + 3 (2c_2 - c_1)st^2 + (2c_1 - c_2)t^3). \end{align}One then checks that
\begin{align} H_{{\mathcal{G}}_{c_1,c_2}}(u,s,t) &= \frac{1}{3} \begin{vmatrix} \dfrac{\partial^2 {\mathcal{G}}}{\partial u^2} & \dfrac{\partial^2 {\mathcal{G}}}{\partial u \partial s} & \dfrac{\partial^2 {\mathcal{G}}}{\partial u \partial t} \\ \dfrac{\partial^2 {\mathcal{G}}}{\partial u \partial s} & \dfrac{\partial^2 {\mathcal{G}}}{\partial s^2} & \dfrac{\partial^2 {\mathcal{G}}}{\partial s \partial t} \\ \dfrac{\partial^2 {\mathcal{G}}}{\partial u \partial t} & \dfrac{\partial^2 {\mathcal{G}}}{\partial s \partial t} & \dfrac{\partial^2 {\mathcal{G}}}{\partial t^2} \end{vmatrix} \nonumber\\ & = 54c{\mathcal{G}}_{c_1,c_2}(u,s,t). \end{align} In other words, 
$H_{{\mathcal {G}}_{c_1,c_2}}$ is proportional to 
${\mathcal {G}}_{c_1,c_2}$. The following lemma implies that 
${\mathcal {G}}_{c_1,c_2}$ is a decomposable form; that is, it splits into a product of three linear forms over 
${\mathbb {C}}$. This fact is well known; see, for example, Theorem 1 in [Reference BrookfieldBro16] for a modern reference.
Lemma 4.1 Let 
$G(x_1, x_2, x_3) \in {\mathbb {C}}[x_1, x_2, x_3]$ be a ternary cubic form which does not have a square linear factor. Then 
$G$ is the product of three linear forms if and only if 
$G$ is proportional to its Hessian 
$H_G$.
Proof. Recall that the intersection points of the cubic curve 
$C_G$ in 
${\mathbb {P}}^2({\mathbb {C}})$ defined by 
$G = 0$ with the curve defined by 
$H_G = 0$ are exactly the inflection points of 
$C_G$. If 
$G$ is proportional to 
$H_G$, then these two curves are identical, so every point of 
$C_G$ is an inflection point. This implies that every component of 
$C_G$ is a line. The converse follows easily by explicit calculation.
In fact, it is easily checked that 
${\mathcal {G}}_{c_1,c_2}(u,s,t)$ must necessarily split over 
${\mathbb {R}}$.
4.1 Proof of the upper bound in Theorem 1.1
We consider dyadic ranges for 
$a,c$. In particular, we suppose that
\begin{equation} T_1 < c \leq 2T_1, \quad T_2 < a \leq 2T_2, \end{equation}
satisfying 
$T_1 T_2 \ll X^2$. We note the fact that there must exist 
$u \in {\mathbb {Q}}$ with 
$3u \in {\mathbb {Z}}$ such that
\begin{equation} 3|u^2 - ac|,\quad |u^3 - 3acu - bc| \leq X. \end{equation}
Put 
$N(T_1, T_2)$ for the number of quintuples 
$(u, c_1, c_2, s, t)$ which satisfies (4.5).
We view the expression
\begin{equation} f(u) = u^3 - 3acu + bc \end{equation}
as a polynomial in 
$u$. By assumption, it has positive discriminant. We then use the cubic equation for cubic polynomials with positive discriminant. The following formula is given in [Reference WeissteinWei].
Lemma 4.2 (Cubic formula for cubic polynomials with three real roots)
Let 
${f(x) = x^3 - 3px + q}$ be a real polynomial with three distinct real roots, so that 
$p > 0$. Then the roots 
$r_1, r_2, r_3$ of 
$f$ are given by
\[ r_1 = 2p^{1/2} \cos\biggl(\frac{\theta}{3}\biggr), \quad r_2 = 2p^{1/2} \cos \biggl(\frac{\theta + 2 \pi}{3}\biggr), \quad r_3 = 2p^{1/2} \cos \biggl(\frac{\theta + 4 \pi}{3}\biggr), \]where
\[ \theta = \arccos \biggl(\frac{q}{2p^{3/2}}\biggr). \] We write the form 
${\mathcal {G}}_{c_1,c_2}(u,s,t)$ given by (4.2) as
\begin{equation} {\mathcal{G}}_{c_1, c_2}(u,s,t) = (u - \xi_1 s - \xi_2 t)(u - \xi_2 s + (\xi_1 + \xi_2) t)(u + (\xi_1 + \xi_2)s - \xi_1 t ) = L_1 L_2 L_3. \end{equation}
say, with 
$\xi _1, \xi _2 \in \overline {{\mathbb {Q}}} \cap {\mathbb {R}}$. Note that
\[ \xi_1 \xi_2 (\xi_1 + \xi_2) = c(2c_1 - c_2) \asymp T_1^{3/2}, \]
hence 
$\xi _1, \xi _2 \ll T_1^{1/2}$.
We proceed to show that very small values of 
$T_1, T_2$ do not cause any issues.
Lemma 4.3 Suppose that 
$T_1 T_2 \ll X^{2/3}$. Then 
$N(T_1, T_2) \ll X$.
Proof. The proof follows easily from the observation that the number of possible choices for 
$u$ is 
$O(X^{1/3})$.
For the following, we assume that 
$T_1 T_2 \gg X^{2/3}$.
We consider 
$u$ in a dyadic interval 
$(Y/2, Y]$ for some 
$Y \ll X$. We show that when 
$Y$ is appreciably larger or smaller than 
$\sqrt {T_1 T_2}$, then the contribution to 
$N(T_1, T_2)$ will be negligible. Indeed, if 
$Y$ is much smaller or larger than 
$\sqrt {T_1 T_2}$, then
\[ L_i(u,s,t) \gg \max \{Y, \sqrt{T_1 T_2} \} \gg \sqrt{T_1 T_2} \]
for 
$i = 1,2,3$. Hence
\[ (T_1 T_2)^{3/2} \ll |{\mathcal{G}}_{c_1, c_2}(u,s,t)| \leq X, \]
which implies that 
$T_1 T_2 \ll X^{2/3}$ and we are done by Lemma 4.3. We may, thus, assume that 
$Y \asymp \sqrt {T_1 T_2}$.
For a given quintuple 
$(u, c_1, c_2, s, t)$ we order the linear factors 
$L_1, L_2, L_3$ by
\[ |L_1| \leq |L_2| \leq |L_3|. \]
If 
$|L_1| \gg \sqrt {T_1 T_2}$, then we see that 
$T_1 T_2 \ll X^{2/3}$ and again we are done by Lemma 4.3. Hence, we may assume that 
$|L_1| = o(\sqrt {T_1 T_2})$. Note that we must have 
$|L_3| \gg \sqrt {T_1 T_2}$. These observations imply that
\[ \biggl\lvert \frac{\partial}{\partial u} {\mathcal{G}}_{c_1, c_2}(u,s,t) \biggr\rvert = \lvert L_1 L_2 + L_1 L_3 + L_2 L_3 \rvert \gg \lvert L_2 L_3 \rvert, \]whence
\[ |L_2| \ll \frac{X}{\sqrt{T_1 T_2}}. \]Put
\[ L_i(u,s,t) = u - \ell_i(s,t), \quad i = 1,2,3. \]
The binary cubic form 
$n_{c_1, c_2}(s,t)$ is precisely given by
\[ c n_{c_1, c_2}(s,t) = (\ell_1(s,t) - \ell_2(s,t))(\ell_1(s,t) - \ell_3(s,t))(\ell_2(s,t) - \ell_3(s,t)). \]
As 
$\ell _i - \ell _j = L_i - L_j$ for 
$1 \leq i < j \leq 3$, it follows that 
$|\ell _1 - \ell _2| = |L_1 - L_2| \ll X (T_1 T_2)^{-1/2}$ and 
$|\ell _1 - \ell _3|, |\ell _2 - \ell _3| \asymp \sqrt {T_1 T_2}$. Hence,
\begin{equation} c \cdot n_{c_1, c_2}(s,t) \ll X \sqrt{T_1 T_2}. \end{equation}Next let us put
\[ f_{\pm X}(u) = u^3 - 3acu - bc \pm X \]
and let 
$r_i^\pm$ be the corresponding roots of 
$f_{\pm X}$. The possible solutions 
$u$ to (4.5) given 
$c_1, c_2, s,t$ then lie in the three intervals
\[ [r_1^{-}, r_1^{+}], \quad [r_2^{-}, r_2^+], \quad [r_3^-, r_3^+]. \]Note that these intervals need not be disjoint. Typically, we expect that these intervals are very short: the only exception is when
\[ \theta = \arccos\biggl(\frac{bc}{2(ac)^{3/2}}\biggr) \]given as in Lemma 4.2 is very close to zero. We quantify this by writing
\[ \frac{bc}{2(ac)^{3/2}} = 1 - \frac{\eta}{2(ac)^{3/2}}. \]This implies that
\begin{align*} \cos \theta & = 1 - \frac{\theta^2}{2} + O(\theta^4) \\ & = 1 - \frac{\eta}{2(ac)^{3/2}}, \end{align*}which shows that
\[ \theta^2 + O(\theta^4) = \frac{\eta}{(ac)^{3/2}}. \]
This bound is trivial if 
$\eta (ac)^{-3/2} \gg 1$ but measures how close 
$\theta$ is to zero when 
$\eta = o((ac)^{3/2})$.
We now note that, by (4.8), 
$\theta$ will be very close to zero if 
$T_1 T_2 \gg X$.
Lemma 4.4 Suppose that 
$T_1 T_2 \gg X$ and let 
$f(x)$ be given as in (4.6). Then 
$\theta$, defined as in Lemma 4.2, satisfies 
$\theta = O (X/T_1 T_2 )$.
Proof. We consider 
$n = n_{c_1, c_2}(s,t)$ in the equation
\begin{equation} 4ca^3 = b^2 + 3n^2 \end{equation}
and factoring over 
${\mathbb {Z}}[\sqrt {-3}]$, we write the right-hand side as
\[ (b + n \sqrt{-3})(b - n \sqrt{-3}). \]Viewing the first vector as a complex number and expressing it in polar coordinates, we see that
\[ b + n \sqrt{-3} = 2(ca^3)^{1/2} e^{i \theta} \]
with 
$\theta$ as in the statement of the lemma. Further, we have
\[ n = \frac{2(ca^3)^{1/2}}{\sqrt{3}} \sin(\theta). \]
By our bounds on 
$n$ given in (4.8) we see that
\begin{equation} \sin(\theta) = O \biggl(\frac{X \sqrt{T_1 T_2}}{(T_1 T_2)^{3/2}} \biggr) = O \biggl(\frac{X}{T_1 T_2}\biggr). \end{equation}
By looking at the Taylor expansion of 
$\sin (\theta )$ around 
$0$ we conclude that 
$\theta = O(X (T_1 T_2)^{-1} )$, as desired.
In particular, Lemma 4.4 implies that whenever 
$T_1 T_2 \gg X$, we have 
$\eta /(ac)^{3/2} \ll 1$.
We first assume that 
$\eta /(ac)^{3/2} \gg 1$, and so 
$T_1 T_2 \ll X$. In this case, we see that 
$\theta$ is bounded away from zero. We expand the series of
\[ \cos\biggl(\frac{\theta}{3}\biggr), \quad \sin \biggl(\frac{\theta}{3}\biggr) \]and note that
\[ \cos(\alpha + 2\pi/3) = \frac{-1}{2} \cos \alpha - \frac{\sqrt{3}}{2} \sin \alpha, \quad \cos(\alpha + 4\pi/3) = \frac{-1}{2} \cos \alpha + \frac{\sqrt{3}}{2} \sin \alpha. \]If we write
\[ \theta_{\sharp} = \arccos \biggl(\frac{bc + X}{2(ac)^{3/2}} \biggr) \quad \text{and} \quad \theta_{\flat} = \arccos \biggl(\frac{bc - X}{2(ac)^{3/2}} \biggr), \]we see that
\begin{equation} \cos\biggl(\frac{\theta_{\sharp}}{3}\biggr) - \cos\biggl(\frac{\theta_{\flat}}{3}\biggr) = O (\lvert \theta_\sharp - \theta_\flat \rvert ) = O \biggl(\frac{X}{(ac)^{3/2}}\biggr), \end{equation}
because 
$\max \{\theta _\sharp, \theta _\flat \} \gg 1$. Similarly, 
$|\sin (\theta _\sharp /3) - \sin (\theta _\flat /3)| = O(X/(ac)^{3/2})$ and by Lemma 4.2 we conclude that 
$u$ must lie in a union of three intervals each having length 
$O (X (T_1 T_2)^{-1} )$. This immediately shows that
\begin{equation} \sum_{T_1 T_2 \ll X} N^{{\dagger}}(T_1, T_2) \ll \sum_{T_1 T_2 \ll X} T_1 T_2 = O(X \log X), \end{equation}
where the 
${{\dagger}}$ indicates only those 
$(c_1, c_2, s, t)$ for which 
$\eta /(ac)^{3/2} \gg 1$ are counted. Here we used the trivial bound 
$O(T_1 T_2)$ to count such 
$(c_1, c_2, s,t)$ and for each such quadruple with 
$\eta /(ac)^{3/2} \gg 1$ there are 
$O(X (T_1 T_2)^{-1} + 1)$ possibilities for 
$u$.
We now turn our attention to the case when 
$\eta /(ac)^{3/2} \ll 1$ (but with no restriction on the size of 
$T_1 T_2$). In this case, we note that (4.11) still holds, because
\[ \theta_\sharp^2 - \theta_\flat^2 = O \biggl(\frac{((\eta + X)^{1/2} - (\eta - X)^{1/2})(\eta^{1/2}) }{(T_1 T_2)^{3/2}} \biggr) = O\biggl(\frac{X}{(T_1 T_2)^{3/2}}\biggr). \]Hence, we see
\begin{align*} \biggl\lvert \cos\biggl(\frac{\theta_\sharp + 2\pi}{3} \biggr) - \cos \biggl(\frac{\theta_\flat + 2 \pi}{3}\biggr) \biggr\rvert & = O \biggl(\frac{X}{(T_1 T_2)^{3/2}}\biggr) + \frac{|\theta_\sharp - \theta_\flat|}{2 \sqrt{3}} + O (|\theta_\sharp - \theta_\flat|^3 )\\ & \asymp \frac{X}{\eta^{1/2} (T_1 T_2)^{3/4}}. \end{align*}
If 
$\eta$ is much smaller than 
$X$, then we no longer have disjoint intervals, and the longest interval has length 
$O (X^{1/2}/(T_1 T_2)^{1/4} )$. We see then that the number of possible 
$u$ is
\begin{equation} \begin{cases} O\biggl(\dfrac{X}{\eta^{1/2} (T_1 T_2)^{1/4}} + 1 \biggr) & \text{if } \eta \gg X \\ O \biggl(\dfrac{X^{1/2}}{(T_1 T_2)^{1/4}} + 1 \biggr) & \text{if } \eta \ll X. \end{cases} \end{equation} Put 
$N(T_1, T_2, T_3)$ for the set of quintuples 
$(u, c_1, c_2, s, t)$ for which 
$a = s^2 -st + t^2, c = c_1^2 - c_1 c_2 + c_2^2$ satisfies (4.9) and 
$T_3 < \eta \leq 2T_3$.
We factor 
$b + n \sqrt {-3}$ over 
${\mathbb {Z}}[\sqrt {-3}] \subset {\mathbb {C}}$ into 
${\mathbf {c}} \cdot {\mathbf {a}}^3$, say, where
\[ {\mathbf{c}} = c^{1/2} e^{i \gamma} \]and
\[ {\mathbf{a}} = a^{1/2} e^{i \alpha}. \]We then have
\begin{equation} \gamma + 3 \alpha + 2 k \pi = \theta = O\biggl(\frac{T_3^{1/2}}{(T_1 T_2)^{3/4}}\biggr), \end{equation}
where 
$k = 0, 1, 2$. The situation is now essentially symmetric in 
${\mathbf {a}}, {\mathbf {c}}$. Suppose, say, that 
$T_1 \ll T_2$ (so, in particular, 
$T_1 \ll X$). Then we first fix a vector 
${\mathbf {c}}$, and then choose a vector having norm 
$a \in (T_2, 2T_2]$ lying in one of three sectors of angle 
$O (X (T_1 T_2)^{-1} )$. Equation (4.14) gives three sectors depending on the value of 
$k$. Call one of these sectors 
${\mathcal {A}}_\gamma$, say. If we have two vectors
\[ {\mathbf{a}}_1 = p_1 + \sqrt{-3} \cdot q_1, \quad {\mathbf{a}}_2 = p_2 + \sqrt{-3} \cdot q_2 \in {\mathcal{A}}_\gamma, \]
with corresponding angles 
$\alpha _1, \alpha _2$, then
\[ \sqrt{3} \cdot |p_1 q_2 - p_2 q_1| = \lVert {\mathbf{a}}_1 \rVert \lVert {\mathbf{a}}_2 \rVert |\sin(\alpha_1 - \alpha_2)| = O \biggl( \frac{T_3^{1/2}}{(T_1 T_2)^{3/4}} \cdot T_2\biggr) = O\biggl(\frac{T_3^{1/2} T_2^{1/4}}{T_1^{3/4}}\biggr). \]
For each 
$\kappa = O (T_3^{1/2} T_2^{1/4} /T_1^{3/4} )$ with 
$|p_1 q_2 - p_2 q_1| = \kappa$ there are at most 
$O(1)$ possibilities for 
${\mathbf {a}}_2 \in {\mathcal {A}}_\gamma$ once 
${\mathbf {a}}_1$ is fixed, because any different solution would be separated by 
$\lVert {\mathbf {a}}_1 \rVert \gg T_2^{1/2}$. Hence, having fixed 
${\mathbf {c}}$ we see that 
${\mathcal {A}}_\gamma$ contains 
$O (T_3^{1/2} T_2^{1/4} /T_1^{3/4} + 1 )$ possibilities for 
${\mathbf {a}}$. Thus, the number of choices for 
${\mathbf {a}}, {\mathbf {c}}$ is
\[ O (T_3^{1/2} T_1^{1/4} T_2^{1/4} + T_1 ). \]
If instead we have 
$T_2 \leq T_1$, then we switch tracks and fix 
${\mathbf {a}}$ first. The argument proceeds in an identical manner except now there is only one sector 
${\mathcal {B}}_\alpha$, say. Using symmetry in this way allows us to conclude that there are
\begin{equation} O (T_3^{1/2} T_1^{1/4} T_2^{1/4} + \min \{T_1, T_2 \}) \end{equation}
possibilities for 
${\mathbf {a}}, {\mathbf {c}}$.
By (4.13), the number of choices for 
$u$ is then 
$O({X}/{T_3^{1/2} (T_1 T_2)^{1/4}} + 1 )$ if 
$T_3 \gg X$. Thus, we have
\[ N(T_1, T_2, T_3) = O \biggl(X + T_3^{1/2} T_1^{1/4} T_2^{1/4} + \frac{X^{1/2} \min\{T_1, T_2\}}{(T_1 T_2)^{1/4}} + \min\{T_1, T_2 \}\biggr). \]
Noting that 
$\theta \ll X (T_1 T_2)^{-1}$ by (4.10), we see that
\[ T_3 \asymp \eta \ll \theta^2 (T_1 T_2)^{3/2} \ll \frac{X^2}{T_1^{1/2} T_2^{1/2}}. \]This implies that
\[ T_3^{1/2} T_1^{1/4} T_2^{1/4} \ll \frac{X}{T_1^{1/4} T_2^{1/4}} \cdot (T_1 T_2)^{1/4} \ll X. \]
Further, we see that 
$(T_1 T_2)^{1/4} \gg (\min \{T_1, T_2\})^{1/2}$, hence
\[ \frac{X^{1/2} \min\{T_1, T_2\}}{(T_1 T_2)^{1/4}} \ll X^{1/2} \min\{T_1, T_2\}^{1/2}. \]We thus obtain
\begin{align*} &\sum_{X \ll T_3 \ll X^2/(T_1^{1/2} T_2^{1/2})} \sum_{X^{2/3} \ll T_1 T_2 \ll X^2} N(T_1, T_2, T_3) \\ &\quad \ll \sum_{T_3 \ll X^2} \sum_{\substack{T_1 \ll X \\ T_1 \ll T_2 \ll X^2/T_1}} O (X + X^{1/2} T_1^{1/2} + T_1 ) \\ & \quad\ll X (\log X)^2. \end{align*}
If instead 
$T_3 \ll X$, then we use the second bound from (4.13), which shows that
\begin{align*} N(T_1, T_2, T_3) & = O \biggl(X^{1/2} T_3^{1/2} + T_3^{1/2} T_1^{1/4} T_2^{1/4} + \frac{X^{1/2} \min \{T_1, T_2\}}{(T_1 T_2)^{1/4}} + \min\{T_1, T_2\}\biggr) \\ & = O(X^{1/2} T_3^{1/2} + T_3^{1/2} T_1^{1/4} T_2^{1/4} + X^{1/2} \min\{T_1, T_2\}^{1/2} + \min\{T_1, T_2\} ). \end{align*}
Summing over dyadic ranges we again obtain the bound 
$O(X (\log X)^2)$. This is sufficient for the proof of the upper bound of Theorem 1.1.
4.2 Proof of the lower bound in Theorem 1.1
For the lower bound, we have that the set
\[ S(X) = \{x^3 + ax^2 + (a-3)x - 1 : a \in [-X,X] \cap {\mathbb{Z}}\} \]
contains 
$2X + O(1)$ elements. Let 
$f_a$ denote the element in 
$S(X)$ corresponding to the parameter 
$a$. Then 
$\Delta (f_a) = (a^2 - 3a + 9)^2$, so 
$f_a$ is either an abelian cubic or is totally reducible over 
${\mathbb {Q}}$. The latter situation occurs only when 
$f_a$ has a rational integer root. However, the constant coefficient of 
$f_a$ is 
$-1$, so this root must be 
$\pm 1$. We then check that
\[ f_a(1) = 2a - 3, f_a(-1) = 1 \]
are both odd, so they cannot be zero. Hence, 
$f_a$ is irreducible for all 
$a \in {\mathbb {Z}}$ and, thus, 
$f_a$ is an abelian cubic for all 
$a \in {\mathbb {Z}}$. This provides the required lower bound.
We remark that the family 
$S(X)$ is well known; see, for example, [Reference StewartSte91] and [Reference SmithSmi99].
5. Counting monic abelian cubics by invariants
In this section, we prove Theorem 1.3. As in all cases our parametrization demands that 
$\gcd (s,t) = 1$, we first address this issue. Put
\[ \mathcal{S}(T) = \{(s,t) \in {\mathbb{Z}}^2 : \gcd(s,t) = 1, s^2 - st + t^2 \leq T\} \]
and 
$S(T) = \# \mathcal {S}(T)$. Next, put 
${\mathcal {Z}}(T) = \{(s,t) \in {\mathbb {Z}}^2 : s^2 - st + t^2 \leq T\}$ and 
$Z(T) = \# {\mathcal {Z}}(T)$. Then for any positive number 
$M$ we have
\begin{equation} \mathcal{S}(T) = \prod_{\substack{p < M \\ p \ne 3}} \biggl(1 - \frac{1}{p^2}\biggr) Z(T) + O \biggl(\sum_{M < p \ll T^{1/2} } \frac{Z(T)}{p^2} \biggr). \end{equation}Note that the infinite product satisfies
\begin{align*} \prod_{p > M} \biggl(1 - \frac{1}{p^2}\biggr) & = \exp \biggl(\sum_{p > M} \log\biggl(1 - \frac{1}{p^2}\biggr)\biggr) \\ & = \exp\biggl(\sum_{p > M} \biggl(- \frac{1}{p^2} - \frac{1}{2p^4} - \frac{1}{3p^6} - \cdots\biggr)\biggr) \\ & = \exp \biggl(- \frac{c_p}{p^2} \biggr), \end{align*}
where 
$c_p = \sum _{n = 1}^\infty ({1}/{n p^{2n - 2}})$ is an absolute constant. It follows that
\[ \prod_{p > M} \biggl(1 - \frac{1}{p^2}\biggr) = 1 + O(p^{-2}). \]From here one concludes that
\begin{equation} S(T) = \frac{27}{4\pi^2} \cdot \frac{\pi T}{\sqrt{3}} + O(T^{1/2}). \end{equation} We proceed to treat the first case given by (1.9). Thus, we are required to count the solutions 
$(c_1, c_2, s, t)$ satisfying the inequality
\begin{equation} (c_1^2 - c_1 c_2 + c_2^2)(s^2 - st + t^2) \leq X^{1/3}/9 \end{equation}
and 
$\gcd (s,t) = 1, 3 \nmid s^2 - st + t^2$. We then have
\begin{equation} \sum_{c = c_1^2 - c_1 c_2 + c_2^2 \leq X^{1/3}} S(X^{1/3}/9c) = \sum_{c_1^2 - c_1 c_2 + c_2^2 \leq X^{1/3}} \biggl(\frac{X^{1/3}}{\pi \sqrt{3} c} + O\biggl(\frac{X^{1/6}}{c^{1/2}}\biggr)\biggr). \end{equation}
Let 
$r_3(n) = \# \{(s,t) \in {\mathbb {Z}}^2 : n = s^2 - st + t^2\}$. Observe that
\[ \sum_{n \leq Y} r_3(n) = \# \{(s,t) \in {\mathbb{Z}}^2 : s^2 - st + t^2 \leq Y\} = \frac{\pi Y}{\sqrt{3}} + O (Y^{1/2}). \]
Indeed, the middle term above is precisely the number of integral points inside the ellipse defined by the inequality 
$s^2 - st + t^2 \leq Y$. We then have, for any 
$\alpha > 0$,
\begin{align*} \sum_{c_1^2 - c_1 c_2 + c_2^2 \leq Y} (c_1^2 - c_1 c_2 + c_2^2)^{-\alpha} & = \sum_{n \leq Y} \frac{r_3(n)}{n^\alpha} \\ & = Y^{-\alpha} \sum_{n \leq Y} r_3(n) + \int_1^{Y}\frac{\sum_{n \leq t} r_3(n)}{t^{\alpha + 1}}\, {d} t \\ & = \frac{\pi Y^{1 - \alpha}}{\sqrt{3}} + \int_1^{Y} \biggl( \frac{\pi}{\sqrt{3} t^{\alpha}} + O \biggl(\frac{1}{t^{\alpha + 1/2}}\biggr)\biggr) \, {d} t. \end{align*}
The values we require to evaluate (5.4) are 
$\alpha = 1$ and 
$\alpha = 1/2$, giving the term
\[ \frac{ X^{1/3} \log X}{4} + O (X^{1/3}). \]
However, we must remember to impose the condition that 
$s^2 - st + t^2 \not \equiv 0 \pmod {3}$, which introduces a factor of 
$2/3$ to the main term. Hence, we obtain the asymptotic form
\begin{equation} \frac{ X^{1/3} \log X}{6} + O (X^{1/3}). \end{equation}The cases corresponding to (3.4) and (3.6) correspond to the inequalities
\begin{equation} (c_1^2 - c_1 3c_2 + 9c_2^2)(s^2 - st + t^2) \leq X^{1/3}/3 \end{equation}and
\begin{equation} (c_1^2 - c_1 3c_2 + 9c_2^2)(s^2 - st + t^2) \leq X^{1/3}, \end{equation}
respectively. However, there are now additional congruence relations that must be satisfied by 
$c_1, c_2, s,t$ as indicated in Theorem 1.2. For the second case we must have 
$c_1 \not \equiv 0 \pmod {3}$ and 
$s^2 - st + t^2 \not \equiv 0 \pmod {3}$. These conditions introduce a factor of 
$4/9$. This gives that there are
\begin{equation} \frac{X^{1/3} \log X}{3} + O (X^{1/3}) \end{equation}possibilities in this case. Finally, in the third case we apply the same congruence restrictions, resulting in the estimate
\begin{equation} X^{1/3} \log X + O (X^{1/3}). \end{equation}Thus, we see that
\begin{align*} {\mathcal{M}}_{\text{BS}}(X) & = \frac{1}{12} (2 + 4 + 12) X^{1/3} \log X + O (X^{1/3}) \\ & = \frac{3X^{1/3} \log X}{2} + O (X^{1/3}), \end{align*}as desired.
6. Some algebraic consequences
In this section, we record some nice algebraic consequences of the methods we develop in this paper which may be of independent interest. First, we give another proof of the following well-known theorem in algebraic number theory.
Theorem 6.1 The 
$3$-torsion part of narrow class groups of quadratic fields are in one-to-one bijection with maximal, irreducible nowhere totally ramified cubic rings.
6.1 Proof of Theorem 6.1
Let 
${\mathcal {R}}_2, {\mathcal {R}}_3$ denote the 
$\operatorname {GL}_2({\mathbb {Z}})$-equivalence classes of binary quadratic and cubic forms, respectively. We show that the map 
$\phi _{3,2} : {\mathcal {R}}_3 \rightarrow {\mathcal {R}}_2$ sending a binary cubic form 
$F$ to its Hessian covariant 
$H_F$ induces a bijection between the two objects in the theorem. Indeed it is well known that 
$\operatorname {GL}_2({\mathbb {Z}})$-classes of binary cubic forms with square-free discriminant precisely correspond to rings of integers of cubic fields which are nowhere totally ramified, and 
$\operatorname {GL}_2({\mathbb {Z}})$-classes of binary quadratic forms correspond to ideal classes of quadratic fields.
Let 
$F$ be a binary cubic form with integer coefficients. As 
$\Delta (H_F) = -3 \Delta (F)$, it follows that 
$F$ has square-free discriminant only if 
$H_F$ is primitive. For a given binary quadratic form 
$g(x,y) = ax^2 + bxy + cy^2$ with co-prime integer coefficients and non-zero discriminant, we have that an element 
$F = F_{a_3, a_2} \in V_g({\mathbb {C}})$ with integer coefficients given in Proposition 3.1 has discriminant equal to
\[ \Delta(F_{a_3,a_2}) = \frac{g(a_2, -3a_3)^2(4ac - b^2 )}{3a^4}. \]
We now apply an element of 
$\operatorname {GL}_2({\mathbb {Z}})$ to 
$g$ (respectively, 
$F$) to replace 
$a$ with a prime 
$p$ representable by 
$g$ which does not divide 
$\Delta (g)$. The prime 
$p$ can be interpreted as representing the narrow class associated to 
$g$. Moreover, we see that 
$\Delta (F)$ can be square-free only if 
$g$ represents 
$p^2$ as well.
As 
$g$ represents 
$p$, it follows that 
$p$ splits in 
${\mathbb {Q}}\big(\sqrt {\Delta (g)}\big)$. We thus factor 
$(p) = \mathfrak {p}_1 \mathfrak {p}_2$ and without loss of generality, we assume that the ideal class corresponding to 
$g$ is represented by 
$\mathfrak {p}_1$. As 
$g$ also represents 
$p^2$, which has the possible factorizations
\[ (p^2) = (p)(p), \mathfrak{p}_1^2 \mathfrak{p}_2^2 , \mathfrak{p}_2^2 \mathfrak{p}_1^2, \]
it follows that 
$\mathfrak {p}_1^2$ or 
$\mathfrak {p}_2^2$ must be in the same class as 
$\mathfrak {p}_1$ because the first case corresponds to imprimitive representations. Indeed, examining the congruence conditions in (3.2) shows that the second case also cannot happen. Thus, 
$\mathfrak {p}_1, \mathfrak {p}_2^2$ must lie in the same class. Note that the class 
$[\mathfrak {p}_2]$ of 
$\mathfrak {p}_2$ is the inverse of the class 
$\mathfrak {p}_1$, whence 
$[\mathfrak {p}_1]^3 = \text {Id}$. This shows that 
$g$ is an order-3 element in the ideal class group of 
${\mathbb {Q}}\big(\sqrt {\Delta (g)}\big)$. This establishes the desired bijection.
6.2 Proof of Theorem 1.4
In this subsection, we give a proof of Theorem 1.4, which asserts that all semi-stable abelian elliptic curves have a common 
$2$-torsion field, equal to the maximal real subfield of 
${\mathbb {Q}}(\zeta _9)$.
The cubic polynomials we are considering take the shape
\begin{equation} f(x) = x^3 - 3(s^2 - st + t^2)x \pm (s^3 - 6s^2 t + 3st^2 + t^3), \end{equation}
by Proposition 9.6 in [Reference CohenCoh07]. By explicit calculation, we see that the Hessian covariant of 
$F(x,y) = y^3 f(x/y)$ is proportional to
\[ g(x,y) = (s^2 - st + t^2)x^2 \pm (s^3 - 6s^2 t + 3st^2 + t^3)xy + (s^2 - st + t^2)^2 y^2. \]One then checks that
\[ g(x,y) = u^2 + uv + v^2, \]where
\[ u = sx + (s^2 - t^2)y, v = -tx + (2st - s^2)y. \]
Moreover, for 
$G(x,y) = x^3 + 3x^2 y - y^3$, we have
\[ G(u,v) = (s^3 - 3s^2 t + t^3)F(x,y). \]
This shows that 
$G$ and 
$F$ have the same splitting fields. Note that
\[ \theta_0 = \arccos\biggl(\frac{-1}{2}\biggr) = \frac{\pi}{3}. \]
It then follows from Lemma 4.2 that the roots 
$r_1, r_2, r_3$ of 
$G(x,1)$ are given by
\[ r_1 = 2 \cos(\theta_0/3) = 2 \cos\biggl(\frac{2\pi}{9}\biggr), \quad r_2 = 2 \cos \biggl(\frac{8\pi}{9}\biggr),\quad r_3 = 2 \cos\biggl(\frac{14 \pi}{9}\biggr). \]
These are precisely equal to 
$\zeta _9 + \zeta _9^{-1}, \zeta _9^2 + \zeta _9^{-2}, \zeta _9^4 + \zeta _9^{-4}$, where 
$\zeta _9 = \exp (2\pi i/9)$ is a primitive ninth root of unity. This completes the proof.
