For positive integers 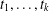 $t_{1},\ldots ,t_{k}$, let
$t_{1},\ldots ,t_{k}$, let 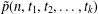 $\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ (respectively
$\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ (respectively 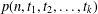 $p(n,t_{1},t_{2},\ldots ,t_{k})$) be the number of partitions of
$p(n,t_{1},t_{2},\ldots ,t_{k})$) be the number of partitions of  $n$ such that, if
$n$ such that, if 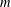 $m$ is the smallest part, then each of
$m$ is the smallest part, then each of  $m+t_{1},m+t_{1}+t_{2},\ldots ,m+t_{1}+t_{2}+\cdots +t_{k-1}$ appears as a part and the largest part is at most (respectively equal to)
$m+t_{1},m+t_{1}+t_{2},\ldots ,m+t_{1}+t_{2}+\cdots +t_{k-1}$ appears as a part and the largest part is at most (respectively equal to)  $m+t_{1}+t_{2}+\cdots +t_{k}$. Andrews et al. [‘Partitions with fixed differences between largest and smallest parts’, Proc. Amer. Math. Soc.143 (2015), 4283–4289] found an explicit formula for the generating function of
$m+t_{1}+t_{2}+\cdots +t_{k}$. Andrews et al. [‘Partitions with fixed differences between largest and smallest parts’, Proc. Amer. Math. Soc.143 (2015), 4283–4289] found an explicit formula for the generating function of 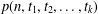 $p(n,t_{1},t_{2},\ldots ,t_{k})$. We establish a
$p(n,t_{1},t_{2},\ldots ,t_{k})$. We establish a 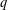 $q$-series identity from which the formulae for the generating functions of
$q$-series identity from which the formulae for the generating functions of 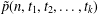 $\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ and
$\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ and 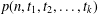 $p(n,t_{1},t_{2},\ldots ,t_{k})$ can be obtained.
$p(n,t_{1},t_{2},\ldots ,t_{k})$ can be obtained.
 $K_{16}$
$K_{16}$
 $ax^{2}+by^{2}+cz^{2}$ AND
$ax^{2}+by^{2}+cz^{2}$ AND  $ax^{2}+by^{2}+cz^{2}+dw^{2}$
$ax^{2}+by^{2}+cz^{2}+dw^{2}$
 $L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES
$L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES
 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
 $U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
$U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
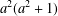 $a^{2}(a^{2}+1)$
$a^{2}(a^{2}+1)$
 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II