Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T00:26:06.512Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW PROOF OF THE CARLITZ–LUTZ THEOREM

Part of: Finite fields and commutative rings (number-theoretic aspects) General field theory

Published online by Cambridge University Press:  10 July 2019

RACHID BOUMAHDI Open the ORCID record for RACHID BOUMAHDI [Opens in a new window] ,
OMAR KIHEL Open the ORCID record for OMAR KIHEL [Opens in a new window] ,
JESSE LARONE Open the ORCID record for JESSE LARONE [Opens in a new window]  and
MAKHLOUF YADJEL Open the ORCID record for MAKHLOUF YADJEL [Opens in a new window]
RACHID BOUMAHDI
Affiliation:
La3c Laboratory, Faculty of Mathematics, USTHB University, Algiers, Algeria email r_boumehdi@esi.dz
OMAR KIHEL
Affiliation:
Department of Mathematics, Brock University, Ontario, CanadaL2S 3A1 email okihel@brocku.ca
JESSE LARONE*
Affiliation:
Département de mathématiques et de statistique, Université Laval, Québec, CanadaG1V 0A6 email jesse.larone.1@ulaval.ca
MAKHLOUF YADJEL
Affiliation:
La3c Laboratory, Faculty of Mathematics, USTHB University, Algiers, Algeria email yadmakhlouf@hotmail.fr
*
✉jesse.larone.1@ulaval.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A polynomial 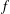$f$ over a finite field $\mathbb{F}_{q}$ can be classified as a permutation polynomial by the Hermite–Dickson criterion, which consists of conditions on the powers 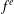$f^{e}$ for each $e$ from 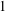$1$ to $q-2$, as well as the existence of a unique solution to 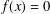$f(x)=0$ in 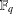$\mathbb{F}_{q}$. Carlitz and Lutz gave a variant of the criterion. In this paper, we provide an alternate proof to the theorem of Carlitz and Lutz.

Keywords

permutation polynomialHermite–Dickson theorem

MSC classification

Primary: 11T06: Polynomials
Secondary: 12E20: Finite fields (field-theoretic aspects)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 56 - 60
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The second and third authors were supported by NSERC.

References

Ayad, M., Belghaba, K. and Kihel, O., ‘On permutation binomials over finite fields’, Bull. Aust. Math. Soc. 89(1) (2014), 112–124.Google Scholar
Carlitz, L. and Lutz, J. A., ‘A characterization of permutation polynomials over a finite field’, Amer. Math. Monthly 85 (1978), 746–748.Google Scholar
Dickson, L. E., Linear Groups with an Exposition of the Galois Field Theory (Dover, New York, 1958).Google Scholar
Lidl, R. and Mullen, G. L., ‘Does a polynomial permute the elements of the field?’, Amer. Math. Monthly 95 (1988), 243–246.Google Scholar
Lidl, R. and Niedereiter, H., Finite Fields, Encyclopedia of Mathematics and its Applications, 20 (Cambridge University Press, Cambridge, 2008).Google Scholar
Macdonald, I. G., Symmetric Functions and Hall Polynomials (Clarendon Press, Oxford, 1998).Google Scholar