In the present paper, we use a coarse-graining approach to investigate the nonlinear redistribution of free energy in both position and scale space for weakly collisional magnetised plasma turbulence. For this purpose, we use high-resolution numerical simulations of gyrokinetic (GK) turbulence that span the proton–electron range of scales, in a straight magnetic guide field geometry. Accounting for the averaged effect of the particles’ fast gyro-motion on the slow plasma fluctuations, the GK approximation captures the dominant energy redistribution mechanisms in strongly magnetised plasma turbulence. Here, the GK system is coarse grained with respect to a cut-off scale, separating in real space the contributions to the nonlinear interactions from the coarse-grid scales and the sub-grid scales (SGS). We concentrate on the analysis of nonlinear SGS effects. Not only does this allow us to investigate the flux of free energy across the scales, but also to now analyse its spatial density. We find that the net value of scale flux is an order of magnitude smaller than both the positive and negative flux density contributions. The dependence of the results on the filter type is also analysed. Moreover, we investigate the advection of energy in position space. This rather novel approach for GK turbulence can help in the development of SGS models that account for advective unstable structures for space and fusion plasmas, and with the analysis of the turbulent transport saturation.

The possibility of controlling the electrostatic field distribution in plasma has yielded wide prospects for modern technologies. As a magnetic field primarily allows for creating electric fields in plasma, it serves as an additional obstacle for the current flow through a medium. In the present paper, an axially symmetric system is considered in which the magnetic field is directed along the axis and concentric electrodes are located at the ends. The electrodes are negatively biased. A model which solves the problem of the radial distribution of the plasma potential inside the cylindrical plasma column supported by the end electrodes is proposed. The most commonly encountered configurations of the electrical connection for the end electrodes are considered, and the particular solutions to the problem of the radial distribution are presented. The contribution of ions and electrons to the transverse conductivity is evaluated in detail. The influence of a thermionic element on the radial profile of the plasma potential is considered. To verify the proposed model, an experimental study of the reflex discharge is carried out with both cold electrodes and a thermionic element on the axis. A comparison of the computational model results with experimental data is given. The presented model makes it possible to solve the problem concerning the plasma potential distribution in the case of an arbitrary number of end electrodes, and also to take into account the inhomogeneity of the distribution of plasma density, neutral gas pressure and electron temperature along the radius.

Arched magnetized structures are a common occurrence in space and laboratory plasmas. Results from a laboratory experiment on spatio-temporal evolution of an arched magnetized plasma ($\beta \approx 10^{-3}$, Lundquist number $\approx 10^{4}$, plasma radius/ion gyroradius $\approx 20$) in a sheared magnetic configuration are presented. The experiment is designed to model conditions relevant to the formation and destabilization of similar structures in the solar atmosphere. The magnitude of a nearly horizontal overlying magnetic field was varied to study its effects on the writhe and twist of the arched plasma. In addition, the direction of the guiding magnetic field along the arch was varied to investigate its role in the formation of either forward- or reverse-S shaped plasma structures. The electrical current in the arched plasma was well below the current required to make it kink unstable. A significant increase in the writhe of the arched plasma was observed with larger magnitudes of overlying magnetic field. A forward-S shaped arched plasma was observed for a guiding magnetic field oriented nearly antiparallel to the initial arched plasma current, while the parallel orientation yielded the reverse-S shaped arched plasma.

Kinetic-ballooning-mode (KBM) turbulence is studied via gyrokinetic flux-tube simulations in three magnetic equilibria that exhibit small average magnetic shear: the Helically Symmetric eXperiment (HSX), the helical-axis Heliotron-J and a circular tokamak geometry. For HSX, the onset of KBM being the dominant instability at low wavenumber occurs at a critical value of normalized plasma pressure $\beta ^{\rm KBM}_{\rm crit}$ that is an order of magnitude smaller than the magnetohydrodynamic (MHD) ballooning limit $\beta ^{\rm MHD}_{\rm crit}$ when a strong ion temperature gradient (ITG) is present. However, $\beta ^{\rm KBM}_{\rm crit}$ increases and approaches the MHD ballooning limit as the ITG tends to zero. For these configurations, $\beta ^{\rm KBM}_{\rm crit}$ also increases as the magnitude of the average magnetic shear increases, regardless of the sign of the normalized magnetic shear. Simulations of Heliotron-J and a circular axisymmetric geometry display behaviour similar to HSX with respect to $\beta ^{\rm KBM}_{\rm crit}$. Despite large KBM growth rates at long wavelengths in HSX, saturation of KBM turbulence with $\beta > \beta _{\rm crit}^{\rm KBM}$ is achievable in HSX and results in lower heat transport relative to the electrostatic limit by a factor of roughly five. Nonlinear simulations also show that KBM transport dominates the dynamics when KBMs are destabilized linearly, even if KBM growth rates are subdominant to ITG growth rates.

The effect on dynamo action of an anisotropic electrical conductivity conjugated to an anisotropic magnetic permeability is considered. Not only is the dynamo fully axisymmetric, but it requires only a simple differential rotation, which twice challenges the well-established dynamo theory. Stability analysis is conducted entirely analytically, leading to an explicit expression of the dynamo threshold. The results show a competition between the anisotropy of electrical conductivity and that of magnetic permeability, the dynamo effect becoming impossible if the two anisotropies are identical. For isotropic electrical conductivity, Cowling's neutral point argument does imply the absence of an azimuthal component of current density, but does not prevent the dynamo effect as long as the magnetic permeability is anisotropic.

A method of random forcing with a constant power input for two-dimensional gyrokinetic turbulence simulations is developed for the study of stationary plasma turbulence. The property that the forcing term injects the energy at a constant rate enables turbulence to be set up in the desired range and energy dissipation channels to be assessed quantitatively in a statistically steady state. Using the developed method, turbulence is demonstrated in the large-scale fluid and small-scale kinetic regimes, where the theoretically predicted scaling laws are reproduced successfully.

The purpose of the present paper is to investigate the generation of soft X-ray emission from an anharmonic collisional nanoplasma by a laser–nanocluster interaction. The electric field of the laser beam interacts with the nanocluster and leads to ionization of the cluster atoms, which then produces a nanoplasma. Because of the nonlinear restoring force in an anharmonic nanoplasma, the fluctuations and heating rate of, as well as the power radiated by, the electrons in the nanocluster plasma will be notably different from those arising from a linear restoring force. By comparing the nonlinear restoring force state (which arises from an anharmonic cluster) with that of the linear restoring force (in harmonic clusters), the cluster temperature specifically changes at the resonant frequency relative to the linear restoring force, while the variation of the anharmonic cluster radius is almost identical to that of the harmonic cluster radius. In addition, it is revealed that a sharp peak of X-ray emission arises after some picoseconds in deuterium, helium, neon and argon clusters.

In the ion cyclotron range of frequency (ICRF), the presence of a lower hybrid (LH) resonance can appear in the edge of a tokamak plasma and lead to deleterious edge power depositions. An analytic formula for these losses is derived in the cold plasma approximation and for a slab geometry using an asymptotic approach and an analytical continuation near the LH resonance. The way to minimize these losses in a large machine like ITER is discussed. An internal verification between the power loss computed with the semi-analytical code ANTITER IV for ion cyclotron resonance heating (ICRH) and the analytic result is performed. This allows us to check the precision of the numerical integration of the singular set of cold plasma wave differential equations. The set of cold plasma equations used is general and can be applied in other parameters domain.

We construct smooth, non-symmetric plasma equilibria which possess closed, nested flux surfaces and solve the magnetohydrostatic (steady three-dimensional incompressible Euler) equations with a small force. The solutions are also ‘nearly’ quasisymmetric. The primary idea is, given a desired quasisymmetry direction $\xi$, to change the smooth structure on space so that the vector field $\xi$ is Killing for the new metric and construct $\xi$–symmetric solutions of the magnetohydrostatic equations on that background by solving a generalized Grad–Shafranov equation. If $\xi$ is close to a symmetry of Euclidean space, then these are solutions on flat space up to a small forcing.

We derive the two-dimensional counter-differential rotation equilibria of two-component plasmas, composed of both ion and electron ($e^-$) clouds with finite temperatures, for the first time. In the equilibrium found in this study, as the density of the $e^{-}$ cloud is always larger than that of the ion cloud, the entire system is a type of non-neutral plasma. Consequently, a bell-shaped negative potential well is formed in the two-component plasma. The self-electric field is also non-uniform along the $r$-axis. Moreover, the radii of the ion and $e^{-}$ plasmas are different. Nonetheless, the pure ion as well as $e^{-}$ plasmas exhibit corresponding rigid rotations around the plasma axis with different fluid velocities, as in a two-fluid plasma. Furthermore, the $e^{-}$ plasma rotates in the same direction as that of $\boldsymbol {E \times B}$, whereas the ion plasma counter-rotates overall. This counter-rotation is attributed to the contribution of the diamagnetic drift of the ion plasma because of its finite pressure.

An interesting aspect of complex plasma is its ability to self-organize into a variety of structural configurations and undergo transitions between these states. A striking phenomenon is the isotropic-to-string transition observed in electrorheological complex plasma under the influence of a symmetric ion wake field. Such transitions have been investigated using the Plasma Kristall-4 (PK-4) microgravity laboratory on the International Space Station. Recent experiments and numerical simulations have shown that, under PK-4-relevant discharge conditions, the seemingly homogeneous direct current discharge column is highly inhomogeneous, with large axial electric field oscillations associated with ionization waves occurring on microsecond time scales. A multi-scale numerical model of the dust–plasma interactions is employed to investigate the role of the electric field in the charge of individual dust grains, the ion wake field and the order of string-like structures. Results are compared with those for dust strings formed in similar conditions in the PK-4 experiment.

An encoder–decoder neural network has been used to examine the possibility for acceleration of a partial integro-differential equation, the Fokker–Planck–Landau collision operator. This is part of the governing equation in the massively parallel particle-in-cell code XGC, which is used to study turbulence in fusion energy devices. The neural network emphasizes physics-inspired learning, where it is taught to respect physical conservation constraints of the collision operator by including them in the training loss, along with the $\ell _2$ loss. In particular, network architectures used for the computer vision task of semantic segmentation have been used for training. A penalization method is used to enforce the ‘soft’ constraints of the system and integrate error in the conservation properties into the loss function. During training, quantities representing the particle density, momentum and energy for all species of the system are calculated at each configuration vertex, mirroring the procedure in XGC. This simple training has produced a median relative loss, across configuration space, of the order of $10^{-4}$, which is low enough if the error is of random nature, but not if it is of drift nature in time steps. The run time for the current Picard iterative solver of the operator is $O(n^2)$, where $n$ is the number of plasma species. As the XGC1 code begins to attack problems including a larger number of species, the collision operator will become expensive computationally, making the neural network solver even more important, especially since its training only scales as $O(n)$. A wide enough range of collisionality has been considered in the training data to ensure the full domain of collision physics is captured. An advanced technique to decrease the losses further will be subject of a subsequent report. Eventual work will include expansion of the network to include multiple plasma species.

A new paradigm for rapid stellarator configuration design has been recently demonstrated, in which the shapes of quasisymmetric or omnigenous flux surfaces are computed directly using an expansion in small distance from the magnetic axis. To further develop this approach, here we derive several other quantities of interest that can be rapidly computed from this near-axis expansion. First, the $\boldsymbol {\nabla }\boldsymbol {B}$ and $\boldsymbol {\nabla }\boldsymbol {\nabla }\boldsymbol {B}$ tensors are computed, which can be used for direct derivative-based optimization of electromagnetic coil shapes to achieve the desired magnetic configuration. Moreover, if the norm of these tensors is large compared with the field strength for a given magnetic field, the field must have a short length scale, suggesting it may be hard to produce with coils that are suitably far away. Second, we evaluate the minor radius at which the flux surface shapes would become singular, providing a lower bound on the achievable aspect ratio. This bound is also shown to be related to an equilibrium beta limit. Finally, for configurations that are constructed to achieve a desired magnetic field strength to first order in the expansion, we compute the error field that arises due to second-order terms.

Compton scattering of gamma rays propagating in a pair plasma can drive the formation of a relativistic electron positron beam. This process is scrutinized theoretically and numerically via particle-in-cell simulations. In addition, we determine in which conditions the beam can prompt a beam-plasma instability and convert its kinetic energy into magnetic energy. We argue that such conditions can be met at the photosphere radius of bright gamma-ray bursts.

A model is presented for the ion distribution function in a plasma at a solid target with a magnetic field $\boldsymbol {B}$ inclined at a small angle, 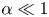$\alpha \ll 1$ (in radians), to the target. Adiabatic electrons are assumed, requiring 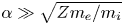$\alpha \gg \sqrt {Zm_{e}/m_{i}}$, where 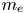$m_{e}$ and 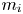$m_{i}$ are the electron and ion mass, respectively, and 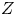$Z$ is the charge state of the ion. An electric field 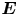$\boldsymbol {E}$ is present to repel electrons, and so the characteristic size of the electrostatic potential 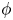$\phi$ is set by the electron temperature 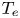$T_{e}$, 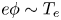$e\phi \sim T_{e}$, where 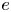$e$ is the proton charge. An asymptotic scale separation between the Debye length 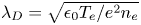$\lambda _{D} = \sqrt {\epsilon _0 T_{{e}} / e^{2} n_{{e}} }$, the ion sound gyro-radius $\rho _{s} = \sqrt { m_{i} ( ZT_{e} + T_{i} ) } / (ZeB)$ and the size of the collisional region 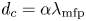$d_{c} = \alpha \lambda _{\textrm {mfp}}$ is assumed, $\lambda _{D} \ll \rho _{s} \ll d_{c}$. Here $\epsilon _0$ is the permittivity of free space, 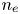$n_{e}$ is the electron density, 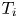$T_{i}$ is the ion temperature, 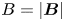$B= |\boldsymbol {B}|$ and 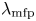$\lambda _{\textrm {mfp}}$ is the collisional mean free path of an ion. The form of the ion distribution function is assumed at distances 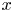$x$ from the wall such that $\rho _{s} \ll x \ll d_{c}$, that is, collisions are not treated. A self-consistent solution of the electrostatic potential for 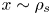$x \sim \rho _{s}$ is required to solve for the quasi-periodic ion trajectories and for the ion distribution function at the target. The large gyro-orbit model presented here allows to bypass the numerical solution of 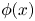$\phi (x)$ and results in an analytical expression for the ion distribution function at the target. It assumes that $\tau =T_{i}/(ZT_{e})\gg 1$, and ignores the electric force on the quasi-periodic ion trajectory until close to the target. For $\tau \gtrsim 1$, the model provides an extremely fast approximation to energy–angle distributions of ions at the target. These can be used to make sputtering predictions.

The dissipation of ion-acoustic surface waves propagating in a semi-bounded and collisional plasma which has a boundary with vacuum is theoretically investigated and this result is used for the analysis of edge-relevant plasma simulated by Divertor Plasma Simulator-2 (DiPS-2). The collisional damping of the surface wave is investigated for weakly ionized plasmas by comparing the collisionless Landau damping with the collisional damping as follows: (1) the ratio of ion temperature $({T_i})$ to electron temperature $({T_e})$ should be very small for the weak collisionality $({T_i}/{T_e} \ll 1)$; (2) the effect of collisionless Landau damping is dominant for the small parallel wavenumber, and the decay constant is given as $\gamma \approx{-} \sqrt {\mathrm{\pi }/2} {k_\parallel }{\lambda _{De}}\omega _{pi}^2/{\omega _{pe}}$; and (3) the collisional damping dominates for the large parallel wavenumber, and the decay constant is given as $\gamma \approx{-} {\nu _{in}}/16$, where ${\nu _{in}}$ is the ion–neutral collisional frequency. An experimental simulation of the above theoretical prediction has been done in the argon plasma of DiPS-2, which has the following parameters: plasma density ${n_e} = (\textrm{2--9)} \times \textrm{1}{\textrm{0}^{11}}\;\textrm{c}{\textrm{m}^{ - 3}}$, ${T_e} = 3.7- 3.8\;\textrm{eV}$, ${T_i} = 0.2- 0.3\;\textrm{eV}$ and collision frequency ${\nu _{in}} = 23- 127\;\textrm{kHz}$. Although the wavelength should be specified with the given parameters of DiPS-2, the collisional damping is found to be $\gamma = ( - 0.9\;\textrm{to}\; - 5) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$ for ${k_\parallel }{\lambda _{De}} = 10$, while the Landau damping is found to be $\gamma = ( - 4\;\textrm{to}\; - 9) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$ for ${k_\parallel }{\lambda _{De}} = 0.1$.

The fundamental nature of turbulent density fluctuations in standard Wendelstein 7-X (W7-X) stellarator discharges is investigated experimentally via phase contrast imaging (PCI) in combination with gyrokinetic simulations with the code GENE. We find that density fluctuations are ion-temperature-gradient-driven and radially localised in the outer half of the plasma. It is shown that the line-integrated PCI measurements cover the right range of wavenumbers and a favourable toroidal and poloidal location to capture some of the strongest density fluctuations in W7-X. Due to the radial localisation of fluctuations, measured wavenumber–frequency spectra exhibit a dominant phase velocity, which can be related to the $\boldsymbol {E\times B}$ rotation velocity at the radial position of a well in the neoclassical radial electric field. The match is robust against variations of heating power and line-integrated density, which is partly due to the localisation of fluctuations and partly due to effects of the radial gradient in the $\boldsymbol {E\times B}$ velocity profile on the wavenumber–frequency spectrum. The latter effect is studied with a newly built synthetic PCI diagnostic and global gyrokinetic simulations with GENE-3D.

This paper investigates the influence of the driving frequency on the dynamics of a single dust particle in argon radiofrequency discharge. A one-dimensional fluid model is presented and solved in the entire inter-electrode domain using the finite difference method. In order to solve the particle equation of motion, the coefficients describing the amplification and the damping of the dust particle oscillations are analytically calculated around the equilibrium position, these coefficients allow us to find the relation between the plasma and dust parameters. The results obtained cover the discharge characteristics, the charge and the dynamics of the dust particle. It has been found that the driving frequency has a significant effect on not only the discharge properties but also on the damped oscillatory motion and the equilibrium position of the dust particle. Hence, these oscillations become closer to the electrodes with increasing driving frequency whereas the dust equilibrium position becomes relatively farther from the powered electrode when the dust size decreases.

The particle–particle (PP) model has a growing number of applications in plasma simulations, because of its high accuracy of solving Coulomb collisions. One of the main issues restricting the practical use of the PP model is its large computational cost, which is now becoming acceptable thanks to state-of-art parallel computing techniques. Another issue is the singularity that occurs when two particles are too close. The most effective approach of avoiding the singularity would be to simulate particles with only like charges plus a neutralizing field, such that the short-range collisions are equivalent to those of using unlike charges. In this paper, we introduce a way of adding the neutralizing field by using the analytical solution of the electric field in the domain filled with uniformly distributed charges, for applications with homogeneous and quasi-neutral plasmas under a reflective boundary condition. Two most common Cartesian domain geometries, cubic and spherical, are considered. The model is verified by comparing simulation results with an analytical solution of an electron–ion temperature relaxation problem, and a corresponding simulation using unlike charges. In addition, it is found that a PP simulation using like charges can achieve a significant speed-up of 100 compared with a corresponding simulation using unlike charges, due to the capability of using larger time steps while maintaining the same energy conservation.

We show that the Weibel or current filamentation instability can lead to the emission of circularly polarized radiation. Using particle-in-cell simulations and a radiation post-processing numerical algorithm, we demonstrate that the level of circular polarization increases with the initial plasma magnetization, saturating at ${\sim }13\,\%$ when the magnetization, given by the ratio of magnetic energy density to the electron kinetic energy density, is larger than 0.05. Furthermore, we show that this effect requires an ion–electron mass ratio greater than unity. These findings, which could also be tested in currently available laboratory conditions, show that the recent observation of circular polarization in gamma-ray burst afterglows could be attributed to the presence of magnetized current filaments driven by the Weibel or current filamentation instability.