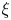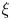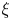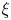1. Introduction
Let ![]() $T\subset \mathbb {R}^3$ be a domain with smooth boundary. The three-dimensional magneto hydrostatic (MHS) equations on
$T\subset \mathbb {R}^3$ be a domain with smooth boundary. The three-dimensional magneto hydrostatic (MHS) equations on ![]() $T$ read
$T$ read
where ![]() $J= \boldsymbol {\nabla }\times B$ is the current,
$J= \boldsymbol {\nabla }\times B$ is the current, ![]() $f$ is an external force and
$f$ is an external force and ![]() $P$ is the pressure. The solution
$P$ is the pressure. The solution ![]() $B$ to (1.1)–(1.3) can be interpreted as either a stationary fluid velocity field which solves the time-independent Euler equation, or as a steady self-supporting magnetic field in a continuous medium with trivial flow velocity. The latter interpretation is robust across a variety of magnetohydrodynamic models (e.g. compressible, incompressible, non-ideal) and makes the system (1.1)–(1.3) central to the study of plasma confinement fusion.
$B$ to (1.1)–(1.3) can be interpreted as either a stationary fluid velocity field which solves the time-independent Euler equation, or as a steady self-supporting magnetic field in a continuous medium with trivial flow velocity. The latter interpretation is robust across a variety of magnetohydrodynamic models (e.g. compressible, incompressible, non-ideal) and makes the system (1.1)–(1.3) central to the study of plasma confinement fusion.
In view of this, there is a long-standing scientific program to identify and construct MHS equilibria which are effective at confining ions during a nuclear fusion reaction. The most basic requirement for confinement is the existence of a ‘flux function’ ![]() $\psi$, whose level sets foliate the domain
$\psi$, whose level sets foliate the domain ![]() $T$ and which satisfies
$T$ and which satisfies ![]() $B\boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$. To first approximation, ions move along the integral curves of
$B\boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$. To first approximation, ions move along the integral curves of ![]() $B$ and so this condition ensures that particle trajectories are approximately constrained to the level sets of
$B$ and so this condition ensures that particle trajectories are approximately constrained to the level sets of ![]() $\psi$. For this reason, it is desirable to seek equilibria with nested flux surfaces (isosurfaces of
$\psi$. For this reason, it is desirable to seek equilibria with nested flux surfaces (isosurfaces of ![]() $\psi$) which foliate the plasma domain. When
$\psi$) which foliate the plasma domain. When ![]() $T$ is the axisymmetric torus, it is natural to look for such solutions in the form of axisymmetric magnetic fields. If
$T$ is the axisymmetric torus, it is natural to look for such solutions in the form of axisymmetric magnetic fields. If ![]() $(R, \varPhi , Z)$ denote the usual cylindrical coordinates on
$(R, \varPhi , Z)$ denote the usual cylindrical coordinates on ![]() $\mathbb {R}^3$ and the centreline of the torus lies in the
$\mathbb {R}^3$ and the centreline of the torus lies in the ![]() $Z = 0$ plane, axisymmetric solutions take the form
$Z = 0$ plane, axisymmetric solutions take the form
with flux function ![]() $\psi _0$. In order for
$\psi _0$. In order for ![]() $B_0$ to satisfy (1.1) with
$B_0$ to satisfy (1.1) with ![]() $P_0 = P_0(\psi _0)$, taking
$P_0 = P_0(\psi _0)$, taking ![]() $f = 0$ momentarily for simplicity and taking
$f = 0$ momentarily for simplicity and taking ![]() $T$ to be the torus with inner radius
$T$ to be the torus with inner radius ![]() $R_0 -1$ and outer radius
$R_0 -1$ and outer radius ![]() $R_0 + 1$, say, the flux function needs to satisfy the axisymmetric Grad–Shafranov equation (Shafranov Reference Shafranov1966; Grad Reference Grad1967)
$R_0 + 1$, say, the flux function needs to satisfy the axisymmetric Grad–Shafranov equation (Shafranov Reference Shafranov1966; Grad Reference Grad1967)
where ![]() $D_0$ denotes the cross-section of the torus (unit disk) in the
$D_0$ denotes the cross-section of the torus (unit disk) in the ![]() $\varPhi = 0$ half-plane centred at
$\varPhi = 0$ half-plane centred at ![]() $R = R_0$. Conversely, if
$R = R_0$. Conversely, if ![]() $\psi _0$ is any solutionFootnote 1 to (1.5) with
$\psi _0$ is any solutionFootnote 1 to (1.5) with ![]() $e_\varPhi \boldsymbol {\cdot }\boldsymbol {\nabla } \psi _0 = 0$ then the vector field
$e_\varPhi \boldsymbol {\cdot }\boldsymbol {\nabla } \psi _0 = 0$ then the vector field ![]() $B_0$ defined in (1.4) is divergence-free and satisfies (1.1). If
$B_0$ defined in (1.4) is divergence-free and satisfies (1.1). If ![]() $\psi _0$ is constant on
$\psi _0$ is constant on ![]() $\partial T$,
$\partial T$, ![]() $B_0$ satisfies (1.3).
$B_0$ satisfies (1.3).
Unfortunately, these tokamak equilibria come with a slew of problems from the point of view of plasma confinement fusion (Landreman Reference Landreman2019). For example, to achieve improved confinement it is desirable for the magnetic field to ‘twist’ as it wraps around the torus and this can only be accomplished in axisymmetry with a large plasma current, ![]() $J$. Such plasma configurations are hard to control in practice. One approach to finding equilibria with better confinement properties is to consider equilibria in geometries which have the desired twist built in. This is the basic design principle behind the stellarator (Garren & Boozer Reference Garren and Boozer1991). It is still desirable for these configurations to possess a form of symmetry, which is known as quasisymmetry.
$J$. Such plasma configurations are hard to control in practice. One approach to finding equilibria with better confinement properties is to consider equilibria in geometries which have the desired twist built in. This is the basic design principle behind the stellarator (Garren & Boozer Reference Garren and Boozer1991). It is still desirable for these configurations to possess a form of symmetry, which is known as quasisymmetry.
Definition 1.1 (Weak quasisymmetry, Rodriguez, Helander & Bhattacharjee (Reference Rodriguez, Helander and Bhattacharjee2020))
Let ![]() $\xi$ be a non-vanishing vector field tangent to
$\xi$ be a non-vanishing vector field tangent to ![]() $\partial T$. We say that
$\partial T$. We say that ![]() $\xi$ is a quasisymmetry and the field
$\xi$ is a quasisymmetry and the field ![]() $B$ is quasisymmetric with respect to
$B$ is quasisymmetric with respect to ![]() $\xi$ if
$\xi$ if
for some function ![]() $\psi : T\to \mathbb {R}$.
$\psi : T\to \mathbb {R}$.
The significance of the condition (1.8) is that it implies ![]() $B\boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ and
$B\boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ and ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ and so quasisymmetric solutions possess flux functions which are symmetric with respect to
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ and so quasisymmetric solutions possess flux functions which are symmetric with respect to ![]() $\xi$. In Rodriguez et al. (Reference Rodriguez, Helander and Bhattacharjee2020), the authors argue that (1.7)–(1.9) form sufficient conditions that ensure first-order (in gyroradius) particle confinement, hence the terminology of weak quasisymmetry. In the confinement fusion literature (Landreman Reference Landreman2019; Burby, Kallinikos & MacKay Reference Burby, Kallinikos and MacKay2020), one encounters the following alternative definition which is actually stronger than the above. It replaces (1.9) with
$\xi$. In Rodriguez et al. (Reference Rodriguez, Helander and Bhattacharjee2020), the authors argue that (1.7)–(1.9) form sufficient conditions that ensure first-order (in gyroradius) particle confinement, hence the terminology of weak quasisymmetry. In the confinement fusion literature (Landreman Reference Landreman2019; Burby, Kallinikos & MacKay Reference Burby, Kallinikos and MacKay2020), one encounters the following alternative definition which is actually stronger than the above. It replaces (1.9) with
We term this set of conditions strong quasisymmetry. When ![]() $f=0$ it is this stronger form of quasisymmetry which is equivalent to other definitions in the plasma fusion literature involving Boozer angles, see § 8 of Landreman (Reference Landreman2019). If
$f=0$ it is this stronger form of quasisymmetry which is equivalent to other definitions in the plasma fusion literature involving Boozer angles, see § 8 of Landreman (Reference Landreman2019). If ![]() $\textrm {div} B = 0$ then (1.9) requires only that a single component of (1.10) vanish,
$\textrm {div} B = 0$ then (1.9) requires only that a single component of (1.10) vanish, ![]() $B\boldsymbol {\cdot } ( \xi \times J - \boldsymbol {\nabla } (B\boldsymbol {\cdot } \xi )) = 0$.Footnote 2
In light of this, the additional content of strong quasisymmetry (1.7), (1.8) and (1.10) is the assumption that the other two components of
$B\boldsymbol {\cdot } ( \xi \times J - \boldsymbol {\nabla } (B\boldsymbol {\cdot } \xi )) = 0$.Footnote 2
In light of this, the additional content of strong quasisymmetry (1.7), (1.8) and (1.10) is the assumption that the other two components of ![]() $\xi \times J - \boldsymbol {\nabla } (B\boldsymbol {\cdot } \xi )$ vanish. It turns out that when there is no force and the equilibria are toroidal, strong quasisymmetry is equivalent to Definition 1.1.Footnote 3
$\xi \times J - \boldsymbol {\nabla } (B\boldsymbol {\cdot } \xi )$ vanish. It turns out that when there is no force and the equilibria are toroidal, strong quasisymmetry is equivalent to Definition 1.1.Footnote 3
From (1.8), if ![]() $\xi \boldsymbol {\cdot } B$ is constant on surfaces of constant
$\xi \boldsymbol {\cdot } B$ is constant on surfaces of constant ![]() $\psi$,
$\psi$, ![]() $\xi \boldsymbol {\cdot } B = C(\psi )$ (by a result in Burby et al. (Reference Burby, Kallinikos and MacKay2020), any solution of (1.1) with
$\xi \boldsymbol {\cdot } B = C(\psi )$ (by a result in Burby et al. (Reference Burby, Kallinikos and MacKay2020), any solution of (1.1) with ![]() $f = 0$ which satisfies (1.7)–(1.9) satisfies this condition), it follows that
$f = 0$ which satisfies (1.7)–(1.9) satisfies this condition), it follows that ![]() $B$ is of the form
$B$ is of the form
and when ![]() $f = 0$, the requirement that (1.1) holds implies that
$f = 0$, the requirement that (1.1) holds implies that ![]() $\psi$ must satisfy the quasisymmetric Grad–Shafranov equation (introduced in Burby et al. (Reference Burby, Kallinikos and MacKay2020)) which reads
$\psi$ must satisfy the quasisymmetric Grad–Shafranov equation (introduced in Burby et al. (Reference Burby, Kallinikos and MacKay2020)) which reads
Equations (1.2), (1.7) and (1.9) can be thought of as constraints relating ![]() $\psi$ to the deformation tensor of
$\psi$ to the deformation tensor of ![]() $\xi$, the symmetric two-tensor
$\xi$, the symmetric two-tensor ![]() $\mathcal {L}_\xi \delta$ defined by
$\mathcal {L}_\xi \delta$ defined by
where ![]() $\boldsymbol {\nabla }$ denotes covariant differentiation with respect to the Euclidean metric. Recall that
$\boldsymbol {\nabla }$ denotes covariant differentiation with respect to the Euclidean metric. Recall that ![]() $\xi$ generates an isometry of Euclidean space if and only if
$\xi$ generates an isometry of Euclidean space if and only if ![]() $\mathcal {L}_\xi \delta = 0$, in which case
$\mathcal {L}_\xi \delta = 0$, in which case ![]() $\xi$ is called a Killing field for the metric
$\xi$ is called a Killing field for the metric ![]() $\delta$. Assuming that
$\delta$. Assuming that ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ and
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ and ![]() $\textrm {div} \xi = 0$, from (1.12) we find
$\textrm {div} \xi = 0$, from (1.12) we find
and expanding the condition (1.9) we find
see lemma C.6 of appendix C. Equation (1.17) is a complicated relationship between ![]() $\psi , C(\psi )$ and
$\psi , C(\psi )$ and ![]() $\xi$ but notice that it holds trivially (assuming only that
$\xi$ but notice that it holds trivially (assuming only that ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$) whenever when
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$) whenever when ![]() $\xi$ is a Killing field. It is well known that in Euclidean space the only Killing fields are linear combinations of translations and rotations. Therefore, up to a multiplicative constant, the only such field compatible with the geometry of the axisymmetric torus is
$\xi$ is a Killing field. It is well known that in Euclidean space the only Killing fields are linear combinations of translations and rotations. Therefore, up to a multiplicative constant, the only such field compatible with the geometry of the axisymmetric torus is ![]() $\xi = R e_\varPhi$ and as mentioned above, such solutions have problematic confinement properties. We have arrived at the following problem.
$\xi = R e_\varPhi$ and as mentioned above, such solutions have problematic confinement properties. We have arrived at the following problem.
Problem Given a toroidal domain ![]() $T$, construct a function
$T$, construct a function ![]() $\psi :T\to \mathbb {R}$ with nested flux surfaces and a divergence-free vector field
$\psi :T\to \mathbb {R}$ with nested flux surfaces and a divergence-free vector field ![]() $\xi$ which does not generate an isometry of
$\xi$ which does not generate an isometry of ![]() $\mathbb {R}^3$ and is tangent to
$\mathbb {R}^3$ and is tangent to ![]() $\partial T$, so that (1.13), (1.9), the nonlinear constraints (1.16), (1.17) and
$\partial T$, so that (1.13), (1.9), the nonlinear constraints (1.16), (1.17) and ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ all hold.
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$ all hold.
It is not clear that there are any smooth solutions ![]() $\psi , \xi$ to the above problem. In fact, in 1967 (long before the above notion of quasisymmetry was introduced), Grad & Rubin (Reference Grad and Rubin1958) and Grad (Reference Grad1967, Reference Grad1985) conjectured that the only smooth solutions to (1.1)–(1.3) possessing a good flux function have a Euclidean symmetry,Footnote 4 and this would in particular rule out any solutions of the above type. Since Grad's work, there have been some constructions of non-symmetric equilibria an infinite cylindrical domains (Salat & Kaiser Reference Salat and Kaiser1995; Kaiser & Salat Reference Kaiser and Salat1997). As these are unbounded in extent, they have limited practical appeal for the perspective of confinement. No such examples of smooth solutions have been rigorously demonstrated on toroidal domains, although there has been some work on suggestive formal near-axis expansions (Bernardin, Moses & Tataronis Reference Bernardin, Moses and Tataronis1986; Weitzner Reference Weitzner2014; Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2019) and non-symmetric weak solution equilibria with pressure jumps have been rigorously constructed (Bruno & Laurence Reference Bruno and Laurence1996) which may have practical implications for the confinement fusion program (Hudson et al. Reference Hudson, Dewar, Hole and McGann2011, Reference Hudson, Dewar, Dennis, Hole, McGann, Von Nessi and Lazerson2012).Footnote 5
$\psi , \xi$ to the above problem. In fact, in 1967 (long before the above notion of quasisymmetry was introduced), Grad & Rubin (Reference Grad and Rubin1958) and Grad (Reference Grad1967, Reference Grad1985) conjectured that the only smooth solutions to (1.1)–(1.3) possessing a good flux function have a Euclidean symmetry,Footnote 4 and this would in particular rule out any solutions of the above type. Since Grad's work, there have been some constructions of non-symmetric equilibria an infinite cylindrical domains (Salat & Kaiser Reference Salat and Kaiser1995; Kaiser & Salat Reference Kaiser and Salat1997). As these are unbounded in extent, they have limited practical appeal for the perspective of confinement. No such examples of smooth solutions have been rigorously demonstrated on toroidal domains, although there has been some work on suggestive formal near-axis expansions (Bernardin, Moses & Tataronis Reference Bernardin, Moses and Tataronis1986; Weitzner Reference Weitzner2014; Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2019) and non-symmetric weak solution equilibria with pressure jumps have been rigorously constructed (Bruno & Laurence Reference Bruno and Laurence1996) which may have practical implications for the confinement fusion program (Hudson et al. Reference Hudson, Dewar, Hole and McGann2011, Reference Hudson, Dewar, Dennis, Hole, McGann, Von Nessi and Lazerson2012).Footnote 5
We do not address Grad's conjecture here and our goal is instead to present a robust method for constructing solutions to (1.1) with small force and which are approximately quasisymmetric with respect to a given vector field ![]() $\xi$ (sufficiently close to the axisymmetric vector field
$\xi$ (sufficiently close to the axisymmetric vector field ![]() $\xi _0 = R e_\varPhi$), in the sense that (1.8) holds but that (1.9) holds up to a small error.
$\xi _0 = R e_\varPhi$), in the sense that (1.8) holds but that (1.9) holds up to a small error.
In addition to the non-trivial constraint (1.9), there are two serious difficulties in constructing solutions to (1.1)–(1.3) of the form (1.12) with given symmetry direction ![]() $\xi$. The first is that by (1.16), unlike in the axisymmetric setting, vector fields of the form (1.12) need not be divergence-free. The second difficulty is that for arbitrary
$\xi$. The first is that by (1.16), unlike in the axisymmetric setting, vector fields of the form (1.12) need not be divergence-free. The second difficulty is that for arbitrary ![]() $\xi$, it is not at all clear that the equations (1.13) and (1.14) admit any solutions with
$\xi$, it is not at all clear that the equations (1.13) and (1.14) admit any solutions with ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$, since the coefficients appearing in (1.13)–(1.14) need not be invariant under
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$, since the coefficients appearing in (1.13)–(1.14) need not be invariant under ![]() $\xi$. Both of these difficulties can be traced to the fact that
$\xi$. Both of these difficulties can be traced to the fact that ![]() $\xi$ need not be a Killing field with respect to the Euclidean metric. To circumvent these issues, inspired by Lichtenfelz, Misiolek & Preston (Reference Lichtenfelz, Misiolek and Preston2019) and Burby, Kallinikos & MacKay (Reference Burby, Kallinikos and MacKay2020), we replace the metric structure of
$\xi$ need not be a Killing field with respect to the Euclidean metric. To circumvent these issues, inspired by Lichtenfelz, Misiolek & Preston (Reference Lichtenfelz, Misiolek and Preston2019) and Burby, Kallinikos & MacKay (Reference Burby, Kallinikos and MacKay2020), we replace the metric structure of ![]() $(\mathbb {R}^3, \delta )$ with
$(\mathbb {R}^3, \delta )$ with ![]() $(\mathbb {R}^3, g)$ for a metric
$(\mathbb {R}^3, g)$ for a metric ![]() $g$ for which
$g$ for which ![]() $\xi$ is a Killing field. The resulting magnetic field will not satisfy the usual MHS equations (1.1), but provided
$\xi$ is a Killing field. The resulting magnetic field will not satisfy the usual MHS equations (1.1), but provided ![]() $\xi$ is sufficiently close to Killing for the Euclidean metric, the error will be small. We now explain the idea.
$\xi$ is sufficiently close to Killing for the Euclidean metric, the error will be small. We now explain the idea.
Let us suppose that given ![]() $\xi$, we can find a metric
$\xi$, we can find a metric ![]() $g$ on
$g$ on ![]() $\mathbb {R}^3$ for which
$\mathbb {R}^3$ for which ![]() $\mathcal {L}_\xi g= 0$, that is, for which
$\mathcal {L}_\xi g= 0$, that is, for which ![]() $\xi$ generates an isometry (we give an explicit construction of such metrics for a large class of vector fields
$\xi$ generates an isometry (we give an explicit construction of such metrics for a large class of vector fields ![]() $\xi$ after the upcoming statement of theorem 1.3). We then consider the following generalization of the ansatz (1.12), introduced in Burby et al. (Reference Burby, Kallinikos and MacKay2020):
$\xi$ after the upcoming statement of theorem 1.3). We then consider the following generalization of the ansatz (1.12), introduced in Burby et al. (Reference Burby, Kallinikos and MacKay2020):
Here, ![]() $|\xi |_g, \times _g, \boldsymbol {\nabla }_g$ denote the analogues of the usual Euclidean quantities
$|\xi |_g, \times _g, \boldsymbol {\nabla }_g$ denote the analogues of the usual Euclidean quantities ![]() $|\xi |,\times \boldsymbol {\nabla }$ with respect to the metric
$|\xi |,\times \boldsymbol {\nabla }$ with respect to the metric ![]() $g$ (see appendix B). In lemma C.3 we use the fact that
$g$ (see appendix B). In lemma C.3 we use the fact that ![]() $\mathcal {L}_\xi g = 0$ to show that vector fields of this form are divergence free assuming only that
$\mathcal {L}_\xi g = 0$ to show that vector fields of this form are divergence free assuming only that ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$,
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } \psi = 0$,
and also that ![]() $\psi$ is a flux function for
$\psi$ is a flux function for ![]() $B_g$,
$B_g$,
We emphasize the somewhat surprising fact that even though the definition (1.18) involves the metric ![]() $g$ in a non-trivial way, it is designed that way so that the identities (1.19) and (1.20) involve only Euclidean quantities. We remark that
$g$ in a non-trivial way, it is designed that way so that the identities (1.19) and (1.20) involve only Euclidean quantities. We remark that ![]() $B_g$ will not be divergence-free with respect to the
$B_g$ will not be divergence-free with respect to the ![]() $g$ metric.
$g$ metric.
We then seek ![]() $B_g$ of the form (1.18) which satisfy the MHS with respect to the metric
$B_g$ of the form (1.18) which satisfy the MHS with respect to the metric ![]() $g$,
$g$,
This ansatz leads to the generalized Grad–Shafranov equation for ![]() $\psi$,
$\psi$,
 \begin{gather} \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) - C(\psi) \frac{\xi}{|\xi|_g^2} \cdot_g \textrm{curl}_g \left(\frac{\xi}{|\xi|_g^2}\right) + \frac{C(\psi)C'(\psi)}{\sqrt{|g|}|\xi|_g^2}+ \frac{P'(\psi)}{\sqrt{|g|}} = 0, \quad \text{in} \ T, \end{gather}
\begin{gather} \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) - C(\psi) \frac{\xi}{|\xi|_g^2} \cdot_g \textrm{curl}_g \left(\frac{\xi}{|\xi|_g^2}\right) + \frac{C(\psi)C'(\psi)}{\sqrt{|g|}|\xi|_g^2}+ \frac{P'(\psi)}{\sqrt{|g|}} = 0, \quad \text{in} \ T, \end{gather}
where ![]() $|\xi |_g, \cdot _g, \textrm {curl}_g$ denote the magnitude, dot product and curl with respect to the metric
$|\xi |_g, \cdot _g, \textrm {curl}_g$ denote the magnitude, dot product and curl with respect to the metric ![]() $g$ (see appendix B for the definitions and appendix C for the derivation of (1.22) from (1.18) and (1.21)). Note that (1.22) and (1.23) reduces to (1.13) and (1.14) when
$g$ (see appendix B for the definitions and appendix C for the derivation of (1.22) from (1.18) and (1.21)). Note that (1.22) and (1.23) reduces to (1.13) and (1.14) when ![]() $g=\delta$, and when
$g=\delta$, and when ![]() $g$ is the circle-averaged metric, it agrees with the equation derived in Burby et al. (Reference Burby, Kallinikos and MacKay2020). As shown in Burby et al. (Reference Burby, Kallinikos and MacKay2020), all solutions of MHS (1.1)–(1.3) without force and non-vanishing pressure gradient must have a flux function satisfying (1.22) where
$g$ is the circle-averaged metric, it agrees with the equation derived in Burby et al. (Reference Burby, Kallinikos and MacKay2020). As shown in Burby et al. (Reference Burby, Kallinikos and MacKay2020), all solutions of MHS (1.1)–(1.3) without force and non-vanishing pressure gradient must have a flux function satisfying (1.22) where ![]() $g$ is the circle-averaged metric discussed below. In light of this, the study of the generalized Grad–Shafranov equation (1.22) is of fundamental importance in the study of solutions to MHS with a generalized symmetry.
$g$ is the circle-averaged metric discussed below. In light of this, the study of the generalized Grad–Shafranov equation (1.22) is of fundamental importance in the study of solutions to MHS with a generalized symmetry.
As another consequence of the fact that ![]() $\mathcal {L}_\xi g= 0$, the coefficients in (1.22) are invariant under
$\mathcal {L}_\xi g= 0$, the coefficients in (1.22) are invariant under ![]() $\xi$ and so (1.22), unlike (1.14), is consistent with the requirement
$\xi$ and so (1.22), unlike (1.14), is consistent with the requirement ![]() $\xi \boldsymbol {\cdot }\boldsymbol {\nabla } \psi = 0$. The downside is that the equation (1.21) does not agree with (1.1) unless
$\xi \boldsymbol {\cdot }\boldsymbol {\nabla } \psi = 0$. The downside is that the equation (1.21) does not agree with (1.1) unless ![]() $g = \delta$ and so
$g = \delta$ and so ![]() $B_g$ will not satisfy the original MHS equations. However, if we can arrange for the metric
$B_g$ will not satisfy the original MHS equations. However, if we can arrange for the metric ![]() $g$ to be sufficiently close to the Euclidean metric
$g$ to be sufficiently close to the Euclidean metric ![]() $\delta$, then
$\delta$, then ![]() $B_g$ will satisfy the usual MHS equations
$B_g$ will satisfy the usual MHS equations ![]() $\textrm {curl} B_g \times B_g - \boldsymbol {\nabla } P = 0$ up to a small error. Our approach will be to solve the generalized Grad–Shafranov equation (1.22) by deforming an appropriate solution
$\textrm {curl} B_g \times B_g - \boldsymbol {\nabla } P = 0$ up to a small error. Our approach will be to solve the generalized Grad–Shafranov equation (1.22) by deforming an appropriate solution ![]() $\psi _0$ of the axisymmetric Grad–Shafranov equation (1.5), using the methods from Constantin, Drivas & Ginsberg (Reference Constantin, Drivas and Ginsberg2020). In particular, we seek a diffeomorphism
$\psi _0$ of the axisymmetric Grad–Shafranov equation (1.5), using the methods from Constantin, Drivas & Ginsberg (Reference Constantin, Drivas and Ginsberg2020). In particular, we seek a diffeomorphism ![]() $\gamma : D_0 \to D$ and requiring that
$\gamma : D_0 \to D$ and requiring that ![]() $\psi = \psi _0\circ \gamma ^{-1}$. It turns out (see § 2) that this reduces to a system of nonlinear elliptic equations for the components of
$\psi = \psi _0\circ \gamma ^{-1}$. It turns out (see § 2) that this reduces to a system of nonlinear elliptic equations for the components of ![]() $\gamma$ which can be solved by a iteration.
$\gamma$ which can be solved by a iteration.
In what follows, ![]() $T_0$ denotes the axisymmetric torus
$T_0$ denotes the axisymmetric torus
with thickness ![]() $0 < a \ll R_0$. Let
$0 < a \ll R_0$. Let ![]() $\xi _0 = R e_\varPhi$ be the generator of rotations in the
$\xi _0 = R e_\varPhi$ be the generator of rotations in the ![]() $Z = 0$ plane. Let
$Z = 0$ plane. Let ![]() $D$ be any domain in the half-plane
$D$ be any domain in the half-plane ![]() $\{\varPhi = 0\}$ sufficiently close to
$\{\varPhi = 0\}$ sufficiently close to ![]() $D_0$. Suppose that
$D_0$. Suppose that ![]() $\xi$ is a vector field which is sufficiently close to the rotation field
$\xi$ is a vector field which is sufficiently close to the rotation field ![]() $\xi _0$ with the property that all the orbits of
$\xi _0$ with the property that all the orbits of ![]() $\xi$ starting from
$\xi$ starting from ![]() $D$ are periodic (with possibly different period
$D$ are periodic (with possibly different period ![]() $\tau (p)$). In this case we define the toroidal domain
$\tau (p)$). In this case we define the toroidal domain
where ![]() $\varphi _s(p)$ denotes the time-
$\varphi _s(p)$ denotes the time-![]() $s$ flow of
$s$ flow of ![]() $\xi$ starting from
$\xi$ starting from ![]() $p \in D$,
$p \in D$,
In this setting we say that the toroidal domain ![]() $T$ is swept out by
$T$ is swept out by ![]() $\xi$ from
$\xi$ from ![]() $D$.
$D$.
Our first result is that, given a toroidal domain ![]() $T$ swept out by a vector field
$T$ swept out by a vector field ![]() $\xi$ as above, sufficiently close to the axisymmetric torus
$\xi$ as above, sufficiently close to the axisymmetric torus ![]() $T_0$, we can find a flux function satisfying the generalized Grad–Shafranov equation (1.22). The proof is constructive and relies on deforming a known axisymmetric steady state satisfying mild conditions (H1)–(H2) stated in § 2.
$T_0$, we can find a flux function satisfying the generalized Grad–Shafranov equation (1.22). The proof is constructive and relies on deforming a known axisymmetric steady state satisfying mild conditions (H1)–(H2) stated in § 2.
Theorem 1.2 Fix ![]() $k \geq 0, \alpha > 0$ and let
$k \geq 0, \alpha > 0$ and let ![]() $\xi \in C^{k+2,\alpha }(\mathbb {R}^3)$ be a divergence-free vector field, sufficiently close in
$\xi \in C^{k+2,\alpha }(\mathbb {R}^3)$ be a divergence-free vector field, sufficiently close in ![]() $C^{k+2,\alpha }$ to the rotation vector field
$C^{k+2,\alpha }$ to the rotation vector field ![]() $\xi _0 = R e_\varPhi$. Let
$\xi _0 = R e_\varPhi$. Let ![]() $D$ be a domain sufficiently close to
$D$ be a domain sufficiently close to ![]() $D_0$ in
$D_0$ in ![]() $C^{k+2,\alpha }$ in the sense that
$C^{k+2,\alpha }$ in the sense that ![]() $D = \{(r, \theta ) \, |\, 0 \leq r \leq \mathfrak {b}(\theta ), \theta \in \mathbb {S}^1\}$ for a function
$D = \{(r, \theta ) \, |\, 0 \leq r \leq \mathfrak {b}(\theta ), \theta \in \mathbb {S}^1\}$ for a function ![]() $\mathfrak {b}:\mathbb {S}^1 \to \mathbb {R}$ sufficiently close to 1 in
$\mathfrak {b}:\mathbb {S}^1 \to \mathbb {R}$ sufficiently close to 1 in ![]() $C^{k+2,\alpha }(\mathbb {S}^1)$. Let
$C^{k+2,\alpha }(\mathbb {S}^1)$. Let ![]() $\psi _0 \in C^{k+2,\alpha }(D_0)$ be a solution of (1.5)–(1.6) with pressure
$\psi _0 \in C^{k+2,\alpha }(D_0)$ be a solution of (1.5)–(1.6) with pressure ![]() $P_0 \in C^{k+1,\alpha }(\mathbb {R})$ and with
$P_0 \in C^{k+1,\alpha }(\mathbb {R})$ and with ![]() $C_0 \in C^{k+1,\alpha }(\mathbb {R})$ satisfying
$C_0 \in C^{k+1,\alpha }(\mathbb {R})$ satisfying ![]() $(\mathrm {H1})$–
$(\mathrm {H1})$–![]() $(\mathrm {H2})$.
$(\mathrm {H2})$.
Suppose, moreover, that ![]() $\xi$ has closed integral curves that sweep out a toroidal domain
$\xi$ has closed integral curves that sweep out a toroidal domain ![]() $T$ from
$T$ from ![]() $D$. Suppose that there is a metric
$D$. Suppose that there is a metric ![]() $g\in C^{k+2,\alpha }(\mathbb {R}^3)$ with the property
$g\in C^{k+2,\alpha }(\mathbb {R}^3)$ with the property ![]() $\mathcal {L}_\xi g= 0$ which is sufficiently close to the Euclidean metric. Then, for any given
$\mathcal {L}_\xi g= 0$ which is sufficiently close to the Euclidean metric. Then, for any given ![]() $C\in C^{k+1,\alpha }(\mathbb {R})$ sufficiently close to
$C\in C^{k+1,\alpha }(\mathbb {R})$ sufficiently close to ![]() $C_0$, there is a flux function
$C_0$, there is a flux function ![]() $\psi \in C^{k+2,\alpha }(T)$, and a pressure
$\psi \in C^{k+2,\alpha }(T)$, and a pressure ![]() $P = P(\psi ) \in C^{k+1,\alpha }(T)$ so that
$P = P(\psi ) \in C^{k+1,\alpha }(T)$ so that ![]() $\psi$ satisfies the generalized Grad–Shafranov equation (1.22) and the boundary condition (1.23). Moreover, the level sets of
$\psi$ satisfies the generalized Grad–Shafranov equation (1.22) and the boundary condition (1.23). Moreover, the level sets of ![]() $\psi$ are diffeomorphic to the level sets of
$\psi$ are diffeomorphic to the level sets of ![]() $\psi _0$.
$\psi _0$.
As a consequence of the above theorem, we are able to produce magnetic fields with nested flux surfaces and a global symmetry that solve MHS up to a small force whose magnitude is controlled by the deviation of the symmetry from being Euclidean. These fields satisfy two of the three quasisymmetry conditions, the third holding approximately. The resulting magnetic field possesses flux surfaces which have the same topology as the axisymmetric base state.
Theorem 1.3 Suppose the hypotheses of the previous theorem hold. For any given ![]() $C\in C^{k+1,\alpha }(\mathbb {R})$ sufficiently close to
$C\in C^{k+1,\alpha }(\mathbb {R})$ sufficiently close to ![]() $C_0$, there is a flux function
$C_0$, there is a flux function ![]() $\psi \in C^{k+2,\alpha }(T)$, and a pressure
$\psi \in C^{k+2,\alpha }(T)$, and a pressure ![]() $P = P(\psi ) \in C^{k+1,\alpha }(T)$ so that the magnetic field
$P = P(\psi ) \in C^{k+1,\alpha }(T)$ so that the magnetic field ![]() $B$ defined by (1.18) satisfies
$B$ defined by (1.18) satisfies ![]() $B\boldsymbol {\cdot } \boldsymbol {\nabla }\psi = 0$,
$B\boldsymbol {\cdot } \boldsymbol {\nabla }\psi = 0$, ![]() $B\times \xi = \boldsymbol {\nabla } \psi$ as well as MHS (1.1)–(1.3) with a force
$B\times \xi = \boldsymbol {\nabla } \psi$ as well as MHS (1.1)–(1.3) with a force ![]() $f$ obeying
$f$ obeying
where ![]() $c:= c(\|\xi \|_{C^{k+2,\alpha }(T)},\| \psi \|_{C^{k+2,\alpha }(T)},\| P_0\|_{C^{k+1,\alpha }(\mathbb {R})},\| C_0\|_{C^{k+1,\alpha }(\mathbb {R})})$. Moreover, the flux surfaces of
$c:= c(\|\xi \|_{C^{k+2,\alpha }(T)},\| \psi \|_{C^{k+2,\alpha }(T)},\| P_0\|_{C^{k+1,\alpha }(\mathbb {R})},\| C_0\|_{C^{k+1,\alpha }(\mathbb {R})})$. Moreover, the flux surfaces of ![]() $B$ (isosurfaces of
$B$ (isosurfaces of ![]() $\psi$) are diffeomorphic to the isosurfaces of
$\psi$) are diffeomorphic to the isosurfaces of ![]() $\psi _0$, and
$\psi _0$, and ![]() $\psi$ is a solution of the generalized Grad–Shafranov equation (1.22).
$\psi$ is a solution of the generalized Grad–Shafranov equation (1.22).
The point of the bound (1.27) is that if ![]() $\xi$ is a Killing field for the Euclidean metric
$\xi$ is a Killing field for the Euclidean metric ![]() $\delta$ then we can take
$\delta$ then we can take ![]() $g = \delta$ in the above and by (1.27), the
$g = \delta$ in the above and by (1.27), the ![]() $B$ is then an exact solution of the MHS equations (1.1) with
$B$ is then an exact solution of the MHS equations (1.1) with ![]() $f = 0$. In this sense, (1.27) shows that one can construct approximate solutions to MHS with symmetry direction
$f = 0$. In this sense, (1.27) shows that one can construct approximate solutions to MHS with symmetry direction ![]() $\xi$ with error proportional to how far
$\xi$ with error proportional to how far ![]() $\xi$ is from being a symmetry of
$\xi$ is from being a symmetry of ![]() $\mathbb {R}^3$. We remark that the proof is quantitative in that all the small parameters can be explicitly defined in terms of the inputs
$\mathbb {R}^3$. We remark that the proof is quantitative in that all the small parameters can be explicitly defined in terms of the inputs ![]() $\psi _0$,
$\psi _0$, ![]() $C_0$,
$C_0$, ![]() $P_0$ and
$P_0$ and ![]() $\xi$. Let us also remark that one is not free to choose
$\xi$. Let us also remark that one is not free to choose ![]() $P$ from the outset and it is instead determined in the course of the proof to enforce a certain compatibility condition, see § 2.
$P$ from the outset and it is instead determined in the course of the proof to enforce a certain compatibility condition, see § 2.
The above theorem is perturbative, in the sense that the resulting magnetic field will be approximately axisymmetric and have a flux function close to a given ![]() $\psi _0$ satisfying the axisymmetric Grad–Shafranov equation (1.5). As will be discussed in the upcoming section, the result follows from a theorem in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) by deforming the given solution
$\psi _0$ satisfying the axisymmetric Grad–Shafranov equation (1.5). As will be discussed in the upcoming section, the result follows from a theorem in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) by deforming the given solution ![]() $\psi _0$ of the axisymmetric Grad–Shafranov equation (1.5) into a solution of the generalized Grad–Shafranov equation (1.22). The same theorem from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) in fact allows one to deform a given solution
$\psi _0$ of the axisymmetric Grad–Shafranov equation (1.5) into a solution of the generalized Grad–Shafranov equation (1.22). The same theorem from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) in fact allows one to deform a given solution ![]() $\psi _1$ to (1.22) for given
$\psi _1$ to (1.22) for given ![]() $\xi = \xi _1$ into a solution
$\xi = \xi _1$ into a solution ![]() $\psi _2$ to (1.22) with nearby, but different,
$\psi _2$ to (1.22) with nearby, but different, ![]() $\xi = \xi _2$. Given a desired
$\xi = \xi _2$. Given a desired ![]() $\xi$, if one can produce a sequence of vector fields
$\xi$, if one can produce a sequence of vector fields ![]() $\xi _0, \xi _1,\ldots , \xi _{N-1}, \xi _N = \xi$ in such a way that the resulting solutions
$\xi _0, \xi _1,\ldots , \xi _{N-1}, \xi _N = \xi$ in such a way that the resulting solutions ![]() $\psi _0, \psi _1,\ldots , \psi _{N-1}$ all satisfy the conditions (H1)–(H2) this would produce a flux function satisfying (1.22) far from axisymmetry. Note, however, that the resulting force in (1.1) could be quite large.
$\psi _0, \psi _1,\ldots , \psi _{N-1}$ all satisfy the conditions (H1)–(H2) this would produce a flux function satisfying (1.22) far from axisymmetry. Note, however, that the resulting force in (1.1) could be quite large.
If one is only interested in constructing approximate equilibria, this can be achieved simply by pushing forward a given axisymmetric state by a volume-preserving diffeomorphishm. The resulting flux function need not satisfy the generalized Grad–Shafranov equation (1.22). On the other hand, the construction in theorem 1.2 does ensure that the generalized Grad–Shafranov equation is exactly satisfied. In light of the fact that Burby et al. (Reference Burby, Kallinikos and MacKay2020) show that all unforced solutions to (1.1) and (1.3) must satisfy the equation (1.22), our theorem may provide a path towards obtaining non-axisymmetric solutions without force.
We now describe how to produce a base state ![]() $\psi _0$ and metric
$\psi _0$ and metric ![]() $g$ which are suitable inputs for theorem 1.2. In appendix A, we provide an example of a base state
$g$ which are suitable inputs for theorem 1.2. In appendix A, we provide an example of a base state ![]() $\psi _0$ satisfying (H1)–(H2) living on a large aspect ratio torus. This is obtained as a perturbation of an explicit profile on an ‘infinite aspect ratio’ torus. It should be stressed that the conditions (H1)–(H2) are not very stringent and should hold for a wide class of axisymmetric solutions that possess simple nested flux surfaces (which could, for example, be numerically obtained). Next, we describe two large classes of vector fields
$\psi _0$ satisfying (H1)–(H2) living on a large aspect ratio torus. This is obtained as a perturbation of an explicit profile on an ‘infinite aspect ratio’ torus. It should be stressed that the conditions (H1)–(H2) are not very stringent and should hold for a wide class of axisymmetric solutions that possess simple nested flux surfaces (which could, for example, be numerically obtained). Next, we describe two large classes of vector fields ![]() $\xi$ and metrics
$\xi$ and metrics ![]() $g$ satisfying the hypotheses of our theorem.
$g$ satisfying the hypotheses of our theorem.
Remark (Designer metrics) We provide two possible ways of constructing a ‘near’ Euclidean metric given a ‘near’ isometry ![]() $\xi$.
$\xi$.
(i) (Deformed metric) Suppose that the torus
 $T$ is given by
$T$ is given by  $T = f(T_0)$ where
$T = f(T_0)$ where  $f$ is a diffeomorphism defined in a neighbourhood of
$f$ is a diffeomorphism defined in a neighbourhood of  $T_0$ and which is sufficiently close to the identity. Then we can take
$T_0$ and which is sufficiently close to the identity. Then we can take  $\xi = \textrm {d}f(\xi _0)$ where
$\xi = \textrm {d}f(\xi _0)$ where  $\textrm {d}f$ denotes the differential and let
$\textrm {d}f$ denotes the differential and let  $g = f^*\delta$ denote the pullback of the Euclidean metric
$g = f^*\delta$ denote the pullback of the Euclidean metric  $\delta$ by
$\delta$ by  $f$. Because the Lie derivative is invariant under diffeomorphisms, we have
$f$. Because the Lie derivative is invariant under diffeomorphisms, we have  $\xi$ is a Killing field for
$\xi$ is a Killing field for  $g$ since
$g$ since  $\mathcal {L}_\xi g = f^* (L_{\xi _0} \delta ) = 0$.
$\mathcal {L}_\xi g = f^* (L_{\xi _0} \delta ) = 0$.(ii) (Circle-averaged metric) Suppose the orbits of
 $\xi$ starting from
$\xi$ starting from  $D$ are all
$D$ are all  $2{\rm \pi}$-periodic. In this case we say that
$2{\rm \pi}$-periodic. In this case we say that  $\xi$ generates a circle action. Defining the circle-averaged metric
$\xi$ generates a circle action. Defining the circle-averaged metric  $g$,
(1.28)it follows by a simple computation that
$g$,
(1.28)it follows by a simple computation that \begin{equation} g = \frac{1}{2{\rm \pi}}\int_{0}^{2{\rm \pi}} \varphi_s^* \delta \, \textrm{d} s, \end{equation}
\begin{equation} g = \frac{1}{2{\rm \pi}}\int_{0}^{2{\rm \pi}} \varphi_s^* \delta \, \textrm{d} s, \end{equation} $\mathcal {L}_\xi g = 0$. Moreover, when
$\mathcal {L}_\xi g = 0$. Moreover, when  $\xi$ is a Killing field for Euclidean space,
$\xi$ is a Killing field for Euclidean space,  $g = \delta$. This metric was introduced by Burby et al. (Reference Burby, Kallinikos and MacKay2020). As motivation for the appearance of this particular metric, consider the MHS in terms of one-forms
$g = \delta$. This metric was introduced by Burby et al. (Reference Burby, Kallinikos and MacKay2020). As motivation for the appearance of this particular metric, consider the MHS in terms of one-forms  $\mathcal {L}_B(B^\flat ) = \textrm {d} P$ (see Arnold & Khesin Reference Arnold and Khesin1999). In this representation, it is clear that the metric appears linearly (in the definition of
$\mathcal {L}_B(B^\flat ) = \textrm {d} P$ (see Arnold & Khesin Reference Arnold and Khesin1999). In this representation, it is clear that the metric appears linearly (in the definition of  $\flat$). Therefore, if
$\flat$). Therefore, if  $B$ and
$B$ and  $P$ are invariant under the flow of
$P$ are invariant under the flow of  $\xi$, then one finds
$\xi$, then one finds  $\mathcal {L}_B(B^{\bar {\flat }}) = \textrm {d} P$ where
$\mathcal {L}_B(B^{\bar {\flat }}) = \textrm {d} P$ where  $\bar {\flat }$ denotes the operation of lowering the index with respect to the circle-averaged metric. Raising indices with
$\bar {\flat }$ denotes the operation of lowering the index with respect to the circle-averaged metric. Raising indices with  $g$, we find that any such MHS solution on Euclidean space is also a solution of the circle-averaged equation (MHS with respect to the metric
$g$, we find that any such MHS solution on Euclidean space is also a solution of the circle-averaged equation (MHS with respect to the metric  $g$).
$g$).
We conclude with some remarks about achieving exact quasisymmetry. By construction, the magnetic field ![]() $B$ from the previous theorem will satisfy (1.8) but will only approximately satisfy the property (1.9) of quasisymmetry. Thus, our fields confine particles to zeroth but not first order in the guiding centre approximation (Rodriguez et al. Reference Rodriguez, Helander and Bhattacharjee2020). The error from being an exact weak quasisymmetry can be easily quantified; for a vector field
$B$ from the previous theorem will satisfy (1.8) but will only approximately satisfy the property (1.9) of quasisymmetry. Thus, our fields confine particles to zeroth but not first order in the guiding centre approximation (Rodriguez et al. Reference Rodriguez, Helander and Bhattacharjee2020). The error from being an exact weak quasisymmetry can be easily quantified; for a vector field ![]() $B_g$ of the form (1.18), assuming that
$B_g$ of the form (1.18), assuming that ![]() $g$ is such that
$g$ is such that ![]() $\mathcal {L}_\xi g = 0$ the condition (1.9) reads
$\mathcal {L}_\xi g = 0$ the condition (1.9) reads
 \begin{align} \xi \boldsymbol{\cdot}\boldsymbol{\nabla} |B_g| &= \frac{C^2(\psi)}{2|\xi|_g^4|B_g|} \left[ (\mathcal{L}_\xi \delta) (\xi ,\xi) +2 C^{{-}1}(\psi) (\mathcal{L}_\xi \delta) (\xi ,\boldsymbol{\nabla}_g^\perp \psi ) \right.\nonumber\\ &\quad\left.+\,C^{{-}2}(\psi) (\mathcal{L}_\xi \delta) (\boldsymbol{\nabla}_g^\perp \psi ,\boldsymbol{\nabla}_g^\perp \psi ) \right], \end{align}
\begin{align} \xi \boldsymbol{\cdot}\boldsymbol{\nabla} |B_g| &= \frac{C^2(\psi)}{2|\xi|_g^4|B_g|} \left[ (\mathcal{L}_\xi \delta) (\xi ,\xi) +2 C^{{-}1}(\psi) (\mathcal{L}_\xi \delta) (\xi ,\boldsymbol{\nabla}_g^\perp \psi ) \right.\nonumber\\ &\quad\left.+\,C^{{-}2}(\psi) (\mathcal{L}_\xi \delta) (\boldsymbol{\nabla}_g^\perp \psi ,\boldsymbol{\nabla}_g^\perp \psi ) \right], \end{align}
see lemma C.6. Since (1.29) involves the Euclidean deformation tensor alone, it is controlled by the deviation of ![]() $\xi$ from being a Euclidean isometry and our solution will have
$\xi$ from being a Euclidean isometry and our solution will have ![]() $\xi \boldsymbol {\cdot }\boldsymbol {\nabla } |B_g|$ small. The error from being a strong quasisymmetry is also quantifiably small.
$\xi \boldsymbol {\cdot }\boldsymbol {\nabla } |B_g|$ small. The error from being a strong quasisymmetry is also quantifiably small.
It is worth remarking that there are additional freedoms in our construction that could, in principle, be used to further constrain the constructed solution. Specifically, in our theorem, we treat ![]() $\xi$ as a fixed vector field sufficiently close to
$\xi$ as a fixed vector field sufficiently close to ![]() $\xi _0$ and we made the somewhat arbitrary choice that the map
$\xi _0$ and we made the somewhat arbitrary choice that the map ![]() $\gamma$ should be volume preserving. The results in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) actually allow one to construct the map
$\gamma$ should be volume preserving. The results in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) actually allow one to construct the map ![]() $\gamma$ so that
$\gamma$ so that ![]() $\det \boldsymbol {\nabla } \gamma := \rho$ is any given function, sufficiently close to one; in fact by iterating that result, one can additionally achieve that
$\det \boldsymbol {\nabla } \gamma := \rho$ is any given function, sufficiently close to one; in fact by iterating that result, one can additionally achieve that ![]() $\det \boldsymbol {\nabla } \gamma = X(\phi , \eta , \partial \phi , \partial \eta ,\partial \partial _s\phi ,\partial \partial _s\eta )$ for a suitable nonlinearity
$\det \boldsymbol {\nabla } \gamma = X(\phi , \eta , \partial \phi , \partial \eta ,\partial \partial _s\phi ,\partial \partial _s\eta )$ for a suitable nonlinearity ![]() $X$ sufficiently close to one when
$X$ sufficiently close to one when ![]() $\phi , \eta = 0$. Using this freedom, it is possible to show that, under some (possibly restrictive and undesirable) assumptions on the field
$\phi , \eta = 0$. Using this freedom, it is possible to show that, under some (possibly restrictive and undesirable) assumptions on the field ![]() $\xi$, the Jacobian
$\xi$, the Jacobian ![]() $\rho$ can be used to achieve exact quasisymmetry on a slice of the torus (namely on the cross-section
$\rho$ can be used to achieve exact quasisymmetry on a slice of the torus (namely on the cross-section ![]() $D$). Ensuring this property holds seems of little practical interest for ion confinement in a stellarator, since particles starting on the slice will immediately leave. In contrast, Garren and Boozer Garren & Boozer (Reference Garren and Boozer1991) and Plunk & Helander (Reference Plunk and Helander2018) show that exact quasisymmetry is possible to achieve on one flux surface while maintaining the MHS force balance, which is of greater relevance to confinement in a stellarator. It is unknown whether or not quasisymmetry can be achieved in a volume. We leave open the question of whether or not, using our approach, a carefully designed field
$D$). Ensuring this property holds seems of little practical interest for ion confinement in a stellarator, since particles starting on the slice will immediately leave. In contrast, Garren and Boozer Garren & Boozer (Reference Garren and Boozer1991) and Plunk & Helander (Reference Plunk and Helander2018) show that exact quasisymmetry is possible to achieve on one flux surface while maintaining the MHS force balance, which is of greater relevance to confinement in a stellarator. It is unknown whether or not quasisymmetry can be achieved in a volume. We leave open the question of whether or not, using our approach, a carefully designed field ![]() $\xi$ (perhaps constructed dynamically alongside the solution) can be used to ensure quasisymmetry on a flux surface or a volume.
$\xi$ (perhaps constructed dynamically alongside the solution) can be used to ensure quasisymmetry on a flux surface or a volume.
2. Proof of theorem 1.3
We start by giving an outline of the arguments used to establish the main theorem. All details can be found in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020).
Let ![]() $D_0, D, \psi _0, \xi , g$ be as in the statement of theorem 1.3. We will start by constructing a solution
$D_0, D, \psi _0, \xi , g$ be as in the statement of theorem 1.3. We will start by constructing a solution ![]() $\psi$ to the generalized Grad–Shafranov equation (1.22) of the form
$\psi$ to the generalized Grad–Shafranov equation (1.22) of the form ![]() $\psi = \psi _0\circ \gamma ^{-1}$ for a diffeormorphism
$\psi = \psi _0\circ \gamma ^{-1}$ for a diffeormorphism ![]() $\gamma : D_0 \to D$ which is to be determined. With the toroidal coordinates
$\gamma : D_0 \to D$ which is to be determined. With the toroidal coordinates ![]() $(r, \theta , \varphi )$ defined as in (A 1a–c), for functions
$(r, \theta , \varphi )$ defined as in (A 1a–c), for functions ![]() $\eta , \phi$ independent of
$\eta , \phi$ independent of ![]() $\varphi$, write
$\varphi$, write ![]() $\nabla \eta = \partial _r \eta e_r + ({1}/{r}) \partial _\theta \eta e_\theta$ and
$\nabla \eta = \partial _r \eta e_r + ({1}/{r}) \partial _\theta \eta e_\theta$ and ![]() $\boldsymbol {\nabla }^\perp \phi = -\partial _r \phi e_\theta + ({1}/{r}) \partial _\theta f e_r$. We will look for
$\boldsymbol {\nabla }^\perp \phi = -\partial _r \phi e_\theta + ({1}/{r}) \partial _\theta f e_r$. We will look for ![]() $\gamma (r, \theta ) = (r, \theta ) +\boldsymbol {\nabla } \eta (r, \theta ) + \boldsymbol {\nabla }^\perp \phi (r, \theta )$ and the functions
$\gamma (r, \theta ) = (r, \theta ) +\boldsymbol {\nabla } \eta (r, \theta ) + \boldsymbol {\nabla }^\perp \phi (r, \theta )$ and the functions ![]() $\eta , \phi$ are the unknowns. For simplicity, using the assumption that
$\eta , \phi$ are the unknowns. For simplicity, using the assumption that ![]() $\textrm {Vol}\ D = \textrm {Vol}\ D_0$, we will require that
$\textrm {Vol}\ D = \textrm {Vol}\ D_0$, we will require that ![]() $\det \boldsymbol {\nabla } \gamma ^{-1} = 1$. After a short calculation, this condition reads
$\det \boldsymbol {\nabla } \gamma ^{-1} = 1$. After a short calculation, this condition reads
where ![]() $\mathcal {N}_{\eta }[\phi , \eta ] = \mathcal {N}_\eta (\partial \phi , \partial \eta , \partial ^2\phi ,\partial ^2 \eta )$ is a quadratic nonlinearity. We will pose boundary conditions momentarily. We think of this equation as determining
$\mathcal {N}_{\eta }[\phi , \eta ] = \mathcal {N}_\eta (\partial \phi , \partial \eta , \partial ^2\phi ,\partial ^2 \eta )$ is a quadratic nonlinearity. We will pose boundary conditions momentarily. We think of this equation as determining ![]() $\eta$ at the linear level from
$\eta$ at the linear level from ![]() $\phi$ and it remains to determine
$\phi$ and it remains to determine ![]() $\phi$ in a such a way that
$\phi$ in a such a way that ![]() $\psi = \psi _0\circ \gamma ^{-1}$ is a solution to (1.22). We now describe how this is done.
$\psi = \psi _0\circ \gamma ^{-1}$ is a solution to (1.22). We now describe how this is done.
The Grad–Shafranov equation (1.5) is of the form
with nonlinearities ![]() $F_0 = P'_0,$
$F_0 = P'_0,$ ![]() $G_0 = ({1}/{R^2}) C_0C_0'(\psi _0)$ and where the operator
$G_0 = ({1}/{R^2}) C_0C_0'(\psi _0)$ and where the operator ![]() $L_0$ is elliptic. Similarly, we write the generalized Grad–Shafranov (1.22) in the form
$L_0$ is elliptic. Similarly, we write the generalized Grad–Shafranov (1.22) in the form
At this stage, the function ![]() $F$ (which is related to the pressure of the solution in our application) is actually undetermined and will be chosen momentarily, while
$F$ (which is related to the pressure of the solution in our application) is actually undetermined and will be chosen momentarily, while ![]() $G$ can be chosen to be any function sufficiently close to
$G$ can be chosen to be any function sufficiently close to ![]() $G_0$.
$G_0$.
A calculation (see appendix B of Constantin et al. (Reference Constantin, Drivas and Ginsberg2020)) shows that provided ![]() $\det \boldsymbol {\nabla } \gamma ^{-1} = 1$, we have
$\det \boldsymbol {\nabla } \gamma ^{-1} = 1$, we have
where we have introduced the notation ![]() $\partial _s = \boldsymbol {\nabla } \psi _0\boldsymbol {\cdot } \boldsymbol {\nabla }^\perp$ for the ‘streamline derivative’. Then
$\partial _s = \boldsymbol {\nabla } \psi _0\boldsymbol {\cdot } \boldsymbol {\nabla }^\perp$ for the ‘streamline derivative’. Then ![]() $\partial _s$ is tangent to level sets of
$\partial _s$ is tangent to level sets of ![]() $\psi _0$. After a computation, composing both sides of (2.3) with
$\psi _0$. After a computation, composing both sides of (2.3) with ![]() $\gamma ^{-1}$ and using (2.4), (2.3) takes the form
$\gamma ^{-1}$ and using (2.4), (2.3) takes the form
where ![]() $\mathcal {L}_{\psi _0}$ is the linearization of
$\mathcal {L}_{\psi _0}$ is the linearization of ![]() $L_0$ around
$L_0$ around ![]() $\psi _0$, for a function
$\psi _0$, for a function ![]() $\mathcal {N}_\phi [\phi , \eta ] = \mathcal {N}_\phi (\partial \phi , \partial \eta , \partial \partial _s\phi , \partial \partial _s\eta )$ (whose explicit form can be found in appendix B of Constantin et al. (Reference Constantin, Drivas and Ginsberg2020)), which consists of terms which are linear in
$\mathcal {N}_\phi [\phi , \eta ] = \mathcal {N}_\phi (\partial \phi , \partial \eta , \partial \partial _s\phi , \partial \partial _s\eta )$ (whose explicit form can be found in appendix B of Constantin et al. (Reference Constantin, Drivas and Ginsberg2020)), which consists of terms which are linear in ![]() $\eta$ and its derivatives, and either nonlinear or weakly linear in derivatives of
$\eta$ and its derivatives, and either nonlinear or weakly linear in derivatives of ![]() $\phi$, meaning it involves terms which can bounded by
$\phi$, meaning it involves terms which can bounded by ![]() $\epsilon |\partial \phi |$, for example. This latter point is a consequence of the assumption that
$\epsilon |\partial \phi |$, for example. This latter point is a consequence of the assumption that ![]() $\xi - \xi _0$ is sufficiently small. Notice that at the linear level this is an equation for
$\xi - \xi _0$ is sufficiently small. Notice that at the linear level this is an equation for ![]() $\partial _s\phi$ and not
$\partial _s\phi$ and not ![]() $\phi$ itself. In order for this equation to be solvable for
$\phi$ itself. In order for this equation to be solvable for ![]() $\phi$ at the linear level (given appropriate boundary conditions), there are two requirements. The first is that
$\phi$ at the linear level (given appropriate boundary conditions), there are two requirements. The first is that ![]() $\mathscr {L}_{\psi _0}$ should be invertible. The second is a somewhat subtle condition which is easiest to understand in the simple model case. In order to solve the problem
$\mathscr {L}_{\psi _0}$ should be invertible. The second is a somewhat subtle condition which is easiest to understand in the simple model case. In order to solve the problem ![]() $\Delta \partial _\theta u = f,$ in the unit disk, say (with arbitrary boundary conditions), it is clearly necessary that
$\Delta \partial _\theta u = f,$ in the unit disk, say (with arbitrary boundary conditions), it is clearly necessary that ![]() $\int _{0}^{2{\rm \pi} } f \, \textrm {d}\theta = 0$. We will now impose a condition on (2.5) which is analogous to this one and which will determine the function
$\int _{0}^{2{\rm \pi} } f \, \textrm {d}\theta = 0$. We will now impose a condition on (2.5) which is analogous to this one and which will determine the function ![]() $F$ at the linear level. Assume that the Dirichlet problem for
$F$ at the linear level. Assume that the Dirichlet problem for ![]() $\mathscr {L}_{\psi _0}$,
$\mathscr {L}_{\psi _0}$,
 \begin{gather} \left.\begin{array}{ll@{}} \mathscr{L}_{\psi_0} u = f, & \text{in } D_0,\\ u = 0, & \text{on } \partial D_0, \end{array}\right\} \end{gather}
\begin{gather} \left.\begin{array}{ll@{}} \mathscr{L}_{\psi_0} u = f, & \text{in } D_0,\\ u = 0, & \text{on } \partial D_0, \end{array}\right\} \end{gather}
has a unique solution for ![]() $f \in L^2$, say. Writing
$f \in L^2$, say. Writing ![]() $\mathscr {L}^{-1}_{\psi _0} f = u$, if we apply
$\mathscr {L}^{-1}_{\psi _0} f = u$, if we apply ![]() $\mathscr {L}^{-1}_{\psi _0}$ to both sides of (2.5) and integrating with respect to
$\mathscr {L}^{-1}_{\psi _0}$ to both sides of (2.5) and integrating with respect to ![]() $ds$ over the streamline
$ds$ over the streamline ![]() $\{\psi _0 = c\}$ (considered as a subset of the two-dimensional set
$\{\psi _0 = c\}$ (considered as a subset of the two-dimensional set ![]() $D_0$) we find
$D_0$) we find
This is an equation which must be solved for ![]() $F$. Writing
$F$. Writing ![]() $T(c)q = \oint _{\{\psi _0 = c\}} \mathscr {L}_{\psi _0}^{-1} q \, \textrm {d} s$, given
$T(c)q = \oint _{\{\psi _0 = c\}} \mathscr {L}_{\psi _0}^{-1} q \, \textrm {d} s$, given ![]() $R$ depending only on the streamline
$R$ depending only on the streamline ![]() $R = R(c)$, we would like to be able to find
$R = R(c)$, we would like to be able to find ![]() $q = q(c)$ with
$q = q(c)$ with ![]() $T(c)q =R$. This is a complicated problem which would be hard to address directly, however, in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) we show that such
$T(c)q =R$. This is a complicated problem which would be hard to address directly, however, in Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) we show that such ![]() $q$ can be found, assuming that the following hypotheses hold.
$q$ can be found, assuming that the following hypotheses hold.
Hypothesis 1 (H1) The operator ![]() $\mathscr {L}_{\psi _0}$ is positive definite.
$\mathscr {L}_{\psi _0}$ is positive definite.
Hypothesis 2 (H2) There exists a constant ![]() $C>0$ such that we have
$C>0$ such that we have
where ![]() $\ell$ is the arclength parameter.
$\ell$ is the arclength parameter.
Notice that the hypothesis (H1), in particular, ensures that the operator ![]() $\mathscr {L}_{\psi _0}^{-1}$ is well-defined. This is a condition on
$\mathscr {L}_{\psi _0}^{-1}$ is well-defined. This is a condition on ![]() $P_0, C_0$. Hypothesis (H2) concerns the travel time
$P_0, C_0$. Hypothesis (H2) concerns the travel time ![]() $\mu (c)$ for a particle governed by the Hamiltonian system
$\mu (c)$ for a particle governed by the Hamiltonian system ![]() $\dot {x}= \boldsymbol {\nabla }^\perp \psi _0(x)$ and moving along the streamline of
$\dot {x}= \boldsymbol {\nabla }^\perp \psi _0(x)$ and moving along the streamline of ![]() $\{\psi _0=c\}$. It is easy to see that it holds provided
$\{\psi _0=c\}$. It is easy to see that it holds provided ![]() $\psi _0$ has at most one critical point in
$\psi _0$ has at most one critical point in ![]() $D_0 = T_0 \cap \{\varphi = 0\}$ and that it vanishes no faster than to first order there. We remark that (H2) is trivially satisfied if
$D_0 = T_0 \cap \{\varphi = 0\}$ and that it vanishes no faster than to first order there. We remark that (H2) is trivially satisfied if ![]() $|\boldsymbol {\nabla } \psi _0|$ is bounded below in the domain
$|\boldsymbol {\nabla } \psi _0|$ is bounded below in the domain ![]() $D_0$. This could be accomplished if, for example, one worked on a ‘hollowed out’ toroidal domain.
$D_0$. This could be accomplished if, for example, one worked on a ‘hollowed out’ toroidal domain.
We now discuss the boundary conditions. Assume that ![]() $D$ is the interior of a Jordan curve
$D$ is the interior of a Jordan curve ![]() $B$,
$B$,
We also write ![]() $\partial D_0 =\{p \in \mathbb {R}^2 \, |\, \mathfrak {b}_0(r,\theta ) = 0\}$ where
$\partial D_0 =\{p \in \mathbb {R}^2 \, |\, \mathfrak {b}_0(r,\theta ) = 0\}$ where ![]() $\mathfrak {b}_0$ is chosen with
$\mathfrak {b}_0$ is chosen with ![]() $|\boldsymbol {\nabla } \mathfrak {b}_0| = 1, \boldsymbol {\nabla } \psi _0\boldsymbol {\cdot } \boldsymbol {\nabla } \mathfrak {b}_0 > 0$. We write
$|\boldsymbol {\nabla } \mathfrak {b}_0| = 1, \boldsymbol {\nabla } \psi _0\boldsymbol {\cdot } \boldsymbol {\nabla } \mathfrak {b}_0 > 0$. We write ![]() $\gamma - \textrm {id} = \boldsymbol {\nabla } \eta + \boldsymbol {\nabla }^\perp \phi = \alpha e_x + \beta e_y$ where
$\gamma - \textrm {id} = \boldsymbol {\nabla } \eta + \boldsymbol {\nabla }^\perp \phi = \alpha e_x + \beta e_y$ where ![]() $(x,y)$ are rectangular coordinates. Using that
$(x,y)$ are rectangular coordinates. Using that ![]() $\mathfrak {B}_0|_{\partial D_0} = 0$, the requirement that
$\mathfrak {B}_0|_{\partial D_0} = 0$, the requirement that ![]() $\gamma :\partial D_0 \to \partial D$ can be written as
$\gamma :\partial D_0 \to \partial D$ can be written as
where ![]() $\delta \mathfrak {b} = \mathfrak {b} - \mathfrak {b}_0$, and where the remainder
$\delta \mathfrak {b} = \mathfrak {b} - \mathfrak {b}_0$, and where the remainder ![]() $\mathfrak {b}_1$ is
$\mathfrak {b}_1$ is
Returning to ![]() $\phi , \eta$, we have
$\phi , \eta$, we have
By the choice of ![]() $\mathfrak {b}_0$, we have
$\mathfrak {b}_0$, we have ![]() $\boldsymbol {\nabla } \eta \boldsymbol {\cdot } \boldsymbol {\nabla } \mathfrak {b}_0 =\partial _n \eta$ where
$\boldsymbol {\nabla } \eta \boldsymbol {\cdot } \boldsymbol {\nabla } \mathfrak {b}_0 =\partial _n \eta$ where ![]() $n$ is the outward-facing normal to
$n$ is the outward-facing normal to ![]() $\partial D_0$. Additionally, using that
$\partial D_0$. Additionally, using that ![]() $\psi _0$ is constant on the boundary we have
$\psi _0$ is constant on the boundary we have ![]() $\boldsymbol {\nabla }^\perp \mathfrak {b}_0 = {\boldsymbol {\nabla }^\perp \psi _0}/{|\boldsymbol {\nabla }\psi _0|}$, and using (2.12) and these observations, the formula (2.10) becomes
$\boldsymbol {\nabla }^\perp \mathfrak {b}_0 = {\boldsymbol {\nabla }^\perp \psi _0}/{|\boldsymbol {\nabla }\psi _0|}$, and using (2.12) and these observations, the formula (2.10) becomes
This is one boundary condition for the two functions ![]() $\phi , \eta$. Again we need to ensure that this equation is compatible with the requirement
$\phi , \eta$. Again we need to ensure that this equation is compatible with the requirement ![]() $\oint _{\{\psi _0 = \psi _0|_{\partial D_0}\}} \partial _s\phi \, \textrm {d} s = 0$. We therefore take
$\oint _{\{\psi _0 = \psi _0|_{\partial D_0}\}} \partial _s\phi \, \textrm {d} s = 0$. We therefore take ![]() $\partial _n\eta$ constant on the boundary and impose the following nonlinear boundary conditions:
$\partial _n\eta$ constant on the boundary and impose the following nonlinear boundary conditions:
 \begin{gather}\partial_s \phi = |\boldsymbol{\nabla} \psi_0| \left(-\mathfrak{b}_1(\phi, \eta) +\frac{ \oint_{\partial D_0} \mathfrak{b}_1(\phi, \eta)\, {\textrm{d}\ell}}{\textrm{length}(\partial D_0)} \right) \quad \text{on } \partial D_0. \end{gather}
\begin{gather}\partial_s \phi = |\boldsymbol{\nabla} \psi_0| \left(-\mathfrak{b}_1(\phi, \eta) +\frac{ \oint_{\partial D_0} \mathfrak{b}_1(\phi, \eta)\, {\textrm{d}\ell}}{\textrm{length}(\partial D_0)} \right) \quad \text{on } \partial D_0. \end{gather} We now summarize the result of the above calculation. The function ![]() $\psi = \psi _0\circ \gamma ^{-1}$ is a solution of the equation (2.3) in
$\psi = \psi _0\circ \gamma ^{-1}$ is a solution of the equation (2.3) in ![]() $D$ with constant boundary value provided the diffeomorphism
$D$ with constant boundary value provided the diffeomorphism ![]() $\gamma$ is of the form
$\gamma$ is of the form ![]() $\gamma = \textrm {id} + \boldsymbol {\nabla } \eta + \boldsymbol {\nabla }^\perp \phi$ and the functions
$\gamma = \textrm {id} + \boldsymbol {\nabla } \eta + \boldsymbol {\nabla }^\perp \phi$ and the functions ![]() $\eta , \phi :D_0 \to \mathbb {R}$ satisfy the elliptic equations
$\eta , \phi :D_0 \to \mathbb {R}$ satisfy the elliptic equations
 \begin{gather} \left.\begin{array}{ll@{}} \Delta \eta = \mathcal{N}_\eta[\phi, \eta] & \text{in } D_0, \\ \mathscr{L}_{\psi_0} \partial_s\phi= \mathcal{N}_\phi[\phi, \eta]+ F(\psi_0) - F_0(\psi_0) + G(\psi_0, r, \theta) - G_0(\psi_0, r, \theta), & \text{in } D_0, \end{array}\right\} \end{gather}
\begin{gather} \left.\begin{array}{ll@{}} \Delta \eta = \mathcal{N}_\eta[\phi, \eta] & \text{in } D_0, \\ \mathscr{L}_{\psi_0} \partial_s\phi= \mathcal{N}_\phi[\phi, \eta]+ F(\psi_0) - F_0(\psi_0) + G(\psi_0, r, \theta) - G_0(\psi_0, r, \theta), & \text{in } D_0, \end{array}\right\} \end{gather}
where ![]() $F$ is determined by solving
$F$ is determined by solving
and where ![]() $\eta , \phi$ satisfy the boundary conditions (2.14) and (2.15).
$\eta , \phi$ satisfy the boundary conditions (2.14) and (2.15).
This nonlinear system can be solved by the following iteration scheme. Given ![]() $\eta ^{N-1}, \phi ^{N-1}$, define
$\eta ^{N-1}, \phi ^{N-1}$, define ![]() $F^N = F^N(c)$ by solving
$F^N = F^N(c)$ by solving
Then solve for ![]() $\eta ^N, \varPhi ^N$ satisfying
$\eta ^N, \varPhi ^N$ satisfying
 \begin{gather} \left.\begin{array}{ll@{}} \Delta \eta^{N} = \mathcal{N}_\eta[\phi^{N-1}, \eta^{N-1}] & \text{in } D_0,\\ \mathscr{L}_{\psi_0} \varPhi^{N} = \mathcal{N}_\phi[\phi^{N-1}, \eta^{N-1}] + F^N - F_0 + G - G_0 & \text{in } D_0, \end{array}\right\} \end{gather}
\begin{gather} \left.\begin{array}{ll@{}} \Delta \eta^{N} = \mathcal{N}_\eta[\phi^{N-1}, \eta^{N-1}] & \text{in } D_0,\\ \mathscr{L}_{\psi_0} \varPhi^{N} = \mathcal{N}_\phi[\phi^{N-1}, \eta^{N-1}] + F^N - F_0 + G - G_0 & \text{in } D_0, \end{array}\right\} \end{gather}with boundary conditions
 \begin{equation} \left.\begin{gathered} \partial_n \eta^N = \int_{D_0} \mathcal{N}_{\eta}[\phi^{N-1}, \eta^{N-1}]\, \textrm{d} x,\\ \varPhi^N = |\boldsymbol{\nabla} \psi_0| \left(-\mathfrak{b}_1(\phi^{N-1}, \eta^{N-1}) +\dfrac{ \oint_{\partial D_0} \mathfrak{b}_1(\phi^{N-1}, \eta^{N-1})\, {\textrm{d}\ell}}{\textrm{length}(\partial D_0)} \right) \quad \text{on } \partial D_0. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \partial_n \eta^N = \int_{D_0} \mathcal{N}_{\eta}[\phi^{N-1}, \eta^{N-1}]\, \textrm{d} x,\\ \varPhi^N = |\boldsymbol{\nabla} \psi_0| \left(-\mathfrak{b}_1(\phi^{N-1}, \eta^{N-1}) +\dfrac{ \oint_{\partial D_0} \mathfrak{b}_1(\phi^{N-1}, \eta^{N-1})\, {\textrm{d}\ell}}{\textrm{length}(\partial D_0)} \right) \quad \text{on } \partial D_0. \end{gathered}\right\} \end{equation} The boundary condition for ![]() $\eta ^N$ has been chosen so that the Neumann problem (2.19) and (2.20) is solvable. Once
$\eta ^N$ has been chosen so that the Neumann problem (2.19) and (2.20) is solvable. Once ![]() $\varPhi ^N$ has been found, as a consequence of the choice of
$\varPhi ^N$ has been found, as a consequence of the choice of ![]() $F^N$ it can be shown that
$F^N$ it can be shown that ![]() $\oint _{\{\psi _0 = c\}} \varPhi ^N \, \textrm {d} s = 0$ for all
$\oint _{\{\psi _0 = c\}} \varPhi ^N \, \textrm {d} s = 0$ for all ![]() $c$, and so
$c$, and so ![]() $\varPhi ^N = \partial _s\phi ^N$ for a function
$\varPhi ^N = \partial _s\phi ^N$ for a function ![]() $\phi ^N$ which is determined up to a constant, which can be fixed throughout the iteration by requiring that
$\phi ^N$ which is determined up to a constant, which can be fixed throughout the iteration by requiring that ![]() $\int _{D_0} \phi ^N = 0$. In Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) we prove that this iteration converges in a suitable topology. We remark that the boundary condition (2.20) is not the same as the boundary condition in (2.14) but as a consequence of
$\int _{D_0} \phi ^N = 0$. In Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) we prove that this iteration converges in a suitable topology. We remark that the boundary condition (2.20) is not the same as the boundary condition in (2.14) but as a consequence of ![]() $\textrm {Vol}\ D_0 = \textrm {Vol}\ D$, they agree after taking
$\textrm {Vol}\ D_0 = \textrm {Vol}\ D$, they agree after taking ![]() $N\to \infty$.
$N\to \infty$.
Proof of theorems 1.2 and 1.3 We first reduce the problem to solving a certain elliptic problem on the domain ![]() $D$. Given a (local) coordinate system
$D$. Given a (local) coordinate system ![]() $(x_1, x_2)$ defined on a neighbourhood of
$(x_1, x_2)$ defined on a neighbourhood of ![]() $D$, we can extend it to a (local) coordinate system on a neighbourhood of the torus
$D$, we can extend it to a (local) coordinate system on a neighbourhood of the torus ![]() $T$ by pulling back along the flow of
$T$ by pulling back along the flow of ![]() $\xi$. Explicitly, given
$\xi$. Explicitly, given ![]() $p \in T$, there is a unique
$p \in T$, there is a unique ![]() $p_0 \in D$ and a unique smallest
$p_0 \in D$ and a unique smallest ![]() $x_3 > 0$ so that
$x_3 > 0$ so that ![]() $\varPhi _{x_3}(p_0) = p$ where
$\varPhi _{x_3}(p_0) = p$ where ![]() $\varPhi _s(p_0)$ denotes the time-
$\varPhi _s(p_0)$ denotes the time-![]() $s$ flow of
$s$ flow of ![]() $\xi$ starting from a point
$\xi$ starting from a point ![]() $p_0 \in D$, because the integral curves of
$p_0 \in D$, because the integral curves of ![]() $\xi$ are closed. Then the map
$\xi$ are closed. Then the map ![]() $\varPsi : T \to D \times \mathbb {R}$ defined by
$\varPsi : T \to D \times \mathbb {R}$ defined by ![]() $\varPsi (p) = (p_0, x_3)$ is a (local) diffeomorphism onto its image. In these coordinates,
$\varPsi (p) = (p_0, x_3)$ is a (local) diffeomorphism onto its image. In these coordinates, ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } f = ({\partial }/{\partial x^3}) f$ for any function
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } f = ({\partial }/{\partial x^3}) f$ for any function ![]() $f$. We now express the given metric
$f$. We now express the given metric ![]() $g$ in this coordinates,
$g$ in this coordinates, ![]() $g = \sum _{i,j = 1}^3 g_{ij}(x_1,x_2,x_3)\, {\textrm {d} x}^i\,\textrm {d}x^j$, where
$g = \sum _{i,j = 1}^3 g_{ij}(x_1,x_2,x_3)\, {\textrm {d} x}^i\,\textrm {d}x^j$, where ![]() $g_{ij} = g(\partial _{x^i}, \partial _{x^i})$. By the definition of the Lie derivative of the metric we have
$g_{ij} = g(\partial _{x^i}, \partial _{x^i})$. By the definition of the Lie derivative of the metric we have
since by assumption ![]() $\mathcal {L}_\xi g = 0$ and since
$\mathcal {L}_\xi g = 0$ and since ![]() $[\xi , \partial _{x^\ell }] = [\partial _{x^3}, \partial _{x^\ell }]= 0$ by construction. In this coordinate system, the Grad–Shafranov equation is the following three-dimensional elliptic equation:
$[\xi , \partial _{x^\ell }] = [\partial _{x^3}, \partial _{x^\ell }]= 0$ by construction. In this coordinate system, the Grad–Shafranov equation is the following three-dimensional elliptic equation:
 \begin{equation} L \psi := \sum_{i,j = 1}^3 a_{\xi,g}^{ij} \partial_{x^i}\partial_{x^j}\psi + \sum_{i = 1}^3 b_{\xi,g}^i \partial_{x^i} \psi + G_{\xi,g}(x_1, x_2, x_3, C, \psi)+ \frac{1}{\sqrt{|g|}}P'(\psi) =0, \quad \text{in } T, \end{equation}
\begin{equation} L \psi := \sum_{i,j = 1}^3 a_{\xi,g}^{ij} \partial_{x^i}\partial_{x^j}\psi + \sum_{i = 1}^3 b_{\xi,g}^i \partial_{x^i} \psi + G_{\xi,g}(x_1, x_2, x_3, C, \psi)+ \frac{1}{\sqrt{|g|}}P'(\psi) =0, \quad \text{in } T, \end{equation}
for coefficients ![]() $a_{\xi ,g}^{ij}, b_{\xi ,g}^j$ and a function
$a_{\xi ,g}^{ij}, b_{\xi ,g}^j$ and a function ![]() $G_{\xi ,g}$, depending on
$G_{\xi ,g}$, depending on ![]() $x_1, x_2, x_3$ which are all computed explicitly in appendix D. The crucial point is that all of these quantities are independent of
$x_1, x_2, x_3$ which are all computed explicitly in appendix D. The crucial point is that all of these quantities are independent of ![]() $x_3$, because they involve algebraic functions of components of the metric.
$x_3$, because they involve algebraic functions of components of the metric.
We can therefore look for a two-dimensional solution, ![]() $\bar {\psi } = \bar {\psi }(x_1, x_2)$, of the equation
$\bar {\psi } = \bar {\psi }(x_1, x_2)$, of the equation
 \begin{equation} \sum_{i,j = 1}^2 a_{\xi,g}^{ij}(x_1, x_2) \partial_{x^i} \partial_{x^j} \bar{\psi} + \sum_{i = 1}^2 b_{\xi, g}^i(x_1, x_2) \partial_{x^j} \bar{\psi} +G_{\xi,g}(x_1, x_2, C, \bar{\psi}) + \frac{1}{\sqrt{|g|}}P'(\bar{\psi}) = 0, \end{equation}
\begin{equation} \sum_{i,j = 1}^2 a_{\xi,g}^{ij}(x_1, x_2) \partial_{x^i} \partial_{x^j} \bar{\psi} + \sum_{i = 1}^2 b_{\xi, g}^i(x_1, x_2) \partial_{x^j} \bar{\psi} +G_{\xi,g}(x_1, x_2, C, \bar{\psi}) + \frac{1}{\sqrt{|g|}}P'(\bar{\psi}) = 0, \end{equation}
in ![]() $D$ with
$D$ with ![]() $\bar {\psi }$ constant on
$\bar {\psi }$ constant on ![]() $\partial D$. Given such
$\partial D$. Given such ![]() $\bar {\psi }$, we can recover
$\bar {\psi }$, we can recover ![]() $\psi$ satisfying (2.22) by setting
$\psi$ satisfying (2.22) by setting ![]() $\psi (x_1, x_2, x_3) = \bar {\psi }(x_1, x_2)$, i.e. by extending
$\psi (x_1, x_2, x_3) = \bar {\psi }(x_1, x_2)$, i.e. by extending ![]() $\bar {\psi }$ to be constant along integral curves of
$\bar {\psi }$ to be constant along integral curves of ![]() $\xi$. Since the integral curves of
$\xi$. Since the integral curves of ![]() $\xi$ are closed it follows that
$\xi$ are closed it follows that ![]() $\psi$ is as smooth as
$\psi$ is as smooth as ![]() $\bar {\psi }$, and by construction we have
$\bar {\psi }$, and by construction we have ![]() $\mathcal {L}_\xi \psi = 0$. Also since
$\mathcal {L}_\xi \psi = 0$. Also since ![]() $\xi$ is tangent to
$\xi$ is tangent to ![]() $\partial T$ it follows that the resulting
$\partial T$ it follows that the resulting ![]() $\psi$ is constant there.
$\psi$ is constant there.
Supposing that we have a solution ![]() $\bar {\psi }$ as above, by lemma C.3, defining
$\bar {\psi }$ as above, by lemma C.3, defining ![]() $B$ as in (1.18) provides a magnetic field satisfying
$B$ as in (1.18) provides a magnetic field satisfying ![]() $\textrm {div} B = 0$ and which satisfies the MHS equations with respect to
$\textrm {div} B = 0$ and which satisfies the MHS equations with respect to ![]() $g$,
$g$, ![]() $\textrm {curl}_g B \times _g B_g = \boldsymbol {\nabla }_g P$ exactly, by lemma C.5. As a consequence,
$\textrm {curl}_g B \times _g B_g = \boldsymbol {\nabla }_g P$ exactly, by lemma C.5. As a consequence, ![]() $B$ satisfies the usual MHS equations with forcing,
$B$ satisfies the usual MHS equations with forcing,
From the formulae for ![]() $\textrm {curl}_g, \times _g$ in appendix B, it is clear this satisfies a bound of the form (1.27), completing the proof of theorem 1.3.
$\textrm {curl}_g, \times _g$ in appendix B, it is clear this satisfies a bound of the form (1.27), completing the proof of theorem 1.3.
We have therefore reduced the problem to solving the generalized Grad–Shafranov equation for a function ![]() $\bar {\psi }: D \to \mathbb {R}$. In what follows we will abuse notation and just write
$\bar {\psi }: D \to \mathbb {R}$. In what follows we will abuse notation and just write ![]() $\psi = \bar {\psi }$. Using, for example, variational methods (proposition 11.4 of Taylor (Reference Taylor1996)), in principle one can find a weak solution to this equation in
$\psi = \bar {\psi }$. Using, for example, variational methods (proposition 11.4 of Taylor (Reference Taylor1996)), in principle one can find a weak solution to this equation in ![]() $H^1_0$. Unfortunately, these solutions need not be smooth and, more importantly, the structure of the level sets cannot be specified. In particular, the flux function may possess ‘magnetic islands’. We provide here an explicit construction of classical solutions which allows for control of flux surfaces, based on the approach of Constantin et al. (Reference Constantin, Drivas and Ginsberg2020). As explained above, the method there is to deform a solution
$H^1_0$. Unfortunately, these solutions need not be smooth and, more importantly, the structure of the level sets cannot be specified. In particular, the flux function may possess ‘magnetic islands’. We provide here an explicit construction of classical solutions which allows for control of flux surfaces, based on the approach of Constantin et al. (Reference Constantin, Drivas and Ginsberg2020). As explained above, the method there is to deform a solution ![]() $\psi _0$ to the axisymmetric Grad–Shafranov equations into a solution to (2.23) and this has the benefit of ensuring that the level sets of the resulting
$\psi _0$ to the axisymmetric Grad–Shafranov equations into a solution to (2.23) and this has the benefit of ensuring that the level sets of the resulting ![]() $\psi$ are tori, as well as providing a simple algorithm to compute the solution.
$\psi$ are tori, as well as providing a simple algorithm to compute the solution.
Let ![]() $\psi _0:D_0 \to \mathbb {R}$ be a solution to the axisymmetric Grad–Shafranov equation (1.5) with
$\psi _0:D_0 \to \mathbb {R}$ be a solution to the axisymmetric Grad–Shafranov equation (1.5) with ![]() $\psi _0|_{\partial D_0}$ constant, satisfying the mild hypotheses (H1) and (H2) (see appendix A for an example of such a flux function). We begin by writing the axisymmetric Grad–Shafranov equation on the unit disk
$\psi _0|_{\partial D_0}$ constant, satisfying the mild hypotheses (H1) and (H2) (see appendix A for an example of such a flux function). We begin by writing the axisymmetric Grad–Shafranov equation on the unit disk ![]() $D_0$ in the same coordinate system
$D_0$ in the same coordinate system ![]() $(x_1, x_2)$ as above. Letting
$(x_1, x_2)$ as above. Letting ![]() $h_{ij}$ denote the components of the Euclidean metric restricted to
$h_{ij}$ denote the components of the Euclidean metric restricted to ![]() $D_0$ in this coordinate system, on
$D_0$ in this coordinate system, on ![]() $D_0$ we have
$D_0$ we have
 \begin{align} L_0\psi_0 &:= \sum_{i,j = 1}^2 \tilde{a}^{ij}_{\xi_0,\delta}(x_1, x_2) \partial_{x^i} \partial_{x^j}\psi_0 + \sum_{i = 1}^2 \tilde{b}^i_{\xi_0,\delta}(x_1, x_2) \partial_{x^i} \psi_0 + \tilde{G}_{\xi_0,\delta}(x_1, x_2, C_0, \psi_0)\nonumber\\ & \quad + \frac{1}{\sqrt{|h|}} P_0'(\psi_0) =0, \end{align}
\begin{align} L_0\psi_0 &:= \sum_{i,j = 1}^2 \tilde{a}^{ij}_{\xi_0,\delta}(x_1, x_2) \partial_{x^i} \partial_{x^j}\psi_0 + \sum_{i = 1}^2 \tilde{b}^i_{\xi_0,\delta}(x_1, x_2) \partial_{x^i} \psi_0 + \tilde{G}_{\xi_0,\delta}(x_1, x_2, C_0, \psi_0)\nonumber\\ & \quad + \frac{1}{\sqrt{|h|}} P_0'(\psi_0) =0, \end{align}
where ![]() $|h|$ denotes the determinant of the matrix
$|h|$ denotes the determinant of the matrix ![]() $h_{ij}$,
$h_{ij}$, ![]() $\xi _0 = R e_\varPhi$ is the generator of rotations in the
$\xi _0 = R e_\varPhi$ is the generator of rotations in the ![]() $Z = 0$ plane, and
$Z = 0$ plane, and ![]() $\tilde {a}^{ij}_{\xi _0,\delta }, \tilde {b}^i_{\xi _0,\delta }, \tilde {G}_{\xi _0,\delta }$ can be computed explicitly by changing variables in (1.5),
$\tilde {a}^{ij}_{\xi _0,\delta }, \tilde {b}^i_{\xi _0,\delta }, \tilde {G}_{\xi _0,\delta }$ can be computed explicitly by changing variables in (1.5),
 \begin{equation} \left.\begin{gathered} \tilde{a}^{ij}_{\xi_0,\delta} = \frac{\sqrt{|h|}}{|\xi_0|^2} h^{ij},\quad \tilde{b}^i_{\xi_0,\delta} = \sum_{j =1,2} \frac{1}{\sqrt{|h|}} \partial_{x^i} \left(\frac{\sqrt{|h|}}{|\xi_0|^2} h^{ij}\right),\\ \tilde{G}_{\xi_0,\delta} =\frac{C(\psi)}{|\xi_0|^2}\left(\frac{C'(\psi)}{ \sqrt{|h|}} - \xi_0\cdot \textrm{curl} \xi_0\right). \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \tilde{a}^{ij}_{\xi_0,\delta} = \frac{\sqrt{|h|}}{|\xi_0|^2} h^{ij},\quad \tilde{b}^i_{\xi_0,\delta} = \sum_{j =1,2} \frac{1}{\sqrt{|h|}} \partial_{x^i} \left(\frac{\sqrt{|h|}}{|\xi_0|^2} h^{ij}\right),\\ \tilde{G}_{\xi_0,\delta} =\frac{C(\psi)}{|\xi_0|^2}\left(\frac{C'(\psi)}{ \sqrt{|h|}} - \xi_0\cdot \textrm{curl} \xi_0\right). \end{gathered}\right\} \end{equation}
In order to appeal to the results of Constantin et al. (Reference Constantin, Drivas and Ginsberg2020) we need that the coefficients of ![]() $L$ are close to those of
$L$ are close to those of ![]() $L_0$, that
$L_0$, that ![]() $G_{\xi _0,\delta }$ is close to
$G_{\xi _0,\delta }$ is close to ![]() $G_{\xi , g}$ and that the domain
$G_{\xi , g}$ and that the domain ![]() $D$ is close to
$D$ is close to ![]() $D_0$. For simplicity, we take the function
$D_0$. For simplicity, we take the function ![]() $C$ in (2.23) to just be
$C$ in (2.23) to just be ![]() $C_0$, though this is not essential. From the formulae in appendix D we have
$C_0$, though this is not essential. From the formulae in appendix D we have
 \begin{align} & \sum_{i,j =1}^2\|a_{\xi,g}^{ij} - \tilde{a}_{\xi_0,\delta}^{ij}\|_{C^{k,\alpha}} +\sum_{i = 1}^2\|b_{\xi,g}^i - \tilde{b}_{\xi_0,\delta}^i\|_{C^{k,\alpha}} + \|G_{\xi,g} - \tilde{G}_{\xi_0,\delta}\|_{C^{k,\alpha}}\nonumber\\ &\quad \leq c\|g - \delta\|_{C^{k+1,\alpha}} +c\|\xi - \xi_0\|_{C^{k+1,\alpha}}, \end{align}
\begin{align} & \sum_{i,j =1}^2\|a_{\xi,g}^{ij} - \tilde{a}_{\xi_0,\delta}^{ij}\|_{C^{k,\alpha}} +\sum_{i = 1}^2\|b_{\xi,g}^i - \tilde{b}_{\xi_0,\delta}^i\|_{C^{k,\alpha}} + \|G_{\xi,g} - \tilde{G}_{\xi_0,\delta}\|_{C^{k,\alpha}}\nonumber\\ &\quad \leq c\|g - \delta\|_{C^{k+1,\alpha}} +c\|\xi - \xi_0\|_{C^{k+1,\alpha}}, \end{align}
where ![]() $c$ is a constant depending on
$c$ is a constant depending on ![]() $k, \alpha , \sum _{i,j = 1}^3\|g\|_{C^{k+2,\alpha }}$ and
$k, \alpha , \sum _{i,j = 1}^3\|g\|_{C^{k+2,\alpha }}$ and ![]() $\|C_0\|_{C^{k+3,\alpha }}$. Here, and in what follows, we are writing
$\|C_0\|_{C^{k+3,\alpha }}$. Here, and in what follows, we are writing ![]() $C^{k+2,\alpha } = C^{k+2,\alpha }(U)$ where
$C^{k+2,\alpha } = C^{k+2,\alpha }(U)$ where ![]() $U$ is a domain containing both
$U$ is a domain containing both ![]() $D$ and
$D$ and ![]() $D_0$. By theorem 3.1 from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020), there is
$D_0$. By theorem 3.1 from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020), there is ![]() $\epsilon > 0$ depending on
$\epsilon > 0$ depending on ![]() $k, \alpha , \psi _0, D_0$ so that if the following holds,
$k, \alpha , \psi _0, D_0$ so that if the following holds,
 \begin{align} \sum_{i,j =1}^2\|a_{\xi,g}^{ij} - \tilde{a}_{\xi_0,\delta}^{ij}\|_{C^{k,\alpha}} +\sum_{i = 1}^2\|b_{\xi,g}^i - \tilde{b}_{\xi_0,\delta}^i\|_{C^{k,\alpha}} + \|G_{\xi,g} - \tilde{G}_{\xi_0,\delta}\|_{C^{k,\alpha}} + \|\mathfrak{b} - \mathfrak{b_0}\|_{C^{k+2,\alpha}} \leq \epsilon \end{align}
\begin{align} \sum_{i,j =1}^2\|a_{\xi,g}^{ij} - \tilde{a}_{\xi_0,\delta}^{ij}\|_{C^{k,\alpha}} +\sum_{i = 1}^2\|b_{\xi,g}^i - \tilde{b}_{\xi_0,\delta}^i\|_{C^{k,\alpha}} + \|G_{\xi,g} - \tilde{G}_{\xi_0,\delta}\|_{C^{k,\alpha}} + \|\mathfrak{b} - \mathfrak{b_0}\|_{C^{k+2,\alpha}} \leq \epsilon \end{align}
and the hypotheses (H1) and (H2) hold, there is a function ![]() $\psi \in C^{k,\alpha }$ of the form
$\psi \in C^{k,\alpha }$ of the form ![]() $\psi = \psi _0\circ \gamma ^{-1}$ where
$\psi = \psi _0\circ \gamma ^{-1}$ where ![]() $\gamma : D_0 \to D$ is a diffeomorphism and
$\gamma : D_0 \to D$ is a diffeomorphism and ![]() $\psi$ satisfies the generalized Grad–Shafranov equation (1.22) for some pressure profile
$\psi$ satisfies the generalized Grad–Shafranov equation (1.22) for some pressure profile ![]() $P$ which is close to
$P$ which is close to ![]() $P_0$. We now take
$P_0$. We now take ![]() $\|g - \delta \|_{C^{k+1,\alpha }},\|\xi - \xi _0\|_{C^{k+2,\alpha }}$ and
$\|g - \delta \|_{C^{k+1,\alpha }},\|\xi - \xi _0\|_{C^{k+2,\alpha }}$ and ![]() $\|\mathfrak {b} - \mathfrak {b}_0\|_{C^{k+2,\alpha }}$ small enough that (2.28) holds and let
$\|\mathfrak {b} - \mathfrak {b}_0\|_{C^{k+2,\alpha }}$ small enough that (2.28) holds and let ![]() $\psi$ be the flux function guaranteed by theorem 3.1 from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020). This completes the proof of theorem 1.2.
$\psi$ be the flux function guaranteed by theorem 3.1 from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020). This completes the proof of theorem 1.2.

Figure 1. Tokamak and stellarator geometries.
Acknowledgements
We thank A. Bhattacharjee, J. Burby, A. Cerfon, N. Kallinikos, M. Landreman, R. MacKay and G. Misiołek for insightful discussions.
Funding
The work of P.C. was partially supported by NSF grant DMS-1713985 and by the Simons Center for Hidden Symmetries and Fusion Energy award ![]() $\# 601960$. Research of T.D. was partially supported by NSF grant DMS-1703997. Research of D.G. was partially supported by the Simons Center for Hidden Symmetries and Fusion Energy.
$\# 601960$. Research of T.D. was partially supported by NSF grant DMS-1703997. Research of D.G. was partially supported by the Simons Center for Hidden Symmetries and Fusion Energy.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Flux function satisfying our hypotheses
The purpose of this section is to give a simple example of a flux function satisfying the hypotheses (H1)–(H2). We will work in toroidal coordinates ![]() $(r, \theta , \varphi )$ defined by
$(r, \theta , \varphi )$ defined by
where ![]() $(R, Z, \varPhi )$ are the usual cylindrical coordinates on
$(R, Z, \varPhi )$ are the usual cylindrical coordinates on ![]() $\mathbb {R}^3$. In these coordinates, (1.5) becomes
$\mathbb {R}^3$. In these coordinates, (1.5) becomes
The flux function we exhibit is not an exact solution of (A2) but satisfies it when the aspect ratio of the torus is taken to infinity. Using theorem 3.1 from Constantin et al. (Reference Constantin, Drivas and Ginsberg2020), one can show that there exist solutions on the true axisymmetric torus with large aspect ratio nearby this example. Although they do not have a simple analytical form, they will continue to satisfy (H1)–(H2) as these are open conditions.
We consider the torus where ![]() $r$ ranges in
$r$ ranges in ![]() $[0, r_0]$ with
$[0, r_0]$ with ![]() $0< r_0<R_0$ for
$0< r_0<R_0$ for ![]() $R_0 > 1$ and solve the equation (A2) with the choices
$R_0 > 1$ and solve the equation (A2) with the choices
for ![]() $\epsilon \ll 1$ (this is to regularize the square root) and for some constants
$\epsilon \ll 1$ (this is to regularize the square root) and for some constants ![]() $\bar {\psi }, \bar {c}$ and
$\bar {\psi }, \bar {c}$ and ![]() $\bar {p}$. The functions
$\bar {p}$. The functions ![]() $C_0$ and
$C_0$ and ![]() $P_0$ are both infinitely differentiable functions of
$P_0$ are both infinitely differentiable functions of ![]() $\psi$. Note that the pressure vanishes at the outer boundary where
$\psi$. Note that the pressure vanishes at the outer boundary where ![]() $\psi _0$ is zero, and so this boundary may be interpreted as vacuum. For special choices of constants,
$\psi _0$ is zero, and so this boundary may be interpreted as vacuum. For special choices of constants, ![]() ${\psi }_0$ solves the ‘infinite aspect ratio’ Grad–Shafranov equation ((A2) as
${\psi }_0$ solves the ‘infinite aspect ratio’ Grad–Shafranov equation ((A2) as ![]() $R_0\gg 1$)
$R_0\gg 1$)
since ![]() $\partial _r^2\psi _0 = -2\bar {\psi }/r_0^2$,
$\partial _r^2\psi _0 = -2\bar {\psi }/r_0^2$, ![]() $R_0^2 P_0'(\psi _0)= \bar {p}/r_0^2$ and
$R_0^2 P_0'(\psi _0)= \bar {p}/r_0^2$ and ![]() $C_0C_0'(\psi _0)= \bar {c}^2$. Thus
$C_0C_0'(\psi _0)= \bar {c}^2$. Thus ![]() $\psi _0$ is a solution if
$\psi _0$ is a solution if ![]() $\bar {p} = 2\bar {\psi }- (\bar {c}r_0)^2$.
$\bar {p} = 2\bar {\psi }- (\bar {c}r_0)^2$.
Appendix B. Geometric identities
In this section we recall some basic definitions and facts from Riemannian geometry which will be used in the upcoming sections. These are standard and we include the details for the convenience of the reader. Throughout we fix a Riemannian metric ![]() $g$. In our applications, we will take either
$g$. In our applications, we will take either ![]() $g = \delta$, the Euclidean metric, or
$g = \delta$, the Euclidean metric, or ![]() $g$ will be a metric with
$g$ will be a metric with ![]() $\mathcal {L}_\xi g = 0$ for a given vector field
$\mathcal {L}_\xi g = 0$ for a given vector field ![]() $\xi$. We let
$\xi$. We let ![]() $\flat , \sharp$ denote the usual operations of lowering and raising indices with respect to
$\flat , \sharp$ denote the usual operations of lowering and raising indices with respect to ![]() $g$. If
$g$. If ![]() $X = X^i \partial _{x^i}$ is a vector field and
$X = X^i \partial _{x^i}$ is a vector field and ![]() $\beta = \beta _i \,{\textrm {d} x}^i$ is a one-form, where
$\beta = \beta _i \,{\textrm {d} x}^i$ is a one-form, where ![]() $\{x^i\}_{i = 1}^3$ are arbitrary local coordinates, then
$\{x^i\}_{i = 1}^3$ are arbitrary local coordinates, then
We write ![]() $\boldsymbol {\nabla }_g f$ for the gradient of
$\boldsymbol {\nabla }_g f$ for the gradient of ![]() $f$ with respect to the metric
$f$ with respect to the metric ![]() $g$,
$g$,
In an arbitrary coordinate system ![]() $\{x^i\}_{i = 1}^3$, if
$\{x^i\}_{i = 1}^3$, if ![]() $X = X^i \partial _i$ is a vector field and
$X = X^i \partial _i$ is a vector field and ![]() $\beta = \beta _i\, {\textrm {d} x}^i$ is a one-form then
$\beta = \beta _i\, {\textrm {d} x}^i$ is a one-form then ![]() $\boldsymbol {\nabla } X, \boldsymbol {\nabla } \beta$ have components
$\boldsymbol {\nabla } X, \boldsymbol {\nabla } \beta$ have components
where ![]() $\varGamma ^i_{jk}$ are the Christoffel symbols in this coordinate system, defined by
$\varGamma ^i_{jk}$ are the Christoffel symbols in this coordinate system, defined by
Here we are writing ![]() $g_{ij}$ for the components of the metric in this corodinate system and
$g_{ij}$ for the components of the metric in this corodinate system and ![]() $g^{ij}$ for the components of the inverse metric. The
$g^{ij}$ for the components of the inverse metric. The ![]() $\varGamma$ are symmetric in the lower indices,
$\varGamma$ are symmetric in the lower indices,
We also note that covariant differentiation commutes with lowering and raising indices since
Let us also recall that the divergence of a vector field can be written as
where ![]() $|g| =\det g$ denotes the determinant of the matrix with components
$|g| =\det g$ denotes the determinant of the matrix with components ![]() $g_{ij}$.
$g_{ij}$.
We let ![]() $\mathcal {L}_X$ denote the Lie derivative in the direction
$\mathcal {L}_X$ denote the Lie derivative in the direction ![]() $X$. If
$X$. If ![]() $f$ is a function then
$f$ is a function then ![]() $\mathcal {L}_X\, f$ is defined by
$\mathcal {L}_X\, f$ is defined by
For a vector field ![]() $Y$,
$Y$, ![]() $\mathcal {L}_X Y$ is the commutator
$\mathcal {L}_X Y$ is the commutator ![]() $\mathcal {L}_XY = [X, Y]$. In an arbitrary coordinate system,
$\mathcal {L}_XY = [X, Y]$. In an arbitrary coordinate system, ![]() $\mathcal {L}_X Y = (\mathcal {L}_X Y)^i\partial _i$ with
$\mathcal {L}_X Y = (\mathcal {L}_X Y)^i\partial _i$ with
Many of our results will be stated in terms of the deformation tensor of ![]() $X$, denoted
$X$, denoted ![]() $\mathcal {L}_X g$, which is the
$\mathcal {L}_X g$, which is the ![]() $(0,2)$ tensor defined by the formula
$(0,2)$ tensor defined by the formula
In an arbitrary coordinate system, ![]() $\mathcal {L}_X g = \mathcal {L}_X g_{ij} \,{\textrm {d} x}^i \,{\textrm {d} x}^j$ and a standard calculation shows that
$\mathcal {L}_X g = \mathcal {L}_X g_{ij} \,{\textrm {d} x}^i \,{\textrm {d} x}^j$ and a standard calculation shows that
where ![]() $\boldsymbol {\nabla }$ denotes covariant differentiation (B 3a,b). We will often abuse notation and write
$\boldsymbol {\nabla }$ denotes covariant differentiation (B 3a,b). We will often abuse notation and write ![]() $\mathcal {L}_X g(Y,\cdot )$ for the vector field with components
$\mathcal {L}_X g(Y,\cdot )$ for the vector field with components
Let ![]() $*_g$ denote the Hodge star with respect to the Riemannian volume form
$*_g$ denote the Hodge star with respect to the Riemannian volume form ![]() $\textrm {d}\mu = \sqrt {|g|}\, {\textrm {d} x}^1 \wedge {\textrm {d} x}^2\wedge {\textrm {d} x}^3$. For the general definition, see Lee (Reference Lee2013). For our purposes we will only need to compute
$\textrm {d}\mu = \sqrt {|g|}\, {\textrm {d} x}^1 \wedge {\textrm {d} x}^2\wedge {\textrm {d} x}^3$. For the general definition, see Lee (Reference Lee2013). For our purposes we will only need to compute ![]() $*_g \omega$ when
$*_g \omega$ when ![]() $\omega$ is a two-form. With
$\omega$ is a two-form. With ![]() $\epsilon _{ijk}$ denoting the Levi–Civita symbol, so that
$\epsilon _{ijk}$ denoting the Levi–Civita symbol, so that ![]() $\epsilon _{ijk}$ denotes the sign of the permutation taking
$\epsilon _{ijk}$ denotes the sign of the permutation taking ![]() $(1,2,3)$ to
$(1,2,3)$ to ![]() $(i,j,k)$, we have
$(i,j,k)$, we have
If ![]() $\beta = \beta _{ij} \,{\textrm {d} x}^i\wedge {\textrm {d} x}^j$ is a two-form then from the above formula,
$\beta = \beta _{ij} \,{\textrm {d} x}^i\wedge {\textrm {d} x}^j$ is a two-form then from the above formula,
Let ![]() $d$ denote exterior differentiation. If
$d$ denote exterior differentiation. If ![]() $\beta$ is a one-form then
$\beta$ is a one-form then ![]() $d \beta$ is defined by
$d \beta$ is defined by
We will use the following identity relating ![]() $*_g, d$ and covariant differentiation
$*_g, d$ and covariant differentiation ![]() $\boldsymbol {\nabla }$. If
$\boldsymbol {\nabla }$. If ![]() $\omega =\omega _{ij} \,{\textrm {d} x}^i\, {\textrm {d} x}^j$ is a
$\omega =\omega _{ij} \,{\textrm {d} x}^i\, {\textrm {d} x}^j$ is a ![]() $(0,2)$-tensor then
$(0,2)$-tensor then
Given vector fields ![]() $X, Y$, let
$X, Y$, let ![]() $X \times _g Y$ be the vector field
$X \times _g Y$ be the vector field
Explicitly, ![]() $X \times _g Y = (X \times _g Y)^\ell \partial _\ell$ with
$X \times _g Y = (X \times _g Y)^\ell \partial _\ell$ with ![]() $(X \times _g Y)^k = \sqrt {|g|} g^{k\ell } \epsilon _{ij\ell } X^i Y^j.$ The curl of a vector field,
$(X \times _g Y)^k = \sqrt {|g|} g^{k\ell } \epsilon _{ij\ell } X^i Y^j.$ The curl of a vector field, ![]() $\textrm {curl}_g X$, is then defined by
$\textrm {curl}_g X$, is then defined by
or, in components,
where the second equality follows from a direct calculation involving the formula for the Christoffel symbols (B4).
We now collect some basic vector calculus identities.
Lemma B.1 Define ![]() $\times _g$ by (B17),
$\times _g$ by (B17), ![]() $\textrm {curl}_g$ by (B18) and
$\textrm {curl}_g$ by (B18) and ![]() $\boldsymbol {\nabla }_g$ by (B 2a,b). Suppose that
$\boldsymbol {\nabla }_g$ by (B 2a,b). Suppose that ![]() $M$ is a subset of
$M$ is a subset of ![]() $R^3$. Let
$R^3$. Let ![]() $\times , \cdot$ denote the usual cross and dot products in Euclidean space. Then we have
$\times , \cdot$ denote the usual cross and dot products in Euclidean space. Then we have
 \begin{gather} \left. \begin{gathered} (X \times_g Y)\cdot_g Z = \sqrt{|g|} X\times Y \cdot Z,\\ \textrm{curl}_g (f\, X) = \boldsymbol{\nabla}_g f \times_g X + f \textrm{curl}_g X, \\ \textrm{curl}_g \boldsymbol{\nabla}_g f = 0, \end{gathered}\right\} \end{gather}
\begin{gather} \left. \begin{gathered} (X \times_g Y)\cdot_g Z = \sqrt{|g|} X\times Y \cdot Z,\\ \textrm{curl}_g (f\, X) = \boldsymbol{\nabla}_g f \times_g X + f \textrm{curl}_g X, \\ \textrm{curl}_g \boldsymbol{\nabla}_g f = 0, \end{gathered}\right\} \end{gather}Proof. The first three identities are immediate. The last identity is proved by changing coordinates as in the proof of the upcoming identity (B.3), and we omit the proof.
We will also need the following slightly more complicated identities in the next section.
Lemma B.2 Let ![]() $\boldsymbol {\nabla }_g$ denote covariant differentiation. For any vector fields
$\boldsymbol {\nabla }_g$ denote covariant differentiation. For any vector fields ![]() $X, Y$,
$X, Y$,
where ![]() $\boldsymbol {\nabla }_X := X^i \boldsymbol {\nabla }_i$, and where
$\boldsymbol {\nabla }_X := X^i \boldsymbol {\nabla }_i$, and where ![]() $\mathcal {L}_Xg$, defined in (B 11a,b) denotes the deformation tensor of
$\mathcal {L}_Xg$, defined in (B 11a,b) denotes the deformation tensor of ![]() $X$, and we are using the notation (B12).
$X$, and we are using the notation (B12).
Proof. We begin by writing
Using (B 16a,b) and writing ![]() $X_i = g_{ij} X^j, Y_k = g_{k\ell } Y^\ell$,
$X_i = g_{ij} X^j, Y_k = g_{k\ell } Y^\ell$,
The first two terms are ![]() $X_i \textrm {div}_g Y - Y_i \textrm {div}_g X$. If we raise the index on the last two terms (using (B6)) and use (B5) then we see
$X_i \textrm {div}_g Y - Y_i \textrm {div}_g X$. If we raise the index on the last two terms (using (B6)) and use (B5) then we see
which gives (B22). To prove (B23) we start by computing ![]() $X \times _g \textrm {curl}_g X$. Writing
$X \times _g \textrm {curl}_g X$. Writing ![]() $\beta = X^\flat$, a direct calculation using (B19) shows that
$\beta = X^\flat$, a direct calculation using (B19) shows that
and that
The identity (B23) follows at any given point ![]() $P$ after changing coordinates near
$P$ after changing coordinates near ![]() $P$ so that expressed in these coordinates, the metric is given by
$P$ so that expressed in these coordinates, the metric is given by ![]() $\textrm {diag}(1,1,1)$.
$\textrm {diag}(1,1,1)$.
To prove (B24), we write
and so it follows from the definition of the covariant derivative that
and expanding the definition of the Christoffel symbols, the right-hand side is
To prove (B25), we use (B6) and write
 \begin{align} \textrm{div}_g (X\times_g Y) = \boldsymbol{\nabla}_i (\sqrt{|g|} g^{ij} \epsilon_{jk\ell} X^k Y^\ell) &= Y^\ell (\sqrt{|g|} g^{ij} \epsilon_{jk\ell} \boldsymbol{\nabla}_i X^k) + X^k (\sqrt{|g|} g^{ij} \epsilon_{jk\ell} \boldsymbol{\nabla}_i Y^\ell)\nonumber\\ &= Y^k (\textrm{curl}_g X)_k- X^k (\textrm{curl}_g Y)_k. \end{align}
\begin{align} \textrm{div}_g (X\times_g Y) = \boldsymbol{\nabla}_i (\sqrt{|g|} g^{ij} \epsilon_{jk\ell} X^k Y^\ell) &= Y^\ell (\sqrt{|g|} g^{ij} \epsilon_{jk\ell} \boldsymbol{\nabla}_i X^k) + X^k (\sqrt{|g|} g^{ij} \epsilon_{jk\ell} \boldsymbol{\nabla}_i Y^\ell)\nonumber\\ &= Y^k (\textrm{curl}_g X)_k- X^k (\textrm{curl}_g Y)_k. \end{align} The following identity involving ![]() $\times$ and
$\times$ and ![]() $\times _g$ is crucial for proving that the vector field
$\times _g$ is crucial for proving that the vector field ![]() ${B}_g$ defined in (1.18) possesses a flux function. This result follows directly from standard vector calculus identities when
${B}_g$ defined in (1.18) possesses a flux function. This result follows directly from standard vector calculus identities when ![]() $g = \delta$.
$g = \delta$.
Lemma B.3 If ![]() $\varphi$ is a function with
$\varphi$ is a function with ![]() $\mathcal {L}_X \varphi = 0$, then with
$\mathcal {L}_X \varphi = 0$, then with ![]() $\boldsymbol {\nabla }$ denoting the Euclidean gradient,
$\boldsymbol {\nabla }$ denoting the Euclidean gradient,
Proof. This follows from a straightforward but tedious argument; we include the details for the convenience of the reader. With ![]() $\omega$ the quantity on the left-hand side of (B36), from the definitions we have
$\omega$ the quantity on the left-hand side of (B36), from the definitions we have
Fix any ![]() $P \in M$ and choose coordinates
$P \in M$ and choose coordinates ![]() $(Z^1, Z^2, Z^3)$ near
$(Z^1, Z^2, Z^3)$ near ![]() $P$, so that at
$P$, so that at ![]() $P$ we have
$P$ we have
We note the following relation which will be useful in what follows: at ![]() $P$, we have
$P$, we have
Expressing ![]() $\omega$ in these coordinates,
$\omega$ in these coordinates, ![]() $\omega = \omega ^a \partial _{Z^a}$ with
$\omega = \omega ^a \partial _{Z^a}$ with ![]() $\omega ^a = ({\partial Z^a}/{\partial x^i})\omega ^i$, evaluating at
$\omega ^a = ({\partial Z^a}/{\partial x^i})\omega ^i$, evaluating at ![]() $P$ and using (B39) to rewrite
$P$ and using (B39) to rewrite ![]() $g^{\ell m}$ and
$g^{\ell m}$ and ![]() $g^{ p q}$, from (B37) we have
$g^{ p q}$, from (B37) we have
 \begin{align} \omega^a &= \sqrt{|g|}\frac{\partial Z^a}{\partial x^i} \delta^{ij}g^{\ell m} g^{pq} \epsilon_{jk\ell}\epsilon_{mnp} X^k X^n \partial_q \varphi\nonumber\\ &= \sqrt{|g|} \frac{\partial Z^a}{\partial x^i} \frac{\partial x^\ell}{\partial Z^b} \frac{\partial x^m}{\partial Z^c} \frac{\partial x^p}{\partial Z^d} \frac{\partial x^k}{\partial Z^{b'}} \frac{\partial x^n}{\partial Z^{c'}} \delta^{bc} \delta^{dd'} \epsilon_{jk\ell}\epsilon_{mnp} X^{b'} X^{c'} \partial_{Z^{d'}}\varphi, \end{align}
\begin{align} \omega^a &= \sqrt{|g|}\frac{\partial Z^a}{\partial x^i} \delta^{ij}g^{\ell m} g^{pq} \epsilon_{jk\ell}\epsilon_{mnp} X^k X^n \partial_q \varphi\nonumber\\ &= \sqrt{|g|} \frac{\partial Z^a}{\partial x^i} \frac{\partial x^\ell}{\partial Z^b} \frac{\partial x^m}{\partial Z^c} \frac{\partial x^p}{\partial Z^d} \frac{\partial x^k}{\partial Z^{b'}} \frac{\partial x^n}{\partial Z^{c'}} \delta^{bc} \delta^{dd'} \epsilon_{jk\ell}\epsilon_{mnp} X^{b'} X^{c'} \partial_{Z^{d'}}\varphi, \end{align}
writing, e.g. ![]() $X^{k} = ({\partial x^k}/{\partial Z^{b'}}) X^{b'}$. Now we note that
$X^{k} = ({\partial x^k}/{\partial Z^{b'}}) X^{b'}$. Now we note that
Indeed, the quantity on the left-hand side of, for example, the first equality is antisymmetric in all three indices, and so is a multiple of ![]() $\epsilon _{cc'd}$ and evaluating at
$\epsilon _{cc'd}$ and evaluating at ![]() $c =1, c' = 2, d = 3$ gives the result. Therefore (B40) reads
$c =1, c' = 2, d = 3$ gives the result. Therefore (B40) reads
 \begin{align} \omega^a &= \sqrt{|g|} \det(\partial_Zx)^2 \delta^{ij} \frac{\partial Z^a}{\partial x^i} \frac{\partial Z^e}{\partial x^j} \delta^{dd'}\delta^{bc}\epsilon_{cc'd}\epsilon_{beb'} X^{b'} X^{c'} \partial_{Z^{d'}} \varphi\nonumber\\ &=\sqrt{|g|} \det(\partial_Zx)^2 \delta^{ij} \frac{\partial Z^a}{\partial x^i} \frac{\partial Z^e}{\partial x^j} \delta^{dd'} \left( \delta_{c'e}\delta_{db'} - \delta_{c'b'}\delta_{de}\right)X^{b'} X^{c'} \partial_{Z^{d'}} \varphi, \end{align}
\begin{align} \omega^a &= \sqrt{|g|} \det(\partial_Zx)^2 \delta^{ij} \frac{\partial Z^a}{\partial x^i} \frac{\partial Z^e}{\partial x^j} \delta^{dd'}\delta^{bc}\epsilon_{cc'd}\epsilon_{beb'} X^{b'} X^{c'} \partial_{Z^{d'}} \varphi\nonumber\\ &=\sqrt{|g|} \det(\partial_Zx)^2 \delta^{ij} \frac{\partial Z^a}{\partial x^i} \frac{\partial Z^e}{\partial x^j} \delta^{dd'} \left( \delta_{c'e}\delta_{db'} - \delta_{c'b'}\delta_{de}\right)X^{b'} X^{c'} \partial_{Z^{d'}} \varphi, \end{align}using a well known identity for the Levi–Civita symbol. Now we note that
by assumption, and so
From (B38), we have ![]() $\sqrt { |g|} (\det \partial _{Z}x)^2 = {1}/{\sqrt {|g|}}$ and so at
$\sqrt { |g|} (\det \partial _{Z}x)^2 = {1}/{\sqrt {|g|}}$ and so at ![]() $P$ we find
$P$ we find
and since ![]() $P$ was arbitrary we get the result.
$P$ was arbitrary we get the result.
We finally record some useful formulae involving Lie derivatives along ![]() $g$ Killing fields.
$g$ Killing fields.
Lemma B.4 Let ![]() $X,Y$ be vector fields and let
$X,Y$ be vector fields and let ![]() $\xi$ be a Killing vector field for the metric
$\xi$ be a Killing vector field for the metric ![]() $g$. Then
$g$. Then
Proof. To prove (B46), we start from the following fact, which can be found on p. 177 of Fecko (Reference Fecko2006). If ![]() $\xi _0$ is a Killing field for a metric
$\xi _0$ is a Killing field for a metric ![]() $g$,
$g$, ![]() $\mathcal {L}_{\xi }g = 0$, then
$\mathcal {L}_{\xi }g = 0$, then ![]() $\mathcal {L}_{\xi } *_g \alpha = *_g\mathcal {L}_{\xi } \alpha$. Similarly,
$\mathcal {L}_{\xi } *_g \alpha = *_g\mathcal {L}_{\xi } \alpha$. Similarly, ![]() $\mathcal {L}_{\xi } X^\flat = (\mathcal {L}_{\xi } X)_{\flat },$ where
$\mathcal {L}_{\xi } X^\flat = (\mathcal {L}_{\xi } X)_{\flat },$ where ![]() $\flat$ denotes lowering indices with
$\flat$ denotes lowering indices with ![]() $g$. For any vector field
$g$. For any vector field ![]() $\xi$, if
$\xi$, if ![]() $\varPhi _s$ denotes its flow, we have the following identity
$\varPhi _s$ denotes its flow, we have the following identity ![]() $\varPhi _s^* *_g \alpha = *_{\varPhi _s^*g} \varPhi _s^* \alpha .$ If
$\varPhi _s^* *_g \alpha = *_{\varPhi _s^*g} \varPhi _s^* \alpha .$ If ![]() $\xi$ is a Killing field for
$\xi$ is a Killing field for ![]() $g$ then this becomes
$g$ then this becomes ![]() $\varPhi _s^* *_g = *_g \varPhi _s^* \alpha .$ Differentiating this at
$\varPhi _s^* *_g = *_g \varPhi _s^* \alpha .$ Differentiating this at ![]() $s = 0$ and using the definition of the Lie derivative gives the result. Now, to get the formula for
$s = 0$ and using the definition of the Lie derivative gives the result. Now, to get the formula for ![]() $\mathcal {L}_\xi (X \times _g Y)$ we then recall that
$\mathcal {L}_\xi (X \times _g Y)$ we then recall that ![]() $(X \times _g Y)_{\flat } = *_g(X^\flat \wedge Y^\flat )$. Using that
$(X \times _g Y)_{\flat } = *_g(X^\flat \wedge Y^\flat )$. Using that ![]() $\mathcal {L}_{\xi }$ commutes with
$\mathcal {L}_{\xi }$ commutes with ![]() $\sharp$,
$\sharp$, ![]() $\flat$, and
$\flat$, and ![]() $*_g$,
$*_g$,
 \begin{align} \mathcal{L}_{\xi} (X \times_g Y) = \mathcal{L}_{\xi} *_g\left( X^\flat \wedge Y_{\flat}\right)^\sharp = *_g\left(\mathcal{L}_{\xi} (X_{\flat} \wedge Y_{\flat} )\right)^\sharp &= *_g\left( (\mathcal{L}_{\xi}X)^\flat \wedge Y_{\flat} + X_{\flat} \wedge (\mathcal{L}_{\xi} Y)_{\flat}\right)^\sharp\nonumber\\ &= \mathcal{L}_{\xi} X \times_g Y + X \times_g \mathcal{L}_{\xi} Y. \end{align}
\begin{align} \mathcal{L}_{\xi} (X \times_g Y) = \mathcal{L}_{\xi} *_g\left( X^\flat \wedge Y_{\flat}\right)^\sharp = *_g\left(\mathcal{L}_{\xi} (X_{\flat} \wedge Y_{\flat} )\right)^\sharp &= *_g\left( (\mathcal{L}_{\xi}X)^\flat \wedge Y_{\flat} + X_{\flat} \wedge (\mathcal{L}_{\xi} Y)_{\flat}\right)^\sharp\nonumber\\ &= \mathcal{L}_{\xi} X \times_g Y + X \times_g \mathcal{L}_{\xi} Y. \end{align}
To prove (B47), recall that ![]() $\textrm {curl}_g X = (*_g \,\textrm {d} X^\flat )^\sharp ,$ where
$\textrm {curl}_g X = (*_g \,\textrm {d} X^\flat )^\sharp ,$ where ![]() $\flat$ and
$\flat$ and ![]() $\sharp$ denote lowering and raising the index with
$\sharp$ denote lowering and raising the index with ![]() $g$. Recall that if
$g$. Recall that if ![]() $\mathcal {L}_{\xi } g= 0$ then
$\mathcal {L}_{\xi } g= 0$ then
After lowering the index on ![]() $\textrm {curl}_g X$ and using the fact that Lie derivatives commute with exterior differentiation,
$\textrm {curl}_g X$ and using the fact that Lie derivatives commute with exterior differentiation, ![]() $\mathcal {L}_{\xi } d = \textrm {d} \mathcal {L}_{\xi }$, we obtain
$\mathcal {L}_{\xi } d = \textrm {d} \mathcal {L}_{\xi }$, we obtain ![]() $\mathcal {L}_{\xi } *_g (\textrm {d} X_{\flat }) = *_g d (\mathcal {L}_{\xi } X)_{\flat }$. Raising the index with
$\mathcal {L}_{\xi } *_g (\textrm {d} X_{\flat }) = *_g d (\mathcal {L}_{\xi } X)_{\flat }$. Raising the index with ![]() $g$ and using (B 49a–c) again we get the result.
$g$ and using (B 49a–c) again we get the result.
Appendix C. Generalized quasisymmetric Grad–Shafranov equation
In this section we summarize the relationship between quasisymmetry and the MHS equation (1.1). Recall that the deformation tensor ![]() $\mathcal {L}_\xi \delta$ is defined by
$\mathcal {L}_\xi \delta$ is defined by
We begin by showing that the ansatz (1.18) is automatically Euclidean divergence-free, has flux surfaces and we write the condition for weak quasisymmetry explicitly for such fields.
Proposition C.1 (Characterization of quasisymmetric ![]() $B_g$ MHS solutions)
$B_g$ MHS solutions)
Let ![]() $\xi$ be a non-vanishing and divergence-free vector field tangent to
$\xi$ be a non-vanishing and divergence-free vector field tangent to ![]() $\partial T$ and let
$\partial T$ and let ![]() $g$ be any metric with
$g$ be any metric with ![]() $\mathcal {L}_\xi g = 0$. Let
$\mathcal {L}_\xi g = 0$. Let ![]() $\psi :T\to \mathbb {R}$ satisfy
$\psi :T\to \mathbb {R}$ satisfy ![]() $\mathcal {L}_\xi \psi =0$ and
$\mathcal {L}_\xi \psi =0$ and ![]() $|\boldsymbol {\nabla } \psi |>0$. Then
$|\boldsymbol {\nabla } \psi |>0$. Then ![]() $B_g$ given by (1.18) is (Euclidean) divergence-free, satisfies (1.8) and is tangent to
$B_g$ given by (1.18) is (Euclidean) divergence-free, satisfies (1.8) and is tangent to ![]() $\partial T$. Moreover,
$\partial T$. Moreover, ![]() $B_g$ is weakly quasisymmetric if and only if
$B_g$ is weakly quasisymmetric if and only if
The field ![]() $B_g$ additionally solves MHS with forcing
$B_g$ additionally solves MHS with forcing ![]() $f$ if and only if
$f$ if and only if ![]() $f \cdot _g \boldsymbol {\nabla }_g^\perp \psi = f \cdot _g \xi = 0,$ and
$f \cdot _g \boldsymbol {\nabla }_g^\perp \psi = f \cdot _g \xi = 0,$ and ![]() $\psi$ satisfies the generalized Grad–Shafranov equation
$\psi$ satisfies the generalized Grad–Shafranov equation
 \begin{equation} \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) - C(\psi) \frac{\xi}{|\xi|_g^2} \cdot_g \textrm{curl}_g \left(\frac{\xi}{|\xi|_g^2}\right) + \frac{C(\psi)C'(\psi)}{\sqrt{|g|}|\xi|_g^2}+ \frac{P'(\psi)}{\sqrt{|g|}} = \frac{f\cdot_g \boldsymbol{\nabla}_g \psi}{\sqrt{|g|}|\boldsymbol{\nabla}_g \psi|_g^2}. \end{equation}
\begin{equation} \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) - C(\psi) \frac{\xi}{|\xi|_g^2} \cdot_g \textrm{curl}_g \left(\frac{\xi}{|\xi|_g^2}\right) + \frac{C(\psi)C'(\psi)}{\sqrt{|g|}|\xi|_g^2}+ \frac{P'(\psi)}{\sqrt{|g|}} = \frac{f\cdot_g \boldsymbol{\nabla}_g \psi}{\sqrt{|g|}|\boldsymbol{\nabla}_g \psi|_g^2}. \end{equation}This section will build up to the proof of proposition C.1 by developing the following lemmas C.4 and C.5. The proof is a straightforward combination of these results. First we record some elementary vector identities.
Lemma C.2 Fix a metric ![]() $g$. Let
$g$. Let ![]() $\xi$ be a vector field with
$\xi$ be a vector field with ![]() $|\xi | \neq 0$ and let
$|\xi | \neq 0$ and let ![]() $\psi : T\to \mathbb {R}$ be a function satisfying
$\psi : T\to \mathbb {R}$ be a function satisfying ![]() $\mathcal {L}_\xi \psi = 0$. Then we have
$\mathcal {L}_\xi \psi = 0$. Then we have
where we have introduced ![]() $\boldsymbol {\nabla }_g^\perp \psi = \xi \times _g \boldsymbol {\nabla }_g \psi$. Thus, the triple
$\boldsymbol {\nabla }_g^\perp \psi = \xi \times _g \boldsymbol {\nabla }_g \psi$. Thus, the triple ![]() $(\boldsymbol {\nabla }_g \psi , \boldsymbol {\nabla }^\perp _g \psi , \xi )$ forms an orthogonal basis of
$(\boldsymbol {\nabla }_g \psi , \boldsymbol {\nabla }^\perp _g \psi , \xi )$ forms an orthogonal basis of ![]() $\mathbb {R}^3$ at each
$\mathbb {R}^3$ at each ![]() $x\in T$ where
$x\in T$ where ![]() $|\boldsymbol {\nabla }_g \psi |_g>0$.
$|\boldsymbol {\nabla }_g \psi |_g>0$.
Proof. Follows from the identity (B21).
The following are the main results in this section and are proved at the end of the section.
Lemma C.3 (Structural properties of ![]() $B_g$)
$B_g$)
Fix a metric ![]() $g$. Let
$g$. Let ![]() $\xi : T\to \mathbb {R}^3$ be a (Euclidean) divergence-free vector field with
$\xi : T\to \mathbb {R}^3$ be a (Euclidean) divergence-free vector field with ![]() $|\xi |_g \neq 0$ which is tangent to
$|\xi |_g \neq 0$ which is tangent to ![]() $\partial T$. Let
$\partial T$. Let ![]() $\psi : T\to \mathbb {R}$ be a function satisfying
$\psi : T\to \mathbb {R}$ be a function satisfying ![]() $\mathcal {L}_\xi \psi = 0$ which is constant on
$\mathcal {L}_\xi \psi = 0$ which is constant on ![]() $\partial T$. Fix
$\partial T$. Fix ![]() $C:\mathbb {R}\to \mathbb {R}$. Then
$C:\mathbb {R}\to \mathbb {R}$. Then ![]() $B_g$ defined in (1.18) satisfies
$B_g$ defined in (1.18) satisfies
For the proof, see § 2. The crucial point here is, despite the fact that ![]() $B_g$ is defined in terms of an arbitrary metric
$B_g$ is defined in terms of an arbitrary metric ![]() $g$, the identities (C5) and (C6) involve the Euclidean metric.
$g$, the identities (C5) and (C6) involve the Euclidean metric.
We now begin the derivation of the Grad–Shafranov equation (1.22) which involves a somewhat lengthy calculation using the above identities. The most important and complicated ingredient is the following formula, which is a direct consequence of lemma C.7, below.
Lemma C.4 (Curl of ![]() $B_g$)
$B_g$)
Fix a metric ![]() $g$. Let
$g$. Let ![]() $\xi$ be a vector field with
$\xi$ be a vector field with ![]() $|\xi | \neq 0$ and let
$|\xi | \neq 0$ and let ![]() $\psi : T\to \mathbb {R}$ be a function satisfying
$\psi : T\to \mathbb {R}$ be a function satisfying ![]() $\mathcal {L}_\xi \psi = 0$. Fix a function
$\mathcal {L}_\xi \psi = 0$. Fix a function ![]() $C:\mathbb {R}\to \mathbb {R}$. Then
$C:\mathbb {R}\to \mathbb {R}$. Then ![]() $B_g$ defined in (1.18) satisfies
$B_g$ defined in (1.18) satisfies
where ![]() $\textrm {curl}_g$ is with respect to the metric
$\textrm {curl}_g$ is with respect to the metric ![]() $g$, defined in (B18), and with
$g$, defined in (B18), and with ![]() $F, G, H$ defined by
$F, G, H$ defined by
 \begin{gather} F:={-}\frac{\sqrt{|g|}}{|\xi|_g^4 |\boldsymbol{\nabla}_g \psi|_g^2} \left[\frac{C(\psi)}{\sqrt{|g|}}(\mathcal{L}_\xi g)(\xi, \boldsymbol{\nabla}_g^\perp \psi) + 2 |\xi|_g^2 | \boldsymbol{\nabla}_g \psi|_g^2 \frac{\mathcal{L}_\xi \sqrt{|g|}}{\sqrt{|g|}} \right.\nonumber\\ \quad \left.- |\xi|_g^2 (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi, \boldsymbol{\nabla}_g \psi) - |\boldsymbol{\nabla}_g \psi|_g^2 (\mathcal{L}_\xi g)(\xi,\xi) \right], \end{gather}
\begin{gather} F:={-}\frac{\sqrt{|g|}}{|\xi|_g^4 |\boldsymbol{\nabla}_g \psi|_g^2} \left[\frac{C(\psi)}{\sqrt{|g|}}(\mathcal{L}_\xi g)(\xi, \boldsymbol{\nabla}_g^\perp \psi) + 2 |\xi|_g^2 | \boldsymbol{\nabla}_g \psi|_g^2 \frac{\mathcal{L}_\xi \sqrt{|g|}}{\sqrt{|g|}} \right.\nonumber\\ \quad \left.- |\xi|_g^2 (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi, \boldsymbol{\nabla}_g \psi) - |\boldsymbol{\nabla}_g \psi|_g^2 (\mathcal{L}_\xi g)(\xi,\xi) \right], \end{gather} \begin{gather} G:= \frac{\sqrt{|g|}}{|\xi|_g^2} \frac{ 1}{|\boldsymbol{\nabla}_g \psi|_g^2} \left[ (\mathcal{L}_\xi g)(B_g, \boldsymbol{\nabla}_g \psi) - |\boldsymbol{\nabla}_g\psi|_g^2 \frac{C'(\psi)}{\sqrt{|g|}} \right] , \end{gather}
\begin{gather} G:= \frac{\sqrt{|g|}}{|\xi|_g^2} \frac{ 1}{|\boldsymbol{\nabla}_g \psi|_g^2} \left[ (\mathcal{L}_\xi g)(B_g, \boldsymbol{\nabla}_g \psi) - |\boldsymbol{\nabla}_g\psi|_g^2 \frac{C'(\psi)}{\sqrt{|g|}} \right] , \end{gather} \begin{gather} H:= \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) + \frac{1}{|\xi|^4_g} C(\psi) \xi \cdot_g \textrm{curl}_g \xi + \frac{\sqrt{|g|}}{|\xi|_g^2} (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi, \xi). \end{gather}
\begin{gather} H:= \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) + \frac{1}{|\xi|^4_g} C(\psi) \xi \cdot_g \textrm{curl}_g \xi + \frac{\sqrt{|g|}}{|\xi|_g^2} (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi, \xi). \end{gather}Lemma C.5 (MHS for ![]() $B_g$)
$B_g$)
Fix a metric ![]() $g$. Let
$g$. Let ![]() $\xi$ be a vector field with
$\xi$ be a vector field with ![]() $|\xi | \neq 0$ and let
$|\xi | \neq 0$ and let ![]() $\psi : T\to \mathbb {R}$ be a function satisfying
$\psi : T\to \mathbb {R}$ be a function satisfying ![]() $\mathcal {L}_\xi \psi = 0$. Fix a function
$\mathcal {L}_\xi \psi = 0$. Fix a function ![]() $C:\mathbb {R}\to \mathbb {R}$. Then
$C:\mathbb {R}\to \mathbb {R}$. Then ![]() $B_g$ defined in (1.18) satisfies
$B_g$ defined in (1.18) satisfies
 \begin{equation} \textrm{curl}_g B_g \times_g B_g - \boldsymbol{\nabla}_g P = \left(C(\psi) G -H- P'\right) \boldsymbol{\nabla}_g \psi - \frac{C(\psi)}{|\xi|_g^2}F \boldsymbol{\nabla}_g^\perp \psi + \frac{|\boldsymbol{\nabla}_g\psi|_g^2}{|\xi|_g^2 } F\xi, \end{equation}
\begin{equation} \textrm{curl}_g B_g \times_g B_g - \boldsymbol{\nabla}_g P = \left(C(\psi) G -H- P'\right) \boldsymbol{\nabla}_g \psi - \frac{C(\psi)}{|\xi|_g^2}F \boldsymbol{\nabla}_g^\perp \psi + \frac{|\boldsymbol{\nabla}_g\psi|_g^2}{|\xi|_g^2 } F\xi, \end{equation}
with ![]() $F$,
$F$, ![]() $G$ and
$G$ and ![]() $H$ defined by (C10), (C11) and (C12). In particular, if
$H$ defined by (C10), (C11) and (C12). In particular, if ![]() $\mathcal {L}_\xi g = 0$ then
$\mathcal {L}_\xi g = 0$ then ![]() $B$ satisfies the MHS equation with force
$B$ satisfies the MHS equation with force ![]() $f$
$f$
if and only if ![]() $f \cdot _g \boldsymbol {\nabla }_g^\perp \psi = f \cdot _g \xi = 0,$ and
$f \cdot _g \boldsymbol {\nabla }_g^\perp \psi = f \cdot _g \xi = 0,$ and ![]() $\psi$ satisfies the generalized Grad–Shafranov equation
$\psi$ satisfies the generalized Grad–Shafranov equation
 \begin{equation} \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) - C(\psi) \frac{\xi}{|\xi|_g^2} \cdot_g \textrm{curl}_g \left(\frac{\xi}{|\xi|_g^2}\right) + \frac{C(\psi)C'(\psi)}{\sqrt{|g|}|\xi|_g^2}+ \frac{P'(\psi)}{\sqrt{|g|}} = \frac{f\cdot_g \boldsymbol{\nabla}_g \psi}{\sqrt{|g|}|\boldsymbol{\nabla}_g \psi|_g^2}. \end{equation}
\begin{equation} \textrm{div}_g\left(\sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi}{|\xi|_g^2} \right) - C(\psi) \frac{\xi}{|\xi|_g^2} \cdot_g \textrm{curl}_g \left(\frac{\xi}{|\xi|_g^2}\right) + \frac{C(\psi)C'(\psi)}{\sqrt{|g|}|\xi|_g^2}+ \frac{P'(\psi)}{\sqrt{|g|}} = \frac{f\cdot_g \boldsymbol{\nabla}_g \psi}{\sqrt{|g|}|\boldsymbol{\nabla}_g \psi|_g^2}. \end{equation} The generalized Grad–Shafranov equation (C15) for vector fields of the form (1.18) was first derived in Burby et al. (Reference Burby, Kallinikos and MacKay2020) when ![]() $g$ was taken to be the circle-averaged metric.
$g$ was taken to be the circle-averaged metric.
Lemma C.6 (Quasisymmetry of ![]() $B_g$)
$B_g$)
Fix a metric ![]() $g$ with
$g$ with ![]() $\mathcal {L}_\xi g = 0$. Let
$\mathcal {L}_\xi g = 0$. Let ![]() $\xi$ be a vector field with
$\xi$ be a vector field with ![]() $|\xi | \neq 0$ and let
$|\xi | \neq 0$ and let ![]() $\psi : T\to \mathbb {R}$ be a function satisfying
$\psi : T\to \mathbb {R}$ be a function satisfying ![]() $\mathcal {L}_\xi \psi = 0$. Fix
$\mathcal {L}_\xi \psi = 0$. Fix ![]() $C:\mathbb {R}\to \mathbb {R}$. Then
$C:\mathbb {R}\to \mathbb {R}$. Then ![]() $B_g$ satisfies
$B_g$ satisfies
C.1. Auxiliary lemmas
We collect some calculations which are useful for the proofs of the other lemmas in the following statement.
Lemma C.7 Fix a metric ![]() $g$. Let
$g$. Let ![]() $\xi$ be a vector field with
$\xi$ be a vector field with ![]() $|\xi | \neq 0$ and let
$|\xi | \neq 0$ and let ![]() $\psi : T\to \mathbb {R}$ be a function satisfying
$\psi : T\to \mathbb {R}$ be a function satisfying ![]() $\mathcal {L}_\xi \psi = 0$. Fix a function
$\mathcal {L}_\xi \psi = 0$. Fix a function ![]() $C:\mathbb {R}\to \mathbb {R}$. Then
$C:\mathbb {R}\to \mathbb {R}$. Then
 \begin{gather}\textrm{div}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) ={-}\frac{\sqrt{|g|}}{|\xi|_g^4}(\mathcal{L}_\xi g)( \xi,\boldsymbol{\nabla}_g^\perp \psi) + \frac{1}{|\xi|_g^2} \mathcal{L}_{\boldsymbol{\nabla}^\perp_g\psi } \sqrt{|g|}, \end{gather}
\begin{gather}\textrm{div}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) ={-}\frac{\sqrt{|g|}}{|\xi|_g^4}(\mathcal{L}_\xi g)( \xi,\boldsymbol{\nabla}_g^\perp \psi) + \frac{1}{|\xi|_g^2} \mathcal{L}_{\boldsymbol{\nabla}^\perp_g\psi } \sqrt{|g|}, \end{gather} \begin{gather} \textrm{curl}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) = \frac{1}{|\xi|_g^4} C(\psi)(\xi \cdot_g \textrm{curl}_g \xi) \xi \nonumber\\ \quad +\, \frac{1}{|\xi|_g^2}\left( \frac{C(\psi) }{|\xi|_g^2|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g \psi )- C'(\psi) \right) \boldsymbol{\nabla}_g^\perp \psi \nonumber\\ \quad -\, \frac{C(\psi) }{|\xi|_g^4|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g^\perp \psi ) \boldsymbol{\nabla}_g \psi , \end{gather}
\begin{gather} \textrm{curl}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) = \frac{1}{|\xi|_g^4} C(\psi)(\xi \cdot_g \textrm{curl}_g \xi) \xi \nonumber\\ \quad +\, \frac{1}{|\xi|_g^2}\left( \frac{C(\psi) }{|\xi|_g^2|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g \psi )- C'(\psi) \right) \boldsymbol{\nabla}_g^\perp \psi \nonumber\\ \quad -\, \frac{C(\psi) }{|\xi|_g^4|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g^\perp \psi ) \boldsymbol{\nabla}_g \psi , \end{gather} \begin{gather} \textrm{curl}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right)\nonumber\\ \quad = \left(\textrm{div}_g \left( \sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi }{|\xi|_g^2} \right)+ \frac{\sqrt{|g|} }{|\xi|_g^4}(\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\xi) \right)\xi \nonumber\\ \qquad +\, \frac{\sqrt{|g|} }{|\xi|_g^4} \left(\mathcal{L}_\xi g(\xi,\xi)- 2|\xi|_g^2 \frac{\mathcal{L}_\xi \sqrt{|g|}}{\sqrt{|g|}} +\frac{|\xi|_g^2}{|\boldsymbol{\nabla}_g \psi|^2}(\mathcal{L}_\xi g)( \boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}_g \psi)\right)\boldsymbol{\nabla}_g \psi\nonumber\\ \qquad +\, \frac{\sqrt{|g|}}{|\xi|_g^4|\boldsymbol{\nabla}_g\psi|^2 }(\mathcal{L}_\xi g)( \boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}_g^\perp \psi)\boldsymbol{\nabla}_g^\perp \psi. \end{gather}
\begin{gather} \textrm{curl}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right)\nonumber\\ \quad = \left(\textrm{div}_g \left( \sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi }{|\xi|_g^2} \right)+ \frac{\sqrt{|g|} }{|\xi|_g^4}(\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\xi) \right)\xi \nonumber\\ \qquad +\, \frac{\sqrt{|g|} }{|\xi|_g^4} \left(\mathcal{L}_\xi g(\xi,\xi)- 2|\xi|_g^2 \frac{\mathcal{L}_\xi \sqrt{|g|}}{\sqrt{|g|}} +\frac{|\xi|_g^2}{|\boldsymbol{\nabla}_g \psi|^2}(\mathcal{L}_\xi g)( \boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}_g \psi)\right)\boldsymbol{\nabla}_g \psi\nonumber\\ \qquad +\, \frac{\sqrt{|g|}}{|\xi|_g^4|\boldsymbol{\nabla}_g\psi|^2 }(\mathcal{L}_\xi g)( \boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}_g^\perp \psi)\boldsymbol{\nabla}_g^\perp \psi. \end{gather}Proof. We will repeatedly use the product rule (B10) as well as the commutator identity
Step 1: identity (C17). To prove (C17) we note
 \begin{align} \textrm{div}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) &= C(\psi) \frac{\textrm{div}_g \xi}{|\xi|_g^2} - |\xi|_g^{{-}4}C(\psi) \mathcal{L}_\xi |\xi|_g^{2}= \frac{C(\psi)}{|\xi|_g^2} \textrm{div}_g \xi \nonumber\\ &\quad - \frac{C(\psi)}{|\xi|_g^4} (\mathcal{L}_\xi g )(\xi,\xi), \end{align}
\begin{align} \textrm{div}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) &= C(\psi) \frac{\textrm{div}_g \xi}{|\xi|_g^2} - |\xi|_g^{{-}4}C(\psi) \mathcal{L}_\xi |\xi|_g^{2}= \frac{C(\psi)}{|\xi|_g^2} \textrm{div}_g \xi \nonumber\\ &\quad - \frac{C(\psi)}{|\xi|_g^4} (\mathcal{L}_\xi g )(\xi,\xi), \end{align}using the product rule (B20).
Step 2: identity (C18). First note that
 \begin{equation} \textrm{div}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right)=\sqrt{|g|} \textrm{div}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) + \frac{1}{|\xi|_g^2} \mathcal{L}_{\boldsymbol{\nabla}^\perp_g\psi } \sqrt{|g|}. \end{equation}
\begin{equation} \textrm{div}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right)=\sqrt{|g|} \textrm{div}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) + \frac{1}{|\xi|_g^2} \mathcal{L}_{\boldsymbol{\nabla}^\perp_g\psi } \sqrt{|g|}. \end{equation}Next we compute
 \begin{align} \textrm{div}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right)&= \frac{1}{|\xi|_g^2}\left(\textrm{div}_g \boldsymbol{\nabla}^\perp_g\psi +|\xi|_g^2 \mathcal{L}_{ \boldsymbol{\nabla}^\perp_g\psi} |\xi|_g^{{-}2} \right)\nonumber\\ &= \frac{1}{|\xi|_g^2}\left(\textrm{div}_g( \xi \times_g \boldsymbol{\nabla}_g \psi) - |\xi|_g^{{-}2}(\xi \times_g \boldsymbol{\nabla}_g \psi) \cdot_g \boldsymbol{\nabla}_g |\xi|_g^{2}\right) \nonumber\\ &= \frac{1}{|\xi|_g^2}\left(\mathcal{L}_{\textrm{curl}_g \xi} \psi - \xi \cdot_g \textrm{curl}_g \boldsymbol{\nabla}_g \psi- |\xi|_g^{{-}2} ( \boldsymbol{\nabla}_g |\xi|_g^{2} \times_g \xi) \cdot_g \boldsymbol{\nabla}_g \psi \right)\nonumber\\ &= \frac{1}{|\xi|_g^2}\left(\mathcal{L}_{\textrm{curl}_g \xi} \psi - |\xi|_g^{{-}2} ( \boldsymbol{\nabla}_g |\xi|_g^{2} \times_g \xi) \cdot_g \boldsymbol{\nabla}_g \psi \right). \end{align}
\begin{align} \textrm{div}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right)&= \frac{1}{|\xi|_g^2}\left(\textrm{div}_g \boldsymbol{\nabla}^\perp_g\psi +|\xi|_g^2 \mathcal{L}_{ \boldsymbol{\nabla}^\perp_g\psi} |\xi|_g^{{-}2} \right)\nonumber\\ &= \frac{1}{|\xi|_g^2}\left(\textrm{div}_g( \xi \times_g \boldsymbol{\nabla}_g \psi) - |\xi|_g^{{-}2}(\xi \times_g \boldsymbol{\nabla}_g \psi) \cdot_g \boldsymbol{\nabla}_g |\xi|_g^{2}\right) \nonumber\\ &= \frac{1}{|\xi|_g^2}\left(\mathcal{L}_{\textrm{curl}_g \xi} \psi - \xi \cdot_g \textrm{curl}_g \boldsymbol{\nabla}_g \psi- |\xi|_g^{{-}2} ( \boldsymbol{\nabla}_g |\xi|_g^{2} \times_g \xi) \cdot_g \boldsymbol{\nabla}_g \psi \right)\nonumber\\ &= \frac{1}{|\xi|_g^2}\left(\mathcal{L}_{\textrm{curl}_g \xi} \psi - |\xi|_g^{{-}2} ( \boldsymbol{\nabla}_g |\xi|_g^{2} \times_g \xi) \cdot_g \boldsymbol{\nabla}_g \psi \right). \end{align}We now simplify the second term in the above. First note the identity (which follows from (B26))
 \begin{align} \xi \times_g \textrm{curl}_g \xi &= \frac{1}{2} \boldsymbol{\nabla}_g |\xi|_g^2 - (\xi \cdot_g \boldsymbol{\nabla}_g) \xi\nonumber\\ &= \boldsymbol{\nabla}_g |\xi|_g^2 - ((\xi \cdot_g \boldsymbol{\nabla}_g) \xi+ \boldsymbol{\nabla}_g \xi \cdot_g \xi)\nonumber\\ & = \boldsymbol{\nabla}_g |\xi|_g^2 - (\mathcal{L}_\xi g)\cdot_g \xi, \end{align}
\begin{align} \xi \times_g \textrm{curl}_g \xi &= \frac{1}{2} \boldsymbol{\nabla}_g |\xi|_g^2 - (\xi \cdot_g \boldsymbol{\nabla}_g) \xi\nonumber\\ &= \boldsymbol{\nabla}_g |\xi|_g^2 - ((\xi \cdot_g \boldsymbol{\nabla}_g) \xi+ \boldsymbol{\nabla}_g \xi \cdot_g \xi)\nonumber\\ & = \boldsymbol{\nabla}_g |\xi|_g^2 - (\mathcal{L}_\xi g)\cdot_g \xi, \end{align}so that
 \begin{align} \boldsymbol{\nabla}_g |\xi|_g^2 \times_g \xi &= (\xi \times_g \textrm{curl}_g \xi )\times_g \xi + ((\mathcal{L}_\xi g)\cdot_g\xi)\times_g\xi\nonumber\\ &= |\xi|_g^2 \textrm{curl}_g \xi - (\xi \cdot_g \textrm{curl}_g \xi) \xi + ((\mathcal{L}_\xi g)\cdot_g \xi) \times_g\xi, \end{align}
\begin{align} \boldsymbol{\nabla}_g |\xi|_g^2 \times_g \xi &= (\xi \times_g \textrm{curl}_g \xi )\times_g \xi + ((\mathcal{L}_\xi g)\cdot_g\xi)\times_g\xi\nonumber\\ &= |\xi|_g^2 \textrm{curl}_g \xi - (\xi \cdot_g \textrm{curl}_g \xi) \xi + ((\mathcal{L}_\xi g)\cdot_g \xi) \times_g\xi, \end{align}where we have used the elementary identity
Noting finally that
using that ![]() $\mathcal {L}_\xi \psi =0$ we have
$\mathcal {L}_\xi \psi =0$ we have
Putting this together with (C24), we obtain the identity (C18).
Step 3: identity (C19). To prove (C19), we note
Using this formula and (C25), we find that
 \begin{align} \textrm{curl}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) &= \frac{1}{|\xi|_g^2}\left({-}C'(\psi) \boldsymbol{\nabla}_g^\perp \psi + C(\psi) \textrm{curl}_g \xi\right) - |\xi|_g^{{-}4} C(\psi) \boldsymbol{\nabla} |\xi|_g^2 \times_g \xi\nonumber\\ &= \frac{1}{|\xi|_g^2}\left({-}C'(\psi) \boldsymbol{\nabla}_g^\perp \psi + C(\psi) \textrm{curl}_g \xi\right)\nonumber\\ &\quad - |\xi|_g^{{-}4} C(\psi)\left(|\xi|_g^2 \textrm{curl}_g \xi - (\xi \cdot_g \textrm{curl}_g \xi) \xi+ (\mathcal{L}_\xi g)\boldsymbol{\cdot} \xi \times_g \xi\right)\nonumber\\ &={-}\frac{C'(\psi)}{|\xi|_g^2} \boldsymbol{\nabla}_g^\perp \psi + |\xi|_g^{{-}4} C(\psi) \left((\xi \cdot_g \textrm{curl}_g \xi) \xi- (\mathcal{L}_\xi g)\boldsymbol{\cdot} \xi \times_g \xi\right). \end{align}
\begin{align} \textrm{curl}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) &= \frac{1}{|\xi|_g^2}\left({-}C'(\psi) \boldsymbol{\nabla}_g^\perp \psi + C(\psi) \textrm{curl}_g \xi\right) - |\xi|_g^{{-}4} C(\psi) \boldsymbol{\nabla} |\xi|_g^2 \times_g \xi\nonumber\\ &= \frac{1}{|\xi|_g^2}\left({-}C'(\psi) \boldsymbol{\nabla}_g^\perp \psi + C(\psi) \textrm{curl}_g \xi\right)\nonumber\\ &\quad - |\xi|_g^{{-}4} C(\psi)\left(|\xi|_g^2 \textrm{curl}_g \xi - (\xi \cdot_g \textrm{curl}_g \xi) \xi+ (\mathcal{L}_\xi g)\boldsymbol{\cdot} \xi \times_g \xi\right)\nonumber\\ &={-}\frac{C'(\psi)}{|\xi|_g^2} \boldsymbol{\nabla}_g^\perp \psi + |\xi|_g^{{-}4} C(\psi) \left((\xi \cdot_g \textrm{curl}_g \xi) \xi- (\mathcal{L}_\xi g)\boldsymbol{\cdot} \xi \times_g \xi\right). \end{align}Note finally using lemma C.2 that
 \begin{align} (\mathcal{L}_\xi g)\cdot_g \xi \times_g \xi&=((\mathcal{L}_\xi g)\cdot_g \xi \times_g \xi) \cdot_g \widehat{\boldsymbol{\nabla}_g \psi}\ \widehat{\boldsymbol{\nabla}_g \psi }+ ((\mathcal{L}_\xi g)\cdot_g \xi \times_g \xi) \cdot_g \widehat{\boldsymbol{\nabla}_g^\perp \psi} \ \widehat{\boldsymbol{\nabla}_g^\perp \psi }\nonumber\\ &= \frac{1}{|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g^\perp \psi ) \boldsymbol{\nabla}_g \psi - \frac{1}{|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g \psi ) \boldsymbol{\nabla}_g^\perp \psi, \end{align}
\begin{align} (\mathcal{L}_\xi g)\cdot_g \xi \times_g \xi&=((\mathcal{L}_\xi g)\cdot_g \xi \times_g \xi) \cdot_g \widehat{\boldsymbol{\nabla}_g \psi}\ \widehat{\boldsymbol{\nabla}_g \psi }+ ((\mathcal{L}_\xi g)\cdot_g \xi \times_g \xi) \cdot_g \widehat{\boldsymbol{\nabla}_g^\perp \psi} \ \widehat{\boldsymbol{\nabla}_g^\perp \psi }\nonumber\\ &= \frac{1}{|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g^\perp \psi ) \boldsymbol{\nabla}_g \psi - \frac{1}{|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g \psi ) \boldsymbol{\nabla}_g^\perp \psi, \end{align}where we used the identity (C28) in passing to the second line together with
Combining this with (C31) gives
 \begin{align} \textrm{curl}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) &={-}\frac{C'(\psi)}{|\xi|_g^2} \boldsymbol{\nabla}_g^\perp \psi + |\xi|_g^{{-}4} C(\psi) (\xi \cdot_g \textrm{curl}_g \xi) \xi \nonumber\\ &\quad+\, \frac{1}{|\xi|_g^2} \left(\frac{C(\psi)}{|\xi|_g^2|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g \psi ) \boldsymbol{\nabla}_g^\perp \psi \right.\nonumber\\ &\quad \left.-\, \frac{C(\psi)}{|\xi|_g^2|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g^\perp \psi ) \boldsymbol{\nabla}_g \psi \right). \end{align}
\begin{align} \textrm{curl}_g \left(C(\psi) \frac{\xi}{|\xi|_g^2} \right) &={-}\frac{C'(\psi)}{|\xi|_g^2} \boldsymbol{\nabla}_g^\perp \psi + |\xi|_g^{{-}4} C(\psi) (\xi \cdot_g \textrm{curl}_g \xi) \xi \nonumber\\ &\quad+\, \frac{1}{|\xi|_g^2} \left(\frac{C(\psi)}{|\xi|_g^2|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g \psi ) \boldsymbol{\nabla}_g^\perp \psi \right.\nonumber\\ &\quad \left.-\, \frac{C(\psi)}{|\xi|_g^2|\boldsymbol{\nabla}_g\psi|_g^2} (\mathcal{L}_\xi g)( \xi, \boldsymbol{\nabla}_g^\perp \psi ) \boldsymbol{\nabla}_g \psi \right). \end{align}Rearrangement establishes (C19).
Step 4: identity (C20). First note that
 \begin{align} \textrm{curl}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) &= \sqrt{|g|} \textrm{curl}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) + \frac{1}{|\xi|_g^2} \boldsymbol{\nabla} \sqrt{|g|} \times_g \boldsymbol{\nabla}^\perp_g\psi\nonumber\\ &= \sqrt{|g|} \textrm{curl}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) + \frac{1}{|\xi|_g^2} (\mathcal{L}_{\boldsymbol{\nabla}_g \psi} \sqrt{|g|}) \xi - \frac{1}{|\xi|_g^2} (\mathcal{L}_{\xi} \sqrt{|g|}) \boldsymbol{\nabla} \psi. \end{align}
\begin{align} \textrm{curl}_g \left(\sqrt{|g|} \frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) &= \sqrt{|g|} \textrm{curl}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) + \frac{1}{|\xi|_g^2} \boldsymbol{\nabla} \sqrt{|g|} \times_g \boldsymbol{\nabla}^\perp_g\psi\nonumber\\ &= \sqrt{|g|} \textrm{curl}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) + \frac{1}{|\xi|_g^2} (\mathcal{L}_{\boldsymbol{\nabla}_g \psi} \sqrt{|g|}) \xi - \frac{1}{|\xi|_g^2} (\mathcal{L}_{\xi} \sqrt{|g|}) \boldsymbol{\nabla} \psi. \end{align}Now, by the identity (B22),
 \begin{align} \textrm{curl}_g \boldsymbol{\nabla}^\perp_g \psi = \textrm{curl}_g (\xi\times_g \boldsymbol{\nabla}_g \psi) &= \xi \varDelta_g \psi - \boldsymbol{\nabla}_g \psi \textrm{div}_g \xi + \mathcal{L}_{\boldsymbol{\nabla}_g \psi}\xi\nonumber\\ & = \xi \varDelta_g \psi - \boldsymbol{\nabla}_g \psi \textrm{div}_g \xi - \mathcal{L}_{\xi}\boldsymbol{\nabla}_g \psi\nonumber\\ &= \xi \varDelta_g \psi - \boldsymbol{\nabla}_g \psi \textrm{div}_g \xi + (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot), \end{align}
\begin{align} \textrm{curl}_g \boldsymbol{\nabla}^\perp_g \psi = \textrm{curl}_g (\xi\times_g \boldsymbol{\nabla}_g \psi) &= \xi \varDelta_g \psi - \boldsymbol{\nabla}_g \psi \textrm{div}_g \xi + \mathcal{L}_{\boldsymbol{\nabla}_g \psi}\xi\nonumber\\ & = \xi \varDelta_g \psi - \boldsymbol{\nabla}_g \psi \textrm{div}_g \xi - \mathcal{L}_{\xi}\boldsymbol{\nabla}_g \psi\nonumber\\ &= \xi \varDelta_g \psi - \boldsymbol{\nabla}_g \psi \textrm{div}_g \xi + (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot), \end{align}
where we used (C21) and ![]() $(\mathcal {L}_\xi g)(\nabla _g \psi ,\cdot )$ is defined as in (B12). Therefore
$(\mathcal {L}_\xi g)(\nabla _g \psi ,\cdot )$ is defined as in (B12). Therefore
 \begin{align} \sqrt{|g|} \textrm{curl}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) &= \frac{\sqrt{|g|} }{|\xi|_g^2}\left( \xi \varDelta_g \psi \!-\! \textrm{div}_g \xi\, \boldsymbol{\nabla}_g \psi \!+\! (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot)\right)-\frac{\sqrt{|g|} }{|\xi|_g^4} \boldsymbol{\nabla}_g |\xi|_g^2 \!\times\! \boldsymbol{\nabla}^\perp_g\psi \nonumber\\ &= \frac{\sqrt{|g|} }{|\xi|_g^2}\left( \xi \varDelta_g \psi - \textrm{div}_g \xi\, \boldsymbol{\nabla}_g \psi + (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot)\right) \nonumber\\ &\quad + \frac{\sqrt{|g|} }{|\xi|_g^4}\left( ( \mathcal{L}_\xi |\xi|_g^2) \boldsymbol{\nabla}_g\psi - (\boldsymbol{\nabla}_g\psi\cdot_g \boldsymbol{\nabla}_g |\xi|_g^2 ) \xi \right)\nonumber\\ &= \sqrt{|g|} \textrm{div}_g \left( \frac{\boldsymbol{\nabla}_g \psi }{|\xi|_g^2} \right) \xi + \frac{\sqrt{|g|} }{|\xi|_g^2}(\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot) \nonumber\\ &\quad + \frac{\sqrt{|g|} }{|\xi|_g^4} \left( \mathcal{L}_\xi g(\xi,\xi)- |\xi|_g^2 \textrm{div}_g \xi \right)\boldsymbol{\nabla}_g \psi\nonumber\\ &= \textrm{div}_g \left( \sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi }{|\xi|_g^2} \right) \xi - \frac{1}{|\xi|_g^2} (\mathcal{L}_{\boldsymbol{\nabla}_g \psi} \sqrt{|g|} ) \xi\nonumber\\ &\quad + \frac{\sqrt{|g|} }{|\xi|_g^2}(\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot) + \frac{1}{|\xi|_g^4} \left(\sqrt{|g|} \mathcal{L}_\xi g(\xi,\xi)- |\xi|_g^2 \mathcal{L}_{\xi} \sqrt{|g|} \right) \boldsymbol{\nabla}_g \psi, \end{align}
\begin{align} \sqrt{|g|} \textrm{curl}_g \left(\frac{\boldsymbol{\nabla}^\perp_g\psi }{|\xi|_g^2} \right) &= \frac{\sqrt{|g|} }{|\xi|_g^2}\left( \xi \varDelta_g \psi \!-\! \textrm{div}_g \xi\, \boldsymbol{\nabla}_g \psi \!+\! (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot)\right)-\frac{\sqrt{|g|} }{|\xi|_g^4} \boldsymbol{\nabla}_g |\xi|_g^2 \!\times\! \boldsymbol{\nabla}^\perp_g\psi \nonumber\\ &= \frac{\sqrt{|g|} }{|\xi|_g^2}\left( \xi \varDelta_g \psi - \textrm{div}_g \xi\, \boldsymbol{\nabla}_g \psi + (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot)\right) \nonumber\\ &\quad + \frac{\sqrt{|g|} }{|\xi|_g^4}\left( ( \mathcal{L}_\xi |\xi|_g^2) \boldsymbol{\nabla}_g\psi - (\boldsymbol{\nabla}_g\psi\cdot_g \boldsymbol{\nabla}_g |\xi|_g^2 ) \xi \right)\nonumber\\ &= \sqrt{|g|} \textrm{div}_g \left( \frac{\boldsymbol{\nabla}_g \psi }{|\xi|_g^2} \right) \xi + \frac{\sqrt{|g|} }{|\xi|_g^2}(\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot) \nonumber\\ &\quad + \frac{\sqrt{|g|} }{|\xi|_g^4} \left( \mathcal{L}_\xi g(\xi,\xi)- |\xi|_g^2 \textrm{div}_g \xi \right)\boldsymbol{\nabla}_g \psi\nonumber\\ &= \textrm{div}_g \left( \sqrt{|g|} \frac{\boldsymbol{\nabla}_g \psi }{|\xi|_g^2} \right) \xi - \frac{1}{|\xi|_g^2} (\mathcal{L}_{\boldsymbol{\nabla}_g \psi} \sqrt{|g|} ) \xi\nonumber\\ &\quad + \frac{\sqrt{|g|} }{|\xi|_g^2}(\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot) + \frac{1}{|\xi|_g^4} \left(\sqrt{|g|} \mathcal{L}_\xi g(\xi,\xi)- |\xi|_g^2 \mathcal{L}_{\xi} \sqrt{|g|} \right) \boldsymbol{\nabla}_g \psi, \end{align}
where we used (C41) to say ![]() $\sqrt {|g|} \textrm {div}_g\xi = \mathcal {L}_{\xi } \sqrt {|g|}$ as well as the identity
$\sqrt {|g|} \textrm {div}_g\xi = \mathcal {L}_{\xi } \sqrt {|g|}$ as well as the identity
Finally, note that we can express
 \begin{align} (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot) &= \frac{1}{|\xi|_g^2} (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\xi ) \xi + \frac{1}{|\xi|_g^2|\boldsymbol{\nabla}_g \psi|_g^2 } (\mathcal{L}_\xi g)( \boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}^\perp_g\psi) \boldsymbol{\nabla}^\perp_g\psi\nonumber\\ &\quad + \frac{1}{|\boldsymbol{\nabla}_g \psi|_g^2 } (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}_g \psi) \boldsymbol{\nabla}_g\psi. \end{align}
\begin{align} (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\cdot) &= \frac{1}{|\xi|_g^2} (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\xi ) \xi + \frac{1}{|\xi|_g^2|\boldsymbol{\nabla}_g \psi|_g^2 } (\mathcal{L}_\xi g)( \boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}^\perp_g\psi) \boldsymbol{\nabla}^\perp_g\psi\nonumber\\ &\quad + \frac{1}{|\boldsymbol{\nabla}_g \psi|_g^2 } (\mathcal{L}_\xi g)(\boldsymbol{\nabla}_g \psi,\boldsymbol{\nabla}_g \psi) \boldsymbol{\nabla}_g\psi. \end{align}This completes the derivation.
C.2. Proof of lemma C.3
The result follows from direct computation as follows.
Step 1: identity (C5). The property of having a flux function (C5) follows from lemma B.3.
Step 2: identity (C6). For the divergence (C6), lemma C.6 gives
Next recall the relation between the divergence on flat and curved backgrounds
Applying this identity to convert (C40) to the divergence using the Euclidean metric, we have
 \begin{align} \textrm{div} B_g &= \textrm{div}_g B_g- \frac{1}{\sqrt{|g|}} \mathcal{L}_{B_g}\sqrt{|g|} = \frac{1}{|\xi|_g^2} \left(C(\psi) \textrm{div}_g\xi - (\mathcal{L}_\xi g)(\xi, B)\right) \nonumber\\ &\quad - \frac{1}{\sqrt{|g|}} \frac{C(\psi) }{|\xi|_g^2} \mathcal{L}_{\xi} \sqrt{|g|}. \end{align}
\begin{align} \textrm{div} B_g &= \textrm{div}_g B_g- \frac{1}{\sqrt{|g|}} \mathcal{L}_{B_g}\sqrt{|g|} = \frac{1}{|\xi|_g^2} \left(C(\psi) \textrm{div}_g\xi - (\mathcal{L}_\xi g)(\xi, B)\right) \nonumber\\ &\quad - \frac{1}{\sqrt{|g|}} \frac{C(\psi) }{|\xi|_g^2} \mathcal{L}_{\xi} \sqrt{|g|}. \end{align}
Using ![]() $\textrm {div} \xi =0$ and (C41) again we find
$\textrm {div} \xi =0$ and (C41) again we find ![]() $\sqrt {|g|} \textrm {div}_g\xi = \mathcal {L}_{\xi } \sqrt {|g|},$ and get the claimed result.
$\sqrt {|g|} \textrm {div}_g\xi = \mathcal {L}_{\xi } \sqrt {|g|},$ and get the claimed result.
Step 3: identity (C7). We have the identity
 \begin{align} \mathcal{L}_\xi B_g&:= \xi \boldsymbol{\cdot} \boldsymbol{\nabla} B_g - B_g\boldsymbol{\cdot} \boldsymbol{\nabla} \xi \nonumber\\ &= \textrm{curl}(B_g \times \xi) + (\textrm{div} B_g) \xi - (\textrm{div} \xi) B_g={-} \frac{1}{|\xi|_g^2} (\mathcal{L}_\xi g)(\xi, B_g) \xi, \end{align}
\begin{align} \mathcal{L}_\xi B_g&:= \xi \boldsymbol{\cdot} \boldsymbol{\nabla} B_g - B_g\boldsymbol{\cdot} \boldsymbol{\nabla} \xi \nonumber\\ &= \textrm{curl}(B_g \times \xi) + (\textrm{div} B_g) \xi - (\textrm{div} \xi) B_g={-} \frac{1}{|\xi|_g^2} (\mathcal{L}_\xi g)(\xi, B_g) \xi, \end{align}
and the result follows from (C5), (C6) and the assumption ![]() $\textrm {div} \xi = 0$.
$\textrm {div} \xi = 0$.
Step 4: identity (C8). Let ![]() $\hat {n}$ be the unit outward normal vector to
$\hat {n}$ be the unit outward normal vector to ![]() $\partial T$. Then we have
$\partial T$. Then we have
since ![]() $\xi \boldsymbol {\cdot } \hat {n}=0$ by assumption. Now, for any vector field
$\xi \boldsymbol {\cdot } \hat {n}=0$ by assumption. Now, for any vector field ![]() $X$ and scalar function
$X$ and scalar function ![]() $f$ we have
$f$ we have
As a result, since ![]() $\psi$ is assumed constant on the boundary, we can choose
$\psi$ is assumed constant on the boundary, we can choose ![]() $\hat {n} = \boldsymbol {\nabla } \psi /|\boldsymbol {\nabla } \psi |$ on the boundary and a standard vector identity shows that
$\hat {n} = \boldsymbol {\nabla } \psi /|\boldsymbol {\nabla } \psi |$ on the boundary and a standard vector identity shows that ![]() $(\xi \times _g \boldsymbol {\nabla }_g \psi )\boldsymbol {\cdot } \hat {n} =0$.
$(\xi \times _g \boldsymbol {\nabla }_g \psi )\boldsymbol {\cdot } \hat {n} =0$.
C.3. Proof of lemma C.6
Proof. Direct computation shows
Since ![]() $\mathcal {L}_\xi g = 0$, from (C7) it follows that
$\mathcal {L}_\xi g = 0$, from (C7) it follows that ![]() $\mathcal {L}_\xi B_g=0$. Thus we have
$\mathcal {L}_\xi B_g=0$. Thus we have
Using ![]() $\mathcal {L}_\xi |\xi |_g^2=0$,
$\mathcal {L}_\xi |\xi |_g^2=0$, ![]() $\mathcal {L}_\xi \xi =0$,
$\mathcal {L}_\xi \xi =0$, ![]() $\mathcal {L}_\xi \psi =0$,
$\mathcal {L}_\xi \psi =0$, ![]() $\mathcal {L}_{\xi } \boldsymbol {\nabla }_g^\perp \psi =0$ and
$\mathcal {L}_{\xi } \boldsymbol {\nabla }_g^\perp \psi =0$ and ![]() $\mathcal {L}_\xi |\xi |^2 = (\mathcal {L}_\xi \delta ) (\xi ,\xi )$ completes the proof.
$\mathcal {L}_\xi |\xi |^2 = (\mathcal {L}_\xi \delta ) (\xi ,\xi )$ completes the proof.
Appendix D. Explicit expression for the generalized Grad–Shafranov equation
Fix a domain ![]() $D$ in the
$D$ in the ![]() $\{\varPhi = 0\}$ half-plane and let
$\{\varPhi = 0\}$ half-plane and let ![]() $\xi$ be a vector field whose orbits starting from
$\xi$ be a vector field whose orbits starting from ![]() $D$ are all periodic (with possibly different period). Fix an arbitrary local coordinate system on
$D$ are all periodic (with possibly different period). Fix an arbitrary local coordinate system on ![]() $D$ and extend it to a coordinate system
$D$ and extend it to a coordinate system ![]() $(x_1, x_2, x_3)$ on the torus
$(x_1, x_2, x_3)$ on the torus ![]() $T$ defined in (1.25) by pulling back along the flow of
$T$ defined in (1.25) by pulling back along the flow of ![]() $\xi$. In these coordinates we have
$\xi$. In these coordinates we have ![]() $\xi \boldsymbol {\cdot } \boldsymbol {\nabla } f = ({\partial }/{\partial x^3}) f$. In this section we express the coefficients appearing in the generalized Grad–Shafranov equation (1.22) in these coordinates. The most complicated part of the calculation is contained in the following lemma.
$\xi \boldsymbol {\cdot } \boldsymbol {\nabla } f = ({\partial }/{\partial x^3}) f$. In this section we express the coefficients appearing in the generalized Grad–Shafranov equation (1.22) in these coordinates. The most complicated part of the calculation is contained in the following lemma.
Lemma D.1 Let ![]() $g$ be an arbitrary metric on
$g$ be an arbitrary metric on ![]() $T$ and let
$T$ and let ![]() $(x_1, x_2, x_3)$ be a coordinate system on
$(x_1, x_2, x_3)$ be a coordinate system on ![]() $T$ as above. Then
$T$ as above. Then
 \begin{align} \textrm{curl}_g \xi \cdot_g \xi &= |g|^{1/2} \left( (\partial_1 g_{23} - \partial_2 g_{13} ) (g^{11} g^{22} - (g^{12})^2)\right.\nonumber\\ &\quad\left.+ (\partial_3 g_{13} - \partial_1 g_{33}) ( g^{21} g^{23} - g^{22} g^{13}) + (\partial_3 g_{23} - \partial_2 g_{33}) ( g^{11} g^{23} - g^{12} g^{13})\right). \end{align}
\begin{align} \textrm{curl}_g \xi \cdot_g \xi &= |g|^{1/2} \left( (\partial_1 g_{23} - \partial_2 g_{13} ) (g^{11} g^{22} - (g^{12})^2)\right.\nonumber\\ &\quad\left.+ (\partial_3 g_{13} - \partial_1 g_{33}) ( g^{21} g^{23} - g^{22} g^{13}) + (\partial_3 g_{23} - \partial_2 g_{33}) ( g^{11} g^{23} - g^{12} g^{13})\right). \end{align}Proof. We use the formula ![]() $\textrm {curl}_g \xi \cdot _g \xi = i_\xi (\textrm {curl}_g \xi )_{\flat } = i_\xi (*_g \,\textrm {d} \alpha ),$ where
$\textrm {curl}_g \xi \cdot _g \xi = i_\xi (\textrm {curl}_g \xi )_{\flat } = i_\xi (*_g \,\textrm {d} \alpha ),$ where ![]() $*_g$ is the Hodge star in terms of
$*_g$ is the Hodge star in terms of ![]() $g$ and
$g$ and ![]() $\alpha = \xi _\flat$ denotes the one-form which is dual to
$\alpha = \xi _\flat$ denotes the one-form which is dual to ![]() $\xi$ with respect to
$\xi$ with respect to ![]() $g$. Explicitly
$g$. Explicitly ![]() $\alpha = \alpha _i \, {\textrm {d} x}^i = g_{ij}\xi ^j \,{\textrm {d} x}^i = g_{i3} \,{\textrm {d} x}^i$. We now compute the terms on the right-hand side of (D1) explicitly and the main step is computing
$\alpha = \alpha _i \, {\textrm {d} x}^i = g_{ij}\xi ^j \,{\textrm {d} x}^i = g_{i3} \,{\textrm {d} x}^i$. We now compute the terms on the right-hand side of (D1) explicitly and the main step is computing ![]() $*_g d\alpha$. Acting on two-forms,
$*_g d\alpha$. Acting on two-forms, ![]() $*_g$ is defined by linearity and the rule
$*_g$ is defined by linearity and the rule
where ![]() $|g| = \det g$ and
$|g| = \det g$ and ![]() $\epsilon _{k\ell m}$ is the Levi–Civita symbol.
$\epsilon _{k\ell m}$ is the Levi–Civita symbol.
Since in our coordinate system ![]() $\xi = \partial _{3}$ we have
$\xi = \partial _{3}$ we have ![]() $i_\xi \,{\textrm {d} x}^m = {\textrm {d} x}^m(\partial _{3}) = \delta ^{m3}$ and so
$i_\xi \,{\textrm {d} x}^m = {\textrm {d} x}^m(\partial _{3}) = \delta ^{m3}$ and so
A straightforward calculation shows
 \begin{equation} \left.\begin{gathered} i_{\xi} *_g ({\textrm{d} x}^1\wedge {\textrm{d} x}^2) = |g|^{1/2} \left( g^{11} g^{22} - (g^{12})^2\right),\\ i_\xi *_g ({\textrm{d} x}^2 \wedge {\textrm{d} x}^3) = |g|^{1/2} \left( g^{21} g^{32} - g^{22}g^{31}\right),\\ i_\xi *_g ({\textrm{d} x}^1 \wedge {\textrm{d} x}^3) = |g|^{1/2} \left(g^{11} g^{32} - g^{12} g^{31}\right). \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} i_{\xi} *_g ({\textrm{d} x}^1\wedge {\textrm{d} x}^2) = |g|^{1/2} \left( g^{11} g^{22} - (g^{12})^2\right),\\ i_\xi *_g ({\textrm{d} x}^2 \wedge {\textrm{d} x}^3) = |g|^{1/2} \left( g^{21} g^{32} - g^{22}g^{31}\right),\\ i_\xi *_g ({\textrm{d} x}^1 \wedge {\textrm{d} x}^3) = |g|^{1/2} \left(g^{11} g^{32} - g^{12} g^{31}\right). \end{gathered}\right\} \end{equation}
Since ![]() $\textrm {d} \alpha = (\partial _1 \alpha _2 - \partial _2 \alpha _1) \,{\textrm {d} x}^1\wedge {\textrm {d} x}^2 + (\partial _1 \alpha _3 - \partial _3 \alpha _1) \,{\textrm {d} x}^1 \wedge {\textrm {d} x}^3 + (\partial _2 \alpha _3 - \partial _3 \alpha _2) \,{\textrm {d} x}^2\wedge {\textrm {d} x}^3,$ we have
$\textrm {d} \alpha = (\partial _1 \alpha _2 - \partial _2 \alpha _1) \,{\textrm {d} x}^1\wedge {\textrm {d} x}^2 + (\partial _1 \alpha _3 - \partial _3 \alpha _1) \,{\textrm {d} x}^1 \wedge {\textrm {d} x}^3 + (\partial _2 \alpha _3 - \partial _3 \alpha _2) \,{\textrm {d} x}^2\wedge {\textrm {d} x}^3,$ we have
 \begin{align} \textrm{curl}_g \xi \cdot_g \xi &= (\partial_1 \alpha_2 \!-\! \partial_2 \alpha_1) i_\xi *_g ({\textrm{d} x}^1\wedge {\textrm{d} x}^2) \!-\! \partial_1 \alpha_3 i_\xi *_g ({\textrm{d} x}^1 \wedge {\textrm{d} x}^3) \!+\! \partial_2 \alpha_3 i_\xi *_g ({\textrm{d} x}^2\wedge {\textrm{d} x}^3) \nonumber\\ &= |g|^{1/2} \left((\partial_1\alpha_2 - \partial_2 \alpha_1) (g^{11} g^{22} - (g^{12})^2) +(\partial_3 \alpha_1 - \partial_1 \alpha_3) ( g^{21} g^{23} - g^{22} g^{13})\right.\nonumber\\ &\quad\left. +\, (\partial_3 \alpha_2 - \partial_2 \alpha_3) ( g^{11} g^{23} - g^{12} g^{13})\right) \end{align}
\begin{align} \textrm{curl}_g \xi \cdot_g \xi &= (\partial_1 \alpha_2 \!-\! \partial_2 \alpha_1) i_\xi *_g ({\textrm{d} x}^1\wedge {\textrm{d} x}^2) \!-\! \partial_1 \alpha_3 i_\xi *_g ({\textrm{d} x}^1 \wedge {\textrm{d} x}^3) \!+\! \partial_2 \alpha_3 i_\xi *_g ({\textrm{d} x}^2\wedge {\textrm{d} x}^3) \nonumber\\ &= |g|^{1/2} \left((\partial_1\alpha_2 - \partial_2 \alpha_1) (g^{11} g^{22} - (g^{12})^2) +(\partial_3 \alpha_1 - \partial_1 \alpha_3) ( g^{21} g^{23} - g^{22} g^{13})\right.\nonumber\\ &\quad\left. +\, (\partial_3 \alpha_2 - \partial_2 \alpha_3) ( g^{11} g^{23} - g^{12} g^{13})\right) \end{align}
which gives (D1) since ![]() $\alpha _i = g_{i3}$.
$\alpha _i = g_{i3}$.
The next lemma follows from the previous one and (C15) after noting that ![]() $|\xi |^2 = g(\xi , \xi ) = g_{33}$.
$|\xi |^2 = g(\xi , \xi ) = g_{33}$.
Lemma D.2 Fix a vector field ![]() $\xi$ and a metric
$\xi$ and a metric ![]() $g$ with
$g$ with ![]() $\mathcal {L}_\xi g = 0$. Let
$\mathcal {L}_\xi g = 0$. Let ![]() $(x_1, x_2, x_3)$ be any coordinate system as in the statement of the previous lemma. Then (C15) with
$(x_1, x_2, x_3)$ be any coordinate system as in the statement of the previous lemma. Then (C15) with ![]() $f = 0$ takes the form
$f = 0$ takes the form
 \begin{equation} \sum_{i,j=1}^{3} a^{ij}_{\xi,g} \partial_i \partial_j \psi + \sum_{i = 1}^3 b_{\xi,g}^i \partial_i \psi + G_{\xi,g}(x_1, x_2, x_3, C, \psi) + \frac{P'(\psi)}{\sqrt{|g|}} = 0, \end{equation}
\begin{equation} \sum_{i,j=1}^{3} a^{ij}_{\xi,g} \partial_i \partial_j \psi + \sum_{i = 1}^3 b_{\xi,g}^i \partial_i \psi + G_{\xi,g}(x_1, x_2, x_3, C, \psi) + \frac{P'(\psi)}{\sqrt{|g|}} = 0, \end{equation}where
 \begin{equation} \left.\begin{gathered} a^{ij}_{\xi,g} = \frac{\sqrt{|g|}}{g_{33}} g^{ij},\quad b^i_{\xi,g} = \sum_{j =1,2} \frac{\sqrt{|g|}}{g_{33}}\partial_j\left( \sqrt{|g|} g^{ij}\right) + g^{ij}\partial_j \left( \frac{\sqrt{|g|}}{g_{33}}\right),\\ G_{\xi,g} =\frac{C(\psi)}{ g_{33}}\left(\frac{C'(\psi)}{ \sqrt{|g|}} - \xi\cdot_g \textrm{curl}_g \xi\right), \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} a^{ij}_{\xi,g} = \frac{\sqrt{|g|}}{g_{33}} g^{ij},\quad b^i_{\xi,g} = \sum_{j =1,2} \frac{\sqrt{|g|}}{g_{33}}\partial_j\left( \sqrt{|g|} g^{ij}\right) + g^{ij}\partial_j \left( \frac{\sqrt{|g|}}{g_{33}}\right),\\ G_{\xi,g} =\frac{C(\psi)}{ g_{33}}\left(\frac{C'(\psi)}{ \sqrt{|g|}} - \xi\cdot_g \textrm{curl}_g \xi\right), \end{gathered}\right\} \end{equation}
where ![]() $\xi \cdot _g\textrm {curl}_g \xi$ is given by (D1).
$\xi \cdot _g\textrm {curl}_g \xi$ is given by (D1).