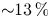1. Introduction
Understanding the origin of polarization in the radiation from charged particles is of central importance in the study of many astrophysical objects like gamma-ray bursts (GRBs) (Wiersema et al. Reference Wiersema, Covino, Toma, Van Der Horst, Varela, Min, Greiner, Starling, Tanvir and Wijers2014; Troja et al. Reference Troja, Lipunov, Mundell, Butler, Watson, Kobayashi, Cenko, Marshall, Ricci and Fruchter2017), supernova remnants (Milne & Dickel Reference Milne and Dickel1974; Bandiera & Petruk Reference Bandiera and Petruk2016), active galactic nuclei (Lopez-Rodriguez et al. Reference Lopez-Rodriguez, Alonso-Herrero, Diaz-Santos, Gonzalez-Martin, Ichikawa, Levenson, Martinez-Paredes, Nikutta, Packham and Perlman2018) and pulsar wind nebulae (Linden Reference Linden2015). The vast majority of theoretical models predict low degrees of linear polarization and virtually no circular polarization (Gruzinov & Waxman Reference Gruzinov and Waxman1999; Medvedev & Loeb Reference Medvedev and Loeb1999; Matsumiya & Ioka Reference Matsumiya and Ioka2003; Sagiv, Waxman & Loeb Reference Sagiv, Waxman and Loeb2004; Toma, Ioka & Nakamura Reference Toma, Ioka and Nakamura2007). This is in contrast with recent observations that demonstrated the existence of circularly polarized radiation emission in the afterglow of GRB 121024A (Wiersema et al. Reference Wiersema, Covino, Toma, Van Der Horst, Varela, Min, Greiner, Starling, Tanvir and Wijers2014). This emphasizes the importance of reinvestigating previous theoretical formulations regarding the origin of circular polarization in these scenarios, and, in particular, at the plasma scale (Sagiv et al. Reference Sagiv, Waxman and Loeb2004; Sinha, Keitel & Kumar Reference Sinha, Keitel and Kumar2019). Here we show that circularly polarized radiation emission can be observed in the context of the Weibel/current filamentation instability (WI/CFI) (Weibel Reference Weibel1959), and we explore the physical conditions under which this can occur.
It has been shown that WI/CFI-mediated collisionless shocks could be a possible mechanism to explain the power-law distribution of charged particles and sub-equipartition magnetic fields believed to be present in GRBs (Spitkovsky Reference Spitkovsky2008; Martins et al. Reference Martins, Fonseca, Silva and Mori2009b; Sironi & Spitkovsky Reference Sironi and Spitkovsky2009a; Fiuza et al. Reference Fiuza, Fonseca, Tonge, Mori and Silva2012; Stockem et al. Reference Stockem, Grismayer, Fonseca and Silva2014; Huntington et al. Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz and Levy2015), and the radiation obtained from charged particle motion in these magnetic fields is attributed to a synchrotron process (Hededal & Nordlund Reference Hededal and Nordlund2005; Sironi & Spitkovsky Reference Sironi and Spitkovsky2009b). However, although the mechanism of radiation in such collisionless shocks was demonstrated, little attention has been paid to the polarization of the radiation emitted.
In this contribution, we show that for plasmas in the presence of an ambient magnetic field, composed of light (e.g. electrons) and heavy (e.g. protons) species, the radiation emitted by the plasma particles due to their motion in fields generated due to WI/CFI is partially circularly polarized. The trajectories of charged particles in the WI/CFI fields are studied using the two-dimensional particle-in-cell (PIC) code OSIRIS (Fonseca et al. Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee and Katsouleas2002, Reference Fonseca, Vieira, Fiúza, Davidson, Tsung, Mori and Silva2013). A semi-analytical model is developed to describe such motion and to estimate the radiation spectra and the degree of circular polarization for a fixed observer for various pitch angles that an electron makes with the WI/CFI magnetic fields in initially magnetized and unmagnetized plasmas. Furthermore, the radiation spectra and the degree of circular polarization are computed from particle trajectories extracted directly from PIC simulations and post-processing them using the radiation code jRad (Martins et al. Reference Martins, Martins, Fonseca and Silva2009a). We show that an initial magnetization leads to transverse symmetry breaking in the pitch angle distribution of electrons confined in a current filament, producing a finite circular polarization in the emitted radiation. Of particular interest is the degree of circular polarization associated with different initial magnetizations.
2. Simulations
We simulate a relativistic cold electron–proton plasma of uniform density and a relativistic factor ![]() $\gamma _0=20$ flowing through a background plasma at rest with identical electron and proton densities. Both electrons and protons are initialized with a small isotropic thermal velocity
$\gamma _0=20$ flowing through a background plasma at rest with identical electron and proton densities. Both electrons and protons are initialized with a small isotropic thermal velocity ![]() $\beta _{th}\approx 10^{-3}$ (
$\beta _{th}\approx 10^{-3}$ (![]() ${=}\sqrt {T/m c^2}$) to initiate the WI/CFI. The flow velocity (along
${=}\sqrt {T/m c^2}$) to initiate the WI/CFI. The flow velocity (along ![]() $z$) is perpendicular to the simulation plane (see figure 1). The computational domain is
$z$) is perpendicular to the simulation plane (see figure 1). The computational domain is ![]() $512\times 512 (c/\omega _{pe})^2$ with periodic boundaries. The cell size is
$512\times 512 (c/\omega _{pe})^2$ with periodic boundaries. The cell size is ![]() ${\rm \Delta} x={\rm \Delta} y=0.1 c/\omega _{pe}$, time step
${\rm \Delta} x={\rm \Delta} y=0.1 c/\omega _{pe}$, time step ![]() ${\rm \Delta} t=0.045 \omega _{pe}^{-1}$ and each cell contains
${\rm \Delta} t=0.045 \omega _{pe}^{-1}$ and each cell contains ![]() $3\times 3$ particles per cell per species, where
$3\times 3$ particles per cell per species, where ![]() $\omega _{pe}=(4{\rm \pi} n_0\,\textrm {e}^2/m_e)^{1/2}$ is the plasma frequency,
$\omega _{pe}=(4{\rm \pi} n_0\,\textrm {e}^2/m_e)^{1/2}$ is the plasma frequency, ![]() $n_0$ is the initial plasma density,
$n_0$ is the initial plasma density, ![]() $m_e$ is the electron mass,
$m_e$ is the electron mass, ![]() $e$ is the electron charge and
$e$ is the electron charge and ![]() $c$ is the velocity of light. We include a uniform out-of-plane (along
$c$ is the velocity of light. We include a uniform out-of-plane (along ![]() $z$) initial magnetic field (
$z$) initial magnetic field (![]() $B_z$) measured in the frame of the background plasma corresponding to a magnetization of the flowing plasma
$B_z$) measured in the frame of the background plasma corresponding to a magnetization of the flowing plasma ![]() $\sigma \equiv B_{z}^2/4{\rm \pi} \gamma _0m_en_0c^2$ which we varied from
$\sigma \equiv B_{z}^2/4{\rm \pi} \gamma _0m_en_0c^2$ which we varied from ![]() $\sigma = 0.0$ to
$\sigma = 0.0$ to ![]() $0.2$ for both signs of
$0.2$ for both signs of ![]() $B_z$. The WI/CFI in interpenetrating plasma flows gives rise to current filaments with an associated azimuthal magnetic field (
$B_z$. The WI/CFI in interpenetrating plasma flows gives rise to current filaments with an associated azimuthal magnetic field (![]() $B_\phi \hat {\boldsymbol {e}}_\phi$) surrounding them. Because the electrons respond at time scales faster than the protons, a space charge radial electric field (
$B_\phi \hat {\boldsymbol {e}}_\phi$) surrounding them. Because the electrons respond at time scales faster than the protons, a space charge radial electric field (![]() $E_r\hat {\boldsymbol {e}}_r$) develops at the edge of the electron filaments. The maximum electron WI/CFI growth rate is given by
$E_r\hat {\boldsymbol {e}}_r$) develops at the edge of the electron filaments. The maximum electron WI/CFI growth rate is given by ![]() $\varGamma _{WI/CFI}\approx |\beta _0|/\sqrt {\gamma _0}\omega _{pe}$ (Silva et al. Reference Silva, Fonseca, Tonge, Mori and Dawson2002; Shukla et al. Reference Shukla, Stockem, Fiúza and Silva2012), where
$\varGamma _{WI/CFI}\approx |\beta _0|/\sqrt {\gamma _0}\omega _{pe}$ (Silva et al. Reference Silva, Fonseca, Tonge, Mori and Dawson2002; Shukla et al. Reference Shukla, Stockem, Fiúza and Silva2012), where ![]() $\beta _0$ is the flow velocity normalized to
$\beta _0$ is the flow velocity normalized to ![]() $c$. For our
$c$. For our ![]() $\gamma _0=20$ this yields
$\gamma _0=20$ this yields ![]() $\varGamma \approx 0.2\omega _{pe}$, and simulations show that the magnetic field saturates in a few 100
$\varGamma \approx 0.2\omega _{pe}$, and simulations show that the magnetic field saturates in a few 100![]() $\omega _{pe}^{-1}$.
$\omega _{pe}^{-1}$.

Figure 1. (a) The spatial distribution of radiated power from electrons in a magnetized current filament of an electron–proton plasma (![]() $m_i/m_e=1836$) with initial magnetization
$m_i/m_e=1836$) with initial magnetization ![]() $\sigma =0.05$ and at time
$\sigma =0.05$ and at time ![]() $t=9000\omega _{pe}^{-1}$. (b) The transverse magnetic field vectors (represented by arrows) arising due to WI/CFI for the same simulation as in (a). Trajectories of 50 electrons trapped in the current filament are shown from time
$t=9000\omega _{pe}^{-1}$. (b) The transverse magnetic field vectors (represented by arrows) arising due to WI/CFI for the same simulation as in (a). Trajectories of 50 electrons trapped in the current filament are shown from time ![]() $t_i=8910\omega _{pe}^{-1}$ to
$t_i=8910\omega _{pe}^{-1}$ to ![]() $t_f=9000\omega _{pe}^{-1}$, with colour scales representing their longitudinal momentum (
$t_f=9000\omega _{pe}^{-1}$, with colour scales representing their longitudinal momentum (![]() $\boldsymbol {p}_z$). (c) The fields and tracks of electrons for the same time period in an unmagnetized electron–proton plasma.
$\boldsymbol {p}_z$). (c) The fields and tracks of electrons for the same time period in an unmagnetized electron–proton plasma.
At the saturation of WI/CFI, there is a strong emission of radiation from the filament edges. This is illustrated in figure 1(a), which shows the radiated power (![]() $P$) from the electrons in a single magnetized current filament. The radiated power is calculated using the relativistic generalization of Larmor's formula,
$P$) from the electrons in a single magnetized current filament. The radiated power is calculated using the relativistic generalization of Larmor's formula, ![]() $P=2/3(\textrm {e}^2/c)\gamma _e^6[\boldsymbol {\dot {\beta }}_e^2-(\boldsymbol {\beta }_e\times \boldsymbol {\dot {\beta }}_e)^2]$, where
$P=2/3(\textrm {e}^2/c)\gamma _e^6[\boldsymbol {\dot {\beta }}_e^2-(\boldsymbol {\beta }_e\times \boldsymbol {\dot {\beta }}_e)^2]$, where ![]() $\boldsymbol {\beta }_e$ is the electron velocity vector normalized to
$\boldsymbol {\beta }_e$ is the electron velocity vector normalized to ![]() $c$,
$c$, ![]() $\boldsymbol {\dot {\beta }}_e$ is the normalized electron acceleration and
$\boldsymbol {\dot {\beta }}_e$ is the normalized electron acceleration and ![]() $\gamma _e$ is the electron Lorentz factor (Jackson Reference Jackson2012). The peak value of
$\gamma _e$ is the electron Lorentz factor (Jackson Reference Jackson2012). The peak value of ![]() $P$ at the filament edges is nearly ten times larger than that within the filament. This is because additional mutually perpendicular strong electric and magnetic fields resulting from WI/CFI lead to a relatively stronger
$P$ at the filament edges is nearly ten times larger than that within the filament. This is because additional mutually perpendicular strong electric and magnetic fields resulting from WI/CFI lead to a relatively stronger ![]() $\boldsymbol {\dot {\beta }}_e$ perpendicular to
$\boldsymbol {\dot {\beta }}_e$ perpendicular to ![]() $\boldsymbol {\beta }_e$ and increased kinetic energies of the electrons at the filament edges, whereas the electrons at the centre gyrate only under the influence of the initial magnetic field and the longitudinal momentum (
$\boldsymbol {\beta }_e$ and increased kinetic energies of the electrons at the filament edges, whereas the electrons at the centre gyrate only under the influence of the initial magnetic field and the longitudinal momentum (![]() $p_z$) is much larger than the transverse momentum (
$p_z$) is much larger than the transverse momentum (![]() $p_x,p_y$). Hence, the electrons at the filament edge primarily contribute to the radiated energy.The electric field of the radiation emitted by an electron is given by (Jackson Reference Jackson2012)
$p_x,p_y$). Hence, the electrons at the filament edge primarily contribute to the radiated energy.The electric field of the radiation emitted by an electron is given by (Jackson Reference Jackson2012)
 \begin{equation} \boldsymbol{E}_\mathrm{rad}(\boldsymbol{r},t) =\frac{e}{c} \left[\frac{\boldsymbol{n}\times[(\boldsymbol{n}-\boldsymbol{\beta}_e)\times \boldsymbol{\dot{\beta}}_e]}{(1-\boldsymbol{\beta}_e\cdot\boldsymbol{n})^3R}\right]_{\textrm{ret}},\end{equation}
\begin{equation} \boldsymbol{E}_\mathrm{rad}(\boldsymbol{r},t) =\frac{e}{c} \left[\frac{\boldsymbol{n}\times[(\boldsymbol{n}-\boldsymbol{\beta}_e)\times \boldsymbol{\dot{\beta}}_e]}{(1-\boldsymbol{\beta}_e\cdot\boldsymbol{n})^3R}\right]_{\textrm{ret}},\end{equation}
where ![]() $\boldsymbol {n}$ is the unit vector from the position of the charge to the observer at a distance
$\boldsymbol {n}$ is the unit vector from the position of the charge to the observer at a distance ![]() $R$ from the particle. The quantities are evaluated at the retarded time
$R$ from the particle. The quantities are evaluated at the retarded time ![]() $t^\prime =t-R/c$. The spectrum of the radiated electric field is determined from the Fourier transform of (2.1) (Jackson Reference Jackson2012):
$t^\prime =t-R/c$. The spectrum of the radiated electric field is determined from the Fourier transform of (2.1) (Jackson Reference Jackson2012):
 \begin{align} \boldsymbol{E}_\mathrm{rad}(\omega)&=\frac{e}{c}\left(\frac{1}{2{\rm \pi}}\right)^{1/2} \int_{-\infty}^{\infty}\frac{\boldsymbol{n}\times[(\boldsymbol{n}-\boldsymbol{\beta}_e)\times \boldsymbol{\dot{\beta}}_e]}{(1-\boldsymbol{\beta}_e\cdot\boldsymbol{n})^2R(t^\prime)}\nonumber\\ &\quad \times \exp({\textrm{i}\omega(t^\prime-\boldsymbol{n}\cdot\boldsymbol{r}(t^\prime)/c)})\,\textrm{d} t^\prime. \end{align}
\begin{align} \boldsymbol{E}_\mathrm{rad}(\omega)&=\frac{e}{c}\left(\frac{1}{2{\rm \pi}}\right)^{1/2} \int_{-\infty}^{\infty}\frac{\boldsymbol{n}\times[(\boldsymbol{n}-\boldsymbol{\beta}_e)\times \boldsymbol{\dot{\beta}}_e]}{(1-\boldsymbol{\beta}_e\cdot\boldsymbol{n})^2R(t^\prime)}\nonumber\\ &\quad \times \exp({\textrm{i}\omega(t^\prime-\boldsymbol{n}\cdot\boldsymbol{r}(t^\prime)/c)})\,\textrm{d} t^\prime. \end{align} The information about the instantaneous position, velocity and acceleration of the electrons can be obtained from the electron trajectories. The electron trajectories, superimposed on the magnetic fields due to WI/CFI for magnetized and unmagnetized plasmas, are shown in figures 1(b) and 1(c), respectively. The electrons have enhanced longitudinal momentum (![]() $p_z$) at the filament edge, which indicates that most of the radiation emitted from them will be collimated in the direction perpendicular to the simulation plane. An initial magnetization causes the electrons to drift along the azimuthal direction, due to a combination of
$p_z$) at the filament edge, which indicates that most of the radiation emitted from them will be collimated in the direction perpendicular to the simulation plane. An initial magnetization causes the electrons to drift along the azimuthal direction, due to a combination of ![]() $\boldsymbol {E}\times \boldsymbol {B}$ and
$\boldsymbol {E}\times \boldsymbol {B}$ and ![]() $\boldsymbol {\nabla }\boldsymbol {B}$ drifts, executing a correlated motion (figure 1b). On the other hand, in an unmagnetized plasma, the electrons scatter at all possible angles from the WI/CFI fields (figure 1c).
$\boldsymbol {\nabla }\boldsymbol {B}$ drifts, executing a correlated motion (figure 1b). On the other hand, in an unmagnetized plasma, the electrons scatter at all possible angles from the WI/CFI fields (figure 1c).
3. Model and comparison with simulations
To formulate a model describing the motion of charged particles in WI/CFI fields, we consider a cylindrical current filament with electrons flowing along the positive ![]() $z$ direction (
$z$ direction (![]() $\hat {\boldsymbol {e}}_z$). The electric and magnetic fields can be described as
$\hat {\boldsymbol {e}}_z$). The electric and magnetic fields can be described as ![]() $\boldsymbol {E}=E_rS(r)\hat {{e}}_r$ and
$\boldsymbol {E}=E_rS(r)\hat {{e}}_r$ and ![]() $\boldsymbol {B}=B_\phi S(r)\hat {\boldsymbol {e}}_\phi +B_{z}\hat {\boldsymbol {e}}_z$, respectively, where
$\boldsymbol {B}=B_\phi S(r)\hat {\boldsymbol {e}}_\phi +B_{z}\hat {\boldsymbol {e}}_z$, respectively, where ![]() $E_r$ and
$E_r$ and ![]() $B_\phi$ are the respective amplitudes of the
$B_\phi$ are the respective amplitudes of the ![]() $\boldsymbol {E}$ and
$\boldsymbol {E}$ and ![]() $\boldsymbol {B}$ fields in the radial and azimuthal directions,
$\boldsymbol {B}$ fields in the radial and azimuthal directions, ![]() $B_z$ is the initial magnetic field and
$B_z$ is the initial magnetic field and ![]() $S(r)$ is the spatial profile. At saturation, the spatial profile of the fields from the simulation closely resembles a Gaussian with
$S(r)$ is the spatial profile. At saturation, the spatial profile of the fields from the simulation closely resembles a Gaussian with ![]() $\textrm {FWHM}\sim 2.5c/\omega _{pe}$. Hence, we substitute
$\textrm {FWHM}\sim 2.5c/\omega _{pe}$. Hence, we substitute ![]() $S(r)=\exp [-(r-r_0)^2/2\eta ^2]$, where
$S(r)=\exp [-(r-r_0)^2/2\eta ^2]$, where ![]() $r_0$ is the filament radius and
$r_0$ is the filament radius and ![]() $\eta =1/\sqrt {2}$. The equation for the electron trajectory obtained by combining the momentum and energy equation is
$\eta =1/\sqrt {2}$. The equation for the electron trajectory obtained by combining the momentum and energy equation is
where the normalizations ![]() $\boldsymbol {E}\equiv e\boldsymbol {E}/(m_e\omega _{pe}c)$;
$\boldsymbol {E}\equiv e\boldsymbol {E}/(m_e\omega _{pe}c)$; ![]() $\boldsymbol {B}\equiv e\boldsymbol {B}/(m_e\omega _{pe}c)$; and
$\boldsymbol {B}\equiv e\boldsymbol {B}/(m_e\omega _{pe}c)$; and ![]() $t\equiv \omega _{pe}t$ have been used. The radiated electric field vectors can be calculated using (2.1) and (3.1) for a given field configuration and initial position and velocity of the particles.
$t\equiv \omega _{pe}t$ have been used. The radiated electric field vectors can be calculated using (2.1) and (3.1) for a given field configuration and initial position and velocity of the particles.
A schematic representation of the geometry of the magnetic field due to the current filaments and the motion of plasma electrons in the frame of the background plasma is shown in figure 2(a). The radiated electric field vectors obtained using (2.1) and (3.1) for electrons making pitch angles ![]() $\psi _1$ (
$\psi _1$ (![]() $<{\rm \pi} /2$) and
$<{\rm \pi} /2$) and ![]() $\psi _2$ (
$\psi _2$ (![]() $>{\rm \pi} /2$) with respect to the direction of the WI/CFI magnetic field at the instant of emission are shown in figure 2(b). The direction of rotation of the radiated electric field vectors shows a left-handed circular polarization for
$>{\rm \pi} /2$) with respect to the direction of the WI/CFI magnetic field at the instant of emission are shown in figure 2(b). The direction of rotation of the radiated electric field vectors shows a left-handed circular polarization for ![]() $\psi _1$ and right-handed circular polarization for
$\psi _1$ and right-handed circular polarization for ![]() $\psi _2$. The handedness of circular polarization depends on the pitch angle. The emission from a single electron whose velocity vector makes a pitch angle
$\psi _2$. The handedness of circular polarization depends on the pitch angle. The emission from a single electron whose velocity vector makes a pitch angle ![]() $\psi$ with the direction of the WI/CFI magnetic field vector at the instant of emission is equivalent to that emitted by a particle moving at a constant speed in a circular path. For the observer lying on the
$\psi$ with the direction of the WI/CFI magnetic field vector at the instant of emission is equivalent to that emitted by a particle moving at a constant speed in a circular path. For the observer lying on the ![]() $z$ axis in the far field, it is reasonable to assume that the angle between the observer and the point of emission
$z$ axis in the far field, it is reasonable to assume that the angle between the observer and the point of emission ![]() $\alpha \approx 0$. Hence, the electric field vectors of the emitted radiation will be oriented in the
$\alpha \approx 0$. Hence, the electric field vectors of the emitted radiation will be oriented in the ![]() $xy$ plane. For a relativistic electron, the radiation lasts for a very short time and is limited within a small angle
$xy$ plane. For a relativistic electron, the radiation lasts for a very short time and is limited within a small angle ![]() $\theta \sim 1/\gamma _e\ll 1$ for a fixed observer. Under this assumption, (2.2) reduces to
$\theta \sim 1/\gamma _e\ll 1$ for a fixed observer. Under this assumption, (2.2) reduces to ![]() $\boldsymbol {E}_\mathrm {rad}= (e/c)(2/3 {\rm \pi} )^{1/2} (\omega /\omega _0 R) [-\textrm {i}(1/\gamma _e^2+({\rm \pi} /2-\psi )^2) K_{2/3}(\xi )\widehat {\boldsymbol {e}_{x}}]$
$\boldsymbol {E}_\mathrm {rad}= (e/c)(2/3 {\rm \pi} )^{1/2} (\omega /\omega _0 R) [-\textrm {i}(1/\gamma _e^2+({\rm \pi} /2-\psi )^2) K_{2/3}(\xi )\widehat {\boldsymbol {e}_{x}}]$ ![]() $+ ({\rm \pi} /2-\psi ) \sqrt {(1/\gamma _e^2+({\rm \pi} /2-\psi )^2)} K_{1/3}(\xi )\widehat {\boldsymbol {e}_{y}} ]$, where
$+ ({\rm \pi} /2-\psi ) \sqrt {(1/\gamma _e^2+({\rm \pi} /2-\psi )^2)} K_{1/3}(\xi )\widehat {\boldsymbol {e}_{y}} ]$, where ![]() $K_{2/3}$ and
$K_{2/3}$ and ![]() $K_{1/3}$ are the modified Bessel functions,
$K_{1/3}$ are the modified Bessel functions, ![]() $\xi =(\omega /\omega _0)(1+\gamma _e^2({\rm \pi} /2-\psi )^2)^{3/2}/3\gamma _e^3$,
$\xi =(\omega /\omega _0)(1+\gamma _e^2({\rm \pi} /2-\psi )^2)^{3/2}/3\gamma _e^3$, ![]() $\omega _0$ is the gyrofrequency and
$\omega _0$ is the gyrofrequency and ![]() $\omega$ is the frequency of radiation (Jackson Reference Jackson2012). It is clear that the polarization of radiation is right-handed or left-handed according to
$\omega$ is the frequency of radiation (Jackson Reference Jackson2012). It is clear that the polarization of radiation is right-handed or left-handed according to ![]() $\psi \gtrless {\rm \pi} /2$ and is consistent with the results from the semi-analytical model shown in figure 2(b1,b2). For a plasma with no initial magnetic field component along
$\psi \gtrless {\rm \pi} /2$ and is consistent with the results from the semi-analytical model shown in figure 2(b1,b2). For a plasma with no initial magnetic field component along ![]() $\hat {\boldsymbol {e}}_z$, the electrons have a symmetric pitch angle distribution for
$\hat {\boldsymbol {e}}_z$, the electrons have a symmetric pitch angle distribution for ![]() $\psi \gtrless {\rm \pi} /2$. Hence, the contributions to the right-handed and left-handed polarizations are equal, resulting in a net zero circular polarization. In a magnetized plasma, the initial magnetic field (
$\psi \gtrless {\rm \pi} /2$. Hence, the contributions to the right-handed and left-handed polarizations are equal, resulting in a net zero circular polarization. In a magnetized plasma, the initial magnetic field (![]() $B_z$) along
$B_z$) along ![]() $\hat {\boldsymbol {e}}_z$ bends the electron trajectory in the
$\hat {\boldsymbol {e}}_z$ bends the electron trajectory in the ![]() $xy$ plane creating an anisotropy in pitch angle distribution. When
$xy$ plane creating an anisotropy in pitch angle distribution. When ![]() $B_z$ is along positive
$B_z$ is along positive ![]() $\hat {\boldsymbol {e}}_z$, the number of electrons with negative pitch angles exceeds the number with positive pitch angles resulting in a net right-handed circular polarization and vice versa when the direction of
$\hat {\boldsymbol {e}}_z$, the number of electrons with negative pitch angles exceeds the number with positive pitch angles resulting in a net right-handed circular polarization and vice versa when the direction of ![]() $B_z$ is reversed. To validate our model, we extracted trajectories of 1000 electrons from a current filament directly from PIC simulations and computed the radiation spectrum and the degree of circular polarization (
$B_z$ is reversed. To validate our model, we extracted trajectories of 1000 electrons from a current filament directly from PIC simulations and computed the radiation spectrum and the degree of circular polarization (![]() $P_c$) of the radiation emitted from them using the post-processing radiation code jRad (Martins et al. Reference Martins, Martins, Fonseca and Silva2009a). Although the OSIRIS simulation is a two-dimensional one, we reconstruct the three-dimensional trajectories as
$P_c$) of the radiation emitted from them using the post-processing radiation code jRad (Martins et al. Reference Martins, Martins, Fonseca and Silva2009a). Although the OSIRIS simulation is a two-dimensional one, we reconstruct the three-dimensional trajectories as ![]() $z=\int p_z(t)/\gamma _e(t)\,\textrm {d} t$. The spectrum was calculated on a two-dimensional virtual detector in the
$z=\int p_z(t)/\gamma _e(t)\,\textrm {d} t$. The spectrum was calculated on a two-dimensional virtual detector in the ![]() $xy$ plane at a distance
$xy$ plane at a distance ![]() $z=1.5\times 10^4c/\omega _{pe}$ and size
$z=1.5\times 10^4c/\omega _{pe}$ and size ![]() $60\,000\times 60\,000(c/\omega _{pe})^2$ divided in
$60\,000\times 60\,000(c/\omega _{pe})^2$ divided in ![]() $100\times 100$ cells to capture the entire emitting region. The detector captured a spectrum of frequencies (
$100\times 100$ cells to capture the entire emitting region. The detector captured a spectrum of frequencies (![]() $\omega$) in the range
$\omega$) in the range ![]() $\omega =(10^0\text {--}10^3)\omega _{pe}^{-1}$ with a resolution of 256 cells per decade in the frequency axis. Radiation was calculated following the trajectories from time
$\omega =(10^0\text {--}10^3)\omega _{pe}^{-1}$ with a resolution of 256 cells per decade in the frequency axis. Radiation was calculated following the trajectories from time ![]() $t_i=6300\omega _{pe}^{-1}$ to
$t_i=6300\omega _{pe}^{-1}$ to ![]() $t_f=9000\omega _{pe}^{-1}$ during which the filament was in a steady state. The degree of circular polarization (
$t_f=9000\omega _{pe}^{-1}$ during which the filament was in a steady state. The degree of circular polarization (![]() $P_c$) was estimated using the relevant Stokes parameters, for which
$P_c$) was estimated using the relevant Stokes parameters, for which ![]() $P_c=V/I$,
$P_c=V/I$, ![]() $V=2\langle Im[(\boldsymbol {\epsilon }_1\cdot \boldsymbol {E}_{\textrm {rad}})^*(\boldsymbol {\epsilon }_2\cdot \boldsymbol {E}_{\textrm {rad}})]\rangle$,
$V=2\langle Im[(\boldsymbol {\epsilon }_1\cdot \boldsymbol {E}_{\textrm {rad}})^*(\boldsymbol {\epsilon }_2\cdot \boldsymbol {E}_{\textrm {rad}})]\rangle$, ![]() $I=|\boldsymbol {\epsilon }_1\cdot \boldsymbol {E}_{\textrm {rad}}|^2+|\boldsymbol {\epsilon }_2\cdot \boldsymbol {E}_{\textrm {rad}}|^2$ and
$I=|\boldsymbol {\epsilon }_1\cdot \boldsymbol {E}_{\textrm {rad}}|^2+|\boldsymbol {\epsilon }_2\cdot \boldsymbol {E}_{\textrm {rad}}|^2$ and ![]() $\boldsymbol {\epsilon }_1$ and
$\boldsymbol {\epsilon }_1$ and ![]() $\boldsymbol {\epsilon }_2$ are the unit vectors perpendicular to the direction of observation. The angular brackets
$\boldsymbol {\epsilon }_2$ are the unit vectors perpendicular to the direction of observation. The angular brackets ![]() $\langle \cdot \rangle$ represent the time average. Figures 3(a) and 3(c) show the spatial distribution of frequency-averaged radiated energy,
$\langle \cdot \rangle$ represent the time average. Figures 3(a) and 3(c) show the spatial distribution of frequency-averaged radiated energy, ![]() $\langle I_{\textrm {rad}}\rangle _\omega =\int I_{\textrm {rad}}\,\textrm {d}\omega /\int \textrm {d}\omega$, from the electrons confined in the current filament of figures 1(b) and 1(c), respectively. Figures 3(b) and 3(d) show the corresponding
$\langle I_{\textrm {rad}}\rangle _\omega =\int I_{\textrm {rad}}\,\textrm {d}\omega /\int \textrm {d}\omega$, from the electrons confined in the current filament of figures 1(b) and 1(c), respectively. Figures 3(b) and 3(d) show the corresponding ![]() $\langle P_c\rangle _\omega =\int P_cI_{\textrm {rad}}\,\textrm {d}\omega /\int I_{\textrm {rad}}\,\textrm {d}\omega$ for the filament. A strong right circular polarization with a peak value of
$\langle P_c\rangle _\omega =\int P_cI_{\textrm {rad}}\,\textrm {d}\omega /\int I_{\textrm {rad}}\,\textrm {d}\omega$ for the filament. A strong right circular polarization with a peak value of ![]() $\langle P_c\rangle _\omega \approx 0.25$ (25 %) is observed for the magnetized filament. For the unmagnetized filament, a nearly equal distribution of left and right circular polarization is observed resulting in a net zero circularly polarized radiation flux. The total circularly polarized radiation flux
$\langle P_c\rangle _\omega \approx 0.25$ (25 %) is observed for the magnetized filament. For the unmagnetized filament, a nearly equal distribution of left and right circular polarization is observed resulting in a net zero circularly polarized radiation flux. The total circularly polarized radiation flux ![]() $\langle P_c\rangle$ can be obtained using the formula
$\langle P_c\rangle$ can be obtained using the formula ![]() $\langle P_c\rangle =\iint P_cI_{\textrm {rad}}\,\textrm {d} A\,\textrm {d}\omega /\iint I_{\textrm {rad}}\,\textrm {d} A\,\textrm {d}\omega$, where
$\langle P_c\rangle =\iint P_cI_{\textrm {rad}}\,\textrm {d} A\,\textrm {d}\omega /\iint I_{\textrm {rad}}\,\textrm {d} A\,\textrm {d}\omega$, where ![]() $A$ is the detector area. For the radiation in figure 1(b),
$A$ is the detector area. For the radiation in figure 1(b), ![]() $\langle P_c\rangle =0.117$ (11.7 %). To confirm that
$\langle P_c\rangle =0.117$ (11.7 %). To confirm that ![]() $\langle P_c\rangle$ is not affected by the time period on which it is averaged, the time of averaging (
$\langle P_c\rangle$ is not affected by the time period on which it is averaged, the time of averaging (![]() $6300\omega _{pe}^{-1}\text {--}9000\omega _{pe}^{-1}$) was divided into three equal segments of interval
$6300\omega _{pe}^{-1}\text {--}9000\omega _{pe}^{-1}$) was divided into three equal segments of interval ![]() $900\omega _{pe}^{-1}$ and
$900\omega _{pe}^{-1}$ and ![]() $\langle P_c\rangle$ was separately calculated for each of these intervals. We found that
$\langle P_c\rangle$ was separately calculated for each of these intervals. We found that ![]() $\langle P_c\rangle$ was equal in all cases with a variation of
$\langle P_c\rangle$ was equal in all cases with a variation of ![]() ${\pm }0.1\,\%$, which indicates that our observations for a single filament are physically meaningful.
${\pm }0.1\,\%$, which indicates that our observations for a single filament are physically meaningful.

Figure 2. (a) A schematic representation of the azimuthal magnetic field due to a cylindrical current filament with a flow along ![]() $z$ with 1 and 2 representing electron trajectories that, at a given time, make pitch angles
$z$ with 1 and 2 representing electron trajectories that, at a given time, make pitch angles ![]() $\psi _1<{\rm \pi} /2$ and
$\psi _1<{\rm \pi} /2$ and ![]() $\psi _2>{\rm \pi} /2$, respectively, with the direction of the WI/CFI magnetic field vector at the time of emission. (b) The trajectories of two electrons from the semi-analytical model for an observer along
$\psi _2>{\rm \pi} /2$, respectively, with the direction of the WI/CFI magnetic field vector at the time of emission. (b) The trajectories of two electrons from the semi-analytical model for an observer along ![]() $\hat {\boldsymbol {e}}_z$ (trajectory 1 (
$\hat {\boldsymbol {e}}_z$ (trajectory 1 (![]() $\psi _1$) in blue and trajectory 2 (
$\psi _1$) in blue and trajectory 2 (![]() $\psi _2$) in red). The electric field vectors (arrows) are attached to each point on the trajectory, and shown more clearly in the zoom (b1,b2). It is clear that, at the time of dominant radiation where the radius of curvature is at a minimum, the radiation from trajectory 1 is left circularly polarized and from trajectory 2 is right circularly polarized because the electric field vectors are rotating clockwise and counterclockwise, respectively.
$\psi _2$) in red). The electric field vectors (arrows) are attached to each point on the trajectory, and shown more clearly in the zoom (b1,b2). It is clear that, at the time of dominant radiation where the radius of curvature is at a minimum, the radiation from trajectory 1 is left circularly polarized and from trajectory 2 is right circularly polarized because the electric field vectors are rotating clockwise and counterclockwise, respectively.

Figure 3. Simulation results from jRad illustrating the key properties of radiation and degree of circular polarization from 1000 electrons trapped in a current filament. (a,c) The frequency-averaged spatial distribution of radiated energy on the detector lying in the ![]() $xy$ plane (parallel to the simulation plane) from the current filament shown in figures 1(c) and 1(b), respectively. (b,d) The frequency-averaged degree of circular polarization corresponding to (a,c). For the unmagnetized filament, there is an almost equal contribution to left and right circular polarization, whereas a magnetized filament produces a strong right circularly polarized radiation with peak value
$xy$ plane (parallel to the simulation plane) from the current filament shown in figures 1(c) and 1(b), respectively. (b,d) The frequency-averaged degree of circular polarization corresponding to (a,c). For the unmagnetized filament, there is an almost equal contribution to left and right circular polarization, whereas a magnetized filament produces a strong right circularly polarized radiation with peak value ![]() ${\sim }25\,\%$. (e) The frequency-averaged spatial distribution of radiated energy on a detector similar to (c) from four magnetized current filaments (with initial magnetization
${\sim }25\,\%$. (e) The frequency-averaged spatial distribution of radiated energy on a detector similar to (c) from four magnetized current filaments (with initial magnetization ![]() $\sigma =0.05$) of electron–proton plasma shown in the inset (a zoom of this inset can be found in figure 5). (f) The frequency-averaged degree of circular polarization corresponding to (e) with the inset showing
$\sigma =0.05$) of electron–proton plasma shown in the inset (a zoom of this inset can be found in figure 5). (f) The frequency-averaged degree of circular polarization corresponding to (e) with the inset showing ![]() $\langle P_c\rangle$ for each of the corresponding filaments. A line-out indicated by a dashed line is also plotted as a solid curve in each panel.
$\langle P_c\rangle$ for each of the corresponding filaments. A line-out indicated by a dashed line is also plotted as a solid curve in each panel.
Furthermore, to check for the effect of multiple filaments, we computed the radiation spectra and ![]() $P_c$ from 1000 electrons distributed equally in four filaments of a magnetized electron–proton plasma of figure 1(b). Figures 3(e) and 3(f) show
$P_c$ from 1000 electrons distributed equally in four filaments of a magnetized electron–proton plasma of figure 1(b). Figures 3(e) and 3(f) show ![]() $\langle I_{\textrm {rad}}\rangle _\omega$ and
$\langle I_{\textrm {rad}}\rangle _\omega$ and ![]() $\langle P_c\rangle _\omega$, respectively, for the four filaments described in the inset of figure 3(e). The radiation spectra and circular polarization are similar to those of the single filament. In addition,
$\langle P_c\rangle _\omega$, respectively, for the four filaments described in the inset of figure 3(e). The radiation spectra and circular polarization are similar to those of the single filament. In addition, ![]() $\langle P_c\rangle$ obtained from each of the filaments (inset of figure 3f) is computed separately and found to be nearly equal (
$\langle P_c\rangle$ obtained from each of the filaments (inset of figure 3f) is computed separately and found to be nearly equal (![]() ${\sim }0.115$). This shows that the anisotropy in pitch angle distribution depends only on the fields and not the filament shape. An important observation is that WI/CFI in magnetized plasmas generates local islands of anisotropic pitch angle distribution. Hence, circular polarization can be observed even in the case of WI/CFI-driven shocks in magnetized spherical jets irrespective of the position of observation in contrast to the model described earlier (Nava, Nakar & Piran Reference Nava, Nakar and Piran2015), which is valid only for collimated jets. To investigate the role of initial magnetization of the plasma,
${\sim }0.115$). This shows that the anisotropy in pitch angle distribution depends only on the fields and not the filament shape. An important observation is that WI/CFI in magnetized plasmas generates local islands of anisotropic pitch angle distribution. Hence, circular polarization can be observed even in the case of WI/CFI-driven shocks in magnetized spherical jets irrespective of the position of observation in contrast to the model described earlier (Nava, Nakar & Piran Reference Nava, Nakar and Piran2015), which is valid only for collimated jets. To investigate the role of initial magnetization of the plasma, ![]() $\langle P_c\rangle$ was calculated from 1000 electrons confined in a single filament of electron–proton plasma with initial magnetizations varying from 0.0 to 0.2 for both signs of
$\langle P_c\rangle$ was calculated from 1000 electrons confined in a single filament of electron–proton plasma with initial magnetizations varying from 0.0 to 0.2 for both signs of ![]() $B_z$. It was found that
$B_z$. It was found that ![]() $\langle P_c\rangle$ increased initially with magnetization and then started to saturate beyond
$\langle P_c\rangle$ increased initially with magnetization and then started to saturate beyond ![]() $\sigma = 0.05$ converging to
$\sigma = 0.05$ converging to ![]() ${\sim }13\,\%$. The level of circular polarization depends on the electron pitch angle distribution, and we have confirmed that the external magnetic field changes this distribution such that finite levels of circular polarization become possible. Specifically, in unmagnetized scenarios, the pitch angle distribution is symmetric about
${\sim }13\,\%$. The level of circular polarization depends on the electron pitch angle distribution, and we have confirmed that the external magnetic field changes this distribution such that finite levels of circular polarization become possible. Specifically, in unmagnetized scenarios, the pitch angle distribution is symmetric about ![]() ${\rm \pi} /2$. Thus, the total level of circular polarization vanishes in this case. In magnetized scenarios, instead, the pitch angle distribution is offset due to the particle drifts that appear in the presence of the external magnetic fields. As the pitch angle distribution becomes asymmetric, the level of circular polarization increases. Other processes can also lead to finite circular polarization levels, for instance (Sinha et al. Reference Sinha, Keitel and Kumar2019) where the generation of circular polarization in a different physical configuration is attributed to an asymmetric energy dissipation mechanism instead of the topological changes in pitch angle distribution discussed here.
${\rm \pi} /2$. Thus, the total level of circular polarization vanishes in this case. In magnetized scenarios, instead, the pitch angle distribution is offset due to the particle drifts that appear in the presence of the external magnetic fields. As the pitch angle distribution becomes asymmetric, the level of circular polarization increases. Other processes can also lead to finite circular polarization levels, for instance (Sinha et al. Reference Sinha, Keitel and Kumar2019) where the generation of circular polarization in a different physical configuration is attributed to an asymmetric energy dissipation mechanism instead of the topological changes in pitch angle distribution discussed here.
For high magnetizations (![]() ${\gtrapprox }0.05$), the cyclotron motion completely dominates over the azimuthal velocity vector leading to a saturation of the pitch angle distribution which results in the saturation of
${\gtrapprox }0.05$), the cyclotron motion completely dominates over the azimuthal velocity vector leading to a saturation of the pitch angle distribution which results in the saturation of ![]() $\langle P_c\rangle$. The handedness of circular polarization changes with the sign of
$\langle P_c\rangle$. The handedness of circular polarization changes with the sign of ![]() $B_z$ because the velocity vector due to cyclotron motion reverses with the sign of
$B_z$ because the velocity vector due to cyclotron motion reverses with the sign of ![]() $B_z$ resulting in an anisotropy in the opposite direction. Furthermore, to understand the effect of plasma composition, i.e. ion–electron mass ratios (
$B_z$ resulting in an anisotropy in the opposite direction. Furthermore, to understand the effect of plasma composition, i.e. ion–electron mass ratios (![]() $m_i/m_e$), we performed simulations for the same magnetizations for plasmas with
$m_i/m_e$), we performed simulations for the same magnetizations for plasmas with ![]() $m_i/m_e=1$ and 918, and compared the degree of circular polarization shown in figure 4. We observed that the values of
$m_i/m_e=1$ and 918, and compared the degree of circular polarization shown in figure 4. We observed that the values of ![]() $\langle P_c\rangle$ for
$\langle P_c\rangle$ for ![]() $m_i/m_e=918$ and 1836 were almost equal. This is because the ion response time scales are very large when compared to electron time scales, resulting in the radiation primarily being emitted only by the electrons and the circular polarization arising only due to the anisotropies in electron pitch angle distribution. For electron–positron plasmas, both species contribute to the emitted radiation. They rotate in opposite directions due to their opposite charge and create anisotropies in mutually opposite directions resulting in a net cancellation of the circular polarization. Although the level of circular polarization is strongly dependent on mass ratio for intermediate values of
$m_i/m_e=918$ and 1836 were almost equal. This is because the ion response time scales are very large when compared to electron time scales, resulting in the radiation primarily being emitted only by the electrons and the circular polarization arising only due to the anisotropies in electron pitch angle distribution. For electron–positron plasmas, both species contribute to the emitted radiation. They rotate in opposite directions due to their opposite charge and create anisotropies in mutually opposite directions resulting in a net cancellation of the circular polarization. Although the level of circular polarization is strongly dependent on mass ratio for intermediate values of ![]() $m_i/m_e$, we did not include this range of mass ratios in figure 4. In this range, it is not possible to find a steady-state filament for comparable time intervals, because filaments evolve rapidly compared to the electron motion. Although a study showing the scaling of polarization as a function of mass ratio may be possible, and could allow for a three-dimensional study at reduced mass ratio, this is beyond the scope of this paper.
$m_i/m_e$, we did not include this range of mass ratios in figure 4. In this range, it is not possible to find a steady-state filament for comparable time intervals, because filaments evolve rapidly compared to the electron motion. Although a study showing the scaling of polarization as a function of mass ratio may be possible, and could allow for a three-dimensional study at reduced mass ratio, this is beyond the scope of this paper.

Figure 4. Simulation results from jRad illustrating the normalized flux of circularly polarized photons (averaged over frequency and spatial domain) from 1000 electrons trapped in a typical current filament arising from interpenetrating flows of electron–positron and electron–ion plasmas for varying magnetizations. Note that here negative ![]() $\sigma$ represents negative
$\sigma$ represents negative ![]() $B_z$.
$B_z$.
4. Conclusions
In conclusion, we have shown that the motion of the charged particles in the fields due to WI/CFI produces strong radiation emission in the direction of the plasma flow. An initial magnetization breaks the symmetry in pitch angle distribution of the electrons resulting in a partially circularly polarized radiation. Results indicate that the anisotropies in pitch angle distribution saturate at high initial magnetizations leading to a saturation in the degree of circular polarization. The emission of circularly polarized radiation is limited to electron–ion plasmas (plasmas with ![]() $m_i/m_e > 1$). For pair plasmas, the electrons and positrons produce circular polarization of opposite handedness resulting in a net zero circular polarization. The simulation set-up mimics the flow believed to be present in astrophysical scenarios. Hence, this study is significant for understanding the origin of circular polarization in the recent observation of GRB afterglow (Wiersema et al. Reference Wiersema, Covino, Toma, Van Der Horst, Varela, Min, Greiner, Starling, Tanvir and Wijers2014). As the anisotropy in pitch angles is local to the current filaments, the treatment is valid even for broader or spherical jets. With the observation of WI/CFI in the laboratory and future proposals to study the interaction of electrically neutral electron–positron beams (fireball beams) with plasma (Fox et al. Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson2013; Huntington et al. Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz and Levy2015; Sarri et al. Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015), it may be possible to design scaled experiments to test the results presented in this contribution and to develop a better understanding of radiation and its polarization in real astrophysical scenarios.
$m_i/m_e > 1$). For pair plasmas, the electrons and positrons produce circular polarization of opposite handedness resulting in a net zero circular polarization. The simulation set-up mimics the flow believed to be present in astrophysical scenarios. Hence, this study is significant for understanding the origin of circular polarization in the recent observation of GRB afterglow (Wiersema et al. Reference Wiersema, Covino, Toma, Van Der Horst, Varela, Min, Greiner, Starling, Tanvir and Wijers2014). As the anisotropy in pitch angles is local to the current filaments, the treatment is valid even for broader or spherical jets. With the observation of WI/CFI in the laboratory and future proposals to study the interaction of electrically neutral electron–positron beams (fireball beams) with plasma (Fox et al. Reference Fox, Fiksel, Bhattacharjee, Chang, Germaschewski, Hu and Nilson2013; Huntington et al. Reference Huntington, Fiuza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz and Levy2015; Sarri et al. Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015), it may be possible to design scaled experiments to test the results presented in this contribution and to develop a better understanding of radiation and its polarization in real astrophysical scenarios.
This work is limited to an idealized two-dimensional system with periodic boundaries. In a more realistic situation, there would be some variation along the out-of-plane direction and boundary effects, especially in the case of jets. While the large-scale field in jets is predicted to be twisted (Nishikawa et al. Reference Nishikawa, Mizuno, Gómez, Duţan, Meli, Niemiec, Kobzar, Pohl, Sol and MacDonald2019), this field can be considered uniform at the kinetic scale that we are examining. On the other hand, three-dimensional simulations of the WI/CFI have shown the development of out-of-plane variations, usually of the order of a few ion inertial lengths (Ruyer et al. Reference Ruyer, Gremillet, Debayle and Bonnaud2015; Fiuza et al. Reference Fiuza, Swadling, Grassi, Rinderknecht, Higginson, Ryutov, Bruulsema, Drake, Funk and Glenzer2020). It is predicted that the WI/CFI will reach a quasi-steady state before a kinking instability aids in the formation of these variations, and eventually leading to full saturation and isotropization (Ruyer & Fiuza Reference Ruyer and Fiuza2018). The electron WI/CFI growth rate is proportional to ![]() $\omega _{pe}/\sqrt {\gamma }$ (time scale of
$\omega _{pe}/\sqrt {\gamma }$ (time scale of ![]() $5 \omega _{pe}^{-1}$ in our simulations) and then the ion WI/CFI scales with the ion plasma frequency
$5 \omega _{pe}^{-1}$ in our simulations) and then the ion WI/CFI scales with the ion plasma frequency ![]() $\omega _{pi} = \sqrt {m_e Z/m_i} \omega _{pe}$ (time scale of
$\omega _{pi} = \sqrt {m_e Z/m_i} \omega _{pe}$ (time scale of ![]() $215\omega _{pe}^{-1}$). The relativistic growth rate of the kinking filaments is proportional to an additional factor of
$215\omega _{pe}^{-1}$). The relativistic growth rate of the kinking filaments is proportional to an additional factor of ![]() $\sqrt {m_e Z/m_i} \sqrt {c/\omega _{pe}R_0}/\gamma$ (Ruyer & Fiuza Reference Ruyer and Fiuza2018), where
$\sqrt {m_e Z/m_i} \sqrt {c/\omega _{pe}R_0}/\gamma$ (Ruyer & Fiuza Reference Ruyer and Fiuza2018), where ![]() $R_0$ is the radius of a filament (time scale of
$R_0$ is the radius of a filament (time scale of ![]() ${\sim }3000 \omega _{pe}^{-1}$ in our simulations). The kinking time scale is long compared to the time for an electron to make a full rotation around one of these filaments
${\sim }3000 \omega _{pe}^{-1}$ in our simulations). The kinking time scale is long compared to the time for an electron to make a full rotation around one of these filaments ![]() ${\sim }90 \omega _{pe}^{-1}$, and comparable to the
${\sim }90 \omega _{pe}^{-1}$, and comparable to the ![]() $2700 \omega _{pe}^{-1}$ that we used in our main result. Note that the out-of-plane magnetic field increases the time scale of the kinking instability, even suppressing it when the out-of-plane field is comparable to the in-plane field (Zenitani & Hoshino Reference Zenitani and Hoshino2008), which leads to longer filaments. Therefore, there is significant time for filaments to saturate and for electrons to radiate with circular polarization. Furthermore, radiation signatures from the region at the boundaries of jets remain a topic for future study. Sharp velocity gradients drive kinetic instabilities such as the Kelvin–Helmholtz instability (Alves et al. Reference Alves, Grismayer, Martins, Fiúza, Fonseca and Silva2012) and the mushroom instability (Alves et al. Reference Alves, Grismayer, Fonseca and Silva2015) (also suppressed by an out-of-plane magnetic field), which may lead to different radiation signatures from our predictions that are relevant in the centre region.
$2700 \omega _{pe}^{-1}$ that we used in our main result. Note that the out-of-plane magnetic field increases the time scale of the kinking instability, even suppressing it when the out-of-plane field is comparable to the in-plane field (Zenitani & Hoshino Reference Zenitani and Hoshino2008), which leads to longer filaments. Therefore, there is significant time for filaments to saturate and for electrons to radiate with circular polarization. Furthermore, radiation signatures from the region at the boundaries of jets remain a topic for future study. Sharp velocity gradients drive kinetic instabilities such as the Kelvin–Helmholtz instability (Alves et al. Reference Alves, Grismayer, Martins, Fiúza, Fonseca and Silva2012) and the mushroom instability (Alves et al. Reference Alves, Grismayer, Fonseca and Silva2015) (also suppressed by an out-of-plane magnetic field), which may lead to different radiation signatures from our predictions that are relevant in the centre region.
Here, we have discussed a new mechanism for the generation of circularly polarized light in contrast with previously discussed mechanisms based on synchrotron radiation (Sazonov Reference Sazonov1969; Melrose Reference Melrose1971; Wiersema et al. Reference Wiersema, Covino, Toma, Van Der Horst, Varela, Min, Greiner, Starling, Tanvir and Wijers2014). We note that the level of polarization in these models scales as ![]() $1/\gamma$, where
$1/\gamma$, where ![]() $\gamma$ is the Lorentz factor of the emitting electrons. Our model appears to follow a similar scaling based on additional simulations not presented in this work.
$\gamma$ is the Lorentz factor of the emitting electrons. Our model appears to follow a similar scaling based on additional simulations not presented in this work.
Acknowledgements
The authors would like to thank Professor M. Medvedev for very insightful discussions. This work was supported by the European Research Council (ERC-2010-AdG grant 267841 and ERC-2015 grant 695008) and FCT (Portugal) grant no. PTDC-FIS-PLA-2940-2014. J.V. acknowledges the support of FCT (Portugal) grant no. SFRH/IF/01635/2015. We acknowledge PRACE for awarding access to resource SuperMUC (Leibniz Research Center) and Fermi (CINECA). We also acknowledge the supercomputing resource IST Cluster at IST.
Editor Antoine C. Bret thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Degree of circular polarization from multiple filaments
Although we have only considered radiation from a single filament, it is important to consider the net effect on the degree of circular polarization due to radiation from multiple filaments. A simple analytical model can be constructed by assuming the current filaments as independent sources of radiation. In the far field, each filament can be described as a point source of radiation with electric field components given by ![]() $E_x(r,t)=A\exp [\textrm {i}(\boldsymbol {k}\cdot \boldsymbol {r}-\omega t)]$ and
$E_x(r,t)=A\exp [\textrm {i}(\boldsymbol {k}\cdot \boldsymbol {r}-\omega t)]$ and ![]() $E_y(r,t)=A\exp [\textrm {i}(\boldsymbol {k}\cdot \boldsymbol {r}-\omega t+\phi )]$, with
$E_y(r,t)=A\exp [\textrm {i}(\boldsymbol {k}\cdot \boldsymbol {r}-\omega t+\phi )]$, with ![]() $\boldsymbol {k}$ being the wave vector,
$\boldsymbol {k}$ being the wave vector, ![]() $\omega$ the frequency and
$\omega$ the frequency and ![]() $\phi$ the phase difference between the components. The degree of circular polarization associated with a single filament is then
$\phi$ the phase difference between the components. The degree of circular polarization associated with a single filament is then ![]() $P_c=\sin (\phi )$, where the light is circularly (elliptically) polarized for
$P_c=\sin (\phi )$, where the light is circularly (elliptically) polarized for ![]() $\phi ={\rm \pi} /2$ (
$\phi ={\rm \pi} /2$ (![]() $\phi <{\rm \pi} /2$). To incorporate the effect of multiple current filaments, we consider the superposition of
$\phi <{\rm \pi} /2$). To incorporate the effect of multiple current filaments, we consider the superposition of ![]() $N$ plane waves with a random phase factor
$N$ plane waves with a random phase factor ![]() $\psi _k$ between them. The resultant electric field components can be written as
$\psi _k$ between them. The resultant electric field components can be written as ![]() $E_x(r,t)=\sum _{n=1}^{N}A_{n}\exp [\textrm {i}(\boldsymbol {k}_{n}\cdot \boldsymbol {r}-\omega _{n}t+\psi _{n})]$ and
$E_x(r,t)=\sum _{n=1}^{N}A_{n}\exp [\textrm {i}(\boldsymbol {k}_{n}\cdot \boldsymbol {r}-\omega _{n}t+\psi _{n})]$ and ![]() $E_y(r,t)=\sum _{m=1}^{N}A_{m}\exp [\textrm {i}(\boldsymbol {k}_m\cdot \boldsymbol {r}-\omega _{m}t+\psi _{m}+\phi _m)]$. The degree of circular polarization (
$E_y(r,t)=\sum _{m=1}^{N}A_{m}\exp [\textrm {i}(\boldsymbol {k}_m\cdot \boldsymbol {r}-\omega _{m}t+\psi _{m}+\phi _m)]$. The degree of circular polarization (![]() $P_c$) is given by the relevant Stokes parameters, for which
$P_c$) is given by the relevant Stokes parameters, for which ![]() $P_c=V/I$,
$P_c=V/I$, ![]() $V=2\langle \mathrm {Im}\{E_x^*E_y\} \rangle$,
$V=2\langle \mathrm {Im}\{E_x^*E_y\} \rangle$, ![]() $I=E_x^* E_x + E_y^* E_y$, and where the angular brackets
$I=E_x^* E_x + E_y^* E_y$, and where the angular brackets ![]() $\langle \cdot \rangle$ represent the time average. Hence,
$\langle \cdot \rangle$ represent the time average. Hence, ![]() $V = 2 \langle \textrm {Im} \{ \sum _{n,m=1}^{N} A_n A_m \exp [\textrm {i} ({\rm \Delta} \boldsymbol {k}_{n,m}\cdot \boldsymbol {r}-{\rm \Delta} \omega _{n,m} t+{\rm \Delta} \psi _{n,m}+\phi _m)]\}\rangle$,
$V = 2 \langle \textrm {Im} \{ \sum _{n,m=1}^{N} A_n A_m \exp [\textrm {i} ({\rm \Delta} \boldsymbol {k}_{n,m}\cdot \boldsymbol {r}-{\rm \Delta} \omega _{n,m} t+{\rm \Delta} \psi _{n,m}+\phi _m)]\}\rangle$, ![]() $I=\sum _{n,m=1}^N A_n A_m \exp [\textrm {i} ({\rm \Delta} \boldsymbol {k}_{n,m}\cdot \boldsymbol {r}-{\rm \Delta} \omega _{n,m} t+{\rm \Delta} \psi _{n,m}][1+\exp (\textrm {i} {\rm \Delta} \phi _{m,n})]$ and
$I=\sum _{n,m=1}^N A_n A_m \exp [\textrm {i} ({\rm \Delta} \boldsymbol {k}_{n,m}\cdot \boldsymbol {r}-{\rm \Delta} \omega _{n,m} t+{\rm \Delta} \psi _{n,m}][1+\exp (\textrm {i} {\rm \Delta} \phi _{m,n})]$ and ![]() ${\rm \Delta} a_{n,m} = a_m-a_n$, where
${\rm \Delta} a_{n,m} = a_m-a_n$, where ![]() $a$ is a generic quantity. If the phase
$a$ is a generic quantity. If the phase ![]() $\psi _n$ is randomly distributed, we can employ the random phase approximation (Silva et al. Reference Silva, Bingham, Dawson and Mori1999), for which
$\psi _n$ is randomly distributed, we can employ the random phase approximation (Silva et al. Reference Silva, Bingham, Dawson and Mori1999), for which ![]() $\langle \exp [\textrm {i} {\rm \Delta} \psi _{n,m}]\rangle _{s}=\delta _{m,n}$, where
$\langle \exp [\textrm {i} {\rm \Delta} \psi _{n,m}]\rangle _{s}=\delta _{m,n}$, where ![]() $\langle \cdot \rangle _s$ is the average over a statistical ensemble of systems differing from one another only in the phase
$\langle \cdot \rangle _s$ is the average over a statistical ensemble of systems differing from one another only in the phase ![]() $\psi$. It is thus straightforward to show that
$\psi$. It is thus straightforward to show that ![]() $V=2\langle \sum _{n=1}^N A_n^* A_n \sum _{m=1}^N \sin (\phi _m)\rangle =\sum _{n=1}^N A_n^* A_n \sum _{m=1}^N \sin (\phi _m)$ and
$V=2\langle \sum _{n=1}^N A_n^* A_n \sum _{m=1}^N \sin (\phi _m)\rangle =\sum _{n=1}^N A_n^* A_n \sum _{m=1}^N \sin (\phi _m)$ and ![]() $I = 2 N \sum _{n=1}^N A_n^* A_n$. Hence, the degree of circular polarization emitted by
$I = 2 N \sum _{n=1}^N A_n^* A_n$. Hence, the degree of circular polarization emitted by ![]() $N$ filaments corresponds to
$N$ filaments corresponds to
 \begin{equation} P_c=\frac{1}{N}\sum_{m=1}^{N}\sin(\phi_m).\end{equation}
\begin{equation} P_c=\frac{1}{N}\sum_{m=1}^{N}\sin(\phi_m).\end{equation}
Equation (A 1) is consistent with our simulation results, where we tracked 1000 electrons distributed equally in four different filaments of the magnetized electron–proton plasma described in figure 5. The inset of figure 3(f) shows ![]() $\langle P_c\rangle$ for the four filaments separately, the average of which is 0.113. The value of
$\langle P_c\rangle$ for the four filaments separately, the average of which is 0.113. The value of ![]() $\langle P_c\rangle$ is 0.115 when calculated from all the four filaments together. We emphasize that (A 1) is valid for an arbitrary large number of filaments, such that our results hold in such scenarios.
$\langle P_c\rangle$ is 0.115 when calculated from all the four filaments together. We emphasize that (A 1) is valid for an arbitrary large number of filaments, such that our results hold in such scenarios.

Figure 5. The transverse magnetic field vectors (represented by arrows) arising due to WI/CFI in a magnetized interpenetrating electron–proton (![]() $m_i/m_e=1836$) plasma flow with initial magnetization
$m_i/m_e=1836$) plasma flow with initial magnetization ![]() $\sigma =0.05$ at time
$\sigma =0.05$ at time ![]() $t=9000\omega _{pe}^{-1}$. The trajectories of 25 electrons each trapped in four different current filaments are shown from time
$t=9000\omega _{pe}^{-1}$. The trajectories of 25 electrons each trapped in four different current filaments are shown from time ![]() $t_i=8910\omega _{pe}^{-1}$ to
$t_i=8910\omega _{pe}^{-1}$ to ![]() $t_f=9000\omega _{pe}^{-1}$, with colour scales representing their longitudinal momentum (
$t_f=9000\omega _{pe}^{-1}$, with colour scales representing their longitudinal momentum (![]() $\boldsymbol {p}_z$).
$\boldsymbol {p}_z$).