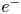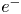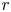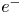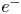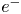1. Introduction
In modern plasma physics research, the two-fluid plasma model (Shumlak et al. Reference Shumlak, Lilly, Reddell, Sousa and Srinivasan2011) is popular for analysing phenomena for which conventional hydorodynamic models, for example single-fluid equations and magnetohydrodynamics (generally abbreviated as MHD), are unsuitable. The two-fluid plasma equations permit a high degree of freedom in determining not only the spatiotemporal evolutions (Zhu, Francisquez & Rogers Reference Zhu, Francisquez and Rogers2017; Morel et al. Reference Morel, Giust, Ardaneh and Courvoisier2021) but also the equilibrium profiles (Ishida, Steinhauer & Peng Reference Ishida, Steinhauer and Peng2010; Kanki & Nagata Reference Kanki and Nagata2019; Ito & Nakajima Reference Ito and Nakajima2021) of the density $n_\sigma$![]() , pressure $p_\sigma$
, pressure $p_\sigma$![]() and mean velocity $\boldsymbol {v}_\sigma$
and mean velocity $\boldsymbol {v}_\sigma$![]() of the ion and electron fluids (hereafter, called plasma); subscript $\sigma$
of the ion and electron fluids (hereafter, called plasma); subscript $\sigma$![]() denotes either $i$
denotes either $i$![]() or $e$
or $e$![]() because the equations comprise two sets of Euler equations as well as Maxwell's equations. However, a fundamental question arises on the assumption (De Jonghe & Keppens Reference De Jonghe and Keppens2020; Mironov Reference Mironov2021; Zhang et al. Reference Zhang, Poedts, Lani, Kuźma and Murawski2021) that the ion and electron plasmas are electrically neutral, although it is not required by the two-fluid plasma model.
because the equations comprise two sets of Euler equations as well as Maxwell's equations. However, a fundamental question arises on the assumption (De Jonghe & Keppens Reference De Jonghe and Keppens2020; Mironov Reference Mironov2021; Zhang et al. Reference Zhang, Poedts, Lani, Kuźma and Murawski2021) that the ion and electron plasmas are electrically neutral, although it is not required by the two-fluid plasma model.
Non-neutral plasma physics (Kabantsev et al. Reference Kabantsev, Chim, O'Neil and Driscoll2014; Danielson et al. Reference Danielson, Dubin, Greaves and Surko2015) provides a novel insight into this question. Non-neutral plasmas are defined as exotic plasmas because they originally include only one charged particle species, for example either pure electrons ($e^-$![]() ) or pure ions ($i^+$
) or pure ions ($i^+$![]() ). Such non-neutral plasmas have been extensively investigated (Kabantsev et al. Reference Kabantsev, Driscoll, Hilsabeck, O'Neil and Yu2001; Romé et al. Reference Romé, Maero, Panzeri and Pozzoli2019; Espinoza-Lozano, Calderón & Velazquez Reference Espinoza-Lozano, Calderón and Velazquez2020) following the experimental verification of their robust rotation equilibrium (Davidson et al. Reference Davidson, Chan, Chen and Lund1991) with the confinement of the pure $e^-$
). Such non-neutral plasmas have been extensively investigated (Kabantsev et al. Reference Kabantsev, Driscoll, Hilsabeck, O'Neil and Yu2001; Romé et al. Reference Romé, Maero, Panzeri and Pozzoli2019; Espinoza-Lozano, Calderón & Velazquez Reference Espinoza-Lozano, Calderón and Velazquez2020) following the experimental verification of their robust rotation equilibrium (Davidson et al. Reference Davidson, Chan, Chen and Lund1991) with the confinement of the pure $e^-$![]() plasma in a linear trap (Malmberg & Driscoll Reference Malmberg and Driscoll1980). Pure $i^+$
plasma in a linear trap (Malmberg & Driscoll Reference Malmberg and Driscoll1980). Pure $i^+$![]() plasmas (Dimonte Reference Dimonte1981; Bollinger, Wineland & Dubin Reference Bollinger, Wineland and Dubin1994; Dubin Reference Dubin2020; Viray, Miller & Raithel Reference Viray, Miller and Raithel2020) have also been studied. Several techniques developed in such experiments have been applied to produce antimatter, and CPT (charge, parity, and time reversal symmetry) sensitivity tests have been performed recently (Higaki et al. Reference Higaki, Kaga, Fukushima, Okamoto, Nagata, Kanai and Yamazaki2017; Fajans & Surko Reference Fajans and Surko2020). Moreover, toroidal $e^-$
plasmas (Dimonte Reference Dimonte1981; Bollinger, Wineland & Dubin Reference Bollinger, Wineland and Dubin1994; Dubin Reference Dubin2020; Viray, Miller & Raithel Reference Viray, Miller and Raithel2020) have also been studied. Several techniques developed in such experiments have been applied to produce antimatter, and CPT (charge, parity, and time reversal symmetry) sensitivity tests have been performed recently (Higaki et al. Reference Higaki, Kaga, Fukushima, Okamoto, Nagata, Kanai and Yamazaki2017; Fajans & Surko Reference Fajans and Surko2020). Moreover, toroidal $e^-$![]() plasmas confined to magnetic surfaces without an externally applied electric field have been investigated (Berkery et al. Reference Berkery, Pedersen, Kremer, Marksteiner, Lefrancois, Hahn and Brenner2007; Himura et al. Reference Himura, Nakamura, Masamune, Isobe and Shimizu2010; Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2012; Khamaru, Ganesh & Sengupta Reference Khamaru, Ganesh and Sengupta2021), and magnetized electron–positron plasmas are being developed (Gilbert et al. Reference Gilbert, Dubin, Greaves and Surko2001; Stoneking et al. Reference Stoneking, Pedersen, Helander, Chen, Hergenhahn, Stenson, Fiksel, von der Linden, Saitoh and Surko2020). In most recent studies, both $i^+$
plasmas confined to magnetic surfaces without an externally applied electric field have been investigated (Berkery et al. Reference Berkery, Pedersen, Kremer, Marksteiner, Lefrancois, Hahn and Brenner2007; Himura et al. Reference Himura, Nakamura, Masamune, Isobe and Shimizu2010; Yoshida et al. Reference Yoshida, Saitoh, Yano, Mikami, Kasaoka, Sakamoto, Morikawa, Furukawa and Mahajan2012; Khamaru, Ganesh & Sengupta Reference Khamaru, Ganesh and Sengupta2021), and magnetized electron–positron plasmas are being developed (Gilbert et al. Reference Gilbert, Dubin, Greaves and Surko2001; Stoneking et al. Reference Stoneking, Pedersen, Helander, Chen, Hergenhahn, Stenson, Fiksel, von der Linden, Saitoh and Surko2020). In most recent studies, both $i^+$![]() and $e^-$
and $e^-$![]() plasmas have been used simultaneously as seed plasmas to explore the unverified physics of the equilibrium and stability of two-fluid plasmas in which $n_i$
plasmas have been used simultaneously as seed plasmas to explore the unverified physics of the equilibrium and stability of two-fluid plasmas in which $n_i$![]() is never equal to $n_e$
is never equal to $n_e$![]() (Himura Reference Himura2016; Akaike & Himura Reference Akaike and Himura2018, Reference Akaike and Himura2019; Yamada et al. Reference Yamada, Himura, Kato, Okada, Sanpei and Masamune2018; Kato et al. Reference Kato, Himura, Sowa and Sanpei2019).
(Himura Reference Himura2016; Akaike & Himura Reference Akaike and Himura2018, Reference Akaike and Himura2019; Yamada et al. Reference Yamada, Himura, Kato, Okada, Sanpei and Masamune2018; Kato et al. Reference Kato, Himura, Sowa and Sanpei2019).
A two-fluid plasma with $n_i \neq n_e$![]() inherently results in a self-electric potential $\phi _s$
inherently results in a self-electric potential $\phi _s$![]() . Therefore, if the plasma is magnetically confined, it is not static but dynamic. The two-fluid plasma needs to keep rotating if it is in equilibrium. Davidson (Davidson Reference Davidson2001) derived a two-dimensional (2-D) differential rotation equilibrium under the assumption that the $i^+$
. Therefore, if the plasma is magnetically confined, it is not static but dynamic. The two-fluid plasma needs to keep rotating if it is in equilibrium. Davidson (Davidson Reference Davidson2001) derived a two-dimensional (2-D) differential rotation equilibrium under the assumption that the $i^+$![]() and $e^-$
and $e^-$![]() plasmas constituting the two-component plasma had zero temperature ($T_i = T_e = 0$
plasmas constituting the two-component plasma had zero temperature ($T_i = T_e = 0$![]() eV), and were cylindrically confined by a linear trap in a uniform axial magnetic field $B_z$
eV), and were cylindrically confined by a linear trap in a uniform axial magnetic field $B_z$![]() , where $B_z$
, where $B_z$![]() was assumed to be considerably larger than the self-magnetic field of the $i^+$
was assumed to be considerably larger than the self-magnetic field of the $i^+$![]() and $e^-$
and $e^-$![]() plasmas (Davidson Reference Davidson2001). In this case, the $i^+$
plasmas (Davidson Reference Davidson2001). In this case, the $i^+$![]() and $e^-$
and $e^-$![]() plasmas are independently rigid-rotated in the same direction but with different angular velocities $\omega _{ri}$
plasmas are independently rigid-rotated in the same direction but with different angular velocities $\omega _{ri}$![]() and $\omega _{re}$
and $\omega _{re}$![]() , respectively, which is unlike the differential rotation observed in the Sun (Balbus et al. Reference Balbus, Bonart, Latter and Weiss2009). In modern terms, the differential rotation equilibrium of the $i^+$
, respectively, which is unlike the differential rotation observed in the Sun (Balbus et al. Reference Balbus, Bonart, Latter and Weiss2009). In modern terms, the differential rotation equilibrium of the $i^+$![]() and $e^-$
and $e^-$![]() plasmas can be described as a two-fluid plasma (Davidson & Uhm Reference Davidson and Uhm1978) because $\boldsymbol {v}_i$
plasmas can be described as a two-fluid plasma (Davidson & Uhm Reference Davidson and Uhm1978) because $\boldsymbol {v}_i$![]() and $\boldsymbol {v}_e$
and $\boldsymbol {v}_e$![]() are different. The solutions for $\omega _{ri}$
are different. The solutions for $\omega _{ri}$![]() and $\omega _{re}$
and $\omega _{re}$![]() for the cold plasma case are expressed as $\omega _{ri}^\pm =-(\omega _{ci}/2)\{1\pm (1-2\omega _{pi}^2(1-1/f)/\omega _{ci}^2)^{{1}/{2}}\}$
for the cold plasma case are expressed as $\omega _{ri}^\pm =-(\omega _{ci}/2)\{1\pm (1-2\omega _{pi}^2(1-1/f)/\omega _{ci}^2)^{{1}/{2}}\}$![]() and $\omega _{re}^\pm =(\omega _{ce}/2)\{1\pm (1-2\omega _{pe}^2(1-f)/\omega _{ce}^2)^{{1}/{2}}\}$
and $\omega _{re}^\pm =(\omega _{ce}/2)\{1\pm (1-2\omega _{pe}^2(1-f)/\omega _{ce}^2)^{{1}/{2}}\}$![]() , where $\omega _{p\sigma }$
, where $\omega _{p\sigma }$![]() and $\omega _{c\sigma }$
and $\omega _{c\sigma }$![]() are the plasma and cyclotron frequencies of the $i^+$
are the plasma and cyclotron frequencies of the $i^+$![]() and $e^-$
and $e^-$![]() plasmas, respectively. Here, $f$
plasmas, respectively. Here, $f$![]() is used as an indicator of the degree of non-neutrality of the two-component plasma: $f \equiv n_{i0}/n_{e0}$
is used as an indicator of the degree of non-neutrality of the two-component plasma: $f \equiv n_{i0}/n_{e0}$![]() , where $n_{i0}$
, where $n_{i0}$![]() and $n_{e0}$
and $n_{e0}$![]() are the densities of the $i^+$
are the densities of the $i^+$![]() and $e^-$
and $e^-$![]() plasmas, respectively. However, to the best of our knowledge, the 2-D differential rotation equilibrium of a two-fluid plasma with finite temperature has not yet been derived. In the case of finite temperature, diamagnetic drift because of the pressure gradient (Bellan Reference Bellan2008), whose direction depends on the polarity of the charge of the plasma species, unlike the $\boldsymbol {E \times B}$
plasmas, respectively. However, to the best of our knowledge, the 2-D differential rotation equilibrium of a two-fluid plasma with finite temperature has not yet been derived. In the case of finite temperature, diamagnetic drift because of the pressure gradient (Bellan Reference Bellan2008), whose direction depends on the polarity of the charge of the plasma species, unlike the $\boldsymbol {E \times B}$![]() drift, occurs in two-fluid plasmas. In this study, we theoretically show that the 2-D differential rotation equilibrium continues to exist even in a two-fluid plasma with finite temperature, for the first time. Similar to the case of a single-component plasma with finite temperature (Davidson & Krall Reference Davidson and Krall1969), $n_i(r)$
drift, occurs in two-fluid plasmas. In this study, we theoretically show that the 2-D differential rotation equilibrium continues to exist even in a two-fluid plasma with finite temperature, for the first time. Similar to the case of a single-component plasma with finite temperature (Davidson & Krall Reference Davidson and Krall1969), $n_i(r)$![]() and $n_e(r)$
and $n_e(r)$![]() develop corresponding bell-shaped profiles at rotational equilibrium. In addition, the plasma radii $r_\sigma$
develop corresponding bell-shaped profiles at rotational equilibrium. In addition, the plasma radii $r_\sigma$![]() of the $i^+$
of the $i^+$![]() and $e^-$
and $e^-$![]() plasmas do not coincide but are different. Consequently, the radial component ($E_r$
plasmas do not coincide but are different. Consequently, the radial component ($E_r$![]() ) of $-\boldsymbol {\nabla } \phi _s$
) of $-\boldsymbol {\nabla } \phi _s$![]() increases nonlinearly. Nevertheless, both $i^+$
increases nonlinearly. Nevertheless, both $i^+$![]() and $e^-$
and $e^-$![]() plasmas continue to exhibit corresponding rigid rotations. More notably, unlike the cold plasma case, the $i^+$
plasmas continue to exhibit corresponding rigid rotations. More notably, unlike the cold plasma case, the $i^+$![]() plasma counter-rotates around the plasma axis in the opposite direction of the $e^-$
plasma counter-rotates around the plasma axis in the opposite direction of the $e^-$![]() plasma, which rotates in the direction of $-\boldsymbol {\nabla } \phi _s \times \boldsymbol {B}$
plasma, which rotates in the direction of $-\boldsymbol {\nabla } \phi _s \times \boldsymbol {B}$![]() for the case where $f < 1$
for the case where $f < 1$![]() , i.e. $n_{i0} < n_{e0}$
, i.e. $n_{i0} < n_{e0}$![]() . This counter-differential rotation equilibrium is attributed to the contribution of the diamagnetic drift of the $i^+$
. This counter-differential rotation equilibrium is attributed to the contribution of the diamagnetic drift of the $i^+$![]() plasma (Bellan Reference Bellan2008).
plasma (Bellan Reference Bellan2008).
2. Derivation of the counter-differential rotation equilibria
Figure 1 depicts a solution of the counter-differential rotation equilibria. An infinitely long lithium-ion (Li$^+$![]() ) plasma column contains an infinitely long $e^-$
) plasma column contains an infinitely long $e^-$![]() plasma confined radially through $\boldsymbol {B}_z=B_0\hat {z}$
plasma confined radially through $\boldsymbol {B}_z=B_0\hat {z}$![]() , where $\hat {z}$
, where $\hat {z}$![]() is the unit vector. The origin of the cylindrical coordinate system ($r$
is the unit vector. The origin of the cylindrical coordinate system ($r$![]() , $\theta$
, $\theta$![]() , $z$
, $z$![]() ) is located at the midplane of the coaxial plasmas, and the $z$
) is located at the midplane of the coaxial plasmas, and the $z$![]() -axis is selected to be parallel to $\boldsymbol {B}_z$
-axis is selected to be parallel to $\boldsymbol {B}_z$![]() . Both Li$^+$
. Both Li$^+$![]() and $e^-$
and $e^-$![]() plasmas have corresponding thermal equilibria and finite pressure $p_\sigma (r)$
plasmas have corresponding thermal equilibria and finite pressure $p_\sigma (r)$![]() . The fluid velocity $\boldsymbol {v}_\sigma$
. The fluid velocity $\boldsymbol {v}_\sigma$![]() is assumed to be non-relativistic. Moreover, the plasma current $e(n_i\boldsymbol {v}_i-n_e\boldsymbol {v}_e)$
is assumed to be non-relativistic. Moreover, the plasma current $e(n_i\boldsymbol {v}_i-n_e\boldsymbol {v}_e)$![]() is insufficient to change $B_z$
is insufficient to change $B_z$![]() because of the low $n_i$
because of the low $n_i$![]() and $n_e$
and $n_e$![]() . One of the possible states likely to exist is the rigid-rotation equilibrium of the two-fluid plasma in which both pure Li$^+$
. One of the possible states likely to exist is the rigid-rotation equilibrium of the two-fluid plasma in which both pure Li$^+$![]() and $e^-$
and $e^-$![]() plasmas can be independently relaxed into their corresponding thermal equilibria. Thus, the $\omega _{r\sigma }$
plasmas can be independently relaxed into their corresponding thermal equilibria. Thus, the $\omega _{r\sigma }$![]() values are constant. In this case, the counter differential rotation equilibrium can be derived as follows.
values are constant. In this case, the counter differential rotation equilibrium can be derived as follows.

Figure 1. Illustration of the differential rigid-rotation equilibrium of a two-component (two-fluid) plasma model with finite $T_\sigma$![]() . To find solutions in the realistic case of laboratory plasmas, we refer to the beam experiment upgrade (BX-U) linear trap experiment (Himura Reference Himura2016; Akaike & Himura Reference Akaike and Himura2018, Reference Akaike and Himura2019; Yamada et al. Reference Yamada, Himura, Kato, Okada, Sanpei and Masamune2018; Kato et al. Reference Kato, Himura, Sowa and Sanpei2019), where Li$^+$
. To find solutions in the realistic case of laboratory plasmas, we refer to the beam experiment upgrade (BX-U) linear trap experiment (Himura Reference Himura2016; Akaike & Himura Reference Akaike and Himura2018, Reference Akaike and Himura2019; Yamada et al. Reference Yamada, Himura, Kato, Okada, Sanpei and Masamune2018; Kato et al. Reference Kato, Himura, Sowa and Sanpei2019), where Li$^+$![]() and $e^-$
and $e^-$![]() plasmas constitute the two-component plasma.
plasmas constitute the two-component plasma.
Because each plasma rotates as a rigid body around the $z$![]() -axis, the $\theta$
-axis, the $\theta$![]() component of $\boldsymbol {v}_\sigma$
component of $\boldsymbol {v}_\sigma$![]() ($v_{\theta \sigma }$
($v_{\theta \sigma }$![]() ) is proportional to $r$
) is proportional to $r$![]() and therefore, $v_{\sigma \theta }=\omega _{r\sigma } r$
and therefore, $v_{\sigma \theta }=\omega _{r\sigma } r$![]() . The term $\boldsymbol {\nabla } p_\sigma$
. The term $\boldsymbol {\nabla } p_\sigma$![]() is equivalent to $k_BT_\sigma \boldsymbol {\nabla } n_\sigma$
is equivalent to $k_BT_\sigma \boldsymbol {\nabla } n_\sigma$![]() because $T_\sigma$
because $T_\sigma$![]() is spatially uniform at thermal equilibrium. Hence, the equation of steady-state motion for both plasmas can be expressed as $m_\sigma n_\sigma (\boldsymbol {v}_\sigma \boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {v}_\sigma = n_\sigma q_\sigma (\boldsymbol {v}_\sigma \times \boldsymbol {B}_z-\boldsymbol {\nabla } \phi _s)- k_B T_\sigma \boldsymbol {\nabla } n_\sigma$
is spatially uniform at thermal equilibrium. Hence, the equation of steady-state motion for both plasmas can be expressed as $m_\sigma n_\sigma (\boldsymbol {v}_\sigma \boldsymbol {\cdot } \boldsymbol {\nabla })\boldsymbol {v}_\sigma = n_\sigma q_\sigma (\boldsymbol {v}_\sigma \times \boldsymbol {B}_z-\boldsymbol {\nabla } \phi _s)- k_B T_\sigma \boldsymbol {\nabla } n_\sigma$![]() , where $m_\sigma$
, where $m_\sigma$![]() and $q_\sigma$
and $q_\sigma$![]() represent the mass number and elementary charge of each species, respectively. Solving this equation for $n_\sigma (r)$
represent the mass number and elementary charge of each species, respectively. Solving this equation for $n_\sigma (r)$![]() ,
,
where
The coefficient $n_{\sigma 0}$![]() on the right-hand side of (2.1) represents the value of $n_\sigma$
on the right-hand side of (2.1) represents the value of $n_\sigma$![]() on the $z$
on the $z$![]() -axis, where $r = 0$
-axis, where $r = 0$![]() . In addition, $\psi _\sigma$
. In addition, $\psi _\sigma$![]() are the corresponding effective potential energies (Davidson Reference Davidson2001) of the singly ionized ions and $e^-$
are the corresponding effective potential energies (Davidson Reference Davidson2001) of the singly ionized ions and $e^-$![]() plasmas. Substituting them in Poisson's equation, the rotation equilibrium equation with finite $T_\sigma$
plasmas. Substituting them in Poisson's equation, the rotation equilibrium equation with finite $T_\sigma$![]() can be expressed as
can be expressed as

To numerically determine the solutions of (2.3), we apply the measured values in the beam experiment upgrade (BX-U) linear trap experiments (Himura Reference Himura2016; Akaike & Himura Reference Akaike and Himura2018, Reference Akaike and Himura2019; Yamada et al. Reference Yamada, Himura, Kato, Okada, Sanpei and Masamune2018; Kato et al. Reference Kato, Himura, Sowa and Sanpei2019), as examples for the calculation. The boundary condition of $\phi _s$![]() is the same as that of the BX-U as well, as listed in table 1. Although the value of $B_0$
is the same as that of the BX-U as well, as listed in table 1. Although the value of $B_0$![]() is variable, it is fixed to 0.13 T in the presented calculation. Lithium (Li$^+$
is variable, it is fixed to 0.13 T in the presented calculation. Lithium (Li$^+$![]() ) is employed as the singly ionized ion. The value of $n_{i0}$
) is employed as the singly ionized ion. The value of $n_{i0}$![]() can be varied in the $10^{11}\text{--}10^{12}$
can be varied in the $10^{11}\text{--}10^{12}$![]() m$^{-3}$
m$^{-3}$![]() range, whereas $n_{e0}$
range, whereas $n_{e0}$![]() is in the $10^{12}\text{--}10^{13}$
is in the $10^{12}\text{--}10^{13}$![]() m$^{-3}$
m$^{-3}$![]() range. For $T_\sigma$
range. For $T_\sigma$![]() , we assume $T_i = T_e = 2$
, we assume $T_i = T_e = 2$![]() eV because the confinement time is considerably greater than the binary collision time. This observation implies two-fluid rotational equilibrium. To determine solutions within the $n_i$
eV because the confinement time is considerably greater than the binary collision time. This observation implies two-fluid rotational equilibrium. To determine solutions within the $n_i$![]() and $n_e$
and $n_e$![]() ranges in table 1, the coefficients of $n_{i0}$
ranges in table 1, the coefficients of $n_{i0}$![]() and $n_{e0}$
and $n_{e0}$![]() are set to $1\times 10^{11}$
are set to $1\times 10^{11}$![]() and $5\times 10^{12}$
and $5\times 10^{12}$![]() m$^{-3}$
m$^{-3}$![]() , respectively. Thus, $n_{i0}/n_{e0} = 0.02$
, respectively. Thus, $n_{i0}/n_{e0} = 0.02$![]() . Under these conditions, the Gauss–Seidel method was employed to solve (2.3). Values of $\omega _{ri}$
. Under these conditions, the Gauss–Seidel method was employed to solve (2.3). Values of $\omega _{ri}$![]() and $\omega _{re}$
and $\omega _{re}$![]() are also computational parameters. First, we obtain $\phi _s (r)$
are also computational parameters. First, we obtain $\phi _s (r)$![]() from (2.2) and (2.3) by substituting independent values into $\omega _{ri}$
from (2.2) and (2.3) by substituting independent values into $\omega _{ri}$![]() and $\omega _{re}$
and $\omega _{re}$![]() one by one. Then, the obtained $\phi _s (r)$
one by one. Then, the obtained $\phi _s (r)$![]() is utilized to calculate the corresponding $n_\sigma (r)$
is utilized to calculate the corresponding $n_\sigma (r)$![]() from (2.1). Using these numerical schemes, we systematically find self-consistent sets of solutions of $\psi _s$
from (2.1). Using these numerical schemes, we systematically find self-consistent sets of solutions of $\psi _s$![]() , $n_i$
, $n_i$![]() and $n_e$
and $n_e$![]() that satisfy (2.1)–(2.3) simultaneously even with finite $T_i$
that satisfy (2.1)–(2.3) simultaneously even with finite $T_i$![]() and $T_e$
and $T_e$![]() , as shown below.
, as shown below.
Table 1. Nominal parameters of the BX-U machine and assumed boundary condition for $\phi _s$![]() in this calculation.
in this calculation.

$^{\textrm {a}}$![]() All the collision times are calculated using the values of $n_i$
All the collision times are calculated using the values of $n_i$![]() and $n_e$
and $n_e$![]() listed above.
listed above.
3. Possible $\omega _{re}$ and $\omega _{ri}$
and $\omega _{ri}$ with which counter-differential rigid-rotation equilibria exist
with which counter-differential rigid-rotation equilibria exist
Figure 2 shows the dependency of $\omega _{r\sigma }$![]() on $n_{i0}/n_{e0}$
on $n_{i0}/n_{e0}$![]() , where $\omega _{r\sigma }$
, where $\omega _{r\sigma }$![]() is normalized by the cyclotron frequency $\omega _{c\sigma }$
is normalized by the cyclotron frequency $\omega _{c\sigma }$![]() . For the three cases where $n_{i0}/n_{e0} = 0.02$
. For the three cases where $n_{i0}/n_{e0} = 0.02$![]() , 0.5 and 0.9, the possible ranges of $\omega _{re}$
, 0.5 and 0.9, the possible ranges of $\omega _{re}$![]() and $\omega _{ri}$
and $\omega _{ri}$![]() in which rigid-rotation equilibria of the two-fluid plasma exist are denoted by the six solid-line sections, where the red and blue colours represent $\omega _{re}$
in which rigid-rotation equilibria of the two-fluid plasma exist are denoted by the six solid-line sections, where the red and blue colours represent $\omega _{re}$![]() and $\omega _{ri}$
and $\omega _{ri}$![]() , respectively.Footnote 1 For the reader's understanding, it should be noted that the value of $\omega _{r\sigma }$
, respectively.Footnote 1 For the reader's understanding, it should be noted that the value of $\omega _{r\sigma }$![]() of a single-component plasma such as pure $e^-$
of a single-component plasma such as pure $e^-$![]() plasma must be either $\omega _{r\sigma }^+$
plasma must be either $\omega _{r\sigma }^+$![]() (fast mode) or $\omega _{r\sigma }^-$
(fast mode) or $\omega _{r\sigma }^-$![]() (slow mode) if $T_\sigma$
(slow mode) if $T_\sigma$![]() is zero. For $T_\sigma \neq 0$
is zero. For $T_\sigma \neq 0$![]() , $\omega _{r\sigma }$
, $\omega _{r\sigma }$![]() of a single-component plasma can take any value between $\omega _{r\sigma }^+$
of a single-component plasma can take any value between $\omega _{r\sigma }^+$![]() and $\omega _{r\sigma }^-$
and $\omega _{r\sigma }^-$![]() . However, for two-fluid plasmas with finite $T_\sigma$
. However, for two-fluid plasmas with finite $T_\sigma$![]() , the possible ranges of both $\omega _{re}$
, the possible ranges of both $\omega _{re}$![]() and $\omega _{ri}$
and $\omega _{ri}$![]() are limited. This is noticeable for $\omega _{ri}$
are limited. This is noticeable for $\omega _{ri}$![]() , as depicted in figure 2. The sign of $\omega _{re}$
, as depicted in figure 2. The sign of $\omega _{re}$![]() is always positive. On the other hand, the sign of $\omega _{ri}$
is always positive. On the other hand, the sign of $\omega _{ri}$![]() is always negative, contrary to the case of one-component pure ion plasmas. The different signs of $\omega _{re}$
is always negative, contrary to the case of one-component pure ion plasmas. The different signs of $\omega _{re}$![]() and $\omega _{ri}$
and $\omega _{ri}$![]() physically imply that the Li$^+$
physically imply that the Li$^+$![]() and $e^-$
and $e^-$![]() plasmas rigid-rotate in opposite directions. As previously mentioned, $B_z$
plasmas rigid-rotate in opposite directions. As previously mentioned, $B_z$![]() is along the positive direction of the $z$
is along the positive direction of the $z$![]() -axis, whereas $E_r (=-\nabla _r \phi _s)$
-axis, whereas $E_r (=-\nabla _r \phi _s)$![]() is from the plasma edge toward the plasma axis, inward. This can be deduced from the fact that $n_{e0}>n_{i0}$
is from the plasma edge toward the plasma axis, inward. This can be deduced from the fact that $n_{e0}>n_{i0}$![]() . Overall, it is recognized that the $e^-$
. Overall, it is recognized that the $e^-$![]() plasma rotates in the direction of $E_r \times B_z$
plasma rotates in the direction of $E_r \times B_z$![]() , whereas the Li$^+$
, whereas the Li$^+$![]() plasma counter-rotates in the opposite direction of $E_r \times B_z$
plasma counter-rotates in the opposite direction of $E_r \times B_z$![]() . Because $\omega _{ri} \neq \omega _{re}$
. Because $\omega _{ri} \neq \omega _{re}$![]() , this can be considered as the counter-differential rotation equilibrium of two-fluid plasmas. As example solutions, we present extraordinary cases. When $\omega _{re}/\omega _{ce}$
, this can be considered as the counter-differential rotation equilibrium of two-fluid plasmas. As example solutions, we present extraordinary cases. When $\omega _{re}/\omega _{ce}$![]() takes a minimum value of $1.6\times 10^{-4}$
takes a minimum value of $1.6\times 10^{-4}$![]() , $\omega _{ri}/\omega _{ci}$
, $\omega _{ri}/\omega _{ci}$![]() can take any value in the $-0.97<\omega _{ri}/\omega _{ci}<-0.05$
can take any value in the $-0.97<\omega _{ri}/\omega _{ci}<-0.05$![]() range. Such arbitrariness is provided by the fact that changes in the profiles of $n_\sigma (r)$
range. Such arbitrariness is provided by the fact that changes in the profiles of $n_\sigma (r)$![]() and $\phi _s (r)$
and $\phi _s (r)$![]() occur self-consistently to satisfy (2.1)–(2.3).
occur self-consistently to satisfy (2.1)–(2.3).

Figure 2. Dependency of $\omega _{r\sigma }$![]() on $n_{i0}/n_{e0}$
on $n_{i0}/n_{e0}$![]() . Here $\omega _{r\sigma }$
. Here $\omega _{r\sigma }$![]() is normalized by the corresponding cyclotron frequency $\omega _{c\sigma }$
is normalized by the corresponding cyclotron frequency $\omega _{c\sigma }$![]() . The dashed (red) curve shows the possible solutions ($\omega _{ri}^+$
. The dashed (red) curve shows the possible solutions ($\omega _{ri}^+$![]() and $\omega _{ri}^-$
and $\omega _{ri}^-$![]() ) for a two-component plasma with $T_i = T_e = 0$
) for a two-component plasma with $T_i = T_e = 0$![]() eV, whereas the dashed (blue) lines indicate the possible solutions ($\omega _{re}^+$
eV, whereas the dashed (blue) lines indicate the possible solutions ($\omega _{re}^+$![]() and $\omega _{re}^-$
and $\omega _{re}^-$![]() ) for a two-component plasma with $T_i = T_e = 0$
) for a two-component plasma with $T_i = T_e = 0$![]() . $T_e = 0$
. $T_e = 0$![]() eV. The values of $n_{e0}$
eV. The values of $n_{e0}$![]() are set to $5\times 10^{12}$
are set to $5\times 10^{12}$![]() m$^{-3}$
m$^{-3}$![]() . As can be observed, for a two-component plasma with finite $T_\sigma$
. As can be observed, for a two-component plasma with finite $T_\sigma$![]() , the possible ranges of $\omega _\sigma$
, the possible ranges of $\omega _\sigma$![]() are limited. These are denoted by the corresponding solid-line sections, where the blue colour represents $e^-$
are limited. These are denoted by the corresponding solid-line sections, where the blue colour represents $e^-$![]() plasma and the red represents Li$^+$
plasma and the red represents Li$^+$![]() plasma.
plasma.
4. The finite temperature effect
The counter-rotation of Li$^+$![]() plasma at rigid-rotor equilibrium is attributed to the finite $p_\sigma$
plasma at rigid-rotor equilibrium is attributed to the finite $p_\sigma$![]() . Figure 3 shows the radial profiles of the azimuthal components of $\boldsymbol {E\times B} \, (\equiv v_\phi = (1/B_0)\, \textrm {d}\phi _s/ \textrm {d} r)$
. Figure 3 shows the radial profiles of the azimuthal components of $\boldsymbol {E\times B} \, (\equiv v_\phi = (1/B_0)\, \textrm {d}\phi _s/ \textrm {d} r)$![]() and the diamagnetic ($\equiv v_{d\sigma } = -(k_B T_\sigma /n_\sigma q_\sigma B_0)\, \textrm {d} n_\sigma / \textrm {d} r$
and the diamagnetic ($\equiv v_{d\sigma } = -(k_B T_\sigma /n_\sigma q_\sigma B_0)\, \textrm {d} n_\sigma / \textrm {d} r$![]() ) drift terms along with $v_{\sigma }$
) drift terms along with $v_{\sigma }$![]() . These are calculated from a typical set of equilibrium solutions of $\phi _s(r)$
. These are calculated from a typical set of equilibrium solutions of $\phi _s(r)$![]() and $n_\sigma (r)$
and $n_\sigma (r)$![]() , as depicted in figure 4. Figure 3 shows that the sign of $v_\phi$
, as depicted in figure 4. Figure 3 shows that the sign of $v_\phi$![]() is positive along the entire $r$
is positive along the entire $r$![]() -axis. However, $|v_\phi |$
-axis. However, $|v_\phi |$![]() is one order of magnitude smaller than the absolute value of $v_{di}$
is one order of magnitude smaller than the absolute value of $v_{di}$![]() , which is negative in the entire plasma, causing counter-rotation. Here, we note that $v_\phi$
, which is negative in the entire plasma, causing counter-rotation. Here, we note that $v_\phi$![]() and $v_{di}$
and $v_{di}$![]() change nonlinearly along the $r$
change nonlinearly along the $r$![]() -axis, which can be clearly recognized in the inset of figure 3. However, $v_{i}$
-axis, which can be clearly recognized in the inset of figure 3. However, $v_{i}$![]() , composed of $v_\phi$
, composed of $v_\phi$![]() and $v_{di}$
and $v_{di}$![]() , increases linearly along the $r$
, increases linearly along the $r$![]() -axis, resulting in rigid-body rotation.
-axis, resulting in rigid-body rotation.

Figure 3. Radial profiles of the azimuthal components of $v_\phi$![]() (black dashed curves), $v_{d\sigma }$
(black dashed curves), $v_{d\sigma }$![]() (red dotted curves for Li$^+$
(red dotted curves for Li$^+$![]() plasma and blue for $e^-$
plasma and blue for $e^-$![]() plasma) and $v_\sigma$
plasma) and $v_\sigma$![]() (two solid red and blue lines) for a typical set of equilibrium solutions obtained for the case where $\omega _{ri} = -3.3\times 10^{5}$
(two solid red and blue lines) for a typical set of equilibrium solutions obtained for the case where $\omega _{ri} = -3.3\times 10^{5}$![]() and $\omega _{re} = 3.6\times 10^{6}$
and $\omega _{re} = 3.6\times 10^{6}$![]() rad s$^{-1}$
rad s$^{-1}$![]() . Both Li$^+$
. Both Li$^+$![]() and $e^-$
and $e^-$![]() exhibit counter-differential rigid-rotation equilibrium.
exhibit counter-differential rigid-rotation equilibrium.

Figure 4. Radial profiles of $\phi _s(r)$![]() and $n_\sigma (r)$
and $n_\sigma (r)$![]() for the set of equilibrium solutions shown in figure 3. Here $r_i$
for the set of equilibrium solutions shown in figure 3. Here $r_i$![]() and $r_e$
and $r_e$![]() are never equal but are different when the two-component (two-fluid) plasma is in counter-differential rigid-rotation equilibrium. In addition, the lengths of $r_i$
are never equal but are different when the two-component (two-fluid) plasma is in counter-differential rigid-rotation equilibrium. In addition, the lengths of $r_i$![]() and $r_e$
and $r_e$![]() in the two-fluid equilibrium are smaller than those calculated for the pure Li$^+$
in the two-fluid equilibrium are smaller than those calculated for the pure Li$^+$![]() and $e^-$
and $e^-$![]() plasmas.
plasmas.
The same linearization occurs for $v_{e}$![]() as well, as depicted in figure 3. Counter-differential rigid-rotation equilibrium is caused by the balance between $p_\sigma$
as well, as depicted in figure 3. Counter-differential rigid-rotation equilibrium is caused by the balance between $p_\sigma$![]() and $\phi _s$
and $\phi _s$![]() perpendicular to $B_z$
perpendicular to $B_z$![]() , which is qualitatively similar to the study of non-uniform $p_\sigma$
, which is qualitatively similar to the study of non-uniform $p_\sigma$![]() and $\phi _s$
and $\phi _s$![]() on toroidal magnetic surfaces (Pedersen & Boozer Reference Pedersen and Boozer2002; Himura et al. Reference Himura, Wakabayashi, Yamamoto, Isobe, Okamura, Matsuoka, Sanpei and Masamune2007).
on toroidal magnetic surfaces (Pedersen & Boozer Reference Pedersen and Boozer2002; Himura et al. Reference Himura, Wakabayashi, Yamamoto, Isobe, Okamura, Matsuoka, Sanpei and Masamune2007).
At counter-differential rotation equilibrium, $n_\sigma (r)$![]() assumes the corresponding bell-shaped profile, which is qualitatively the same as that in the cold plasma case. However, because of finite $T_\sigma$
assumes the corresponding bell-shaped profile, which is qualitatively the same as that in the cold plasma case. However, because of finite $T_\sigma$![]() , the pressure-gradient terms ($k_BT_\sigma \boldsymbol {\nabla } n_\sigma$
, the pressure-gradient terms ($k_BT_\sigma \boldsymbol {\nabla } n_\sigma$![]() ) play dominant roles in maintaining the corresponding rotational equilibria, as mentioned above. In figure 4, the value of $n_{i}(0)$
) play dominant roles in maintaining the corresponding rotational equilibria, as mentioned above. In figure 4, the value of $n_{i}(0)$![]() is approximately $1.4\times 10^{11}$
is approximately $1.4\times 10^{11}$![]() m$^{-3}$
m$^{-3}$![]() , which is greater than $n_{i0}$
, which is greater than $n_{i0}$![]() , whereas $n_{e}(0) \approx 3.5\times 10^{12}$
, whereas $n_{e}(0) \approx 3.5\times 10^{12}$![]() m$^{-3}$
m$^{-3}$![]() is smaller than $n_{e0}$
is smaller than $n_{e0}$![]() . The difference between $n_i$
. The difference between $n_i$![]() and $n_e$
and $n_e$![]() indicates that the two-fluid plasma is electrically non-neutral. Because $n_{i}(0) < n_{e}(0)$
indicates that the two-fluid plasma is electrically non-neutral. Because $n_{i}(0) < n_{e}(0)$![]() , $\phi _s$
, $\phi _s$![]() becomes negative at $r =0$
becomes negative at $r =0$![]() . However, in addition to the plasma axis, the negative $\phi _s$
. However, in addition to the plasma axis, the negative $\phi _s$![]() extends over the entire plasma, regardless of $n_i$
extends over the entire plasma, regardless of $n_i$![]() . The minimum value of $\phi _s$
. The minimum value of $\phi _s$![]() is at $r = 0$
is at $r = 0$![]() , which is approximately $-0.7$
, which is approximately $-0.7$![]() V in this case. The curvature of $\phi _s(r)$
V in this case. The curvature of $\phi _s(r)$![]() becomes convex toward the top, as observable in figure 4.
becomes convex toward the top, as observable in figure 4.
For $n_\sigma (r)$![]() , their maxima appear at the plasma centre ($r=0$
, their maxima appear at the plasma centre ($r=0$![]() ) and decrease monotonically, consistent with $\phi _s(r)$
) and decrease monotonically, consistent with $\phi _s(r)$![]() . However, the remarkable result inferred from the profiles of $n_i(r)$
. However, the remarkable result inferred from the profiles of $n_i(r)$![]() and $n_e(r)$
and $n_e(r)$![]() is that $r_i$
is that $r_i$![]() and $r_e$
and $r_e$![]() never become equal and always remain different. Defining $r_\sigma$
never become equal and always remain different. Defining $r_\sigma$![]() as the distance between the plasma centre and the coordinate, where $n_\sigma$
as the distance between the plasma centre and the coordinate, where $n_\sigma$![]() decreases to 1/10 of $n_\sigma (0)$
decreases to 1/10 of $n_\sigma (0)$![]() (i.e. $n_\sigma (r_\sigma ) / n_\sigma (0) = 1/10$
(i.e. $n_\sigma (r_\sigma ) / n_\sigma (0) = 1/10$![]() ), $r_i$
), $r_i$![]() and $r_e$
and $r_e$![]() are approximately 2.5 and 0.5 cm, respectively, in the presented case.
are approximately 2.5 and 0.5 cm, respectively, in the presented case.
The obtained bell-shaped profiles shown in figure 4 may be due to the finite-temperature effect (Davidson & Krall Reference Davidson and Krall1969) to some extent. However, the past study assumed that the Debye length $\lambda$![]() was sufficiently short compared with the plasma radius $r_p$
was sufficiently short compared with the plasma radius $r_p$![]() . This assumption implied that either $n_e$
. This assumption implied that either $n_e$![]() was relatively high or $r_p$
was relatively high or $r_p$![]() was relatively long. Contrary to these, the present result is obtained from a different parameter regime in which $n_\sigma$
was relatively long. Contrary to these, the present result is obtained from a different parameter regime in which $n_\sigma$![]() is relatively lower and $T_\sigma$
is relatively lower and $T_\sigma$![]() is finite. As a result, $\lambda$
is finite. As a result, $\lambda$![]() has the same order as that of $r_p$
has the same order as that of $r_p$![]() .
.
5. On the radii of single-component and two-fluid plasmas
The lengths of $r_\sigma$![]() reduce when the pure ion as well as $e^-$
reduce when the pure ion as well as $e^-$![]() plasmas with finite $T_\sigma$
plasmas with finite $T_\sigma$![]() are in counter-differential rotation equilibrium together. Substituting the values of $n_{\sigma }(0)$
are in counter-differential rotation equilibrium together. Substituting the values of $n_{\sigma }(0)$![]() in figure 4 in Davidson's formulaFootnote 2 derived for a single-component plasma, $r_i$
in figure 4 in Davidson's formulaFootnote 2 derived for a single-component plasma, $r_i$![]() and $r_e$
and $r_e$![]() are expected to be approximately 6 and 1 cm, respectively. Here, $r_\sigma \approx -\{{\sqrt {k_BT_\sigma /m_\sigma }}/{\omega _{p\sigma }}\} \ln {[({{2(\omega _{r\sigma }\omega _{c\sigma }-\omega _{r\sigma }^2)}/{\omega _{p\sigma }^2}})-1]}$
are expected to be approximately 6 and 1 cm, respectively. Here, $r_\sigma \approx -\{{\sqrt {k_BT_\sigma /m_\sigma }}/{\omega _{p\sigma }}\} \ln {[({{2(\omega _{r\sigma }\omega _{c\sigma }-\omega _{r\sigma }^2)}/{\omega _{p\sigma }^2}})-1]}$![]() . This discrepancy is caused by the increase in $\psi _i$
. This discrepancy is caused by the increase in $\psi _i$![]() of the two-fluid plasma. When a single-component ion plasma is in rotational equilibrium, $\phi _s$
of the two-fluid plasma. When a single-component ion plasma is in rotational equilibrium, $\phi _s$![]() is estimated to be of the order of $er_i^2n_{i0}/\epsilon _0$
is estimated to be of the order of $er_i^2n_{i0}/\epsilon _0$![]() . In addition, $n_{i0}$
. In addition, $n_{i0}$![]() must always be smaller than the Brillouin density (Davidson Reference Davidson2001) such that $\omega _{ri}^-\approx -\omega _{pi}^2/2\omega _{ci}$
must always be smaller than the Brillouin density (Davidson Reference Davidson2001) such that $\omega _{ri}^-\approx -\omega _{pi}^2/2\omega _{ci}$![]() , in the case where $\omega _{ri}^-\ll \omega _{ci}$
, in the case where $\omega _{ri}^-\ll \omega _{ci}$![]() . Substituting these in (2.2), we estimate $\psi _i^0$
. Substituting these in (2.2), we estimate $\psi _i^0$![]() of the single-component ion plasma as
of the single-component ion plasma as
Here, we used the following relationship: $m_ir_i^2\omega _{pi}^2=e^2r^2_in_{i0}/\epsilon _0$![]() . However, in the case of a two-component plasma with $0< n_{i0}< n_{e0}$
. However, in the case of a two-component plasma with $0< n_{i0}< n_{e0}$![]() , $\phi _s\approx er_i^2n_e(0)/\epsilon _0$
, $\phi _s\approx er_i^2n_e(0)/\epsilon _0$![]() and $\omega _{ri}^-\approx (n_{e0}/n_{i0})\omega _{pi}^2/2\omega _{ci}$
and $\omega _{ri}^-\approx (n_{e0}/n_{i0})\omega _{pi}^2/2\omega _{ci}$![]() . Thus, for the counter-differential rotation equilibrium example shown in figures 3 and 4, $\omega _{ri} \approx -(n_{e0}/n_{i0})\omega _{pi}^2/2\omega _{ci}$
. Thus, for the counter-differential rotation equilibrium example shown in figures 3 and 4, $\omega _{ri} \approx -(n_{e0}/n_{i0})\omega _{pi}^2/2\omega _{ci}$![]() because $\omega _{ri}=-0.19\times \omega _{ci}=-1.1\times \omega _{ri}^-$
because $\omega _{ri}=-0.19\times \omega _{ci}=-1.1\times \omega _{ri}^-$![]() . Therefore, $\psi _i$
. Therefore, $\psi _i$![]() of the two-component plasma is derived as
of the two-component plasma is derived as
According to (2.1), an increase in $\psi _i$![]() causes a rapid decrease in $n_i$
causes a rapid decrease in $n_i$![]() as $|r|$
as $|r|$![]() increases, resulting in a narrower $n_i(r)$
increases, resulting in a narrower $n_i(r)$![]() as seen in figure 4. In general, for $0< n_{i0}< n_{e0}$
as seen in figure 4. In general, for $0< n_{i0}< n_{e0}$![]() , $r_i$
, $r_i$![]() of a two-component plasma becomes approximately $\sqrt {n_{i0}/n_{e0}}$
of a two-component plasma becomes approximately $\sqrt {n_{i0}/n_{e0}}$![]() times smaller than that of a single-component ion plasma.
times smaller than that of a single-component ion plasma.
The shorter $r_e$![]() is also explained by the increase in $\psi _e$
is also explained by the increase in $\psi _e$![]() . In the equilibrium depicted in figures 3 and 4, $\omega _{re}/\omega _{ce}$
. In the equilibrium depicted in figures 3 and 4, $\omega _{re}/\omega _{ce}$![]() is $\sim 10^{-4}$
is $\sim 10^{-4}$![]() , which is an order of magnitude greater than the slow mode: $\omega _{re}^-/\omega _{ce}\sim 10^{-5}$
, which is an order of magnitude greater than the slow mode: $\omega _{re}^-/\omega _{ce}\sim 10^{-5}$![]() . In addition, $(1-n_{i0}/n_{e0})\approx 1$
. In addition, $(1-n_{i0}/n_{e0})\approx 1$![]() in this case. Thus, $\phi _s$
in this case. Thus, $\phi _s$![]() is almost the same for the pure $e^-$
is almost the same for the pure $e^-$![]() as well as two-component plasma. We compare the two effective potentials of the two cases. The effective potential of the pure $e^-$
as well as two-component plasma. We compare the two effective potentials of the two cases. The effective potential of the pure $e^-$![]() plasma is $\psi _e^0$
plasma is $\psi _e^0$![]() . Substituting these in (2.1) and (2.2), we estimate $\psi _e$
. Substituting these in (2.1) and (2.2), we estimate $\psi _e$![]() and $\psi _e^0$
and $\psi _e^0$![]() as
as
Based on these considerations, it is concluded that the two-component plasma becomes narrower overall.
6. Summary
In summary, the 2-D rigid-rotation equilibria of electrically non-neutral two-component (two-fluid) plasma with finite $T_\sigma$![]() were presented in this study, for the first time. Furthermore, self-consistent solutions of the differential rigid-rotation equilibria were determined. However, the possible range of $\omega _\sigma$
were presented in this study, for the first time. Furthermore, self-consistent solutions of the differential rigid-rotation equilibria were determined. However, the possible range of $\omega _\sigma$![]() becomes narrower than that of the two-component plasma with $T_\sigma = 0$
becomes narrower than that of the two-component plasma with $T_\sigma = 0$![]() . Remarkably, in contrast to the cold plasma case, the ion plasma is only permitted to counter-rotate because of its diamagnetic drift. In the future, we intend to investigate the following. In this study, three cases of $e^-$
. Remarkably, in contrast to the cold plasma case, the ion plasma is only permitted to counter-rotate because of its diamagnetic drift. In the future, we intend to investigate the following. In this study, three cases of $e^-$![]() rich plasmas ($n_{i0}/n_{e0}= 0.02$
rich plasmas ($n_{i0}/n_{e0}= 0.02$![]() , 0.5, and 0.9) were presented to straightaway show the existence of counter differential rigid-rotation equilibria. A complete set of possible ranges of $\omega _\sigma$
, 0.5, and 0.9) were presented to straightaway show the existence of counter differential rigid-rotation equilibria. A complete set of possible ranges of $\omega _\sigma$![]() for different values of $n_{i0}/n_{e0}$
for different values of $n_{i0}/n_{e0}$![]() will be considered. Cases with $T_i\neq T_e$
will be considered. Cases with $T_i\neq T_e$![]() will be investigated as well. Moreover, in the BX-U experiment, there is no constraint that the two-fluid plasma must rotate rigidly. A more general solution would be to use $\omega _i (r)$
will be investigated as well. Moreover, in the BX-U experiment, there is no constraint that the two-fluid plasma must rotate rigidly. A more general solution would be to use $\omega _i (r)$![]() and $\omega _e (r)$
and $\omega _e (r)$![]() . In fact, the axial length of actual plasmas is finite so that three-dimensional computations are suitable for comparison between experiments and simulations.
. In fact, the axial length of actual plasmas is finite so that three-dimensional computations are suitable for comparison between experiments and simulations.
Finally, in the case of a small fraction of positive ions in an otherwise pure electron plasma, the ion resonance instability has been observed to emerge not only theoretically (Levy, Daugherty & Buneman Reference Levy, Daugherty and Buneman1969) but also experimentally (Marksteiner et al. Reference Marksteiner, Pedersen, Berkery, Hahn, Mendez, de Gevigney and Himura2008). Therefore, a stability analysis would be required for the counter differential rigid-rotation equilibrium with a minimal value of $f$![]() . Since $\lambda \approx r_\sigma$
. Since $\lambda \approx r_\sigma$![]() in the presented parameter regime, collective plasma effects are not expected to be significant. Perhaps, such an instability might not grow as much.
in the presented parameter regime, collective plasma effects are not expected to be significant. Perhaps, such an instability might not grow as much.
Acknowledgements
The authors thank Mr T. Okada of the Kyoto Institute of Technology, Professor E.S. Okada of Osaka University and Dr M. Sengupta of Saskatchewan University for the discussions and comments. We would like to thank Editage (www.editage.com) for English language editing.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Funding
This work is supported by JSPS KAKENHI (grant no. 20KK0063 and 21H01056) and the National Institute for Fusion Science (grant no. NIFS20KOAP035).
Declaration of interest
The authors report no conflict of interest.