Let $\mathbb{N}$ be the set of all non-negative integers. For any integer r and m, let $r+m\mathbb{N}=\{r+mk: k\in\mathbb{N}\}$. For $S\subseteq \mathbb{N}$ and $n\in \mathbb{N}$, let $R_{S}(n)$ denote the number of solutions of the equation $n=s+s'$ with $s, s'\in S$ and $s \lt s'$. Let $r_{1}, r_{2}, m$ be integers with $0 \lt r_{1} \lt r_{2} \lt m$ and $2\mid r_{1}$. In this paper, we prove that there exist two sets C and D with $C\cup D=\mathbb{N}$ and $C\cap D=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N})$ such that $R_{C}(n)=R_{D}(n)$ for all $n\in\mathbb{N}$ if and only if there exists a positive integer l such that $r_{1}=2^{2l+1}-2, r_{2}=2^{2l+1}-1, m=2^{2l+2}-2$.

For 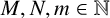$M,N,m\in \mathbb {N}$ with 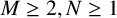$M\geq 2, N\geq 1$ and $m \geq 2$, we define two families of sequences, $\mathcal {B}_{M,N}$ and $\mathcal {B}_{M,N,m}$. The nth term of $\mathcal {B}_{M,N}$ is obtained by expressing n in base M and recombining those digits in base N. The nth term of 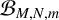$\mathcal {B}_{M,N,m}$ is defined by $\mathcal {B}_{M,N,m}(n):=\mathcal {B}_{M,N}(n) \; (\textrm {mod}\;m)$. The special case $\mathcal {B}_{M,1,m}$, where $N=1$, yields the digit sum sequence 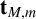$\mathbf {t}_{M,m}$ in base M mod m. We prove that $\mathcal {B}_{M,N}$ is the fixed point of a morphism $\mu _{M,N}$ at letter $0$, similar to a property of 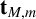$\mathbf {t}_{M,m}$. Additionally, we show that $\mathcal {B}_{M,N,m}$ contains arbitrarily long palindromes if and only if $m=2$, mirroring the behaviour of the digit sum sequence. When $m\geq M$ and N, m are coprime, we establish that 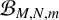$\mathcal {B}_{M,N,m}$ contains no overlaps.

The Thue–Morse sequence $\{t(n)\}_{n\geqslant 0}$ is the indicator function of the parity of the number of ones in the binary expansion of nonnegative integers n, where $t(n)=1$ (resp. $=0$) if the binary expansion of n has an odd (resp. even) number of ones. In this paper, we generalize a recent result of E. Miyanohara by showing that, for a fixed Pisot or Salem number $\beta>\sqrt {\varphi }=1.272019\ldots $, the set of the numbers

$$\begin{align*}1,\quad \sum_{n\geqslant1}\frac{t(n)}{\beta^{n}},\quad \sum_{n\geqslant1}\frac{t(n^2)}{\beta^{n}},\quad \dots, \quad \sum_{n\geqslant1}\frac{t(n^k)}{\beta^{n}},\quad \dots \end{align*}$$

$\mathbb {Q}(\beta )$

$\varphi :=(1+\sqrt {5})/2$

$k\geqslant 1$

$a_1,a_2,\ldots ,a_k\in \mathbb {Q}(\beta )$

$a_1t(n)+a_2t(n^2)+\cdots +a_kt(n^k)\}_{n\geqslant 1}$

Let $\mathbb {N}$ be the set of all nonnegative integers. For $S\subseteq \mathbb {N}$ and $n\in \mathbb {N}$ , let $R_S(n)$ denote the number of solutions of the equation $n=s_1+s_2$ , $s_1,s_2\in S$ and $s_1<s_2$ . Let A be the set of all nonnegative integers which contain an even number of digits $1$ in their binary representations and $B=\mathbb {N}\setminus A$ . Put $A_l=A\cap [0,2^l-1]$ and $B_l=B\cap [0,2^l-1]$ . We prove that if $C \cup D=[0, m]\setminus \{r\}$ with $0<r<m$ , $C \cap D=\emptyset $ and $0 \in C$ , then $R_{C}(n)=R_{D}(n)$ for any nonnegative integer n if and only if there exists an integer $l \geq 1$ such that $m=2^{l}$ , $r=2^{l-1}$ , $C=A_{l-1} \cup (2^{l-1}+1+B_{l-1})$ and $D=B_{l-1} \cup (2^{l-1}+1+A_{l-1})$ . Kiss and Sándor [‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161] proved an analogous result when $C\cup D=[0,m]$ , $0\in C$ and $C\cap D=\{r\}$ .

The Thue–Morse sequence is a prototypical automatic sequence found in diverse areas of mathematics, and in computer science. We study occurrences of factors w within this sequence, or more precisely, the sequence of gaps between consecutive occurrences. This gap sequence is morphic; we prove that it is not automatic as soon as the length of w is at least $2$ , thereby answering a question by J. Shallit in the affirmative. We give an explicit method to compute the discrepancy of the number of occurrences of the block $\mathtt {01}$ in the Thue–Morse sequence. We prove that the sequence of discrepancies is the sequence of output sums of a certain base- $2$ transducer.

The level of distribution of a complex-valued sequence $b$ measures the quality of distribution of $b$ along sparse arithmetic progressions $nd+a$. We prove that the Thue–Morse sequence has level of distribution $1$, which is essentially best possible. More precisely, this sequence gives one of the first nontrivial examples of a sequence satisfying a Bombieri–Vinogradov-type theorem for each exponent $\theta <1$. This result improves on the level of distribution $2/3$ obtained by Müllner and the author. As an application of our method, we show that the subsequence of the Thue–Morse sequence indexed by $\lfloor n^c\rfloor$, where $1 < c < 2$, is simply normal. This result improves on the range $1 < c < 3/2$ obtained by Müllner and the author and closes the gap that appeared when Mauduit and Rivat proved (in particular) that the Thue–Morse sequence along the squares is simply normal.