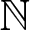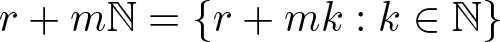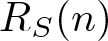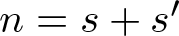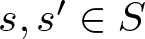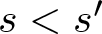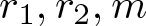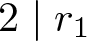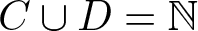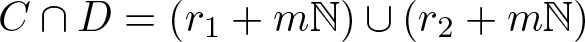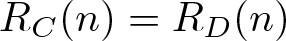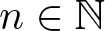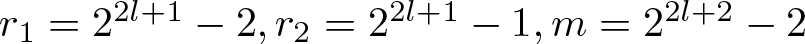1. Introduction
Let 
$\mathbb{N}$ be the set of all non-negative integers. For any integer r and m, let 
$r+m\mathbb{N}=\{r+mk: k\in\mathbb{N}\}$. Let A be the set of all non-negative integers which contain an even number of digits 1 in their binary representations and 
$B=\mathbb{N}\backslash A$. The set A is called Thue–Morse sequence. For any positive integer l, let 
$A_{l}=A\cap [0, 2^{l}-1]$ and 
$B_{l}=B\cap [0, 2^{l}-1]$. For 
$S\subseteq \mathbb{N}$ and 
$n\in \mathbb{N}$, let the representation function 
$R_{S}(n)$ denote the number of solutions of the equation 
$s+s'=n$ with 
$s, s'\in S$ and 
$s \lt s'$. Sárközy asked whether there exist two subsets 
$C, D\subseteq \mathbb{N}$ with 
$|(C\cup D)\backslash (C\cap D)|=\infty$ such that 
$R_{C}(n)=R_{D}(n)$ for all sufficiently large integers n. By using the Thue–Morse sequence, Dombi [Reference Dombi6] answered Sárközy’s problem affirmatively. Later, Lev [Reference Lev10], Sándor [Reference Sándor12] and Tang [Reference Tang17] proved this result by different methods. Partitions of non-negative integers and their corresponding representation functions have been extensively studied by many authors. The related results can be found in [Reference Chen and Tang4, Reference Chen and Wang5, Reference Jiao, Sándor, Yang and Zhou7–Reference Kiss and Sándor9, Reference Sándor12–Reference Tang17, Reference Yang and Chen19].
In 2012, Yu and Tang [Reference Yu and Tang20] began to focus on partitions of non-negative integers with the intersection not empty. They studied the intersection of two sets is an arithmetic progression and posed the following conjecture:
Conjecture 1.1.
Let 
$m\in\mathbb{N}$ and 
$R\subset \{0, 1, \ldots, m-1\}$. If 
$C\cup D=\mathbb{N}$ and 
$C\cap D=\{r+km: k\in\mathbb{N}, r\in R\}$, then 
$R_{C}(n)=R_{D}(n)$ cannot hold for all sufficiently large n.
In 2016, Tang [Reference Tang18] obtained the following theorem.
Theorem A [Reference Tang18, Theorem 1]
Let m be an integer with 
$m\geq 2$. If 
$C\cup D=\mathbb{N}$ and 
$C\cap D=m\mathbb{N}$, then 
$R_{C}(n)=R_{D}(n)$ cannot hold for all large enough integers n.
In 20l6, Chen and Lev [Reference Chen and Lev3] disproved Conjecture 1.1 by the following result.
Theorem B [Reference Chen and Lev3, Theorem 1]
Let l be a positive integer. There exist two sets C and D with 
$C\cup D=\mathbb{N}$ and 
$C\cap D=(2^{2l}-1)+(2^{2l+1}-1)\mathbb{N}$ such that 
$R_{C}(n)=R_{D}(n)$ for every positive integer n.
In [Reference Chen and Lev3], Chen and Lev also proposed the following problem.
Problem 1.2.
Given 
$R_{C}(n)=R_{D}(n)$ for every positive integer n, 
$C\cup D=\mathbb{N}$ and 
$C\cap D=r+m\mathbb{N}$ with 
$r\geq 0$ and 
$m\geq 2$, must there exist an integer 
$l\geq 1$ such that 
$r=2^{2l}-1, m=2^{2l+1}-1$?
Afterwards, Li and Tang [Reference Li and Tang11], Chen, Tang and Yang [Reference Chen, Tang and Yang2] solved Problem 1.2 under the condition 
$0\leq r \lt m$. In 2021, Chen and Chen [Reference Chen and Chen1] solved Problem 1.2 affirmatively.
Theorem C [Reference Chen and Chen1, Theorem 1.1]
Let 
$m\geq 2$ and 
$r\geq 0$ be two integers and let C and D be two sets with 
$C\cup D=\mathbb{N}$ and 
$C\cap D=r+m\mathbb{N}$ such that 
$R_{C}(n)=R_{D}(n)$ for every positive integer n. Then there exists a positive integer l such that 
$r=2^{2l}-1$ and 
$m=2^{2l+1}-1$.
Let 
$r_{1}, r_{2}, m$ be integers with 
$0 \lt r_{1} \lt r_{2} \lt m$. In this paper, we focus on partitions of non-negative integers into two sets 
$C, D$ with 
$C\,\cup\,D=\mathbb{N}$ and 
$C\,\cap\,D=(r_{1}\,+\,m\mathbb{N})\cup (r_{2}\,+\,m\mathbb{N})$ such that 
$R_{C}(n)=R_{D}(n)$ for all 
$n\in\mathbb{N}$ and obtain the following result.
Theorem 1.3. Let 
$r_{1}, r_{2}, m$ be integers with 
$0 \lt r_{1} \lt r_{2} \lt m$ and 
$2\mid r_{1}$. Then there exist two sets C and D with 
$C\cup D=\mathbb{N}$ and 
$C\cap D=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N})$ such that 
$R_{C}(n)=R_{D}(n)$ for all 
$n\in\mathbb{N}$ if and only if there exists a positive integer l such that 
$r_{1}=2^{2l+1}-2, r_{2}=2^{2l+1}-1, m=2^{2l+2}-2$.
Motivated by Theorems B and C, we propose the following conjecture for further research.
Conjecture 1.4.
Let 
$r_{1}, r_{2}, m$ be integers with 
$0 \lt r_{1} \lt r_{2} \lt m$ and 
$2\nmid r_{1}$. Then there exist two sets C and D with 
$C\cup D=\mathbb{N}$ and 
$C\cap D=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N})$ such that 
$R_{C}(n)=R_{D}(n)$ for all 
$n\in \mathbb{N}$ if and only if there exists a positive integer l such that 
$r_{1}=2^{2l}-1, r_{2}=2^{2l+1}+2^{2l}-2, m=2^{2l+2}-2$.
Throughout this paper, let 
$f(x)=a_{0}+a_{1}x+\cdots+a_{n}x^{n}\in\mathbb{Z}[x]$ and for 
$m\leq n$, define
\begin{equation*}(f(x))_{m}=a_{0}+a_{1}x +\cdots+a_{m}x^{m}.\end{equation*} For 
$C, D\subseteq \mathbb{N}$ and 
$n\in \mathbb{N}$, let 
$R_{C, D}(n)$ be the number of solutions of 
$n=c+d$ with 
$c\in C$ and 
$d\in D$. Let 
$C+D=\{c+d: c\in C, d\in D\}$. Let C(x) be the set of integers in C which are less than or equal to x. The characteristic function of C is denoted by
\begin{equation*}\chi_{C}(n)=\begin{cases}1, &n\in C,\\
0, & n\not\in C.
\end{cases}\end{equation*}2. Some lemmas
Lemma 2.1. [Reference Chen and Lev3, Lemma 1]
Suppose that 
$C_{0}, D_{0}\subseteq \mathbb{N}$ satisfy 
$R_{C_{0}}(n)=R_{D_{0}}(n)$ for all 
$n\in \mathbb{N}$, and that m is a non-negative integer with 
$m \notin (C_{0}-D_{0})\cup(D_{0}-C_{0})$. Then, letting
\begin{equation*}C_{1}:=C_{0}\cup (m+D_{0}) \text{and } D_{1}:=D_{0}\cup (m+C_{0}),\end{equation*} we have 
$R_{C_{1}}(n)=R_{D_{1}}(n)$ for all 
$n\in \mathbb{N}$ and furthermore
(i)
$C_{1}\cup D_{1}=(C_{0}\cup D_{0})\cup (m+C_{0}\cup D_{0})$;(ii)
$C_{1}\cap D_{1}\supseteq(C_{0}\cap D_{0})\cup (m+C_{0}\cap D_{0})$, the union being disjoint.
Moreover, if 
$m\notin (C_{0}-C_{0})\cup (D_{0}-D_{0})$, then also in (i) the union is disjoint, and in (ii) the inclusion is in fact an equality. In particular, if 
$C_{0}\cup D_{0}=[0,m-1]$, then 
$C_{1}\cup D_{1}=[0,2m-1]$, and if C 0 and D 0 indeed partition the interval 
$[0, m-1]$, then C 1 and D 1 partition the interval 
$[0, 2m-1]$.
Lemma 2.2. [Reference Kiss and Sándor8, Claim 1]
Let 
$0 \lt r_{1} \lt \cdots \lt r_{s}\leq m$ be integers. Then there exists at most one pair of sets (C, D) such that 
$C\cup D=[0, m], 0\in C, C\cap D=\{r_{1}, \ldots, r_{s}\}$ and 
$R_{C}( n)=R_{D}(n)$ for every 
$n \leq m$.
Lemma 2.3. [Reference Kiss and Sándor8, Claim 3]
If for some positive integer M, the integers 
$M-1, M-2, M-4, M-8, \ldots, M-2^{\lceil \log_{2}M\rceil-1}$ are all contained in the set A, then 
$\lceil \log_{2}M\rceil$ is odd and 
$M=2^{\lceil \log_{2}M\rceil}-1$.
Lemma 2.4. [Reference Kiss and Sándor8, Claim 4]
If for some positive integer M, the integers 
$M-1, M-2, M-4, M-8, \ldots, M-2^{\lceil \log_{2}M\rceil-1}$ are all contained in the set B, then 
$\lceil \log_{2}M\rceil$ is even and 
$M=2^{\lceil \log_{2}M\rceil}-1$.
Lemma 2.5. [Reference Kiss and Sándor8, Theorem 3]
Let C and D be sets of non-negative integers such that 
$C\cup D=[0, m], C\cap D=\emptyset$ and 
$0\in C$. Then 
$R_{C}(n)=R_{D}(n)$ for every positive integer n if and only if there exists a positive integer l such that 
$C=A_{l}$ and 
$D=B_{l}$.
3. Proofs
Proof of Theorem 1.3. (Sufficiency). For any given positive integer l, let
\begin{equation}
m_{i}=\left\{\begin{array}{ll}
2^{i+1}, & 0\leq i\leq 2l-1,\\
2^{i+1}-2, & i=2l,\\
2^{i+1}-2^{i-2l}, & i\geq 2l+1.
\end{array}\right.
\end{equation} For given sets 
$C_{0}=\{0\}, D_{0}=\{1\}$, define
\begin{equation}
C_{i}=C_{i-1}\cup (m_{i-1}+D_{i-1}), \quad D_{i}=D_{i-1}\cup (m_{i-1}+C_{i-1}),\quad i=1, 2, \ldots
\end{equation}and
\begin{equation}
C=\bigcup_{i\in\mathbb{N}}C_{i}, \qquad\qquad D=\bigcup_{i\in\mathbb{N}}D_{i}.
\end{equation} It is clear that C 0 and D 0 partition the interval 
$[0, m_{0}-1]$ and
\begin{equation*}m_{0}=2\notin (C_{0}-D_{0})\cup(D_{0}-C_{0})\cup (C_{0}-C_{0})\cup (D_{0}-D_{0})\end{equation*} and 
$R_{C_{0}}(n)=R_{D_{0}}(n)$ for all 
$n\in \mathbb{N}$ (both representation functions are identically equal to 0). Applying Lemma 2.1 inductively 
$2l-1$ times, we can deduce that for any 
$i\in [0, 2l-1]$, 
$R_{C_{i}}(n)=R_{D_{i}}(n)$ for all 
$n\in\mathbb{N}$, the sets Ci and Di partition the interval 
$[0, m_{i}-1]$ and
\begin{equation*}m_{i}=2^{i+1}\notin (C_{i}-D_{i})\cup(D_{i}-C_{i})\cup (C_{i}-C_{i})\cup (D_{i}-D_{i}).\end{equation*} In particular, 
$R_{C_{2l-1}}(n)=R_{D_{2l-1}}(n)$ for all 
$n\in \mathbb{N}$, the sets 
$C_{2l-1}$ and 
$D_{2l-1}$ partition the interval 
$[0, m_{2l-1}-1]=[0, 2^{2l}-1]$ and
\begin{equation*}m_{2l-1}=2^{2l}\notin (C_{2l-1}-D_{2l-1})\cup(D_{2l-1}-C_{2l-1})\cup (C_{2l-1}-C_{2l-1})\cup (D_{2l-1}-D_{2l-1}).\end{equation*} By Lemma 2.1, we have 
$R_{C_{2l}}(n)=R_{D_{2l}}(n)$ for all 
$n\in \mathbb{N}$, the sets 
$C_{2l}$ and 
$D_{2l}$ partition the interval 
$[0, 2m_{2l-1}-1]=[0, 2^{2l+1}-1]=[0, m_{2l}+1]$. In addition, it is easily seen that 
$\{0, m_{2l}\}\subseteq C_{2l}$ and 
$\{1, m_{2l}+1\}\subseteq D_{2l}$. Then
\begin{equation*}m_{2l}\not\in (C_{2l}-D_{2l})\cup (D_{2l}-C_{2l}), \quad m_{2l}\in (C_{2l}-C_{2l})\cup (D_{2l}-D_{2l}).\end{equation*} By Lemma 2.1, we have 
$R_{C_{2l+1}}(n)=R_{D_{2l+1}}(n)$ for all 
$n\in \mathbb{N}$ and
\begin{align*}
C_{2l+1}\cup D_{2l+1}&= [0, 2m_{2l}+1]=[0, m_{2l+1}-1],\\
C_{2l+1}\cap D_{2l+1}&=(C_{2l}\cup (m_{2l}+D_{2l}))\cap (D_{2l}\cup(m_{2l}+C_{2l}))\\
&=(C_{2l}\cap D_{2l})\cup (C_{2l}\cap (m_{2l}+C_{2l}))\cup (D_{2l}\cap (m_{2l}+D_{2l}))\\
&\,\quad\cup (m_{2l}+C_{2l}\cap D_{2l})\\
&=\{m_{2l},m_{2l}+1\}.
\end{align*} Applying again Lemma 2.1, we can conclude that 
$R_{C_{i}}(n)=R_{D_{i}}(n)$ for all 
$n\in \mathbb{N}$, 
$C_{i}\cup D_{i}=[0, m_{i}-1]$ and 
$C_{i}\cap D_{i}=\{m_{2l}, m_{2l}+1\}+\{0, m_{2l+1}, \ldots, (2^{i-2l}-1)m_{2l+1}\}$ for each 
$i\geq 2l+1$.
Therefore, by the definitions of C and D in (3.1)–(3.3), we have 
$R_{C}(n)=R_{D}(n)$ for all 
$n\in \mathbb{N}$, 
$C\cup D=\mathbb{N}$ and
\begin{equation*}C\cap D=\{m_{2l}, m_{2l}+1\}+m_{2l+1}\mathbb{N}=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N}).\end{equation*}(Necessity). To prove the necessity of Theorem 1.3, we need the following three claims.
Claim 1.
Given 
$0 \lt r_{1} \lt r_{2}\leq m$, there exists at most one pair of sets (C, D) such that 
$C\cup D=\mathbb{N}$, 
$C\cap D=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N})$ and 
$R_{C}(n)=R_{D}(n)$ for all 
$n\in\mathbb{N}$.
Proof of Claim 1
Assume that there exist at least two pairs of sets (C, D) and 
$(C', D')$ which satisfy the conditions
\begin{equation*} C\cup D=\mathbb{N}, C\cap D=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N}), R_{C}(n)=R_{D}(n) \,\text{for all } n\in\mathbb{N},\end{equation*}
\begin{equation*} C'\cup D'=\mathbb{N}, C'\cap D'=(r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N}), R_{C'}(n)=R_{D'}(n) \,\text{for all } n\in\mathbb{N}.\end{equation*} We may assume that 
$0\in C\cap C'$. Let k be the smallest positive integer such that 
$\chi_{C}(k)\neq\chi_{C'}(k)$. Write
\begin{equation*}\big((r_{1}+m\mathbb{N})\cup (r_{2}+m\mathbb{N})\big)\cap [0, k]=\{t_{1}, \ldots, t_{s}\},\end{equation*}
\begin{equation*}C_{1}=C\cap [0, k],\;\; D_{1}=D\cap [0, k],\end{equation*}
\begin{equation*}\quad\!\!\! C_{2}=C'\cap [0, k],\;\; D_{2}=D'\cap [0, k].\end{equation*}Then
\begin{equation}
C_{1}\cup D_{1}=C_{2}\cup D_{2}=[0, k],
\end{equation}
\begin{equation}
\qquad\,\,\,\, C_{1}\cap D_{1}=C_{2}\cap D_{2}=\{t_{1}, \ldots, t_{s}\},
\end{equation}
\begin{equation}
\qquad\,\,\,\,\chi_{C_{1}}(k)\neq \chi_{C_{2}}(k),\;\; 0\in C_{1}\cap C_{2}.
\end{equation} For any integer 
$n\in [0, k]$, by the hypothesis, we have
\begin{align}
R_{C_{1}}(n)&=|\{(c, c'): c \lt c'\leq n, c, c'\in C_{1}, c+c'=n\}|\nonumber\\
&=R_{C}(n)=R_{D}(n)=R_{D_{1}}(n),
\end{align}
\begin{align}
R_{C_{2}}(n)&=|\{(c, c'): c \lt c'\leq n, c, c'\in C_{2}, c+c'=n\}|\nonumber\\
&=R_{C'}(n)=R_{D'}(n)=R_{D_{2}}(n).
\end{align} Thus there exist two pairs of sets 
$(C_{1}, D_{1})$ and 
$(C_{2}, D_{2})$ satisfying (3.4)–(3.8). By Lemma 2.2, this is impossible. This completes the proof of Claim 1.
Claim 2.
Let 
$r_{1}, r_{2}, m$ be integers with 
$0 \lt r_{1} \lt r_{2} \lt r_{1}+r_{2}\leq m$ and 
$2\mid r_{1}$. Let C and D be sets of non-negative integers such that 
$C\cup D=[0, m]$, 
$C\cap D=\{r_{1}, r_{2}\}$ and 
$0\in C$. If 
$R_{C}(n)=R_{D}(n)$ for any integer 
$n\in [0, m]$, then there exists a positive integer l such that 
$r_{1}=2^{2l+1}-2, r_{2}=2^{2l+1}-1$.
Proof of Claim 2
Let
\begin{equation}
p_{C}(x)=\sum\limits_{i=0}^{m}\chi_{C}(i)x^{i}, \;\; p_{D}(x)=\sum\limits_{i=0}^{m}\chi_{D}(i)x^{i}.
\end{equation}Then
\begin{equation}
\frac{1}{2}(p_{C}(x)^{2}-p_{C}(x^{2}))=\sum_{n=0}^{\infty} R_{C}(n)x^{n}, \;\; \frac{1}{2}(p_{D}(x)^{2}-p_{D}(x^{2}))=\sum_{n=0}^{\infty} R_{D}(n)x^{n}.
\end{equation} Since 
$R_{C}(n)=R_{D}(n)$ for any integer 
$n\in [0, m]$, we have
\begin{equation}
\bigg(\sum_{n=0}^{\infty} R_{C}(n)x^{n}\bigg)_{m}=\bigg(\sum_{n=0}^{\infty} R_{D}(n)x^{n}\bigg)_{m}.
\end{equation}
\begin{align*} \bigg(\frac{1}{2}(p_{C}(x)^{2}-p_{C}(x^{2}))\bigg)_{m}&=\bigg(\sum_{n=0}^{\infty} R_{C}(n)x^{n}\bigg)_{m}=\bigg(\sum_{n=0}^{\infty} R_{D}(n)x^{n}\bigg)_{m}\\
&=\bigg(\frac{1}{2}(p_{D}(x)^{2}-p_{D}(x^{2}))\bigg)_{m}.\end{align*} Noting that 
$C\cup D=[0, m]$, 
$C\cap D=\{r_{1}, r_{2}\}$, we have
\begin{equation*} p_{D}(x)=\frac{1-x^{m+1}}{1-x}-p_{C}(x)+x^{r_{1}}+x^{r_{2}}. \end{equation*}Then
\begin{align*}\big(p_{C}(x)^{2}-p_{C}(x^{2})\big)_{m}
&=\bigg(\bigg(\frac{1-x^{m+1}}{1-x}-p_{C}(x)+x^{r_{1}}+x^{r_{2}}\bigg)^{2}\\
&\,\,\quad-\,\bigg(\frac{1-x^{2m+2}}{1-x^{2}}-p_{C}(x^{2})+x^{2r_{1}}+x^{2r_{2}}\bigg)\bigg)_{m}.\end{align*}Thus
\begin{equation}
\begin{array}{rcl}
\big(2p_{C}(x^{2})\big)_{m}&=& \bigg(\frac{1-x^{2m+2}}{1-x^{2}}+2p_{C}(x)x^{r_{1}}+2p_{C}(x)x^{r_{2}}+2p_{C}(x)\frac{1-x^{m+1}}{1-x}\\
&& -\bigg(\frac{1-x^{m+1}}{1-x}\bigg)^{2}-2x^{r_{1}}\frac{1-x^{m+1}}{1-x}-2x^{r_{2}}\frac{1-x^{m+1}}{1-x}-2x^{r_{1}+r_{2}}\bigg)_{m}.
\end{array}
\end{equation} An easy calculation shows that 
$r_{1}\geq 6$, 
$\{0, 3, 5, 6\}\subset C$ and 
$\{1, 2, 4, 7\}\subset D$.
In order to prove 
$r_{2}=r_{1}+1$, we suppose that 
$r_{2}\geq r_{1}+2$ and we will show that this leads to a contradiction.
The coefficient of 
$x^{r_{1}-1}$ in (3.12) is 
$0=2\sum\limits_{i=0}^{r_{1}-1}\chi_{C}(i)-r_{1}$. Since 
$r_{1}\in C$, we have 
$\chi_{C}(r_{1})=1$. Then 
$2\sum\limits_{i=0}^{r_{1}}\chi_{C}(i)=r_{1}+2$. The coefficient of 
$x^{r_{1}}$ in (3.12) is 
$2\chi_{C}\big(\frac{r_{1}}{2}\big)=2\sum\limits_{i=0}^{r_{1}}\chi_{C}(i)-r_{1}=2$. Then 
$\chi_{C}\big(\frac{r_{1}}{2}\big)=1$. The coefficient of 
$x^{r_{1}+1}$ in (3.12) is 
$0=2\sum\limits_{i=0}^{r_{1}+1}\chi_{C}(i)-r_{1}-4=2\chi_{C}(r_{1}+1)-2$. Then 
$\chi_{C}(r_{1}+1)=1$. The coefficient of 
$x^{r_{1}+2}$ in (3.12) is 
$2\chi_{C}\big(\frac{r_{1}+2}{2}\big)=2\sum\limits_{i=0}^{r_{1}+2}\chi_{C}(i)-r_{1}-4$. Then 
$\chi_{C}\big(\frac{r_{1}+2}{2}\big)=\chi_{C}(r_{1}+2)$. If 
$r_{2}=r_{1}+2$, then 
$\chi_{C}(r_{1}+2)=1$. Comparing the coefficients of 
$x^{r_{1}+s}$ with 
$s\in \{3, 4, 5\}$ on the both sides of (3.12), we have
\begin{equation*}
\begin{array}{l}
0=2\sum\limits_{i=0}^{r_{1}+3}\chi_{C}(i)-r_{1}-6,\\
2\chi_{C}\bigg(\frac{r_{1}+4}{2}\bigg)=2\sum\limits_{i=0}^{r_{1}+4}\chi_{C}(i)-r_{1}-8,\\
0=2\sum\limits_{i=0}^{r_{1}+5}\chi_{C}(i)-r_{1}-6.
\end{array}
\end{equation*} Then 
$\chi_{C}(r_{1}+3)=0$, 
$\chi_{C}(r_{1}+4)=1$ and 
$\chi_{C}(r_{1}+5)=-1$, a contradiction. Thus 
$r_{2}\geq r_{1}+3$. The coefficient of 
$x^{r_{1}+3}$ in (3.12) is
\begin{equation*} 0=2\sum\limits_{i=0}^{r_{1}+3}\chi_{C}(i)-r_{1}-4=2\chi_{C}(r_{1}+2)+2\chi_{C}(r_{1}+3).\end{equation*} Then 
$\chi_{C}(r_{1}+2)=\chi_{C}(r_{1}+3)=0$. Thus 
$\chi_{C}\big(\frac{r_{1}+2}{2}\big)=0$ and 
$r_{2}\geq r_{1}+4$. The coefficient of 
$x^{r_{1}+4}$ in (3.12) is
\begin{equation*}2\chi_{C}\bigg(\frac{r_{1}+4}{2}\bigg)=2\sum\limits_{i=0}^{r_{1}+4}\chi_{C}(i)-r_{1}-6=2\chi_{C}(r_{1}+4)-2.\end{equation*} Then 
$\chi_{C}(r_{1}+4)=1$, 
$\chi_{C}\big(\frac{r_{1}+4}{2}\big)=0$ and 
$2\sum\limits_{i=0}^{r_{1}+4}\chi_{C}(i)=r_{1}+6$. By Lemma 2.2, we have
\begin{equation}
C\cap [0, r_{1}-1]=A\cap [0, r_{1}-1], \quad D\cap [0, r_{1}-1]=B\cap [0, r_{1}-1].
\end{equation} Since 
$\chi_{C}\big(\frac{r_{1}+2}{2}\big)=\chi_{C}\big(\frac{r_{1}+4}{2}\big)$ and 
$\frac{r_{1}+4}{2}\leq r_{1}-1$, by (3.13) and the definition of A, we have 
$r_{1}\equiv 0\pmod 4$. It follows that 
$r_{1}\geq 8$ and 
$\chi_{C}\big(\frac{r_{1}+6}{2}\big)=1$.
Let k be a positive even integer such that 
$r_{1}\leq k \lt k+1 \lt \min\{r_{2}, 2r_{1}\}\leq m$. Comparing the coefficients of x k and 
$x^{k+1}$ on the both sides of (3.12) respectively, we have
\begin{equation*} 2\chi_{C}\bigg(\frac{k}{2}\bigg)=2\chi_{C}(k-r_{1})+2\sum\limits_{i=0}^{k}\chi_{C}(i)-k-2,\end{equation*}
\begin{equation*} 0=2\chi_{C}(k+1-r_{1})+2\sum\limits_{i=0}^{k+1}\chi_{C}(i)-k-4.\end{equation*}Subtracting the above two equalities and dividing by 2 we can get
\begin{equation}
\chi_{C}\bigg(\frac{k}{2}\bigg)=\chi_{C}(k-r_{1})-\chi_{C}(k+1-r_{1})-\chi_{C}(k+1)+1.
\end{equation} Since 
$k+1-r_{1} \lt r_{1}, k-r_{1}$ is even, by (3.13), we have
\begin{equation*}\chi_{C}(k-r_{1})+\chi_{C}(k+1-r_{1})=1.\end{equation*} If 
$\chi_{C}(k-r_{1})=0$, then 
$\chi_{C}(k+1-r_{1})=1$. By (3.14), we get 
$\chi_{C}(\frac{k}{2})=0$. If 
$\chi_{C}(k-r_{1})=1$, then 
$\chi_{C}(k+1-r_{1})=0$. By (3.14), we get 
$\chi_{C}(\frac{k}{2})=1$. Thus
\begin{equation}
\chi_{C}(k-r_{1})=\chi_{C}\bigg(\frac{k}{2}\bigg).
\end{equation} If 
$\min\{r_{2}, 2r_{1}\} \gt 2r_{1}-1$, then choose 
$k=2r_{1}-2^{i+1}$ with 
$i\geq 0$ in (3.15), we have
\begin{equation*}\chi_{C}(r_{1}-2^{i+1})=\chi_{C}(r_{1}-2^{i}).\end{equation*}Then
\begin{equation*}\chi_{C}(r_{1}-1)=\chi_{C}(r_{1}-2)=\chi_{C}(r_{1}-4)=\cdots=\chi_{C}(r_{1}-2^{\lceil\log_{2}r_{1}\rceil-1}).\end{equation*} By Lemmas 2.3 and 2.4, we have 
$r_{1}=2^{\lceil\log_{2}r_{1}\rceil}-1$, which contradicts 
$2\mid r_{1}$.
If 
$r_{2}=2r_{1}-1$, then compare the coefficients of 
$x^{r_{2}}$ and 
$x^{r_{2}-1}$ on the both sides of (3.12) respectively, we have
\begin{equation*}0=2\chi_{C}(r_{1}-1)+2\sum\limits_{i=0}^{r_{2}}\chi_{C}(i)-r_{2}-3=2\chi_{C}(r_{1}-1)+2\sum\limits_{i=0}^{r_{2}-1}\chi_{C}(i)-r_{2}-1,\end{equation*}
\begin{equation*}2\chi_{C}(r_{1}-1)=2\chi_{C}(r_{1}-2)+2\sum\limits_{i=0}^{r_{2}-1}\chi_{C}(i)-r_{2}-1.\end{equation*} Then 
$2\chi_{C}(r_{1}-1)=\chi_{C}(r_{1}-2)$. It follows that 
$\chi_{C}(r_{1}-2)=\chi_{C}(r_{1}-1)=0$, which contradicts 
$\chi_{C}(r_{1}-2)+\chi_{C}(r_{1}-1)=1$. Thus 
$r_{2}\leq 2r_{1}-2$.
Let k be a non-negative integer such that 
$2r_{1}\leq 2r_{1}+k \lt 2r_{1}+k+1 \lt r_{1}+r_{2}\leq m$. If k is even, then compare the coefficients of 
$x^{2r_{1}+s}$ with 
$s\in \{k, k+1\}$ on the both sides of (3.12), we have
\begin{equation*}
\begin{array}{l}
2\chi_{C}\bigg(\frac{2r_{1}+k}{2}\bigg)=2\chi_{C}(r_{1}+k)+2\chi_{C}(2r_{1}+k-r_{2})+2\sum\limits_{i=0}^{2r_{1}+k}\chi_{C}(i)-2r_{1}-k-4,\\
0=2\chi_{C}(r_{1}+k+1)+2\chi_{C}(2r_{1}+k+1-r_{2})+2\sum\limits_{i=0}^{2r_{1}+k+1}\chi_{C}(i)-2r_{1}-k-6.
\end{array}
\end{equation*}Subtracting the above two equalities and dividing by 2 we can get
\begin{align}
\chi_{C}\bigg(\frac{2r_{1}+k}{2}\bigg)&=\chi_{C}(r_{1}+k)+\chi_{C}(2r_{1}+k-r_{2})-\chi_{C}(2r_{1}+k+1)\nonumber\\
&\quad-\chi_{C}(r_{1}+k+1)-\chi_{C}(2r_{1}+k+1-r_{2})+1.
\end{align} If k is odd, then compare the coefficients of 
$x^{2r_{1}+s}$ with 
$s\in \{k, k+1\}$ on the both sides of (3.12), we have
\begin{equation*} 0=2\chi_{C}(r_{1}+k)+2\chi_{C}(2r_{1}+k-r_{2})+2\sum\limits_{i=0}^{2r_{1}+k}\chi_{C}(i)-2r_{1}-k-5,\end{equation*}
\begin{equation*} 2\chi_{C}\bigg(\frac{2r_{1}+k+1}{2}\bigg)=2\chi_{C}(r_{1}+k+1)+2\chi_{C}(2r_{1}+k+1-r_{2})+2\sum\limits_{i=0}^{2r_{1}+k+1}\chi_{C}(i)-2r_{1}-k-5.\end{equation*}Subtracting the above two equalities and dividing by 2 we can get
\begin{align}
\chi_{C}\bigg(\frac{2r_{1}+k+1}{2}\bigg)&=\chi_{C}(r_{1}+k+1)+\chi_{C}(2r_{1}+k+1-r_{2})+\chi_{C}(2r_{1}+k+1)\nonumber\\
&\quad-\chi_{C}(r_{1}+k)-\chi_{C}(2r_{1}+k-r_{2}).
\end{align}If r 2 is even, then choose k = 0 and k = 2 in (3.16) respectively, we have
\begin{equation*} \chi_{C}(r_{1})=\chi_{C}(r_{1})+\chi_{C}(2r_{1}-r_{2})-\chi_{C}(2r_{1}+1)-\chi_{C}(r_{1}+1)-\chi_{C}(2r_{1}+1-r_{2})+1,\end{equation*}
\begin{equation*} \chi_{C}(r_{1}+1)=\chi_{C}(r_{1}+2)+\chi_{C}(2r_{1}+2-r_{2})-\chi_{C}(2r_{1}+3)-\chi_{C}(r_{1}+3)-\chi_{C}(2r_{1}+3-r_{2})+1.\end{equation*}Then
\begin{equation*} \chi_{C}(2r_{1}-r_{2})-\chi_{C}(2r_{1}+1)-\chi_{C}(2r_{1}+1-r_{2})=0,\end{equation*}
\begin{equation*} \chi_{C}(2r_{1}+2-r_{2})-\chi_{C}(2r_{1}+3)-\chi_{C}(2r_{1}+3-r_{2})=0.\end{equation*} By (3.13), we have 
$\chi_{C}(2r_{1}-r_{2})+\chi_{C}(2r_{1}+1-r_{2})=1$ and 
$\chi_{C}(2r_{1}+2-r_{2})+\chi_{C}(2r_{1}+3-r_{2})=1$. Then 
$\chi_{C}(2r_{1}-r_{2})=1$ and 
$\chi_{C}(2r_{1}+2-r_{2})=1$. It follows that 
$r_{2}\equiv 2\pmod 4$. The coefficient of 
$x^{r_{2}}$ in (3.12) is
\begin{equation*} 2\chi_{C}\bigg(\frac{r_{2}}{2}\bigg)=2\chi_{C}(r_{2}-r_{1})+2\sum\limits_{i=0}^{r_{2}}\chi_{C}(i)-r_{2}-2\end{equation*} and the coefficient of 
$x^{r_{2}+1}$ in (3.12) is
\begin{equation*} 0=2\chi_{C}(r_{2}+1-r_{1})+2\sum\limits_{i=0}^{r_{2}+1}\chi_{C}(i)-r_{2}-6.\end{equation*}Then
\begin{equation*} \chi_{C}\bigg(\frac{r_{2}}{2}\bigg)=\chi_{C}(r_{2}-r_{1})-\chi_{C}(r_{2}+1-r_{1})-\chi_{C}(r_{2}+1)+2.\end{equation*} By 
$\chi_{C}(r_{2}-r_{1})+\chi_{C}(r_{2}+1-r_{1})=1$, we have 
$\chi_{C}(r_{2}-r_{1})=0$, 
$\chi_{C}(r_{2}+1-r_{1})=1$. By 
$r_{1}\equiv 0\pmod 4$ and 
$r_{2}\equiv 2\pmod 4$, we have 
$\chi_{C}(r_{2}-1-r_{1})=0$, 
$\chi_{C}(r_{2}-2-r_{1})=1$. The coefficient of 
$x^{r_{2}-1}$ in (3.12) is
\begin{equation*} 0=2\chi_{C}(r_{2}-1-r_{1})+2\sum\limits_{i=0}^{r_{2}-1}\chi_{C}(i)-r_{2}-2.\end{equation*} Then 
$2\sum\limits_{i=0}^{r_{2}-1}\chi_{C}(i)=r_{2}+2$. It follows that 
$2\sum\limits_{i=0}^{r_{2}}\chi_{C}(i)=r_{2}+4$ and 
$\chi_{C}\big(\frac{r_{2}}{2}\big)=1$. The coefficient of 
$x^{r_{2}-2}$ in (3.12) is
\begin{equation*} 2\chi_{C}\bigg(\frac{r_{2}-2}{2}\bigg)=2\chi_{C}(r_{2}-2-r_{1})+2\sum\limits_{i=0}^{r_{2}-2}\chi_{C}(i)-r_{2}.\end{equation*} Then 
$\chi_{C}\big(\frac{r_{2}-2}{2}\big)=2-\chi_{C}(r_{2}-1)$. Thus 
$\chi_{C}\big(\frac{r_{2}-2}{2}\big)=\chi_{C}(r_{2}-1)=1$. By (3.13) and 
$\chi_{C}\big(\frac{r_{2}-2}{2}\big)=\chi_{C}\big(\frac{r_{2}}{2}\big)=1$, we have 
$r_{2}\equiv 0\pmod 4$, a contradiction.
If r 2 is odd, then 
$r_{1}+5\leq r_{2}\leq 2r_{1}-3$. The coefficient of 
$x^{r_{1}+5}$ in (3.12) is
\begin{equation*}0=2\sum\limits_{i=0}^{r_{1}+5}\chi_{C}(i)-r_{1}-6=2\chi_{C}(r_{1}+5).\end{equation*} Then 
$\chi_{C}(r_{1}+5)=0$ and so 
$r_{2}\geq r_{1}+7$. The coefficient of 
$x^{r_{1}+6}$ in (3.12) is
\begin{equation*}2\chi_{C}\big(\frac{r_{1}+6}{2}\big)=2\sum\limits_{i=0}^{r_{1}+6}\chi_{C}(i)-r_{1}-6=2\chi_{C}(r_{1}+6).\end{equation*} Then 
$\chi_{C}(r_{1}+6)=\chi_{C}\big(\frac{r_{1}+6}{2}\big)=1$. By choosing k = 3 and k = 5 in (3.17) respectively, we have
\begin{equation*} \chi_{C}(r_{1}+2)=\chi_{C}(r_{1}+4)+\chi_{C}(2r_{1}+4-r_{2})+\chi_{C}(2r_{1}+4)-\chi_{C}(r_{1}+3)-\chi_{C}(2r_{1}+3-r_{2}),\end{equation*}
\begin{equation*} \chi_{C}(r_{1}+3)=\chi_{C}(r_{1}+6)+\chi_{C}(2r_{1}+6-r_{2})+\chi_{C}(2r_{1}+6)-\chi_{C}(r_{1}+5)-\chi_{C}(2r_{1}+5-r_{2}).\end{equation*}Then
\begin{equation*}\chi_{C}(2r_{1}+4-r_{2})+\chi_{C}(2r_{1}+4)-\chi_{C}(2r_{1}+3-r_{2})+1=0, \end{equation*}
\begin{equation*}\chi_{C}(2r_{1}+6-r_{2})+\chi_{C}(2r_{1}+6)-\chi_{C}(2r_{1}+5-r_{2})+1=0. \end{equation*} By (3.13), we have 
$\chi_{C}(2r_{1}+4-r_{2})+\chi_{C}(2r_{1}+3-r_{2})=1$ and 
$\chi_{C}(2r_{1}+6-r_{2})+\chi_{C}(2r_{1}+5-r_{2})=1$. Then 
$\chi_{C}(2r_{1}+3-r_{2})=\chi_{C}(2r_{1}+5-r_{2})=1$. Applying again (3.13), we have 
$r_{2}\equiv 1\pmod 4$. The coefficient of 
$x^{2r_{1}-2}$ in (3.12) is
\begin{equation*} 2\chi_{C}(r_{1}-1)=2\chi_{C}(r_{1}-2)+2\chi_{C}(2r_{1}-2-r_{2})+2\sum\limits_{i=0}^{2r_{1}-2}\chi_{C}(i)-2r_{1}-2\end{equation*} and the coefficient of 
$x^{2r_{1}-1}$ in (3.12) is
\begin{equation*} 0=2\chi_{C}(r_{1}-1)+2\chi_{C}(2r_{1}-1-r_{2})+2\sum\limits_{i=0}^{2r_{1}-1}\chi_{C}(i)-2r_{1}-4.\end{equation*}Subtracting the above two equalities and dividing by 2 we can obtain
\begin{equation*} 2\chi_{C}(r_{1}-1)=1+\chi_{C}(r_{1}-2)+\chi_{C}(2r_{1}-2-r_{2})-\chi_{C}(2r_{1}-1)-\chi_{C}(2r_{1}-1-r_{2}).\end{equation*} Noting that 
$\chi_{C}(r_{1}-2)+\chi_{C}(r_{1}-1)=1$ and 
$\chi_{C}(2r_{1}-2-r_{2})=\chi_{C}(2r_{1}-1-r_{2})$, we have 
$3\chi_{C}(r_{1}-1)=2-\chi_{C}(2r_{1}-1)$. However, it is impossible. Therefore 
$r_{2}=r_{1}+1$.
The remainder of the proof is similar to the proof of [Reference Sun and Pan13, Theorem 1.1]. For the sake of completeness we give the details.
Let k be a positive even integer with 
$r_{2} \lt k \lt k+1 \lt 2r_{1} \lt r_{1}+r_{2}\leq m$. Comparing the coefficients of 
$x^{k-1}, x^{k}$ and 
$x^{k+1}$ on the both sides of (3.12) respectively, we have
\begin{equation*} 0=2\chi_{C}(k-1-r_{1})+2\chi_{C}(k-1-r_{2})+2\sum\limits_{i=0}^{k-1}\chi_{C}(i)-k-4,\end{equation*}
\begin{equation*} 2\chi_{C}\bigg(\frac{k}{2}\bigg)=2\chi_{C}(k-r_{1})+2\chi_{C}(k-r_{2})+2\sum\limits_{i=0}^{k}\chi_{C}(i)-k-4,\end{equation*}
\begin{equation*} 0=2\chi_{C}(k+1-r_{1})+2\chi_{C}(k+1-r_{2})+2\sum\limits_{i=0}^{k+1}\chi_{C}(i)-k-6.\end{equation*}Calculating the above three equalities, we have
\begin{equation}
\chi_{C}\bigg(\frac{k}{2}\bigg)=\chi_{C}(k-r_{1})-\chi_{C}(k-1-r_{2})+\chi_{C}(k),
\end{equation}
\begin{equation}
\chi_{C}\bigg(\frac{k}{2}\bigg)=\chi_{C}(k-r_{2})-\chi_{C}(k+1-r_{1})-\chi_{C}(k+1)+1.
\end{equation} By choosing 
$k=2r_{1}-2$ in (3.19), we have
\begin{equation*} 2\chi_{C}(r_{1}-1)=\chi_{C}(r_{1}-3)-\chi_{C}(2r_{1}-1)+1. \end{equation*} Then 
$\chi_{C}(r_{1}-1)=\chi_{C}(r_{1}-3)$. Thus 
$r_{1}\equiv 2\pmod 4$ and 
$r_{2}\equiv 3\pmod 4$.
If 
$k-1-r_{2}\equiv 0\pmod 4$, then 
$k-r_{1}\equiv 2\pmod 4$ and 
$k\equiv 0\pmod 4$. Thus
\begin{equation*}\chi_{C}\bigg(\frac{k-1-r_{2}}{2}\bigg)+\chi_{C}\bigg(\frac{k-r_{1}}{2}\bigg)=1.\end{equation*}Hence
\begin{equation*}\chi_{C}(k-1-r_{2})+\chi_{C}(k-r_{1})=1.\end{equation*} If 
$\chi_{C}(k-1-r_{2})=0$, then 
$\chi_{C}(k-r_{1})=1$. By (3.18), we have 
$\chi_{C}(\frac{k}{2})=1$. If 
$\chi_{C}(k-1-r_{2})=1$, then 
$\chi_{C}(k-r_{1})=0$. By (3.18), we have 
$\chi_{C}(\frac{k}{2})=0$. Thus 
$\chi_{C}\big(\frac{k}{2}\big)=\chi_{C}(k-r_{1})$ and 
$\chi_{C}\big(\frac{k}{2}\big)+\chi_{C}(k-1-r_{2})=1$. Noting that 
$\chi_{C}(k-1-r_{2})+\chi_{C}(k-r_{2})=1$, we have 
$\chi_{C}\big(\frac{k}{2}\big)=\chi_{C}(k-r_{2})$.
If 
$k-1-r_{2}\equiv 2\pmod 4$, then 
$k-r_{1}\equiv 0\pmod 4$ and 
$k\equiv 2\pmod 4$. By (3.18), we have
\begin{equation*} \chi_{C}\bigg(\frac{k-2}{2}\bigg)=\chi_{C}(k-2-r_{1})-\chi_{C}(k-3-r_{2})+\chi_{C}(k-2).\end{equation*} Then 
$\chi_{C}\big(\frac{k-2}{2}\big)=\chi_{C}(k-2-r_{1})$. Noting that 
$\chi_{C}\big(\frac{k-2}{2}\big)+\chi_{C}\big(\frac{k}{2}\big)=1$ and 
$\chi_{C}(k-1-r_{2})+\chi_{C}(k-r_{2})=1$, we have 
$\chi_{C}\big(\frac{k}{2}\big)=\chi_{C}(k-r_{2})$.
As a result, we can obtain 
$\chi_{C}\big(\frac{k}{2}\big)=\chi_{C}(k-r_{2})$. Put 
$k=2r_{2}-2^{i+1}$ with 
$i\geq 0$. Then 
$\chi_{C}(r_{2}-2^{i})=\chi_{C}(r_{2}-2^{i+1})$. Thus
\begin{equation*}1=\chi_{C}(r_{1})=\chi_{C}(r_{2}-1)=\chi_{C}(r_{2}-2)=\chi_{C}(r_{2}-4)=\cdots=\chi_{C}(r_{2}-2^{\lceil\log_{2}r_{2}\rceil-1}).\end{equation*} By Lemma 2.3, we have 
$r_{1}=2^{2l+1}-2$ and 
$r_{2}=2^{2l+1}-1$ for some positive integer l.
This completes the proof of Claim 2.
Claim 3.
Let l be a positive integer and let 
$E, F$ be two sets of non-negative integers with 
$E\cup F=[0, 3 \cdot 2^{2l+1}-4], 0\in E$ and 
$E\cap F=\{2^{2l+1}-2, 2^{2l+1}-1\}$. Then 
$R_{E}(n)=R_{F}(n)$ for any integer 
$n\in [0, 3\cdot 2^{2l+1}-4]$ if and only if
\begin{align*}
E &= A_{2l+1}\cup (2^{2l+1}-2+B_{2l+1})\cup (2^{2l+2}-2+(B_{2l+1} \cap [0, 2^{2l+1}-3]))\cup \{3\cdot 2^{2l+1}-4\},\\
F &= B_{2l+1}\cup (2^{2l+1}-2+A_{2l+1})\cup (2^{2l+2}-2+(A_{2l+1}\cap [0, 2^{2l+1}-3])).
\end{align*}Proof of Claim 3.
We first prove the sufficiency of Claim 3. It is easy to verify that 
$E\cup F=[0, 3 \cdot 2^{2l+1}-4]$, 
$0\in E$ and 
$E\cap F=\{2^{2l+1}-2, 2^{2l+1}-1\}$.
If 
$n\in [0, 2^{2l+2}-3]$, then
\begin{align*}
R_{E}(n)&= R_{A_{2l+1}}(n)+R_{A_{2l+1}, 2^{2l+1}-2+B_{2l+1}}(n)+R_{2^{2l+1}-2+B_{2l+1}}(n)\\
&= R_{A_{2l+1}}(n)+ R_{A_{2l+1}, B_{2l+1}}(n-(2^{2l+1}-2))+R_{B_{2l+1}}(n-2(2^{2l+1}-2))
\end{align*}and
\begin{align*}
R_{F}(n)&= R_{B_{2l+1}}(n)+R_{2^{2l+1}-2+A_{2l+1}, B_{2l+1}}(n)+R_{2^{2l+1}-2+A_{2l+1}}(n)\\
&= R_{B_{2l+1}}(n)+ R_{A_{2l+1}, B_{2l+1}}(n-(2^{2l+1}-2))+R_{A_{2l+1}}(n-2(2^{2l+1}-2)).
\end{align*} By Lemma 2.5, for all 
$k\in\mathbb{N}$, we have 
$R_{A_{2l+1}}(k)=R_{B_{2l+1}}(k)$. Then 
$R_{E}(n)=R_{F}(n)$.
If 
$n\in [2^{2l+2}-2, 3\cdot 2^{2l+1}-5]$, then
\begin{align*}
R_{E}(n)&= R_{A_{2l+1}, 2^{2l+1}-2+B_{2l+1}}(n)+R_{2^{2l+1}-2+B_{2l+1}}(n)\\
&\quad+\,R_{A_{2l+1}, 2^{2l+2}-2+(B_{2l+1}\cap [0, 2^{2l+1}-3])}(n)\\
&= R_{A_{2l+1}, B_{2l+1}}(n-(2^{2l+1}-2))+R_{B_{2l+1}}(n-2(2^{2l+1}-2))\\
&\quad+\,R_{A_{2l+1}, B_{2l+1}}(n-(2^{2l+2}-2))
\end{align*}and
\begin{align*}
R_{F}(n)&= R_{B_{2l+1}, 2^{2l+1}-2+A_{2l+1}}(n)+R_{2^{2l+1}-2+A_{2l+1}}(n)\\
&\quad+\,R_{B_{2l+1}, 2^{2l+2}-2+(A_{2l+1}\cap [0, 2^{2l+1}-3])}(n)\\
&=R_{B_{2l+1}, A_{2l+1}}(n-(2^{2l+1}-2))+R_{A_{2l+1}}(n-2(2^{2l+1}-2))\\
&\quad+\,R_{B_{2l+1}, A_{2l+1}}(n-(2^{2l+2}-2)).
\end{align*} By Lemma 2.5, 
$R_{A_{2l+1}}(k)=R_{B_{2l+1}}(k)$ holds for all 
$k\in\mathbb{N}$ and then 
$R_{E}(n)=R_{F}(n)$.
By 
$3\cdot 2^{2l+1}-4=(2^{2l+1}-2)+(2^{2l+2}-2)$ in D, we have
\begin{equation*} R_{C}(3\cdot 2^{2l+1}-4)=1+R_{B_{2l+1}}(2^{2l+1})+R_{A_{2l+1}, B_{2l+1}}(2^{2l+1}-2)\end{equation*}and
\begin{equation*} R_{D}(3\cdot 2^{2l+1}-4)=1+R_{A_{2l+1}}(2^{2l+1})+R_{B_{2l+1}, A_{2l+1}}(2^{2l+1}-2).\end{equation*} Thus 
$R_{C}(3\cdot 2^{2l+1}-4)=R_{D}(3\cdot 2^{2l+1}-4)$.
The necessity of Claim 3 follows from Lemma 2.2 and the sufficiency of Claim 3.
This completes the proof of Claim 3.
Now let
\begin{equation*}C_{1}=C\cap [0, m-1+r_{1}], \quad D_{1}=D\cap [0, m-1+r_{1}].\end{equation*}Then
\begin{equation*}C_{1}\cup D_{1}=[0, m-1+r_{1}], \quad C_{1}\cap D_{1}=\{r_{1}, r_{2}\}.\end{equation*} Moreover, for any integer 
$n\in [0, m-1+r_{1}]$, we have
\begin{align*}
R_{C_{1}}(n)&= |\{(c, c'): c \lt c'\leq n, c, c'\in C_{1}, c+c'=n\}|\\
&= |\{(c, c'): c \lt c'\leq n, c, c'\in C, c+c'=n\}|\\
&= R_{C}(n),
\end{align*}
\begin{align*}
R_{D_{1}}(n)&= |\{(d, d'): d \lt d'\leq n, d, d' \in D_{1}, d+d'=n\}|\\
&= |\{(d, d'): d \lt d'\leq n, d, d' \in D, d+d'=n\}|\\
&= R_{D}(n).
\end{align*} Thus for any integer 
$n\in [0, m-1+r_{1}]$, we have
\begin{equation*}R_{C_{1}}(n)=R_{C}(n)=R_{D}(n)=R_{D_{1}}(n).\end{equation*} Noting that 
$r_{2}\leq m-1$, we see that 
$r_{1}+r_{2}\leq m-1+r_{1}$. By Claim 2, there exists a positive integer l such that 
$r_{1}=2^{2l+1}-2, r_{2}=2^{2l+1}-1$.
Let E and F be as in Claim 3. If 
$m\geq 2^{2l+2}-1$ and 
$0\in C$, then 
$m-1+r_{1}\geq 3\cdot 2^{2l+1}-4$ and
\begin{equation*} C(3\cdot 2^{2l+1}-4)\cup D(3\cdot 2^{2l+1}-4)=[0, 3\cdot 2^{2l+1}-4],\end{equation*}
\begin{equation*} C(3\cdot 2^{2l+1}-4)\cap D(3\cdot 2^{2l+1}-4)=\{2^{2l+1}-2, 2^{2l+1}-1\}.\end{equation*} Moreover, 
$R_{C(3 \cdot 2^{2l+1}-4)}(n)=R_{C}(n)=R_{D}(n)=R_{D(3 \cdot 2^{2l+1}-4)}(n)$ for all 
$n\in [0, 3 \cdot 2^{2l+1}-4]$. By Lemma 2.2, we have
\begin{equation*} C(3\cdot 2^{2l+1}-4)= E,\quad D(3\cdot 2^{2l+1}-4)=F.\end{equation*}By
\begin{equation*} R_{C}(3\cdot 2^{2l+1}-3)=\chi_{C}(3\cdot 2^{2l+1}-3)+R_{A_{2l+1}, B_{2l+1}}(2^{2l+1}-1)+R_{B_{2l+1}}(2^{2l+1}+1)-1,\end{equation*}
\begin{equation*} R_{D}(3\cdot 2^{2l+1}-3)=R_{B_{2l+1}, A_{2l+1}}(2^{2l+1}-1)+R_{A_{2l+1}}(2^{2l+1}+1)-1,\end{equation*} we know that 
$R_{C}(3\cdot 2^{2l+1}-3)=R_{D}(3\cdot 2^{2l+1}-3)$ if and only if 
$\chi_{C}(3\cdot 2^{2l+1}-3)=0$, that is, 
$3\cdot 2^{2l+1}-3 \in D$. Noting that 
$2^{2l+1}-2\in A_{2l+1}, 2^{2l+1}-1\in B_{2l+1}$, 
$3\cdot 2^{2l+1}-2=(2^{2l+1}-1)+(2^{2l+2}-1)$ in C and 
$3\cdot 2^{2l+1}-2=1+(3\cdot 2^{2l+1}-3)$ in D, we obtain
\begin{align*}
R_{C}(3\cdot 2^{2l+1}-2)&=1+\chi_{C}(3\cdot 2^{2l+1}-2)+R_{A_{2l+1}, B_{2l+1}}(2^{2l+1})+R_{B_{2l+1}}(2^{2l+1}+2)\\
&\quad-\,\chi_{A_{2l+1}}(3\cdot 2^{2l+1}-2-(2^{2l+2}-2+2^{2l+1}-1))\\
&=1+\chi_{C}(3\cdot 2^{2l+1}-2)+R_{A_{2l+1}, B_{2l+1}}(2^{2l+1})+R_{B_{2l+1}}(2^{2l+1}+2)
\end{align*}and
\begin{align*}
R_{D}(3\cdot 2^{2l+1}-2)&= 1+R_{B_{2l+1}, A_{2l+1}}(2^{2l+1})+R_{A_{2l+1}}(2^{2l+1}+2)\\
&\quad-\,\chi_{B_{2l+1}}(3\cdot 2^{2l+1}-2-(2^{2l+2}-2+2^{2l+1}-2))\\
&= R_{B_{2l+1}, A_{2l+1}}(2^{2l+1})+R_{A_{2l+1}}(2^{2l+1}+2).
\end{align*} Thus by Lemma 2.5, we have 
$R_{C}(3\cdot 2^{2l+1}-2) \gt R_{D}(3\cdot 2^{2l+1}-2)$, which is impossible. Therefore 
$m\leq 2^{2l+2}-2$.
Now we assume that 
$2^{2l+1} \leq m\leq 2^{2l+2}-3$ and 
$0\in C$. Let
\begin{equation*}M=r_{1}+m=2^{2l+1}-2+m.\end{equation*} Since 
$2^{2l+2}-2\leq M\leq 3\cdot 2^{2l+1}-5$, by Lemma 2.2, we have
\begin{equation}
E(M)\cup F(M)=[0, M], \quad E(M)\cap F(M)=\{2^{2l+1}-2, 2^{2l+1}-1\},
\end{equation}
\begin{equation}
R_{E(M)}(n)=R_{E}(n)=R_{F}(n)=R_{F(M)}(n) \,\text{for any integer } n\in [0, M].
\end{equation}Moreover,
\begin{equation}
C(M) \cup D(M-1)=[0, M],\quad C(M) \cap D(M-1)=\{2^{2l+1}-2, 2^{2l+1}-1\}.
\end{equation} Since 
$R_{C}(n)=R_{D}(n)$ for all 
$n\in\mathbb{N}$ and 
$0\not\in D$, we have
\begin{equation}
R_{C(M)}(n)=R_{C}(n)=R_{D}(n)=R_{D(M-1)}(n)
\end{equation} for any integer 
$n\in [0, M]$. By (3.20)–(3.23) and Lemma 2.2, we have
\begin{equation}
C(M)=E(M), \quad D(M-1)=F(M).
\end{equation} Then 
$\chi_{E}(M)=1$, 
$\chi_{F}(M)=0$.
By 
$2^{2l+1}-3\in A_{2l+1}$, we have 
$3\,\cdot\,2^{2l+1}-5\in F$. Then 
$M \lt 3\,\cdot\,2^{2l+1}-5$. If 
$\chi_{E}(M+1)=1$, then 
$\chi_{F}(M+1)=0$ and 
$C(M+1)=E(M+1), D(M+1)=F(M+1)\cup \{M, M+1\}$. Thus
\begin{align*}
R_{C}(M+1)&= |\{(c, c'): 0\leq c \lt c'\leq M+1, c, c'\in C, c+c'=M+1\}|\\
&= |\{(c, c'): 0\leq c \lt c'\leq M+1, c, c'\in C(M+1), c+c'=M+1\}|\\
&= R_{E(M+1)}(M+1)
\end{align*}and
\begin{align*}
R_{D}(M+1)&= |\{(d, d'): 1\leq d \lt d'\leq M+1, d, d'\in D, d+d'=M+1\}|\\
&= |\{(d, d'): 1\leq d \lt d'\leq M+1, d, d'\in D(M+1), d+d'=M+1\}|\\
&= 1+|\{(d, d'): 1\leq d \lt d'\leq M+1, d, d'\in F(M+1), d+d'=M+1\}|\\
&= 1+R_{F(M+1)}(M+1).
\end{align*} By Claim 3, we have 
$R_{E(M+1)}(M+1)=R_{F(M+1)}(M+1)$. Then 
$R_{C}(M+1)\neq R_{D}(M+1)$, a contradiction. Thus 
$\chi_{E}(M+1)=0$ and 
$\chi_{F}(M+1)=1$.
Let t be an arbitrary positive integer such that 
$M \lt M+t \lt M+t+1\leq 3\cdot 2^{2l+1}-4$. Then 
$1\leq t\leq 2^{2l+1}-3$. Define the sets S and T by
\begin{equation*}S=(E\cap C)(M+t)\cup (F(M+t)\backslash D(M+t)),\end{equation*}
\begin{equation*}T=(F\cap D)(M+t)\cup (E(M+t)\backslash C(M+t)).\end{equation*}Noting that
\begin{equation*}E(M+t)\cup F(M+t)=[0, M+t]=(C(M+t)\backslash \{M+1\})\cup (D(M+t)\backslash \{M\}),\end{equation*}
\begin{equation*}E(M+t)\cap F(M+t)=\{2^{2l+1}-2, 2^{2l+1}-1\},\end{equation*}we have
\begin{equation*}S\subseteq C(M+t)\backslash \{M+1\}, \quad T\subseteq D(M+t)\backslash \{M\},\end{equation*}
\begin{equation*}S\cup T=(C(M+t)\backslash \{M+1\})\cup (D(M+t)\backslash \{M\}),\end{equation*}
\begin{equation*}S\cap T=\{2^{2l+1}-2, 2^{2l+1}-1\}=(C(M+t)\backslash \{M+1\})\cap (D(M+t)\backslash \{M\}).\end{equation*}Then
\begin{equation*}|S|+|T|=|S\cup T|+|S\cap T|=|C(M+t)\backslash \{M+1\}|+|D(M+t)\backslash \{M\}|.\end{equation*}It follows that
\begin{equation}
S=C(M+t)\backslash \{M+1\}, \quad T=D(M+t)\backslash \{M\}.
\end{equation} For 
$M+t\leq n\leq 3\cdot 2^{2l+1}-4$, let
\begin{align*}
N_{1}(t, n)&= R_{E(2^{2l+1}-3), E(M+t)\backslash C(M+t)}(n),\\
N_{2}(t, n)&= R_{F(2^{2l+1}-3), E(M+t)\backslash C(M+t)}(n),\\
N_{3}(t, n)&= R_{E(2^{2l+1}-3), F(M+t)\backslash D(M+t)}(n),\\
N_{4}(t, n)&= R_{F(2^{2l+1}-3), F(M+t)\backslash D(M+t)}(n).
\end{align*}We claim that
\begin{equation}
|E(M+t)\backslash C(M+t)|=N_{1}(t, n)+N_{2}(t, n),
\end{equation}
\begin{equation}
|F(M+t)\backslash D(M+t)|=N_{3}(t, n)+N_{4}(t, n).
\end{equation} In fact, if 
$E(M+t)\backslash C(M+t)=\emptyset$, then 
$N_{1}(t, n)=N_{2}(t, n)=0$; if
\begin{equation*}E(M+t)\backslash C(M+t)=\{c_{1}, \ldots, c_{u}\}\end{equation*} for some positive integer u, then by (3.24), we have 
$c_{i}\geq M+1$ and so 
$0\leq n-c_{i}\leq 2^{2l+1}-3$ for 
$i\in [1, u]$. In view of
\begin{equation*}E(2^{2l+1}-3)\cup F(2^{2l+1}-3)=[0, 2^{2l+1}-3], \quad E(2^{2l+1}-3)\cap F(2^{2l+1}-3)=\emptyset,\end{equation*}we have
\begin{equation*}N_{1}(t, n)+N_{2}(t, n)=\sum\limits_{i=1}^{u}\chi_{E(2^{2l+1}-3)}(n-c_{i})+\sum\limits_{i=1}^{u}\chi_{F(2^{2l+1}-3)}(n-c_{i})=u.\end{equation*}Thus (3.26) holds. Similarly, we can deduce (3.27) holds.
By 
$M+t \lt 3\cdot 2^{2l+1}-4 \lt 2^{2l+3}-4\leq 2M$, we can obtain
\begin{align*} R_{E(M+t)}(n)&=R_{(E\cap C)(M+t)}(n)+R_{E(2^{2l+1}-3), E(M+t)\backslash C(M+t)}(n)\nonumber\\
&=R_{(E\cap C)(M+t)}(n)+N_{1}(t, n).\end{align*}
\begin{align}
R_{C(M+t)}(n)&= R_{C(M+t)\backslash \{M+1\}}(n)+\chi_{C(M+t)\backslash \{M+1\}}(n-M-1)\nonumber\\
&= R_{(E\cap C)(M+t)}(n)+R_{E(2^{2l+1}-3), F(M+t)\backslash D(M+t)}(n)+\chi_{E}(n-M-1)\nonumber\\
&= R_{E(M+t)}(n)-N_{1}(t, n)+N_{3}(t, n)+\chi_{E}(n-M-1).
\end{align}Similarly, we can get
\begin{align}
R_{D(M+t)}(n)&=R_{D(M+t)\backslash \{M\}}(n)+\chi_{D(M+t)\backslash \{M\}}(n-M)\nonumber\\
&=R_{(F\cap D)(M+t)}(n)+R_{F(2^{2l+1}-3), E(M+t)\backslash C(M+t)}(n)+\chi_{F}(n-M)\nonumber\\
&=R_{F(M+t)}(n)-N_{4}(t, n)+N_{2}(t, n)+\chi_{F}(n-M).
\end{align} By choosing 
$n=M+t$ and 
$n=M+t+1$ in (3.28) respectively, we have
\begin{equation}
R_{C(M+t)}(M+t)=R_{E(M+t)}(M+t)-N_{1}(t, M+t)+N_{3}(t, M+t)+\chi_{E}(t-1)
\end{equation}and
\begin{align}
R_{C(M+t+1)}(M+t+1)&= R_{C(M+t)}(M+t+1)+\chi_{C}(M+t+1\nonumber)\\
&=R_{E(M+t+1)}(M+t+1)-\chi_{E}(M+t+1)-N_{1}(t, M+t+1) \nonumber\\
&\quad+\,N_{3}(t, M+t+1)+\chi_{E}(t)+\chi_{C}(M+t+1).
\end{align} By choosing 
$n=M+t$ and 
$n=M+t+1$ in (3.29) respectively, we have
\begin{equation}
R_{D(M+t)}(M+t)=R_{F(M+t)}(M+t)-N_{4}(t, M+t)+N_{2}(t, M+t)+\chi_{F}(t)
\end{equation}and
\begin{align}
R_{D(M+t+1)}(M+t+1)&= R_{D(M+t)}(M+t+1)\nonumber\\
&=R_{F(M+t+1)}(M+t+1)-N_{4}(t, M+t+1) \nonumber\\
&\quad+\,N_{2}(t, M+t+1)+\chi_{F}(t+1).
\end{align} Note that 
$R_{C(n)}(n)=R_{D(n)}(n)$ and 
$R_{E(n)}(n)=R_{F(n)}(n)$. By (3.30)–(3.33), we have
\begin{equation*} N_{1}(t, M+t)+N_{2}(t, M+t)+\chi_{F}(t)=N_{3}(t, M+t)+N_{4}(t, M+t)+\chi_{E}(t-1)\end{equation*}and
\begin{align*}
& N_{1}(t, M+t+1)+N_{2}(t, M+t+1)+\chi_{E}(M+t+1)+\chi_{F}(t+1)\\
&=\ N_{3}(t, M+t+1)+N_{4}(t, M+t+1)+\chi_{E}(t)+\chi_{C}(M+t+1).
\end{align*}
\begin{equation*} |E(M+t)\backslash C(M+t)|+\chi_{F}(t)=|F(M+t)\backslash D(M+t)|+\chi_{E}(t-1)\end{equation*}and
\begin{align*}
& |E(M+t)\backslash C(M+t)|+\chi_{E}(M+t+1)+\chi_{F}(t+1)\\
&=\ |F(M+t)\backslash D(M+t)|+\chi_{E}(t)+\chi_{C}(M+t+1).
\end{align*}Then
\begin{equation}
\chi_{F}(t)+\chi_{E}(t)+\chi_{C}(M+t+1)=\chi_{E}(t-1)+\chi_{E}(M+t+1)+\chi_{F}(t+1).
\end{equation}If M is even, then we can write
\begin{equation*}M=(2^{2l+2}-2)+\sum\limits_{i=1}^{2l}b_{i}2^{i},\end{equation*} where 
$b_{i}\in \{0, 1\}$. It follows from 
$\chi_{F}(M)=0$ that 
$\chi_{B_{2l+1}}\big(\sum\limits_{i=1}^{2l}b_{i}2^{i}\big)=1$. By choosing 
$M+t+1=3\cdot 2^{2l+1}-4$ in (3.34), we see that t is odd and
\begin{equation*}\chi_{F}(t+1)=\chi_{F}\big(2^{21+1}-2-\sum\limits_{i=1}^{2l}b_{i}2^{i}\big)=\chi_{B_{2l+1}}\big(\sum\limits_{i=1}^{2l}(1-b_{i})2^{i}\big)=1.\end{equation*} Then 
$\chi_{E}(t+1)=0$. It follows from 
$\chi_{F}(t)+\chi_{E}(t)=1$ and 
$\chi_{E}(3\cdot 2^{2l+1}-4)=1$ that 
$\chi_{E}(t-1)=0$ and 
$\chi_{F}(t-1)=1$. Since 
$\chi_{E}(t-1)+\chi_{E}(t)=1$, we have 
$\chi_{E}(t)=1$ and 
$\chi_{F}(t)=0$. Noting that 
$\chi_{E}(t-1)=\chi_{E}(t+1)$, we have 
$t\equiv 3\pmod 4$ and so 
$t\geq 3$. Then 
$\chi_{E}(t-2)=0$. By choosing 
$M+(t-1)+1=3\cdot 2^{2l+1}-5$ in (3.34), we have
\begin{equation*}\chi_{F}(t-1)+\chi_{E}(t-1)+\chi_{C}(M+(t-1)+1)=\chi_{E}(t-2)+\chi_{E}(M+(t-1)+1)+\chi_{F}(t).\end{equation*} It follows from 
$\chi_{E}(M+(t-1)+1)=\chi_{E}(3\cdot 2^{2l+1}-5)=0$ that 
$\chi_{C}(M+(t-1)+1)=-1$, which is clearly false.
If M is odd, then we can write
\begin{equation*}M=(2^{2l+2}-2)+\sum\limits_{i=0}^{f}2^{i}+\sum\limits_{i=f+2}^{2l}b_{i}2^{i},\end{equation*} where 
$f\in\{0, 1, \ldots, 2l-1\}$ and 
$b_{i}\in \{0, 1\}$. It follows from 
$\chi_{E}(M+1)=0$ and 
$\chi_{F}(M)=0$ that
\begin{equation*}\chi_{A_{2l+1}}\bigg(2^{f+1}+\sum\limits_{i=f+2}^{2l}b_{i}2^{i}\bigg)=1, \quad \chi_{B_{2l+1}}\bigg(\sum\limits_{i=0}^{f}2^{i}+\sum\limits_{i=f+2}^{2l}b_{i}2^{i}\bigg)=1.\end{equation*} Then f is odd. By choosing 
$M+t+1=3\cdot 2^{2l+1}-4$ in (3.34), we see that t is even and
\begin{equation*}\chi_{F}(t+1)=\chi_{F}\bigg(2^{21+1}-2-\sum\limits_{i=0}^{f}2^{i}-\sum\limits_{i=f+2}^{2l}b_{i}2^{i}\bigg)=\chi_{B_{2l+1}}\big(2^{f+1}-1+\sum\limits_{i=f+2}^{2l}(1-b_{i})2^{i}\big)=1.\end{equation*} Then 
$\chi_{E}(t+1)=0$ and 
$\chi_{F}(t)=0$. Thus 
$\chi_{E}(t)=1$. It follows from 
$\chi_{E}(3\cdot 2^{2l+1}-4)=1$ that 
$\chi_{E}(t-1)=0$ and 
$\chi_{F}(t-1)=1$. Since 
$\chi_{E}(t-1)=\chi_{E}(t+1)$, we have 
$t\equiv 0\pmod 4$ and so 
$t\geq 4$. Then 
$\chi_{E}(t-2)=\chi_{E}(t-3)=1$ and 
$\chi_{F}(t-2)=0$. By choosing 
$M+(t-2)+1=3\cdot 2^{2l+1}-6$ in (3.34), we have
\begin{equation*}\chi_{F}(t-2)+\chi_{E}(t-2)+\chi_{C}(M+(t-2)+1)=\chi_{E}(t-3)+\chi_{E}(M+(t-2)+1)+\chi_{F}(t-1).\end{equation*} It follows from 
$\chi_{E}(M+(t-2)+1)=\chi_{E}(3\cdot 2^{2l+1}-6)=1$ that 
$\chi_{C}(M+(t-2)+1)=2$, which is also impossible. Therefore 
$m=2^{2l+2}-2$.
This completes the proof of Theorem 1.3.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 12371003).
