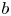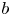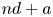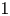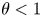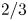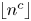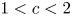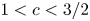1. Introduction
The Thue–Morse sequence 
$\mathbf {t}$ is one of the most easily defined automatic sequences. Like any automatic sequence, it can be defined using a uniform morphism over a finite alphabet: 
$\mathbf {t}$ is the unique fixed point of the substitution 
$\mathtt 0\mapsto \mathtt 0\mathtt 1$, 
$\mathtt 1\mapsto \mathtt 1\mathtt 0$ that starts with 
$\mathtt 0$. Therefore, 
$\mathbf {t}=(\mathtt 0\mathtt 1\mathtt 1\mathtt 0\mathtt 1\mathtt 0\mathtt 0\mathtt 1\mathtt 1\mathtt 0\mathtt 0\mathtt 1\mathtt 0\mathtt 1\mathtt 1\mathtt 0\ldots )$. Alternatively, this sequence can be defined using the binary sum-of-digits function 
$s$, which counts the number of 
$\mathtt 1$s in the binary expansion of a nonnegative integer 
$n$: we have 
$\mathbf {t}(n)=\mathtt 0$ if and only if 
$s(n)\equiv 0\bmod 2$. The equivalence of these two definitions can be proved via a third description: start with the one-element sequence 
$\mathbf {t}^{(0)} := (\mathtt 0)$ and define 
$\mathbf {t}^{(n+1)}$ by concatenating 
$\mathbf {t}^{(n)}$ and the Boolean complement 
$\neg \mathbf {t}^{(n)}$. Then 
$\mathbf {t}$ is the (pointwise) limit of this sequence of finite words. In this work, we will adopt the second viewpoint. In fact, in the proofs we will work with the sequence 
$(-1)^{s(n)}$ instead of 
$\mathbf {t}$, and we also call this sequence the Thue–Morse sequence by slight abuse of notation. When working with exponential sums, we will always use the ‘multiplicative version’ 
$(-1)^{s(n)}$. For an overview on the Thue–Morse sequence, we refer the reader to the article by Allouche and Shallit [Reference Allouche and ShallitAS99], which points out occurrences of this sequence in different fields of mathematics and offers a good bibliography. We also wish to mention the survey paper [Reference MauduitMau01] by Mauduit on the Thue–Morse sequence. For a comprehensive treatment of automatic and morphic sequences, see the book [Reference Allouche and ShallitAS03] by Allouche and Shallit.
The main topic of this article is the study of 
$\mathbf {t}$ along arithmetic progressions and, more generally, along Beatty sequences 
$\lfloor n\alpha +\beta \rfloor$, where 
$\alpha$ and 
$\beta$ are real numbers and 
$\alpha \geq 0$. This topic can be traced back at least to Gel'fond [Reference Gel'fondGel68], who proved the following theorem on the base-
$q$ sum-of-digits function 
$s_q$ defined by 
$s_q(\varepsilon _\nu q^\nu +\cdots +\varepsilon _0q^0)=\varepsilon _\nu +\cdots +\varepsilon _0$ for 
$\varepsilon _i\in \{0,\ldots ,q-1\}$.
Theorem A (Gel'fond) Let 
$q,m,d,b,a$ be integers and 
$q,m,d\geq 2$. Suppose that 
$\gcd (m, q-1)=1$. Then
\[ \lvert\{1\leq n\leq x: n\equiv a\bmod d, s_q(n)\equiv b\bmod m\}\rvert =\frac{x}{dm}+\mathcal{O}(x^\lambda) \]
for some 
$\lambda <1$ independent of 
$x,d,a$ and 
$b$.
We are particularly interested in the error term for sparse arithmetic progressions, having large common difference 
$d$. This leads us directly to the other main concept of this paper, the notion of level of distribution. (We use this term in the same way as Goldston et al. [Reference Goldston, Pintz and YıldırımGPY09]; the term is also used for a very similar concept by other authors. Moreover, the term exponent of distribution is also common.) Very roughly speaking, the level of distribution is a measure of how well a given sequence behaves on arithmetic progressions. A formal definition can be found in the article [Reference Fouvry and MauduitFM96a] by Fouvry and Mauduit. We adapt this definition.
Definition 1 Let 
$c=(c_n)_{n\geq 0}$ be a sequence of complex numbers and, for each integer 
$d\geq 1$, let 
$\mathcal {Q}(d)$ and 
$\mathcal {R}(d)\neq \emptyset$ be subsets of 
$\mathbb {Z}/d\mathbb {Z}$ such that 
$\mathcal {Q}(d)\subseteq \mathcal {R}(d)$. The sequence 
$c$ has level of distribution 
$\theta$ with respect to 
$\mathcal {Q}$ and 
$\mathcal {R}$ if for all 
$\varepsilon >0$ and 
$A>0$ we have for all 
$x\geq 1$ that
\[ \sum_{1\leq d\leq D}\max_{0\leq y\leq x}\max_{\substack{0\leq a < d\\ a+d\mathbb{Z}\in \mathcal{Q}(d)}} \bigg\lvert\sum_{\substack{0\leq n < y\\ n\equiv a \bmod d}}c_n -\frac 1{\lvert \mathcal{R}(d)\rvert}\sum_{\substack{0\leq n < y\\n+d\mathbb{Z}\in \mathcal{R}(d)}}c_n \bigg\rvert\ll (\log 2x)^{{-}A}\sum_{0\leq n < x}\lvert c_n\rvert, \]
where 
$D=x^{\theta -\varepsilon }$. The implied constant may depend on 
$A$ and 
$\varepsilon$. In this definition, the maximum over the empty index set is defined to be 
$0$.
The most well-known cases are 
$\mathcal {R}(d)=\mathbb {Z}/d\mathbb {Z}$ or 
$\mathcal {R}(d)=(\mathbb {Z}/d\mathbb {Z})^\ast$; the treatment of the main term
\[ \frac 1{\lvert \mathcal{R}(d)\rvert}\sum_{\substack{0\leq n < y\\ n+d\mathbb{Z}\in \mathcal{R}(d)}}c_n \]
is usually the easy part of an estimate as in the definition. In the case of the Bombieri–Vinogradov theorem, we use 
$\mathcal {R}(d)=(\mathbb {Z}/d\mathbb {Z})^\ast$, since the prime numbers are distributed evenly in the residue classes relatively prime to 
$d$. The summands in Definition 1 measure the maximal deviation of a sum over an arithmetic progression from the expected value, where the maximum is taken over a set 
$\mathcal {Q}(d)$ of residue classes and the length of the progression may also vary.
The level of distribution is an important concept in sieve theory. As a striking application, a variant of this concept was used in the paper by Zhang [Reference ZhangZha14] on bounded gaps between primes. For more information on this subject, we refer the reader to the survey by Kontorovich [Reference KontorovichKon14]. Moreover, we wish to draw the attention of the reader to the book [Reference Friedlander and IwaniecFI10] on sieve theory by Friedlander and Iwaniec, in particular Chapter 22 on the level of distribution.
We are ready to present our main result. Note that we use 
$\mathcal {O}_\varepsilon$ to indicate that the implied constant may depend on 
$\varepsilon$.
Theorem 1.1 The Thue–Morse sequence has level of distribution 
$1$ with respect to 
$\mathcal {Q}$ and 
$\mathcal {R}$ given by 
$\mathcal {Q}(d)=\mathcal {R}(d)=\mathbb {Z}/d\mathbb {Z}$. More precisely, for all 
$\varepsilon >0$, we have
\[ \sum_{1\leq d\leq D}\max_{\substack{y,z\geq 0\\ z-y\leq x}} \max_{0\leq a < d}\bigg\lvert\sum_{\substack{y\leq n < z\\n\equiv a\bmod d}}({-}1)^{s(n)} \bigg\rvert=\mathcal{O}_\varepsilon(x^{1-\eta}) \]
for some 
$\eta >0$ depending on 
$\varepsilon$, where 
$D=x^{1-\varepsilon }$.
Before presenting some history, we wish to say a word about the proof: we are going to reduce the problem to the estimation of a certain Gowers uniformity norm of the Thue–Morse sequence. These expressions appear by repeated application of Van der Corput's inequality and have the form
\[ \sum_{\substack{0\leq n<2^\rho\\ 0\leq r_1,\ldots,r_k< 2^\rho}} \prod_{\varepsilon\in\{0,1\}^k}({-}1)^{s_\rho(n+\varepsilon\cdot r)}, \]
where 
$\varepsilon \cdot r=\sum _{1\leq i\leq k}\varepsilon _ir_i$ and 
$s_\rho$ is the truncated sum-of-digits function in base 
$2$ defined by 
$s_\rho (n)=s(n\bmod 2^\rho )$. Note that, strictly speaking, this is not the Gowers norm of the Thue–Morse sequence, but the Gowers norm of order 
$k$ of the projection of 
$(-1)^{s(n)}$ to 
$\mathbb {Z}/2^\rho \mathbb {Z}$. The proof of a very similar statement was given recently by Konieczny [Reference KoniecznyKon19], and we use the proof from that paper to prove our estimate.
Gowers norms are certain averaged multiple correlations and were introduced by Gowers [Reference GowersGow98, Reference GowersGow01], who used them to give a new proof of Szemerédi's theorem. These norms are a central tool in higher order Fourier analysis [Reference TaoTao12]; this theory can be used to study questions in additive combinatorics, such as the behaviour of an arithmetic function 
$f$ on arithmetic progressions 
$n,n+d,n+2d,\ldots ,n+(\ell -1)d$. In the ground-breaking paper [Reference Green and TaoGT08] by Green and Tao, Gowers norms were used to prove the existence of arbitrarily long arithmetic progressions in the primes. Our result is a statement on arithmetic progressions too; although it is different in nature, Gowers norms are applicable here.
In order to put Theorem 1.1 into context, we present some related theorems. The well-known Bombieri–Vinogradov theorem concerns the level of distribution of the von Mangoldt function 
$\Lambda$, which is defined by 
$\Lambda (n)=\log p$ if 
$n=p^\ell$ for some prime 
$p$ and some 
$\ell \geq 1$ and 
$\Lambda (n)=0$ otherwise. This theorem states that 
$\Lambda$ has level of distribution 
$1/2$ with respect to 
$\mathcal {Q}$ and 
$\mathcal {R}$ given by 
$\mathcal {Q}(d)=\mathcal {R}(d)=(\mathbb {Z}/d\mathbb {Z})^*$.
Theorem B (Bombieri–Vinogradov) Let 
$d\geq 1$ and 
$a$ be integers and define
\[ \psi(x;d,a) = \sum_{\substack{1\leq n\leq x\\n\equiv a\bmod d}}\Lambda(n). \]
For all real numbers 
$A>0$ there exist 
$B>0$ and a constant 
$C$ such that setting 
$D=x^{1/2}(\log x)^{-B}$ we have for all 
$x\geq 2$
\[ \sum_{1\leq d\leq D}\max_{1\leq y\leq x} \max_{\substack{0\leq a < d\\ \gcd(a,d)=1}} \bigg\lvert\psi(y;d,a)-\frac y{\varphi(d)}\bigg\rvert\leq Cx(\log x)^{{-}A}. \]
Here 
$\varphi$ denotes Euler's totient function.
No improvement on the level of distribution 
$1/2$ in this theorem is currently known. Meanwhile the Elliott–Halberstam conjecture [Reference Elliott and HalberstamEH70] states that we can choose 
$D=x^{1-\varepsilon }$ for any 
$\varepsilon >0$. That is, it is conjectured that the primes have level of distribution 
$1$. Improvements on the exponent 
$1/2$ exist for certain sequences of integers; we refer to the articles [Reference FouvryFou82, Reference FouvryFou84] by Fouvry, [Reference Fouvry and IwaniecFI80] by Fouvry and Iwaniec and [Reference Friedlander and IwaniecFI85] by Friedlander and Iwaniec. Moreover, we mention the series [Reference Bombieri, Friedlander and IwaniecBFI86, Reference Bombieri, Friedlander and IwaniecBFI87, Reference Bombieri, Friedlander and IwaniecBFI89] by Bombieri et al. concerning this topic. In this context, we also note the result of Goldston et al. [Reference Goldston, Pintz and YıldırımGPY09], who showed in particular the following conditional result: if the primes have level of distribution 
$\theta$ for some 
$\theta >1/2$, then there exists a constant 
$C$ such that 
$p_{n+1}-p_n < C$ infinitely often, where 
$p_n$ is the 
$n$th prime. In a ground-breaking paper we mentioned before, Zhang [Reference ZhangZha14] used the Goldston et al. method and a variant of the Bombieri–Vinogradov theorem to prove the above result unconditionally. Maynard [Reference MaynardMay15] later proved the bounded gaps result using only the classical Bombieri–Vinogradov theorem.
Improvements on the level 
$1/2$ are also known for the sum-of-digits function modulo 
$m$. Fouvry and Mauduit [Reference Fouvry and MauduitFM96b] established 
$0.5924$ as a level of distribution of the Thue–Morse sequence, with respect to 
$\mathcal {Q}$ and 
$\mathcal {R}$, where 
$\mathcal {Q}(d)=\mathcal {R}(d)=\mathbb {Z}/d\mathbb {Z}$.
Theorem C (Fouvry–Mauduit) Set
\[ A(x;d,a)=\lvert\{0\leq n < x:\mathbf{t}(n)=\mathtt 0, n\equiv a\bmod d\}\rvert. \]Then
\begin{equation} \sum_{1\leq d\leq D}\max_{1\leq y\leq x}\max_{0\leq a < d} \bigg \lvert A(y;d,a)-\frac y{2d} \bigg \rvert \leq Cx(\log 2x)^{{-}A} \end{equation}
for all real 
$A$ and 
$D=x^{0.5924}$, where 
$C$ may depend on 
$A$.
More generally, for 
$m\geq 2$, they also studied the sum-of-digits function in base 
$2$ modulo 
$m$, obtaining the weaker level of distribution 
$0.55711$. Using sieve theory, they applied this result to the study of the sum of digits modulo 
$m$ of numbers having at most two prime factors. Later, Mauduit and Rivat [Reference Mauduit and RivatMR10], in an important paper, managed to treat the sum of digits modulo 
$m$ of prime numbers, thereby answering one of the questions posed by Gel'fond [Reference Gel'fondGel68].
Müllner and the author [Reference Müllner and SpiegelhoferMS17] improved the exponent 
$0.5924$ to 
$2/3-\varepsilon$, thereby establishing 
$2/3$ as an admissible level of distribution of the Thue–Morse sequence.
Fouvry and Mauduit [Reference Fouvry and MauduitFM96a] also considered, more generally, the sum-of-digits function 
$s_q$ in base 
$q$ modulo an integer 
$m$ such that 
$\gcd (m,q-1)=1$. They obtained the result that the level of distribution approaches 
$1$ as the base 
$q$ gets larger.
Theorem D (Fouvry–Mauduit) Let 
$q\geq 2$, 
$m\geq 1$ and 
$b$ be integers such that 
${\gcd (m,q-1)=1}$. There exists 
$\theta _q>0$ such that for all 
$A$ and 
$\varepsilon >0$ we have for all 
$x\geq 1$
\[ \sum_{1\leq d\leq D}\max_{0\leq y\leq x}\max_{0\leq a < d} \bigg\lvert\sum_{\substack{n < y,s_q(n)\equiv b\bmod m\\n\equiv a\bmod d}}1- \frac 1d\sum_{n < y,s_q(n)\equiv b\bmod m}1\bigg\rvert =\mathcal{O}_{m,q,A,\varepsilon}(x(\log 2x)^{{-}A}), \]
where 
$D=x^{\theta _q-\varepsilon }$. The implied constant depends at most on 
$m$, 
$q$, 
$A$ and 
$\varepsilon$. As 
$q\rightarrow \infty$, the value of 
$\theta _q$ tends to 
$1$.
As an application of this theorem, they considered the sum of digits in base 
$q$ of integers having at most two prime factors; moreover, they studied the sum 
$\sum _{n < x,s_q(n)\equiv b\bmod m}\Lambda _\ell (n)$, where 
$\Lambda _\ell$ is the generalized von Mangoldt function of order 
$\ell \geq 2$ [Reference Fouvry and MauduitFM96a, Corollaire 2].
Theorem D motivates us to look for sequences having level of distribution equal to 
$1$. In the paper by Fouvry and Mauduit [Reference Fouvry and MauduitFM96a] cited above, for example, a list of sequences having this property is given. Also, we note [Reference Friedlander and IwaniecFI10, Chapter 22.3], which studies the level of distribution for additive convolutions, giving further examples. However, in these examples, other than the trivial example 
$c_n=1$ for all 
$n$, the maximum over 
$a$ does not play a rôle: the set 
$\mathcal {Q}(d)$ consists of at most one element.
We are interested in sequences 
$c$ having level of distribution 
$1$ and such that the set 
$\mathcal {Q}(d)$ contains ‘many’ residue classes. In other words, we want to find analogues of the Elliott–Halberstam conjecture. Requiring monotonicity of 
$c$, examples can be constructed easily: 
$c(n)=n$ is such an example and, more generally, increasing sequences 
$c$ satisfying certain growth conditions have this property. Apart from such ‘trivial’ sequences, no other examples seem to be known. Our Theorem 1.1, giving such an example, might therefore be of interest.
We believe that our method can be adapted to 
$s_q(n)\bmod m$ for all 
$m\geq 1$ and general bases 
$q\geq 2$, which would yield 
$\theta _q=1$ for all 
$q\geq 2$ in Theorem D.
The second focus of this paper concerns Piatetski-Shapiro sequences, which are sequences of the form 
$(\lfloor n^c\rfloor )_{n\geq 0}$ for some 
$c\geq 1$. In order to state the second main theorem, we do not need additional preparation.
Theorem 1.2 Let 
$1 < c < 2$. The Thue–Morse sequence along 
$\lfloor n^c\rfloor$ is simply normal. That is, each of the letters 
$\mathtt 0$ and 
$\mathtt 1$ appears with asymptotic frequency 
$1/2$ in 
$n\mapsto \mathbf {t}(\lfloor n^c\rfloor )$.
In our earlier paper [Reference Müllner and SpiegelhoferMS17] with Müllner, this theorem is proved via a Beatty sequence variant of Theorem 1.1. That theorem in turn is proved by arguments analogous to the arguments in the proof of Theorem 1.1 and reduces to the same estimate of the Gowers uniformity norm of Thue–Morse. Theorem 1.2 is therefore an application of the method of proof of Theorem 1.1.
Again, we present some historical background. Studying Piatetski-Shapiro subsequences of a given sequence can be seen as a step towards proving theorems on polynomial subsequences. For example, it is unknown whether there are infinitely many primes of the form 
$n^2+1$; therefore, it is of interest to consider primes of the form 
$\lfloor n^c\rfloor$ for 
$1 < c < 2$ and prove an asymptotic formula for the number of such primes. Piatetski-Shapiro [Reference Piatetski-ShapiroPia53] proved such a formula for 
$1 < c < 12/11$, and the currently best known bound is 
$1 < c < 2817/2426$ due to Rivat and Sargos [Reference Rivat and SargosRS01]. In a similar way, the study of the sum-of-digits function along 
$\lfloor n^c\rfloor$ can be justified. It is another problem posed by Gel'fond [Reference Gel'fondGel68] to study the distribution of the sum of digits of polynomial sequences in residue classes. Since this problem could not be solved at first, Mauduit and Rivat [Reference Mauduit and RivatMR95, Reference Mauduit and RivatMR05] considered 
$q$-multiplicative functions along 
$\lfloor n^c\rfloor$ (where a 
$q$-multiplicative function 
$f:\mathbb {N}\rightarrow \{z\in \mathbb {C}:\lvert z\rvert =1\}$ satisfies 
$f(aq^m+b)=f(aq^m)f(b)$ for nonnegative integers 
$a,b,m$ such that 
$b < q^m$) and they obtained an asymptotic formula for 
$c < 7/5$.
Theorem E (Mauduit–Rivat) Let 
$1 < c < 7/5$ and set 
$\gamma =1/c$. For all 
$\delta \in (0,(7-5c)/9)$ there exists a constant 
$C > 0$ such that for all 
$q$-multiplicative functions 
$f:\mathbb {N}\rightarrow \{z\in \mathbb {C}:\lvert z\rvert =1\}$ and all 
$x\geq 1$ we have
\[ \bigg\lvert\sum_{1\leq n\leq x}f(\lfloor n^c\rfloor) -\sum_{1\leq m\leq x^c}\gamma m^{\gamma-1}f(m)\bigg\rvert\leq Cx^{1-\delta}. \] Since the Thue–Morse sequence is 
$2$-multiplicative, it follows in particular that the subsequence indexed by 
$\lfloor n^c\rfloor$ assumes each of the two values 
$\mathtt 0$, 
$\mathtt 1$ with asymptotic frequency 
$1/2$, as long as 
$1 < c < 7/5$. This means that this subsequence is simply normal. In the paper [Reference Deshouillers, Drmota and MorgenbesserDDM12] by Deshouillers et al., a statement as in Theorem E for arbitrary automatic sequences and 
$1 < c < 7/5$ is proved. Moreover, we wish to note the paper [Reference MorgenbesserMor11] by Morgenbesser, who proved uniform distribution of 
$s_q(\lfloor n^c\rfloor )$ in residue classes for all noninteger 
$c > 0$, as long as the base 
$q$ is large enough (depending on 
$c$).
Some progress on Gel'fond's question on polynomials was made by Drmota and Rivat [Reference Drmota and RivatDR05] and by Dartyge and Tenenbaum [Reference Dartyge and TenenbaumDT06]; finally, Mauduit and Rivat [Reference Mauduit and RivatMR09] managed to answer Gel'fond's question for the polynomial 
$n^2$. This latter paper was generalized by Drmota et al. [Reference Drmota, Mauduit and RivatDMR19], who showed that in fact 
$\mathbf {t}(n^2)$ defines a normal sequence, by which we understand an infinite sequence on 
$\{\mathtt 0,\mathtt 1\}$ such that every finite sequence of length 
$L$ occurs as a factor (contiguous finite subsequence) with asymptotic frequency 
$2^{-L}$. This result also generalizes a paper by Moshe [Reference MosheMos07], who showed that every finite word on 
$\{\mathtt 0,\mathtt 1\}$ occurs as a factor of 
$n\mapsto \mathbf {t}(n^2)$ at least once.
However, the distribution of the sum of digits of 
$\lfloor n^c\rfloor$ in residue classes, for 
$c\in [7/5,2)$, remained an open problem. Progress in this direction was made by the author [Reference SpiegelhoferSpi14], who improved the bound on 
$c$ to 
$1 < c\leq 1.42$ for the Thue–Morse sequence. The key idea in that paper is to approximate 
$\lfloor n^c\rfloor$ by a Beatty sequence 
$\lfloor n\alpha +\beta \rfloor$ and thus reduce the problem to a linear one. Müllner and the author [Reference Müllner and SpiegelhoferMS17], using the same linearization argument and a Bombieri–Vinogradov-type theorem for the Thue–Morse sequence on Beatty sequences, were able to extend this range to 
$1 < c < 3/2$. In that paper, we also handled occurrences of factors in Piatetski-Shapiro subsequences of 
$\mathbf {t}$, thus showing that 
$\mathbf {t}(\lfloor n^c\rfloor )$ defines a normal sequence for 
$1 < c < 3/2$.
Theorem F (Müllner–Spiegelhofer) Let 
$1 < c < 3/2$. Then the sequence 
$\mathbf {u}=(\mathbf {t}(\lfloor n^c\rfloor ))_{n\geq 0}$ is normal. More precisely, for any 
$L\geq 1$ there exist an exponent 
$\eta > 0$ and a constant 
$C$ such that
\[ \big\lvert \lvert\{n < N:\mathbf{u}(n+i)=\omega_i\textrm{ for }0\leq i < L\}\rvert-N/2^L\big\rvert\leq CN^{1-\eta} \]
for all 
$(\omega _0,\ldots ,\omega _{L-1})\in \{\mathtt 0,\mathtt 1\}^L$.
This theorem also improved on an earlier result by the author [Reference SpiegelhoferSpi15], who obtained normality for 
$1 < c < 4/3$, using an estimate for Fourier coefficients related to the Thue–Morse sequence provided by Drmota et al. [Reference Drmota, Mauduit and RivatDMR19].
Our Theorem 1.2 finally closes the gap in the set of exponents 
$c$ such that we have an asymptotic formula for Thue–Morse on 
$\lfloor n^c\rfloor$. This gap appeared with the Mauduit–Rivat result on squares [Reference Mauduit and RivatMR09]; at that time, the gap was 
$[7/5,2)$: now, after our paper with Müllner [Reference Müllner and SpiegelhoferMS17], it was only left to close the smaller gap 
$[3/2,2)$.
However, the case 
$c > 2$ remains open for now for 
$c\in \mathbb {Z}$ (which is contained in Gel'fond's problem on polynomial subsequences) as well as for Piatetski-Shapiro sequences. For example, it is a notorious open question to prove that 
$\mathtt 0$ occurs with frequency 
$1/2$ in 
$n\mapsto \mathbf {t}(n^3)$.
Mauduit [Reference MauduitMau01, Conjecture 1] conjectured that
\[ \lim_{N\rightarrow\infty}\frac 1N \{1\leq n\leq N:s_q(\lfloor n^c\rfloor)\equiv b\bmod m\}=\frac 1m \]
for almost all 
$c > 1$ with respect to Lebesgue measure, where 
$q\geq 2$, 
$m\geq 1$ and 
$b$ are integers. While this almost-all result is known for 
$1 < c < 2$, as he notes just before this conjecture, we believe (as we noted before) that our method can be adapted to generalize our results to general sequences 
$s_q(n) \bmod m$ and thus to prove the asymptotic identity for all 
$c\in (1,2)$. However, while we are confident that the asymptotic identity in Mauduit's conjecture holds for all noninteger 
$c > 1$, the case 
$c > 2$ cannot yet be handled by our methods.
We note that it would definitely be interesting to generalize the normality result from Theorem F to all exponents 
$1 < c < 2$.
Notation. For a real number 
$x$, we write 
$e(x)=\exp (2\pi i x)$, 
$\{x\}=x-\lfloor x\rfloor$, 
$\lVert x\rVert =\min _{n\in \mathbb {Z}}\lvert x-n\rvert$ and 
$\langle \cdot \rangle =\lfloor x+1/2\rfloor$ (the ‘nearest integer’ to 
$x$). For a prime number 
$p$ let 
$\nu _p(n)$ be the exponent of 
$p$ in the prime factorization of 
$n$. We define the truncated binary sum-of-digits function
\[ s_\lambda(n) := s(n'), \]
where 
$0\leq n'<2^\lambda$ and 
$n'\equiv n\bmod 2^\lambda$, which is the 
$2^\lambda$-periodic extension of the restriction of 
$s$ to 
$\{0,\ldots ,2^\lambda -1\}$. For 
$\mu \leq \lambda$ we define the two-fold restricted binary sum-of-digits function
\[ s_{\mu,\lambda}(n)=s_\lambda(n)-s_\mu(n). \]
For a real number 
$x\geq 0$ we set
\[ \log^+\! x=\max\{1,\log x\}. \]
The symbol 
$\mathbb {N}$ denotes the set of nonnegative integers.
Constants implied by the symbols 
$\ll$ and 
$\mathcal {O}$ may depend on the variable 
$k$ (which describes the number of times that we apply Van der Corput's inequality), but are otherwise absolute. Exceptions to this rule will be indicated in the text.
2. Results
In order to (re)state our main theorem, we introduce some notation. Let 
$\alpha ,\beta ,y$ and 
$z$ be nonnegative real numbers such that 
$\alpha \geq 1$. We define
\[ A(y,z;\alpha,\beta)=\lvert\{y\leq m < z:\mathbf{t}(m)=\mathtt 0\text{ and } \exists n\in\mathbb{Z}\text{ such that }m=\lfloor n\alpha+\beta\rfloor\}\rvert. \]
For integers 
$d=\alpha$ and 
$a=\beta$, we clearly have
\[ A(y,z;d,a)=\lvert\{y\leq m < z:\mathbf{t}(m)=\mathtt 0\textrm{ and } m\equiv a\bmod d\}\rvert. \]Our main theorem is the following result.
Theorem 2.1 Let 
$\varepsilon > 0$. There exist 
$\eta > 0$ and 
$C$ such that
\[ \sum_{1\leq d\leq D}\max_{\substack{y,z\geq 0\\z-y\leq x}}\max_{0\leq a < d} \bigg\lvert A(y,z;d,a) - \frac{z-y}{2d} \bigg\rvert \leq Cx^{1-\eta} \]
for all 
$x\geq 1$ and 
$D=x^{1-\varepsilon }$.
Note that this theorem allows intervals 
$[y,z)$ for arbitrary 
$y\geq 0$, which is more general than our definition of a level of distribution. Noting that 
$1-2\mathbf {t}(n)=(-1)^{s(n)}$, we obtain the form of this theorem given in the introduction.
As a corollary we obtain an estimate for the least element 
$m$ in an arithmetic progression such that 
$\mathbf {t}(m)=\mathtt 1$. For most common differences 
$d$, we do not have to search for a long time until we encounter the first 
$\mathtt 1$.
Corollary 2.2 For 
$d\geq 1$ and 
$a\geq 0$ we define
\[ m(d,a)=\min\{n\in\mathbb{N}:\mathbf{t}(nd+a)=\mathtt 1\}. \]
For each 
$\varepsilon >0$ we have, as 
$D\rightarrow \infty$,
\[ \Big\lvert\Big\{d < D:\max_{a\geq 0}m(d,a)\geq d^\varepsilon\Big\}\Big\rvert=o(D). \] We note that Dartyge and Tenenbaum considered (among many other things) the homogeneous problem concerning 
$a=0$: they proved in particular [Reference Dartyge and TenenbaumDT06, Théorème 2.5] that for any function 
$\xi (d)$ tending to 
$\infty$, we have 
$m(d,0)\leq \xi (d)$ for almost all 
$d$ in the sense of asymptotic density. The added value of our corollary lies in the fact that the maximum is taken over all arithmetic progressions having a given common difference and a given number of terms. We also wish to note that Morgenbesser et al. [Reference Morgenbesser, Shallit and StollMSS11] proved in particular that 
$m(d,0)\leq d+4$ for all nonnegative integers 
$d$.
Our second result concerns Piatetski-Shapiro subsequences of the Thue–Morse sequence.
Theorem 2.3 Let 
$1 < c < 2$. Then the sequence 
$n\mapsto \mathbf {t}(\lfloor n^c\rfloor )$ is simply normal. More precisely, there exist an exponent 
$\eta > 0$ and a constant 
$C$ such that
\[ \bigg\lvert\frac 1N\lvert\{0\leq n < N:\mathbf{t}(\lfloor n^c\rfloor)=\mathtt 0\}\rvert- \frac 12\bigg\rvert\leq CN^{-\eta}. \] In order to prove this theorem, we use the general argument presented in § 4.2 of [Reference Müllner and SpiegelhoferMS17]. This argument uses linear approximation of 
$\lfloor n^c\rfloor$ by 
$\lfloor n\alpha +\beta \rfloor$ and thus reduces the problem to Beatty sequences. Therefore, Theorem 2.3 is a corollary of the following Beatty sequence version of a statement on the level of distribution.
Theorem 2.4 Let 
$0 < \theta _1\leq \theta _2<1$. There exist 
$\eta > 0$ and 
$C$ such that
\[ \int_{D}^{2D}\max_{\substack{y,z\geq 0\\z-y\leq x}}\max_{\beta\geq 0} \bigg\lvert A(y,z;\alpha,\beta) - \frac{z-y}{2\alpha} \bigg\rvert\, d\alpha \leq Cx^{1-\eta} \]
for all 
$x$ and 
$D$ such that 
$x\geq 1$ and 
$x^{\theta _1}\leq D\leq x^{\theta _2}$.
In order to derive Theorem 2.3 from this result, it is essential that we have the maximum over 
$\beta$ inside the integral over 
$\alpha$, since we need to approximate 
$\lfloor n^c\rfloor$ by inhomogeneous (shifted) Beatty sequences 
$\lfloor n\alpha +\beta \rfloor$.
Concerning Theorem 2.1, we can obtain a weakened version of this result, without the maximum over 
$a$, using Martin et al. [Reference Martin, Mauduit and RivatMMR14].
Remark. Martin et al. [Reference Martin, Mauduit and RivatMMR14, Proposition 3] proved an estimate of a sum of type II containing the following special case: let 
$a_m$ and 
$b_n$ be complex numbers satisfying 
$\lvert a_m\rvert \leq 1$ and 
$\lvert b_n\rvert \leq 1$. Assume that 
$x\geq 2$, 
$0 < \varepsilon \leq 1/2$, 
$x^\varepsilon \leq M,N\leq x$ and 
$MN\leq x$. Then
\[ S_0=\sum_{M < m\leq 2M}\sum_{\substack{N < n\leq 2N\\mn\leq x}} a_mb_n ({-}1)^{s(mn)}\leq Cx^{1-\eta} \]
for an absolute constant 
$C$ and some 
$\eta > 0$ only depending on 
$\varepsilon$. By dyadic decomposition and using the trivial estimate for 
$n < x^\varepsilon$, we obtain
\[ \sum_{M < m\leq 2M}\bigg\lvert\sum_{\substack{0\leq n\leq 2N\\mn\leq x}} ({-}1)^{s(mn)}\bigg \rvert\ll_\varepsilon x^{1-\eta}\log N+Mx^\varepsilon \]
for 
$M$ and 
$N$ satisfying the same restrictions and with an implied constant that may depend on 
$\varepsilon$. Let 
$x$ be given and assume that 
$x^\varepsilon \leq M\leq x^\theta$ for some 
$\theta \in (1/2,1)$. Set 
$\varepsilon =1-\theta \leq 1/2$ and 
$N=x/M$. Then 
$N\geq x^\varepsilon$ and the condition 
$mn\leq x$ implies that 
$n\leq 2N$. Using dyadic decomposition again, this time in the variable 
$m$, we obtain
\[ \sum_{x^\varepsilon < m\leq D} \bigg \lvert\sum_{\substack{0\leq u\leq x\\u\equiv 0\bmod m}}({-}1)^{s(u)}\bigg \rvert \ll_\varepsilon x^{1-\eta}\log^2x+Mx^{\varepsilon}\log x \]
for 
$D=x^\theta$. Finally, we use Fouvry and Mauduit [Reference Fouvry and MauduitFM96b] in order to handle residue classes having small modulus 
$m$, that is, 
$m\leq x^\varepsilon$. We note (as we did in [Reference Müllner and SpiegelhoferMS17]) that the error term in their estimate [Reference Fouvry and MauduitFM96b, (1.6)] is in fact 
$x^{1-\eta }$ for some 
$\eta > 0$; this follows from Théorème 2 in the same paper [Reference Fouvry and MauduitFM96b]. We obtain
\[ \sum_{1\leq d\leq D} \bigg \lvert\sum_{\substack{0\leq u\leq x\\ n\equiv 0\bmod d}}({-}1)^{s(u)}\bigg \rvert \leq C x^{1-\eta} \]
for 
$D=x^\theta$ and some 
$\eta > 0$ and 
$C$ depending on 
$\theta$. This is a weak version of a statement of the type ‘the Thue–Morse sequence has level of distribution 
$1$’, where 
$\mathcal {Q}(d)$ has only one element. We note that we could also handle the maximum over 
$y\leq x$, using the factor 
$e(\beta mn)$ that appears in [Reference Martin, Mauduit and RivatMMR14, Proposition 3]. The added value of our paper (compare also to the remark after Corollary 2.2) lies in the maximum over the residue classes modulo 
$d$.
Finally, we note the following open questions concerning Theorems 2.1 and 2.3.
(i) In Theorem 2.1, can we choose
$D=x(\log x)^{-B}$ for some $B>0$, using $x(\log x)^{-A}$ as error term?(ii) Does Theorem 2.3 hold for
$\lfloor x^2(\log x)^{-C}\rfloor$ (and similar sequences, possibly with a worse error term) in place of $\lfloor x^c\rfloor$?
Plan of the paper. In § 3 we state two results (Propositions 3.1 and 3.2) from which Theorems 2.1 and 2.4 follow; moreover, we prove an important Gowers uniformity norm estimate for the Thue–Morse sequence in Proposition 3.3. We also give an idea of the proof of Proposition 3.1. Using Proposition 3.1, the proof of Corollary 2.2 is very short and we present it in that section. In § 4 we state lemmas needed for proving the results from § 3. Section 5 is devoted to proving Propositions 3.1 and 3.2. Finally, in §§ 5.1 and 5.2, we prove Proposition 3.3 and a technical lemma appearing in the proof of Propositions 3.1 and 3.2.
3. Auxiliary results
It will be sufficient to prove the following two propositions in order to obtain our main theorems. To see this, we follow our earlier paper with Müllner [Reference Müllner and SpiegelhoferMS17, Section 4.1] and Fouvry and Mauduit [Reference Fouvry and MauduitFM96b] for handling small 
$d$. In fact, as we noted before, their Théorème 2 holds with an improved error term. Moreover, the proof of this result also reveals that the result holds for arbitrarily shifted intervals 
$[y,z)$.
Proposition 3.1 For real numbers 
$N,D\geq 1$ and 
$\xi$ set
\begin{equation} S_0 = S_0(N,D,\xi)=\sum_{D\leq d < 2D} \max_{a\geq 0}\bigg \lvert \sum_{0\leq n < N} e\bigg(\frac 12s(nd+a)\bigg)e(n\xi) \bigg \rvert. \end{equation}
Let 
$\rho _2\geq \rho _1 > 0$. There exist an 
$\eta > 0$ and a constant 
$C$ such that
\begin{equation} \frac{S_0}{ND} \leq CN^{-\eta} \end{equation}
holds for all 
$\xi \in \mathbb {R}$ and all real numbers 
$N,D\geq 1$ satisfying 
$N^{\rho _1}\leq D \leq N^{\rho _2}$.
With the help of this proposition, it is not difficult to prove Corollary 2.2: we have 
$\lvert \{d\in [D,2D):\max _{a\geq 0}m(d,a)\geq N\}\rvert \leq CDN^{-\eta }$ for all 
$N,D$ such that 
$N^{\rho _1}\leq D\leq N^{\rho _2}$ and some 
$C > 0$, 
$\eta > 0$. This is the case since we cannot have more than 
$CDN^{-\eta }$ many trivial sums in the expression 
$S_0$; this means that for each nontrivial summand we encounter at least one 
$\mathtt 1$ for each 
$a$. It follows that 
$\lvert \{d\in [D,2D):\max _{a\geq 0}m(d,a)\geq D^\varepsilon \}\rvert \leq CD^{1-\eta '}$ for all 
$\varepsilon > 0$. By dyadic decomposition the statement of the corollary follows.
Proposition 3.2 For real numbers 
$D,N\geq 1$ and 
$\xi$ set
\begin{equation} S_0 = S_0(N,D,\xi)=\int_{D}^{2D}\max_{\beta\geq 0}\bigg \lvert \sum_{0\leq n < N}e\bigg(\frac 12s(\lfloor n\alpha+\beta\rfloor)\bigg)e(n\xi) \bigg \rvert \, d \alpha. \end{equation}
Let 
$\rho _2\geq \rho _1>0$. There exist 
$\eta > 0$ and a constant 
$C$ such that
\begin{equation} \frac{S_0}{ND}\leq CN^{-\eta} \end{equation}
holds for all real numbers 
$D,N\geq 1$ satisfying 
$N^{\rho _1}\leq D \leq N^{\rho _2}$ and for all 
$\xi \in \mathbb {R}$.
In the proof of these results, we will use the following essential estimate of a Gowers uniformity norm of the Thue–Morse sequence (see Konieczny [Reference KoniecznyKon19]).
Proposition 3.3 Let 
$k\geq 2$ be an integer. There exist some 
$\eta >0$ and some 
$C$ such that
\[ \frac 1{2^{(k+1)\rho}} \sum_{\substack{0\leq n < 2^\rho\\0\leq r_1,\ldots,r_k < 2^\rho}} e\bigg(\frac 12\sum_{\varepsilon\in\{0,1\}^k}s_\rho(n+\varepsilon\cdot r)\bigg)\leq C 2^{-\rho\eta} \]
for all 
$\rho \geq 0$, where 
$\varepsilon \cdot r=\sum _{1\leq i\leq k}\varepsilon _ir_i$.
Remark. Since the paper [Reference KoniecznyKon19] by Konieczny also handles the Rudin–Shapiro sequence, it is certainly possible to prove analogous theorems for this sequence instead of the Thue–Morse sequence.
We wish to give a rough idea of the proof of Proposition 3.1 (Proposition 3.2 being proved essentially in the same way).
Idea of the proof of Proposition 3.1. The key idea is to reduce the number of digits that have to be taken into account and thus to replace the sum-of-digits function 
$s$ by its truncated version 
$s_\rho$. Here 
$2^\rho$ will be significantly smaller than 
$N$, so that (we simplify things a bit to convey the idea) we may replace the sum over 
$s(nd+a)$ by a full sum over the periodic function 
$s_\rho (n)$. This reducing of the digits is achieved by a refinement of the method used by Müllner and the author [Reference Müllner and SpiegelhoferMS17], which in turn builds on the ideas from the papers [Reference Mauduit and RivatMR09, Reference Mauduit and RivatMR10] by Mauduit and Rivat.
First, we apply Van der Corput's inequality and use a ‘carry propagation lemma’ in order to replace 
$s$ by 
$s_\lambda$. In general, 
$2^\lambda$ will be much larger than 
$N$, so that we have to reduce 
$\lambda$ further. The next step is to apply the generalized Van der Corput inequality repeatedly. With each application, we remove 
$\mu$ many digits. This is achieved by appealing to the Dirichlet approximation theorem, by which we can find a multiple of 
$\alpha =d/2^{j\mu }$ that is close to a multiple of 
$2^\mu$. This property can be used to discard the 
$\mu$ lowest digits.
By this repeated application the estimate is reduced to an estimate of a Gowers uniformity norm of the Thue–Morse sequence, and we use the method of proof of Konieczny [Reference KoniecznyKon19] in order to obtain this estimate. The application of Van der Corput's inequality in the context of digital problems is well established, beginning with the work of Mauduit and Rivat [Reference Mauduit and RivatMR09, Reference Mauduit and RivatMR10]. The combination with Gowers norms however is novel, and we think that this connection is a fruitful one: iterated application of Van der Corput's inequality leads to multiple correlations, which in a natural way lead to Gowers norms.
4. Lemmas
We have the following series of lemmas that can also be found in our earlier paper with Müllner [Reference Müllner and SpiegelhoferMS17]. The first lemma can be proved by elementary considerations.
Lemma 4.1 Let 
$a,b\in \mathbb {R}$ and 
$n\in \mathbb {N}$.
\begin{align} & \text{If $\lVert a\rVert < \varepsilon$ and $\lVert b\rVert\geq \varepsilon$, then $\lfloor a+b\rfloor=\langle a\rangle+\lfloor b\rfloor$,} \end{align}
\begin{align} & \lVert na\rVert \leq n\lVert a\rVert, \end{align}
\begin{align} & \text{If $\lVert a\rVert < \varepsilon$ and $2n\varepsilon < 1$, then $\langle na\rangle=n\langle a\rangle$.} \end{align}As an essential tool, we will use repeatedly the following generalized Van der Corput inequality [Reference Mauduit and RivatMR09, Lemme 17].
Lemma 4.2 Let 
$I$ be a finite interval in 
$\mathbb {Z}$ containing 
$N$ integers and let 
$z_n$ be a complex number for 
$n\in I$. For all integers 
$K\geq 1$ and 
$R\geq 1$ we have
\begin{equation} \bigg \lvert\sum_{n\in I}z_n\bigg \rvert^2\leq \frac{N+K(R-1)}R \sum_{0\leq\lvert r\rvert < R}\bigg(1-\frac{\lvert r\rvert}R\bigg) \sum_{\substack{n\in I\\ n+Kr\in I}}z_{n+Kr}\overline{z_n}. \end{equation} Assume that 
$\alpha$ is a real number and 
$N$ is a nonnegative integer. We define the discrepancy of the sequence 
$n\alpha$ modulo 
$1$:
\[ D_N(\alpha)=\sup_{\substack{0\leq x\leq 1\\y\in\mathbb{R}}} \bigg\lvert \frac 1N\sum_{n < N}1_{[0,x)+y+\mathbb{Z}}(n\alpha)-x\bigg\rvert. \]
Applying this definition, using 
$x=1/(KT)$, 
$y=t/(KT)$, and 
$\alpha /K$ instead of 
$\alpha$, we obtain the following lemma.
Lemma 4.3 Let 
$J$ be an interval in 
$\mathbb {R}$ containing 
$N$ integers and let 
$\alpha$ and 
$\beta$ be real numbers. Assume that 
$t,T,\ell$ and 
$L$ are integers such that 
$0\leq t < T$ and 
$0\leq \ell < L$. Then
\[ \bigg\lvert\bigg\{n\in J: \frac tT\leq \{n\alpha+\beta\} < \frac{t+1}T, \lfloor n\alpha+\beta\rfloor\equiv \ell\bmod L\bigg\}\bigg\rvert =\frac N{LT} + \mathcal{O}\bigg(ND_N\bigg(\frac \alpha L\bigg)\bigg) \]with an absolute implied constant.
In the estimation of our error terms, we will use the following mean discrepancy results (Lemma 3.4 in [Reference Müllner and SpiegelhoferMS17]).
Lemma 4.4 For integers 
$\mu \geq 0$ and 
$N\geq 1$ we have
\[ \sum_{0\leq d < 2^{\mu}}D_N\bigg(\frac d{2^\mu}\bigg) \leq C_1\frac{N+2^\mu}{N}(\log^+\! N)^2. \]Also, the estimate
\[ \int_0^1 D_N(\alpha)\, d\alpha\leq C_2 \frac{(\log^+\! N)^2}{N} \]
holds. The constants 
$C_1$ and 
$C_2$ in these estimates are absolute.
The following ‘carry propagation lemma’ will allow us to replace the sum-of-digits function 
$s$ by its truncated version 
$s_\lambda$. Statements of this type were used by Mauduit and Rivat in their papers on the sum of digits of primes and squares [Reference Mauduit and RivatMR09, Reference Mauduit and RivatMR10].
Lemma 4.5 Let 
$r,N,\lambda$ be nonnegative integers and 
$\alpha > 0,\beta \geq 0$ real numbers. Assume that 
$I$ is an interval containing 
$N$ integers. Then
\begin{align*} & \lvert \{n\in I:s(\lfloor(n+r)\alpha+\beta\rfloor)-s(\lfloor n\alpha+\beta\rfloor)\neq s_\lambda(\lfloor(n+r)\alpha+\beta\rfloor)-s_\lambda(\lfloor n\alpha+\beta\rfloor)\}\rvert\\ &\quad \leq r(N\alpha/2^\lambda+2). \end{align*} Let 
$\mathcal {F}_n$ be the set of rational numbers 
$p/q$ such that 
$1\leq q\leq n$, the Farey series of order 
$n$. Each 
$a\in \mathcal {F}_n$ has two neighbours 
$a_L,a_R\in \mathcal {F}_n$ satisfying 
$a_L < a < a_R$ and 
$(a_L,a)\cap \mathcal {F}_n=(a,a_R)\cap \mathcal {F}_n=\emptyset$. We have the following elementary lemma concerning this set (see [Reference Hardy and WrightHW54, Chapter 3]).
Lemma 4.6 Assume that 
$a/b$ and 
$c/d$ are reduced fractions such that 
$b,d > 0$ and 
$a/b < c/d$. Then 
$a/b < (a+c)/(b+d) < c/d$. If 
$a/b$ and 
$c/d$ are neighbours in the Farey series 
$\mathcal {F}_n$, then 
$bc-ad=1$ and 
$b+d>n$; moreover,
\[ (a+c)/(b+d)-a/b < \frac 1{bn}\quad\text{and}\quad c/d-(a+c)/(b+d) < \frac 1{dn}. \] Let 
$\alpha \in \mathbb {R}$ and 
$Q$ a positive integer. We assign a fraction 
$p_Q(\alpha )/q_Q(\alpha )$ to 
$\alpha$ according to the Farey dissection of the reals: consider reduced fractions 
$a/b < c/d$ that are neighbours in the Farey series 
$\mathcal {F}_Q$ such that 
$a/b\leq \alpha < c/d$. If 
$\alpha <(a+c)/(b+d)$, then set 
$p_Q(\alpha )=a$ and 
$q_Q(\alpha )=b$, otherwise set 
$p_Q(\alpha )=c$ and 
$q_Q(\alpha )=d$. Lemma 4.6 implies that
\begin{equation} \lvert q_Q(\alpha)\alpha-p_Q(\alpha)\rvert < Q^{{-}1}. \end{equation}
We will call an interval of the form 
$\{\alpha \in \mathbb {R}:p_Q(\alpha )=p, q_Q(\alpha )=q\}$ a Farey interval around 
$p/q$.
5. Proof of Propositions 3.1 and 3.2
As in the proof of Proposition 2.5 in [Reference Müllner and SpiegelhoferMS17], for (3.2) and (3.4) to hold it is sufficient to prove that there exist 
$\eta >0$ and a constant 
$C$ such that
\[ \frac{S_0(N,2^\nu,\xi)}{N2^\nu}\leq CN^{-\eta} \]
for all real numbers 
$\xi$ and for all positive integers 
$N$ and 
$\nu$ such that there exists a real number 
$D\geq 1$ satisfying 
$N^{\rho _1}\leq D\leq N^{\rho _2}$ and 
$D<2^\nu \leq 2D$, where 
$S_0$ is defined according to (3.1) or (3.3).
In order to treat the two propositions to some extent in parallel, we will work with two measures 
$\boldsymbol \mu$: for Proposition 3.1, we take the measure defined by 
$\boldsymbol \mu (A)=\lvert A\cap \mathbb {Z}\rvert$, counting the number of integers inside a set, while for Proposition 3.2, 
$\boldsymbol \mu$ is the Lebesgue measure. We note that in this proof, implied constants in estimates depend only on the variable 
$k$, whose meaning will become clear later.
By Cauchy–Schwarz, followed by Van der Corput's inequality (4.4) (
$R_0$ will be specified later), we obtain
\begin{align*} \lvert S_0(N,2^\nu,\xi)\rvert^2 &\leq 2^\nu \frac{N+R_0}{R_0}\int_{2^\nu}^{2^{\nu+1}} \sup_{\beta\geq 0}\sum_{0\leq \lvert r_0\rvert < R_0} \bigg(1-\frac{\lvert r_0\rvert}{R_0}\bigg)e(r_0\xi)\\ &\quad \times\sum_{\substack{0\leq n < N\\0\leq n+r_0 < N}} e\bigg(\frac 12 s(\lfloor(n+r_0)\alpha+\beta\rfloor) -\frac 12 s(\lfloor n\alpha+\beta\rfloor)\bigg) d \boldsymbol\mu(\alpha). \end{align*} We apply the carry propagation lemma (Lemma 4.5), treat the summand 
$r_0=0$ separately and omit the condition 
$0\leq n+r_0 < N$. Moreover, we consider 
$r_0$ and 
$-r_0$ synchronously. In this way we obtain for all 
$\lambda \geq 0$
\begin{align*} \lvert S_0(N,2^\nu,\xi)\rvert^2 &\ll (2^\nu N)^2 E_0 +\frac{2^\nu N}{R_0}\sum_{1\leq r_0 < R_0}\\ &\quad \times\int_{2^\nu}^{2^{\nu+1}}\sup_{\beta\geq~0} \bigg\lvert\sum_{0\leq n < N}e\bigg(\frac 12 s_\lambda(\lfloor(n+r_0)\alpha+\beta\rfloor) -\frac 12 s_\lambda(\lfloor n\alpha+\beta\rfloor)\bigg)\bigg\rvert\, d\boldsymbol\mu(\alpha), \end{align*}where
\[ E_0=\frac 1{R_0}+\frac{R_0 2^\nu}{2^\lambda}+\frac {R_0}N. \] We apply Cauchy–Schwarz on the sum over 
$r_0$ and the integral over 
$\alpha$ in order to prepare our expression for another application of Van der Corput's inequality. It follows that
\[ \lvert S_0(N,2^\nu,\xi)\rvert^4\ll \frac{2^{3\nu}N^2}{R_0}\sum_{1\leq r_0 < R_0} \int_{2^\nu}^{2^{\nu+1}}\sup_{\beta\geq 0} \lvert S_1\rvert^2\, d\boldsymbol\mu(\alpha) +(2^\nu N)^4 E_0, \]where
\[ S_1=\sum_{0\leq n < N}e\bigg(\frac 12 s_\lambda(\lfloor (n+r_0)\alpha+\beta\rfloor) -\frac 12s_\lambda(\lfloor n\alpha+\beta\rfloor)\bigg). \]
(Note that the error term is also squared, but if it is larger than or equal to 
$1$, the estimate is trivial anyway. We will use this argument again in a moment.) We apply Van der Corput's inequality (4.4) with 
$R=R_1$ and 
$K=K_1$ to be chosen later:
\begin{align*} \lvert S_1\rvert^2 &\leq \frac{N+K_1(R_1-1)}{R_1}\sum_{0\leq\lvert r_1\rvert < R_1} \bigg(1-\frac{\lvert r_1\rvert}{R_1}\bigg)\\ &\quad \times\sum_{\substack{0\leq n < N\\0\leq n+r_1K_1 < N}} e\bigg(\frac 12\sum_{\varepsilon_0,\varepsilon_1\in\{0,1\}} s_{\lambda}(\lfloor(n+\varepsilon_0r_0+\varepsilon_1r_1K_1)\alpha+\beta\rfloor)\bigg); \end{align*}
therefore, combining the summands for 
$r_1$ and 
$-r_1$ and omitting the condition 
$0\leq n+r_1K_1 < N$,
\[ \lvert S_0(N,2^\nu,\xi)\rvert^4\ll \frac{2^{3\nu}N^3}{R_0\,R_1}\sum_{\substack{1\leq r_0 < R_0\\0\leq r_1 < R_1}} \int_{2^\nu}^{2^{\nu+1}}\sup_{\beta\geq 0}\lvert S_2\rvert \,d\boldsymbol\mu(\alpha)+(2^\nu N)^4(E_0+E_1), \]where
\[ S_2 =\sum_{0\leq n < N}e\bigg(\frac 12\sum_{\varepsilon_0,\varepsilon_1\in\{0,1\}} s_{\lambda}(\lfloor(n+\varepsilon_0r_0+\varepsilon_1r_1K_1)\alpha+\beta\rfloor)\bigg) \]and
\[ E_1=\frac{R_1K_1}{N}. \]
Cauchy–Schwarz over 
$r_0$, 
$r_1$ and 
$\alpha$ yields
\[ \lvert S_0(N,\nu,\xi)\rvert^8\ll\frac{2^{7\nu}N^6}{R_0R_1} \sum_{\substack{1\leq r_0 < R_0\\0\leq r_1 < R_1}}\int_{2^\nu}^{2^{\nu+1}} \sup_{\beta\geq 0}\lvert S_2\rvert^2\, d\boldsymbol\mu(\alpha)+ (2^\nu N)^8(E_0+E_1). \]
We apply Van der Corput's inequality with 
$R=R_2$ and 
$K=K_2$ to be chosen later:
\[ \frac{\lvert S_0(N,2^\nu,\xi)\rvert^8}{(2^\nu N)^8}\ll(E_0+E_1+E_2)+\frac{1}{R_0R_1R_2 2^\nu N} \sum_{\substack{1\leq r_0 < R_0\\0\leq r_1 < R_1\\0\leq r_2 < R_2}} \int_{2^\nu}^{2^{\nu+1}}\sup_{\beta\geq 0}\lvert S_3\rvert\, d\boldsymbol\mu(\alpha), \]where
\[ S_3=\sum_{0\leq n < N}e\bigg(\frac 12 \sum_{\varepsilon_0,\varepsilon_1,\varepsilon_2\in\{0,1\}}s_{\lambda} (\lfloor n\alpha+\beta+\varepsilon_0r_0\alpha+\varepsilon_1r_1K_1\alpha+ \varepsilon_2r_2K_2\alpha\rfloor)\bigg) \]
and 
$E_2=R_2K_2/N.$ Continuing in this manner and replacing the range of integration (we note that we are going to choose 
$\lambda > \nu$ later), we obtain
\begin{align} \bigg\lvert \frac{S_0(N,2^\nu,\xi)}{2^\nu N}\bigg\rvert^{2^{k+1}} &\ll (E_0+E_1+\cdots+E_k) \nonumber\\ &\quad +\frac{1}{R_0R_1\cdots R_k 2^\nu N} \sum_{\substack{1\leq r_0 < R_0\\ 0\leq r_i < R_i, 1\leq i\leq k}} \int_0^{2^\lambda}\sup_{\beta\geq 0} \lvert S_4\rvert \,d\boldsymbol\mu(\alpha), \end{align}where
\[ S_4=\sum_{0\leq n < N}e\bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_{\lambda}(\lfloor n\alpha+\beta+\varepsilon_0r_0\alpha+\varepsilon_1r_1K_1\alpha+ \cdots+\varepsilon_kr_kK_k\alpha\rfloor)\bigg) \]and
\begin{align*} E_0&=\frac 1{R_0}+\frac{R_0\, 2^\nu}{2^\lambda}+\frac {R_0}N,\\ E_i&=\frac{R_i\,K_i}{N}\quad\textrm{for }1\leq i\leq k. \end{align*} Now we choose the multiples 
$K_1,\ldots ,K_k$ in such a way that the number of digits to be taken into account is reduced from 
$\lambda$ to 
$\rho := \lambda -(k+1)\mu$, where 
$\mu$ is chosen later. For this we use Farey series; see (4.5). Let
\begin{align*} K_1&=q_{2^{2\mu+2\sigma}}\bigg(\frac{\alpha}{2^{2\mu}}\bigg) q_{2^\sigma} \bigg(\frac{p_{2^{2\mu+2\sigma}}(\alpha/2^{2\mu})}{2^{(k-1)\mu}}\bigg);\\ K_i&=q_{2^{\mu+2\sigma}}\bigg(\frac{\alpha}{2^{(i+1)\mu}}\bigg) q_{2^\sigma} \bigg(\frac{p_{2^{\mu+2\sigma}}(\alpha/2^{(i+1)\mu})}{2^{(k-i)\mu}}\bigg) \quad\textrm{for }2\leq i < k; \\ K_k&=q_{2^{\mu+\sigma}}\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg), \end{align*}
where 
$\sigma$ is chosen later. Moreover, we set
\begin{align*} M_1&=p_{2^{2\mu+2\sigma}}\bigg(\frac{\alpha}{2^{2\mu}}\bigg) q_{2^\sigma} \bigg(\frac{p_{2^{2\mu+2\sigma}}(\alpha/2^{2\mu})}{2^{(m-1)\mu}}\bigg);\\ M_i&=p_{2^{\mu+2\sigma}}\bigg(\frac{\alpha}{2^{(i+1)\mu}}\bigg) q_{2^\sigma} \bigg(\frac{p_{2^{\mu+2\sigma}}(\alpha/2^{(i+1)\mu})}{2^{(k-i)\mu}}\bigg) \quad\textrm{for }2\leq i < k;\\ M_k&=p_{2^{\mu+\sigma}}\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg). \end{align*} By Lemma 4.6, estimating the second factor in the definition of 
$K_i$ and 
$M_i$ by 
$2^\sigma$, we have
\begin{align} \lvert K_1\alpha-2^{2\mu}M_1\rvert& < 2^{-\sigma};\nonumber\\ \bigg\lvert \frac{K_i\alpha}{2^{i\mu}}-2^\mu M_i\bigg\rvert& < 2^{-\sigma}\quad\textrm{for }2\leq i < k;\\ \bigg\lvert \frac{K_k\alpha}{2^{k\mu}}-2^\mu M_k\bigg\rvert& < 2^{-\sigma}. \nonumber\end{align} We are going to use these inequalities in order to replace 
$r_iK_i\alpha$ in the sum 
$S_4$, starting with 
$r_1K_1\alpha$. We treat the case when 
$\alpha$ is an integer first: in this case, 
$K_1\alpha =2^{2\mu }M_1$, and by the fact that the arguments of 
$s_\lambda$ corresponding to 
$\varepsilon _1=0,1$ differ by a multiple of 
$2^{2\mu }$, we may shift the argument by 
$2\mu$ digits and thus reduce the number of digits to be taken into account from 
$\lambda$ to 
$\lambda -2\mu$:
\begin{align*} S_4 &= \sum_{0\leq n < N}e\bigg(\frac 12 \sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_{2\mu,\lambda}(\lfloor n\alpha+\beta \\ &\quad +\varepsilon_0r_0\alpha +\varepsilon_1r_1M_12^{2\mu} +\varepsilon_2r_2K_2\alpha +\cdots+\varepsilon_kr_kK_k\alpha\rfloor)\bigg)\\ &= \sum_{0\leq n < N}e\bigg(\frac 12 \sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_{\lambda-2\mu}\bigg(\bigg\lfloor \frac{n\alpha+\beta}{2^{2\mu}} +\frac{\varepsilon_0r_0\alpha}{2^{2\mu}} +\varepsilon_1r_1M_1 \\ &\quad +\frac{\varepsilon_2r_2K_2\alpha}{2^{2\mu}} +\cdots+\frac{\varepsilon_kr_kK_k\alpha}{2^{2\mu}}\bigg\rfloor\bigg)\bigg). \end{align*}
In the case 
$\alpha \not \in \mathbb {Z}$, we use the inequalities (5.2) and the argument that 
$n\alpha$-sequences are usually not close to an integer. This can be made precise as follows. Assume that
\begin{equation} \lVert n\alpha+\beta'\rVert\geq R_1/2^\sigma, \end{equation}
where 
$\beta '=\beta +\varepsilon _0r_0\alpha +\varepsilon _2r_2K_2\alpha +\cdots +\varepsilon _kr_kK_k\alpha$, and that 
$2R_1 < 2^\sigma$. Using the inequality (4.3) in Lemma 4.1 with 
$\varepsilon =1/2^\sigma$, where 
$\sigma \geq 1$ is chosen later, and (4.5), we obtain
\[ \langle r_1K_1\alpha\rangle=r_1\langle K_1\alpha\rangle=r_12^{2\mu} M_1. \]
Applying (4.1), setting 
$\varepsilon =R_1/2^\sigma$, we see that (5.3) together with (5.2) implies that
\[ \lfloor n\alpha+r_1K_1\alpha+\beta'\rfloor =\lfloor n\alpha+r_12^{2\mu}M_1+\beta'\rfloor. \]
The number of 
$n$ where hypothesis (5.3) fails for some 
$\varepsilon _0,\varepsilon _2,\ldots ,\varepsilon _k$ can be estimated by discrepancy estimates for 
$\{n\alpha \}$-sequences: for all positive integers 
$N$ and 
$2R_1 < 2^\sigma$ we have
\begin{align*} & \lvert\{n\in [0,N-1]:\lVert n\alpha+\beta'\rVert\leq R_1/2^\sigma\}\rvert\\ &\quad =\lvert\{n\in [0,N-1]:n\alpha+\beta'\in [{-}R_1/2^\sigma,R_1/2^\sigma]+\mathbb{Z}\}\rvert\\ &\quad =\lvert\{n\in [0,N-1]:n\alpha\in [0,2R_1/2^\sigma]-\beta'-R_1/2^\sigma+\mathbb{Z}\}\rvert\\ &\quad \leq ND_N(\alpha)+2R_1N/2^\sigma. \end{align*}
Therefore, the number of 
$n\in [0,N-1]$ such that there exist 
$\varepsilon _0,\varepsilon _2,\ldots ,\varepsilon _k\in \{0,1\}$ with 
$\lVert n\alpha +\beta '\rVert \leq R_1/2^\sigma$ is bounded by 
$2^kN(D_N(\alpha )+2R_1/2^\sigma )$, which is 
$\ll N(D_N(\alpha )+2R_1/2^\sigma )$ by our convention that implied constants may depend on 
$k$.
We replace 
$K_1\alpha$ by 
$2^{2\mu }M_1$ and subsequently shift the digits by 
$2\mu$ and obtain
\begin{align*} S_4 &= \sum_{0\leq n < N}e\bigg(\frac 12 \sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_{\lambda-2\mu}\bigg(\bigg\lfloor \frac{n\alpha+\beta}{2^{2\mu}} +\frac{\varepsilon_0r_0\alpha}{2^{2\mu}} +\varepsilon_1r_1M_1\\ &\quad +\frac{\varepsilon_2r_2K_2\alpha}{2^{2\mu}} +\cdots+\frac{\varepsilon_kr_kK_k\alpha}{2^{2\mu}}\bigg\rfloor\bigg)\bigg) +\mathcal{O}(N D_N(\alpha)+NR_1/2^\sigma). \end{align*} Repeating this argument for all 
$i\in \{2,\ldots ,k\}$ we obtain
\begin{align*} S_4 &= N\mathcal{O}\bigg(\widetilde D_N(\alpha)+D_N\bigg(\frac{\alpha}{2^{2\mu}}\bigg)+ \cdots+D_N\bigg(\frac{\alpha}{2^{k\mu}}\bigg)+\frac{R_1+\cdots+R_k}{2^\sigma}\bigg)\\ &\quad +\sum_{0\leq n < N}e\bigg(\frac 12 \sum_{\varepsilon_1,\ldots,\varepsilon_k\in\{0,1\}} s_{\lambda-(k+1)\mu}\bigg(\bigg\lfloor \frac{n\alpha+\beta}{2^{(k+1)\mu}} + \frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}} +\sum_{1\leq i\leq k} \frac{\varepsilon_ir_iM_i}{2^{(k-i)\mu}}\bigg\rfloor\bigg)\bigg), \end{align*}
where 
$\widetilde D_N(\alpha )=D_N(\alpha )$ if 
$\alpha \not \in \mathbb {Z}$ and 
$\widetilde D_N(\alpha )=0$ otherwise.
Now the second factor in the definition of 
$K_i$ comes into play. We use the definition of 
$M_i$ together with the approximation property (4.5), and apply the discrepancy estimate for 
$\{n\alpha \}$-sequences again, to obtain
\begin{equation} S_4=N\mathcal{O}\bigg(\widetilde D_N(\alpha)+D_N\bigg(\frac{\alpha}{2^{2\mu}}\bigg)+ \cdots+D_N\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg)+\frac{R_1+\cdots+R_k}{2^\sigma}\bigg)+S_5, \end{equation}where
\[ S_5=\sum_{0\leq n < N}e\bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_{\lambda-(k+1)\mu}\bigg(\bigg\lfloor \frac{n\alpha+\beta}{2^{(k+1)\mu}}+ \frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\bigg\rfloor+\sum_{1\leq i\leq k} \varepsilon_ir_i\mathfrak p_i\bigg)\bigg) \]and
\begin{align} \mathfrak p_1 &= p_{2^\sigma}\bigg(\frac{p_{2^{2\mu+2\sigma}}(\alpha/2^{2\mu})}{2^{(k-1)\mu}}\bigg); \nonumber\\ \mathfrak p_i &= p_{2^\sigma}\bigg(\frac{p_{2^{\mu+2\sigma}}(\alpha/2^{(i+1)\mu})} {2^{(k-i)\mu}}\bigg)\quad\textrm{for }2\leq i < k;\\ \mathfrak p_k&= p_{2^{\mu+\sigma}}\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg). \nonumber \end{align} Our next goal is to remove the Beatty sequence occurring in 
$S_5$, and also to remove the integers 
$\mathfrak p_i$. The resulting expression can be handled by the Gowers norm estimate given in Proposition 3.3, which will finish the proof.
We start by splitting the Beatty sequence into two summands. Let 
$t,T$ be integers such that 
$0\leq t < T$ and define
\[ S_6 = \sum_{\substack{0\leq n < N\\ t/T\leq\{{(n\alpha+\beta)}/{2^{(k+1)\mu}}\} < {(t+1)}/T}} e\bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_{\lambda-(k+1)\mu}\bigg(\bigg\lfloor \frac{n\alpha+\beta+\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\bigg\rfloor \!+\!\sum_{1\leq i\leq k}\varepsilon_ir_i\mathfrak p_i\bigg)\bigg). \]We define
\[ G=\bigg\{1\leq t < T: \bigg[\frac tT+\frac {\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}, \frac{t+1}T+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\bigg) \cap \mathbb{Z}= \emptyset\bigg\}. \]
Clearly, we have 
$\lvert G\rvert \geq T-2$, since we have to exclude at most one 
$t$. For 
$t\in \{0,\ldots ,T-1\}\setminus G$ we estimate 
$S_6$ trivially, using Lemma 4.3: we obtain
\begin{equation} S_6\ll \frac NT+ND_N\bigg(\frac {\alpha}{2^{(k+1)\mu} }\bigg). \end{equation}
Assume that 
$t\in G$ and that 
$t/T\leq \{(n\alpha +\beta )/2^{(k+1)\mu }\}<(t+1)/T$. Then
\[ \bigg\lfloor \frac{n\alpha+\beta}{2^{(k+1)\mu}}\bigg\rfloor+ \frac tT+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\leq \frac{n\alpha+\beta+\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}< \bigg\lfloor \frac{n\alpha+\beta}{2^{(k+1)\mu}}\bigg\rfloor+ \frac {t+1}T+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}} \]
and the assumption 
$t\in G$ gives
\[ \bigg\lfloor\frac{n\alpha+\beta+\varepsilon_0r_0\alpha}{2^{(k+1)\mu} }\bigg\rfloor =\bigg\lfloor\frac{n\alpha+\beta}{2^{(k+1)\mu} }\bigg\rfloor+ \bigg\lfloor\frac tT+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu} }\bigg\rfloor \]
for 
$\varepsilon _0\in \{0,1\}$. From these observations we obtain for 
$t\in G$:
\begin{align*} S_6 &= \sum_{0\leq m < 2^\rho}\sum_{\substack{0\leq n < N\\ t/T\leq\{{(n\alpha+\beta)}/{2^{(k+1)\mu}}\} < {(t+1)}/T\\ \lfloor{(n\alpha+\beta)}/{2^{(k+1)\mu} }\rfloor\equiv m\bmod 2^\rho}}\\ &\quad \times e\bigg(\frac 12 \sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_\rho\bigg(m+\bigg\lfloor \frac tT+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\bigg\rfloor +\sum_{1\leq i\leq k}\varepsilon_ir_i\mathfrak p_i\bigg)\bigg). \end{align*}
Note that the Beatty sequence 
$\lfloor (n\alpha +\beta )/2^{(k+1)\mu }\rfloor$ does not occur in the summand any more. We may therefore remove the second summation by estimating the number of times the three conditions under the summation sign are satisfied. At this point we want to stress the fact that 
$N$ is going to be significantly larger than 
$2^\rho =2^{\lambda -(k+1)\mu }$. Using Lemma 4.3 and the usually very small discrepancy of 
$n\alpha$-sequences, this fact will enable us to remove the summation over 
$n$, while introducing only a negligible error term for most 
$\alpha$. This is the point in the proof where the successive ‘cutting away’ of binary digits with the help of Farey series pays off.
By Lemma 4.3, applied with 
$L=2^\rho$, and noting that 
$\lambda =(k+1)\mu +\rho$, we obtain for 
$t\in G$
\begin{equation} S_6=\frac{N}{2^\rho T}S_7+\mathcal{O}\bigg(2^\rho ND_N\bigg(\frac \alpha{2^\lambda} \bigg)\bigg), \end{equation}where
\[ S_7=\sum_{0\leq m < 2^\rho}e\bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_\rho\bigg(m+\bigg\lfloor\frac tT+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\bigg\rfloor +\sum_{1\leq i\leq k}\varepsilon_ir_i\mathfrak p_i\bigg)\bigg). \]
We note the important fact that this expression is independent of 
$\beta$. This will allow us to remove the maximum over 
$\beta$ inside the integral over 
$\alpha$ and thus prove the strong statement on the level of distribution.
We wish to simplify this expression in such a way that Proposition 3.3 is applicable. To this end, we use the summation over 
$r_i$ and the integral over 
$\alpha$. We define
\[ S_8=\int_0^{2^\lambda}\sum_{\substack{0\leq r_1,\ldots,r_k < 2^\rho}} \lvert S_7\rvert\, d\boldsymbol\mu(\alpha), \]
which is an expression that will appear when we expand the original sum 
$S_0$.
We are going to apply the argument that for most 
$\alpha < 2^\lambda$ (with respect to 
$\boldsymbol \mu$) the 
$2$-adic valuation of 
$\mathfrak p_1,\ldots ,\mathfrak p_k$ is small. For these 
$\alpha$, the term 
$r_i\mathfrak p_i\bmod 2^\rho$ attains each 
$m\in \{0,\ldots ,2^\rho -1\}$ not too often, as 
$r_i$ varies. We may therefore replace 
$r_i\mathfrak p_1$ by 
$r_i$ and thus obtain full sums over 
$r_i$: at this point, we set
\[ R_i=2^\rho\quad\mbox{for}\ 1\leq i\leq k. \]In order to make this argument work, we are going to utilize the following technical result, the proof of which we give in § 5.2.
Lemma 5.1 Let 
$\mu ,\lambda ,\sigma ,\gamma ,k$ be nonnegative integers such that 
$k\geq 2$ and
\begin{equation} \begin{array}{ll} \lambda\geq (k+1)\mu,&\gamma \leq \lambda-(k+1)\mu,\\ \mu\geq 4\sigma,& \sigma \geq \gamma\geq 1. \end{array} \end{equation}
Let 
$\mathfrak p_1,\ldots ,\mathfrak p_k$ be defined by (5.5) and set
\[ A=\{\alpha\in\{0,\ldots,2^\lambda-1\}:2^{3\gamma}\mid \mathfrak p_i\textrm{ for some }i=1,\ldots,k\}. \]Then
\[ \lvert A\rvert=\mathcal{O}(2^{\lambda-\gamma}). \]Analogously, if
\[ A=\{\alpha\in[0,2^\lambda]:2^{3\gamma}\mid \mathfrak p_i\textrm{ for some }i=1,\ldots,k\}, \]then
\[ \boldsymbol\lambda(A)=\mathcal{O}(2^{\lambda-\gamma}), \]
where 
$\boldsymbol \lambda$ is the Lebesgue measure. The implied constants only depend on 
$m$ (and are independent of 
$\mu ,\lambda ,\sigma$ and 
$\gamma$).
Let 
$A$ be defined as in this lemma. We choose 
$R_i=2^\rho$ for 
$1\leq i\leq k$.
Assume that 
$\alpha \not \in A$. Then, by an elementary argument, 
$r_i\mathfrak p_i\bmod 2^\rho$ attains each value not more than 
$2^{3\gamma }$ times, as 
$r_i$ runs through 
$\{0,\ldots ,2^\rho -1\}$. The contribution for 
$\alpha \in A$ will be estimated trivially by the lemma. We obtain
\[ S_8\leq 2^{3\gamma k}\int_0^{2^\lambda}\sum_{0\leq r_1,\ldots,r_k < 2^\rho} \lvert S_9\rvert d\boldsymbol\mu(\alpha)+ \mathcal{O}(2^{\lambda+(k+1)\rho-\gamma}), \]where
\[ S_9=\sum_{0\leq n < 2^\rho}e\bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_\rho\bigg(n+\bigg\lfloor\frac tT+\frac{\varepsilon_0r_0\alpha}{2^{(k+1)\mu}}\bigg\rfloor +\sum_{1\leq i\leq k} \varepsilon_ir_i\bigg)\bigg). \]
The next step is removing the remaining floor function, using the integral over 
$\alpha$. In the continuous case, the expression 
$\lfloor t/T+r_0K_0\alpha /2^{(k+1)\mu }\rfloor \bmod 2^\rho$ runs through 
$\{0,\ldots ,2^\rho -1\}$ in a completely uniform manner. That is, for 
$r_0\neq 0$ and 
$0\leq m < 2^\rho$ we have
\[ \boldsymbol\lambda(\{\alpha\in[0,2^\lambda]: \lfloor t/T+r_0\alpha/2^{(k+1)\mu}\rfloor\equiv m\bmod 2^\rho\})=2^{\lambda-\rho}, \]
where 
$\boldsymbol \lambda$ is the Lebesgue measure. We consider the discrete case. Assume that 
$r_0\leq 2^{(k+1)\mu }$ (we will choose 
$R_0$ very small at the end of the proof, so that this will be satisfied). Then the set of 
$\alpha \in \{0,\ldots ,2^\lambda -1\}$ such that 
$\lfloor t/T+r_0\alpha /2^{(k+1)\mu }\rfloor \equiv m\bmod 2^\rho$ decomposes into at most 
$r_0+1$ intervals (note that 
$\lambda =(k+1)\mu +\rho$), each having 
$\leq 2^{(k+1)\mu }/r_0+1$ elements. In total we have 
$\ll 2^{\lambda -\rho }$ elements, where the implied constant is absolute. It follows that
\[ S_8\ll 2^{\lambda+(k+1)\rho-\gamma}+2^{\lambda-\rho+3\gamma k} \sum_{0\leq r_0,\ldots,r_k < 2^\rho}\lvert S_{10}(r_0,\ldots,r_k)\rvert, \]where
\[ S_{10}(r_0,\ldots,r_k)=\sum_{0\leq n < 2^\rho}e \bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_\rho\bigg(n+\sum_{0\leq i\leq k}\varepsilon_i r_i\bigg)\bigg). \]
As a final step in the procedure of reducing the main theorems to Proposition 3.3, we are going to remove the absolute value around 
$S_{10}$. For brevity, we set
\[ g(n)=\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} s_\rho\bigg(n+\sum_{0\leq i\leq k}\varepsilon_i r_i\bigg). \]
By the 
$2^\rho$-periodicity of 
$g$ we have
\begin{align*} &\sum_{0\leq r_0,\ldots,r_k < 2^\rho}\lvert S_{10}(r_0,\ldots,r_k)\rvert^2\\ &\quad =\sum_{0\leq r_0,\ldots,r_k < 2^\rho}\sum_{0\leq n_1,n_2 < 2^\rho} e\bigg(\frac 12 g(n_1)+\frac 12g(n_2)\bigg)\\ &\quad =\sum_{0\leq r_0,\ldots,r_k < 2^\rho}\sum_{0\leq n_1 < 2^\rho} \sum_{0\leq r_{k+1} < 2^\rho}e\bigg(\frac 12 g(n_1)+\frac 12g(n_1+r_{k+1})\bigg)\\ &\quad =\sum_{0\leq r_0,\ldots,r_{k+1} < 2^\rho}\sum_{0\leq n_1 < 2^\rho} e\bigg(\frac 12 g(n_1)+\frac 12g(n_1+r_{k+1})\bigg)\\ &\quad =\sum_{0\leq r_0,\ldots,r_{k+1} < 2^\rho}\sum_{0\leq n_1 < 2^\rho} e\bigg(\frac 12\sum_{\varepsilon_0,\ldots,\varepsilon_k\in\{0,1\}} \sum_{\varepsilon_{k+1}\in\{0,1\}} s_\rho(n_1+\varepsilon\cdot r+\varepsilon_{k+1}r_{k+1})\bigg)\\ &\quad =\sum_{0\leq r_0,\ldots,r_{k+1} < 2^\rho}S_{10}(r_0,\ldots,r_{k+1}). \end{align*}
We have therefore removed the absolute value around 
$S_{10}$ for the price of an additional variable 
$r_{k+1}$; see also [Reference Green and TaoGT10, Section 4] for this type of argument. This means that we have reduced our main theorems to Proposition 3.3.
By this proposition and Cauchy–Schwarz we obtain
\begin{equation} S_8\ll 2^{\lambda+(k+1)\rho}(2^{-\gamma}+2^{3\gamma k-\eta\rho}) \end{equation}
for some 
$\eta > 0$.
It remains to collect the error terms and to choose values for the free variables. Using (5.7) and (5.6), we obtain
\begin{align*} S_5 &\ll \sum_{t\not\in G}\bigg(\frac NT+ND_N\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg)\bigg) +\sum_{t\in G}\bigg(\frac N{2^\rho T}S_7+2^\rho N D_N\bigg(\frac{\alpha}{2^\lambda}\bigg)\bigg)\\ &\ll\frac N{2^\rho T}\sum_{t\in G}S_7 +\frac NT+ND_N\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg)+2^\rho N TD_N\bigg(\frac{\alpha}{2^\lambda}\bigg) \end{align*}and by (5.4) and (5.1) we obtain
\begin{align} & \bigg\lvert\frac{S_0(N,\nu,\xi)}{2^\nu N}\bigg\rvert^{2^{k+1} }\nonumber\\ &\quad \ll \mathcal{O}\bigg(\frac 1{R_0}+\frac{R_02^\nu}{2^\lambda}+\frac{R_0}{N}+ \frac{R_1K_1}{N}+\cdots+\frac{R_kK_k}{N}\bigg) \nonumber\\ &\, \, \quad\quad +\frac 1{2^\nu N}\int_0^{2^\lambda}N \mathcal{O}\bigg(\widetilde D_N(\alpha)+D_N\bigg(\frac{\alpha}{2^{2\mu}}\bigg)+ \cdots+D_N\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg)+ \frac{R_1+\cdots+R_k}{2^\sigma}\bigg) d\boldsymbol\mu(\alpha) \nonumber\\ &\, \, \quad\quad +\frac 1{2^\nu N}\int_0^{2^\lambda} \mathcal{O}\bigg(\frac NT+ND_N\bigg(\frac{\alpha}{2^{(k+1)\mu}}\bigg)+ 2^\rho TN D_N\bigg(\frac{\alpha}{2^\lambda}\bigg)\bigg) d\boldsymbol\mu(\alpha) \nonumber\\ &\, \, \quad\quad +\frac 1{R_0\cdots R_k2^\nu N}\frac N{2^\rho T}\sum_{t\in G}\sum_{1\leq r_0 < R_0} \int_0^{2^\lambda}\sum_{\substack{0\leq r_1,\ldots,r_k < 2^\rho}} \lvert S_7\rvert \,d\boldsymbol\mu(\alpha). \end{align} We employ the mean discrepancy estimates from Lemma 4.4. Assume that 
$\delta \leq \lambda$. In the continuous case we have
\[ \frac 1{2^\nu}\int_0^{2^\lambda}D_N\bigg(\frac \alpha{2^\delta}\bigg) d\alpha \ll 2^{\lambda-\nu-\delta}\int_0^{2^\delta}D_N\bigg(\frac \alpha{2^\delta}\bigg) d\alpha \ll 2^{\lambda-\nu}\frac{(\log^+\! N)^2}N, \]while the discrete case gives
\[ \frac 1{2^\nu}\sum_{0\leq d < 2^\lambda}D_N\bigg(\frac d{2^\delta}\bigg) \ll 2^{\lambda-\delta-\nu}\frac{N+2^\delta}N(\log^+\! N)^2 =2^{\lambda-\nu}(\log^+\! N)^2\bigg(\frac 1N+\frac 1{2^\delta}\bigg). \]
In total, noting that 
$\lambda \geq (k+1)\mu$, the discrepancy terms can be estimated by
\[{\ll} 2^{\lambda-\nu}(\log^+\! N)^2 2^\rho T\bigg(\frac 1N+\frac 1{2^{2\mu}}\bigg). \]By (5.9), the last summand in (5.10) can be estimated by
\[{\ll} 2^{\lambda-\nu}(2^{-\gamma}+2^{3\gamma k-\eta\rho}). \]
Moreover, using the facts that 
$R_1=\cdots =R_k=2^\rho$ and 
$K_i\leq 2^{2\mu +3\sigma }$ for 
$1\leq i\leq k$, we obtain
\begin{align} \bigg\lvert\frac{S_0(N,\nu,\xi)}{2^\nu N}\bigg\rvert^{2^{k+1} } &\ll \frac 1{R_0}+\frac{R_02^\nu}{2^\lambda}+\frac{R_0}{N}+\frac{2^{\rho+2\mu+3\sigma}}{N} \nonumber\\ &\quad +2^{\lambda-\nu}(\log^+\! N)^2 2^\rho T\bigg(\frac 1N+\frac 1{2^{2\mu}}\bigg) +2^{\rho-\sigma+\lambda-\nu} +\frac 1T +2^{\lambda-\nu}(2^{-\gamma}+2^{3\gamma k-\eta\rho}) \end{align}
with some implied constant only depending on 
$k$. Collecting also the requirements on the variables we assumed in the course of our calculation, we see that this estimate is valid as long as
\begin{equation} \begin{array}{ll} R_0,\ T\geq 1,\ k\geq 2,\ \gamma, \nu,\lambda,\rho,\mu\geq 0, & R_1=\cdots=R_k=2^\rho,\\ \lambda>\nu,& \rho=\lambda-(k+1)\mu,\\ \gamma\leq \rho<\sigma-1,& \mu\geq 4\sigma,\\ R_0\leq 2^{(k+1)\mu}.\end{array}\end{equation} It remains to choose the variables within these constraints. Choose the integer 
$j\geq 1$ in such a way that 
$N^{j-1}\leq 2^\nu < N^j$ and set 
$k=3j-1$. Clearly, 
$k\geq 2$. We define
\[ \mu=\bigg\lfloor\frac{\nu}{k+1+1/8}\bigg\rfloor,\quad \sigma=\lfloor \mu/4\rfloor,\quad \widetilde\rho=\nu-(k+1)\mu. \]
We obtain the inequalities 
$N\geq 2^{3\mu }$, 
$\mu \geq 4\sigma$, 
$\widetilde \rho \geq 0$. Moreover, for large 
$\nu$ we obtain 
$\widetilde \rho \sim \mu /8$.
Choose 
$\gamma =\lfloor \widetilde \rho \eta /(6k)\rfloor$ and 
$R_0=\lfloor 2^{\gamma /4}\rfloor$. Then the last summand in (5.11) is 
$\ll 2^{\lambda -\nu }(2^{-\gamma }+2^{-\widetilde \rho \eta /2})\ll 2^{\lambda -\nu -\gamma }$. Finally, set 
$\lambda =\nu +\lfloor \gamma /2\rfloor$, 
$T=2^\gamma$ and 
$\rho =\lambda -(k+1)\mu$. It follows that 
$\rho =\widetilde \rho +\lfloor \gamma /2\rfloor \sim (\mu /8)(1+\eta /(12k))\leq \mu /8+\mu /192$. Using these definitions, it is not hard to see that, for large 
$N$ and 
$\nu$, the requirements (5.12) are met.
Using the statements 
$N^{\rho _1}\leq D\leq N^{\rho _2}$ and 
$D < 2^\nu \leq 2D$ we can easily estimate (5.11) term by term and conclude that 
$S_0(N,\nu ,\xi )/(2^\nu N)\leq C N^{-\eta '}$ for some 
$\eta '> 0$ and some constant 
$C$. This finishes the proof of Propositions 3.1 and 3.2 and therefore of our main theorems. It remains to prove our auxiliary results.
5.1 Proof of Proposition 3.3
We utilize ideas from the paper [Reference KoniecznyKon19] by Konieczny. In that paper, he uses the Gowers norm on intervals in 
$\mathbb {Z}$, while we are concerned with the cyclic group 
$\mathbb {Z}/2^\rho \mathbb {Z}$. The proof of Proposition 3.3 is analogous to Konieczny's proof. In fact, it is possible to relate the two notions of Gowers norms to each other and therefore avoid going into the details of the proof in [Reference KoniecznyKon19] (Konieczny, private communication; we also thank the anonymous referee for pointing out this possibility). In this paper, however, we chose to follow the proof from [Reference KoniecznyKon19], as the argument is interesting and not unreasonably long.
Set
\[ A_\rho(\mathbf{a})=\frac 1{2^{(k+1)\rho}}\sum_{\substack{0\leq n < 2^\rho\\0\leq r_1,\ldots,r_k < 2^\rho}} e\bigg(\frac 12\sum_{\varepsilon\in\{0,1\}^k}s_\rho(n+\varepsilon\cdot r+\mathbf{a}_\varepsilon)\bigg). \]
Then, in analogy to equation (16) of [Reference KoniecznyKon19], we get after a similar calculation (using 
$k\geq 2$) that
\begin{equation} A_{\rho+1}(\mathbf{a})=\frac{({-}1)^{\lvert \mathbf{a}\rvert}}{2^{k+1}} \sum_{e_0,\ldots,e_k\in\{0,1\}} A_\rho(\delta(\mathbf{a},e)), \end{equation}
where 
$\lvert \mathbf {a}\rvert = \sum _{\varepsilon \in \{0,1\}^k} \mathbf {a}_\varepsilon$ and
\[ \delta(\mathbf{a},e)_\varepsilon= \bigg\lfloor \frac{\mathbf{a}_\varepsilon+e_0+\sum_{1\leq i\leq k}\varepsilon_ie_i}2\bigg\rfloor. \] We define a directed graph with weighted edges according to (5.13). The set of vertices is given by the set of families 
$\mathbf {a}\in \mathbb {Z}^{\{0,1\}^k}$. There is an edge from 
$\mathbf {a}$ to 
$\mathbf {b}$ if and only if there is an 
$e=(e_0,\ldots ,e_k)\in \{0,1\}^{k+1}$ such that 
$\delta (\mathbf {a},e)=\mathbf {b}$ and this edge has the weight
\[ w(\mathbf{a},\mathbf{b})=\frac{({-}1)^{\lvert \mathbf{a}\rvert}}{2^{k+1}} \lvert\{e\in\{0,1\}^{k+1}:\delta(\mathbf{a},e)=\mathbf{b}\}\rvert. \]Note that
\begin{equation} \sum_{\mathbf{b}\in\mathbb{Z}^{\{0,1\}^k}}\lvert w(\mathbf{a},\mathbf{b})\rvert=1, \end{equation}
which we will need later. We are interested in the subgraph 
$(V,E,w)$ induced by the set of vertices reachable from 
$\mathbf 0$. This graph is finite: we have
\[ \max_{\varepsilon\in\{0,1\}^k}\lvert \delta(\mathbf{a},e)_\varepsilon\rvert \leq \frac 12\Big(\max_{\varepsilon\in\{0,1\}^k}\lvert \mathbf{a}_\varepsilon\rvert+k+1\Big) \]
and, by induction, it follows that 
$\max _{\varepsilon \in \{0,1\}^k}\lvert \mathbf {a}_\varepsilon \rvert < k+1$ for all 
$\mathbf {a}\in V$, which implies the finiteness of 
$V$.
This subgraph is strongly connected. We prove this by showing that 
$\mathbf 0$ is reachable from each 
$\mathbf {a}\in V$. This follows immediately by considering the path given by the edges 
$(\mathbf {a}^{(0)},\mathbf {a}^{(1)})$, 
$(\mathbf {a}^{(1)},\mathbf {a}^{(2)})$,…,
$(\mathbf {a}^{(j)},\mathbf {a}^{(j+1)})$ defined by 
$\mathbf {a}^{(0)}=\mathbf {a}$ and 
$\mathbf {a}^{(i+1)}=\delta (\mathbf {a}^{(i)},(0,\ldots ,0))$. It is clear from the definition of 
$\delta$ that such a path reaches 
$\mathbf 0$ if 
$j$ is large enough.
We wish to apply (5.13) recursively. We therefore define, for two vertices 
$\mathbf {a}, \mathbf {b}\in V$ and a positive integer 
$j$, the weight 
$w_j(\mathbf {a},\mathbf {b})$ as the sum of all weights of paths of length 
$j$ from 
$\mathbf {a}$ to 
$\mathbf {b}$. (Here the weight of a path is the product of the weights of the edges.)
In order to prove Proposition 3.3, it is sufficient to prove that there is a 
$j$ such that
\[ \sum_{\mathbf{b}\in V}\lvert w_j(\mathbf{a},\mathbf{b})\rvert < 1 \]
for all 
$\mathbf {a}\in V$. In order to prove this, it is sufficient, by the strong connectedness of the graph and (5.14), to prove that there are two paths of the same length from 
$\mathbf 0$ to 
$\mathbf 0$ such that their respective weights have different sign. One of these paths is the trivial one, choosing 
$e_0=\cdots =e_j=0$ in each step. This path has positive weight.
For the second path, we follow Konieczny [Reference KoniecznyKon19, proof of Proposition 2.3]. As in that paper, we define 
$\mathbf {a}^{(0)}=\mathbf {a}^{(j+1)}=\mathbf 0$ and, for 
$1\leq i\leq j$,
\[ \mathbf{a}^{(i)}_\varepsilon=\begin{cases} 1, & \textrm{if }\varepsilon_1=\cdots=\varepsilon_i=1;\\ 0, & \textrm{otherwise.} \end{cases} \]
Assuming for a moment that there is an edge from 
$\mathbf {a}^{(i)}$ to 
$\mathbf {a}^{(i+1)}$ for all 
$i\in \{0,\ldots ,j\}$, it is easy to see that each edge 
$(\mathbf {a}^{(i)},\mathbf {a}^{(i+1)})$ has positive weight for 
$0\leq i < j$, while 
$(\mathbf {a}^{(j)},\mathbf {a}^{(j+1)})$ has negative weight. Proving that these vertices indeed define a path is contained completely in the argument given in [Reference KoniecznyKon19]. This finishes the proof of Lemma 3.3.
5.2 Proof of Lemma 5.1
We choose an integer 
$\gamma >0$ and bound the size of the set of 
$\alpha < 2^\lambda$ such that 
$2^{3\gamma }\mid \mathfrak p_i$ for some 
$i\in \{1,\ldots ,k\}$. We will need the following two lemmas.
Lemma 5.2 Let 
$\boldsymbol \lambda$ be the Lebesgue measure. Assume that 
$K\geq 1$ and 
$\gamma \geq 0$ are integers. Then
\[ \boldsymbol\lambda (\{x\in[0,1]:2^\gamma\mid q_K(x)\})\ll \frac 1{2^\gamma}+\frac 1K. \]The constant in this estimate is absolute.
Proof. We have to sum up the lengths of the Farey intervals around 
$p/q$ such that 
$2^\gamma \mid q$. By Lemma 4.6, each such fraction contributes at most 
$2/(Kq)$. By summing over 
$p\in \{1,\ldots ,q\}$, this gives a contribution 
$2/K$ for each multiple 
$q$ of 
$2^\gamma$ and we obtain a total contribution
\[{\ll} \sum_{\substack{1\leq q\leq K\\ 2^\gamma\mid q}} \frac 1K\leq \frac 1{2^\gamma}+\frac 1K. \]Lemma 5.3 Let 
$x_0,\ldots ,x_{M-1}\in [0,1]$ and 
$\delta > 0$. Assume that 
$\lVert x_i-x_j\rVert \geq \delta$ for 
$i\neq j$. Then
\[ \lvert \{n\in \{0,\ldots,M-1\}:2^\gamma\mid q_K(x_i)\}\rvert\ll \frac{K^2}{2^\gamma}+\frac 1\delta\bigg(\frac 1{2^\gamma}+\frac 1K\bigg). \]The implied constant is absolute.
Proof. In each Farey interval around 
$p/q$ such that 
$q$ is divisible by 
$2^\gamma$ there are at most 
$2/(Kq\delta )+1$ many points 
$x_i$. By summing over 
$p$ and 
$q$, we can bound the number of points in such intervals by
\begin{align*} \ll \sum_{\substack{1\leq q\leq K\\2^\gamma\mid q}} \sum_{1\leq p\leq q}\bigg(\frac 1{qK\delta}+1\bigg) &= \sum_{\substack{1\leq q\leq K\\2^\gamma\mid q}} \bigg(\frac 1{K\delta}+q\bigg)=(K2^{-\gamma}+1)\frac 1{K\delta}+ \sum_{\substack{1\leq q\leq K\\2^\gamma\mid q}}q\\ &\leq \frac 1{2^\gamma \delta}+\frac 1{K\delta}+ 2^\gamma \sum_{1\leq q'\leq\lfloor K2^{-\gamma} \rfloor }q' \ll\frac{K^2}{2^\gamma}+\frac 1{2^\gamma\delta}+\frac 1{K\delta}. \end{align*} We proceed to the proof of Lemma 5.1. Consider 
$\mathfrak p_1$ and the case ‘
$\alpha$ discrete’. In this case, we have 
$p_{2^{2\mu +2\sigma }}(\alpha /2^{2\mu })=\alpha$. Assume therefore that 
$\alpha =\alpha _0+2^{(k-1)\mu }\alpha _1$, where 
$\alpha _0\in \{0,\ldots ,2^{(k-1)\mu }-1\}$ and 
$\alpha _1\in \{0,\ldots ,2^{\lambda -(k-1)\mu }-1\}$.
Then
\[ \mathfrak p_1=p_{2^\sigma}(\alpha/2^{(k-1)\mu}) =p_{2^\sigma}(\alpha_0/2^{(k-1)\mu})+ q_{2^\sigma}(\alpha_0/2^{(k-1)\mu})\alpha_1. \]
By Lemma 5.3, using also (5.8), it follows that the number of 
$\alpha _0\in \{0,\ldots ,2^{(k-1)\mu }-1\}$ such that 
$2^\gamma \nmid q_{2^\sigma }(\alpha _0/2^{(k-1)\mu })$ is 
$2^{(k-1)\mu }(1-\mathcal {O}(2^{-\gamma }))$. For each such 
$\alpha _0$, we let 
$\alpha _1$ run through 
$\{0,\ldots ,2^{\lambda -(k-1)\mu }-1\}$. Then two occurrences 
$\alpha _1$, 
$\alpha _1'$ such that 
$2^{2\gamma }\mid \mathfrak p_1$ are separated by at least 
$2^\gamma$ steps; it follows that the number of such 
$\alpha _1$ is bounded by 
$2^{\lambda -(k-1)\mu -\gamma }$. Putting these errors together, we see that the number of 
$\alpha \in \{0,\ldots ,2^\lambda -1\}$ such that 
$2^{2\gamma }\nmid \mathfrak p_1$ is given by 
$2^{(k-1)\mu }(1-\mathcal {O}(2^{-\gamma }))2^{\lambda -(k-1)\mu }(1-\mathcal {O}(2^{-\gamma }))= 2^\lambda (1-\mathcal {O}(2^{-\gamma }))$.
Next, we consider the continuous case. We write 
$\alpha =\alpha _0+2^{2\mu }\alpha _1+2^{(k+1)\mu }\alpha _2$ , where 
$\alpha _0\in [0,2^{2\mu })$ is real and 
$\alpha _1 < 2^{(k-1)\mu }$ and 
$\alpha _2 < 2^{\lambda -(k+1)\mu }$ are nonnegative integers. Set 
$p=p_{2^{2\mu +2\sigma }}(\alpha _0/2^{2\mu })$ and 
$q=q_{2^{2\mu +2\sigma }}(\alpha _0/2^{2\mu })$. Then
\[ \frac{p_{2^{2\mu+2\sigma}}(\alpha/2^{2\mu})}{2^{(k-1)\mu}} =\frac{p+(\alpha_1+2^{(k-1)\mu}\alpha_2)q}{2^{(k-1)\mu}} =\frac{p+\alpha_1q}{2^{(k-1)\mu}}+\alpha_2q. \] By the approximation property (4.5) (note that 
$\sigma \geq 1$) we have
\begin{align*} \mathfrak p_1 &= \bigg\langle\bigg(\frac{p+\alpha_1q}{2^{(k-1)\mu}}+\alpha_2q\bigg) q_{2^\sigma} \bigg(\frac{p+\alpha_1q}{2^{(k-1)\mu}}\bigg)\bigg\rangle\\ &= \bigg\langle\frac{p+\alpha_1q}{2^{(k-1)\mu}} q_{2^\sigma} \bigg(\frac{p+\alpha_1q}{2^{(k-1)\mu}}\bigg)\bigg\rangle +\alpha_2q\, q_{2^\sigma}\bigg(\frac{p+\alpha_1q}{2^{(k-1)\mu}}\bigg) \end{align*}
and we note that the first summand does not depend on 
$\alpha _2$.
As 
$\alpha _0$ runs through 
$[0,2^{2\mu }]$, we have by Lemma 5.2 that 
$2^\gamma \nmid q$ in a set of measure 
$2^{2\mu }(1-\mathcal {O}(2^{-\gamma }+2^{-2\mu -2\sigma }))$. By (5.8), this is 
$2^{2\mu }(1-\mathcal {O}(2^{-\gamma }))$. Assume that 
$\alpha _0$ is such that 
$2^\gamma \nmid q$ and set 
$\gamma '=\nu _2(q)<\gamma$. Next, we let 
$\alpha _1$ run. We choose 
$x_j=\{(p+jq)/2^{(k-1)\mu }\}$ for 
$0\leq j < 2^{(k-1)\mu -\gamma '}$ and we note that these points satisfy 
$\lVert x_i-x_j\rVert \geq 1/2^{(k-1)\mu -\gamma '}$ for 
$i\neq j$. By Lemma 5.3 it follows that
\[ \bigg\{\alpha_1\in\{0,\ldots,2^{(k-1)\mu-\gamma'}-1\}: 2^\gamma\mid q_{2^\sigma}\bigg(\frac{p+\alpha_1 q}{2^{(k-1)\mu}}\bigg)\bigg\} \ll\frac{2^{2\sigma}}{2^{\gamma}}+2^{(k-1)\mu-\gamma'}\bigg(\frac 1{2^\gamma}+\frac 1{2^{\sigma}}\bigg). \]
By (5.8), this is 
$\ll 2^{(k-1)\mu -\gamma '-\gamma }$. Performing this also for the other intervals of length 
$2^{(k-1)\mu -\gamma '}$, we obtain
\[ \bigg\{\alpha_1\in\{0,\ldots,2^{(k-1)\mu}-1\}: 2^\gamma\mid q_{2^\sigma}\bigg(\frac{p+\alpha_1 q}{2^{(k-1)\mu}}\bigg)\bigg\}\ll 2^{(k-1)\mu-\gamma}. \] Finally, 
$\alpha _2$ runs through 
$\{0,\ldots ,2^{\lambda -(k+1)\mu }-1\}$ and we consider 
$\mathfrak p_1$. For given good 
$\alpha _1$ and 
$\alpha _0$ (such that 
$2^\gamma \nmid q$ and 
$2^\gamma \nmid q_{2^\sigma }((p+\alpha _1 q)/2^{(k-1)\mu })$), 
$\mathfrak p_1$ is an arithmetic progression in 
$\alpha _2$ whose common difference is not divisible by 
$2^{2\gamma }$. Similarly to the discrete case, it follows that 
$\mathfrak p_1$ is divisible by 
$2^{3\gamma }$ for at most 
$2^{\lambda -(k+1)\mu -\gamma }$ many 
$\alpha _2$. It follows that there is a set of measure
\[ 2^{2\mu}(1-\mathcal{O}(2^{-\gamma}))2^{(k-1)\mu}(1-\mathcal{O}(2^{-\gamma})) 2^{\lambda-(k+1)\mu}(1-\mathcal{O}(2^{-\gamma}))=2^\lambda(1-\mathcal{O}(2^{-\gamma})) \]
of 
$\alpha < 2^\lambda$ such that 
$2^{3\gamma }\nmid \mathfrak p_1$.
The cases 
$2\leq i\leq k$ do not require any new ideas; we only give a sketch of a proof. Let 
$2\leq i < k$. We treat the discrete and continuous cases in parallel. We write 
$\alpha =\alpha _0+2^{(i+1)\mu }\alpha _1+2^{(k+1)\mu }\alpha _2$, where 
$\alpha _0 < 2^{(i+1)\mu }$, and 
$\alpha _1 < 2^{(k-i)\mu }$ and 
$\alpha _2 < 2^{\lambda -(k+1)\mu }$ are nonnegative integers. Set 
$p=p_{2^{\mu +2\sigma }}(\alpha _0/2^{(i+1)\mu })$ and 
$q=q_{2^{\mu +2\sigma }}(\alpha _0/2^{(i+1)\mu })$. Then
\[ \mathfrak p_i=\bigg\langle\frac{p+\alpha_1q}{2^{(k-i)\mu}} q_{2^\sigma} \bigg(\frac{p+\alpha_1q}{2^{(k-i)\mu}}\bigg)\bigg\rangle +\alpha_2q q_{2^\sigma}\bigg(\frac{p+\alpha_1q}{2^{(k-i)\mu}}\bigg), \]
as before. By Lemmas 5.2 and 5.3, we have 
$2^\gamma \nmid q$ for 
$\alpha _0$ in a set of measure 
$2^{(i+1)\mu }(1-\mathcal {O}(2^{-\gamma }))$, where we used 
$2\mu +4\sigma \leq (i+1)\mu$ in the discrete case. (We note that this last inequality is the reason for defining 
$\mathfrak p_1$ separately, using 
$2^{2\mu }$ instead of 
$2^\mu$.) The remaining steps are as before and this case is finished.
Finally, in the case 
$i=k$, we write 
$\alpha =\alpha _0+2^{(k+1)\mu }\alpha _1$, where 
$\alpha _0<(k+1)\mu$ and 
$\alpha _1\in \{0,\ldots ,2^{\lambda -(k+1)\mu }-1\}$. Then
\[ \mathfrak p_k=p_{2^{\mu+\sigma}}(\alpha_0/2^{(k+1)\mu})+q_{2^{\mu+\sigma}} (\alpha_0/2^{(k+1)\mu})\alpha_1. \]
By Lemmas 5.2 and 5.3 and (5.8), we have 
$2^\gamma \mid q_{2^{\mu +\sigma }}(\alpha _0/2^{(k+1)\mu })$ for 
$\alpha _0$ in a set of measure 
$\mathcal {O}(2^{(k+1)\mu -\gamma })$ and the statement follows as before.
In total, we have a set of measure 
$2^\lambda (1-\mathcal {O}(2^{-\gamma }))$ of 
$\alpha < 2^\lambda$ such that 
$2^{3\gamma }\nmid \mathfrak p_i$ for all 
$i$.
Acknowledgments
The author wishes to thank Thomas Stoll for helpful discussions during his stay in Nancy, France, where the work on this project began. Moreover, the author wishes to thank Michael Drmota and Clemens Müllner for several fruitful discussions on the topic, and the anonymous referees for numerous suggestions. Finally, the author is indebted to Etienne Fouvry, Jakub Konieczny, Christian Mauduit and Gwendal Collet for valuable advice.
