 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur  $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
 ${\mathbb Q}$
${\mathbb Q}$
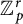 ${\mathbb Z}_p^r$
(1)
${\mathbb Z}_p^r$
(1)
 $p$-adic curves
$p$-adic curves
 $p$-adic
$p$-adic  $L$-functions at near-central points
$L$-functions at near-central points