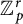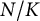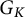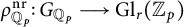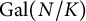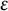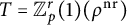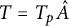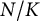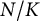1 Introduction
Let p be a prime and
![]() $N/K$
a finite Galois extension of p-adic number fields with group
$N/K$
a finite Galois extension of p-adic number fields with group
![]() $G := \mathrm {Gal}(N/K)$
. We write
$G := \mathrm {Gal}(N/K)$
. We write
![]() $G_K$
(resp.
$G_K$
(resp.
![]() $G_N$
) for the absolute Galois group of K (resp. N), and for each finite extension
$G_N$
) for the absolute Galois group of K (resp. N), and for each finite extension
![]() $E/{{{\mathbb Q}}_{p}}$
, we let
$E/{{{\mathbb Q}}_{p}}$
, we let
![]() $F_E$
denote the arithmetic Frobenius automorphism. Let V denote a p-adic representation of
$F_E$
denote the arithmetic Frobenius automorphism. Let V denote a p-adic representation of
![]() $G_K$
, and let
$G_K$
, and let
![]() $T \subseteq V$
be a
$T \subseteq V$
be a
![]() $G_K$
-stable
$G_K$
-stable
![]() ${\mathbb Z}_{p}$
-sublattice such that
${\mathbb Z}_{p}$
-sublattice such that
![]() $V = {{\mathbb Q}}_{p} \otimes _{{\mathbb Z}_{p}} T$
.
$V = {{\mathbb Q}}_{p} \otimes _{{\mathbb Z}_{p}} T$
.
As in [Reference Izychev and VenjakobIV16, Reference Bley and CobbeBC17], we write
![]() $C_{EP}^{na}(N/K, V)$
for the equivariant
$C_{EP}^{na}(N/K, V)$
for the equivariant
![]() $\varepsilon $
-constant conjecture (see, for example, Conjecture 3.1.1 in [Reference Bley and CobbeBC17]). For more details and some remarks on the history of the conjecture, we refer the interested reader to the introduction and Section 3.1 of [Reference Bley and CobbeBC17].
$\varepsilon $
-constant conjecture (see, for example, Conjecture 3.1.1 in [Reference Bley and CobbeBC17]). For more details and some remarks on the history of the conjecture, we refer the interested reader to the introduction and Section 3.1 of [Reference Bley and CobbeBC17].
In this manuscript, we will consider
![]() $C_{EP}^{na}(N/K, V)$
for higher dimensional unramified twists of
$C_{EP}^{na}(N/K, V)$
for higher dimensional unramified twists of
![]() ${\mathbb Z}_p^r(1)$
(which should be considered as the Tate module associated with
${\mathbb Z}_p^r(1)$
(which should be considered as the Tate module associated with
![]() $\mathbb {G}_m^r$
). More precisely, by [Reference CobbeCob18, Proposition 1.6], each matrix
$\mathbb {G}_m^r$
). More precisely, by [Reference CobbeCob18, Proposition 1.6], each matrix
![]() $U \in \mathrm {Gl}_r({\mathbb Z}_{p})$
gives rise to an unramified representation of
$U \in \mathrm {Gl}_r({\mathbb Z}_{p})$
gives rise to an unramified representation of
![]() $G_K$
by setting
$G_K$
by setting
![]() $\rho ^{\mathrm {nr}}(F_K) := U$
. We will be concerned with the module
$\rho ^{\mathrm {nr}}(F_K) := U$
. We will be concerned with the module
![]() $T={\mathbb Z}_p^r(1)(\rho ^{\mathrm {nr}})$
, which by [Reference CobbeCob18, Proposition 1.11] can be considered as the Tate module of an r-dimensional Lubin–Tate formal group.
$T={\mathbb Z}_p^r(1)(\rho ^{\mathrm {nr}})$
, which by [Reference CobbeCob18, Proposition 1.11] can be considered as the Tate module of an r-dimensional Lubin–Tate formal group.
We recall that for
![]() $r=1$
and representations
$r=1$
and representations
![]() $\rho ^{\mathrm {nr}}$
which are restrictions of unramified representations
$\rho ^{\mathrm {nr}}$
which are restrictions of unramified representations
![]() $\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}} : G_{{{\mathbb Q}}_{p}} \longrightarrow {\mathbb Z}_{p}^{\times }$
, Izychev and Venjakob in [Reference Izychev and VenjakobIV16] have proved the validity of
$\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}} : G_{{{\mathbb Q}}_{p}} \longrightarrow {\mathbb Z}_{p}^{\times }$
, Izychev and Venjakob in [Reference Izychev and VenjakobIV16] have proved the validity of
![]() $C_{EP}^{na}(N/K, V)$
for tame extensions
$C_{EP}^{na}(N/K, V)$
for tame extensions
![]() $N/K$
. The main result of [Reference Bley and CobbeBC17, Theorem 1] shows that
$N/K$
. The main result of [Reference Bley and CobbeBC17, Theorem 1] shows that
![]() $C_{EP}^{na}(N/K, V)$
holds for certain weakly and wildly ramified finite abelian extensions
$C_{EP}^{na}(N/K, V)$
holds for certain weakly and wildly ramified finite abelian extensions
![]() $N/K$
. In this context, we recall that
$N/K$
. In this context, we recall that
![]() $N/K$
is weakly ramified if the second ramification group in lower numbering is trivial. Generalizing these results, we will show the following theorem.
$N/K$
is weakly ramified if the second ramification group in lower numbering is trivial. Generalizing these results, we will show the following theorem.
Theorem 1.1 Let
![]() $N/K$
be a tame extension of p-adic number fields, and let
$N/K$
be a tame extension of p-adic number fields, and let
be an unramified representation of
![]() $G_{{\mathbb Q}_{p}}$
. Let
$G_{{\mathbb Q}_{p}}$
. Let
![]() $\rho ^{\mathrm {nr}}$
denote the restriction of
$\rho ^{\mathrm {nr}}$
denote the restriction of
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
![]() $G_K$
. Then,
$G_K$
. Then,
![]() $C_{EP}^{na}(N/K, V)$
is true for
$C_{EP}^{na}(N/K, V)$
is true for
![]() $N/K$
and
$N/K$
and
![]() $V = {\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}})$
, if
$V = {\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}})$
, if
![]() $\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
.
$\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
.
Remarks 1.2
-
(1) The condition
 $\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
holds, if and only if
$\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
holds, if and only if
 $H^2(N, T)$
is finite (see Section 2). It is also equivalent to
$H^2(N, T)$
is finite (see Section 2). It is also equivalent to
 $\left ( \mathbb Z_p^r(\rho ^{\mathrm {nr}}) \right )^{G_N} = 0$
.
$\left ( \mathbb Z_p^r(\rho ^{\mathrm {nr}}) \right )^{G_N} = 0$
. -
(2) If
 $r=1$
, then
$r=1$
, then
 $\det (\rho ^{\mathrm {nr}}(F_N) - 1) = 0$
if and only if
$\det (\rho ^{\mathrm {nr}}(F_N) - 1) = 0$
if and only if
 $\rho ^{\mathrm {nr}} |_{G_N} = 1$
. If
$\rho ^{\mathrm {nr}} |_{G_N} = 1$
. If
 $r> 1$
, then there are “mixed” cases where both
$r> 1$
, then there are “mixed” cases where both
 $\rho ^{\mathrm {nr}} |_{G_N} \ne 1$
and
$\rho ^{\mathrm {nr}} |_{G_N} \ne 1$
and
 $\det (\rho ^{\mathrm {nr}}(F_N) - 1) = 0$
(see, e.g., [Reference CobbeCob18, Example 3.18]).
$\det (\rho ^{\mathrm {nr}}(F_N) - 1) = 0$
(see, e.g., [Reference CobbeCob18, Example 3.18]). -
(3) If
 $\rho ^{\mathrm {nr}} |_{G_N}=1$
, then twisting commutes with taking
$\rho ^{\mathrm {nr}} |_{G_N}=1$
, then twisting commutes with taking
 $G_N$
-cohomology, so that we expect that
$G_N$
-cohomology, so that we expect that
 $C_{EP}^{na}(N/K, V)$
can be proved relying on the fact that the conjecture is known in the untwisted case by [Reference BreuningBre04b]. In the case
$C_{EP}^{na}(N/K, V)$
can be proved relying on the fact that the conjecture is known in the untwisted case by [Reference BreuningBre04b]. In the case
 $r=1$
, this is sketched in [Reference Izychev and VenjakobIV16, Appendix A.1]; however, for
$r=1$
, this is sketched in [Reference Izychev and VenjakobIV16, Appendix A.1]; however, for
 $r>1$
, we have not checked the details.
$r>1$
, we have not checked the details.
In the weakly ramified setting, we will prove the following theorem.
Theorem 1.3 Let p be an odd prime. Let
![]() $K/{\mathbb Q}_p$
be the unramified extension of degree m, and let
$K/{\mathbb Q}_p$
be the unramified extension of degree m, and let
![]() $N/K$
be a weakly and wildly ramified finite abelian extension with cyclic ramification group. Let d denote the inertia degree of
$N/K$
be a weakly and wildly ramified finite abelian extension with cyclic ramification group. Let d denote the inertia degree of
![]() $N/K$
, let
$N/K$
, let
![]() $\tilde d$
denote the order of
$\tilde d$
denote the order of
![]() $\rho ^{\mathrm {nr}}(F_N) \text { mod } p$
in
$\rho ^{\mathrm {nr}}(F_N) \text { mod } p$
in
![]() $\mathrm {Gl}_r({{\mathbb Z}_{p}}/p{{\mathbb Z}_{p}})$
, and assume that m and d are relatively prime. Let
$\mathrm {Gl}_r({{\mathbb Z}_{p}}/p{{\mathbb Z}_{p}})$
, and assume that m and d are relatively prime. Let
be an unramified representation of
![]() $G_{{\mathbb Q}_{p}}$
, and let
$G_{{\mathbb Q}_{p}}$
, and let
![]() $\rho ^{\mathrm {nr}}$
denote the restriction of
$\rho ^{\mathrm {nr}}$
denote the restriction of
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
![]() $G_K$
. Assume that
$G_K$
. Assume that
![]() $\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
and, in addition, that one of the following three conditions holds:
$\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
and, in addition, that one of the following three conditions holds:
-
(a)
 $\rho ^{\mathrm {nr}}(F_N)-1$
is invertible modulo p;
$\rho ^{\mathrm {nr}}(F_N)-1$
is invertible modulo p; -
(b)
 $\rho ^{\mathrm {nr}}(F_N)\equiv 1\pmod {p}$
;
$\rho ^{\mathrm {nr}}(F_N)\equiv 1\pmod {p}$
; -
(c)
 $\gcd (\tilde d,m)=1$
and
$\gcd (\tilde d,m)=1$
and
 $\det (\rho ^{\mathrm {nr}}(F_N)^{\tilde d} - 1) \ne 0$
.
$\det (\rho ^{\mathrm {nr}}(F_N)^{\tilde d} - 1) \ne 0$
.
Then,
![]() $C_{EP}^{na}(N/K, V)$
is true for
$C_{EP}^{na}(N/K, V)$
is true for
![]() $N/K$
and
$N/K$
and
![]() $V = {\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}})$
.
$V = {\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}})$
.
Remarks 1.4
-
(a) In the case
 $r=1$
, we define as in [Reference Bley and CobbeBC17, equation (14)] a nonnegative integer
$r=1$
, we define as in [Reference Bley and CobbeBC17, equation (14)] a nonnegative integer
 $\omega = \omega _N := v_p(1-\rho ^{\mathrm {nr}}(F_N))$
. Note that the conditions (a) and (b) concerning the reduction of
$\omega = \omega _N := v_p(1-\rho ^{\mathrm {nr}}(F_N))$
. Note that the conditions (a) and (b) concerning the reduction of
 $\rho ^{\mathrm {nr}}(F_N)$
modulo p generalize the cases
$\rho ^{\mathrm {nr}}(F_N)$
modulo p generalize the cases
 $\omega =0$
and
$\omega =0$
and
 $\omega>0$
, which were studied separately in [Reference Bley and CobbeBC17], and which exhaust all the possible cases when
$\omega>0$
, which were studied separately in [Reference Bley and CobbeBC17], and which exhaust all the possible cases when
 $r=1$
. In the higher dimensional setting of the present paper, however, this is not true, even under the assumption
$r=1$
. In the higher dimensional setting of the present paper, however, this is not true, even under the assumption
 $\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
. To deal with the remaining cases, our strategy of proof is to replace the field N by its unramified extension of degree
$\det (\rho ^{\mathrm {nr}}(F_N) - 1) \ne 0$
. To deal with the remaining cases, our strategy of proof is to replace the field N by its unramified extension of degree
 $\tilde d$
and to use functoriality with respect to change of fields (see Prop. 7.2). For technical reasons, this forces us to require hypothesis (c).
$\tilde d$
and to use functoriality with respect to change of fields (see Prop. 7.2). For technical reasons, this forces us to require hypothesis (c). -
(b) By [Reference CobbeCob18, Lemma 1.1], we know that
 $\tilde d$
is a divisor of
$\tilde d$
is a divisor of
 $p^st$
with
$p^st$
with
 $s = (r-1)r/2$
and
$s = (r-1)r/2$
and
 $t = \prod _{i=1}^r(p^i-1)$
.
$t = \prod _{i=1}^r(p^i-1)$
.
In a more geometrical setting, if
![]() $A/{\mathbb Q}_p$
is an abelian variety of dimension r with good ordinary reduction, then by [Reference CobbeCob18, Proposition 1.12] the Tate module of the associated formal group
$A/{\mathbb Q}_p$
is an abelian variety of dimension r with good ordinary reduction, then by [Reference CobbeCob18, Proposition 1.12] the Tate module of the associated formal group
![]() $\hat {A}$
is isomorphic to
$\hat {A}$
is isomorphic to
![]() $\mathbb Z_p^r(1)(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
for an appropriate choice of
$\mathbb Z_p^r(1)(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
for an appropriate choice of
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
. Here, it is worth to remark that the converse is not true, i.e., not every module
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
. Here, it is worth to remark that the converse is not true, i.e., not every module
![]() $\mathbb Z_p^r(1)(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
comes from an abelian variety with good ordinary reduction. In this setting, by a result of Mazur [Reference MazurMaz72, Corollary 4.38], we know that
$\mathbb Z_p^r(1)(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
comes from an abelian variety with good ordinary reduction. In this setting, by a result of Mazur [Reference MazurMaz72, Corollary 4.38], we know that
![]() $\det (\rho ^{\mathrm {nr}}(F_L) - 1) \ne 0$
is automatically satisfied for any finite extension
$\det (\rho ^{\mathrm {nr}}(F_L) - 1) \ne 0$
is automatically satisfied for any finite extension
![]() $L/{{\mathbb Q}_{p}}$
(see Lemma 8.1).
$L/{{\mathbb Q}_{p}}$
(see Lemma 8.1).
Theorem 1.5 Let
![]() $N/K$
be a tame extension of p-adic number fields, and let
$N/K$
be a tame extension of p-adic number fields, and let
![]() $A/{\mathbb Q}_p$
be an r-dimensional abelian variety with good ordinary reduction. Let
$A/{\mathbb Q}_p$
be an r-dimensional abelian variety with good ordinary reduction. Let
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
be the unramified representation induced by the Tate module
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
be the unramified representation induced by the Tate module
![]() $T_p\hat A$
of the formal group
$T_p\hat A$
of the formal group
![]() $\hat A$
of A, and let
$\hat A$
of A, and let
![]() $\rho ^{\mathrm {nr}}$
be the restriction of
$\rho ^{\mathrm {nr}}$
be the restriction of
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
![]() $G_K$
. Then,
$G_K$
. Then,
![]() $C_{EP}^{na}(N/K, V)$
is true for
$C_{EP}^{na}(N/K, V)$
is true for
![]() $V = {\mathbb Q}_p\otimes _{{\mathbb Z}_{p}}T_p\hat A$
.
$V = {\mathbb Q}_p\otimes _{{\mathbb Z}_{p}}T_p\hat A$
.
Theorem 1.6 Let p be an odd prime, and let
![]() $A/{\mathbb Q}_p$
be an r-dimensional abelian variety with good ordinary reduction. Let
$A/{\mathbb Q}_p$
be an r-dimensional abelian variety with good ordinary reduction. Let
![]() $K/{{\mathbb Q}_{p}}$
be the unramified extension of degree m, and let
$K/{{\mathbb Q}_{p}}$
be the unramified extension of degree m, and let
![]() $N/K$
be a weakly and wildly ramified finite abelian extension with cyclic ramification group. Let
$N/K$
be a weakly and wildly ramified finite abelian extension with cyclic ramification group. Let
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
be the unramified representation induced by the Tate module
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
be the unramified representation induced by the Tate module
![]() $T_p\hat A$
of the formal group
$T_p\hat A$
of the formal group
![]() $\hat A$
of A, and let
$\hat A$
of A, and let
![]() $\rho ^{\mathrm {nr}}$
be the restriction of
$\rho ^{\mathrm {nr}}$
be the restriction of
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
to
![]() $G_K$
. Let d denote the inertia degree of
$G_K$
. Let d denote the inertia degree of
![]() $N/K$
, and let
$N/K$
, and let
![]() $\tilde d$
denote the order of
$\tilde d$
denote the order of
![]() $\rho ^{\mathrm {nr}}(F_N) \text { mod } p$
in
$\rho ^{\mathrm {nr}}(F_N) \text { mod } p$
in
![]() $\mathrm {Gl}_r({{\mathbb Z}_{p}}/p{{\mathbb Z}_{p}})$
. Assume that m and d are relatively prime, and, in addition, that one of the following conditions holds:
$\mathrm {Gl}_r({{\mathbb Z}_{p}}/p{{\mathbb Z}_{p}})$
. Assume that m and d are relatively prime, and, in addition, that one of the following conditions holds:
-
(a)
 $\rho ^{\mathrm {nr}}(F_N)-1$
is invertible modulo p;
$\rho ^{\mathrm {nr}}(F_N)-1$
is invertible modulo p; -
(b)
 $\rho ^{\mathrm {nr}}(F_N)\equiv 1\pmod {p}$
;
$\rho ^{\mathrm {nr}}(F_N)\equiv 1\pmod {p}$
; -
(c)
 $(m, \tilde d) = 1$
.
$(m, \tilde d) = 1$
.
Then,
![]() $C_{EP}^{na}(N/K, V)$
is true for
$C_{EP}^{na}(N/K, V)$
is true for
![]() $V = {\mathbb Q}_p\otimes _{{\mathbb Z}_{p}}T_p\hat A$
.
$V = {\mathbb Q}_p\otimes _{{\mathbb Z}_{p}}T_p\hat A$
.
To conclude this introduction, we reference forthcoming work of Nickel [Reference NickelNic18] and a forthcoming joint paper of Burns and Nickel [Reference Burns and NickelBN] where an Iwasawa theoretic approach to
![]() $C_{EP}^{na}(N/K, V)$
is developed. In a little more detail, Nickel formulates an Iwasawa theoretic analogue of
$C_{EP}^{na}(N/K, V)$
is developed. In a little more detail, Nickel formulates an Iwasawa theoretic analogue of
![]() $C_{EP}^{na}(N/K, {{\mathbb Q}_{p}}(1))$
, call it
$C_{EP}^{na}(N/K, {{\mathbb Q}_{p}}(1))$
, call it
![]() $C_{EP}^{na}(N_{\infty }/K, {{\mathbb Q}_{p}}(1))$
for the purpose of this introduction, for the extension
$C_{EP}^{na}(N_{\infty }/K, {{\mathbb Q}_{p}}(1))$
for the purpose of this introduction, for the extension
![]() $N_{\infty }/K$
where
$N_{\infty }/K$
where
![]() $N_{\infty }/N$
is the unramified
$N_{\infty }/N$
is the unramified
![]() ${{\mathbb Z}_{p}}$
-extension of N. Then, in a second paper, Burns and Nickel show that
${{\mathbb Z}_{p}}$
-extension of N. Then, in a second paper, Burns and Nickel show that
![]() $C_{EP}^{na}(N_{\infty }/K, {{\mathbb Q}_{p}}(1))$
holds if and only if
$C_{EP}^{na}(N_{\infty }/K, {{\mathbb Q}_{p}}(1))$
holds if and only if
![]() $C_{EP}^{na}(E/F, {{\mathbb Q}_{p}}(1))$
holds for all finite Galois extensions
$C_{EP}^{na}(E/F, {{\mathbb Q}_{p}}(1))$
holds for all finite Galois extensions
![]() $E/F$
such that
$E/F$
such that
![]() $K \subseteq F \subseteq E \subseteq N_{\infty }$
. Furthermore, they prove a certain twist invariance of the conjecture. If
$K \subseteq F \subseteq E \subseteq N_{\infty }$
. Furthermore, they prove a certain twist invariance of the conjecture. If
![]() $\chi ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
is a one-dimensional unramified character, they show that
$\chi ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
is a one-dimensional unramified character, they show that
![]() $C_{EP}^{na}(N_{\infty } N'/K, {{\mathbb Q}_{p}}(1))$
holds if and only if
$C_{EP}^{na}(N_{\infty } N'/K, {{\mathbb Q}_{p}}(1))$
holds if and only if
![]() $C_{EP}^{na}(E/F, {{\mathbb Q}_{p}}(1)(\chi ^{\mathrm {nr}}))$
holds for all finite Galois extensions
$C_{EP}^{na}(E/F, {{\mathbb Q}_{p}}(1)(\chi ^{\mathrm {nr}}))$
holds for all finite Galois extensions
![]() $E/F$
such that
$E/F$
such that
![]() $K \subseteq F \subseteq E \subseteq N_{\infty } N'$
where
$K \subseteq F \subseteq E \subseteq N_{\infty } N'$
where
![]() $N'/N$
is a certain unramified extension of degree dividing
$N'/N$
is a certain unramified extension of degree dividing
![]() $p-1$
. It will be very interesting to see how this Iwasawa theoretic approach will carry over to the higher dimensional case.
$p-1$
. It will be very interesting to see how this Iwasawa theoretic approach will carry over to the higher dimensional case.
1.1 Notations
We will mostly rely on the notation of [Reference Bley and CobbeBC17, Reference CobbeCob18]. For a field L, we write
![]() $L^c$
for its algebraic closure; for any subfield L of
$L^c$
for its algebraic closure; for any subfield L of
![]() ${\mathbb Q}_p^c$
, we let
${\mathbb Q}_p^c$
, we let
![]() $\bar L$
denote the p-adic completion of L. In this paper,
$\bar L$
denote the p-adic completion of L. In this paper,
![]() $N/K$
will always denote a finite Galois extension of p-adic number fields. We write
$N/K$
will always denote a finite Galois extension of p-adic number fields. We write
![]() $N^{\mathrm {nr}}$
for the maximal unramified extension, and then set
$N^{\mathrm {nr}}$
for the maximal unramified extension, and then set
![]() $N_0=\overline {N^{\mathrm {nr}}}$
and denote by
$N_0=\overline {N^{\mathrm {nr}}}$
and denote by
![]() $\widehat {N_0^{\times }}$
the p-completion of
$\widehat {N_0^{\times }}$
the p-completion of
![]() $N_0^{\times }$
. Let
$N_0^{\times }$
. Let
![]() $N_1$
be the maximal unramified subextension of
$N_1$
be the maximal unramified subextension of
![]() $N/{{\mathbb Q}_{p}}$
. We will denote by
$N/{{\mathbb Q}_{p}}$
. We will denote by
![]() $e_{N/K}$
and
$e_{N/K}$
and
![]() $d_{N/K}$
the ramification index and the inertia degree of
$d_{N/K}$
the ramification index and the inertia degree of
![]() $N/K$
,
$N/K$
,
![]() $\mathcal {O}_N$
will be the ring of integers of N, and
$\mathcal {O}_N$
will be the ring of integers of N, and
![]() $U_N$
will be its group of units. We also set
$U_N$
will be its group of units. We also set
![]() $\Lambda _N=\prod _r \widehat {N_0^{\times }}(\rho ^{\mathrm {nr}})$
,
$\Lambda _N=\prod _r \widehat {N_0^{\times }}(\rho ^{\mathrm {nr}})$
,
![]() $\Upsilon _N=\prod _r \widehat {U_{N_0}}(\rho ^{\mathrm {nr}})$
, and
$\Upsilon _N=\prod _r \widehat {U_{N_0}}(\rho ^{\mathrm {nr}})$
, and
![]() $\mathcal Z=\mathbb Z_p^r(\rho ^{\mathrm {nr}})$
, and we will mostly use an additive notation for the (twisted) action of the absolute Galois group
$\mathcal Z=\mathbb Z_p^r(\rho ^{\mathrm {nr}})$
, and we will mostly use an additive notation for the (twisted) action of the absolute Galois group
![]() $G_N$
. The elements fixed by the action of
$G_N$
. The elements fixed by the action of
![]() $G_N$
will be denoted by
$G_N$
will be denoted by
![]() $\Lambda _N^{G_N}$
,
$\Lambda _N^{G_N}$
,
![]() $\Upsilon _N^{G_N}$
, and
$\Upsilon _N^{G_N}$
, and
![]() $\mathcal Z^{G_N}$
, respectively.
$\mathcal Z^{G_N}$
, respectively.
Let
![]() $\varphi $
be the absolute Frobenius automorphism, let
$\varphi $
be the absolute Frobenius automorphism, let
![]() $F_N$
be the Frobenius automorphism of N, and let
$F_N$
be the Frobenius automorphism of N, and let
![]() $F=F_K$
be the Frobenius of K.
$F=F_K$
be the Frobenius of K.
For an r-dimensional formal group
![]() $\mathcal F$
, we denote by
$\mathcal F$
, we denote by
![]() $\mathcal F(\mathfrak p_N^{(r)})$
the group structure on
$\mathcal F(\mathfrak p_N^{(r)})$
the group structure on
![]() $\prod _r\mathfrak p_N$
induced by
$\prod _r\mathfrak p_N$
induced by
![]() $\mathcal F$
.
$\mathcal F$
.
For any ring R, we denote by
![]() $M_r(R)$
the ring of
$M_r(R)$
the ring of
![]() $r\times r$
matrices with coefficients in R and by
$r\times r$
matrices with coefficients in R and by
![]() $\mathrm {Gl}_r(R)$
the group of invertible matrices. A unity matrix will always be denoted simply by
$\mathrm {Gl}_r(R)$
the group of invertible matrices. A unity matrix will always be denoted simply by
![]() $1$
. In addition, we write
$1$
. In addition, we write
![]() $Z(R)$
for the centre of R.
$Z(R)$
for the centre of R.
If
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Sigma $
are unital rings and
$\Sigma $
are unital rings and
![]() $\Lambda \longrightarrow \Sigma $
a ring homomorphism, then we write
$\Lambda \longrightarrow \Sigma $
a ring homomorphism, then we write
![]() $K_0(\Lambda , \Sigma )$
for the relative algebraic K-group defined by Swan [Reference SwanSwa70, p. 215]. If
$K_0(\Lambda , \Sigma )$
for the relative algebraic K-group defined by Swan [Reference SwanSwa70, p. 215]. If
![]() $\Sigma = L[G]$
for a finite group G and a field extension
$\Sigma = L[G]$
for a finite group G and a field extension
![]() $L/{{\mathbb Q}_{p}}$
, we write
$L/{{\mathbb Q}_{p}}$
, we write
![]() $\mathrm {Nrd}_{\Sigma } \colon K_1(\Sigma ) \longrightarrow Z(\Sigma )^{\times }$
for the map on
$\mathrm {Nrd}_{\Sigma } \colon K_1(\Sigma ) \longrightarrow Z(\Sigma )^{\times }$
for the map on
![]() $K_1$
induced by the reduced norm map. We will only be concerned with cases where
$K_1$
induced by the reduced norm map. We will only be concerned with cases where
![]() $\mathrm {Nrd}_{\Sigma }$
is an isomorphism. In this case, we set
$\mathrm {Nrd}_{\Sigma }$
is an isomorphism. In this case, we set
![]() $\hat \partial ^1_{\Lambda , \Sigma } := \partial ^1_{\Lambda , \Sigma } \circ \mathrm {Nrd}_{\Sigma }^{-1}\colon Z(\Sigma )^{\times } \longrightarrow K_0(\Lambda , \Sigma )$
where
$\hat \partial ^1_{\Lambda , \Sigma } := \partial ^1_{\Lambda , \Sigma } \circ \mathrm {Nrd}_{\Sigma }^{-1}\colon Z(\Sigma )^{\times } \longrightarrow K_0(\Lambda , \Sigma )$
where
![]() $\partial ^1_{\Lambda , \Sigma } \colon K_1(\Sigma ) \longrightarrow K_0(\Lambda , \Sigma )$
is the canonical map. If there is no danger of confusion, we will often abbreviate
$\partial ^1_{\Lambda , \Sigma } \colon K_1(\Sigma ) \longrightarrow K_0(\Lambda , \Sigma )$
is the canonical map. If there is no danger of confusion, we will often abbreviate
![]() $\hat \partial ^1_{\Lambda , \Sigma }$
to
$\hat \partial ^1_{\Lambda , \Sigma }$
to
![]() $\hat \partial ^1$
.
$\hat \partial ^1$
.
For any
![]() ${{\mathbb Z}_{p}}$
-module X and any ring extension
${{\mathbb Z}_{p}}$
-module X and any ring extension
![]() $R/{{\mathbb Z}_{p}}$
, we set
$R/{{\mathbb Z}_{p}}$
, we set
![]() $X_R := R \otimes _{{\mathbb Z}_{p}} X$
.
$X_R := R \otimes _{{\mathbb Z}_{p}} X$
.
1.2 Plan of the manuscript
We will start recalling some results on the cohomology of
![]() $\mathbb Z_p^r(1)$
which are proved in [Reference CobbeCob18]. We will also formulate a finiteness hypothesis (F), which we will assume throughout the paper, and we will show some basic consequences of (F). After a short digression on the formal logarithm and exponential function in higher dimension in Section 3, we can start our study of the conjecture
$\mathbb Z_p^r(1)$
which are proved in [Reference CobbeCob18]. We will also formulate a finiteness hypothesis (F), which we will assume throughout the paper, and we will show some basic consequences of (F). After a short digression on the formal logarithm and exponential function in higher dimension in Section 3, we can start our study of the conjecture
![]() $C_{EP}^{na}(N/K, V)$
.
$C_{EP}^{na}(N/K, V)$
.
As in [Reference Bley and CobbeBC17], which was motivated by the work in [Reference Izychev and VenjakobIV16], we define an element
 $$ \begin{align} \begin{aligned} R_{N/K}&= C_{N/K} + U_{\mathrm{cris}}+rm\hat\partial^1_{{\mathbb Z_p[G]}, {B_{\mathrm{dR}}}[G]}(t) - m U_{tw}(\rho^{\mathrm{nr}}_{{\mathbb Q}_{p}}) \\ &\ \kern1pt\qquad\quad- r U_{N/K} + \hat\partial^1_{{\mathbb Z_p[G]}, {B_{\mathrm{dR}}}[G]}(\varepsilon_D(N/K,V)) \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} R_{N/K}&= C_{N/K} + U_{\mathrm{cris}}+rm\hat\partial^1_{{\mathbb Z_p[G]}, {B_{\mathrm{dR}}}[G]}(t) - m U_{tw}(\rho^{\mathrm{nr}}_{{\mathbb Q}_{p}}) \\ &\ \kern1pt\qquad\quad- r U_{N/K} + \hat\partial^1_{{\mathbb Z_p[G]}, {B_{\mathrm{dR}}}[G]}(\varepsilon_D(N/K,V)) \end{aligned}\end{align} $$
in the relative algebraic K-group
![]() $K_0({\mathbb Z_p[G]},{{\mathbb Q}_p[G]})$
. The conjecture
$K_0({\mathbb Z_p[G]},{{\mathbb Q}_p[G]})$
. The conjecture
![]() $C_{EP}^{na}(N/K, V)$
is then equivalent to the vanishing of
$C_{EP}^{na}(N/K, V)$
is then equivalent to the vanishing of
![]() $R_{N/K}$
.
$R_{N/K}$
.
Actually, the element
![]() $R_{N/K}$
as defined in (1.1) differs from [Reference Bley and CobbeBC17, equation (17)] by the term
$R_{N/K}$
as defined in (1.1) differs from [Reference Bley and CobbeBC17, equation (17)] by the term
![]() $m U_{tw}(\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}})$
. This new term emerges from the computation of the cohomological term
$m U_{tw}(\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}})$
. This new term emerges from the computation of the cohomological term
![]() $C_{N/K}$
, which was slightly incorrect in [Reference Bley and CobbeBC17], and has to be compensated in the definition of
$C_{N/K}$
, which was slightly incorrect in [Reference Bley and CobbeBC17], and has to be compensated in the definition of
![]() $R_{N/K}$
. For more details on this issue, we refer the reader to Remark 6.6.
$R_{N/K}$
. For more details on this issue, we refer the reader to Remark 6.6.
We will explicitly compute the terms
![]() $C_{N/K}$
,
$C_{N/K}$
,
![]() $U_{\mathrm {cris}}$
, and
$U_{\mathrm {cris}}$
, and
![]() $\hat \partial ^1_{{\mathbb Z_p[G]}, {B_{\mathrm {dR}}}[G]}(\varepsilon _D(N/K,V))$
in the definition of
$\hat \partial ^1_{{\mathbb Z_p[G]}, {B_{\mathrm {dR}}}[G]}(\varepsilon _D(N/K,V))$
in the definition of
![]() $R_{N/K}$
and then use these results to prove
$R_{N/K}$
and then use these results to prove
![]() $C_{EP}^{na}(N/K, V)$
when
$C_{EP}^{na}(N/K, V)$
when
![]() $N/K$
is tame (Theorem 1.1) and, under some additional hypotheses, also when
$N/K$
is tame (Theorem 1.1) and, under some additional hypotheses, also when
![]() $N/K$
is weakly and wildly ramified (Theorem 1.3). This generalizes previous work for
$N/K$
is weakly and wildly ramified (Theorem 1.3). This generalizes previous work for
![]() $r = 1$
of Izychev and Venjakob in [Reference Izychev and VenjakobIV16] in the tame case and the authors in [Reference Bley and CobbeBC17] in the weakly ramified case.
$r = 1$
of Izychev and Venjakob in [Reference Izychev and VenjakobIV16] in the tame case and the authors in [Reference Bley and CobbeBC17] in the weakly ramified case.
2 The cohomology of
 ${\mathbb Z}_p^r(1)(\rho ^{\text {nr}})$
${\mathbb Z}_p^r(1)(\rho ^{\text {nr}})$
Let
![]() $u \in \mathrm {Gl}_r({{\mathbb Z}_{p}})$
, and let
$u \in \mathrm {Gl}_r({{\mathbb Z}_{p}})$
, and let
![]() $\rho ^{\mathrm {nr}} = \rho _u \colon G_{{\mathbb Q}_{p}} \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
denote the unramified representation attached to u by [Reference CobbeCob18, Proposition 1.6]. By [Reference HazewinkelHaz78, Section 13.3], there is a unique r-dimensional Lubin–Tate formal group
$\rho ^{\mathrm {nr}} = \rho _u \colon G_{{\mathbb Q}_{p}} \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
denote the unramified representation attached to u by [Reference CobbeCob18, Proposition 1.6]. By [Reference HazewinkelHaz78, Section 13.3], there is a unique r-dimensional Lubin–Tate formal group
![]() $\mathcal F = \mathcal F_{pu^{-1}}$
attached to the parameter
$\mathcal F = \mathcal F_{pu^{-1}}$
attached to the parameter
![]() $pu^{-1}$
. As in [Reference CobbeCob18, Proposition 1.10], we can construct an isomorphism
$pu^{-1}$
. As in [Reference CobbeCob18, Proposition 1.10], we can construct an isomorphism
![]() $\theta \colon \mathcal F \longrightarrow \mathbb {G}_m^r$
defined over the completion
$\theta \colon \mathcal F \longrightarrow \mathbb {G}_m^r$
defined over the completion
![]() $\overline {{{\mathbb Q}_p^{\mathrm {nr}}}}$
of
$\overline {{{\mathbb Q}_p^{\mathrm {nr}}}}$
of
![]() ${{\mathbb Q}_p^{\mathrm {nr}}}$
such that
${{\mathbb Q}_p^{\mathrm {nr}}}$
such that
where
![]() $\varepsilon \in \mathrm {Gl}_r(\overline {\mathbb Z_p^{\mathrm {nr}}})$
has the defining property
$\varepsilon \in \mathrm {Gl}_r(\overline {\mathbb Z_p^{\mathrm {nr}}})$
has the defining property
![]() $\varphi (\varepsilon ^{-1})\varepsilon = u^{-1}$
. In the following, we set
$\varphi (\varepsilon ^{-1})\varepsilon = u^{-1}$
. In the following, we set
![]() $T := \mathbb Z_p^r(1)(\rho ^{\mathrm {nr}})$
, and for future reference, we recall that T is isomorphic to the p-adic Tate module
$T := \mathbb Z_p^r(1)(\rho ^{\mathrm {nr}})$
, and for future reference, we recall that T is isomorphic to the p-adic Tate module
![]() $T_p\mathcal F$
of
$T_p\mathcal F$
of
![]() $\mathcal F$
by [Reference CobbeCob18, Proposition 1.11].
$\mathcal F$
by [Reference CobbeCob18, Proposition 1.11].
Let
![]() $N/{{\mathbb Q}_{p}}$
be a finite field extension, and let
$N/{{\mathbb Q}_{p}}$
be a finite field extension, and let
![]() $N_0 = \overline {N^{\mathrm {nr}}}$
denote the completion of the maximal unramified extension of N. Following [Reference CobbeCob18], we define
$N_0 = \overline {N^{\mathrm {nr}}}$
denote the completion of the maximal unramified extension of N. Following [Reference CobbeCob18], we define
Then, by [Reference CobbeCob18, Corollary 3.16], we have
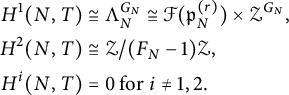 $$ \begin{align*} H^1(N, T) &\cong \Lambda_N^{G_N} \cong \mathcal F(\mathfrak p_N^{(r)}) \times \mathcal{Z}^{G_N}, \\ H^2(N, T) &\cong \mathcal{Z} / (F_N - 1)\mathcal{Z}, \\ H^i(N, T) &= 0 \text{ for } i \ne 1,2. \end{align*} $$
$$ \begin{align*} H^1(N, T) &\cong \Lambda_N^{G_N} \cong \mathcal F(\mathfrak p_N^{(r)}) \times \mathcal{Z}^{G_N}, \\ H^2(N, T) &\cong \mathcal{Z} / (F_N - 1)\mathcal{Z}, \\ H^i(N, T) &= 0 \text{ for } i \ne 1,2. \end{align*} $$
Remark 2.1 We point out that the above isomorphisms are induced by the explicit representative
![]() $C^{\bullet }_{N, \mathcal F}$
of
$C^{\bullet }_{N, \mathcal F}$
of
![]() $R\Gamma (N, T)$
constructed in [Reference CobbeCob18, Theorem 3.15]. In the formulation of
$R\Gamma (N, T)$
constructed in [Reference CobbeCob18, Theorem 3.15]. In the formulation of
![]() $C_{EP}^{na}(N/K, V)$
, however, we will use the identification of the cohomology modules resulting from the use of continuous cochain cohomology. We will address this problem in Section 6.1.
$C_{EP}^{na}(N/K, V)$
, however, we will use the identification of the cohomology modules resulting from the use of continuous cochain cohomology. We will address this problem in Section 6.1.
For each finite field extension
![]() $N/{{\mathbb Q}_{p}}$
, we set
$N/{{\mathbb Q}_{p}}$
, we set
and in the sequel, always assume the following finiteness hypothesis.
Hypothesis (F):
![]() $\det (U_N - 1) \ne 0$
.
$\det (U_N - 1) \ne 0$
.
This hypothesis clearly implies (and, in fact, is equivalent to)
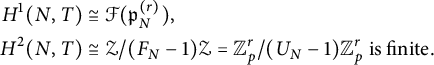 $$ \begin{align*} H^1(N, T) &\cong {\mathcal F}({\mathfrak p}_N^{(r)}), \\ H^2(N, T) &\cong {\mathcal{Z}} / (F_N - 1){\mathcal{Z}} = {\mathbb Z}_p^r / (U_N-1){\mathbb Z}_p^r \text{ is finite}. \end{align*} $$
$$ \begin{align*} H^1(N, T) &\cong {\mathcal F}({\mathfrak p}_N^{(r)}), \\ H^2(N, T) &\cong {\mathcal{Z}} / (F_N - 1){\mathcal{Z}} = {\mathbb Z}_p^r / (U_N-1){\mathbb Z}_p^r \text{ is finite}. \end{align*} $$
The elementary divisor theorem immediately implies
where
![]() $v_p$
denotes the normalized p-adic valuation.
$v_p$
denotes the normalized p-adic valuation.
We first study the case when
![]() $N/K$
is tame.
$N/K$
is tame.
Proposition 2.2 Let
![]() $N/K$
be a finite Galois extension with Galois group
$N/K$
be a finite Galois extension with Galois group
![]() $G = {\mathrm {Gal}}(N/K)$
. Assume that Hypothesis (F) holds. If
$G = {\mathrm {Gal}}(N/K)$
. Assume that Hypothesis (F) holds. If
![]() $N/K$
is tame, then both
$N/K$
is tame, then both
![]() $H^1(N, T)$
and
$H^1(N, T)$
and
![]() $H^2(N, T)$
are G-cohomologically trivial.
$H^2(N, T)$
are G-cohomologically trivial.
Proof By [Reference CobbeCob18, Theorem 3.3 and Lemma 2.2], it suffices to show that
![]() $\mathcal {Z} / (F_N - 1)\mathcal {Z} = {\mathbb Z}_p^r / (U_N - 1){\mathbb Z}_p^r$
is cohomologically trivial.
$\mathcal {Z} / (F_N - 1)\mathcal {Z} = {\mathbb Z}_p^r / (U_N - 1){\mathbb Z}_p^r$
is cohomologically trivial.
We set
![]() $M := \mathcal {Z} / (F_N - 1)\mathcal {Z}$
and write
$M := \mathcal {Z} / (F_N - 1)\mathcal {Z}$
and write
![]() $I = I_{N/K}$
for the inertia group. By [Reference Ellerbrock and NickelEN18, Lemma 2.3], it suffices to show that
$I = I_{N/K}$
for the inertia group. By [Reference Ellerbrock and NickelEN18, Lemma 2.3], it suffices to show that
![]() ${\hat H}^i(G/I, M^I) = 0$
and
${\hat H}^i(G/I, M^I) = 0$
and
![]() ${\hat H}^i(I, M) = 0$
for all
${\hat H}^i(I, M) = 0$
for all
![]() $i \in {\mathbb Z}$
, where
$i \in {\mathbb Z}$
, where
![]() ${\hat H}^i$
denotes Tate cohomology. Because M is a (finite) p-group and
${\hat H}^i$
denotes Tate cohomology. Because M is a (finite) p-group and
![]() $p \nmid \#I$
, we get
$p \nmid \#I$
, we get
![]() $\hat H^i(I, M) = 0$
. Hence, it suffices to show that
$\hat H^i(I, M) = 0$
. Hence, it suffices to show that
![]() $\hat H^i(G/I, M^I) = 0$
for all
$\hat H^i(G/I, M^I) = 0$
for all
![]() $i \in \mathbb Z$
. Because
$i \in \mathbb Z$
. Because
![]() $G/I$
is cyclic and M finite, a standard Herbrand quotient argument shows that it is then enough to prove that
$G/I$
is cyclic and M finite, a standard Herbrand quotient argument shows that it is then enough to prove that
![]() $\hat H^{-1}(G/I, M^I) = 0$
. Note that
$\hat H^{-1}(G/I, M^I) = 0$
. Note that
![]() $M^I = M$
. The long exact cohomology sequence attached to the short exact sequence
$M^I = M$
. The long exact cohomology sequence attached to the short exact sequence
of
![]() $G/I$
-modules yields the exact sequence
$G/I$
-modules yields the exact sequence
With
![]() $F_N = F_K^{d_{N/K}}$
, one has
$F_N = F_K^{d_{N/K}}$
, one has
![]() $U_N = U_K^{d_{N/K}}$
and
$U_N = U_K^{d_{N/K}}$
and
Because
![]() $U_N - 1$
is invertible, the same is true for
$U_N - 1$
is invertible, the same is true for
![]() $1 - U_K$
; hence,
$1 - U_K$
; hence,
![]() $\mathcal {Z}^{G/I} = 0$
and
$\mathcal {Z}^{G/I} = 0$
and
![]() $\hat {H}^{0}(G/I, \mathcal {Z} ) = 0$
. To show that
$\hat {H}^{0}(G/I, \mathcal {Z} ) = 0$
. To show that
![]() $\hat {H}^{-1}(G/I, \mathcal {Z} ) = 0$
, we note that the above identity also implies that
$\hat {H}^{-1}(G/I, \mathcal {Z} ) = 0$
, we note that the above identity also implies that
![]() $1 + U_K + \cdots + U_K^{d_{N/K}-1}$
is invertible, and hence, the kernel of the norm map is trivial. Consequently,
$1 + U_K + \cdots + U_K^{d_{N/K}-1}$
is invertible, and hence, the kernel of the norm map is trivial. Consequently,
![]() $\hat {H}^{-1}(G/I, \mathcal {Z} ) = 0$
.▪
$\hat {H}^{-1}(G/I, \mathcal {Z} ) = 0$
.▪
Because of Proposition 2.2, the tame case is much more accessible to proofs of conjecture
![]() $C_{EP}^{na}(N/K, V)$
than the wild case. Conversely, the following lemma shows that in the generic wild case, the cohomology modules are not cohomologically trivial.
$C_{EP}^{na}(N/K, V)$
than the wild case. Conversely, the following lemma shows that in the generic wild case, the cohomology modules are not cohomologically trivial.
Lemma 2.3 Assume that Hypothesis (F) holds. Then, the following are equivalent:
-
(i)
 $H^2(N,T)$
is trivial.
$H^2(N,T)$
is trivial. -
(ii)
 $U_N - 1 \in \mathrm {Gl}_r({{\mathbb Z}_p})$
.
$U_N - 1 \in \mathrm {Gl}_r({{\mathbb Z}_p})$
.
If
![]() $N/K$
is wildly ramified, then this is also equivalent to:
$N/K$
is wildly ramified, then this is also equivalent to:
-
(iii)
 $H^1(N,T)$
is cohomologically trivial.
$H^1(N,T)$
is cohomologically trivial. -
(iv)
 $H^2(N,T)$
is cohomologically trivial.
$H^2(N,T)$
is cohomologically trivial.
Proof The equivalence of (i) and (ii) is clear. The equivalence of (iii) and (iv) follows from [Reference CobbeCob18, Theorem 3.3 and Lemma 2.2]. To see the equivalence of (i) and (iv) in the wildly ramified case, it suffices to note that I acts trivially on
![]() $M := H^2(N,T) = \mathcal {Z} / (F_N - 1)\mathcal {Z}$
. If P denotes a subgroup of I of order p, then one obviously has
$M := H^2(N,T) = \mathcal {Z} / (F_N - 1)\mathcal {Z}$
. If P denotes a subgroup of I of order p, then one obviously has
▪
3 Formal logarithm and exponential function in higher dimensions
In this section, we prove some results which are probably well known, but for which we could not find a precise reference in the literature. Throughout this subsection, we let L be a finite extension of
![]() ${{\mathbb Q}_{p}}$
and
${{\mathbb Q}_{p}}$
and
![]() $v_L$
the normalized valuation of L.
$v_L$
the normalized valuation of L.
The statement and the proof of the following lemma generalize [Reference FröhlichFrö68, Chapter IV, Section 1, Proposition 1] to a higher dimensional setting. We set
![]() $X := (X_1, \ldots , X_r)$
, and for a homomorphism
$X := (X_1, \ldots , X_r)$
, and for a homomorphism
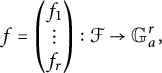 $$ \begin{align*} f=\begin{pmatrix}f_1\\ \vdots \\ f_r\end{pmatrix}:\mathcal F\to \mathbb G_a^r, \end{align*} $$
$$ \begin{align*} f=\begin{pmatrix}f_1\\ \vdots \\ f_r\end{pmatrix}:\mathcal F\to \mathbb G_a^r, \end{align*} $$
we write
![]() $J_f(X):=\left (\frac {\partial f_i}{\partial X_j}\right )_{1\leq i,j\leq r}$
for the Jacobian of f.
$J_f(X):=\left (\frac {\partial f_i}{\partial X_j}\right )_{1\leq i,j\leq r}$
for the Jacobian of f.
Lemma 3.1 Let
![]() $\mathcal F$
be an r-dimensional commutative formal group defined over
$\mathcal F$
be an r-dimensional commutative formal group defined over
![]() $\mathbb Z_p$
. Then, there exists a unique isomorphism
$\mathbb Z_p$
. Then, there exists a unique isomorphism
![]() $\log _{\mathcal F}:\mathcal F\to \mathbb {G}_a^r$
defined over
$\log _{\mathcal F}:\mathcal F\to \mathbb {G}_a^r$
defined over
![]() ${\mathbb Q}_p$
, so that the Jacobian
${\mathbb Q}_p$
, so that the Jacobian
![]() $J_{\log _{\mathcal F}}(X)$
satisfies
$J_{\log _{\mathcal F}}(X)$
satisfies
![]() $J_{\log _{\mathcal F}}(0)=1$
. Furthermore,
$J_{\log _{\mathcal F}}(0)=1$
. Furthermore,
![]() $J_{\log _{\mathcal F}}(X)\in \mathrm {Gl}_r(\mathbb Z_p[[X]])$
and
$J_{\log _{\mathcal F}}(X)\in \mathrm {Gl}_r(\mathbb Z_p[[X]])$
and
![]() $\log _{\mathcal F}(x)$
converges for all
$\log _{\mathcal F}(x)$
converges for all
![]() $x{\,=\,}(x_1,\dots ,x_r) {\,\in\,} L^{(r)}$
satisfying
$x{\,=\,}(x_1,\dots ,x_r) {\,\in\,} L^{(r)}$
satisfying
![]() $\min \{v_L(x_1),\dots ,v_L(x_r)\}{\,>\,}0$
.
$\min \{v_L(x_1),\dots ,v_L(x_r)\}{\,>\,}0$
.
Proof By [Reference FröhlichFrö68, Chapter II, Section 2, Theorem 1 and Corollary 1], there exists an isomorphism
![]() $g:\mathcal F\to \mathbb {G}_a^r$
defined over
$g:\mathcal F\to \mathbb {G}_a^r$
defined over
![]() ${\mathbb Q}_p$
. It is then clear that the Jacobian
${\mathbb Q}_p$
. It is then clear that the Jacobian
![]() $J_g(0)$
is an invertible matrix. We also note that
$J_g(0)$
is an invertible matrix. We also note that
![]() $J_g(0)^{-1}X$
defines an isomorphism
$J_g(0)^{-1}X$
defines an isomorphism
![]() $g_1:\mathbb {G}_a^r\to \mathbb {G}_a^r$
. Thus, the composition
$g_1:\mathbb {G}_a^r\to \mathbb {G}_a^r$
. Thus, the composition
![]() $\log _{\mathcal F}=g_1\circ g:\mathcal F\to \mathbb {G}_a^r$
is an isomorphism satisfying our normalization
$\log _{\mathcal F}=g_1\circ g:\mathcal F\to \mathbb {G}_a^r$
is an isomorphism satisfying our normalization
![]() $J_{\log _{\mathcal F}}(0)=J_{g_1}(g(0))J_g(0)=J_g(0)^{-1}J_g(0)=1$
.
$J_{\log _{\mathcal F}}(0)=J_{g_1}(g(0))J_g(0)=J_g(0)^{-1}J_g(0)=1$
.
To prove uniqueness, we assume that
![]() $f:\mathcal F\to \mathbb {G}_a^r$
is another isomorphism with
$f:\mathcal F\to \mathbb {G}_a^r$
is another isomorphism with
![]() $J_f(0)=1$
. Then,
$J_f(0)=1$
. Then,
It is easy to see that the isomorphisms
![]() $\mathbb {G}_a^r\to \mathbb {G}_a^r$
over
$\mathbb {G}_a^r\to \mathbb {G}_a^r$
over
![]() ${\mathbb Q}_p$
are in one-to-one correspondence with the matrices in
${\mathbb Q}_p$
are in one-to-one correspondence with the matrices in
![]() $\mathrm {Gl}_r({\mathbb Q}_p)$
. Hence, we deduce that
$\mathrm {Gl}_r({\mathbb Q}_p)$
. Hence, we deduce that
![]() $\log _{\mathcal F}\circ f^{-1}$
is the identity map, i.e.,
$\log _{\mathcal F}\circ f^{-1}$
is the identity map, i.e.,
![]() $f=\log _{\mathcal F}$
.
$f=\log _{\mathcal F}$
.
To show that
![]() $J_{\log _{\mathcal F}}(X)\in M_r(\mathbb Z_p[[X]])$
, we write
$J_{\log _{\mathcal F}}(X)\in M_r(\mathbb Z_p[[X]])$
, we write
We view both sides as formal series in the variables Y, calculate the Jacobians, and evaluate at
![]() $Y=0$
:
$Y=0$
:
As a consequence, we obtain
We let
![]() $\mathfrak a$
denote the ideal of
$\mathfrak a$
denote the ideal of
![]() ${{\mathbb Z}_{p}}[[X]]$
which is generated by
${{\mathbb Z}_{p}}[[X]]$
which is generated by
![]() $X_1, \ldots , X_r$
and note that
$X_1, \ldots , X_r$
and note that
![]() $p{{\mathbb Z}_{p}}[[X]] + \mathfrak a$
is the maximal ideal of the local ring
$p{{\mathbb Z}_{p}}[[X]] + \mathfrak a$
is the maximal ideal of the local ring
![]() ${{\mathbb Z}_{p}}[[X]]$
. By the axioms of formal groups, it follows that
${{\mathbb Z}_{p}}[[X]]$
. By the axioms of formal groups, it follows that
![]() $J_{\mathcal F(X,\cdot )}(0) = 1 + M$
with a matrix
$J_{\mathcal F(X,\cdot )}(0) = 1 + M$
with a matrix
![]() $M\in M_r(\mathbb Z_p[[X]])$
with coefficients in
$M\in M_r(\mathbb Z_p[[X]])$
with coefficients in
![]() $\mathfrak a$
. Hence,
$\mathfrak a$
. Hence,
![]() $\det (J_{\mathcal F(X,\cdot )}(0)) \equiv 1 \pmod {\mathfrak a}$
, and we deduce that
$\det (J_{\mathcal F(X,\cdot )}(0)) \equiv 1 \pmod {\mathfrak a}$
, and we deduce that
![]() $\det (J_{\mathcal F(X,\cdot )}(0))$
is a unit in
$\det (J_{\mathcal F(X,\cdot )}(0))$
is a unit in
![]() ${{\mathbb Z}_{p}}[[X]]$
. It follows that
${{\mathbb Z}_{p}}[[X]]$
. It follows that
![]() $J_{\mathcal F(X,\cdot )}(0)$
is invertible in
$J_{\mathcal F(X,\cdot )}(0)$
is invertible in
![]() $M_r({{\mathbb Z}_{p}}[[X]])$
, so that its inverse
$M_r({{\mathbb Z}_{p}}[[X]])$
, so that its inverse
![]() $J_{\log _{\mathcal F}}(X)$
has integral coefficients and is, in fact, in
$J_{\log _{\mathcal F}}(X)$
has integral coefficients and is, in fact, in
![]() $\mathrm {Gl}_r(\mathbb Z_p[[X]])$
.
$\mathrm {Gl}_r(\mathbb Z_p[[X]])$
.
Hence, a general term of any component
![]() $\log _{\mathcal F,i}$
of
$\log _{\mathcal F,i}$
of
![]() $\log _{\mathcal F}$
is of the form
$\log _{\mathcal F}$
is of the form
![]() $\frac {a}{m}\prod _{i=1}^r X_i^{n_i}$
, with
$\frac {a}{m}\prod _{i=1}^r X_i^{n_i}$
, with
![]() $m=\gcd (n_1,\dots ,n_r)$
and
$m=\gcd (n_1,\dots ,n_r)$
and
![]() $a\in \mathbb Z_p$
. If we set
$a\in \mathbb Z_p$
. If we set
![]() $n=\sum _{i=1}^r n_i$
, then
$n=\sum _{i=1}^r n_i$
, then
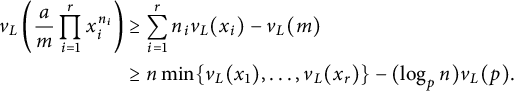 $$ \begin{align*} v_L\left(\frac{a}{m}\prod_{i=1}^r x_i^{n_i}\right)&\geq\sum_{i=1}^r n_iv_L(x_i)-v_L(m)\\ &\ge n\min\{v_L(x_1),\dots,v_L(x_r)\}-(\log_p n)v_L(p). \end{align*} $$
$$ \begin{align*} v_L\left(\frac{a}{m}\prod_{i=1}^r x_i^{n_i}\right)&\geq\sum_{i=1}^r n_iv_L(x_i)-v_L(m)\\ &\ge n\min\{v_L(x_1),\dots,v_L(x_r)\}-(\log_p n)v_L(p). \end{align*} $$
This last expression tends to infinity when the total degree n tends to infinity.▪
As usual, we write
![]() $\exp _{\mathcal F}$
for the inverse of
$\exp _{\mathcal F}$
for the inverse of
![]() $\log _{\mathcal F}$
. To obtain information on the convergence of
$\log _{\mathcal F}$
. To obtain information on the convergence of
![]() $\exp _{\mathcal F}$
, we will need the following lemma whose proof is inspired by the proof of [Reference SilvermanSil09, Lemma IV.5.4].
$\exp _{\mathcal F}$
, we will need the following lemma whose proof is inspired by the proof of [Reference SilvermanSil09, Lemma IV.5.4].
Lemma 3.2 Let
![]() $f,g\in {\mathbb Q}_p[[X]]^r$
be power series without constant term such that
$f,g\in {\mathbb Q}_p[[X]]^r$
be power series without constant term such that
![]() $f(g(X))=X$
for
$f(g(X))=X$
for
![]() $X=(X_1,\dots ,X_r)$
. Assume that
$X=(X_1,\dots ,X_r)$
. Assume that
![]() $J_g(X)\in M_r(\mathbb Z_p[[X]])$
and
$J_g(X)\in M_r(\mathbb Z_p[[X]])$
and
![]() $J_g(0)=1$
. Then, for all
$J_g(0)=1$
. Then, for all
![]() $s\in \mathbb N$
and for all
$s\in \mathbb N$
and for all
![]() $i, n_1,\dots ,n_s\in \{1,\dots ,r\}$
, we have
$i, n_1,\dots ,n_s\in \{1,\dots ,r\}$
, we have
Proof In a first step, we prove the following claim.
Claim: For all
![]() $s \in {\mathbb N}$
and all
$s \in {\mathbb N}$
and all
![]() $n_1,\dots ,n_s\in \{1,\dots ,r\}$
, the expression
$n_1,\dots ,n_s\in \{1,\dots ,r\}$
, the expression
 $$ \begin{align} \sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\frac{\partial^s f_i}{\partial X_{m_1}\cdots \partial X_{m_s}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_s}}{\partial X_{n_s}} \end{align} $$
$$ \begin{align} \sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\frac{\partial^s f_i}{\partial X_{m_1}\cdots \partial X_{m_s}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_s}}{\partial X_{n_s}} \end{align} $$
is a polynomial in
![]() $\frac {\partial ^t f_i}{\partial X_{k_1}\cdots \partial X_{k_t}}(g(X))$
with
$\frac {\partial ^t f_i}{\partial X_{k_1}\cdots \partial X_{k_t}}(g(X))$
with
![]() $1\leq t\leq s-1$
,
$1\leq t\leq s-1$
,
![]() $k_1,\dots ,k_t\in \{1,\dots ,r\}$
and coefficients in
$k_1,\dots ,k_t\in \{1,\dots ,r\}$
and coefficients in
![]() $\mathbb Z_p[[X]]$
.
$\mathbb Z_p[[X]]$
.
Indeed, the chain rule for
![]() $\frac {\partial }{\partial X_{n_{1}}}$
applied to
$\frac {\partial }{\partial X_{n_{1}}}$
applied to
![]() $f_i(g(X))=X_i$
yields
$f_i(g(X))=X_i$
yields
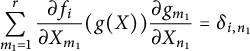 $$ \begin{align} \sum_{m_1=1}^r\frac{\partial f_i}{\partial X_{m_1}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}=\delta_{i,n_1} \end{align} $$
$$ \begin{align} \sum_{m_1=1}^r\frac{\partial f_i}{\partial X_{m_1}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}=\delta_{i,n_1} \end{align} $$
and thus establishes the claim for
![]() $s=1$
.
$s=1$
.
For the inductive step, we apply
![]() $\frac {\partial }{\partial X_{n_{s+1}}}$
to the expression in (3.1), and again, by the chain rule, we obtain
$\frac {\partial }{\partial X_{n_{s+1}}}$
to the expression in (3.1), and again, by the chain rule, we obtain
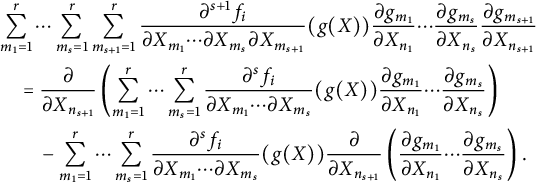 $$ \begin{align*} \begin{aligned} &\sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\sum_{m_{s+1}=1}^r\frac{\partial^{s+1} f_i}{\partial X_{m_1}\cdots \partial X_{m_s}\partial X_{m_{s+1}}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_{s}}}{\partial X_{n_{s}}} \frac{\partial g_{m_{s+1}}}{\partial X_{n_{s+1}}} \\ &\quad = \frac{\partial}{\partial X_{n_{s+1}}}\left(\sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\frac{\partial^s f_i}{\partial X_{m_1}\cdots\partial X_{m_s}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_s}}{\partial X_{n_s}}\right)\\ &\qquad - \sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\frac{\partial^s f_i}{\partial X_{m_1}\cdots\partial X_{m_s}}(g(X))\frac{\partial}{\partial X_{n_{s+1}}}\left(\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_s}}{\partial X_{n_s}}\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\sum_{m_{s+1}=1}^r\frac{\partial^{s+1} f_i}{\partial X_{m_1}\cdots \partial X_{m_s}\partial X_{m_{s+1}}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_{s}}}{\partial X_{n_{s}}} \frac{\partial g_{m_{s+1}}}{\partial X_{n_{s+1}}} \\ &\quad = \frac{\partial}{\partial X_{n_{s+1}}}\left(\sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\frac{\partial^s f_i}{\partial X_{m_1}\cdots\partial X_{m_s}}(g(X))\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_s}}{\partial X_{n_s}}\right)\\ &\qquad - \sum_{m_1=1}^r\cdots\sum_{m_s=1}^r\frac{\partial^s f_i}{\partial X_{m_1}\cdots\partial X_{m_s}}(g(X))\frac{\partial}{\partial X_{n_{s+1}}}\left(\frac{\partial g_{m_1}}{\partial X_{n_1}}\cdots \frac{\partial g_{m_s}}{\partial X_{n_s}}\right). \end{aligned} \end{align*} $$
Using the inductive hypothesis for the first term on the right-hand side and the assumption
![]() $J_g(X) \in M_r({{\mathbb Z}_{p}}[[X]])$
for the second, one proves the above claim.
$J_g(X) \in M_r({{\mathbb Z}_{p}}[[X]])$
for the second, one proves the above claim.
In order to prove the assertion of the lemma, we again proceed by induction on s. For
![]() $s=1$
, we specialize (3.2) at
$s=1$
, we specialize (3.2) at
![]() $X=0$
and obtain from
$X=0$
and obtain from
![]() $g(0) = 0$
$g(0) = 0$
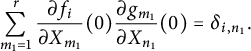 $$ \begin{align*} \sum_{m_1=1}^r\frac{\partial f_i}{\partial X_{m_1}}(0)\frac{\partial g_{m_1}}{\partial X_{n_1}}(0)=\delta_{i,n_1}. \end{align*} $$
$$ \begin{align*} \sum_{m_1=1}^r\frac{\partial f_i}{\partial X_{m_1}}(0)\frac{\partial g_{m_1}}{\partial X_{n_1}}(0)=\delta_{i,n_1}. \end{align*} $$
Because
![]() $J_g(0) = 1$
, this implies
$J_g(0) = 1$
, this implies
![]() $\frac {\partial f_i}{\partial X_{n_1}}(0) = \delta _{i,n_1} \in {{\mathbb Z}_{p}}$
.
$\frac {\partial f_i}{\partial X_{n_1}}(0) = \delta _{i,n_1} \in {{\mathbb Z}_{p}}$
.
For the inductive step, we specialize (3.1) at
![]() $X=0$
, and because
$X=0$
, and because
![]() $J_g(0)=1$
, we simply obtain
$J_g(0)=1$
, we simply obtain
By the above claim and the inductive hypothesis, this is an element in
![]() ${{\mathbb Z}_{p}}$
.▪
${{\mathbb Z}_{p}}$
.▪
Lemma 3.3 The isomorphism
![]() $\exp _{\mathcal F}$
converges for all
$\exp _{\mathcal F}$
converges for all
![]() $x=(x_1,\dots ,x_r) \in L^{(r)}$
satisfying
$x=(x_1,\dots ,x_r) \in L^{(r)}$
satisfying
![]() $\min \{v_L(x_1),\dots ,v_L(x_r)\}>v_L(p)/(p-1)$
.
$\min \{v_L(x_1),\dots ,v_L(x_r)\}>v_L(p)/(p-1)$
.
Proof By Lemmas 3.1 and 3.2, we have
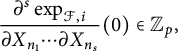 $$ \begin{align*} \frac{\partial^s \exp_{\mathcal F,i}}{\partial X_{n_1}\cdots\partial X_{n_s}}(0)\in\mathbb Z_p, \end{align*} $$
$$ \begin{align*} \frac{\partial^s \exp_{\mathcal F,i}}{\partial X_{n_1}\cdots\partial X_{n_s}}(0)\in\mathbb Z_p, \end{align*} $$
for any
![]() $s\in \mathbb N$
and
$s\in \mathbb N$
and
![]() $i, n_1,\dots ,n_s\in \{1,\dots ,r\}$
. It follows that each component
$i, n_1,\dots ,n_s\in \{1,\dots ,r\}$
. It follows that each component
![]() $\exp _{\mathcal F,i}$
of
$\exp _{\mathcal F,i}$
of
![]() $\exp _{\mathcal F}$
is of the form
$\exp _{\mathcal F}$
is of the form
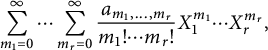 $$ \begin{align*} \sum_{m_1=0}^{\infty}\cdots\sum_{m_r=0}^{\infty} \frac{a_{m_1,\dots,m_r}}{m_1!\cdots m_r!}X_1^{m_1}\cdots X_r^{m_r}, \end{align*} $$
$$ \begin{align*} \sum_{m_1=0}^{\infty}\cdots\sum_{m_r=0}^{\infty} \frac{a_{m_1,\dots,m_r}}{m_1!\cdots m_r!}X_1^{m_1}\cdots X_r^{m_r}, \end{align*} $$
for some
![]() $a_{m_1,\dots ,m_r}\in \mathbb Z_p$
. As in the proof of [Reference SilvermanSil09, Lemma IV.6.3(b)], we can show that
$a_{m_1,\dots ,m_r}\in \mathbb Z_p$
. As in the proof of [Reference SilvermanSil09, Lemma IV.6.3(b)], we can show that
 $$ \begin{align*} v_L\left(\frac{a_{m_1,\dots,m_r}}{m_1!\cdots m_r!}x_1^{m_1}\cdots x_r^{m_r}\right) \ge \sum_{i=0, m_i\ne 0}^r \left( v_L(x_i) + (m_i-1) \left(v_L(x_i) - \frac{v_L(p)}{p-1}\right) \right), \end{align*} $$
$$ \begin{align*} v_L\left(\frac{a_{m_1,\dots,m_r}}{m_1!\cdots m_r!}x_1^{m_1}\cdots x_r^{m_r}\right) \ge \sum_{i=0, m_i\ne 0}^r \left( v_L(x_i) + (m_i-1) \left(v_L(x_i) - \frac{v_L(p)}{p-1}\right) \right), \end{align*} $$
which under our assumption tends to infinity as the total degree tends to infinity.▪
We summarize our discussion in the next proposition.
Proposition 3.4 Let L be a finite extension of
![]() ${{{\mathbb Q}}_{p}}$
with normalized valuation
${{{\mathbb Q}}_{p}}$
with normalized valuation
![]() $v_L$
. Let
$v_L$
. Let
![]() $n> \frac {v_L(p)}{p-1}$
be an integer. Then, the formal logarithm induces an isomorphism
$n> \frac {v_L(p)}{p-1}$
be an integer. Then, the formal logarithm induces an isomorphism
with inverse induced by
![]() $\exp _{\mathcal F}$
.
$\exp _{\mathcal F}$
.
Proof Given the results of this section, the proposition follows as in the proof of [Reference SilvermanSil09, Theorem IV.6.4].▪
4 Computation of the term
 $U_{\mathrm {cris}}$
$U_{\mathrm {cris}}$
4.1 Some preliminary results
We will apply the notation introduced and explained in [Reference Benois and BergerBB08, Section 1.1]. In particular,
![]() $B_{\mathrm {cris}}, B_{\mathrm {st}}$
, and
$B_{\mathrm {cris}}, B_{\mathrm {st}}$
, and
![]() ${B_{\mathrm {dR}}}$
denote the p-adic period rings constructed by Fontaine. We recall that the field
${B_{\mathrm {dR}}}$
denote the p-adic period rings constructed by Fontaine. We recall that the field
![]() ${B_{\mathrm {dR}}} = B_{\mathrm {dR}}^+[1/t]$
is a
${B_{\mathrm {dR}}} = B_{\mathrm {dR}}^+[1/t]$
is a
![]() ${{\mathbb Q}_{p}}$
-algebra which contains
${{\mathbb Q}_{p}}$
-algebra which contains
![]() ${{\mathbb Q}_p^c}$
and carries an action of
${{\mathbb Q}_p^c}$
and carries an action of
![]() $G_{{{\mathbb Q}_{p}}}$
. The uniformizing element
$G_{{{\mathbb Q}_{p}}}$
. The uniformizing element
![]() $t = \log [\varepsilon ]$
depends on the choice of
$t = \log [\varepsilon ]$
depends on the choice of
![]() $\varepsilon = \left ( \zeta _{p^n} \right )_{n \ge 0}$
where the primitive
$\varepsilon = \left ( \zeta _{p^n} \right )_{n \ge 0}$
where the primitive
![]() $p^n$
-th roots of unity
$p^n$
-th roots of unity
![]() $\zeta _{p^n}$
are compatible with respect to
$\zeta _{p^n}$
are compatible with respect to
![]() $x \mapsto x^p$
. We let
$x \mapsto x^p$
. We let
![]() $\chi _{cyc} \colon G_{{{\mathbb Q}_{p}}} \longrightarrow \mathbb Z_p^{\times }$
denote the cyclotomic character which is uniquely determined by the requirement
$\chi _{cyc} \colon G_{{{\mathbb Q}_{p}}} \longrightarrow \mathbb Z_p^{\times }$
denote the cyclotomic character which is uniquely determined by the requirement
![]() $\zeta _{p^n}^{\sigma } = \zeta _{p^n}^{\chi _{cyc}(\sigma )}$
for all
$\zeta _{p^n}^{\sigma } = \zeta _{p^n}^{\chi _{cyc}(\sigma )}$
for all
![]() $n \ge 0$
and all
$n \ge 0$
and all
![]() $\sigma \in G_{{{\mathbb Q}_{p}}}$
. In particular, we have
$\sigma \in G_{{{\mathbb Q}_{p}}}$
. In particular, we have
![]() $\sigma (t) = \chi _{cyc}(\sigma )t$
for all
$\sigma (t) = \chi _{cyc}(\sigma )t$
for all
![]() $\sigma \in G_{{{{\mathbb Q}}_{p}}}$
.
$\sigma \in G_{{{{\mathbb Q}}_{p}}}$
.
The subring
![]() $B_{\mathrm {cris}}$
of
$B_{\mathrm {cris}}$
of
![]() ${B_{\mathrm {dR}}}$
contains the element t, and, in addition, there is a Frobenius endomorphism
${B_{\mathrm {dR}}}$
contains the element t, and, in addition, there is a Frobenius endomorphism
![]() $\phi $
acting on
$\phi $
acting on
![]() $B_{\mathrm {cris}}$
. In Section 4.2, we will frequently use the formula
$B_{\mathrm {cris}}$
. In Section 4.2, we will frequently use the formula
![]() $\phi (t) = pt$
. If V is a p-adic representation of
$\phi (t) = pt$
. If V is a p-adic representation of
![]() $G_K$
, we put
$G_K$
, we put
The K-vector space
![]() $D_{\mathrm {dR}}^K(V)$
is finite dimensional and filtered. The tangent space of V over K is defined by
$D_{\mathrm {dR}}^K(V)$
is finite dimensional and filtered. The tangent space of V over K is defined by
Finally, we write
![]() $\exp _V \colon t_V(K) \longrightarrow H^1(K, V)$
for the exponential map of Bloch and Kato. Note here that
$\exp _V \colon t_V(K) \longrightarrow H^1(K, V)$
for the exponential map of Bloch and Kato. Note here that
![]() $H^1(K, V)$
is defined using continuous cochain cohomology (see Remark 2.1).
$H^1(K, V)$
is defined using continuous cochain cohomology (see Remark 2.1).
For any
![]() ${{\mathbb Q}_{p}}$
-vector space W, we write
${{\mathbb Q}_{p}}$
-vector space W, we write
![]() $W^* = \mathrm {Hom}_{{\mathbb Q}_{p}}(W, {{\mathbb Q}_{p}})$
for its
$W^* = \mathrm {Hom}_{{\mathbb Q}_{p}}(W, {{\mathbb Q}_{p}})$
for its
![]() ${{\mathbb Q}_{p}}$
-linear dual. For convenience, we usually write
${{\mathbb Q}_{p}}$
-linear dual. For convenience, we usually write
![]() $t^*_V(K)$
instead of
$t^*_V(K)$
instead of
![]() $t_V(K)^*$
.
$t_V(K)^*$
.
We fix a matrix
![]() $T^{\mathrm {nr}}\in \mathrm {Gl}_r(\overline {\mathbb Z}_p^{\mathrm {nr}})$
, so that
$T^{\mathrm {nr}}\in \mathrm {Gl}_r(\overline {\mathbb Z}_p^{\mathrm {nr}})$
, so that
![]() $\varphi (T^{\mathrm {nr}})(T^{\mathrm {nr}})^{-1}=u^{-1}$
, which exists by [Reference CobbeCob18, Lemma 1.9].
$\varphi (T^{\mathrm {nr}})(T^{\mathrm {nr}})^{-1}=u^{-1}$
, which exists by [Reference CobbeCob18, Lemma 1.9].
Lemma 4.1 Let
![]() $v_1^*,\dots ,v_r^*$
denote the elements of the canonical
$v_1^*,\dots ,v_r^*$
denote the elements of the canonical
![]() ${{\mathbb Q}_{p}}$
-basis of
${{\mathbb Q}_{p}}$
-basis of
![]() $V^*(1)$
. Then,
$V^*(1)$
. Then,
![]() $e_i^*=\sum _{n=1}^r (T^{\mathrm {nr}})^{-1}_{i,n}\otimes v_n^*$
,
$e_i^*=\sum _{n=1}^r (T^{\mathrm {nr}})^{-1}_{i,n}\otimes v_n^*$
,
![]() $i = 1, \ldots , r$
, constitute a basis of
$i = 1, \ldots , r$
, constitute a basis of
![]() $D_{\mathrm {cris}}^N(V^*(1))$
as an
$D_{\mathrm {cris}}^N(V^*(1))$
as an
![]() $N_1$
-vector space and of
$N_1$
-vector space and of
![]() $D_{\mathrm {dR}}^N(V^*(1))$
as an N-vector space. In addition, each element
$D_{\mathrm {dR}}^N(V^*(1))$
as an N-vector space. In addition, each element
![]() $e_i^*$
is fixed by the action of the Galois group
$e_i^*$
is fixed by the action of the Galois group
![]() $G_{{\mathbb Q}_{p}}$
.
$G_{{\mathbb Q}_{p}}$
.
Proof The following proof is the r-dimensional generalization of the first part of the proof of [Reference Bley and CobbeBC17, Lemma 5.2.1].
By definition, we have
![]() $T^{\mathrm {nr}}=u\varphi (T^{\mathrm {nr}})$
, and by induction, we deduce
$T^{\mathrm {nr}}=u\varphi (T^{\mathrm {nr}})$
, and by induction, we deduce
![]() $F_N(T^{\mathrm {nr}})=\varphi ^{d_N}(T^{\mathrm {nr}})=u^{-d_N}T^{\mathrm {nr}}$
, and hence
$F_N(T^{\mathrm {nr}})=\varphi ^{d_N}(T^{\mathrm {nr}})=u^{-d_N}T^{\mathrm {nr}}$
, and hence
![]() $u^{d_N}F_N(T^{\mathrm {nr}})=T^{\mathrm {nr}}$
.
$u^{d_N}F_N(T^{\mathrm {nr}})=T^{\mathrm {nr}}$
.
First of all, recall that the completion
![]() $\overline {\mathbb Z}_p^{\mathrm {nr}}$
of
$\overline {\mathbb Z}_p^{\mathrm {nr}}$
of
![]() ${\mathbb Z}_p^{\mathrm {nr}}$
is contained both in
${\mathbb Z}_p^{\mathrm {nr}}$
is contained both in
![]() $B_{\mathrm {cris}}$
and
$B_{\mathrm {cris}}$
and
![]() ${B_{\mathrm {dR}}}$
. We now prove that the elements
${B_{\mathrm {dR}}}$
. We now prove that the elements
![]() $e_i^*$
are fixed by the absolute Galois group
$e_i^*$
are fixed by the absolute Galois group
![]() $G_{{\mathbb Q}_{p}}$
, which will show that the
$G_{{\mathbb Q}_{p}}$
, which will show that the
![]() $e_i^*$
are contained in both
$e_i^*$
are contained in both
![]() $D_{\mathrm {cris}}^N(V^*(1))$
and
$D_{\mathrm {cris}}^N(V^*(1))$
and
![]() $D_{\mathrm {dR}}^N(V^*(1))$
. We note that the inertia group
$D_{\mathrm {dR}}^N(V^*(1))$
. We note that the inertia group
![]() $I_{{\mathbb Q}_{p}}$
acts trivially on
$I_{{\mathbb Q}_{p}}$
acts trivially on
![]() $V^*(1)$
, and hence, it remains to prove that
$V^*(1)$
, and hence, it remains to prove that
![]() $e_i^*$
is fixed by
$e_i^*$
is fixed by
![]() $\varphi $
. We first need to calculate
$\varphi $
. We first need to calculate
![]() $\varphi (v_i^*)$
. Here, we use the definitions and the fact that the elements
$\varphi (v_i^*)$
. Here, we use the definitions and the fact that the elements
![]() $v_i$
constitute the canonical basis of
$v_i$
constitute the canonical basis of
![]() ${\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
:
${\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
:
 $$ \begin{align*} \varphi(v_i^*)(v_j)=v_i^*(u^{-1}v_j)=v_i^*\left(\sum_{k=1}^r (u^{-1})_{k,j}v_k\right)=(u^{-1})_{i,j}.\end{align*} $$
$$ \begin{align*} \varphi(v_i^*)(v_j)=v_i^*(u^{-1}v_j)=v_i^*\left(\sum_{k=1}^r (u^{-1})_{k,j}v_k\right)=(u^{-1})_{i,j}.\end{align*} $$
Hence,
 $$ \begin{align*} \varphi(v_i^*)=\sum_{j=1}^r (u^{-1})_{i,j}v_j^*,\end{align*} $$
$$ \begin{align*} \varphi(v_i^*)=\sum_{j=1}^r (u^{-1})_{i,j}v_j^*,\end{align*} $$
and we conclude that
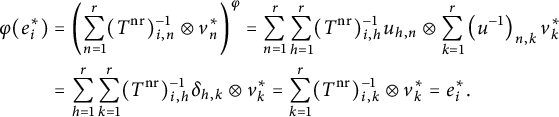 $$ \begin{align*} \begin{aligned} \varphi(e_i^*)&=\left(\sum_{n=1}^r (T^{\mathrm{nr}})^{-1}_{i,n}\otimes v_n^*\right)^{\varphi}=\sum_{n=1}^r \sum_{h=1}^r (T^{\mathrm{nr}})^{-1}_{i,h}u_{h,n}\otimes \sum_{k=1}^r\left(u^{-1}\right)_{n,k}v_{k}^*\\ &=\sum_{h=1}^r\sum_{k=1}^r (T^{\mathrm{nr}})^{-1}_{i,h} \delta_{h,k}\otimes v_k^*=\sum_{k=1}^r (T^{\mathrm{nr}})^{-1}_{i,k} \otimes v_k^*=e_i^*. \end{aligned}\end{align*} $$
$$ \begin{align*} \begin{aligned} \varphi(e_i^*)&=\left(\sum_{n=1}^r (T^{\mathrm{nr}})^{-1}_{i,n}\otimes v_n^*\right)^{\varphi}=\sum_{n=1}^r \sum_{h=1}^r (T^{\mathrm{nr}})^{-1}_{i,h}u_{h,n}\otimes \sum_{k=1}^r\left(u^{-1}\right)_{n,k}v_{k}^*\\ &=\sum_{h=1}^r\sum_{k=1}^r (T^{\mathrm{nr}})^{-1}_{i,h} \delta_{h,k}\otimes v_k^*=\sum_{k=1}^r (T^{\mathrm{nr}})^{-1}_{i,k} \otimes v_k^*=e_i^*. \end{aligned}\end{align*} $$
Because
![]() $T^{\mathrm {nr}} \in \mathrm {Gl}_r(\overline {\mathbb Z}_p^{\mathrm {nr}}) \subseteq \mathrm {Gl}_r(B_{\mathrm {cris}})$
, the elements
$T^{\mathrm {nr}} \in \mathrm {Gl}_r(\overline {\mathbb Z}_p^{\mathrm {nr}}) \subseteq \mathrm {Gl}_r(B_{\mathrm {cris}})$
, the elements
![]() $e_1^*,\dots ,e_r^*$
are a
$e_1^*,\dots ,e_r^*$
are a
![]() $B_{\mathrm {cris}}$
-basis of
$B_{\mathrm {cris}}$
-basis of
![]() $B_{\mathrm {cris}} \otimes _{{\mathbb Q}_{p}} V^*(1)$
. As
$B_{\mathrm {cris}} \otimes _{{\mathbb Q}_{p}} V^*(1)$
. As
![]() $N_1$
is a subfield of
$N_1$
is a subfield of
![]() $B_{\mathrm {cris}}$
, we see that
$B_{\mathrm {cris}}$
, we see that
![]() $e_1^*,\dots ,e_r^*$
are linearly independent over
$e_1^*,\dots ,e_r^*$
are linearly independent over
![]() $N_1$
. This concludes the proof that the elements
$N_1$
. This concludes the proof that the elements
![]() $e_i^*$
constitute a basis of
$e_i^*$
constitute a basis of
![]() $D_{\mathrm {cris}}^N(V^*(1))$
, because
$D_{\mathrm {cris}}^N(V^*(1))$
, because
![]() $\dim _{N_1}D_{\mathrm {cris}}^N(V^*(1))\leq \dim _{{\mathbb Q}_{p}}(V^*(1))=r$
. In particular, this also proves that
$\dim _{N_1}D_{\mathrm {cris}}^N(V^*(1))\leq \dim _{{\mathbb Q}_{p}}(V^*(1))=r$
. In particular, this also proves that
![]() $V^*(1)$
is cristalline. Then, the elements
$V^*(1)$
is cristalline. Then, the elements
![]() $e_1^*,\dots ,e_r^*$
must also be a basis of the N-vector space
$e_1^*,\dots ,e_r^*$
must also be a basis of the N-vector space
![]() $D_{\mathrm {dR}}^N(V^*(1))=N\otimes _{N_1}D_{\mathrm {cris}}^N(V^*(1))$
.▪
$D_{\mathrm {dR}}^N(V^*(1))=N\otimes _{N_1}D_{\mathrm {cris}}^N(V^*(1))$
.▪
Lemma 4.2 Let
![]() $v_1,\dots ,v_r$
be the elements of the canonical
$v_1,\dots ,v_r$
be the elements of the canonical
![]() ${{\mathbb Q}_{p}}$
-basis of V. The elements
${{\mathbb Q}_{p}}$
-basis of V. The elements
![]() $e_i=\sum _{n=1}^r t^{-1} T^{\mathrm {nr}}_{n,i}\otimes v_n$
,
$e_i=\sum _{n=1}^r t^{-1} T^{\mathrm {nr}}_{n,i}\otimes v_n$
,
![]() $i = 1, \ldots , r$
, constitute a basis of
$i = 1, \ldots , r$
, constitute a basis of
![]() $D_{\mathrm {cris}}^N(V)$
as an
$D_{\mathrm {cris}}^N(V)$
as an
![]() $N_1$
-vector space and of
$N_1$
-vector space and of
![]() $D_{\mathrm {dR}}^N(V)$
as an N-vector space. In addition, each element
$D_{\mathrm {dR}}^N(V)$
as an N-vector space. In addition, each element
![]() $e_i$
is fixed by the action of the Galois group
$e_i$
is fixed by the action of the Galois group
![]() $G_{{\mathbb Q}_{p}}$
.
$G_{{\mathbb Q}_{p}}$
.
Proof For
![]() $\sigma \in I_{{\mathbb Q}_{p}}$
we compute
$\sigma \in I_{{\mathbb Q}_{p}}$
we compute
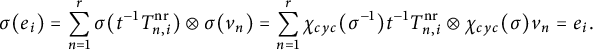 $$ \begin{align*} \sigma(e_i) = \sum_{n=1}^r \sigma(t^{-1} T^{\mathrm{nr}}_{n,i}) \otimes \sigma(v_n) = \sum_{n=1}^r \chi_{cyc}(\sigma^{-1})t^{-1} T^{\mathrm{nr}}_{n,i} \otimes \chi_{cyc}(\sigma)v_n = e_i. \end{align*} $$
$$ \begin{align*} \sigma(e_i) = \sum_{n=1}^r \sigma(t^{-1} T^{\mathrm{nr}}_{n,i}) \otimes \sigma(v_n) = \sum_{n=1}^r \chi_{cyc}(\sigma^{-1})t^{-1} T^{\mathrm{nr}}_{n,i} \otimes \chi_{cyc}(\sigma)v_n = e_i. \end{align*} $$
Hence, the elements
![]() $e_i$
are fixed by the inertia group, and a similar computation as in the proof of Lemma 4.1 shows that
$e_i$
are fixed by the inertia group, and a similar computation as in the proof of Lemma 4.1 shows that
![]() $\varphi (e_i) = e_i$
. The proof follows as above.▪
$\varphi (e_i) = e_i$
. The proof follows as above.▪
Lemma 4.3 Let
![]() $\tilde v_1,\dots ,\tilde v_r$
be the elements of the canonical
$\tilde v_1,\dots ,\tilde v_r$
be the elements of the canonical
![]() ${{\mathbb Q}_{p}}$
-basis of
${{\mathbb Q}_{p}}$
-basis of
![]() $V(-1)$
. The elements
$V(-1)$
. The elements
![]() $\tilde e_i=\sum _{n=1}^r T^{\mathrm {nr}}_{n,i}\otimes \tilde v_n$
are a basis of
$\tilde e_i=\sum _{n=1}^r T^{\mathrm {nr}}_{n,i}\otimes \tilde v_n$
are a basis of
![]() $D_{\mathrm {cris}}^N(V(-1))$
as an
$D_{\mathrm {cris}}^N(V(-1))$
as an
![]() $N_1$
-vector space and of
$N_1$
-vector space and of
![]() $D_{\mathrm {dR}}^N(V(-1))$
as an N-vector space. In addition, each element
$D_{\mathrm {dR}}^N(V(-1))$
as an N-vector space. In addition, each element
![]() $\tilde e_i$
is fixed by the action of the Galois group
$\tilde e_i$
is fixed by the action of the Galois group
![]() $G_{{\mathbb Q}_{p}}$
.
$G_{{\mathbb Q}_{p}}$
.
Proof Similar as above.▪
4.2 Computation of
 $U_{\text {cris}}$
$U_{\text {cris}}$
We recall that
![]() $V = {\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}})$
and
$V = {\mathbb Q}_p^r(1)(\rho ^{\mathrm {nr}})$
and
![]() $V^*(1) = {\mathbb Q}_p^r((\rho ^{\mathrm {nr}})^{-1})$
and that we always assume Hypothesis (F). The following lemma (and its proof) is the analogue of [Reference Bley and CobbeBC17, Lemma 5.1.2].
$V^*(1) = {\mathbb Q}_p^r((\rho ^{\mathrm {nr}})^{-1})$
and that we always assume Hypothesis (F). The following lemma (and its proof) is the analogue of [Reference Bley and CobbeBC17, Lemma 5.1.2].
Lemma 4.4 We have:
-
(1)
 $t_{V^*(1)}(N)=0$
.
$t_{V^*(1)}(N)=0$
. -
(2)
 $H_f^1(N,V^*(1))=0$
.
$H_f^1(N,V^*(1))=0$
. -
(3)
 $H_f^1(N,V)= H^1_e(N,V) = H^1(N,V)$
.
$H_f^1(N,V)= H^1_e(N,V) = H^1(N,V)$
.
Proof Proofs are as for [Reference Bley and CobbeBC17, Lemma 5.1.2]. For the proof of part (c), we also need that by Lemma 4.7 below the endomorphism
![]() $1 - \phi $
of
$1 - \phi $
of
![]() $D_{\mathrm {cris}}^N(V)$
is an isomorphism.▪
$D_{\mathrm {cris}}^N(V)$
is an isomorphism.▪
By the above lemma, [Reference CobbeCob18, Corollary 3.16], and [Reference Bley and CobbeBC17, equation (30)], the seven-term exact sequence [Reference Bley and CobbeBC17, equation (5)] degenerates into the two exact sequences
and
The term
![]() $U_{\mathrm {cris}}\in K_0({\mathbb Z}_p[G],{\mathbb Q}_p[G])$
is defined by [Reference Bley and CobbeBC17, equation (26)]. We recall that for a ring R, the abelian group
$U_{\mathrm {cris}}\in K_0({\mathbb Z}_p[G],{\mathbb Q}_p[G])$
is defined by [Reference Bley and CobbeBC17, equation (26)]. We recall that for a ring R, the abelian group
![]() $K_1(R)$
is generated by elements
$K_1(R)$
is generated by elements
![]() $[P,\alpha ]$
, where P is a finitely generated projective R-module and
$[P,\alpha ]$
, where P is a finitely generated projective R-module and
![]() $\alpha $
is an automorphism of P. By the computations in loc. cit. (see, in particular, [Reference Bley and CobbeBC17, equation (32)]), we obtain
$\alpha $
is an automorphism of P. By the computations in loc. cit. (see, in particular, [Reference Bley and CobbeBC17, equation (32)]), we obtain
Before computing
![]() $U_{\mathrm {cris}}$
, we need an easy lemma from linear algebra.
$U_{\mathrm {cris}}$
, we need an easy lemma from linear algebra.
Lemma 4.5 Let R be a unital commutative ring, and let
 $$ \begin{align*} M=\begin{pmatrix}1&0&0&\cdots&0&B_1\\ A&1&0&\cdots&0&B_2\\ 0&A&1&\cdots&0&B_3\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&1&B_{n-1}\\ 0&0&0&\cdots&A&1+B_n\end{pmatrix}\in M_{nr}(R) \end{align*} $$
$$ \begin{align*} M=\begin{pmatrix}1&0&0&\cdots&0&B_1\\ A&1&0&\cdots&0&B_2\\ 0&A&1&\cdots&0&B_3\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&1&B_{n-1}\\ 0&0&0&\cdots&A&1+B_n\end{pmatrix}\in M_{nr}(R) \end{align*} $$
be a block matrix, with
![]() $n^2$
square blocks of the same size. Let
$n^2$
square blocks of the same size. Let
![]() $\det =\det _R$
denote the determinant over R. Then,
$\det =\det _R$
denote the determinant over R. Then,
 $$ \begin{align*}\det(M)=\det\left(1+\sum_{i=0}^{n-1}(-A)^{i}B_{n-i}\right).\end{align*} $$
$$ \begin{align*}\det(M)=\det\left(1+\sum_{i=0}^{n-1}(-A)^{i}B_{n-i}\right).\end{align*} $$
Proof By Gaussian elimination, we obtain the matrix
 $$ \begin{align*} \begin{pmatrix}1&0&0&\cdots&0&B_1\\ 0&1&0&\cdots&0&B_2-AB_1\\ 0&0&1&\cdots&0&B_3-AB_2+A^2B_1\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&1&\sum_{i=0}^{n-2}(-A)^i B_{n-1-i}\\ 0&0&0&\cdots&0&1+\sum_{i=0}^{n-1}(-A)^i B_{n-i}\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix}1&0&0&\cdots&0&B_1\\ 0&1&0&\cdots&0&B_2-AB_1\\ 0&0&1&\cdots&0&B_3-AB_2+A^2B_1\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&1&\sum_{i=0}^{n-2}(-A)^i B_{n-1-i}\\ 0&0&0&\cdots&0&1+\sum_{i=0}^{n-1}(-A)^i B_{n-i}\end{pmatrix}. \end{align*} $$
▪
The Wedderburn decomposition of
![]() ${{\mathbb Q}_p[G]}$
induces a decomposition of
${{\mathbb Q}_p[G]}$
induces a decomposition of
![]() $Z({{\mathbb Q}_p[G]})$
as a finite direct sum
$Z({{\mathbb Q}_p[G]})$
as a finite direct sum
![]() $\bigoplus _{i} F_i$
of suitable finite field extensions
$\bigoplus _{i} F_i$
of suitable finite field extensions
![]() $F_i/{{\mathbb Q}_{p}}$
. If
$F_i/{{\mathbb Q}_{p}}$
. If
![]() $x \in Z({{\mathbb Q}_p[G]})$
, we let
$x \in Z({{\mathbb Q}_p[G]})$
, we let
![]() ${}^*x \in Z({{\mathbb Q}_p[G]})^{\times }$
denote the invertible element which is given by
${}^*x \in Z({{\mathbb Q}_p[G]})^{\times }$
denote the invertible element which is given by
![]() $({}^*x_i)$
with
$({}^*x_i)$
with
![]() ${}^*x_i = 1$
if
${}^*x_i = 1$
if
![]() $x_i = 0$
and
$x_i = 0$
and
![]() ${}^*x_i = x_i$
otherwise.
${}^*x_i = x_i$
otherwise.
We now generalize [Reference Bley and CobbeBC17, Lemmas 5.2.1 and 5.2.2], and in this way, explicitly compute the element
![]() $U_{\mathrm {cris}}$
. Recall that
$U_{\mathrm {cris}}$
. Recall that
![]() $F = F_K= \varphi ^{d_K}$
is the Frobenius element of K. We write
$F = F_K= \varphi ^{d_K}$
is the Frobenius element of K. We write
![]() $I = I_{N/K}$
for the inertia subgroup of the Galois extension
$I = I_{N/K}$
for the inertia subgroup of the Galois extension
![]() $N/K$
.
$N/K$
.
Lemma 4.6 The endomorphism
![]() $1-\phi ^*$
of
$1-\phi ^*$
of
![]() $D_{\mathrm {cris}}^N(V^*(1))^*$
is an isomorphism. Furthermore, we have
$D_{\mathrm {cris}}^N(V^*(1))^*$
is an isomorphism. Furthermore, we have
in
![]() $K_0({{\mathbb Z}_p[G]},\!{{\mathbb Q}_p[G]})$
.
$K_0({{\mathbb Z}_p[G]},\!{{\mathbb Q}_p[G]})$
.
Proof We have to compute
![]() $\phi (e_i^*)$
. Using the
$\phi (e_i^*)$
. Using the
![]() $\varphi $
-semilinearity of
$\varphi $
-semilinearity of
![]() $\phi $
, we compute
$\phi $
, we compute
 $$ \begin{align*}\begin{aligned}\phi(e_i^*)&=\sum_{n=1}^r\varphi((T^{\mathrm{nr}})^{-1})_{i,n}\otimes v_n^*=\sum_{n=1}^r ((T^{\mathrm{nr}})^{-1} u)_{i,n}\otimes v_n^*\\ &=\sum_{n=1}^r ((T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}(T^{\mathrm{nr}})^{-1})_{i,n}\otimes v_n^*=\sum_{n=1}^r\sum_{\ell=1}^r ((T^{\mathrm{nr}})^{-1} u T^{\mathrm{nr}})_{i,\ell}(T^{\mathrm{nr}})^{-1}_{\ell,n}\otimes v_n^*\\ &=\sum_{\ell=1}^r ((T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}})_{i,\ell}e_{\ell}^*.\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned}\phi(e_i^*)&=\sum_{n=1}^r\varphi((T^{\mathrm{nr}})^{-1})_{i,n}\otimes v_n^*=\sum_{n=1}^r ((T^{\mathrm{nr}})^{-1} u)_{i,n}\otimes v_n^*\\ &=\sum_{n=1}^r ((T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}(T^{\mathrm{nr}})^{-1})_{i,n}\otimes v_n^*=\sum_{n=1}^r\sum_{\ell=1}^r ((T^{\mathrm{nr}})^{-1} u T^{\mathrm{nr}})_{i,\ell}(T^{\mathrm{nr}})^{-1}_{\ell,n}\otimes v_n^*\\ &=\sum_{\ell=1}^r ((T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}})_{i,\ell}e_{\ell}^*.\end{aligned}\end{align*} $$
We fix a normal basis element
![]() $\theta $
of
$\theta $
of
![]() $N_1/{{\mathbb Q}}_p$
. Then,
$N_1/{{\mathbb Q}}_p$
. Then,
![]() $w_{i,j}:=\varphi ^{-j}(\theta ) e_i^*$
, for
$w_{i,j}:=\varphi ^{-j}(\theta ) e_i^*$
, for
![]() $i=1,\dots ,r$
and
$i=1,\dots ,r$
and
![]() $j=0,\dots ,d_K-1$
, is a
$j=0,\dots ,d_K-1$
, is a
![]() ${\mathbb Q}_p[G/I]$
-basis of
${\mathbb Q}_p[G/I]$
-basis of
![]() $D_{\mathrm {cris}}^N(V^*(1))$
. Let
$D_{\mathrm {cris}}^N(V^*(1))$
. Let
![]() $\psi _{i,j}\in D_{\mathrm {cris}}^N(V^*(1))^*$
for
$\psi _{i,j}\in D_{\mathrm {cris}}^N(V^*(1))^*$
for
![]() $i=1,\dots ,r$
and
$i=1,\dots ,r$
and
![]() $j=0,\dots ,d_K-1$
be the dual
$j=0,\dots ,d_K-1$
be the dual
![]() ${\mathbb Q}_p[G/I]$
-basis.
${\mathbb Q}_p[G/I]$
-basis.
For
![]() $0<i,h\leq r$
,
$0<i,h\leq r$
,
![]() $0\leq j,k<d_K-1$
, and
$0\leq j,k<d_K-1$
, and
![]() $0\leq n\leq d-1$
, we have
$0\leq n\leq d-1$
, we have
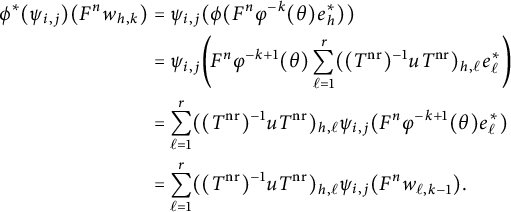 $$ \begin{align*} \begin{aligned} \phi^{*}(\psi_{i,j}) (F^n w_{h,k}) &= \psi_{i,j} (\phi(F^n \varphi^{-k}(\theta) e_h^{*})) \\&= \psi_{i,j}\!\left(\!F^n \varphi^{-k+1}(\theta) \sum_{\ell=1}^r ((T^{\text{nr}})^{-1} uT^{\text{nr}})_{h,\ell}e_{\ell}^{*}\right)\\ &=\sum_{\ell=1}^r ((T^{\text{nr}})^{-1} u T^{\text{nr}})_{h,\ell}\psi_{i,j}(F^n \varphi^{-k+1}(\theta) e_{\ell}^{*})\\&=\sum_{\ell=1}^r ((T^{\text{nr}})^{-1} uT^{\text{nr}})_{h,\ell}\psi_{i,j}(F^n w_{\ell,k-1}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \phi^{*}(\psi_{i,j}) (F^n w_{h,k}) &= \psi_{i,j} (\phi(F^n \varphi^{-k}(\theta) e_h^{*})) \\&= \psi_{i,j}\!\left(\!F^n \varphi^{-k+1}(\theta) \sum_{\ell=1}^r ((T^{\text{nr}})^{-1} uT^{\text{nr}})_{h,\ell}e_{\ell}^{*}\right)\\ &=\sum_{\ell=1}^r ((T^{\text{nr}})^{-1} u T^{\text{nr}})_{h,\ell}\psi_{i,j}(F^n \varphi^{-k+1}(\theta) e_{\ell}^{*})\\&=\sum_{\ell=1}^r ((T^{\text{nr}})^{-1} uT^{\text{nr}})_{h,\ell}\psi_{i,j}(F^n w_{\ell,k-1}). \end{aligned} \end{align*} $$
If
![]() $n=0$
,
$n=0$
,
![]() $k=j+1$
, and any
$k=j+1$
, and any
![]() $0<h\leq r$
, this is equal to
$0<h\leq r$
, this is equal to
![]() $((T^{\mathrm {nr}})^{-1} uT^{\mathrm {nr}})_{h,i}$
; it is
$((T^{\mathrm {nr}})^{-1} uT^{\mathrm {nr}})_{h,i}$
; it is
![]() $0$
otherwise. Hence,
$0$
otherwise. Hence,
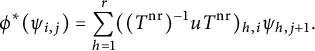 $$ \begin{align*}\phi^*(\psi_{i,j})=\sum_{h=1}^r ((T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}})_{h,i}\psi_{h,j+1}.\end{align*} $$
$$ \begin{align*}\phi^*(\psi_{i,j})=\sum_{h=1}^r ((T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}})_{h,i}\psi_{h,j+1}.\end{align*} $$
Analogously, for
![]() $0<i\leq r$
and
$0<i\leq r$
and
![]() $j=d_K-1$
, we have
$j=d_K-1$
, we have
 $$ \begin{align*} \phi^*(\psi_{i,d_K-1})=\sum_{h=1}^r ((T^{\mathrm{nr}})^{-1} u T^{\mathrm{nr}})_{h,i}F^{-1}\psi_{h,0}. \end{align*} $$
$$ \begin{align*} \phi^*(\psi_{i,d_K-1})=\sum_{h=1}^r ((T^{\mathrm{nr}})^{-1} u T^{\mathrm{nr}})_{h,i}F^{-1}\psi_{h,0}. \end{align*} $$
Note here that
![]() $\phi ^*$
is indeed defined over
$\phi ^*$
is indeed defined over
![]() ${\mathbb Q}_p[G/I]$
, because
${\mathbb Q}_p[G/I]$
, because
![]() $(T^{\mathrm {nr}})^{-1}uT^{\mathrm {nr}}\in M_r({\mathbb Q}_p)$
.
$(T^{\mathrm {nr}})^{-1}uT^{\mathrm {nr}}\in M_r({\mathbb Q}_p)$
.
With respect to the
![]() ${{\mathbb Q}_{p}}[G/I]$
-basis
${{\mathbb Q}_{p}}[G/I]$
-basis
![]() $\psi _{i,j}$
the matrix associated to
$\psi _{i,j}$
the matrix associated to
![]() $1-\phi ^*$
is given by
$1-\phi ^*$
is given by
 $$ \begin{align*} \begin{pmatrix}1&0&0&\cdots&0&-F^{-1}(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}\\ -(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}&1&0&\cdots&0&0\\ 0&-(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}&1&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&1&0\\ 0&0&0&\cdots&-(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}&1\end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix}1&0&0&\cdots&0&-F^{-1}(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}\\ -(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}&1&0&\cdots&0&0\\ 0&-(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}&1&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&1&0\\ 0&0&0&\cdots&-(T^{\mathrm{nr}})^{-1} uT^{\mathrm{nr}}&1\end{pmatrix}. \end{align*} $$
In this matrix, each entry is an
![]() $r\times r$
matrix with coefficients in
$r\times r$
matrix with coefficients in
![]() ${\mathbb Q}_p[G/I]$
(recall that
${\mathbb Q}_p[G/I]$
(recall that
![]() $F=F_K$
generates
$F=F_K$
generates
![]() $G/I$
). In the following, we write
$G/I$
). In the following, we write
![]() $\det $
for the determinant over the commutative ring
$\det $
for the determinant over the commutative ring
![]() ${\mathbb Q}_p[G/I]$
. By Lemma 4.5, the determinant of the above matrix is
${\mathbb Q}_p[G/I]$
. By Lemma 4.5, the determinant of the above matrix is
![]() $\det (1-F^{-1}(T^{\mathrm {nr}})^{-1} u^{d_K}T^{\mathrm {nr}})=\det (1-F^{-1}u^{d_K})$
. Because this determinant computes the reduced norm of
$\det (1-F^{-1}(T^{\mathrm {nr}})^{-1} u^{d_K}T^{\mathrm {nr}})=\det (1-F^{-1}u^{d_K})$
. Because this determinant computes the reduced norm of
![]() $1-\phi ^*$
, the equality in the lemma follows.
$1-\phi ^*$
, the equality in the lemma follows.
To conclude that
![]() $1-\phi ^*$
is an isomorphism, it is now enough to notice that
$1-\phi ^*$
is an isomorphism, it is now enough to notice that
which is invertible, because, by Hypothesis (F), we always have
![]() $\det (U_N-1)\neq 0$
.▪
$\det (U_N-1)\neq 0$
.▪
Lemma 4.7 The endomorphism
![]() $1 - \phi $
of
$1 - \phi $
of
![]() $D_{\mathrm {cris}}^N(V)$
is an isomorphism, and we have
$D_{\mathrm {cris}}^N(V)$
is an isomorphism, and we have
in
![]() $K_0({{\mathbb Z}_p[G]}, {{\mathbb Q}_p[G]})$
.
$K_0({{\mathbb Z}_p[G]}, {{\mathbb Q}_p[G]})$
.
Proof The proof is analogous to the proof of the previous lemma.
To show that
![]() $\det (1-F(pu)^{-d_K})$
is invertible in
$\det (1-F(pu)^{-d_K})$
is invertible in
![]() ${{\mathbb Q}_{p}}[G/I]$
, it is enough to notice that
${{\mathbb Q}_{p}}[G/I]$
, it is enough to notice that
![]() $\sum _{i=0}^{\infty } (F^{-1}(pu)^{d_K})^i$
converges in the matrix ring
$\sum _{i=0}^{\infty } (F^{-1}(pu)^{d_K})^i$
converges in the matrix ring
![]() $M_r({{\mathbb Z}_p}[G/I])$
and is the inverse of
$M_r({{\mathbb Z}_p}[G/I])$
and is the inverse of
▪
Proposition 4.8 We have
We conclude this section by proving some functorial properties for the term
![]() $U_{\mathrm {cris}}$
. To that end, we let L be an intermediate field of
$U_{\mathrm {cris}}$
. To that end, we let L be an intermediate field of
![]() $N/K$
and set
$N/K$
and set
![]() $H := \mathrm {Gal}(N/L)$
. Then, we let
$H := \mathrm {Gal}(N/L)$
. Then, we let
denote the natural restriction of scalars homomorphism, and if H is normal in G, then
denotes the homomorphism which is induced by the functor
![]() $\mathrm {Hom}_{\mathbb Z[H]}(\mathbb Z,\cdot )=(\cdot )^H$
.
$\mathrm {Hom}_{\mathbb Z[H]}(\mathbb Z,\cdot )=(\cdot )^H$
.
Lemma 4.9 Let L be an intermediate field of
![]() $N/K$
and
$N/K$
and
![]() $H=\mathrm {Gal}(N/L)$
. Then:
$H=\mathrm {Gal}(N/L)$
. Then:
-
(1)
 $\rho ^G_H(U_{\mathrm {cris},N/K})=U_{\mathrm {cris},N/L}$
.
$\rho ^G_H(U_{\mathrm {cris},N/K})=U_{\mathrm {cris},N/L}$
. -
(2) If H is normal in G, then
 $q^G_{G/H}(U_{\mathrm {cris},N/K})=U_{\mathrm {cris},L/K}$
.
$q^G_{G/H}(U_{\mathrm {cris},N/K})=U_{\mathrm {cris},L/K}$
.
Proof Let
![]() $u_{\mathrm {cris},N/K}\in Z({{\mathbb Q}_{p}}[G])^{\times }$
be such that
$u_{\mathrm {cris},N/K}\in Z({{\mathbb Q}_{p}}[G])^{\times }$
be such that
![]() $\hat \partial _{{{\mathbb Z}_p[G]}, {\mathbb Q_p[G]}}^1(u_{\mathrm {cris},N/K})=U_{\mathrm {cris},N/K}$
. We will use an analogous notation for all the other Galois extensions involved in the proof.
$\hat \partial _{{{\mathbb Z}_p[G]}, {\mathbb Q_p[G]}}^1(u_{\mathrm {cris},N/K})=U_{\mathrm {cris},N/K}$
. We will use an analogous notation for all the other Galois extensions involved in the proof.
Then, for any irreducible character
![]() $\chi $
of G, we can take
$\chi $
of G, we can take
 $$ \begin{align*} (u_{\mathrm{cris},N/K})_{\chi}= \begin{cases} \frac{\det(1-\chi(F)(pu)^{-d_K})}{\det(1-u^{d_K}\chi(F)^{-1})}&\text{if }\chi|_{I_{N/K}}=1,\\ 1&\text{if }\chi|_{I_{N/K}} \neq 1. \end{cases} \end{align*} $$
$$ \begin{align*} (u_{\mathrm{cris},N/K})_{\chi}= \begin{cases} \frac{\det(1-\chi(F)(pu)^{-d_K})}{\det(1-u^{d_K}\chi(F)^{-1})}&\text{if }\chi|_{I_{N/K}}=1,\\ 1&\text{if }\chi|_{I_{N/K}} \neq 1. \end{cases} \end{align*} $$
For two (virtual) characters
![]() $\chi _1$
and
$\chi _1$
and
![]() $\chi _2$
of a finite group J, we write
$\chi _2$
of a finite group J, we write
![]() $\langle \chi _1, \chi _2\rangle _J$
for the standard scalar product.
$\langle \chi _1, \chi _2\rangle _J$
for the standard scalar product.
-
(1) By [Reference Bley and WilsonBW09, Section 6.1], we have
Because $$ \begin{align*} \rho^G_H(u_{\mathrm{cris},N/K})= \left( \prod_{\chi\in\mathrm{Irr}(G)}(u_{\mathrm{cris},N/K})_{\chi}^{\langle\chi,\mathrm{Ind}^G_H\psi\rangle_G} \right)_{\psi\in \mathrm{Irr}({H})}. \end{align*} $$
$$ \begin{align*} \rho^G_H(u_{\mathrm{cris},N/K})= \left( \prod_{\chi\in\mathrm{Irr}(G)}(u_{\mathrm{cris},N/K})_{\chi}^{\langle\chi,\mathrm{Ind}^G_H\psi\rangle_G} \right)_{\psi\in \mathrm{Irr}({H})}. \end{align*} $$
 $\langle \chi ,\mathrm {Ind}^G_H\psi \rangle _G = \langle \chi |_H,\psi \rangle _H$
by Frobenius reciprocity, we obtain If
$\langle \chi ,\mathrm {Ind}^G_H\psi \rangle _G = \langle \chi |_H,\psi \rangle _H$
by Frobenius reciprocity, we obtain If $$ \begin{align*} (u_{\mathrm{cris},N/K})_{\chi}^{\langle \chi,\mathrm{Ind}_H^G\psi\rangle_G} =\begin{cases}1&\text{if }\chi|_{I_{N/K}}\neq 1,\\ u_{\mathrm{cris},N/K}& \text{if }\chi|_{I_{N/K}}=1 \text{ and } \chi|_H = \psi,\\ 1&\text{if }\chi|_{I_{N/K}}=1 \text{ and } \chi|_H \neq \psi. \end{cases} \end{align*} $$
$$ \begin{align*} (u_{\mathrm{cris},N/K})_{\chi}^{\langle \chi,\mathrm{Ind}_H^G\psi\rangle_G} =\begin{cases}1&\text{if }\chi|_{I_{N/K}}\neq 1,\\ u_{\mathrm{cris},N/K}& \text{if }\chi|_{I_{N/K}}=1 \text{ and } \chi|_H = \psi,\\ 1&\text{if }\chi|_{I_{N/K}}=1 \text{ and } \chi|_H \neq \psi. \end{cases} \end{align*} $$
 $\psi |_{I_{N/L}} \ne 1$
, then
$\psi |_{I_{N/L}} \ne 1$
, then
 $\chi |_{I_{N/K}} \ne 1$
whenever
$\chi |_{I_{N/K}} \ne 1$
whenever
 $\langle \chi |_H, \psi \rangle _H \ne 0$
. Thus,
$\langle \chi |_H, \psi \rangle _H \ne 0$
. Thus,
 $\rho ^G_H(u_{\mathrm {cris},N/K})_{\psi } = 1$
for those characters
$\rho ^G_H(u_{\mathrm {cris},N/K})_{\psi } = 1$
for those characters
 $\psi $
.
$\psi $
.
On the other hand, if
 $\psi |_{I_{N/L}} = 1$
, then
$\psi |_{I_{N/L}} = 1$
, then
 $\psi $
is a character of the cyclic group
$\psi $
is a character of the cyclic group
 $\overline {H} := H/I_{N/L} = \langle F_L \rangle $
. Each character
$\overline {H} := H/I_{N/L} = \langle F_L \rangle $
. Each character
 $\chi \in \mathrm {Irr}(G)$
with
$\chi \in \mathrm {Irr}(G)$
with
 $(u_{\mathrm {cris},N/K})_{\chi } \ne 1$
is actually a character of
$(u_{\mathrm {cris},N/K})_{\chi } \ne 1$
is actually a character of
 $\overline {G} := G / I_{N/K} = \langle F_K \rangle $
. Note that we can naturally identify
$\overline {G} := G / I_{N/K} = \langle F_K \rangle $
. Note that we can naturally identify
 $\overline {H}$
with a subgroup of
$\overline {H}$
with a subgroup of
 $\overline {G}$
and recall that
$\overline {G}$
and recall that
 $|\overline {G} / \overline {H}| = d_{L/K}$
.
$|\overline {G} / \overline {H}| = d_{L/K}$
.We therefore obtain
We consider the numerator and the denominator separately and use, in each case, the polynomial identity $$ \begin{align*} \prod_{\chi\in\mathrm{Irr}(G)}(u_{\mathrm{cris},N/K})_{\chi}^{\langle\chi,\mathrm{Ind}^G_H\psi\rangle_G} = \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} \frac{\det(1 - \chi(F_K)(pu)^{-d_K})}{\det(1 - u^{d_K}\chi(F_K)^{-1})}. \end{align*} $$
$$ \begin{align*} \prod_{\chi\in\mathrm{Irr}(G)}(u_{\mathrm{cris},N/K})_{\chi}^{\langle\chi,\mathrm{Ind}^G_H\psi\rangle_G} = \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} \frac{\det(1 - \chi(F_K)(pu)^{-d_K})}{\det(1 - u^{d_K}\chi(F_K)^{-1})}. \end{align*} $$
 $$ \begin{align*} \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} (X - \chi(F_K)) = X^{d_{L/K}} - \psi(F_L). \end{align*} $$
$$ \begin{align*} \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} (X - \chi(F_K)) = X^{d_{L/K}} - \psi(F_L). \end{align*} $$
For the numerator, we compute
and a similar computation for the denominator shows claim (a). $$ \begin{align*} & \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} \det(1 - \chi(F_K)(pu)^{-d_K}) \\ &= \det \left( \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} (pu)^{-d_K} \left( (pu)^{d_K} - \chi(F_K) \right) \right) \\ &= \det \left( (pu)^{-d_K d_{L/K}} \left( (pu)^{d_K d_{L/K}} - \psi(F_L) \right) \right) \\ &= \det \left( 1 - (pu)^{-d_L} \psi(F_L)\right), \end{align*} $$
$$ \begin{align*} & \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} \det(1 - \chi(F_K)(pu)^{-d_K}) \\ &= \det \left( \prod_{\chi \in \mathrm{Irr}(\overline{G}), \chi|_{\overline{H}} = \psi} (pu)^{-d_K} \left( (pu)^{d_K} - \chi(F_K) \right) \right) \\ &= \det \left( (pu)^{-d_K d_{L/K}} \left( (pu)^{d_K d_{L/K}} - \psi(F_L) \right) \right) \\ &= \det \left( 1 - (pu)^{-d_L} \psi(F_L)\right), \end{align*} $$
-
(2) For any character
 $\psi $
of
$\psi $
of
 $G/H$
, we write
$G/H$
, we write
 $\mathrm {infl}(\psi )$
for the inflated character of G. By [Reference Bley and WilsonBW09, Section 6.3],
$\mathrm {infl}(\psi )$
for the inflated character of G. By [Reference Bley and WilsonBW09, Section 6.3],
 $q^G_{G/H}(u_{\mathrm {cris},N/K})_{\psi }=(u_{\mathrm {cris},N/K})_{\mathrm {infl}(\psi )}$
for any
$q^G_{G/H}(u_{\mathrm {cris},N/K})_{\psi }=(u_{\mathrm {cris},N/K})_{\mathrm {infl}(\psi )}$
for any
 $\psi \in \mathrm {Irr}(G/H)$
. This is equal to
$\psi \in \mathrm {Irr}(G/H)$
. This is equal to
 $(u_{\mathrm {cris},L/K})_{\psi }$
, because
$(u_{\mathrm {cris},L/K})_{\psi }$
, because
 $I_{L/K} = I_{N/K}H/H$
and
$I_{L/K} = I_{N/K}H/H$
and
 $\mathrm {infl}(\psi )(F_K)=\psi (F_K)$
.▪
$\mathrm {infl}(\psi )(F_K)=\psi (F_K)$
.▪
5 Computation of epsilon constants
As in [Reference Izychev and VenjakobIV16, Section 2.3], we define
 $$ \begin{align*} \varepsilon_D(N/K,V)&=(\varepsilon(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{\mathbb Q}_p}(V\otimes\rho_{\chi}^*)), \psi_{\xi}, \mu_{{\mathbb Q}_{p}}))_{\chi\in\mathrm{Irr}(G)} \in\!\!\!\!\prod_{\chi\in\mathrm{Irr}(G)} ({\mathbb Q}_{p}^{c})^{\times} \\&\cong Z({{\mathbb Q}_p^c}[G])^{\times}. \end{align*} $$
$$ \begin{align*} \varepsilon_D(N/K,V)&=(\varepsilon(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{\mathbb Q}_p}(V\otimes\rho_{\chi}^*)), \psi_{\xi}, \mu_{{\mathbb Q}_{p}}))_{\chi\in\mathrm{Irr}(G)} \in\!\!\!\!\prod_{\chi\in\mathrm{Irr}(G)} ({\mathbb Q}_{p}^{c})^{\times} \\&\cong Z({{\mathbb Q}_p^c}[G])^{\times}. \end{align*} $$
For all unexplained notation, we refer the reader to [Reference Izychev and VenjakobIV16, Section 2.3]. If there is no danger of confusion, we sometimes drop
![]() $\psi _{\xi }$
and
$\psi _{\xi }$
and
![]() $\mu _{{\mathbb Q}_{p}}$
from our notation. Still following [Reference Izychev and VenjakobIV16] (see the proof of Lemma 4.1 of loc. cit.), we obtain
$\mu _{{\mathbb Q}_{p}}$
from our notation. Still following [Reference Izychev and VenjakobIV16] (see the proof of Lemma 4.1 of loc. cit.), we obtain
For an extension
![]() $L/K$
of p-adic fields, we write
$L/K$
of p-adic fields, we write
![]() $\mathfrak D_{L/K} = \pi _L^{s_{L/K}}\mathcal {O}_L$
for the different of
$\mathfrak D_{L/K} = \pi _L^{s_{L/K}}\mathcal {O}_L$
for the different of
![]() $L/K$
; in the case
$L/K$
; in the case
![]() $K={\mathbb Q}_p$
, we use the notations
$K={\mathbb Q}_p$
, we use the notations
![]() $\mathfrak D_L$
for
$\mathfrak D_L$
for
![]() $\mathfrak D_{L/{\mathbb Q}_p}$
and
$\mathfrak D_{L/{\mathbb Q}_p}$
and
![]() $s_L$
for
$s_L$
for
![]() $s_{L/{\mathbb Q}_p}$
. If
$s_{L/{\mathbb Q}_p}$
. If
![]() $M/L$
is a finite abelian extension and
$M/L$
is a finite abelian extension and
![]() $\eta $
an irreducible character of
$\eta $
an irreducible character of
![]() $\mathrm {Gal}(M/L)$
, then we let
$\mathrm {Gal}(M/L)$
, then we let
![]() $\tau _L(\eta )$
denote the abelian local Galois Gauß sum defined, e.g., in [Reference Pickett and VinatierPV13, p. 1184]. For the definition of Galois Gauß sums for a finite Galois extension
$\tau _L(\eta )$
denote the abelian local Galois Gauß sum defined, e.g., in [Reference Pickett and VinatierPV13, p. 1184]. For the definition of Galois Gauß sums for a finite Galois extension
![]() $M/L$
, we refer the reader to [Reference FröhlichFrö83, Chapter I, Section 5].
$M/L$
, we refer the reader to [Reference FröhlichFrö83, Chapter I, Section 5].
Proposition 5.1 We have the equality
 $$ \begin{align*}\begin{aligned} &\hat\partial_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}^1\left( \varepsilon_D(N/K, V)\right) \\ &\qquad= \hat\partial_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}^1\left( \left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})} \cdot \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r} \right)_{\chi \in \mathrm{Irr}(G)} \right),\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\hat\partial_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}^1\left( \varepsilon_D(N/K, V)\right) \\ &\qquad= \hat\partial_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}^1\left( \left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})} \cdot \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r} \right)_{\chi \in \mathrm{Irr}(G)} \right),\end{aligned} \end{align*} $$
where we write
![]() $\mathfrak f(\chi ) = \pi _K^{m_{\chi }}\mathcal {O}_K$
for the Artin conductor of
$\mathfrak f(\chi ) = \pi _K^{m_{\chi }}\mathcal {O}_K$
for the Artin conductor of
![]() $\chi $
.
$\chi $
.
Proof In the proof, we will use the list of properties in [Reference Benois and BergerBB08, Section 2.3]. The field K of loc. cit. corresponds to
![]() ${{\mathbb Q}_{p}}$
in our situation. Hence, if
${{\mathbb Q}_{p}}$
in our situation. Hence, if
![]() $\psi $
denotes the standard additive character, we have
$\psi $
denotes the standard additive character, we have
![]() $n(\psi ) = 0$
for its conductor.
$n(\psi ) = 0$
for its conductor.
Because V is cristalline, the
![]() $N_1$
-basis
$N_1$
-basis
![]() $\{e_i\}$
constructed in Lemma 4.2 is also a
$\{e_i\}$
constructed in Lemma 4.2 is also a
![]() ${{\mathbb Q}_p^{\mathrm {nr}}}$
-basis of
${{\mathbb Q}_p^{\mathrm {nr}}}$
-basis of
![]() $D_{\mathrm {pst}}(V)$
. A straightforward computation (see the proof of Lemma 4.6 for a similar computation) shows that
$D_{\mathrm {pst}}(V)$
. A straightforward computation (see the proof of Lemma 4.6 for a similar computation) shows that
 $$ \begin{align} \phi(e_i) = \sum_{h=1}^r p^{-1} ((T^{\mathrm{nr}})^{-1} u^{-1} T^{\mathrm{nr}})_{h,i}e_h. \end{align} $$
$$ \begin{align} \phi(e_i) = \sum_{h=1}^r p^{-1} ((T^{\mathrm{nr}})^{-1} u^{-1} T^{\mathrm{nr}})_{h,i}e_h. \end{align} $$
As in the proof of Lemma 4.2, any element
![]() $\sigma $
of the absolute inertia group acts trivially on the basis elements
$\sigma $
of the absolute inertia group acts trivially on the basis elements
![]() $e_i$
, whence
$e_i$
, whence
![]() $D_{\mathrm {pst}}(V)$
is unramified.
$D_{\mathrm {pst}}(V)$
is unramified.
Applying (5.1) and [Reference Benois and BergerBB08, Section 2.3, proprieté (6)], we obtain
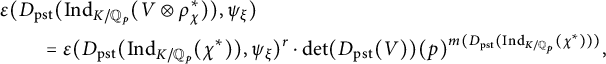 $$ \begin{align*}\begin{aligned} & \varepsilon(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{\mathbb Q}_p}(V\otimes\rho_{\chi}^*)),\psi_{\xi}) \\ &\qquad= \varepsilon(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*)),\psi_{\xi})^{r} \cdot \det(D_{\mathrm{pst}}(V))(p)^{m(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*)))}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} & \varepsilon(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{\mathbb Q}_p}(V\otimes\rho_{\chi}^*)),\psi_{\xi}) \\ &\qquad= \varepsilon(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*)),\psi_{\xi})^{r} \cdot \det(D_{\mathrm{pst}}(V))(p)^{m(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*)))}, \end{aligned}\end{align*} $$
where
![]() $m(D_{\mathrm {pst}}(\mathrm {Ind}_{K/{{\mathbb Q}_{p}}}(\chi ^{{*}})))$
is the exponent of the Artin conductor.
$m(D_{\mathrm {pst}}(\mathrm {Ind}_{K/{{\mathbb Q}_{p}}}(\chi ^{{*}})))$
is the exponent of the Artin conductor.
We consider the first factor and note that
so that we deduce from [Reference Bley and CobbeBC17, Proposition 6.1.3] that
As a consequence of [Reference MartinetMar77, Proposition II.4.1(ii)], we get
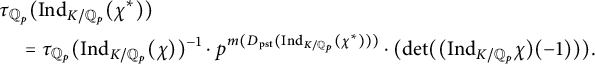 $$ \begin{align*} &\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*) ) \\&\quad = \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-1} \cdot p^{m(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*)))} \cdot (\det((\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}\chi)(-1))). \end{align*} $$
$$ \begin{align*} &\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*) ) \\&\quad = \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-1} \cdot p^{m(D_{\mathrm{pst}}(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi^*)))} \cdot (\det((\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}\chi)(-1))). \end{align*} $$
For the second factor, we first note that
By [Reference Benois and BergerBB08, p. 625], the action of the Weil group
![]() $W_{{{\mathbb Q}_{p}}}$
on
$W_{{{\mathbb Q}_{p}}}$
on
![]() $D_{\mathrm {pst}}(V)$
is defined, so that the action of the geometric Frobenius
$D_{\mathrm {pst}}(V)$
is defined, so that the action of the geometric Frobenius
![]() $\varphi ^{-1}$
coincides with the usual action of
$\varphi ^{-1}$
coincides with the usual action of
![]() $\varphi ^{-1} \phi $
on
$\varphi ^{-1} \phi $
on
![]() $D_{\mathrm {pst}}(V)$
. We recall from (5.2) that with respect to the basis
$D_{\mathrm {pst}}(V)$
. We recall from (5.2) that with respect to the basis
![]() $\{e_i\}$
of
$\{e_i\}$
of
![]() $D_{\mathrm {pst}}(V)$
the element
$D_{\mathrm {pst}}(V)$
the element
![]() $\varphi ^{-1}\phi $
acts as
$\varphi ^{-1}\phi $
acts as
![]() $\varphi ^{-1}( p^{-1}(T^{\mathrm {nr}})^{-1} u^{-1}T^{\mathrm {nr}})$
on
$\varphi ^{-1}( p^{-1}(T^{\mathrm {nr}})^{-1} u^{-1}T^{\mathrm {nr}})$
on
![]() $D_{\mathrm {pst}}(V)$
, so that we derive
$D_{\mathrm {pst}}(V)$
, so that we derive
![]() $\det (\varphi ^{-1},D_{\mathrm {pst}}(V)) = p^{-r}\det (u^{-1})$
.
$\det (\varphi ^{-1},D_{\mathrm {pst}}(V)) = p^{-r}\det (u^{-1})$
.
Finally, by [Reference NeukirchNeu92, Chapter VII, Theorem 11.7], we get
so that
We conclude that
 $$ \begin{align*} \varepsilon_D(N/K, V)_{\chi} &= \left( \det(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi))(-1) \right)^{r} \cdot \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\\ &\quad \cdot \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r}. \end{align*} $$
$$ \begin{align*} \varepsilon_D(N/K, V)_{\chi} &= \left( \det(\mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi))(-1) \right)^{r} \cdot \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\\ &\quad \cdot \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r}. \end{align*} $$
The proposition is now immediate from [Reference Bley and CobbeBC17, Lemma 6.2.2], which shows that
▪
Concerning functoriality with respect to change of fields, we have the following lemma.
Lemma 5.2 Let L be an intermediate field of
![]() $N/K$
and
$N/K$
and
![]() $H=\mathrm {Gal}(N/L)$
.
$H=\mathrm {Gal}(N/L)$
.
-
(1)
 $\rho ^G_H(\hat \partial ^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}(\varepsilon _D(N/K, V)))=\hat \partial ^1_{{{\mathbb Z}_p}[H], {\mathbb Q}_p^c[H]}(\varepsilon _D(N/L, V))$
.
$\rho ^G_H(\hat \partial ^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}(\varepsilon _D(N/K, V)))=\hat \partial ^1_{{{\mathbb Z}_p}[H], {\mathbb Q}_p^c[H]}(\varepsilon _D(N/L, V))$
. -
(2) If H is normal in G, then
 $$ \begin{align*} q^G_{G/H}(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}(\varepsilon_D(N/K, V)))=\hat\partial^1_{{{\mathbb Z}_p}[G/H], {\mathbb Q}_p^c[G/H]}(\varepsilon_D(L/K, V)). \end{align*} $$
$$ \begin{align*} q^G_{G/H}(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}(\varepsilon_D(N/K, V)))=\hat\partial^1_{{{\mathbb Z}_p}[G/H], {\mathbb Q}_p^c[G/H]}(\varepsilon_D(L/K, V)). \end{align*} $$
Proof By Proposition 5.1, we have
 $$ \begin{align*} & \rho^G_H(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}(\varepsilon_D(N/K, V))) \\ &\quad = \rho^G_H\left(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]} \left( \left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})} \cdot \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r} \right)_{\chi \in \mathrm{Irr}(G)} \right) \right). \end{align*} $$
$$ \begin{align*} & \rho^G_H(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]}(\varepsilon_D(N/K, V))) \\ &\quad = \rho^G_H\left(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]} \left( \left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})} \cdot \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r} \right)_{\chi \in \mathrm{Irr}(G)} \right) \right). \end{align*} $$
By [Reference BreuningBre04b, Lemma 2.3], we have
 $$ \begin{align*} &\rho^G_H(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]} \left( \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r} \right)_{\chi \in \mathrm{Irr}(G)} )\\&\quad = \hat\partial^1_{{{\mathbb Z}_p}[H], {\mathbb Q}_p^c[H]} \left( \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{L/{{\mathbb Q}_{p}}}(\psi) )^{-r} \right)_{\psi \in \mathrm{Irr}(H)}, \end{align*} $$
$$ \begin{align*} &\rho^G_H(\hat\partial^1_{{{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G]} \left( \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) )^{-r} \right)_{\chi \in \mathrm{Irr}(G)} )\\&\quad = \hat\partial^1_{{{\mathbb Z}_p}[H], {\mathbb Q}_p^c[H]} \left( \tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{L/{{\mathbb Q}_{p}}}(\psi) )^{-r} \right)_{\psi \in \mathrm{Irr}(H)}, \end{align*} $$
whereas [Reference Bley and WilsonBW09, Section 6.1] implies
with
From [Reference NeukirchNeu92, Theorem VII.11.7] and the obvious relation
we derive
where
![]() $\mathfrak d_{L/K}$
denotes the discriminant of
$\mathfrak d_{L/K}$
denotes the discriminant of
![]() $L/K$
. This implies
$L/K$
. This implies
Furthermore, we note
Hence, we deduce from
![]() $d_L = d_Kd_{L/K}$
$d_L = d_Kd_{L/K}$
 $$ \begin{align*} \begin{aligned} &\sum_{\chi\in\mathrm{Irr}(G)}d_K(s_K\chi(1) + m_{\chi})\langle\chi,\mathrm{ind}^G_H\psi\rangle_G\\ &\qquad=d_K( s_Ke_{L/K}d_{L/K}\psi(1)+d_{L/K}s_{L/K}\psi(1)+d_{L/K}m_{\psi})\\ &\qquad=d_L s_K e_{L/K}\psi(1)+d_Ls_{L/K}\psi(1)+d_{L}m_{\psi}\\ &\qquad=d_L \psi(1) (s_K e_{L/K}+s_{L/K})+d_{L}m_{\psi}\\ &\qquad=d_L \psi(1)s_L+d_{L}m_{\psi}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\sum_{\chi\in\mathrm{Irr}(G)}d_K(s_K\chi(1) + m_{\chi})\langle\chi,\mathrm{ind}^G_H\psi\rangle_G\\ &\qquad=d_K( s_Ke_{L/K}d_{L/K}\psi(1)+d_{L/K}s_{L/K}\psi(1)+d_{L/K}m_{\psi})\\ &\qquad=d_L s_K e_{L/K}\psi(1)+d_Ls_{L/K}\psi(1)+d_{L}m_{\psi}\\ &\qquad=d_L \psi(1) (s_K e_{L/K}+s_{L/K})+d_{L}m_{\psi}\\ &\qquad=d_L \psi(1)s_L+d_{L}m_{\psi}, \end{aligned} \end{align*} $$
where the last equality follows from the multiplicativity of differents (see [Reference NeukirchNeu92, Theorem III.2.2(i)]). The first functoriality property is now obvious.
The second functoriality property follows easily from [Reference BreuningBre04b, Lemma 2.3] and [Reference NeukirchNeu92, Lemma VII.11.7(ii)].▪
6 Computation of the cohomological term
6.1 Identifying cohomology
In the following, we will take the opportunity to clarify some of the constructions of [Reference Bley and CobbeBC17, Section 7.1, p. 356]. This is necessary, because, in the definition of
![]() $C_{N/K}$
, we use the identification of
$C_{N/K}$
, we use the identification of
![]() $H^1(N, T)$
with
$H^1(N, T)$
with
![]() $\mathcal F(\mathfrak p_N^{(r)})$
coming from continuous cochain cohomology combined with Kummer theory, whereas in the computations in [Reference Bley and CobbeBC17, Section 7.1], we use the identification coming from [Reference Bley and CobbeBC17, Theorem 4.3.1] combined with [Reference Bley and CobbeBC17, Lemma 4.1.1]. In this manuscript, we work in the r-dimensional setting based on the results of [Reference CobbeCob18, Section 3], where the special case
$\mathcal F(\mathfrak p_N^{(r)})$
coming from continuous cochain cohomology combined with Kummer theory, whereas in the computations in [Reference Bley and CobbeBC17, Section 7.1], we use the identification coming from [Reference Bley and CobbeBC17, Theorem 4.3.1] combined with [Reference Bley and CobbeBC17, Lemma 4.1.1]. In this manuscript, we work in the r-dimensional setting based on the results of [Reference CobbeCob18, Section 3], where the special case
![]() $r=1$
covers the situation of [Reference Bley and CobbeBC17].
$r=1$
covers the situation of [Reference Bley and CobbeBC17].
Let
with nontrivial modules in degrees
![]() $0$
,
$0$
,
![]() $1$
, and
$1$
, and
![]() $2$
, be the complex of [Reference CobbeCob18, Theorem 3.12], and let
$2$
, be the complex of [Reference CobbeCob18, Theorem 3.12], and let
with nontrivial modules in degrees
![]() $1$
and
$1$
and
![]() $2$
, be the complex of [Reference CobbeCob18, Theorem 3.15]. We also deduce from [Reference CobbeCob18, Theorem 3.3] combined with [Reference CobbeCob18, Lemma 2.1] the short exact sequence
$2$
, be the complex of [Reference CobbeCob18, Theorem 3.15]. We also deduce from [Reference CobbeCob18, Theorem 3.3] combined with [Reference CobbeCob18, Lemma 2.1] the short exact sequence
In the sequel, we will use dotted arrows for morphisms in the derived category and solid arrows for those which are actual morphisms of complexes.
In the proof of [Reference CobbeCob18, Theorem 3.12], we construct an isomorphism
in the derived category which induces the identity on
![]() $H^0$
. In a second step (see [Reference CobbeCob18, Corollary 3.13]), we produce quasi-isomorphisms
$H^0$
. In a second step (see [Reference CobbeCob18, Corollary 3.13]), we produce quasi-isomorphisms
where
 $$ \begin{align*} P^{\bullet} &:= [P^{-1} \longrightarrow P^0 \longrightarrow P^1\longrightarrow {\mathbb Q}_p^r/(F_N-1)\cdot\mathbb Q_p^r(\rho^{\mathrm{nr}})], \\ \tilde P^{\bullet} &:= [P^{-1} \longrightarrow P^0 \longrightarrow P^1]. \end{align*} $$
$$ \begin{align*} P^{\bullet} &:= [P^{-1} \longrightarrow P^0 \longrightarrow P^1\longrightarrow {\mathbb Q}_p^r/(F_N-1)\cdot\mathbb Q_p^r(\rho^{\mathrm{nr}})], \\ \tilde P^{\bullet} &:= [P^{-1} \longrightarrow P^0 \longrightarrow P^1]. \end{align*} $$
Here, the
![]() ${\mathbb Z}_p[G]$
-modules
${\mathbb Z}_p[G]$
-modules
![]() $P^{-1}, P^{0}, P^1$
are finitely generated and projective, and the uniquely divisible module
$P^{-1}, P^{0}, P^1$
are finitely generated and projective, and the uniquely divisible module
![]() $\mathbb Q_p^r(\rho ^{\mathrm {nr}})/(F_N-1)\cdot \mathbb Q_p^r(\rho ^{\mathrm {nr}})$
is G-cohomologically trivial. Composing
$\mathbb Q_p^r(\rho ^{\mathrm {nr}})/(F_N-1)\cdot \mathbb Q_p^r(\rho ^{\mathrm {nr}})$
is G-cohomologically trivial. Composing
![]() $\eta $
and
$\eta $
and
![]() $\tau $
, we obtain an isomorphism
$\tau $
, we obtain an isomorphism
in the derived category. Passing to the projective limit in [Reference CobbeCob18, Lemma 3.14], we obtain another quasi-isomorphism
![]() $\varphi \colon \tilde P^{\bullet } \stackrel \sim \longrightarrow R\Gamma (N, T)[1]$
and thus obtain the following commutative diagram in the derived category:
$\varphi \colon \tilde P^{\bullet } \stackrel \sim \longrightarrow R\Gamma (N, T)[1]$
and thus obtain the following commutative diagram in the derived category:

On
![]() $H^0$
, we therefore obtain the commutative diagram:
$H^0$
, we therefore obtain the commutative diagram:
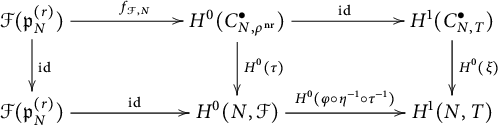
By the proof of [Reference Bley and CobbeBC17, Theorem 4.3.1] (which is used also for [Reference CobbeCob18, Theorem 3.15]), we know that the composite
is the Kummer map
![]() $\partial _{Ku,n}$
resulting from the distinguished triangle
$\partial _{Ku,n}$
resulting from the distinguished triangle
By the universal property of projective limits, we obtain
6.2 Definition of the twist invariant
In this subsection, we define an invariant
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
in the relative algebraic K-group
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
in the relative algebraic K-group
![]() $K_0({{\mathbb Z}_p[G]}, \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
. We recall that
$K_0({{\mathbb Z}_p[G]}, \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
. We recall that
![]() $T^{\mathrm {nr}} \in \mathrm {Gl}_r(\overline {{\mathbb Z}_p^{\mathrm {nr}}})$
satisfies the matrix equality
$T^{\mathrm {nr}} \in \mathrm {Gl}_r(\overline {{\mathbb Z}_p^{\mathrm {nr}}})$
satisfies the matrix equality
This equality determines
![]() $T^{\mathrm {nr}}$
up to right multiplication by a matrix
$T^{\mathrm {nr}}$
up to right multiplication by a matrix
![]() $S \in \mathrm {Gl}_r({{\mathbb Z}_p})$
; explicitly, if
$S \in \mathrm {Gl}_r({{\mathbb Z}_p})$
; explicitly, if
![]() $\tilde {T}^{\mathrm {nr}}$
is a second matrix satisfying (6.4), then
$\tilde {T}^{\mathrm {nr}}$
is a second matrix satisfying (6.4), then
![]() $T^{\mathrm {nr}} = \tilde {T}^{\mathrm {nr}}S$
. It is thus immediate that the element
$T^{\mathrm {nr}} = \tilde {T}^{\mathrm {nr}}S$
. It is thus immediate that the element
does not depend on the specific choice of
![]() $T^{\mathrm {nr}}$
satisfying (6.4).
$T^{\mathrm {nr}}$
satisfying (6.4).
Remark 6.1 The element
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
clearly becomes trivial under the canonical map
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
clearly becomes trivial under the canonical map
![]() $K_0({{\mathbb Z}_p[G]}, \overline {\mathbb Q_p^{\mathrm {nr}}}[G]) \longrightarrow K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
.
$K_0({{\mathbb Z}_p[G]}, \overline {\mathbb Q_p^{\mathrm {nr}}}[G]) \longrightarrow K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
.
6.3 The cohomological term
 $C_{N/K}$
$C_{N/K}$
In this subsection, we clarify and correct the computation of the cohomological term
![]() $C_{N/K}$
of [Reference Bley and CobbeBC17, Section 7.1]. In particular, we produce a detailed proof of [Reference Bley and CobbeBC17, Lemma 7.1.2], which in loc. cit. was quoted from [Reference Izychev and VenjakobIV16, Lemma 6.1]. It is this part of the computation where the new term
$C_{N/K}$
of [Reference Bley and CobbeBC17, Section 7.1]. In particular, we produce a detailed proof of [Reference Bley and CobbeBC17, Lemma 7.1.2], which in loc. cit. was quoted from [Reference Izychev and VenjakobIV16, Lemma 6.1]. It is this part of the computation where the new term
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
emerges.
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
emerges.
We recall that we throughout assume Hypothesis (F), in particular,
![]() $\rho ^{\mathrm {nr}} |_{G_N} \ne 1$
. Then, by [Reference Bley and CobbeBC17, equations (15) and (16)], the cohomological term
$\rho ^{\mathrm {nr}} |_{G_N} \ne 1$
. Then, by [Reference Bley and CobbeBC17, equations (15) and (16)], the cohomological term
![]() $C_{N/K}$
is defined by
$C_{N/K}$
is defined by
where
We fix a
![]() ${{\mathbb Z}_p}[G]$
-projective sublattice
${{\mathbb Z}_p}[G]$
-projective sublattice
![]() $\mathcal L\subseteq \mathcal {O}_N$
such that the exponential map
$\mathcal L\subseteq \mathcal {O}_N$
such that the exponential map
![]() $\exp _{\mathcal F}$
of Lemma 3.3 converges on
$\exp _{\mathcal F}$
of Lemma 3.3 converges on
![]() $\mathcal {L}^{(r)}$
. We set
$\mathcal {L}^{(r)}$
. We set
![]() $X(\mathcal {L}):=\exp _{\mathcal F}(\mathcal {L}^{(r)})$
and note that
$X(\mathcal {L}):=\exp _{\mathcal F}(\mathcal {L}^{(r)})$
and note that
![]() $X(\mathcal {L}) \subseteq \mathcal F(\mathfrak p_N^{(r)})$
.
$X(\mathcal {L}) \subseteq \mathcal F(\mathfrak p_N^{(r)})$
.
The embedding
![]() $X(\mathcal {L}) \hookrightarrow{f_{{\mathcal F},{\mathcal N}}} H^1(C_{N, T}^{\bullet })$
, where
$X(\mathcal {L}) \hookrightarrow{f_{{\mathcal F},{\mathcal N}}} H^1(C_{N, T}^{\bullet })$
, where
![]() $f_{{\mathcal F},{\mathcal N}}$
is the first map in the exact sequence (6.1), induces an injective map of complexes
$f_{{\mathcal F},{\mathcal N}}$
is the first map in the exact sequence (6.1), induces an injective map of complexes
![]() $X(\mathcal {L})[-1] \longrightarrow C_{N,T}^{\bullet }$
. We set
$X(\mathcal {L})[-1] \longrightarrow C_{N,T}^{\bullet }$
. We set
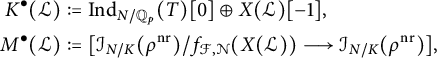 $$ \begin{align} K^{\bullet}(\mathcal{L}) &:= \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(T)[0] \oplus X(\mathcal{L})[-1], \nonumber \\ M^{\bullet}(\mathcal{L}) &:= [ \mathcal{I}_{N/K}(\rho^{\mathrm{nr}}) / f_{{\mathcal F},{\mathcal N}}(X(\mathcal{L})) \longrightarrow \mathcal{I}_{N/K}(\rho^{\mathrm{nr}}) ], \end{align} $$
$$ \begin{align} K^{\bullet}(\mathcal{L}) &:= \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(T)[0] \oplus X(\mathcal{L})[-1], \nonumber \\ M^{\bullet}(\mathcal{L}) &:= [ \mathcal{I}_{N/K}(\rho^{\mathrm{nr}}) / f_{{\mathcal F},{\mathcal N}}(X(\mathcal{L})) \longrightarrow \mathcal{I}_{N/K}(\rho^{\mathrm{nr}}) ], \end{align} $$
with modules in degrees
![]() $1$
and
$1$
and
![]() $2$
, and have thus constructed an exact sequence of complexes
$2$
, and have thus constructed an exact sequence of complexes
We first rewrite
![]() $C_{N/K}$
in terms of the middle complex and obtain
$C_{N/K}$
in terms of the middle complex and obtain
with
![]() $\xi $
as in (6.2). We then use additivity of refined Euler characteristics in distinguished triangles and derive
$\xi $
as in (6.2). We then use additivity of refined Euler characteristics in distinguished triangles and derive
where
![]() $\lambda $
is the following composite map:
$\lambda $
is the following composite map:
 $$ \begin{align*} && X(\mathcal{L})_{{B_{\mathrm{dR}}}} = \mathcal F(\mathfrak p_N^{(r)})_{{B_{\mathrm{dR}}}} \xrightarrow{f_{{\mathcal F},{\mathcal N}}} H^1(C_{N,T}^{\bullet})_{{B_{\mathrm{dR}}}} \\ && \xrightarrow{H^0(\xi)} H^1(N, T)_{{B_{\mathrm{dR}}}} \xrightarrow{comp_V\circ\exp_V^{-1}} (\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(T))_{{B_{\mathrm{dR}}}}. \end{align*} $$
$$ \begin{align*} && X(\mathcal{L})_{{B_{\mathrm{dR}}}} = \mathcal F(\mathfrak p_N^{(r)})_{{B_{\mathrm{dR}}}} \xrightarrow{f_{{\mathcal F},{\mathcal N}}} H^1(C_{N,T}^{\bullet})_{{B_{\mathrm{dR}}}} \\ && \xrightarrow{H^0(\xi)} H^1(N, T)_{{B_{\mathrm{dR}}}} \xrightarrow{comp_V\circ\exp_V^{-1}} (\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(T))_{{B_{\mathrm{dR}}}}. \end{align*} $$
Then, the term
![]() $\chi _{{{\mathbb Z}_p[G]},{{B_{\mathrm {dR}}}[G]}}( M^{\bullet }(\mathcal {L}), 0)$
is precisely the term which is computed in [Reference Bley and CobbeBC17, Section 7.2] in the one-dimensional weakly ramified case. We will compute this term in arbitrary dimension
$\chi _{{{\mathbb Z}_p[G]},{{B_{\mathrm {dR}}}[G]}}( M^{\bullet }(\mathcal {L}), 0)$
is precisely the term which is computed in [Reference Bley and CobbeBC17, Section 7.2] in the one-dimensional weakly ramified case. We will compute this term in arbitrary dimension
![]() $r \ge 1$
in Section 6.4 in the tame case and in Section 6.5 in the weakly ramified case.
$r \ge 1$
in Section 6.4 in the tame case and in Section 6.5 in the weakly ramified case.
For the first term, we obtain
 $$ \begin{align} [X(\mathcal{L}), \lambda, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(T)] = \left[X(\mathcal L),\lambda_2,\bigoplus_{i=1}^r\mathcal L e_i\right]+ \left[\bigoplus_{i=1}^r\mathcal L e_i,\mathrm{comp}_V,\mathrm{Ind}_{N/\mathbb Q_p}T\right], \end{align} $$
$$ \begin{align} [X(\mathcal{L}), \lambda, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(T)] = \left[X(\mathcal L),\lambda_2,\bigoplus_{i=1}^r\mathcal L e_i\right]+ \left[\bigoplus_{i=1}^r\mathcal L e_i,\mathrm{comp}_V,\mathrm{Ind}_{N/\mathbb Q_p}T\right], \end{align} $$
where the elements
![]() $e_1, \ldots , e_r$
are defined in Lemma 4.2 and
$e_1, \ldots , e_r$
are defined in Lemma 4.2 and
![]() $\lambda _2$
is the composite map
$\lambda _2$
is the composite map
Note that
![]() $e_1, \ldots , e_r$
constitute an N-basis of
$e_1, \ldots , e_r$
constitute an N-basis of
![]() $D_{\mathrm {dR}}^N(V) = t_V(N)$
.
$D_{\mathrm {dR}}^N(V) = t_V(N)$
.
In the next three lemmas, we will compute the summands in (6.10).
Lemma 6.2 With
![]() $\lambda _2$
denoting the composite map defined in (6.11), we have
$\lambda _2$
denoting the composite map defined in (6.11), we have
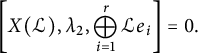 $$ \begin{align*} \left[X(\mathcal L),\lambda_2,\bigoplus_{i=1}^r\mathcal L e_i\right]=0. \end{align*} $$
$$ \begin{align*} \left[X(\mathcal L),\lambda_2,\bigoplus_{i=1}^r\mathcal L e_i\right]=0. \end{align*} $$
Proof This proof is an expanded version of the arguments of [Reference Izychev and VenjakobIV16, p. 509].
Recall the isomorphism
![]() $\theta :\mathcal F\to \mathbb {G}_m^r$
from (2.1), which satisfies
$\theta :\mathcal F\to \mathbb {G}_m^r$
from (2.1), which satisfies
![]() $\theta (x)\equiv \varepsilon ^{-1}x\pmod {\deg \geq 2}$
. Let
$\theta (x)\equiv \varepsilon ^{-1}x\pmod {\deg \geq 2}$
. Let
![]() $\pi _{{B_{\mathrm {dR}}}}:{B_{\mathrm {dR}}}^+\to \mathbb C_p$
be the natural projection to the residue field. Similarly to [Reference Bloch, Kato, Cartier, Illusie, Katz, Laumon, Manin and RibetBK90, p. 360], we can construct a commutative diagram of exact sequences:
$\pi _{{B_{\mathrm {dR}}}}:{B_{\mathrm {dR}}}^+\to \mathbb C_p$
be the natural projection to the residue field. Similarly to [Reference Bloch, Kato, Cartier, Illusie, Katz, Laumon, Manin and RibetBK90, p. 360], we can construct a commutative diagram of exact sequences:
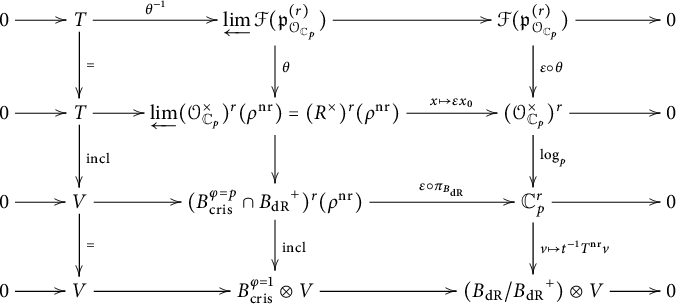
Note that (differently from [Reference Bloch, Kato, Cartier, Illusie, Katz, Laumon, Manin and RibetBK90]) some of the objects are twisted by
![]() $\rho ^{\mathrm {nr}}$
in order to make all maps
$\rho ^{\mathrm {nr}}$
in order to make all maps
![]() $G_N$
-invariant;
$G_N$
-invariant;
![]() $\varepsilon $
always denotes multiplication by the element
$\varepsilon $
always denotes multiplication by the element
![]() $\varepsilon \in \overline {{\mathbb Q_p^{\mathrm {nr}}}}$
which occurs in (2.1). We observe that by Lemma 3.1 we have the equality
$\varepsilon \in \overline {{\mathbb Q_p^{\mathrm {nr}}}}$
which occurs in (2.1). We observe that by Lemma 3.1 we have the equality
![]() $\log _p\circ \varepsilon \circ \theta =\log _{\mathcal F}$
.
$\log _p\circ \varepsilon \circ \theta =\log _{\mathcal F}$
.
Taking
![]() $G_N$
-fixed elements and cohomology, we obtain
$G_N$
-fixed elements and cohomology, we obtain

where the map s is such that
![]() $s(v_i)=e_i$
for all i. Note that this diagram is the higher dimensional version of [Reference Izychev and VenjakobIV16, equation (3.4)]. It makes the identification s of
$s(v_i)=e_i$
for all i. Note that this diagram is the higher dimensional version of [Reference Izychev and VenjakobIV16, equation (3.4)]. It makes the identification s of
![]() $N^r$
and the tangent space
$N^r$
and the tangent space
![]() $t_V(N)$
explicit.
$t_V(N)$
explicit.
We rewrite
![]() $\lambda _2$
in terms of the maps in the last diagram and get
$\lambda _2$
in terms of the maps in the last diagram and get

By diagram (6.3), we see that
![]() $(\partial _{Ku}^{-1}\circ H^0(\xi )\circ f_{{\mathcal F},{\mathcal N}})(X(\mathcal {L})) = X(\mathcal {L})$
, so that it remains to show
$(\partial _{Ku}^{-1}\circ H^0(\xi )\circ f_{{\mathcal F},{\mathcal N}})(X(\mathcal {L})) = X(\mathcal {L})$
, so that it remains to show
which is immediate from
![]() $\log _{\mathcal F}(X(\mathcal {L})) = \mathcal {L}^{(r)}$
and
$\log _{\mathcal F}(X(\mathcal {L})) = \mathcal {L}^{(r)}$
and
![]() $s(v_i)=e_i$
for
$s(v_i)=e_i$
for
![]() $i=1, \ldots ,r$
.▪
$i=1, \ldots ,r$
.▪
Lemma 6.3 With notation as in (6.10) and
![]() $m := [K : {{\mathbb Q}_{p}}]$
, we have
$m := [K : {{\mathbb Q}_{p}}]$
, we have
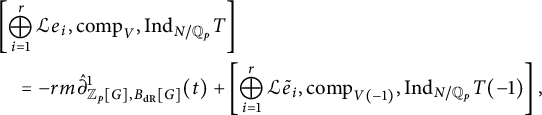 $$ \begin{align*} & \left[\bigoplus_{i=1}^r\mathcal L e_i,\mathrm{comp}_V,\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T\right] \\ &\quad = -r m \hat\partial_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}^1(t)+ \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right], \end{align*} $$
$$ \begin{align*} & \left[\bigoplus_{i=1}^r\mathcal L e_i,\mathrm{comp}_V,\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T\right] \\ &\quad = -r m \hat\partial_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}^1(t)+ \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right], \end{align*} $$
where the elements
![]() $\tilde e_i$
are defined in Lemma 4.3.
$\tilde e_i$
are defined in Lemma 4.3.
Proof It is easy to see that in the r-dimensional setting, we also have a diagram as in [Reference Izychev and VenjakobIV16, equation (6.1)]. If we denote the vertical maps in this diagram by
![]() $f_1$
and
$f_1$
and
![]() $f_2$
, then
$f_2$
, then
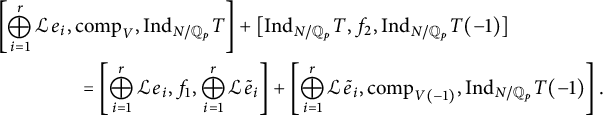 $$ \begin{align*} \begin{aligned} &\left[\bigoplus_{i=1}^r\mathcal L e_i,\mathrm{comp}_V,\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T\right]+ [\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T,f_2,\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)]\\ &\qquad\qquad=\left[\bigoplus_{i=1}^r\mathcal L e_i,f_1,\bigoplus_{i=1}^r\mathcal L \tilde e_i\right]+ \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\left[\bigoplus_{i=1}^r\mathcal L e_i,\mathrm{comp}_V,\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T\right]+ [\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T,f_2,\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)]\\ &\qquad\qquad=\left[\bigoplus_{i=1}^r\mathcal L e_i,f_1,\bigoplus_{i=1}^r\mathcal L \tilde e_i\right]+ \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right]. \end{aligned} \end{align*} $$
Because
![]() $f_1$
sends each basis element
$f_1$
sends each basis element
![]() $e_i$
to
$e_i$
to
![]() $\tilde e_i$
, the first summand on the right-hand side is trivial. Both
$\tilde e_i$
, the first summand on the right-hand side is trivial. Both
![]() $\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T$
and
$\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T$
and
![]() $\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T(-1)$
are isomorphic to
$\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T(-1)$
are isomorphic to
![]() ${{\mathbb Z}_p}[G]^{rm}$
as
${{\mathbb Z}_p}[G]^{rm}$
as
![]() ${{\mathbb Z}_p}[G]$
-modules. Via these isomorphisms, the map
${{\mathbb Z}_p}[G]$
-modules. Via these isomorphisms, the map
![]() $f_2$
corresponds to multiplication by t, and so we obtain
$f_2$
corresponds to multiplication by t, and so we obtain
▪
Let
![]() $\beta \in N$
be a normal basis element of
$\beta \in N$
be a normal basis element of
![]() $N/K$
, i.e.,
$N/K$
, i.e.,
![]() $N = K[G]\beta $
. Let
$N = K[G]\beta $
. Let
be defined by
where
![]() $\mathfrak d_K$
denotes the discriminant of
$\mathfrak d_K$
denotes the discriminant of
![]() $K/{{\mathbb Q}_{p}}$
and
$K/{{\mathbb Q}_{p}}$
and
![]() $\mathcal N_{K/{{\mathbb Q}_{p}}}(\beta | \chi )$
the usual norm resolvent (see, e.g., [Reference Pickett and VinatierPV13, Section 2.2]).
$\mathcal N_{K/{{\mathbb Q}_{p}}}(\beta | \chi )$
the usual norm resolvent (see, e.g., [Reference Pickett and VinatierPV13, Section 2.2]).
We also recall the definition of the twist invariant
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
in Section 6.2. The next lemma corrects an error in [Reference Bley and CobbeBC17, Lemma 7.1.2] where we just quoted the proof of [Reference Izychev and VenjakobIV16, Lemma 6.1]. However, whereas we work in the relative group
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
in Section 6.2. The next lemma corrects an error in [Reference Bley and CobbeBC17, Lemma 7.1.2] where we just quoted the proof of [Reference Izychev and VenjakobIV16, Lemma 6.1]. However, whereas we work in the relative group
![]() $K_0({{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]})$
, the authors of loc. cit. work in
$K_0({{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]})$
, the authors of loc. cit. work in
![]() $K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], {{B_{\mathrm {dR}}}[G]})$
where
$K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], {{B_{\mathrm {dR}}}[G]})$
where
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
vanishes by Remark 6.1.
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
vanishes by Remark 6.1.
Lemma 6.4 With
![]() $m = [K:{{\mathbb Q}_{p}}]$
and
$m = [K:{{\mathbb Q}_{p}}]$
and
![]() $\hat \partial ^1 = \hat \partial ^1_{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}$
, we have
$\hat \partial ^1 = \hat \partial ^1_{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}$
, we have
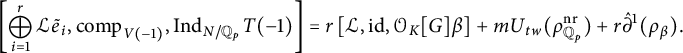 $$ \begin{align*} \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right] = r\left[\mathcal{L}, \mathrm{id}, {\mathcal{O}_K[G]} \beta \right] + m U_{tw}(\rho^{\mathrm{nr}}_{{\mathbb Q}_{p}}) + r\hat\partial^1(\rho_{\beta}). \end{align*} $$
$$ \begin{align*} \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right] = r\left[\mathcal{L}, \mathrm{id}, {\mathcal{O}_K[G]} \beta \right] + m U_{tw}(\rho^{\mathrm{nr}}_{{\mathbb Q}_{p}}) + r\hat\partial^1(\rho_{\beta}). \end{align*} $$
Proof We let
![]() $T_{\mathrm {triv}} = {\mathbb Z}_p^{(r)}$
and
$T_{\mathrm {triv}} = {\mathbb Z}_p^{(r)}$
and
![]() $V_{\mathrm {triv}}=\mathbb Q_p^{(r)}$
denote the trivial representations. Let
$V_{\mathrm {triv}}=\mathbb Q_p^{(r)}$
denote the trivial representations. Let
![]() $z_1, \ldots , z_r$
denote the canonical
$z_1, \ldots , z_r$
denote the canonical
![]() ${{\mathbb Z}_p}$
-basis of
${{\mathbb Z}_p}$
-basis of
![]() $T_{\mathrm {triv}}$
.
$T_{\mathrm {triv}}$
.
In the following, we choose to use for each
![]() $G_N$
-representation W
$G_N$
-representation W
as the definition for the induction. Note that if
![]() $L/{{\mathbb Q}_{p}}$
is any field extension (e.g.,
$L/{{\mathbb Q}_{p}}$
is any field extension (e.g.,
![]() $L = {B_{\mathrm {dR}}}$
) which carries an action of
$L = {B_{\mathrm {dR}}}$
) which carries an action of
![]() $G_{{\mathbb Q}_{p}}$
and W is an L-space, then
$G_{{\mathbb Q}_{p}}$
and W is an L-space, then
![]() $ \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(W)$
is also an L-space with
$ \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(W)$
is also an L-space with
![]() $(\alpha x)(\sigma ) = \sigma (\alpha ) x(\sigma )$
for all
$(\alpha x)(\sigma ) = \sigma (\alpha ) x(\sigma )$
for all
![]() $\alpha \in L$
and
$\alpha \in L$
and
![]() $\sigma \in G_{{\mathbb Q}_{p}}$
. We also note that
$\sigma \in G_{{\mathbb Q}_{p}}$
. We also note that
is a well-defined isomorphism of
![]() $L[G]$
-modules. For the comparison isomorphism
$L[G]$
-modules. For the comparison isomorphism
![]() $\mathrm {comp}_W$
, we then obtain the following simple description:
$\mathrm {comp}_W$
, we then obtain the following simple description:
 $$ \begin{align*} \mathrm{comp}_W \colon L \otimes_{{\mathbb Q}_{p}} \left( L \otimes_{{\mathbb Q}_{p}} W \right)^{G_N} &\longrightarrow \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(L \otimes_{{\mathbb Q}_{p}} W), \\ l \otimes z &\mapsto l y_z , \end{align*} $$
$$ \begin{align*} \mathrm{comp}_W \colon L \otimes_{{\mathbb Q}_{p}} \left( L \otimes_{{\mathbb Q}_{p}} W \right)^{G_N} &\longrightarrow \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}(L \otimes_{{\mathbb Q}_{p}} W), \\ l \otimes z &\mapsto l y_z , \end{align*} $$
where
![]() $l \in L$
,
$l \in L$
,
![]() $z \in \left ( L \otimes _{{\mathbb Q}_{p}} W \right )^{G_N}$
and
$z \in \left ( L \otimes _{{\mathbb Q}_{p}} W \right )^{G_N}$
and
![]() $y_z(\sigma ) := z$
for all
$y_z(\sigma ) := z$
for all
![]() $\sigma \in G_{{\mathbb Q}_{p}}$
(and hence,
$\sigma \in G_{{\mathbb Q}_{p}}$
(and hence,
![]() $(ly_z)(\sigma ) = \sigma (l)z$
).
$(ly_z)(\sigma ) = \sigma (l)z$
).
We define a G-equivariant isomorphism
and
Then, similar as in the proof of [Reference Izychev and VenjakobIV16, Lemma 6.1], we obtain a commutative diagram:
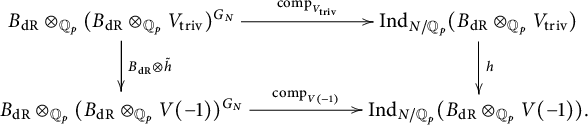
As a consequence, we derive
 $$ \begin{align*}\begin{aligned} & \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right] \\ &\quad = \left[\bigoplus_{i=1}^r\mathcal L z_i,{B_{\mathrm{dR}}} \otimes \tilde h, \bigoplus_{i=1}^r\mathcal L \tilde e_i \right] + \left[\bigoplus_{i=1}^r\mathcal L z_i, \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] \\ &\qquad\qquad + \left[ \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} , h, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1) \right] \\ &\quad = \left[\bigoplus_{i=1}^r\mathcal L z_i, \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] + \left[ \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} , h, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1) \right] \\ &\quad = r \left[ \mathcal{L}, \mathrm{id}, {\mathcal{O}_K[G]} \beta \right] + \left[\bigoplus_{i=1}^r({\mathcal{O}_K[G]} \beta z_i), \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] \\ &\qquad\qquad + \left[ \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} , h, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1) \right] \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} & \left[\bigoplus_{i=1}^r\mathcal L \tilde e_i,\mathrm{comp}_{V(-1)},\mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1)\right] \\ &\quad = \left[\bigoplus_{i=1}^r\mathcal L z_i,{B_{\mathrm{dR}}} \otimes \tilde h, \bigoplus_{i=1}^r\mathcal L \tilde e_i \right] + \left[\bigoplus_{i=1}^r\mathcal L z_i, \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] \\ &\qquad\qquad + \left[ \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} , h, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1) \right] \\ &\quad = \left[\bigoplus_{i=1}^r\mathcal L z_i, \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] + \left[ \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} , h, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1) \right] \\ &\quad = r \left[ \mathcal{L}, \mathrm{id}, {\mathcal{O}_K[G]} \beta \right] + \left[\bigoplus_{i=1}^r({\mathcal{O}_K[G]} \beta z_i), \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] \\ &\qquad\qquad + \left[ \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} , h, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T(-1) \right] \end{aligned}\end{align*} $$
The computations in [Reference Izychev and VenjakobIV16, pp. 512–513] show that
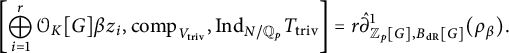 $$ \begin{align*} \left[\bigoplus_{i=1}^r\mathcal O_K[G]\beta z_i, \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] = r \hat\partial_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}^1(\rho_{\beta}). \end{align*} $$
$$ \begin{align*} \left[\bigoplus_{i=1}^r\mathcal O_K[G]\beta z_i, \mathrm{comp}_{V_{\mathrm{triv}}}, \mathrm{Ind}_{N/{{\mathbb Q}_{p}}}T_{\mathrm{triv}} \right] = r \hat\partial_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}^1(\rho_{\beta}). \end{align*} $$
It finally remains to prove that
To that end, we write
and define elements
![]() $x_{ij} \in \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T_{\mathrm {triv}})$
and
$x_{ij} \in \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T_{\mathrm {triv}})$
and
![]() $y_{ij} \in \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T(-1))$
, for
$y_{ij} \in \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T(-1))$
, for
![]() $i = 1, \ldots ,m$
and
$i = 1, \ldots ,m$
and
![]() $j = 1, \ldots , r$
, by
$j = 1, \ldots , r$
, by
 $$ \begin{align*} x_{ij}(\rho\sigma_k) = \begin{cases} z_j, & \text{ if } i=k \text{ and } \bar\rho = 1, \\ 0, & \text{ otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} x_{ij}(\rho\sigma_k) = \begin{cases} z_j, & \text{ if } i=k \text{ and } \bar\rho = 1, \\ 0, & \text{ otherwise}, \end{cases} \end{align*} $$
and
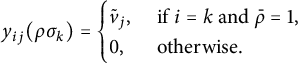 $$ \begin{align*} y_{ij}(\rho\sigma_k) = \begin{cases} \tilde v_j, & \text{ if } i=k \text{ and } \bar\rho = 1, \\ 0, & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} y_{ij}(\rho\sigma_k) = \begin{cases} \tilde v_j, & \text{ if } i=k \text{ and } \bar\rho = 1, \\ 0, & \text{ otherwise}. \end{cases} \end{align*} $$
Without loss of generality, we assume
![]() $\rho =1$
for
$\rho =1$
for
![]() $\bar \rho =1$
. Then, the
$\bar \rho =1$
. Then, the
![]() $x_{ij}$
, respectively, the
$x_{ij}$
, respectively, the
![]() $y_{ij}$
, constitute a
$y_{ij}$
, constitute a
![]() ${{\mathbb Z}_p[G]}$
-basis of
${{\mathbb Z}_p[G]}$
-basis of
![]() $\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T_{\mathrm {triv}})$
, respectively,
$\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T_{\mathrm {triv}})$
, respectively,
![]() $\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T(-1))$
.
$\mathrm {Ind}_{N/{{\mathbb Q}_{p}}}(T(-1))$
.
For fixed i and j and for
![]() $1 \le k \le m$
, we compute
$1 \le k \le m$
, we compute
 $$ \begin{align*} \left( h(x_{ij}) \right) (\rho\sigma_k) = \begin{cases} \tilde e_j, & \text{ if } i=k \text{ and } \bar\rho = 1, \\ 0, & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \left( h(x_{ij}) \right) (\rho\sigma_k) = \begin{cases} \tilde e_j, & \text{ if } i=k \text{ and } \bar\rho = 1, \\ 0, & \text{ otherwise}. \end{cases} \end{align*} $$
For
![]() $1 \le s \le m$
and
$1 \le s \le m$
and
![]() $1 \le t \le r$
, let
$1 \le t \le r$
, let
![]() $\xi _{st}$
be indeterminates (with values in
$\xi _{st}$
be indeterminates (with values in
![]() ${B_{\mathrm {dR}}}$
). Then,
${B_{\mathrm {dR}}}$
). Then,
 $$ \begin{align*} \left( \sum_{s,t} \xi_{st} y_{st} \right) (\rho\sigma_k) = \begin{cases} \sum_t (\rho\sigma_k)(\xi_{kt}) \tilde v_t, & \text{ if } \bar\rho = 1, \\ 0, & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \left( \sum_{s,t} \xi_{st} y_{st} \right) (\rho\sigma_k) = \begin{cases} \sum_t (\rho\sigma_k)(\xi_{kt}) \tilde v_t, & \text{ if } \bar\rho = 1, \\ 0, & \text{ otherwise}. \end{cases} \end{align*} $$
Because
![]() $\tilde e_j = \sum _t T^{\mathrm {nr}}_{tj} \otimes \tilde v_t$
, we obtain
$\tilde e_j = \sum _t T^{\mathrm {nr}}_{tj} \otimes \tilde v_t$
, we obtain
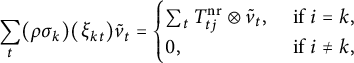 $$ \begin{align*} \sum_t (\rho\sigma_k)(\xi_{kt}) \tilde v_t = \begin{cases} \sum_t T^{\mathrm{nr}}_{tj} \otimes \tilde v_t, & \text{ if } i=k, \\ 0, & \text{ if } i \ne k, \end{cases} \end{align*} $$
$$ \begin{align*} \sum_t (\rho\sigma_k)(\xi_{kt}) \tilde v_t = \begin{cases} \sum_t T^{\mathrm{nr}}_{tj} \otimes \tilde v_t, & \text{ if } i=k, \\ 0, & \text{ if } i \ne k, \end{cases} \end{align*} $$
and hence, for all
![]() $1\leq t\leq r$
,
$1\leq t\leq r$
,
We conclude that with respect to the chosen basis, the map h is represented by a block matrix of the form
 $$ \begin{align*} C = \left( \begin{array}{ccc} \sigma_1^{-1}(T^{\mathrm{nr}}) & & \\ & \ddots & \\ & & \sigma_m^{-1}(T^{\mathrm{nr}}) \end{array} \right). \end{align*} $$
$$ \begin{align*} C = \left( \begin{array}{ccc} \sigma_1^{-1}(T^{\mathrm{nr}}) & & \\ & \ddots & \\ & & \sigma_m^{-1}(T^{\mathrm{nr}}) \end{array} \right). \end{align*} $$
We recall that
![]() $\varphi (T^{\mathrm {nr}}) = u^{-1}T^{\mathrm {nr}}$
and fix
$\varphi (T^{\mathrm {nr}}) = u^{-1}T^{\mathrm {nr}}$
and fix
![]() $\alpha _i \in \hat {\mathbb z}$
such that
$\alpha _i \in \hat {\mathbb z}$
such that
![]() $\sigma _i |_{\mathbb Q_p^{\mathrm {nr}}} = \varphi ^{\alpha _i}$
. Note that for all
$\sigma _i |_{\mathbb Q_p^{\mathrm {nr}}} = \varphi ^{\alpha _i}$
. Note that for all
![]() $n\in {\mathbb z}$
,
$n\in {\mathbb z}$
,
![]() $\varphi ^{-n}(T^{\mathrm {nr}})\cdot (T^{\mathrm {nr}})^{-1}=u^n$
, which coincides with
$\varphi ^{-n}(T^{\mathrm {nr}})\cdot (T^{\mathrm {nr}})^{-1}=u^n$
, which coincides with
![]() $\rho ^{\mathrm {nr}}(\varphi ^n)$
. By a continuity argument, we have
$\rho ^{\mathrm {nr}}(\varphi ^n)$
. By a continuity argument, we have
![]() $\varphi ^{-\alpha _i}(T^{\mathrm {nr}})\cdot (T^{\mathrm {nr}})^{-1}=u^{\alpha _i}$
, where
$\varphi ^{-\alpha _i}(T^{\mathrm {nr}})\cdot (T^{\mathrm {nr}})^{-1}=u^{\alpha _i}$
, where
![]() $u^{\alpha _i}$
is well defined by [Reference CobbeCob18, Lemma 1.5]. Then,
$u^{\alpha _i}$
is well defined by [Reference CobbeCob18, Lemma 1.5]. Then,
 $$ \begin{align*} \det(C) = \prod_{i=1}^m \det\left( u^{\alpha_i}T^{\mathrm{nr}} \right) = \det(u)^{\alpha} \det(T^{\mathrm{nr}})^m \end{align*} $$
$$ \begin{align*} \det(C) = \prod_{i=1}^m \det\left( u^{\alpha_i}T^{\mathrm{nr}} \right) = \det(u)^{\alpha} \det(T^{\mathrm{nr}})^m \end{align*} $$
with
![]() $\alpha = \sum _i \alpha _i$
. Because
$\alpha = \sum _i \alpha _i$
. Because
![]() $\det (u)^{\alpha } \in {\mathbb Z}_p^{\times } \subseteq {{\mathbb Z}_p[G]}^{\times }$
, the result follows from the definition of
$\det (u)^{\alpha } \in {\mathbb Z}_p^{\times } \subseteq {{\mathbb Z}_p[G]}^{\times }$
, the result follows from the definition of
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
.▪
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
.▪
We summarize the results of the previous lemmas in the following proposition.
Proposition 6.5 With
![]() $\hat \partial ^1 = \hat \partial _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}^1$
and
$\hat \partial ^1 = \hat \partial _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}^1$
and
![]() $\chi = \chi _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}$
, we have
$\chi = \chi _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}$
, we have
Remark 6.6 To compare Proposition 6.5 and [Reference Bley and CobbeBC17, equation (55)], we first note that in loc. cit., we have
![]() $\mathcal {L} = {\mathcal {O}_K[G]} \beta $
. The additional new term
$\mathcal {L} = {\mathcal {O}_K[G]} \beta $
. The additional new term
![]() $U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
emerges from the computations in Lemma 6.4. The error does not affect the validity of any of the arguments in [Reference Bley and CobbeBC17]; it just forces us to adapt our definition of
$U_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
emerges from the computations in Lemma 6.4. The error does not affect the validity of any of the arguments in [Reference Bley and CobbeBC17]; it just forces us to adapt our definition of
![]() $R_{N/K}$
and
$R_{N/K}$
and
![]() $\tilde {R}_{N/K}$
.
$\tilde {R}_{N/K}$
.
To finish the proof of the conjecture, it is necessary to compute explicitly the term
![]() $\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
. For this, we will consider the tame and the weakly ramified case separately.
$\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
. For this, we will consider the tame and the weakly ramified case separately.
6.4 The tame case
In this subsection, we let
![]() $N/K$
be tame und compute the term
$N/K$
be tame und compute the term
![]() $\chi _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}(M^{\bullet }(\mathcal {L}), 0)$
from (6.9). In the tame case, by results of Ullom, we can and will use
$\chi _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}(M^{\bullet }(\mathcal {L}), 0)$
from (6.9). In the tame case, by results of Ullom, we can and will use
![]() $\mathcal {L} = \mathfrak p_N^{\nu }$
for a large enough positive integer
$\mathcal {L} = \mathfrak p_N^{\nu }$
for a large enough positive integer
![]() $\nu $
and we also fix
$\nu $
and we also fix
![]() $\beta \in \mathcal {O}_N$
such that
$\beta \in \mathcal {O}_N$
such that
![]() $\mathcal {O}_N={\mathcal {O}_K[G]} \beta $
.
$\mathcal {O}_N={\mathcal {O}_K[G]} \beta $
.
Proposition 6.7 We have
Proof The key point in the proof is that by Proposition 2.2 the cohomology modules of
![]() $M^{\bullet }(\mathcal {L})$
are perfect, so that we can compute the refined Euler characteristic of
$M^{\bullet }(\mathcal {L})$
are perfect, so that we can compute the refined Euler characteristic of
![]() $M^{\bullet }(\mathcal {L})$
in terms of cohomology without explicitly using the complex. In a little more detail, we note that the mapping cone of
$M^{\bullet }(\mathcal {L})$
in terms of cohomology without explicitly using the complex. In a little more detail, we note that the mapping cone of
where the map in degree
![]() $1$
is induced by
$1$
is induced by
![]() $f_{{\mathcal F},{\mathcal N}}$
, is isomorphic to
$f_{{\mathcal F},{\mathcal N}}$
, is isomorphic to
![]() $H^2(N, T)[2]$
. We also recall from Section 2 that we identify
$H^2(N, T)[2]$
. We also recall from Section 2 that we identify
![]() $H^2(N, T)$
with
$H^2(N, T)$
with
![]() $\mathcal {Z} / (F_N -1)\mathcal {Z}$
. Hence, we conclude from [Reference Breuning and BurnsBB05, Theorem 5.7] that
$\mathcal {Z} / (F_N -1)\mathcal {Z}$
. Hence, we conclude from [Reference Breuning and BurnsBB05, Theorem 5.7] that
 $$ \begin{align*} \begin{aligned} &\chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}(M^{\bullet}(\mathcal{L}), 0)\\ &\qquad=\chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}\left( \mathcal F(\mathfrak p_N^{(r)})/X(\mathcal L)[1],0 \right) + \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}(\mathcal{Z} / (F_N -1)\mathcal{Z}, 0). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}(M^{\bullet}(\mathcal{L}), 0)\\ &\qquad=\chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}\left( \mathcal F(\mathfrak p_N^{(r)})/X(\mathcal L)[1],0 \right) + \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}(\mathcal{Z} / (F_N -1)\mathcal{Z}, 0). \end{aligned} \end{align*} $$
To compute the first summand, we observe that by Proposition 3.4 we have
![]() $X(\mathcal {L}) = \mathcal F\left ( (\mathfrak p_N^{\nu })^{(r)}\right )$
. Because, for each integer
$X(\mathcal {L}) = \mathcal F\left ( (\mathfrak p_N^{\nu })^{(r)}\right )$
. Because, for each integer
![]() $i \ge 0$
, the identity map induces isomorphisms
$i \ge 0$
, the identity map induces isomorphisms
a standard argument shows that
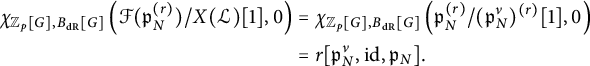 $$ \begin{align*} \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}\left( \mathcal F(\mathfrak p_N^{(r)})/X(\mathcal L)[1],0 \right) &= \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}\left( \mathfrak p_N^{(r)} / (\mathfrak p_N^{\nu})^{(r)} [1],0 \right) \\& = r [\mathfrak p_N^{\nu}, \mathrm{id}, \mathfrak p_N]. \end{align*} $$
$$ \begin{align*} \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}\left( \mathcal F(\mathfrak p_N^{(r)})/X(\mathcal L)[1],0 \right) &= \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}\left( \mathfrak p_N^{(r)} / (\mathfrak p_N^{\nu})^{(r)} [1],0 \right) \\& = r [\mathfrak p_N^{\nu}, \mathrm{id}, \mathfrak p_N]. \end{align*} $$
For the computation of the second term, we consider the short exact sequence of G-modules
where
![]() $\pi (z(\bar g))=g\cdot (z+(F_N-1)\mathcal {Z})$
for all
$\pi (z(\bar g))=g\cdot (z+(F_N-1)\mathcal {Z})$
for all
![]() $z\in {\mathbb Z}_p^r$
and
$z\in {\mathbb Z}_p^r$
and
![]() $g\in G$
and where G acts on
$g\in G$
and where G acts on
![]() $\mathcal {Z} / (F_N -1)\mathcal {Z}$
through any lift of its elements to
$\mathcal {Z} / (F_N -1)\mathcal {Z}$
through any lift of its elements to
![]() $G_K$
(which is well defined, because elements of
$G_K$
(which is well defined, because elements of
![]() $G_N$
act trivially).
$G_N$
act trivially).
Let
![]() $x=\sum _{i=0}^{d-1}\alpha _i F^{-i}\in {\mathbb Z}_p^r[G/I]$
be an element in the kernel of the map on the left. Then,
$x=\sum _{i=0}^{d-1}\alpha _i F^{-i}\in {\mathbb Z}_p^r[G/I]$
be an element in the kernel of the map on the left. Then,
![]() $u^{d_K}\alpha _{i-1}-\alpha _i=0$
for all i. Hence,
$u^{d_K}\alpha _{i-1}-\alpha _i=0$
for all i. Hence,
![]() $(u^{dd_K}-1)\alpha _i=0$
, and by the assumption
$(u^{dd_K}-1)\alpha _i=0$
, and by the assumption
![]() $\mathcal Z^{G_N}=1$
, it follows that
$\mathcal Z^{G_N}=1$
, it follows that
![]() $\alpha _i=0$
for all i. Hence, the map on the left is injective.
$\alpha _i=0$
for all i. Hence, the map on the left is injective.
Next, we see that
![]() $\pi ((F^{-1}u^{d_K}-1)e_i)=(\rho ^{\mathrm {nr}}(F^{-1})u^{d_K}-1)e_i=0$
.
$\pi ((F^{-1}u^{d_K}-1)e_i)=(\rho ^{\mathrm {nr}}(F^{-1})u^{d_K}-1)e_i=0$
.
Conversely, let
![]() $x=\sum _{i=0}^{d-1}\alpha _i F^{-i}\in {\mathbb Z}_p^r[G/I]$
be such that
$x=\sum _{i=0}^{d-1}\alpha _i F^{-i}\in {\mathbb Z}_p^r[G/I]$
be such that
![]() $\pi (x)=0$
. Modulo the image of
$\pi (x)=0$
. Modulo the image of
![]() $F^{-1}u^{d_K}-1$
, x has a representative
$F^{-1}u^{d_K}-1$
, x has a representative
![]() $y\in {\mathbb Z}_p^r$
. We must show that
$y\in {\mathbb Z}_p^r$
. We must show that
![]() $y\in \mathrm {im}(F^{-1}u^{d_K}-1)$
. Because
$y\in \mathrm {im}(F^{-1}u^{d_K}-1)$
. Because
![]() $\pi (y)=0$
, there exists
$\pi (y)=0$
, there exists
![]() $z\in {\mathbb Z}_p^r$
such that
$z\in {\mathbb Z}_p^r$
such that
![]() $y=(u^{dd_K}-1)z=((F^{-1}u^{d_K})^d-1)z$
, which is in the image of
$y=(u^{dd_K}-1)z=((F^{-1}u^{d_K})^d-1)z$
, which is in the image of
![]() $F^{-1}u^{d_K}-1$
. Hence, we have exactness in the middle term.
$F^{-1}u^{d_K}-1$
. Hence, we have exactness in the middle term.
To prove the exactness of the sequence, it remains to check the surjectivity of the map on the right, which is obvious.
Because we are considering the case of a tame extension,
![]() ${\mathbb Z}_p^r[G/I]$
is a projective
${\mathbb Z}_p^r[G/I]$
is a projective
![]() ${\mathbb Z}_p[G]$
-module and we have:
${\mathbb Z}_p[G]$
-module and we have:
The results follows.▪
6.5 The weakly ramified case
In this subsection, we let p be an odd prime. Let
![]() $K/{{\mathbb Q}_{p}}$
be the unramified extension of degree m. We let
$K/{{\mathbb Q}_{p}}$
be the unramified extension of degree m. We let
![]() $N/K$
be a weakly and wildly ramified finite abelian extension with cyclic ramification group. We let
$N/K$
be a weakly and wildly ramified finite abelian extension with cyclic ramification group. We let
![]() $d = d_{N/K}$
be the inertia degree of
$d = d_{N/K}$
be the inertia degree of
![]() $N/K$
and assume that m and d are relatively prime.
$N/K$
and assume that m and d are relatively prime.
The aim of this subsection is to compute the term
![]() $\chi _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}(M^{\bullet }(\lambda ), 0)$
from (6.9) in this weakly and wildly ramified situation. For that purpose, we aim to generalize the methods of [Reference Bley and CobbeBC17]; however, this forces us to introduce a further technical condition which might be either
$\chi _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}(M^{\bullet }(\lambda ), 0)$
from (6.9) in this weakly and wildly ramified situation. For that purpose, we aim to generalize the methods of [Reference Bley and CobbeBC17]; however, this forces us to introduce a further technical condition which might be either
Hypothesis (T):
![]() $U_N \equiv 1 \pmod {p}$
$U_N \equiv 1 \pmod {p}$
or
Hypothesis (I):
![]() $U_N - 1$
is invertible modulo p.
$U_N - 1$
is invertible modulo p.
Here, (T) stands for trivial reduction modulo p and (I) for invertible modulo p. If we set
![]() $\omega := v_p(\det (U_N-1))$
, then we have the following equivalences:
$\omega := v_p(\det (U_N-1))$
, then we have the following equivalences:
Note also that Hypothesis (T) immediately implies
![]() $\omega> 0$
. However, in the higher dimensional setting, there are mixed cases, where none of our hypotheses holds.
$\omega> 0$
. However, in the higher dimensional setting, there are mixed cases, where none of our hypotheses holds.
As in [Reference Bley and CobbeBC17], we have a diagram of fields as follows:

Here,
![]() $K'/K$
is the maximal unramified subextension of
$K'/K$
is the maximal unramified subextension of
![]() $N/K$
,
$N/K$
,
![]() $M/K$
is a weakly and wildly ramified cyclic extension of degree p, and
$M/K$
is a weakly and wildly ramified cyclic extension of degree p, and
![]() $N = MK'$
. Because
$N = MK'$
. Because
![]() $\gcd (m,d)=1$
, there exists
$\gcd (m,d)=1$
, there exists
![]() $\tilde K'/\mathbb Q_p$
of degree d such that
$\tilde K'/\mathbb Q_p$
of degree d such that
![]() $K'=K\tilde K'$
.
$K'=K\tilde K'$
.
The following lemma generalizes [Reference Bley and CobbeBC17, Lemma 7.2.1].
Lemma 6.8 For
![]() $n \ge 2$
, one has
$n \ge 2$
, one has
Moreover,
Proof For
![]() $n \ge 2$
, the formal logarithm induces an isomorphism
$n \ge 2$
, the formal logarithm induces an isomorphism
![]() $\mathcal F((\mathfrak p_N^n)^{(r)}) \cong (\mathfrak p_N^n)^{(r)}$
of
$\mathcal F((\mathfrak p_N^n)^{(r)}) \cong (\mathfrak p_N^n)^{(r)}$
of
![]() ${{\mathbb Z}_p[G]}$
-modules by Proposition 3.4. Hence, the first assertion follows from [Reference KöckKöc04, Theorem 1.1 and Proposition 1.3].
${{\mathbb Z}_p[G]}$
-modules by Proposition 3.4. Hence, the first assertion follows from [Reference KöckKöc04, Theorem 1.1 and Proposition 1.3].
We henceforth assume
![]() $n=1$
. By Lemma 2.3, we know that
$n=1$
. By Lemma 2.3, we know that
![]() $\mathcal F(\mathfrak p_N^{(r)})$
is cohomologically trivial, if and only if Hypothesis (I) holds. Hence, it suffices to prove that
$\mathcal F(\mathfrak p_N^{(r)})$
is cohomologically trivial, if and only if Hypothesis (I) holds. Hence, it suffices to prove that
![]() $\mathcal F(\mathfrak p_N^{(r)})$
is torsion-free. By [Reference CobbeCob18, Lemma 2.1], the module
$\mathcal F(\mathfrak p_N^{(r)})$
is torsion-free. By [Reference CobbeCob18, Lemma 2.1], the module
![]() $\mathcal F(\mathfrak p_N^{(r)})$
is isomorphic to
$\mathcal F(\mathfrak p_N^{(r)})$
is isomorphic to
![]() $\left ( \prod _r \widehat {N_0^{\times }} (\rho ^{\mathrm {nr}})\right )^{G_N}$
which is torsion-free. Indeed, any tuple
$\left ( \prod _r \widehat {N_0^{\times }} (\rho ^{\mathrm {nr}})\right )^{G_N}$
which is torsion-free. Indeed, any tuple
![]() $(\zeta _1, \ldots , \zeta _r)$
of pth roots of unity
$(\zeta _1, \ldots , \zeta _r)$
of pth roots of unity
![]() $\zeta _1, \ldots , \zeta _r \in \widehat {N_0^{\times }} \cong {{\mathbb Z}_p} \times U_{N_0}^{(1)}$
must be contained in N (because
$\zeta _1, \ldots , \zeta _r \in \widehat {N_0^{\times }} \cong {{\mathbb Z}_p} \times U_{N_0}^{(1)}$
must be contained in N (because
![]() $N_0/N$
is unramified). Hence,
$N_0/N$
is unramified). Hence,
![]() $(\zeta _1, \ldots , \zeta _r)$
is fixed by
$(\zeta _1, \ldots , \zeta _r)$
is fixed by
![]() $G_N$
, if and only if it is fixed by
$G_N$
, if and only if it is fixed by
![]() $F_N$
, if and only if
$F_N$
, if and only if
![]() $\zeta _1 = \cdots = \zeta _r = 1$
(using Hypothesis (I)).▪
$\zeta _1 = \cdots = \zeta _r = 1$
(using Hypothesis (I)).▪
By Lemma 6.8, we can and will take
![]() $\mathcal {L} = \mathfrak p_N^{p+1}$
and thus obtain
$\mathcal {L} = \mathfrak p_N^{p+1}$
and thus obtain
We recall some of the notations from [Reference Bley and CobbeBC17]. We put
![]() $q=p^m$
,
$q=p^m$
,
![]() $b=F^{-1}$
and consider an element
$b=F^{-1}$
and consider an element
![]() $a\in \mathrm {Gal}(N^{\mathrm {nr}}/K)$
such that
$a\in \mathrm {Gal}(N^{\mathrm {nr}}/K)$
such that
![]() $\mathrm {Gal}(M/K)=\langle a|_M\rangle $
,
$\mathrm {Gal}(M/K)=\langle a|_M\rangle $
,
![]() $a|_{K^{\mathrm {nr}}}=1$
. Because there will be no ambiguity, we will denote by the same letters
$a|_{K^{\mathrm {nr}}}=1$
. Because there will be no ambiguity, we will denote by the same letters
![]() $a,b$
their restrictions to N. Then,
$a,b$
their restrictions to N. Then,
![]() $\mathrm {Gal}(N/K) = \langle a,b \rangle $
and
$\mathrm {Gal}(N/K) = \langle a,b \rangle $
and
![]() $\mathrm {ord}(a)=p, \mathrm {ord}(b) = d$
. We also define
$\mathrm {ord}(a)=p, \mathrm {ord}(b) = d$
. We also define
![]() $\mathcal T_a := \sum _{i=0}^{p-1}a^i$
.
$\mathcal T_a := \sum _{i=0}^{p-1}a^i$
.
Let
![]() $\theta _1\in M$
be such that
$\theta _1\in M$
be such that
![]() $\mathcal T_{M/K}\theta _1=p$
, where
$\mathcal T_{M/K}\theta _1=p$
, where
![]() $\mathcal T_{M/K}$
denotes the trace map from M to K, and
$\mathcal T_{M/K}$
denotes the trace map from M to K, and
![]() $\mathcal {O}_K[\mathrm {Gal}(M/K)]\theta _1=\mathfrak p_M$
. Let
$\mathcal {O}_K[\mathrm {Gal}(M/K)]\theta _1=\mathfrak p_M$
. Let
![]() $\theta _2$
(resp. A) be a normal integral basis generator of trace one for the extension
$\theta _2$
(resp. A) be a normal integral basis generator of trace one for the extension
![]() $\tilde K'/\mathbb Q_p$
(resp.
$\tilde K'/\mathbb Q_p$
(resp.
![]() $K/\mathbb Q_p$
). Let
$K/\mathbb Q_p$
). Let
![]() $\alpha _1\in \mathcal {O}_K^{\times }$
be such that
$\alpha _1\in \mathcal {O}_K^{\times }$
be such that
![]() $\theta _1^{a-1}\equiv 1-\alpha _1\theta _1\pmod {\mathfrak p_M^2}$
. If we set
$\theta _1^{a-1}\equiv 1-\alpha _1\theta _1\pmod {\mathfrak p_M^2}$
. If we set
then these elements form a
![]() ${{\mathbb Z}_p}$
-basis of
${{\mathbb Z}_p}$
-basis of
![]() $\mathcal {O}_K$
(see [Reference Bley and CobbeBC17, equation (60)]).
$\mathcal {O}_K$
(see [Reference Bley and CobbeBC17, equation (60)]).
Furthermore, we use [Reference CobbeCob18, Lemma 2.4] to find for
![]() $i=1, \ldots ,r$
an element
$i=1, \ldots ,r$
an element
![]() $\gamma _i\in \prod _r U_{N_0}^{(1)}$
such that
$\gamma _i\in \prod _r U_{N_0}^{(1)}$
such that
where
with the nontrivial entry is the ith component.
Let
 $$ \begin{align*} W_{\geq n}=\bigoplus_{j=n}^{p-1}\bigoplus_{k=1}^{m}{\mathbb Z}_p[G]^r v_{k,j} \cong \bigoplus_{j=n}^{p-1}\bigoplus_{k=1}^m{\mathbb Z}_p[G]^r\alpha_kw_j = \bigoplus_{j=n}^{p-1}{\mathcal{O}_K[G]}^r w_j \end{align*} $$
$$ \begin{align*} W_{\geq n}=\bigoplus_{j=n}^{p-1}\bigoplus_{k=1}^{m}{\mathbb Z}_p[G]^r v_{k,j} \cong \bigoplus_{j=n}^{p-1}\bigoplus_{k=1}^m{\mathbb Z}_p[G]^r\alpha_kw_j = \bigoplus_{j=n}^{p-1}{\mathcal{O}_K[G]}^r w_j \end{align*} $$
and put
If we write
![]() $e_1, \ldots , e_r$
for the standard
$e_1, \ldots , e_r$
for the standard
![]() ${{\mathbb Z}_p}$
-basis of
${{\mathbb Z}_p}$
-basis of
![]() ${{\mathbb Z}_p}^{(r)}$
, then a general element of W is of the form
${{\mathbb Z}_p}^{(r)}$
, then a general element of W is of the form
 $$ \begin{align*} \sum_{i=1}^r \sum_{j=1}^{p-1} \sum_{k=1}^m \lambda_{i,j,k}e_i v_{k,j} = \sum_{i=1}^r \sum_{j=1}^{p-1} \mu_{i,j,k}e_i w_{j} \end{align*} $$
$$ \begin{align*} \sum_{i=1}^r \sum_{j=1}^{p-1} \sum_{k=1}^m \lambda_{i,j,k}e_i v_{k,j} = \sum_{i=1}^r \sum_{j=1}^{p-1} \mu_{i,j,k}e_i w_{j} \end{align*} $$
with
![]() $\lambda _{i,j,k} \in {{\mathbb Z}_p[G]}$
or
$\lambda _{i,j,k} \in {{\mathbb Z}_p[G]}$
or
![]() $\mu _{i,j} \in {\mathcal {O}_K[G]}$
. We will apply this convention analogously for the modules
$\mu _{i,j} \in {\mathcal {O}_K[G]}$
. We will apply this convention analogously for the modules
![]() $W'$
and
$W'$
and
![]() $ W_{\geq n}$
.
$ W_{\geq n}$
.
We define a matrix
![]() $E \in M_r(\mathcal O_{K'})$
by
$E \in M_r(\mathcal O_{K'})$
by
 $$ \begin{align} E= \begin{cases}1&\text{under Hypothesis (I)}\\ \sum_{i=0}^{dm-1}(A\theta_2)^{\varphi^i}u^{-i}&\text{under Hypothesis (T)} \end{cases} \end{align} $$
$$ \begin{align} E= \begin{cases}1&\text{under Hypothesis (I)}\\ \sum_{i=0}^{dm-1}(A\theta_2)^{\varphi^i}u^{-i}&\text{under Hypothesis (T)} \end{cases} \end{align} $$
and a matrix
 $$ \begin{align} \tilde u= \begin{cases}1&\text{under Hypothesis (I)}\\ u&\text{under Hypothesis (T)}. \end{cases} \end{align} $$
$$ \begin{align} \tilde u= \begin{cases}1&\text{under Hypothesis (I)}\\ u&\text{under Hypothesis (T)}. \end{cases} \end{align} $$
We also recall that in [Reference CobbeCob18, Lemma 1.9], we constructed an element
![]() $\varepsilon \in \mathrm {Gl}_r(\overline {{\mathbb Z}_p^{\mathrm {nr}}})$
such that
$\varepsilon \in \mathrm {Gl}_r(\overline {{\mathbb Z}_p^{\mathrm {nr}}})$
such that
![]() $u=\varepsilon ^{-1}\cdot \varphi (\varepsilon )$
.
$u=\varepsilon ^{-1}\cdot \varphi (\varepsilon )$
.
Lemma 6.9 The following assertions hold:
-
(1)
 $E\in \mathrm {Gl}_r(\mathcal {O}_{K'})$
.
$E\in \mathrm {Gl}_r(\mathcal {O}_{K'})$
. -
(2)
 $\varphi (E)\equiv \tilde u E \equiv E\tilde u \pmod {p\mathcal {O}_{K'}}$
.
$\varphi (E)\equiv \tilde u E \equiv E\tilde u \pmod {p\mathcal {O}_{K'}}$
. -
(3)
 $\varphi (\varepsilon ^{-1} E)\equiv u^{-1}\tilde u \varepsilon ^{-1} E \pmod {p}$
.
$\varphi (\varepsilon ^{-1} E)\equiv u^{-1}\tilde u \varepsilon ^{-1} E \pmod {p}$
.
Proof Let
![]() $H=\mathrm {Gal}(K'/\mathbb Q_p)$
and let
$H=\mathrm {Gal}(K'/\mathbb Q_p)$
and let
![]() $f \colon H\to K'$
be defined by
$f \colon H\to K'$
be defined by
![]() $f(\sigma )=(A\theta _2)^{\sigma ^{-1}}$
. Then, applying [Reference WashingtonWas97, Lemma 5.26(a)], we obtain
$f(\sigma )=(A\theta _2)^{\sigma ^{-1}}$
. Then, applying [Reference WashingtonWas97, Lemma 5.26(a)], we obtain
 $$ \begin{align*} \det((A\theta_2)^{\tau\sigma^{-1}})_{\sigma,\tau\in H}=\prod_{\chi\in \hat H}\sum_{\sigma\in H}(A\theta_2)^{\sigma^{-1}}\chi(\sigma). \end{align*} $$
$$ \begin{align*} \det((A\theta_2)^{\tau\sigma^{-1}})_{\sigma,\tau\in H}=\prod_{\chi\in \hat H}\sum_{\sigma\in H}(A\theta_2)^{\sigma^{-1}}\chi(\sigma). \end{align*} $$
Because
![]() $A\theta _2$
is an integral normal basis generator and
$A\theta _2$
is an integral normal basis generator and
![]() $K'/\mathbb Q_p$
is unramified, the left-hand side
$K'/\mathbb Q_p$
is unramified, the left-hand side
![]() $\det (\tau \sigma ^{-1}(A\theta _2))_{\sigma ,\tau \in H}$
is a unit (whose square is the discriminant of
$\det (\tau \sigma ^{-1}(A\theta _2))_{\sigma ,\tau \in H}$
is a unit (whose square is the discriminant of
![]() $K'/\mathbb Q_p$
). Therefore, for each character
$K'/\mathbb Q_p$
). Therefore, for each character
![]() $\chi \in \hat H$
, the factor
$\chi \in \hat H$
, the factor
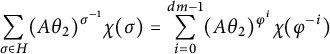 $$ \begin{align*} \sum_{\sigma\in H}(A\theta_2)^{\sigma^{-1}}\chi(\sigma)=\sum_{i=0}^{dm-1}(A\theta_2)^{\varphi^{i}}\chi(\varphi^{-i}) \end{align*} $$
$$ \begin{align*} \sum_{\sigma\in H}(A\theta_2)^{\sigma^{-1}}\chi(\sigma)=\sum_{i=0}^{dm-1}(A\theta_2)^{\varphi^{i}}\chi(\varphi^{-i}) \end{align*} $$
is a unit, and hence,
![]() $\sum _{i=0}^{dm-1}(A\theta _2)^{\varphi ^{i}}\varphi ^{-i}$
is a unit in the maximal order
$\sum _{i=0}^{dm-1}(A\theta _2)^{\varphi ^{i}}\varphi ^{-i}$
is a unit in the maximal order
![]() ${\mathcal M}$
of
${\mathcal M}$
of
![]() $K'[H]$
. Because
$K'[H]$
. Because
![]() $\sum _{i=0}^{dm-1}(A\theta _2)^{\varphi ^{i}}\varphi ^{-i}\in \mathcal O_{K'}[H]$
, we deduce from the well-known fact
$\sum _{i=0}^{dm-1}(A\theta _2)^{\varphi ^{i}}\varphi ^{-i}\in \mathcal O_{K'}[H]$
, we deduce from the well-known fact
that
![]() $\sum _{i=0}^{dm-1}(A\theta _2)^{\varphi ^{i}}\varphi ^{-i}\in \mathcal O_{K'}[H]^{\times }$
. We now apply the character
$\sum _{i=0}^{dm-1}(A\theta _2)^{\varphi ^{i}}\varphi ^{-i}\in \mathcal O_{K'}[H]^{\times }$
. We now apply the character
![]() $\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
and easily derive (a).
$\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}}$
and easily derive (a).
For the proof of (b), we can assume Hypothesis (T) and we compute
 $$ \begin{align*} \varphi(E) = \sum_{i=0}^{dm-1} (A\theta_2)^{\varphi^{i+1}}u^{-(i+1)} u \equiv Eu \equiv uE \pmod{p\mathcal{O}_{K'}}, \end{align*} $$
$$ \begin{align*} \varphi(E) = \sum_{i=0}^{dm-1} (A\theta_2)^{\varphi^{i+1}}u^{-(i+1)} u \equiv Eu \equiv uE \pmod{p\mathcal{O}_{K'}}, \end{align*} $$
where the congruences hold, because we have
![]() $u^{md} \equiv 1\pmod {p}$
by hypothesis (T).
$u^{md} \equiv 1\pmod {p}$
by hypothesis (T).
If Hypothesis (T) holds, then part (c) is an immediate consequence of [Reference CobbeCob18, Lemma 1.9]. Under Hypothesis (I), it follows from the definitions.▪
Generalizing the approach of [Reference Bley and CobbeBC17, Section 6.3], we define a
![]() ${{\mathbb Z}_p[G]}$
-module homomorphism
${{\mathbb Z}_p[G]}$
-module homomorphism
by
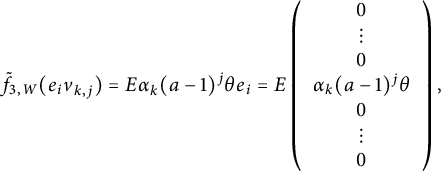 $$ \begin{align*} \tilde f_{3,W}(e_iv_{k,j})=E\alpha_k(a-1)^j\theta e_i = E \left( \begin{array}{c} 0 \\ \vdots \\ 0 \\ \alpha_k (a-1)^j\theta \\ 0 \\ \vdots \\ 0 \end{array} \right), \end{align*} $$
$$ \begin{align*} \tilde f_{3,W}(e_iv_{k,j})=E\alpha_k(a-1)^j\theta e_i = E \left( \begin{array}{c} 0 \\ \vdots \\ 0 \\ \alpha_k (a-1)^j\theta \\ 0 \\ \vdots \\ 0 \end{array} \right), \end{align*} $$
for all
![]() $i,j,k$
, where
$i,j,k$
, where
![]() $\theta =\theta _1\theta _2$
. We denote by
$\theta =\theta _1\theta _2$
. We denote by
![]() $f_{3,W}$
the composition of
$f_{3,W}$
the composition of
![]() $\tilde f_{3,W}$
with the projection to
$\tilde f_{3,W}$
with the projection to
![]() $\mathcal F(\mathfrak p_N^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})$
.
$\mathcal F(\mathfrak p_N^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})$
.
In order to generalize [Reference Bley and CobbeBC17, Lemma 7.2.4], we first need a higher dimensional version of [Reference Bley and CobbeBC16, Lemma 4.1.7].
Lemma 6.10 For
![]() $\nu \in \mathcal {O}_K[G]$
,
$\nu \in \mathcal {O}_K[G]$
,
![]() $i=1,\dots ,r$
and
$i=1,\dots ,r$
and
![]() $j=0,\dots ,p-1$
, we have
$j=0,\dots ,p-1$
, we have
Proof We write
![]() $\nu =\sum _{h,l,k}\nu _{h,l,k}a^hb^l\alpha _k$
for some
$\nu =\sum _{h,l,k}\nu _{h,l,k}a^hb^l\alpha _k$
for some
![]() $\nu _{h,l,k}\in {\mathbb Z}_p$
. Then,
$\nu _{h,l,k}\in {\mathbb Z}_p$
. Then,
 $$ \begin{align*}f_{3,W}\left(\sum_{h,l,k}\nu_{h,l,k}a^hb^le_i\alpha_k w_j\right)=\sum_{h,l,k}\nu_{h,l,k}a^hb^l \cdot E \alpha_k (a-1)^j \theta e_i\in\mathfrak p_N^{j+1}e_i\end{align*} $$
$$ \begin{align*}f_{3,W}\left(\sum_{h,l,k}\nu_{h,l,k}a^hb^le_i\alpha_k w_j\right)=\sum_{h,l,k}\nu_{h,l,k}a^hb^l \cdot E \alpha_k (a-1)^j \theta e_i\in\mathfrak p_N^{j+1}e_i\end{align*} $$
by [Reference Bley and CobbeBC16, Lemma 3.2.5]. Using the isomorphism in (6.12), this is congruent to
▪
Lemma 6.11 The map
![]() $f_{3,W}$
is surjective. More precisely, for
$f_{3,W}$
is surjective. More precisely, for
![]() $j\geq 0$
,
$j\geq 0$
,
Proof For
![]() $j=p$
,
$j=p$
,
![]() $W_{\geq p}=\{0\}$
and
$W_{\geq p}=\{0\}$
and
![]() $\mathcal F((\mathfrak p_N^{p+1})^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})=\{0\}$
, so the result is trivial.
$\mathcal F((\mathfrak p_N^{p+1})^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})=\{0\}$
, so the result is trivial.
We assume the result for
![]() $j+1$
and proceed by descending induction. Let
$j+1$
and proceed by descending induction. Let
![]() $x\in \mathcal F((\mathfrak p_N^{j+1})^{(r)})$
. As in the proof of [Reference Bley and CobbeBC17, Lemma 7.2.4], there exist
$x\in \mathcal F((\mathfrak p_N^{j+1})^{(r)})$
. As in the proof of [Reference Bley and CobbeBC17, Lemma 7.2.4], there exist
![]() $\nu _{h,\ell ,i,k}\in {\mathbb Z}_p$
such that
$\nu _{h,\ell ,i,k}\in {\mathbb Z}_p$
such that
 $$ \begin{align*} \begin{aligned} x&\equiv E\sum_{h,\ell,i,k} \nu_{h,\ell,i,k}a^hb^{\ell}\alpha_k(a-1)^j\theta e_i\pmod{\mathfrak p_N^{j+2}}\\ &\equiv \sum_{h,\ell,i,k}\tilde u^{m\ell} E^{\varphi^{-m\ell}} \nu_{h,\ell,i,k}a^hb^{\ell}\alpha_k(a-1)^j\theta e_i\pmod{\mathfrak p_N^{j+2}}\\ &\equiv \sum_{h,\ell,i,k}\tilde u^{m\ell} \nu_{h,\ell,i,k}a^hb^{\ell} E \alpha_k(a-1)^j\theta e_i\pmod{\mathfrak p_N^{j+2}}\\ &\equiv \tilde f_{3,W}\left(\sum_{h,\ell,i,k}\tilde u^{ml} \nu_{h,\ell,i,k}a^hb^{\ell} e_i\alpha_k w_j\right)\pmod{\mathfrak p_N^{j+2}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} x&\equiv E\sum_{h,\ell,i,k} \nu_{h,\ell,i,k}a^hb^{\ell}\alpha_k(a-1)^j\theta e_i\pmod{\mathfrak p_N^{j+2}}\\ &\equiv \sum_{h,\ell,i,k}\tilde u^{m\ell} E^{\varphi^{-m\ell}} \nu_{h,\ell,i,k}a^hb^{\ell}\alpha_k(a-1)^j\theta e_i\pmod{\mathfrak p_N^{j+2}}\\ &\equiv \sum_{h,\ell,i,k}\tilde u^{m\ell} \nu_{h,\ell,i,k}a^hb^{\ell} E \alpha_k(a-1)^j\theta e_i\pmod{\mathfrak p_N^{j+2}}\\ &\equiv \tilde f_{3,W}\left(\sum_{h,\ell,i,k}\tilde u^{ml} \nu_{h,\ell,i,k}a^hb^{\ell} e_i\alpha_k w_j\right)\pmod{\mathfrak p_N^{j+2}}. \end{aligned} \end{align*} $$
This means that the class
![]() $\pi (x)$
of x in
$\pi (x)$
of x in
![]() $\mathcal F(\mathfrak p_N^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})$
is the sum of an element in the image of
$\mathcal F(\mathfrak p_N^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})$
is the sum of an element in the image of
![]() $W_{\geq j}$
and an element in
$W_{\geq j}$
and an element in
![]() $\mathcal F((\mathfrak p_N^{j+2})^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})$
, which is by assumption in the image of
$\mathcal F((\mathfrak p_N^{j+2})^{(r)})/\mathcal F((\mathfrak p_N^{p+1})^{(r)})$
, which is by assumption in the image of
![]() $W_{\geq j+1}\subseteq W_{\geq j}$
.▪
$W_{\geq j+1}\subseteq W_{\geq j}$
.▪
Lemma 6.12 Let
![]() $1\leq i\leq r$
,
$1\leq i\leq r$
,
![]() $0\leq j\leq p-1$
,
$0\leq j\leq p-1$
,
![]() $1\leq k\leq m$
. Then there exists
$1\leq k\leq m$
. Then there exists
![]() $\mu _{i,j,k}\in W_{\geq j+2}$
such that the element
$\mu _{i,j,k}\in W_{\geq j+2}$
such that the element
is in the kernel of
![]() $f_{3,W}$
. Here,
$f_{3,W}$
. Here,
![]() $w_p$
should be interpreted as
$w_p$
should be interpreted as
![]() $0$
.
$0$
.
Proof As in the proof of [Reference Bley and CobbeBC17, Lemma 7.2.5], we see that the formal subtraction of X and Y takes the form
with
![]() $A_h\in M_r({\mathbb Z}_p)$
for
$A_h\in M_r({\mathbb Z}_p)$
for
![]() $h=1,\dots ,r$
. In analogy to the proof of [Reference Bley and CobbeBC17, Lemma 7.2.5], we set
$h=1,\dots ,r$
. In analogy to the proof of [Reference Bley and CobbeBC17, Lemma 7.2.5], we set
and we obtain that
![]() $x -_{\mathcal F} y -_{\mathcal F} z \equiv 0\pmod {\mathcal F((\mathfrak p_N^{j+3})^{(r)})}$
. Therefore,
$x -_{\mathcal F} y -_{\mathcal F} z \equiv 0\pmod {\mathcal F((\mathfrak p_N^{j+3})^{(r)})}$
. Therefore,
and we conclude the proof of the lemma using Lemma 6.11.▪
Lemma 6.13 The elements
 $$ \begin{align*} r_{i,m}=\mathcal T_a e_i \alpha_m w_0+\varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon^{-1}b^{-\tilde m} e_i \left(\alpha_1-\sum_{i=2}^m\alpha_i\right)w_{p-1}-e_i \alpha_m w_{p-1}, \end{align*} $$
$$ \begin{align*} r_{i,m}=\mathcal T_a e_i \alpha_m w_0+\varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon^{-1}b^{-\tilde m} e_i \left(\alpha_1-\sum_{i=2}^m\alpha_i\right)w_{p-1}-e_i \alpha_m w_{p-1}, \end{align*} $$
for
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $1< k<m$
, are in the kernel of
$1< k<m$
, are in the kernel of
![]() $f_{3,W}$
. Note that
$f_{3,W}$
. Note that
![]() $\varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon ^{-1}$
has coefficients in
$\varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon ^{-1}$
has coefficients in
![]() ${\mathbb Z}_p^{\mathrm {nr}}$
and is fixed by
${\mathbb Z}_p^{\mathrm {nr}}$
and is fixed by
![]() $\varphi $
; hence, it has coefficients in
$\varphi $
; hence, it has coefficients in
![]() ${{\mathbb Z}_p}$
.
${{\mathbb Z}_p}$
.
Proof We denote by
![]() $v_j$
the jth component of a vector v. Using [Reference Bley and CobbeBC16, Lemma 3.2.2] and Lemma 6.9(c), we calculate
$v_j$
the jth component of a vector v. Using [Reference Bley and CobbeBC16, Lemma 3.2.2] and Lemma 6.9(c), we calculate
 $$ \begin{align*} \begin{aligned}(\mathcal{N}_{N_0/K_0}(\varepsilon^{-1}E\alpha_k\theta e_i))_j&=\mathcal{N}_{N_0/K_0}(\theta_1){(\varepsilon^{-1}E\alpha_k\theta_2 e_i)_j}^p\\ &\equiv -\alpha_k^p\theta_2^p\alpha_1^{1-p}p{(\varepsilon^{-1}E e_i)_j}^p\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\equiv -\alpha_k^p\theta_2^p\alpha_1^{1-p}p(\varphi(\varepsilon^{-1}E) e_i)_j\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\equiv -\alpha_k^p\theta_2^p\alpha_1^{1-p}p \left(u^{-1}\tilde u\varepsilon^{-1}E e_i\right)_j\pmod{\mathfrak p_{N_0}^{p+1}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned}(\mathcal{N}_{N_0/K_0}(\varepsilon^{-1}E\alpha_k\theta e_i))_j&=\mathcal{N}_{N_0/K_0}(\theta_1){(\varepsilon^{-1}E\alpha_k\theta_2 e_i)_j}^p\\ &\equiv -\alpha_k^p\theta_2^p\alpha_1^{1-p}p{(\varepsilon^{-1}E e_i)_j}^p\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\equiv -\alpha_k^p\theta_2^p\alpha_1^{1-p}p(\varphi(\varepsilon^{-1}E) e_i)_j\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\equiv -\alpha_k^p\theta_2^p\alpha_1^{1-p}p \left(u^{-1}\tilde u\varepsilon^{-1}E e_i\right)_j\pmod{\mathfrak p_{N_0}^{p+1}}. \end{aligned} \end{align*} $$
We also compute
With this in mind, we can do analogous calculations to those in [Reference Bley and CobbeBC16, Lemma 4.2.6] and [Reference Bley and CobbeBC17, Lemma 7.2.6] and obtain
 $$ \begin{align*} f_{3,W}(\mathcal T_a e_i \alpha_k w_0)\equiv \varepsilon\left(\alpha_k\theta_2-\alpha_{1}\left(\frac{\alpha_k}{\alpha_1}\right)^p\theta_2^{b^{-\tilde m}}u^{-1}\tilde u\right)p\varepsilon^{-1}E e_i\pmod{\mathfrak p_{N_0}^{p+1}}. \end{align*} $$
$$ \begin{align*} f_{3,W}(\mathcal T_a e_i \alpha_k w_0)\equiv \varepsilon\left(\alpha_k\theta_2-\alpha_{1}\left(\frac{\alpha_k}{\alpha_1}\right)^p\theta_2^{b^{-\tilde m}}u^{-1}\tilde u\right)p\varepsilon^{-1}E e_i\pmod{\mathfrak p_{N_0}^{p+1}}. \end{align*} $$
Furthermore,
 $$ \begin{align*} \begin{aligned} &f_{3,W}(\varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon^{-1}b^{-\tilde m}e_i\alpha_{k+1}w_{p-1})\\ &\qquad\equiv \varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon^{-1}E^{\varphi^{m\tilde m}}\alpha_{k+1}p\theta_2^{b^{-\tilde m}} e_i\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\qquad\equiv \varepsilon u^{-1}\tilde u^{1-m\tilde m}u^{m\tilde m}(\varepsilon^{-1}E)^{\varphi^{m\tilde m}}\alpha_{k+1}p\theta_2^{b^{-\tilde m}} e_i\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\qquad\equiv \varepsilon u^{-1}\tilde u \varepsilon^{-1}E\alpha_{k+1}p\theta_2^{b^{-\tilde m}} e_i\pmod{\mathfrak p_{N_0}^{p+1}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &f_{3,W}(\varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon^{-1}b^{-\tilde m}e_i\alpha_{k+1}w_{p-1})\\ &\qquad\equiv \varepsilon u^{-1}\tilde u^{1-m\tilde m}\varepsilon^{-1}E^{\varphi^{m\tilde m}}\alpha_{k+1}p\theta_2^{b^{-\tilde m}} e_i\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\qquad\equiv \varepsilon u^{-1}\tilde u^{1-m\tilde m}u^{m\tilde m}(\varepsilon^{-1}E)^{\varphi^{m\tilde m}}\alpha_{k+1}p\theta_2^{b^{-\tilde m}} e_i\pmod{\mathfrak p_{N_0}^{p+1}}\\ &\qquad\equiv \varepsilon u^{-1}\tilde u \varepsilon^{-1}E\alpha_{k+1}p\theta_2^{b^{-\tilde m}} e_i\pmod{\mathfrak p_{N_0}^{p+1}}. \end{aligned} \end{align*} $$
It is straightforward to adapt the remaining calculations from [Reference Bley and CobbeBC17, Lemma 7.2.6] and conclude that
![]() $r_{i,k}\in \ker f_{3,W}$
for
$r_{i,k}\in \ker f_{3,W}$
for
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $1< k<m$
. The proof that
$1< k<m$
. The proof that
![]() $r_{i,m}\in \ker f_{3,W}$
is analogous.▪
$r_{i,m}\in \ker f_{3,W}$
is analogous.▪
From now on, we have to distinguish the cases of Hypotheses (T) and (I).
We start assuming Hypothesis (I).
Following the computations in [Reference Bley and CobbeBC17, Section 7.3], we have
Lemma 6.14 The
![]() $pmr$
elements
$pmr$
elements
![]() $r_{i,k},s_{i,j,k}$
, for
$r_{i,k},s_{i,j,k}$
, for
![]() $1\leq i\leq r$
,
$1\leq i\leq r$
,
![]() $0\leq j\leq p-2$
,
$0\leq j\leq p-2$
,
![]() $1\leq k\leq m$
, constitute a
$1\leq k\leq m$
, constitute a
![]() ${{\mathbb Z}_p[G]}$
-basis of
${{\mathbb Z}_p[G]}$
-basis of
![]() $\ker f_{3,W}$
.
$\ker f_{3,W}$
.
Proof We adapt the proof of [Reference Bley and CobbeBC17, Lemmas 7.3.1]. We write the coefficients of the
![]() $e_i\alpha _kw_{p-1}$
-components,
$e_i\alpha _kw_{p-1}$
-components,
![]() $i=1,\dots ,r$
,
$i=1,\dots ,r$
,
![]() $k=1,\dots ,m$
, of the elements
$k=1,\dots ,m$
, of the elements
![]() $r_{i,j}$
,
$r_{i,j}$
,
![]() $j=1,\dots ,m$
, into the columns of an
$j=1,\dots ,m$
, into the columns of an
![]() $mr \times mr$
matrix, which we call
$mr \times mr$
matrix, which we call
![]() ${\mathcal M}$
, and whose entries are
${\mathcal M}$
, and whose entries are
![]() $r\times r$
blocks,
$r\times r$
blocks,
 $$ \begin{align*}{\mathcal M}=\begin{pmatrix} \varepsilon u^{-1}\varepsilon^{-1} b^{-\tilde m}\!-\!1\!\!\!\!\!\!&0&\cdots&0&0&\varepsilon u^{-1}\varepsilon^{-1} b^{-\tilde m}\\ 0&-1&\cdots&0&0&-\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\\ 0&\!\!\!\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\!\!\!&\cdots&0&0&-\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&\cdots&\!\!\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\!\!\!\!\!\!\!&-1&-\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\\ 0&0&\cdots&0&\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}&-1\!-\!\varepsilon u^{-1}\varepsilon^{-1} b^{-\tilde m} \end{pmatrix}\!. \end{align*} $$
$$ \begin{align*}{\mathcal M}=\begin{pmatrix} \varepsilon u^{-1}\varepsilon^{-1} b^{-\tilde m}\!-\!1\!\!\!\!\!\!&0&\cdots&0&0&\varepsilon u^{-1}\varepsilon^{-1} b^{-\tilde m}\\ 0&-1&\cdots&0&0&-\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\\ 0&\!\!\!\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\!\!\!&\cdots&0&0&-\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 0&0&\cdots&\!\!\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\!\!\!\!\!\!\!&-1&-\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}\\ 0&0&\cdots&0&\varepsilon u^{-1}\varepsilon^{-1}b^{-\tilde m}&-1\!-\!\varepsilon u^{-1}\varepsilon^{-1} b^{-\tilde m} \end{pmatrix}\!. \end{align*} $$
By Lemma 4.5 and analogous computations as in [Reference Bley and CobbeBC17], we obtain
The rest of the proof works exactly as in [Reference Bley and CobbeBC17]; note that Hypothesis (I) plays the role of the assumption
![]() $\omega =0$
in the one-dimensional setting.▪
$\omega =0$
in the one-dimensional setting.▪
We recall that
![]() $G = \mathrm {Gal}(N/K) = \langle a \rangle \times \langle b \rangle $
. Any irreducible character
$G = \mathrm {Gal}(N/K) = \langle a \rangle \times \langle b \rangle $
. Any irreducible character
![]() $\psi $
of G decomposes as
$\psi $
of G decomposes as
![]() $\psi = \chi \phi $
, where
$\psi = \chi \phi $
, where
![]() $\chi $
is an irreducible character of
$\chi $
is an irreducible character of
![]() $\langle a \rangle $
and
$\langle a \rangle $
and
![]() $\phi $
an irreducible character of
$\phi $
an irreducible character of
![]() $\langle b \rangle $
. We will denote by
$\langle b \rangle $
. We will denote by
![]() $\chi _0$
the trivial character.
$\chi _0$
the trivial character.
Proposition 6.15 Assume Hypothesis (I). For
![]() $\mathcal {L} = \mathfrak p_N^{p+1}$
, the element
$\mathcal {L} = \mathfrak p_N^{p+1}$
, the element
is contained in
![]() $K_0({{\mathbb Z}_p[G]}, {\mathbb Q_p[G]})$
and represented by
$K_0({{\mathbb Z}_p[G]}, {\mathbb Q_p[G]})$
and represented by
![]() $\varepsilon \in {\mathbb Q_p[G]}^{\times }$
where
$\varepsilon \in {\mathbb Q_p[G]}^{\times }$
where
 $$ \begin{align*} \begin{aligned} \kappa_{\chi\phi}^{}&=\begin{cases}p^{mr}&\text{if } \chi=\chi_0\\ (-1)^{r(m-1)} \det(u^{-m}\phi(b)^{-1} - 1) (\chi(a)-1)^{mr(p-1)}&\text{if } \chi\neq\chi_0.\end{cases}\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \kappa_{\chi\phi}^{}&=\begin{cases}p^{mr}&\text{if } \chi=\chi_0\\ (-1)^{r(m-1)} \det(u^{-m}\phi(b)^{-1} - 1) (\chi(a)-1)^{mr(p-1)}&\text{if } \chi\neq\chi_0.\end{cases}\\ \end{aligned} \end{align*} $$
Proof We choose the elements
![]() $r_{i,k}$
and
$r_{i,k}$
and
![]() $s_{i,j,k}$
of Lemma 6.14 as a
$s_{i,j,k}$
of Lemma 6.14 as a
![]() ${{\mathbb Z}_p[G]}$
-basis of
${{\mathbb Z}_p[G]}$
-basis of
![]() $\ker (f_{3,W})$
and fix the canonical
$\ker (f_{3,W})$
and fix the canonical
![]() ${{\mathbb Z}_p[G]}$
-basis of W. Then,
${{\mathbb Z}_p[G]}$
-basis of W. Then,
is represented by the determinant of
 $$ \begin{align*} {\mathfrak M}=\begin{pmatrix} \mathcal T_aI&(a-1)I&0&\cdots&0&0\\ 0&-I&(a-1)I&\cdots&0&0\\ 0&*&-I&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&*&*&\cdots&-I&(a-1)I\\ {\mathcal M}&*&*&\cdots&*&-I \end{pmatrix}, \end{align*} $$
$$ \begin{align*} {\mathfrak M}=\begin{pmatrix} \mathcal T_aI&(a-1)I&0&\cdots&0&0\\ 0&-I&(a-1)I&\cdots&0&0\\ 0&*&-I&\cdots&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&*&*&\cdots&-I&(a-1)I\\ {\mathcal M}&*&*&\cdots&*&-I \end{pmatrix}, \end{align*} $$
where in the above
![]() $pmr\times pmr$
all the entries are
$pmr\times pmr$
all the entries are
![]() $mr\times mr$
blocks. Recalling that p is odd, we get:
$mr\times mr$
blocks. Recalling that p is odd, we get:
 $$ \begin{align*} \begin{aligned} \det(\chi\phi(\mathfrak M))&=\begin{cases}p^{mr}(-1)^{mr(p-1)}&\text{if } \chi=\chi_0\\ (-1)^{m^2r^2(p-1)}\det(\chi\phi({\mathcal M}))(\chi(a)-1)^{mr(p-1)}&\text{if } \chi\neq\chi_0\end{cases}\\ &=\begin{cases}p^{mr}&\text{if } \chi=\chi_0\\ (-1)^{r(m-1)}\det(u^{-m}\phi(b)^{-1}-1)(\chi(a)-1)^{mr(p-1)}&\text{if } \chi\neq\chi_0.\end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \det(\chi\phi(\mathfrak M))&=\begin{cases}p^{mr}(-1)^{mr(p-1)}&\text{if } \chi=\chi_0\\ (-1)^{m^2r^2(p-1)}\det(\chi\phi({\mathcal M}))(\chi(a)-1)^{mr(p-1)}&\text{if } \chi\neq\chi_0\end{cases}\\ &=\begin{cases}p^{mr}&\text{if } \chi=\chi_0\\ (-1)^{r(m-1)}\det(u^{-m}\phi(b)^{-1}-1)(\chi(a)-1)^{mr(p-1)}&\text{if } \chi\neq\chi_0.\end{cases} \end{aligned} \end{align*} $$
▪
It remains to consider the case of Hypothesis (T). Here, we follow the strategy of [Reference Bley and CobbeBC17, Section 7.4].
Lemma 6.16 There is a commutative diagram of
![]() ${\mathbb Z}_p[G]$
-modules with exact rows
${\mathbb Z}_p[G]$
-modules with exact rows

where
 $$ \begin{align*}\begin{aligned} &\delta_2(e_iz_1)=(u^mb-1)e_iz_0,\\ &\delta_2(e_iz_2)=(a-1)e_iz_0,\\ &\delta_2(e_iv_{j,k})=0,\\ &\tilde f_2(e_iz_0)=[(\theta_1)_i,1,\dots,1],\\ &\tilde f_3(e_iz_1)=[(\theta_1)_i,1,\dots,1],\\ &\tilde f_3(e_iz_2)=[\gamma_i,\dots,\gamma_i],\\ &\tilde f_3(e_iv_{k,j})=f_{{\mathcal F},{\mathcal N}}(\tilde f_{3,W}(e_iv_{k,j})),\\ &\pi(e_iz_0)=e_i, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} &\delta_2(e_iz_1)=(u^mb-1)e_iz_0,\\ &\delta_2(e_iz_2)=(a-1)e_iz_0,\\ &\delta_2(e_iv_{j,k})=0,\\ &\tilde f_2(e_iz_0)=[(\theta_1)_i,1,\dots,1],\\ &\tilde f_3(e_iz_1)=[(\theta_1)_i,1,\dots,1],\\ &\tilde f_3(e_iz_2)=[\gamma_i,\dots,\gamma_i],\\ &\tilde f_3(e_iv_{k,j})=f_{{\mathcal F},{\mathcal N}}(\tilde f_{3,W}(e_iv_{k,j})),\\ &\pi(e_iz_0)=e_i, \end{aligned}\end{align*} $$
for all i, j, and k (recall that
![]() $\gamma _i$
was defined in (6.14)). Furthermore,
$\gamma _i$
was defined in (6.14)). Furthermore,
![]() $X(2)=\ker (\delta _2|_{W'})$
and
$X(2)=\ker (\delta _2|_{W'})$
and
![]() $\tilde f_{3,W}$
is the restriction of
$\tilde f_{3,W}$
is the restriction of
![]() $\tilde f_3$
to
$\tilde f_3$
to
![]() $X(2) \oplus W$
.
$X(2) \oplus W$
.
Proof We recall from [Reference CobbeCob18, Section 2] that the action of
![]() $\mathrm {Gal}(K_0/K) \times G$
on
$\mathrm {Gal}(K_0/K) \times G$
on
![]() $\mathcal {I}_{N/K}(\rho ^{\mathrm {nr}})$
is characterized by
$\mathcal {I}_{N/K}(\rho ^{\mathrm {nr}})$
is characterized by
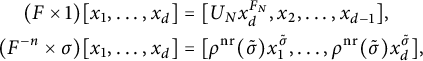 $$ \begin{align*} (F \times 1) [x_1, \ldots, x_d] &= [U_Nx_d^{F_N}, x_2, \ldots, x_{d-1}], \\ (F^{-n} \times \sigma) [x_1, \ldots, x_d] &= [\rho^{\mathrm{nr}}(\tilde\sigma) x_1^{\tilde\sigma}, \ldots, \rho^{\mathrm{nr}}(\tilde\sigma) x_d^{\tilde\sigma}], \end{align*} $$
$$ \begin{align*} (F \times 1) [x_1, \ldots, x_d] &= [U_Nx_d^{F_N}, x_2, \ldots, x_{d-1}], \\ (F^{-n} \times \sigma) [x_1, \ldots, x_d] &= [\rho^{\mathrm{nr}}(\tilde\sigma) x_1^{\tilde\sigma}, \ldots, \rho^{\mathrm{nr}}(\tilde\sigma) x_d^{\tilde\sigma}], \end{align*} $$
where
![]() $x_i \in \prod _r \widehat {N_0^{\times }}$
, the elements
$x_i \in \prod _r \widehat {N_0^{\times }}$
, the elements
![]() $F^{-n}$
and
$F^{-n}$
and
![]() $\sigma \in G$
have the same restriction to
$\sigma \in G$
have the same restriction to
![]() $N \cap K_0$
, and
$N \cap K_0$
, and
![]() $\tilde \sigma \in \mathrm {Gal}(N_0/K)$
is uniquely defined by
$\tilde \sigma \in \mathrm {Gal}(N_0/K)$
is uniquely defined by
![]() $\tilde \sigma |_{K_0} = F^{-n}$
and
$\tilde \sigma |_{K_0} = F^{-n}$
and
![]() $\tilde \sigma |_{N} = \sigma $
. Furthermore, we remark that the action of G on
$\tilde \sigma |_{N} = \sigma $
. Furthermore, we remark that the action of G on
![]() $\mathcal {Z} / (U_N - 1)\mathcal {Z}$
is induced by
$\mathcal {Z} / (U_N - 1)\mathcal {Z}$
is induced by
The bottom sequence is exact by [Reference CobbeCob18, Theorem 3.3 and Lemma 2.1]. The proofs of the exactness of the top sequence as well as the proof of commutativity follow along the lines of proof in the one-dimensional case (see [Reference Bley and CobbeBC17, Lemma 7.4.1]). For example, if we denote the coefficients of
![]() $U_K = u^m$
by
$U_K = u^m$
by
![]() $u_{ij}$
, then
$u_{ij}$
, then
 $$ \begin{align*} \tilde f_2\circ\delta_2(e_iz_1)&=\tilde f_2((u^mb-1)e_i)=\tilde f_2\left(\sum_{j=1}^r bu_{j,i}e_j-e_i\right)\\ &=\sum_{j=1}^r (1\times b)u_{j,i}\cdot [(\theta_1)_j,1,\dots,1]-[(\theta_1)_i,1,\dots,1] \\ &=(1\times b)\cdot [(\theta_1^{u_{1,i}},\theta_1^{u_{2,i}},\dots,\theta_1^{u_{r,i}}),1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=(1\times b)[u(\theta_1)_i,1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=(F\times 1)(F^{-1}\times b)[u(\theta_1)_i,1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=(F\times 1)[u^{-1}u(\theta_1)_i,1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=((F-1)\times 1)\circ \tilde f_3(e_iz_1).\\ \end{align*} $$
$$ \begin{align*} \tilde f_2\circ\delta_2(e_iz_1)&=\tilde f_2((u^mb-1)e_i)=\tilde f_2\left(\sum_{j=1}^r bu_{j,i}e_j-e_i\right)\\ &=\sum_{j=1}^r (1\times b)u_{j,i}\cdot [(\theta_1)_j,1,\dots,1]-[(\theta_1)_i,1,\dots,1] \\ &=(1\times b)\cdot [(\theta_1^{u_{1,i}},\theta_1^{u_{2,i}},\dots,\theta_1^{u_{r,i}}),1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=(1\times b)[u(\theta_1)_i,1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=(F\times 1)(F^{-1}\times b)[u(\theta_1)_i,1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=(F\times 1)[u^{-1}u(\theta_1)_i,1,\dots,1]-[(\theta_1)_i,1,\dots,1]\\ &=((F-1)\times 1)\circ \tilde f_3(e_iz_1).\\ \end{align*} $$
▪
We will need an explicit description of
![]() $X(2)$
, which generalizes the one given in [Reference Bley and CobbeBC17, Lemma 7.4.3].
$X(2)$
, which generalizes the one given in [Reference Bley and CobbeBC17, Lemma 7.4.3].
Lemma 6.17 We have
Proof The proof is just the r-dimensional analogue of that of [Reference Bley and CobbeBC17, Lemma 7.4.3].▪
We let
denote the composite of
![]() $\tilde f_{3,W}$
with the canonical projection. By Lemma 6.11, the homomorphism
$\tilde f_{3,W}$
with the canonical projection. By Lemma 6.11, the homomorphism
![]() $f_{3,W}$
is surjective.
$f_{3,W}$
is surjective.
In the next proposition, which is the analogue of [Reference Bley and CobbeBC17, Lemma 7.4.2], we will obtain an explicit representative for the complex
![]() $M^{\bullet }(\mathcal {L})$
, which we will use to compute the Euler characteristic
$M^{\bullet }(\mathcal {L})$
, which we will use to compute the Euler characteristic
![]() $\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
.
$\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
.
Proposition 6.18 The complex
with modules in degrees
![]() $0,1$
, and
$0,1$
, and
![]() $2$
is a representative of
$2$
is a representative of
![]() $M^{\bullet }(\mathcal {L})$
for
$M^{\bullet }(\mathcal {L})$
for
![]() $\mathcal {L} = \mathfrak p_N^{p+1}$
.
$\mathcal {L} = \mathfrak p_N^{p+1}$
.
Proof If we recall the definition of
![]() $M^{\bullet }(\mathcal {L})$
from (6.8), then it follows readily from Lemmas 6.11 and 6.16 that we have a quasi-isomorphism of complexes
$M^{\bullet }(\mathcal {L})$
from (6.8), then it follows readily from Lemmas 6.11 and 6.16 that we have a quasi-isomorphism of complexes
▪
For the computation of the Euler characteristic of
![]() $M^{\bullet }(\mathcal {L})$
, we continue to closely follow the approach of [Reference Bley and CobbeBC17, Section 7.4]. On these grounds, we will only sketch the proofs, pointing out the parts which are specific for the higher dimensional setting.
$M^{\bullet }(\mathcal {L})$
, we continue to closely follow the approach of [Reference Bley and CobbeBC17, Section 7.4]. On these grounds, we will only sketch the proofs, pointing out the parts which are specific for the higher dimensional setting.
The next result is an analogue of [Reference Bley and CobbeBC17, Lemma 7.4.5] and [Reference Bley and CobbeBC17, Lemma 7.4.6]. Recall that by assumption
![]() $(m,d) = 1$
, and let
$(m,d) = 1$
, and let
![]() $\tilde m$
denote an integer such that
$\tilde m$
denote an integer such that
Lemma 6.19 There exist
![]() $y_{i,1}\in W_{\geq 1}$
such that
$y_{i,1}\in W_{\geq 1}$
such that
 $$ \begin{align*} \begin{aligned} t_{i,1} &:= (a-1)e_iz_1-(u^mb-1)e_iz_2+\\ &\qquad+\left(\sum_{j=2}^{m}\alpha_{j}(u^mb)^{1-(j-2)\tilde m}+\left(\alpha_1-\sum_{j=2}^{m}\alpha_{j}\right)(u^mb)^{\tilde m}\right)e_iw_0+ y_{i,1}\end{aligned}\end{align*} $$
$$ \begin{align*} \begin{aligned} t_{i,1} &:= (a-1)e_iz_1-(u^mb-1)e_iz_2+\\ &\qquad+\left(\sum_{j=2}^{m}\alpha_{j}(u^mb)^{1-(j-2)\tilde m}+\left(\alpha_1-\sum_{j=2}^{m}\alpha_{j}\right)(u^mb)^{\tilde m}\right)e_iw_0+ y_{i,1}\end{aligned}\end{align*} $$
and
 $$ \begin{align*}t_{i,2}:=\begin{cases}\mathcal T_ae_iz_2-\alpha_1 e_i w_{p-1}&\text{if }m=1\\ \mathcal T_ae_iz_2-\alpha_2 e_i w_{p-1}&\text{if }m>1\end{cases}\end{align*} $$
$$ \begin{align*}t_{i,2}:=\begin{cases}\mathcal T_ae_iz_2-\alpha_1 e_i w_{p-1}&\text{if }m=1\\ \mathcal T_ae_iz_2-\alpha_2 e_i w_{p-1}&\text{if }m>1\end{cases}\end{align*} $$
are in the kernel of
![]() $f_{3,W}$
.
$f_{3,W}$
.
Proof Let
![]() $x_2\in \mathcal {O}_{K^{\mathrm {nr}}}$
be such that
$x_2\in \mathcal {O}_{K^{\mathrm {nr}}}$
be such that
![]() $x_2/\alpha _1\pmod {\mathfrak p_{K'}}$
is a root of
$x_2/\alpha _1\pmod {\mathfrak p_{K'}}$
is a root of
![]() $X^p-X+A\theta _2$
, and let
$X^p-X+A\theta _2$
, and let
![]() $(1+x_2\theta _1)_i$
be the element in
$(1+x_2\theta _1)_i$
be the element in
![]() $\prod _r U_{N_0}^{(1)}$
whose ith component is
$\prod _r U_{N_0}^{(1)}$
whose ith component is
![]() $1+x_2\theta _1$
and all the other components are
$1+x_2\theta _1$
and all the other components are
![]() $1$
. By the same proof as in [Reference Bley and CobbeBC17, Lemma 7.2.2], we obtain
$1$
. By the same proof as in [Reference Bley and CobbeBC17, Lemma 7.2.2], we obtain
Therefore, by [Reference CobbeCob18, Lemma 2.4], we may assume
![]() $\gamma _i\equiv (1+x_2\theta _1)_i\pmod {\mathfrak p_{N_0}^2}$
.
$\gamma _i\equiv (1+x_2\theta _1)_i\pmod {\mathfrak p_{N_0}^2}$
.
With this in mind, the proof of the lemma is the same as in [Reference Bley and CobbeBC17, Lemma 7.4.5] and [Reference Bley and CobbeBC17, Lemma 7.4.6].▪
In the case of Hypothesis (T), we need to redefine the elements
![]() $r_{i,1}$
in a different way:
$r_{i,1}$
in a different way:
Lemma 6.20 The elements
belong to
![]() $\ker f_{3,W}\cap W$
, and their
$\ker f_{3,W}\cap W$
, and their
![]() $\alpha _1w_0$
-components are
$\alpha _1w_0$
-components are
![]() $(u^mb)^{\tilde m} \mathcal T_a e_i$
.
$(u^mb)^{\tilde m} \mathcal T_a e_i$
.
Proof Straightforward by the same calculations as in [Reference Bley and CobbeBC16, Lemma 4.2.5].▪
We also redefine the matrix
![]() ${\mathcal M}$
considered in the case of Hypothesis (I) using the elements
${\mathcal M}$
considered in the case of Hypothesis (I) using the elements
![]() $t_{i,2}$
instead of the elements
$t_{i,2}$
instead of the elements
![]() $r_{i,1}$
. For
$r_{i,1}$
. For
![]() $m>1$
, we obtain:
$m>1$
, we obtain:
We call
![]() ${\mathcal M}_1$
the matrix consisting of the first r columns of
${\mathcal M}_1$
the matrix consisting of the first r columns of
![]() ${\mathcal M}$
, and
${\mathcal M}$
, and
![]() $\tilde {\mathcal M}$
the matrix of the remaining columns.
$\tilde {\mathcal M}$
the matrix of the remaining columns.
For
![]() $m=1$
, the matrix
$m=1$
, the matrix
![]() ${\mathcal M}$
is determined only by the
${\mathcal M}$
is determined only by the
![]() $t_{i,2}$
, and, recalling their definition from Lemma 6.19, we get minus the identity matrix.
$t_{i,2}$
, and, recalling their definition from Lemma 6.19, we get minus the identity matrix.
By an easy calculation,
![]() $\det ({\mathcal M})=(-1)^{mr}(\det (u)^mb)^{-\tilde m(m-1)}$
.
$\det ({\mathcal M})=(-1)^{mr}(\det (u)^mb)^{-\tilde m(m-1)}$
.
Lemma 6.21 The
![]() $r(pm+1)$
elements
$r(pm+1)$
elements
![]() $t_{1,i}, t_{2,i}$
, for
$t_{1,i}, t_{2,i}$
, for
![]() $i=1,\dots ,r$
,
$i=1,\dots ,r$
,
![]() $r_{i,k}$
, for
$r_{i,k}$
, for
![]() $i=1,\dots ,r$
,
$i=1,\dots ,r$
,
![]() $k=2,\dots ,m$
, and
$k=2,\dots ,m$
, and
![]() $s_{i,j,k}$
, for
$s_{i,j,k}$
, for
![]() $i=1,\dots ,r$
,
$i=1,\dots ,r$
,
![]() $j=0,\dots ,p-2$
,
$j=0,\dots ,p-2$
,
![]() $k=1,\dots ,m$
, constitute a
$k=1,\dots ,m$
, constitute a
![]() ${\mathbb Z}_p[G]$
-basis of
${\mathbb Z}_p[G]$
-basis of
![]() $\ker (f_{3,W})$
.
$\ker (f_{3,W})$
.
Proof It is enough to follow the proof of [Reference Bley and CobbeBC17, Lemma 7.4.9]. Note that we can construct the matrix
![]() ${\mathcal M}$
as in [Reference Bley and CobbeBC17] and that it also takes exactly the same shape up to the fact that all the entries are
${\mathcal M}$
as in [Reference Bley and CobbeBC17] and that it also takes exactly the same shape up to the fact that all the entries are
![]() $r\times r$
blocks.▪
$r\times r$
blocks.▪
By the same proof as in [Reference Bley and CobbeBC17], we can now reduce the computation of the term
![]() $\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
to the determinant of a matrix
$\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
to the determinant of a matrix
![]() $(w,\mathfrak M)$
, which looks exactly as in [Reference Bley and CobbeBC17], with the convention the elements in
$(w,\mathfrak M)$
, which looks exactly as in [Reference Bley and CobbeBC17], with the convention the elements in
![]() ${{\mathbb Z}_p[G]}$
must be thought as diagonal
${{\mathbb Z}_p[G]}$
must be thought as diagonal
![]() $r\times r$
matrices. So, in particular,
$r\times r$
matrices. So, in particular,
![]() $m\times m$
blocks become
$m\times m$
blocks become
![]() $mr \times mr$
blocks and so on. Of course, for the block
$mr \times mr$
blocks and so on. Of course, for the block
![]() ${\mathcal M}$
, we have to take the one defined above and not that of [Reference Bley and CobbeBC17]. With this in mind, the matrix looks as follows:
${\mathcal M}$
, we have to take the one defined above and not that of [Reference Bley and CobbeBC17]. With this in mind, the matrix looks as follows:
 $$ \begin{align*} {\begin{pmatrix} \frac{\sum_{i=0}^{d-1}(u^{m}b)^i}{u^{dm}-1}&(a-1)I_r&0&0&0&0&\cdots&0&0\\ 0& \!\!\!1-u^mb\!\!\!&\mathcal T_a I_r&0&0&0&\cdots&0&0\\ 0&v&0&\mathcal T_a\tilde I&(a-1)I_{rm}&0&\cdots&0&0\\ 0&*&0&0&-I_{rm}&\!\!(a-1)I_{rm}\!\!&\cdots&0&0\\ 0&*&0&0&*&-I_{rm}&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&*&0&0&*&*&\cdots&-I_{rm}&(a-1)I_{rm}\\ 0&*&{\mathcal M}_1&\tilde {\mathcal M}&*&*&\cdots&*&-I_{rm} \end{pmatrix}}. \end{align*} $$
$$ \begin{align*} {\begin{pmatrix} \frac{\sum_{i=0}^{d-1}(u^{m}b)^i}{u^{dm}-1}&(a-1)I_r&0&0&0&0&\cdots&0&0\\ 0& \!\!\!1-u^mb\!\!\!&\mathcal T_a I_r&0&0&0&\cdots&0&0\\ 0&v&0&\mathcal T_a\tilde I&(a-1)I_{rm}&0&\cdots&0&0\\ 0&*&0&0&-I_{rm}&\!\!(a-1)I_{rm}\!\!&\cdots&0&0\\ 0&*&0&0&*&-I_{rm}&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&*&0&0&*&*&\cdots&-I_{rm}&(a-1)I_{rm}\\ 0&*&{\mathcal M}_1&\tilde {\mathcal M}&*&*&\cdots&*&-I_{rm} \end{pmatrix}}. \end{align*} $$
Here,
![]() $I_{rm}$
(resp.
$I_{rm}$
(resp.
![]() $I_r$
) is the
$I_r$
) is the
![]() $rm\times rm$
(resp.
$rm\times rm$
(resp.
![]() $r\times r$
) identity matrix,
$r\times r$
) identity matrix,
![]() $\tilde I$
is obtained by
$\tilde I$
is obtained by
![]() $I_{rm}$
by removing the first r columns, v is an
$I_{rm}$
by removing the first r columns, v is an
![]() $r \times rm$
matrix, whose first r rows coincide with the matrix
$r \times rm$
matrix, whose first r rows coincide with the matrix
![]() $(u^mb)^{\tilde m}$
, and
$(u^mb)^{\tilde m}$
, and
![]() $\frac {1}{u^{dm}-1}$
is the inverse of the matrix
$\frac {1}{u^{dm}-1}$
is the inverse of the matrix
![]() $u^{dm}-1$
.
$u^{dm}-1$
.
We are ready to record the result of the computation of the refined Euler characteristic of
![]() $M^{\bullet }(\mathcal {L})$
.
$M^{\bullet }(\mathcal {L})$
.
Proposition 6.22 We assume the hypotheses (F) and (T), and let
![]() $\mathcal {L} = \mathfrak p_N^{p+1}$
. Then, the element
$\mathcal {L} = \mathfrak p_N^{p+1}$
. Then, the element
![]() $\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
is contained in
$\chi _{{\mathbb Z}_p[G], {B_{\mathrm {dR}}}[G]}(M^{\bullet }(\mathcal {L}), 0)$
is contained in
![]() $K_0({\mathbb Z}_p[G], {\mathbb Q}_p[G])$
and represented by
$K_0({\mathbb Z}_p[G], {\mathbb Q}_p[G])$
and represented by
![]() $\varepsilon \in {\mathbb Q}_p[G]^{\times }$
where
$\varepsilon \in {\mathbb Q}_p[G]^{\times }$
where
 $$ \begin{align*} \kappa_{\chi\phi}^{}= \begin{cases}(-1)^{r}\frac{\det(u)^{m\tilde m}\phi(b)^{r\tilde m}p^{r m}}{\det(u^m\phi(b)-1)}&\text{if } \chi=\chi_0\\ (-1)^{(m-1)r}(\det(u)^m\phi(b)^r)^{-\tilde m(m-1)}(\chi(a)-1)^{r m(p-1)}&\text{if } \chi\neq\chi_0 \end{cases} \end{align*} $$
$$ \begin{align*} \kappa_{\chi\phi}^{}= \begin{cases}(-1)^{r}\frac{\det(u)^{m\tilde m}\phi(b)^{r\tilde m}p^{r m}}{\det(u^m\phi(b)-1)}&\text{if } \chi=\chi_0\\ (-1)^{(m-1)r}(\det(u)^m\phi(b)^r)^{-\tilde m(m-1)}(\chi(a)-1)^{r m(p-1)}&\text{if } \chi\neq\chi_0 \end{cases} \end{align*} $$
and
![]() $\chi \phi $
is the decomposition explained before Proposition 6.15.
$\chi \phi $
is the decomposition explained before Proposition 6.15.
Proof The proof is a straightforward adaption of the computations in the proof of [Reference Bley and CobbeBC17, Proposition 7.4.10].▪
7 Rationality and functoriality
From now on, we set
![]() $\hat \partial ^1 = \hat \partial _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}^1$
. As in [Reference Bley and CobbeBC17], we consider the term
$\hat \partial ^1 = \hat \partial _{{{\mathbb Z}_p[G]}, {{B_{\mathrm {dR}}}[G]}}^1$
. As in [Reference Bley and CobbeBC17], we consider the term
which a priori lives in
![]() $K_0({{\mathbb Z}_p[G]}, {B_{\mathrm {dR}}}[G])$
. The unramified term
$K_0({{\mathbb Z}_p[G]}, {B_{\mathrm {dR}}}[G])$
. The unramified term
![]() $U_{N/K}$
is defined by Breuning in [Reference BreuningBre04b, Proposition 2.12]. Recall that
$U_{N/K}$
is defined by Breuning in [Reference BreuningBre04b, Proposition 2.12]. Recall that
![]() $R_{N/K}$
differs from [Reference Bley and CobbeBC17, equation (17)], because we have to adapt the definition of
$R_{N/K}$
differs from [Reference Bley and CobbeBC17, equation (17)], because we have to adapt the definition of
![]() $R_{N/K}$
as explained in Remark 6.6.
$R_{N/K}$
as explained in Remark 6.6.
Proposition 7.1 The element
![]() $R_{N/K}$
is rational, i.e.,
$R_{N/K}$
is rational, i.e.,
![]() $R_{N/K}\in K_0({{\mathbb Z}_p[G]}, {{\mathbb Q}_{p}}[G])$
.
$R_{N/K}\in K_0({{\mathbb Z}_p[G]}, {{\mathbb Q}_{p}}[G])$
.
Proof For elements
![]() $x,y \in K_0({{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G])$
, we use the notation
$x,y \in K_0({{\mathbb Z}_p[G]}, {\mathbb Q}_p^c[G])$
, we use the notation
![]() $x \equiv y$
when
$x \equiv y$
when
![]() $x-y \in K_0({{\mathbb Z}_p[G]}, {\mathbb Q_p[G]})$
. By Propositions 4.8, 5.1, and 6.5, we get
$x-y \in K_0({{\mathbb Z}_p[G]}, {\mathbb Q_p[G]})$
. By Propositions 4.8, 5.1, and 6.5, we get
where
![]() $T_{N/K} := \hat \partial \left ( \tau _{{\mathbb Q}_{p}}(\mathrm {Ind}_{K/{{\mathbb Q}_{p}}}(\chi ))_{\chi \in \mathrm {Irr}(G)}\right )$
is precisely the element defined by Breuning in [Reference BreuningBre04b, Section 2.3]. The result now follows, because this is exactly r times the element obtained in [Reference Bley and CobbeBC17, Proposition 7.1.3].▪
$T_{N/K} := \hat \partial \left ( \tau _{{\mathbb Q}_{p}}(\mathrm {Ind}_{K/{{\mathbb Q}_{p}}}(\chi ))_{\chi \in \mathrm {Irr}(G)}\right )$
is precisely the element defined by Breuning in [Reference BreuningBre04b, Section 2.3]. The result now follows, because this is exactly r times the element obtained in [Reference Bley and CobbeBC17, Proposition 7.1.3].▪
Proposition 7.2 Let L be an intermediate field of
![]() $N/K$
and
$N/K$
and
![]() $H=\mathrm {Gal}(N/L)$
. Let
$H=\mathrm {Gal}(N/L)$
. Let
![]() $\rho _H^G$
and
$\rho _H^G$
and
![]() $q_{G/H}^G$
be the restriction and quotient maps from (4.2) and (4.3), respectively. Then,
$q_{G/H}^G$
be the restriction and quotient maps from (4.2) and (4.3), respectively. Then,
-
(1)
 $\rho ^G_H(R_{N/K})=R_{N/L}$
.
$\rho ^G_H(R_{N/K})=R_{N/L}$
. -
(2) If H is normal in G, then
 $q^G_{G/H}(R_{N/K})=R_{L/K}$
.
$q^G_{G/H}(R_{N/K})=R_{L/K}$
.
Proof By definition of the cohomological term, we have
 $$ \begin{align*} R_{N/K} &= -\chi_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}(M^{\bullet}, \exp_{V, N} \circ \mathrm{comp}_{V, N}^{-1}) +rm\hat\partial^1(t) - m U_{tw}(\rho^{\mathrm{nr}}_{{\mathbb Q}_{p}})\\ &\quad +U_{\mathrm{cris}, N/K} - r U_{N/K} + \hat\partial_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}^1(\varepsilon_D(N/K,V)) \end{align*} $$
$$ \begin{align*} R_{N/K} &= -\chi_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}(M^{\bullet}, \exp_{V, N} \circ \mathrm{comp}_{V, N}^{-1}) +rm\hat\partial^1(t) - m U_{tw}(\rho^{\mathrm{nr}}_{{\mathbb Q}_{p}})\\ &\quad +U_{\mathrm{cris}, N/K} - r U_{N/K} + \hat\partial_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}^1(\varepsilon_D(N/K,V)) \end{align*} $$
with
![]() $M^{\bullet } = R\Gamma (N, T) \oplus \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T[0]$
. The functoriality properties of
$M^{\bullet } = R\Gamma (N, T) \oplus \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T[0]$
. The functoriality properties of
![]() $rm\hat \partial ^1(t)$
and
$rm\hat \partial ^1(t)$
and
![]() $mU_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
follow easily using the general formulas in [Reference Bley and WilsonBW09, Sections 6.1 and 6.3]. Recalling also Lemmas 4.9 and 5.2 and [Reference BreuningBre04a, Lemma 4.5], it remains to show
$mU_{tw}(\rho ^{\mathrm {nr}}_{{\mathbb Q}_{p}})$
follow easily using the general formulas in [Reference Bley and WilsonBW09, Sections 6.1 and 6.3]. Recalling also Lemmas 4.9 and 5.2 and [Reference BreuningBre04a, Lemma 4.5], it remains to show
and
 $$ \begin{align} &q^G_{G/H}\left( \chi_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}(M^{\bullet}, \exp_{V, N} \circ \mathrm{comp}_{V, N}^{-1}) \right)\nonumber\\&\quad = \chi_{{\mathbb Z}_p[G/H], {B_{\mathrm{dR}}}[G/H]}(M^{\bullet}, \exp_{V, L} \circ \mathrm{comp}_{V, L}^{-1}). \end{align} $$
$$ \begin{align} &q^G_{G/H}\left( \chi_{{{\mathbb Z}_p[G]}, {{B_{\mathrm{dR}}}[G]}}(M^{\bullet}, \exp_{V, N} \circ \mathrm{comp}_{V, N}^{-1}) \right)\nonumber\\&\quad = \chi_{{\mathbb Z}_p[G/H], {B_{\mathrm{dR}}}[G/H]}(M^{\bullet}, \exp_{V, L} \circ \mathrm{comp}_{V, L}^{-1}). \end{align} $$
The proof of (7.1) follows along the same line of argument as the proof of [Reference BreuningBre04a, Lemma 4.14(1)]. We just have to replace
![]() $A = \mu _{p^n}$
in loc. cit. by
$A = \mu _{p^n}$
in loc. cit. by
![]() $\mathcal F[p^n]$
.
$\mathcal F[p^n]$
.
Because (7.2) is essentially proved in the same way as part (2) of [Reference BreuningBre04b, Lemma 4.14], we only give a brief sketch. As in (17) of loc. cit., we obtain a canonical isomorphism
in the derived category. For each i, the induced map from
![]() $H^i({\mathbb Q}_p^c \otimes R\Gamma (L, T)) \cong {\mathbb Q}_p^c \otimes H^i(L, T)$
to
$H^i({\mathbb Q}_p^c \otimes R\Gamma (L, T)) \cong {\mathbb Q}_p^c \otimes H^i(L, T)$
to
![]() $H^i({\mathbb Q}_p^c \otimes R\mathrm {Hom}_{{\mathbb Z}_p[H]}({{\mathbb Z}_p}, R\Gamma (N, T))) \cong {\mathbb Q}_p^c \otimes H^i(N, T)^H$
is the map induced by the restriction
$H^i({\mathbb Q}_p^c \otimes R\mathrm {Hom}_{{\mathbb Z}_p[H]}({{\mathbb Z}_p}, R\Gamma (N, T))) \cong {\mathbb Q}_p^c \otimes H^i(N, T)^H$
is the map induced by the restriction
![]() $H^i(L, T) \longrightarrow H^i(N, T)$
.
$H^i(L, T) \longrightarrow H^i(N, T)$
.
For
![]() $i=1$
, this restriction map is clearly given by the inclusion
$i=1$
, this restriction map is clearly given by the inclusion
![]() ${\mathcal F}({\mathfrak p}_L^{(r)}) \subseteq {\mathcal F}({\mathfrak p}_N^{(r)})$
, and for
${\mathcal F}({\mathfrak p}_L^{(r)}) \subseteq {\mathcal F}({\mathfrak p}_N^{(r)})$
, and for
![]() $i=2$
, cohomology vanishes after tensoring with
$i=2$
, cohomology vanishes after tensoring with
![]() ${\mathbb Q}_p^c$
by our hypothesis (F).
${\mathbb Q}_p^c$
by our hypothesis (F).
We further note that we have a canonical isomorphism
which is given by
![]() $x \mapsto x$
, if we identify
$x \mapsto x$
, if we identify
![]() $ \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T$
with the set of maps
$ \mathrm {Ind}_{N/{{\mathbb Q}_{p}}}T$
with the set of maps
![]() $x \colon G_{{\mathbb Q}_{p}} \longrightarrow T$
satisfying
$x \colon G_{{\mathbb Q}_{p}} \longrightarrow T$
satisfying
![]() $x(\tau \sigma ) = \tau x(\sigma )$
for all
$x(\tau \sigma ) = \tau x(\sigma )$
for all
![]() $\tau \in G_N$
and
$\tau \in G_N$
and
![]() $\sigma \in G_{{\mathbb Q}_{p}}$
.
$\sigma \in G_{{\mathbb Q}_{p}}$
.
From (7.3) and (7.4), we derive a canonical isomorphism
![]() $M_L^{\bullet } \cong R\mathrm {Hom}_{{\mathbb Z}_p[H]}({{\mathbb Z}_p}, M_N^{\bullet })$
, and it finally remains to show that the induced maps (drawn as dotted arrows below) in the following diagram coincide with
$M_L^{\bullet } \cong R\mathrm {Hom}_{{\mathbb Z}_p[H]}({{\mathbb Z}_p}, M_N^{\bullet })$
, and it finally remains to show that the induced maps (drawn as dotted arrows below) in the following diagram coincide with
![]() $\mathrm {comp}_{V,L}^{-1}$
and
$\mathrm {comp}_{V,L}^{-1}$
and
![]() $\exp _{V, L}$
, respectively:
$\exp _{V, L}$
, respectively:

For
![]() $\exp _V$
, this is immediate, because it is defined as a connecting homomorphism (see, for example, [Reference Benois and BergerBB08, p. 612]) and thus compatible with restriction. In addition, for
$\exp _V$
, this is immediate, because it is defined as a connecting homomorphism (see, for example, [Reference Benois and BergerBB08, p. 612]) and thus compatible with restriction. In addition, for
![]() $\mathrm {comp}_V$
, it follows from the definitions (see [Reference Benois and BergerBB08, p. 625]).▪
$\mathrm {comp}_V$
, it follows from the definitions (see [Reference Benois and BergerBB08, p. 625]).▪
8 Proof of the main results
As in [Reference Bley and CobbeBC17], we also define
so that
![]() $R_{N/K} = \tilde R_{N/K} - rU_{N/K}$
.
$R_{N/K} = \tilde R_{N/K} - rU_{N/K}$
.
We now argue as in the proof of [Reference Bley and CobbeBC17, Proposition 3.2.6] (see page 359 of loc. cit.). By Taylor’s fixed point theorem together with [Reference BreuningBre04b, Proposition 2.12], it can be shown that
![]() $R_{N/K}=0$
in
$R_{N/K}=0$
in
![]() $K_0({{\mathbb Z}_p[G]},{\mathbb Q_p[G]})$
if and only if
$K_0({{\mathbb Z}_p[G]},{\mathbb Q_p[G]})$
if and only if
![]() $\tilde R_{N/K}=0$
in
$\tilde R_{N/K}=0$
in
![]() $K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
.
$K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
.
From Propositions 4.8, 5.1, and 6.5, we conclude that
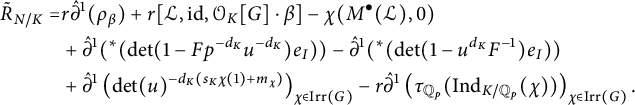 $$ \begin{align} \begin{aligned}\tilde R_{N/K}=& r\hat\partial^1(\rho_{\beta})+r[\mathcal L,\mathrm{id},\mathcal O_K[G]\cdot \beta]- \chi_{}(M^{\bullet}(\mathcal{L}), 0) \\ &+\hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I))-\hat\partial^1({}^*(\det(1-u^{d_K}F^{-1})e_I))\\ &+\hat\partial^1\left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\right)_{\chi \in \mathrm{Irr}(G)} - r\hat\partial^1\left(\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) ) \right)_{\chi \in \mathrm{Irr}(G)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}\tilde R_{N/K}=& r\hat\partial^1(\rho_{\beta})+r[\mathcal L,\mathrm{id},\mathcal O_K[G]\cdot \beta]- \chi_{}(M^{\bullet}(\mathcal{L}), 0) \\ &+\hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I))-\hat\partial^1({}^*(\det(1-u^{d_K}F^{-1})e_I))\\ &+\hat\partial^1\left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\right)_{\chi \in \mathrm{Irr}(G)} - r\hat\partial^1\left(\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) ) \right)_{\chi \in \mathrm{Irr}(G)}. \end{aligned} \end{align} $$
As in the one-dimensional case (see [Reference Bley and CobbeBC17, Proposition 3.2.6]), the following three statements are equivalent in our present setting:
-
(a)
 $C_{EP}^{na}(N/K, V)$
is valid.
$C_{EP}^{na}(N/K, V)$
is valid. -
(b)
 $R_{N/K} = 0$
in
$R_{N/K} = 0$
in
 $K_0({{\mathbb Z}_p[G]}, {\mathbb Q_p[G]})$
.
$K_0({{\mathbb Z}_p[G]}, {\mathbb Q_p[G]})$
. -
(c)
 $\tilde R_{N/K} = 0$
in
$\tilde R_{N/K} = 0$
in
 $K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
.
$K_0(\overline {{\mathbb Z}_p^{\mathrm {nr}}}[G], \overline {\mathbb Q_p^{\mathrm {nr}}}[G])$
.
Proof of Theorem 1.1
It suffices to show that
![]() $\tilde R_{N/K}=0$
. From (8.1) together with Proposition 6.7, we obtain
$\tilde R_{N/K}=0$
. From (8.1) together with Proposition 6.7, we obtain
 $$ \begin{align*} \tilde R_{N/K} &= r\hat\partial^1(\rho_{\beta})+r[\mathfrak p_N, \mathrm{id}, \mathcal{O}_N] + \hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I)) \\ &+\hat\partial^1\left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\right)_{\chi \in \mathrm{Irr}(G)} - r\hat\partial^1\left(\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) ) \right)_{\chi \in \mathrm{Irr}(G)}. \end{align*} $$
$$ \begin{align*} \tilde R_{N/K} &= r\hat\partial^1(\rho_{\beta})+r[\mathfrak p_N, \mathrm{id}, \mathcal{O}_N] + \hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I)) \\ &+\hat\partial^1\left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\right)_{\chi \in \mathrm{Irr}(G)} - r\hat\partial^1\left(\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) ) \right)_{\chi \in \mathrm{Irr}(G)}. \end{align*} $$
The term
vanishes by [Reference Izychev and VenjakobIV16, Lemma 6.2]. Because
![]() $N/K$
is tame, the group ring idempotent
$N/K$
is tame, the group ring idempotent
![]() $e_I$
is contained in
$e_I$
is contained in
![]() ${{\mathbb Z}_p[G]}$
, and it is then easy to show that
${{\mathbb Z}_p[G]}$
, and it is then easy to show that
We conclude that
 $$ \begin{align*} \begin{aligned} \hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I))&=-r\hat\partial^1({}^*(p^{d_K}e_I)) \\ & =-r[\mathfrak p_N,\mathrm{id},\mathcal{O}_N], \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I))&=-r\hat\partial^1({}^*(p^{d_K}e_I)) \\ & =-r[\mathfrak p_N,\mathrm{id},\mathcal{O}_N], \end{aligned} \end{align*} $$
where the last equality follows from [Reference Izychev and VenjakobIV16, equation (6.7)]. In conclusion, we have shown that
We finally conclude as in the proof of [Reference BreuningBre04b, Theorem 3.6] or as in [Reference Izychev and VenjakobIV16, p. 517] to show that
We recall that these proofs crucially use a fundamental result of M. Taylor (see [Reference FröhlichFrö83, Theorem 31]) which computes the quotient of norm resolvents and Galois Gauss sums. We also note that the so-called nonramified characteristic which occurs in these results is an integral unit itself.▪
Proof of Theorem 1.3
The crucial input in our proof is a result of Picket and Vinatier in [Reference Pickett and VinatierPV13]. In [Reference Bley and CobbeBC16, Section 5.1], we used this result to construct an integral normal basis generator
![]() $\beta = p^2\alpha _M\theta _2$
of
$\beta = p^2\alpha _M\theta _2$
of
![]() $\mathcal {L} = \mathfrak p_N^{p+1}$
. Hence, the expression in (8.1) simplifies to
$\mathcal {L} = \mathfrak p_N^{p+1}$
. Hence, the expression in (8.1) simplifies to
 $$ \begin{align} \begin{aligned}\tilde R_{N/K}=& r\hat\partial^1(\rho_{\beta})- \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}(M^{\bullet}(\mathcal{L}), 0) \\ &+\hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I))-\hat\partial^1({}^*(\det(1-u^{d_K}F^{-1})e_I))\\ &+\hat\partial^1\left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\right)_{\chi \in \mathrm{Irr}(G)} - r\hat\partial^1\left(\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) ) \right)_{\chi \in \mathrm{Irr}(G)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}\tilde R_{N/K}=& r\hat\partial^1(\rho_{\beta})- \chi_{{\mathbb Z}_p[G], {B_{\mathrm{dR}}}[G]}(M^{\bullet}(\mathcal{L}), 0) \\ &+\hat\partial^1({}^*(\det(1-Fp^{-d_K}u^{-d_K})e_I))-\hat\partial^1({}^*(\det(1-u^{d_K}F^{-1})e_I))\\ &+\hat\partial^1\left( \det(u)^{-d_K(s_K\chi(1) + m_{\chi})}\right)_{\chi \in \mathrm{Irr}(G)} - r\hat\partial^1\left(\tau_{{\mathbb Q}_{p}}( \mathrm{Ind}_{K/{{\mathbb Q}_{p}}}(\chi) ) \right)_{\chi \in \mathrm{Irr}(G)}. \end{aligned} \end{align} $$
By [Reference Bley and CobbeBC16, Proposition 5.2.1], the element
![]() $\hat \partial ^1(\rho _{\beta }) - \hat \partial ^1\left (\tau _{{\mathbb Q}_{p}}( \mathrm {Ind}_{K/{{\mathbb Q}_{p}}}(\chi ) ) \right )_{\chi \in \mathrm {Irr}(G)}$
is represented by
$\hat \partial ^1(\rho _{\beta }) - \hat \partial ^1\left (\tau _{{\mathbb Q}_{p}}( \mathrm {Ind}_{K/{{\mathbb Q}_{p}}}(\chi ) ) \right )_{\chi \in \mathrm {Irr}(G)}$
is represented by
![]() $\hat \partial ^1(\eta ^{-1})$
with
$\hat \partial ^1(\eta ^{-1})$
with
![]() $\eta $
as in [Reference Bley and CobbeBC16, Proposition. 5.2.1]. Furthermore, recalling that
$\eta $
as in [Reference Bley and CobbeBC16, Proposition. 5.2.1]. Furthermore, recalling that
![]() $m=d_K$
and
$m=d_K$
and
![]() $s_K=0$
,
$s_K=0$
,
From now on, we have to distinguish the three conditions in the statement of the Theorem. Let us start with (a), i.e., Hypothesis (I). In this case,
![]() $\tilde R_{N/K}$
is represented by
$\tilde R_{N/K}$
is represented by
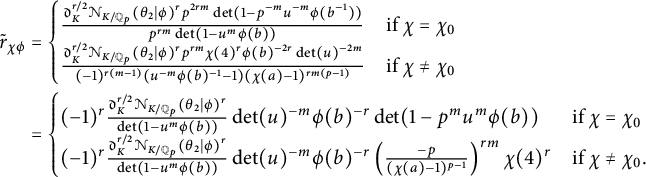 $$ \begin{align*} \begin{aligned} \tilde r_{\chi\phi}&= \begin{cases}\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{2rm}\det(1-p^{-m}u^{-m}\phi(b^{-1}))}{p^{rm}\det(1-u^m\phi(b))}&\text{if } \chi=\chi_0\\ \frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{rm}\chi(4)^r\phi(b)^{-2r} \det(u)^{-2m}}{(-1)^{r(m-1)}(u^{-m}\phi(b)^{-1}-1)(\chi(a)-1)^{rm(p-1)}}&\text{if } \chi\neq\chi_0\end{cases}\\ &=\begin{cases}(-1)^r\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r}{\det(1-u^m\phi(b))}\det(u)^{-m}\phi(b)^{-r}\det(1-p^m u^{m}\phi(b))&\text{if } \chi=\chi_0\\ (-1)^r\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r}{\det(1-u^m\phi(b))}\det(u)^{-m}\phi(b)^{-r}\left(\frac{-p}{(\chi(a)-1)^{p-1}}\right)^{rm}\chi(4)^r&\text{if } \chi\neq\chi_0.\end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tilde r_{\chi\phi}&= \begin{cases}\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{2rm}\det(1-p^{-m}u^{-m}\phi(b^{-1}))}{p^{rm}\det(1-u^m\phi(b))}&\text{if } \chi=\chi_0\\ \frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{rm}\chi(4)^r\phi(b)^{-2r} \det(u)^{-2m}}{(-1)^{r(m-1)}(u^{-m}\phi(b)^{-1}-1)(\chi(a)-1)^{rm(p-1)}}&\text{if } \chi\neq\chi_0\end{cases}\\ &=\begin{cases}(-1)^r\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r}{\det(1-u^m\phi(b))}\det(u)^{-m}\phi(b)^{-r}\det(1-p^m u^{m}\phi(b))&\text{if } \chi=\chi_0\\ (-1)^r\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r}{\det(1-u^m\phi(b))}\det(u)^{-m}\phi(b)^{-r}\left(\frac{-p}{(\chi(a)-1)^{p-1}}\right)^{rm}\chi(4)^r&\text{if } \chi\neq\chi_0.\end{cases} \end{aligned} \end{align*} $$
Let
![]() $W_{\theta _2}\in \mathcal O_p^t[G]\subset \overline {{\mathbb Z}_p^{\mathrm {nr}}}[G]^{\times }$
be defined by
$W_{\theta _2}\in \mathcal O_p^t[G]\subset \overline {{\mathbb Z}_p^{\mathrm {nr}}}[G]^{\times }$
be defined by
So
 $$ \begin{align*}\tilde r=\frac{W_{\theta_2}\det(u)^{-m}b^{-r}}{\det(1-u^m b)} \left(\det(1-p^mu^mb)e_a+(-\tilde u)^m\sigma_4(1-e_a)\right),\end{align*} $$
$$ \begin{align*}\tilde r=\frac{W_{\theta_2}\det(u)^{-m}b^{-r}}{\det(1-u^m b)} \left(\det(1-p^mu^mb)e_a+(-\tilde u)^m\sigma_4(1-e_a)\right),\end{align*} $$
where
![]() $\tilde u\in {\mathbb Z}_p[a]$
is a unit whose augmentation is congruent to
$\tilde u\in {\mathbb Z}_p[a]$
is a unit whose augmentation is congruent to
![]() $1$
modulo p, as in [Reference Bley and CobbeBC17, Section 8]. Then, the proof works as in [Reference Bley and CobbeBC17].
$1$
modulo p, as in [Reference Bley and CobbeBC17, Section 8]. Then, the proof works as in [Reference Bley and CobbeBC17].
Let us now consider case (b), i.e., Hypothesis (T). In this case,
![]() $\tilde R_{N/K}$
is represented by
$\tilde R_{N/K}$
is represented by
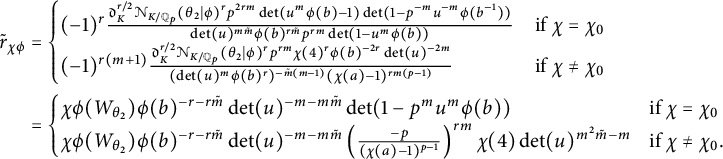 $$ \begin{align*} {\begin{aligned} \tilde r_{\chi\phi}&= \begin{cases}(-1)^{r}\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{2rm}\det(u^m\phi(b)-1)\det(1-p^{-m}u^{-m}\phi(b^{-1}))}{\det(u)^{m\tilde m}\phi(b)^{r\tilde m}p^{rm}\det(1-u^m\phi(b))}&\text{if } \chi=\chi_0\\ (-1)^{r(m+1)}\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{rm}\chi(4)^r\phi(b)^{-2r} \det(u)^{-2m}}{(\det(u)^m\phi(b)^r)^{-\tilde m(m-1)}(\chi(a)-1)^{rm(p-1)}}&\text{if } \chi\neq\chi_0\end{cases}\\ &=\begin{cases}\chi\phi(W_{\theta_2})\phi(b)^{-r-r\tilde m}\det(u)^{-m-m\tilde m}\det(1-p^m u^{m}\phi(b))&\!\text{if } \chi=\chi_0\\ \chi\phi(W_{\theta_2})\phi(b)^{-r-r\tilde m}\det(u)^{-m-m\tilde m}\left(\frac{-p}{(\chi(a)-1)^{p-1}}\right)^{rm}\chi(4)\det(u)^{m^2\tilde m-m}&\!\text{if } \chi\neq\chi_0. \end{cases} \end{aligned}}\end{align*} $$
$$ \begin{align*} {\begin{aligned} \tilde r_{\chi\phi}&= \begin{cases}(-1)^{r}\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{2rm}\det(u^m\phi(b)-1)\det(1-p^{-m}u^{-m}\phi(b^{-1}))}{\det(u)^{m\tilde m}\phi(b)^{r\tilde m}p^{rm}\det(1-u^m\phi(b))}&\text{if } \chi=\chi_0\\ (-1)^{r(m+1)}\frac{\mathfrak d_K^{r/2}\mathcal{N}_{K/{{\mathbb Q}_{p}}}(\theta_2|\phi)^r p^{rm}\chi(4)^r\phi(b)^{-2r} \det(u)^{-2m}}{(\det(u)^m\phi(b)^r)^{-\tilde m(m-1)}(\chi(a)-1)^{rm(p-1)}}&\text{if } \chi\neq\chi_0\end{cases}\\ &=\begin{cases}\chi\phi(W_{\theta_2})\phi(b)^{-r-r\tilde m}\det(u)^{-m-m\tilde m}\det(1-p^m u^{m}\phi(b))&\!\text{if } \chi=\chi_0\\ \chi\phi(W_{\theta_2})\phi(b)^{-r-r\tilde m}\det(u)^{-m-m\tilde m}\left(\frac{-p}{(\chi(a)-1)^{p-1}}\right)^{rm}\chi(4)\det(u)^{m^2\tilde m-m}&\!\text{if } \chi\neq\chi_0. \end{cases} \end{aligned}}\end{align*} $$
So
As in [Reference Bley and CobbeBC17], Hypothesis (T) implies that
![]() $\det (u)^{m^2\tilde m-m}\equiv 1\pmod {1-\zeta _p}$
. Then, the proof works as in [Reference Bley and CobbeBC17], using the computations of the case of Hypothesis (I).
$\det (u)^{m^2\tilde m-m}\equiv 1\pmod {1-\zeta _p}$
. Then, the proof works as in [Reference Bley and CobbeBC17], using the computations of the case of Hypothesis (I).
It remains to consider the case (c). Let
![]() $E/K'$
be the unramified extension of degree
$E/K'$
be the unramified extension of degree
![]() $\tilde d$
. By the functoriality result of Proposition 7.2 (a), it is enough to show
$\tilde d$
. By the functoriality result of Proposition 7.2 (a), it is enough to show
![]() $R_{NE/K}=0$
, which is true, because, for
$R_{NE/K}=0$
, which is true, because, for
![]() $NE/K$
, we can apply part (b) of the theorem.▪
$NE/K$
, we can apply part (b) of the theorem.▪
We finally prove Theorems 1.5 and 1.6. For the definition of the twist matrix of an abelian variety A with good ordinary reduction, we refer the reader to [Reference Lubin and RosenLR78, p. 237]. We recall the following lemma.
Lemma 8.1 Let A be an r-dimensional abelian variety defined over the p-adic number field L with good ordinary reduction, and let U be the twist matrix of A. Then,
![]() $\det (U - 1) \ne 0$
.
$\det (U - 1) \ne 0$
.
Proof This is shown in [Reference MazurMaz72, Corollary 4.38] or in the proof of [Reference Lubin and RosenLR78, Theorem 2].▪
Acknowledgment
We would like to thank Andreas Nickel for sharing with us some of his insights on a particular computation necessary for the proof of Lemma 6.2, which required quite a lot of efforts to be fully clarified. We would also like to thank the referees for their fast and careful reading, as well as their valuable suggestions to improve the exposition, and for correcting some minor mistakes.