The triangle removal states that if G contains $\varepsilon n^2$ edge-disjoint triangles, then G contains $\delta (\varepsilon )n^3$ triangles. Unfortunately, there are no sensible bounds on the order of growth of $\delta (\varepsilon )$, and at any rate, it is known that $\delta (\varepsilon )$ is not polynomial in $\varepsilon $. Csaba recently obtained an asymmetric variant of the triangle removal, stating that if G contains $\varepsilon n^2$ edge-disjoint triangles, then G contains $2^{-\operatorname {\mathrm {poly}}(1/\varepsilon )}\cdot n^5$ copies of $C_5$. To this end, he devised a new variant of Szemerédi’s regularity lemma. We obtain the following results:

• • We first give a regularity-free proof of Csaba’s theorem, which improves the number of copies of $C_5$ to the optimal number $\operatorname {\mathrm {poly}}(\varepsilon )\cdot n^5$.

• • We say that H is $K_3$-abundant if every graph containing $\varepsilon n^2$ edge-disjoint triangles has $\operatorname {\mathrm {poly}}(\varepsilon )\cdot n^{\lvert V(H)\rvert }$ copies of H. It is easy to see that a $K_3$-abundant graph must be triangle-free and tripartite. Given our first result, it is natural to ask if all triangle-free tripartite graphs are $K_3$-abundant. Our second result is that assuming a well-known conjecture of Ruzsa in additive number theory, the answer to this question is negative.

Our proofs use a mix of combinatorial, number-theoretic, probabilistic and Ramsey-type arguments.

For a given graph $H$, we say that a graph $G$ has a perfect $H$-subdivision tiling if $G$ contains a collection of vertex-disjoint subdivisions of $H$ covering all vertices of $G.$ Let $\delta _{\mathrm {sub}}(n, H)$ be the smallest integer $k$ such that any $n$-vertex graph $G$ with minimum degree at least $k$ has a perfect $H$-subdivision tiling. For every graph $H$, we asymptotically determined the value of $\delta _{\mathrm {sub}}(n, H)$. More precisely, for every graph $H$ with at least one edge, there is an integer $\mathrm {hcf}_{\xi }(H)$ and a constant $1 \lt \xi ^*(H)\leq 2$ that can be explicitly determined by structural properties of $H$ such that $\delta _{\mathrm {sub}}(n, H) = \left (1 - \frac {1}{\xi ^*(H)} + o(1) \right )n$ holds for all $n$ and $H$ unless $\mathrm {hcf}_{\xi }(H) = 2$ and $n$ is odd. When $\mathrm {hcf}_{\xi }(H) = 2$ and $n$ is odd, then we show that $\delta _{\mathrm {sub}}(n, H) = \left (\frac {1}{2} + o(1) \right )n$.

Let 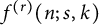$f^{(r)}(n;s,k)$ denote the maximum number of edges in an n-vertex r-uniform hypergraph containing no subgraph with k edges and at most s vertices. Brown, Erdős, and Sós [New directions in the theory of graphs (Proc. Third Ann Arbor Conf., Univ. Michigan 1971), pp. 53–63, Academic Press 1973] conjectured that the limit $\lim _{n\rightarrow \infty }n^{-2}f^{(3)}(n;k+2,k)$ exists for all k. The value of the limit was previously determined for 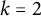$k=2$ in the original paper of Brown, Erdős, and Sós, for 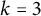$k=3$ by Glock [Bull. Lond. Math. Soc., 51 (2019) 230–236] and for $k=4$ by Glock, Joos, Kim, Kühn, Lichev, and Pikhurko [Proc. Amer. Math. Soc., Series B, 11 (2024) 173–186] while Delcourt and Postle [Proc. Amer. Math. Soc., 152 (2024), 1881–1891] proved the conjecture (without determining the limiting value).

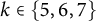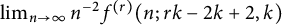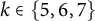In this article, we determine the value of the limit in the Brown–Erdős–Sós problem for $k\in \{5,6,7\}$. More generally, we obtain the value of $\lim _{n\rightarrow \infty }n^{-2}f^{(r)}(n;rk-2k+2,k)$ for all $r\geqslant 3$ and $k\in \{5,6,7\}$. In addition, by combining these new values with recent results of Bennett, Cushman, and Dudek [arxiv:2309.00182, 2023] we obtain new asymptotic values for several generalized Ramsey numbers.

A graph $G$ is $q$-Ramsey for another graph $H$ if in any $q$-edge-colouring of $G$ there is a monochromatic copy of $H$, and the classic Ramsey problem asks for the minimum number of vertices in such a graph. This was broadened in the seminal work of Burr, Erdős, and Lovász to the investigation of other extremal parameters of Ramsey graphs, including the minimum degree.

It is not hard to see that if $G$ is minimally $q$-Ramsey for $H$ we must have $\delta (G) \ge q(\delta (H) - 1) + 1$, and we say that a graph $H$ is $q$-Ramsey simple if this bound can be attained. Grinshpun showed that this is typical of rather sparse graphs, proving that the random graph $G(n,p)$ is almost surely $2$-Ramsey simple when $\frac{\log n}{n} \ll p \ll n^{-2/3}$. In this paper, we explore this question further, asking for which pairs $p = p(n)$ and $q = q(n,p)$ we can expect $G(n,p)$ to be $q$-Ramsey simple.

We first extend Grinshpun’s result by showing that $G(n,p)$ is not just $2$-Ramsey simple, but is in fact $q$-Ramsey simple for any $q = q(n)$, provided $p \ll n^{-1}$ or $\frac{\log n}{n} \ll p \ll n^{-2/3}$. Next, when $p \gg \left ( \frac{\log n}{n} \right )^{1/2}$, we find that $G(n,p)$ is not $q$-Ramsey simple for any $q \ge 2$. Finally, we uncover some interesting behaviour for intermediate edge probabilities. When $n^{-2/3} \ll p \ll n^{-1/2}$, we find that there is some finite threshold $\tilde{q} = \tilde{q}(H)$, depending on the structure of the instance $H \sim G(n,p)$ of the random graph, such that $H$ is $q$-Ramsey simple if and only if $q \le \tilde{q}$. Aside from a couple of logarithmic factors, this resolves the qualitative nature of the Ramsey simplicity of the random graph over the full spectrum of edge probabilities.

We investigate the set $T_{n}$ of the possible number of triangles in a graph on n vertices. The first main result says that every natural number less than $\binom {n}{3} - (\sqrt {2}+o(1) )n^{3/2} $ belongs to $T_{n}$. On the other hand, we show that there is a number $m = \binom {n}{3}-( \sqrt {2} +o(1))n^{3/2}$ that is not a member of $T_{n}$. In addition, we prove that there are two interlacing sequences $\binom {n}{3} - ( \sqrt {2} + o(1) )n^{3/2} = c_{1} \le d_{1} \le c_{2} \le d_{2} \le \cdots \le c_{s} \le d_{s} = \binom {n}{3}$ with $| c_{t} - d_{t}| = n-2-\binom {s - t +1}{2}$ such that $( c_{t}, d_{t} ) \cap T_{n} = \emptyset $ for all t. Moreover, we obtain a generalisation of these results for the set of the possible number of copies of a connected graph H in a graph on n vertices.

For given positive integers $r\ge 3$, $n$ and $e\le \binom{n}{2}$, the famous Erdős–Rademacher problem asks for the minimum number of $r$-cliques in a graph with $n$ vertices and $e$ edges. A conjecture of Lovász and Simonovits from the 1970s states that, for every $r\ge 3$, if $n$ is sufficiently large then, for every $e\le \binom{n}{2}$, at least one extremal graph can be obtained from a complete partite graph by adding a triangle-free graph into one part.

In this note, we explicitly write the minimum number of $r$-cliques predicted by the above conjecture. Also, we describe what we believe to be the set of extremal graphs for any $r\ge 4$ and all large $n$, amending the previous conjecture of Pikhurko and Razborov.

We investigate the list packing number of a graph, the least $k$ such that there are always $k$ disjoint proper list-colourings whenever we have lists all of size $k$ associated to the vertices. We are curious how the behaviour of the list packing number contrasts with that of the list chromatic number, particularly in the context of bounded degree graphs. The main question we pursue is whether every graph with maximum degree $\Delta$ has list packing number at most $\Delta +1$. Our results highlight the subtleties of list packing and the barriers to, for example, pursuing a Brooks’-type theorem for the list packing number.

We say that a graph H dominates another graph H′ if the number of homomorphisms from H′ to any graph G is dominated, in an appropriate sense, by the number of homomorphisms from H to G. We study the family of dominating graphs, those graphs with the property that they dominate all of their subgraphs. It has long been known that even-length paths are dominating in this sense and a result of Hatami implies that all weakly norming graphs are dominating. In a previous paper, we showed that every finite reflection group gives rise to a family of weakly norming, and hence dominating, graphs. Here we revisit this connection to show that there is a much broader class of dominating graphs.

We give a simple method to estimate the number of distinct copies of some classes of spanning subgraphs in hypergraphs with a high minimum degree. In particular, for each $k\geq 2$ and $1\leq \ell \leq k-1$, we show that every $k$-graph on $n$ vertices with minimum codegree at least

\begin{equation*} \left \{\begin {array}{l@{\quad}l} \left (\dfrac {1}{2}+o(1)\right )n & \text { if }(k-\ell )\mid k,\\[5pt] \left (\dfrac {1}{\lceil \frac {k}{k-\ell }\rceil (k-\ell )}+o(1)\right )n & \text { if }(k-\ell )\nmid k, \end {array} \right . \end{equation*}

$\exp\!(n\log n-\Theta (n))$

$\ell$

$(k-\ell )\mid n$

$(k-\ell )\mid k$

$(k-\ell )\nmid k$

$\ell \lt k/2$

Given a graph $F$, we consider the problem of determining the densest possible pseudorandom graph that contains no copy of $F$. We provide an embedding procedure that improves a general result of Conlon, Fox, and Zhao which gives an upper bound on the density. In particular, our result implies that optimally pseudorandom graphs with density greater than $n^{-1/3}$ must contain a copy of the Peterson graph, while the previous best result gives the bound $n^{-1/4}$. Moreover, we conjecture that the exponent $1/3$ in our bound is tight. We also construct the densest known pseudorandom $K_{2,3}$-free graphs that are also triangle-free. Finally, we give a different proof for the densest known construction of clique-free pseudorandom graphs due to Bishnoi, Ihringer, and Pepe that they have no large clique.

Many problems and conjectures in extremal combinatorics concern polynomial inequalities between homomorphism densities of graphs where we allow edges to have real weights. Using the theory of graph limits, we can equivalently evaluate polynomial expressions in homomorphism densities on kernels W, that is, symmetric, bounded and measurable functions W from $[0,1]^2 \to \mathbb {R}$. In 2011, Hatami and Norin proved a fundamental result that it is undecidable to determine the validity of polynomial inequalities in homomorphism densities for graphons (i.e., the case where the range of W is $[0,1]$, which corresponds to unweighted graphs or, equivalently, to graphs with edge weights between $0$ and $1$). The corresponding problem for more general sets of kernels, for example, for all kernels or for kernels with range $[-1,1]$, remains open. For any $a> 0$, we show undecidability of polynomial inequalities for any set of kernels which contains all kernels with range $\{0,a\}$. This result also answers a question raised by Lovász about finding computationally effective certificates for the validity of homomorphism density inequalities in kernels.

In 1964, Erdős proposed the problem of estimating the Turán number of the d-dimensional hypercube $Q_d$. Since $Q_d$ is a bipartite graph with maximum degree d, it follows from results of Füredi and Alon, Krivelevich, Sudakov that $\mathrm {ex}(n,Q_d)=O_d(n^{2-1/d})$. A recent general result of Sudakov and Tomon implies the slightly stronger bound $\mathrm {ex}(n,Q_d)=o(n^{2-1/d})$. We obtain the first power-improvement for this old problem by showing that $\mathrm {ex}(n,Q_d)=O_d\left (n^{2-\frac {1}{d-1}+\frac {1}{(d-1)2^{d-1}}}\right )$. This answers a question of Liu. Moreover, our techniques give a power improvement for a larger class of graphs than cubes.

We use a similar method to prove that any n-vertex, properly edge-coloured graph without a rainbow cycle has at most $O(n(\log n)^2)$ edges, improving the previous best bound of $n(\log n)^{2+o(1)}$ by Tomon. Furthermore, we show that any properly edge-coloured n-vertex graph with $\omega (n\log n)$ edges contains a cycle which is almost rainbow: that is, almost all edges in it have a unique colour. This latter result is tight.

Let G be a graph with m edges, minimum degree $\delta $ and containing no cycle of length 4. Answering a question of Bollobás and Scott, Fan et al. [‘Bisections of graphs without short cycles’, Combinatorics, Probability and Computing 27(1) (2018), 44–59] showed that if (i) G is $2$-connected, or (ii) $\delta \ge 3$, or (iii) $\delta \ge 2$ and the girth of G is at least 5, then G admits a bisection such that $\max \{e(V_1),e(V_2)\}\le (1/4+o(1))m$, where $e(V_i)$ denotes the number of edges of G with both ends in $V_i$. Let $s\ge 2$ be an integer. In this note, we prove that if $\delta \ge 2s-1$ and G contains no $K_{2,s}$ as a subgraph, then G admits a bisection such that $\max \{e(V_1),e(V_2)\}\le (1/4+o(1))m$.

We show that for every $\eta \gt 0$ every sufficiently large $n$-vertex oriented graph $D$ of minimum semidegree exceeding $(1+\eta )\frac k2$ contains every balanced antidirected tree with $k$ edges and bounded maximum degree, if $k\ge \eta n$. In particular, this asymptotically confirms a conjecture of the first author for long antidirected paths and dense digraphs.

Further, we show that in the same setting, $D$ contains every $k$-edge antidirected subdivision of a sufficiently small complete graph, if the paths of the subdivision that have length $1$ or $2$ span a forest. As a special case, we can find all antidirected cycles of length at most $k$.

Finally, we address a conjecture of Addario-Berry, Havet, Linhares Sales, Reed, and Thomassé for antidirected trees in digraphs. We show that this conjecture is asymptotically true in $n$-vertex oriented graphs for all balanced antidirected trees of bounded maximum degree and of size linear in $n$.

For a graph $H$ and a hypercube $Q_n$, $\textrm{ex}(Q_n, H)$ is the largest number of edges in an $H$-free subgraph of $Q_n$. If $\lim _{n \rightarrow \infty } \textrm{ex}(Q_n, H)/|E(Q_n)| \gt 0$, $H$ is said to have a positive Turán density in a hypercube or simply a positive Turán density; otherwise, it has zero Turán density. Determining $\textrm{ex}(Q_n, H)$ and even identifying whether $H$ has a positive or zero Turán density remains a widely open question for general $H$. By relating extremal numbers in a hypercube and certain corresponding hypergraphs, Conlon found a large class of graphs, ones having so-called partite representation, that have zero Turán density. He asked whether this gives a characterisation, that is, whether a graph has zero Turán density if and only if it has partite representation. Here, we show that, as suspected by Conlon, this is not the case. We give an example of a class of graphs which have no partite representation, but on the other hand, have zero Turán density. In addition, we show that any graph whose every block has partite representation has zero Turán density in a hypercube.

Let $\boldsymbol {k} := (k_1,\ldots ,k_s)$ be a sequence of natural numbers. For a graph G, let $F(G;\boldsymbol {k})$ denote the number of colourings of the edges of G with colours $1,\dots ,s$ such that, for every $c \in \{1,\dots ,s\}$, the edges of colour c contain no clique of order $k_c$. Write $F(n;\boldsymbol {k})$ to denote the maximum of $F(G;\boldsymbol {k})$ over all graphs G on n vertices. There are currently very few known exact (or asymptotic) results for this problem, posed by Erdős and Rothschild in 1974. We prove some new exact results for $n \to \infty $:

1. (i) A sufficient condition on $\boldsymbol {k}$ which guarantees that every extremal graph is a complete multipartite graph, which systematically recovers all existing exact results.

2. (ii) Addressing the original question of Erdős and Rothschild, in the case $\boldsymbol {k}=(3,\ldots ,3)$ of length $7$, the unique extremal graph is the complete balanced $8$-partite graph, with colourings coming from Hadamard matrices of order $8$.

3. (iii) In the case $\boldsymbol {k}=(k+1,k)$, for which the sufficient condition in (i) does not hold, for $3 \leq k \leq 10$, the unique extremal graph is complete k-partite with one part of size less than k and the other parts as equal in size as possible.

Given a fixed graph $H$ and a constant $c \in [0,1]$, we can ask what graphs $G$ with edge density $c$ asymptotically maximise the homomorphism density of $H$ in $G$. For all $H$ for which this problem has been solved, the maximum is always asymptotically attained on one of two kinds of graphs: the quasi-star or the quasi-clique. We show that for any $H$ the maximising $G$ is asymptotically a threshold graph, while the quasi-clique and the quasi-star are the simplest threshold graphs, having only two parts. This result gives us a unified framework to derive a number of results on graph homomorphism maximisation, some of which were also found quite recently and independently using several different approaches. We show that there exist graphs $H$ and densities $c$ such that the optimising graph $G$ is neither the quasi-star nor the quasi-clique (Day and Sarkar, SIAM J. Discrete Math. 35(1), 294–306, 2021). We also show that for $c$ large enough all graphs $H$ maximise on the quasi-clique (Gerbner et al., J. Graph Theory 96(1), 34–43, 2021), and for any $c \in [0,1]$ the density of $K_{1,2}$ is always maximised on either the quasi-star or the quasi-clique (Ahlswede and Katona, Acta Math. Hung. 32(1–2), 97–120, 1978). Finally, we extend our results to uniform hypergraphs.

The well-known Erdős-Hajnal conjecture states that for any graph $F$, there exists $\epsilon \gt 0$ such that every $n$-vertex graph $G$ that contains no induced copy of $F$ has a homogeneous set of size at least $n^{\epsilon }$. We consider a variant of the Erdős-Hajnal problem for hypergraphs where we forbid a family of hypergraphs described by their orders and sizes. For graphs, we observe that if we forbid induced subgraphs on $m$ vertices and $f$ edges for any positive $m$ and $0\leq f \leq \binom{m}{2}$, then we obtain large homogeneous sets. For triple systems, in the first nontrivial case $m=4$, for every $S \subseteq \{0,1,2,3,4\}$, we give bounds on the minimum size of a homogeneous set in a triple system where the number of edges spanned by every four vertices is not in $S$. In most cases the bounds are essentially tight. We also determine, for all $S$, whether the growth rate is polynomial or polylogarithmic. Some open problems remain.

We show that for any $\varepsilon \gt 0$ and $\Delta \in \mathbb{N}$, there exists $\alpha \gt 0$ such that for sufficiently large $n$, every $n$-vertex graph $G$ satisfying that $\delta (G)\geq \varepsilon n$ and $e(X, Y)\gt 0$ for every pair of disjoint vertex sets $X, Y\subseteq V(G)$ of size $\alpha n$ contains all spanning trees with maximum degree at most $\Delta$. This strengthens a result of Böttcher, Han, Kohayakawa, Montgomery, Parczyk, and Person.

We show that for every $n\in \mathbb N$ and $\log n\le d\lt n$, if a graph $G$ has $N=\Theta (dn)$ vertices and minimum degree $(1+o(1))\frac{N}{2}$, then it contains a spanning subdivision of every $n$-vertex $d$-regular graph.