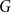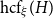1. Introduction
Embedding a large sparse subgraph into a dense graph is one of the most central problems in extremal graph theory. It is well known that any graph
![]() $G$
with a minimum degree of at least
$G$
with a minimum degree of at least
![]() $\lceil \frac {v(G)}{2} \rceil$
has a Hamiltonian cycle, and hence also a perfect matching if the number of vertices
$\lceil \frac {v(G)}{2} \rceil$
has a Hamiltonian cycle, and hence also a perfect matching if the number of vertices
![]() $v(G)$
of
$v(G)$
of
![]() $G$
is even. A perfect matching of a graph
$G$
is even. A perfect matching of a graph
![]() $G$
is a vertex-disjoint collection of edges whose union covers all vertices of
$G$
is a vertex-disjoint collection of edges whose union covers all vertices of
![]() $G$
. A natural generalisation of a perfect matching is a perfect
$G$
. A natural generalisation of a perfect matching is a perfect
![]() $H$
-tiling for a general graph
$H$
-tiling for a general graph
![]() $H$
. We say
$H$
. We say
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-tiling if
$H$
-tiling if
![]() $G$
contains a collection of vertex-disjoint copies of
$G$
contains a collection of vertex-disjoint copies of
![]() $H$
whose union covers all vertices of
$H$
whose union covers all vertices of
![]() $G$
. We note that a perfect
$G$
. We note that a perfect
![]() $H$
-tiling exists only if
$H$
-tiling exists only if
![]() $v(G)$
is divisible by
$v(G)$
is divisible by
![]() $v(H)$
. For a positive integer
$v(H)$
. For a positive integer
![]() $n$
divisible by
$n$
divisible by
![]() $v(H)$
, we denote by
$v(H)$
, we denote by
![]() $\delta (n, H)$
the minimum integer
$\delta (n, H)$
the minimum integer
![]() $k$
such that any
$k$
such that any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with a minimum degree of at least
$G$
with a minimum degree of at least
![]() $k$
has a perfect
$k$
has a perfect
![]() $H$
-tiling. The celebrated Hajnal–Szemerédi [Reference Hajnal and Szemerédi11] theorem states that for any integer
$H$
-tiling. The celebrated Hajnal–Szemerédi [Reference Hajnal and Szemerédi11] theorem states that for any integer
![]() $r \geq 2$
, the number
$r \geq 2$
, the number
![]() $\delta (n, K_r)$
is equal to
$\delta (n, K_r)$
is equal to
![]() $\left (1 - \frac {1}{r}\right )n$
.
$\left (1 - \frac {1}{r}\right )n$
.
An asymptotic version of the Hajnal–Szemerédi theorem for a general graph
![]() $H$
was first proven by Alon and Yuster [Reference Alon and Yuster2]. They showed that if
$H$
was first proven by Alon and Yuster [Reference Alon and Yuster2]. They showed that if
![]() $n$
is divisible by
$n$
is divisible by
![]() $v(H)$
, then
$v(H)$
, then
![]() $\delta (n, H) \leq \left ( 1 - \frac {1}{\chi (H)}\right )n + o(n)$
, where
$\delta (n, H) \leq \left ( 1 - \frac {1}{\chi (H)}\right )n + o(n)$
, where
![]() $\chi (H)$
is the chromatic number of
$\chi (H)$
is the chromatic number of
![]() $H$
. Komlós, Sárkőzy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi18] improved the
$H$
. Komlós, Sárkőzy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi18] improved the
![]() $o(n)$
term in the Alon–Yuster theorem to some constant
$o(n)$
term in the Alon–Yuster theorem to some constant
![]() $C = C(H)$
, which settled the conjecture of Alon and Yuster [Reference Alon and Yuster2]. Another direction for an asymptotic extension of the Hajnal–Szemerédi theorem was proven by Komlós [Reference Komlós17]. Komlós showed that for any
$C = C(H)$
, which settled the conjecture of Alon and Yuster [Reference Alon and Yuster2]. Another direction for an asymptotic extension of the Hajnal–Szemerédi theorem was proven by Komlós [Reference Komlós17]. Komlós showed that for any
![]() $\gamma \gt 0$
, there exists
$\gamma \gt 0$
, there exists
![]() $n_0 = n_0(\gamma , H)$
such that if
$n_0 = n_0(\gamma , H)$
such that if
![]() $n \geq n_0$
, then any
$n \geq n_0$
, then any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
whose minimum degree is at least
$G$
whose minimum degree is at least
![]() $\left (1 - \frac {1}{\chi _{cr}(H)} \right )n$
contains an
$\left (1 - \frac {1}{\chi _{cr}(H)} \right )n$
contains an
![]() $H$
-tiling that covers at least
$H$
-tiling that covers at least
![]() $(1 - \gamma )n$
vertices of
$(1 - \gamma )n$
vertices of
![]() $G$
. Here,
$G$
. Here,
![]() $\chi _{cr}(H)$
denotes the critical chromatic number of
$\chi _{cr}(H)$
denotes the critical chromatic number of
![]() $H$
, which is defined as
$H$
, which is defined as
![]() $\chi _{cr}(H) = \frac {(\chi (H) - 1)v(H)}{v(H) - \sigma (H)}$
, where
$\chi _{cr}(H) = \frac {(\chi (H) - 1)v(H)}{v(H) - \sigma (H)}$
, where
![]() $\sigma (H)$
is the minimum possible size of a colour class among all colourings of
$\sigma (H)$
is the minimum possible size of a colour class among all colourings of
![]() $H$
with
$H$
with
![]() $\chi (H)$
colours. Komlós [Reference Komlós17] conjectured that the number of uncovered vertices can be reduced to a constant, and this conjecture was confirmed by Shokoufandeh and Zhao [Reference Shokoufandeh and Zhao29]. More precisely, the following holds.
$\chi (H)$
colours. Komlós [Reference Komlós17] conjectured that the number of uncovered vertices can be reduced to a constant, and this conjecture was confirmed by Shokoufandeh and Zhao [Reference Shokoufandeh and Zhao29]. More precisely, the following holds.
Theorem 1.1 (Shokoufandeh and Zhao [Reference Shokoufandeh and Zhao29]). Let
![]() $H$
be a graph. Then there exists a constant
$H$
be a graph. Then there exists a constant
![]() $C = C(H)$
, which only depends on
$C = C(H)$
, which only depends on
![]() $H$
, such that any graph
$H$
, such that any graph
![]() $G$
on
$G$
on
![]() $n$
vertices with a minimum degree of at least
$n$
vertices with a minimum degree of at least
![]() $\left (1 - \frac {1}{\chi _{cr}(H)} \right )n$
contains an
$\left (1 - \frac {1}{\chi _{cr}(H)} \right )n$
contains an
![]() $H$
-tiling that covers all but at most
$H$
-tiling that covers all but at most
![]() $C$
vertices of
$C$
vertices of
![]() $G$
.
$G$
.
The almost exact value of
![]() $\delta (n, H)$
for every graph
$\delta (n, H)$
for every graph
![]() $H$
was determined by Kühn and Osthus [Reference Kühn and Osthus23] up to an additive constant depending only on
$H$
was determined by Kühn and Osthus [Reference Kühn and Osthus23] up to an additive constant depending only on
![]() $H$
. To formulate this theorem, we need to define some notations. We say a proper colouring of
$H$
. To formulate this theorem, we need to define some notations. We say a proper colouring of
![]() $H$
is optimal if it uses exactly
$H$
is optimal if it uses exactly
![]() $\chi (H)$
colours. We denote by
$\chi (H)$
colours. We denote by
![]() $\Phi (H)$
the set of all optimal colourings of
$\Phi (H)$
the set of all optimal colourings of
![]() $H$
. Let
$H$
. Let
![]() $\phi \in \Phi (H)$
be an optimal colouring of
$\phi \in \Phi (H)$
be an optimal colouring of
![]() $H$
with the size of colour classes being
$H$
with the size of colour classes being
![]() $x_1 \leq \ldots \leq x_{\chi (H)}$
. Let
$x_1 \leq \ldots \leq x_{\chi (H)}$
. Let
![]() $\mathcal {D}(\phi ) \,:\!=\, \{x_{i+1} - x_i\,:\,i\in [\chi (H)-1]\}$
and
$\mathcal {D}(\phi ) \,:\!=\, \{x_{i+1} - x_i\,:\,i\in [\chi (H)-1]\}$
and
![]() $\mathcal {D}(H) \,:\!=\, \bigcup _{\phi \in \Phi (H)} \mathcal {D}(\phi )$
. We write
$\mathcal {D}(H) \,:\!=\, \bigcup _{\phi \in \Phi (H)} \mathcal {D}(\phi )$
. We write
![]() $\mathrm {hcf}_{\chi }(H)$
for the highest common factor of all integers in
$\mathrm {hcf}_{\chi }(H)$
for the highest common factor of all integers in
![]() $\mathcal {D}(H)$
. (If
$\mathcal {D}(H)$
. (If
![]() $\mathcal {D}(H) = \{0\}$
, we define
$\mathcal {D}(H) = \{0\}$
, we define
![]() $\mathrm {hcf}_{\chi }(H) = \infty .$
) We denote by
$\mathrm {hcf}_{\chi }(H) = \infty .$
) We denote by
![]() $\mathrm {hcf}_{c}(H)$
the highest common factor of all the orders of components in
$\mathrm {hcf}_{c}(H)$
the highest common factor of all the orders of components in
![]() $H$
. For a graph
$H$
. For a graph
![]() $H$
, we define
$H$
, we define
 \begin{align*} \mathrm {hcf}(H) \,:\!=\, \begin{cases} 1 & \text {if } \chi (H) \geq 3 \text { and } \mathrm {hcf}_{\chi }(H) = 1,\\[3pt] 1 & \text {if } \chi (H) = 2, \text { } \mathrm {hcf}_{\chi }(H) \leq 2, \text { and } \mathrm {hcf}_{c}(H) = 1, \\[3pt] 0 & \text {otherwise.} \end{cases} \end{align*}
\begin{align*} \mathrm {hcf}(H) \,:\!=\, \begin{cases} 1 & \text {if } \chi (H) \geq 3 \text { and } \mathrm {hcf}_{\chi }(H) = 1,\\[3pt] 1 & \text {if } \chi (H) = 2, \text { } \mathrm {hcf}_{\chi }(H) \leq 2, \text { and } \mathrm {hcf}_{c}(H) = 1, \\[3pt] 0 & \text {otherwise.} \end{cases} \end{align*}
We define
![]() $\chi ^*(H) = \chi _{cr}(H)$
if
$\chi ^*(H) = \chi _{cr}(H)$
if
![]() $\mathrm {hcf}(H) = 1$
; otherwise,
$\mathrm {hcf}(H) = 1$
; otherwise,
![]() $\chi ^*(H) = \chi (H).$
We are now ready to state the Kühn–Osthus theorem.
$\chi ^*(H) = \chi (H).$
We are now ready to state the Kühn–Osthus theorem.
Theorem 1.2 (Kühn and Osthus [Reference Kühn and Osthus23]). Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $n$
be a positive integer divisible by
$n$
be a positive integer divisible by
![]() $v(H).$
Then there exists a constant
$v(H).$
Then there exists a constant
![]() $C = C(H)$
depending only on
$C = C(H)$
depending only on
![]() $H$
such that
$H$
such that
1.1. Main results
Motivated by the Kühn–Osthus theorem on perfect
![]() $H$
-tilings, several variations of Theorem1.2 have been considered. (For instance, see [Reference Balogh, Li and Treglown5, Reference Freschi and Treglown10, Reference Han, Morris and Treglown12–Reference Hyde, Liu and Treglown14, Reference Kühn and Osthus22, Reference Lo and Markström25]).
$H$
-tilings, several variations of Theorem1.2 have been considered. (For instance, see [Reference Balogh, Li and Treglown5, Reference Freschi and Treglown10, Reference Han, Morris and Treglown12–Reference Hyde, Liu and Treglown14, Reference Kühn and Osthus22, Reference Lo and Markström25]).
In this article, we consider a problem related to the concept of perfect
![]() $H$
-tilings and subdivision embeddings. A graph
$H$
-tilings and subdivision embeddings. A graph
![]() $H^{\prime}$
is a subdivision of
$H^{\prime}$
is a subdivision of
![]() $H$
if
$H$
if
![]() $H^{\prime}$
is obtained from
$H^{\prime}$
is obtained from
![]() $H$
by replacing edges of
$H$
by replacing edges of
![]() $H$
with vertex-disjoint paths while maintaining their endpoints. Since subdivisions maintain the topological structure of the original graph, various problems related to subdivisions have been posed and extensively studied. In particular, finding a sufficient condition on the host graph to contain a subdivision of
$H$
with vertex-disjoint paths while maintaining their endpoints. Since subdivisions maintain the topological structure of the original graph, various problems related to subdivisions have been posed and extensively studied. In particular, finding a sufficient condition on the host graph to contain a subdivision of
![]() $H$
is an important problem in extremal graph theory.
$H$
is an important problem in extremal graph theory.
Let
![]() $H$
and
$H$
and
![]() $G$
be graphs. An
$G$
be graphs. An
![]() $H$
-subdivision tiling is a collection of vertex-disjoint unions of subdivisions of
$H$
-subdivision tiling is a collection of vertex-disjoint unions of subdivisions of
![]() $H$
. We say that
$H$
. We say that
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-subdivision tiling if
$H$
-subdivision tiling if
![]() $G$
has an
$G$
has an
![]() $H$
-subdivision tiling that covers all vertices of
$H$
-subdivision tiling that covers all vertices of
![]() $G$
. A natural question would be to determine the minimum degree threshold for a positive integer
$G$
. A natural question would be to determine the minimum degree threshold for a positive integer
![]() $n$
that ensures the existence of a perfect
$n$
that ensures the existence of a perfect
![]() $H$
-subdivision tiling in any
$H$
-subdivision tiling in any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
. We define this minimum degree threshold as follows.
$G$
. We define this minimum degree threshold as follows.
Definition 1.3.
Let
![]() $H$
be a graph. We denote the minimum degree threshold for perfect
$H$
be a graph. We denote the minimum degree threshold for perfect
![]() $H$
-subdivision tilings by
$H$
-subdivision tilings by
![]() $\delta _{\mathrm {sub}}(n, H)$
, which is the smallest integer
$\delta _{\mathrm {sub}}(n, H)$
, which is the smallest integer
![]() $k$
such that any
$k$
such that any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with a minimum degree of at least
$G$
with a minimum degree of at least
![]() $k$
has a perfect
$k$
has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
If
![]() $H$
has no edges, then a perfect
$H$
has no edges, then a perfect
![]() $H$
-subdivision tiling exists if and only if
$H$
-subdivision tiling exists if and only if
![]() $v(G)$
is divisible by
$v(G)$
is divisible by
![]() $v(H)$
, regardless of the minimum degree
$v(H)$
, regardless of the minimum degree
![]() $\delta (G)$
of
$\delta (G)$
of
![]() $G$
. Thus, from now on, we only consider graphs with at least one edge.
$G$
. Thus, from now on, we only consider graphs with at least one edge.
For most results on embedding large graphs, including perfect
![]() $H$
-tilings and large subdivisions, embedding a graph with more complex structures requires a larger minimum degree threshold. Surprisingly, we observe the opposite phenomenon for perfect subdivision tiling problems. For example, Theorem1.8 states that
$H$
-tilings and large subdivisions, embedding a graph with more complex structures requires a larger minimum degree threshold. Surprisingly, we observe the opposite phenomenon for perfect subdivision tiling problems. For example, Theorem1.8 states that
![]() $\delta _{\mathrm {sub}}(n, K_r)$
decreases as
$\delta _{\mathrm {sub}}(n, K_r)$
decreases as
![]() $r$
increases when
$r$
increases when
![]() $3 \leq r \leq 5$
. This is due to the fact that a larger value of
$3 \leq r \leq 5$
. This is due to the fact that a larger value of
![]() $r$
ensures that
$r$
ensures that
![]() $K_r$
has a bipartite subdivision with a more asymmetric bipartition.
$K_r$
has a bipartite subdivision with a more asymmetric bipartition.
Since embedding bipartite graphs generally requires a lower minimum degree than non-bipartite graphs, we want to cover most of the vertices of the host graph with subdivisions of
![]() $H$
that are bipartite. Suppose every bipartite subdivision of
$H$
that are bipartite. Suppose every bipartite subdivision of
![]() $H$
is, in some sense, balanced. In that case, it cannot be tiled in a highly unbalanced complete bipartite graph that has a lower minimum degree than a balanced complete bipartite graph. For this reason, we need to measure how unbalanced bipartite subdivisions of
$H$
is, in some sense, balanced. In that case, it cannot be tiled in a highly unbalanced complete bipartite graph that has a lower minimum degree than a balanced complete bipartite graph. For this reason, we need to measure how unbalanced bipartite subdivisions of
![]() $H$
can be, as it poses some space barriers to the problem.
$H$
can be, as it poses some space barriers to the problem.
For this purpose, we introduce the following two definitions.
Definition 1.4.
Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $X \subseteq V(H).$
We define a function
$X \subseteq V(H).$
We define a function
![]() $f_H\,:\, 2^{V(H)} \to \mathbb {R}$
as
$f_H\,:\, 2^{V(H)} \to \mathbb {R}$
as
![]() $f_H(X) = \frac {v(H) + e(H[X]) + e(H[Y])}{|X| + e(H[Y])}$
where
$f_H(X) = \frac {v(H) + e(H[X]) + e(H[Y])}{|X| + e(H[Y])}$
where
![]() $Y = V(H) \setminus X.$
$Y = V(H) \setminus X.$
Definition 1.5.
Let
![]() $H$
be a graph. We define
$H$
be a graph. We define
![]() $\xi (H) \,:\!=\, \min \{f_H(X) \,:\, X \subseteq V(H)\}.$
$\xi (H) \,:\!=\, \min \{f_H(X) \,:\, X \subseteq V(H)\}.$
Note that subdividing all edges in
![]() $H[X]$
and
$H[X]$
and
![]() $H[Y]$
yields a bipartite subdivision
$H[Y]$
yields a bipartite subdivision
![]() $H^{\prime}$
of
$H^{\prime}$
of
![]() $H$
, and
$H$
, and
![]() $f_H(X)$
measures the ratio between
$f_H(X)$
measures the ratio between
![]() $V(H^{\prime})$
and one part of its bipartition. The smaller the value of
$V(H^{\prime})$
and one part of its bipartition. The smaller the value of
![]() $f_H$
, the more unbalanced
$f_H$
, the more unbalanced
![]() $H^{\prime}$
is. Later in Observation3.2, we will prove that
$H^{\prime}$
is. Later in Observation3.2, we will prove that
![]() $\xi (H)$
can be used to measure the ratio between the two parts in the most asymmetric bipartite subdivision of
$\xi (H)$
can be used to measure the ratio between the two parts in the most asymmetric bipartite subdivision of
![]() $H$
. Note that we always have
$H$
. Note that we always have
![]() $1 \lt \xi (H) \leq 2$
. Indeed,
$1 \lt \xi (H) \leq 2$
. Indeed,
and for any partition
![]() $X, Y$
of
$X, Y$
of
![]() $V(G)$
, we have
$V(G)$
, we have
so,
![]() $\min \{f_H(X), f_H(Y)\} \leq 2$
.
$\min \{f_H(X), f_H(Y)\} \leq 2$
.
Another crucial factor is the divisibility issue. Assume that all bipartite subdivisions of
![]() $H$
have bipartitions with both parts having the same parity. If
$H$
have bipartitions with both parts having the same parity. If
![]() $G$
is a complete bipartite graph
$G$
is a complete bipartite graph
![]() $K_{a, b}$
with
$K_{a, b}$
with
![]() $a$
and
$a$
and
![]() $b$
having different parity, then we cannot find perfect
$b$
having different parity, then we cannot find perfect
![]() $H$
-subdivision tilings in
$H$
-subdivision tilings in
![]() $G$
, as it poses some divisibility barriers to the problem. Hence, we need to introduce the following definitions concerning the difference between the two parts in bipartitions of subdivisions of
$G$
, as it poses some divisibility barriers to the problem. Hence, we need to introduce the following definitions concerning the difference between the two parts in bipartitions of subdivisions of
![]() $H$
and their highest common factor.
$H$
and their highest common factor.
Definition 1.6.
Let
![]() $H$
be a graph. We define
$H$
be a graph. We define
![]() $\mathcal {C}(H) \,:\!=\, \{(|X| + e(H[Y])) - (|Y| + e(H[X])) \,:\, X \subseteq V(H), Y = V(H) \setminus X\}$
. We denote by
$\mathcal {C}(H) \,:\!=\, \{(|X| + e(H[Y])) - (|Y| + e(H[X])) \,:\, X \subseteq V(H), Y = V(H) \setminus X\}$
. We denote by
![]() $\mathrm {hcf}_{\xi }(H)$
the highest common factor of all integers in
$\mathrm {hcf}_{\xi }(H)$
the highest common factor of all integers in
![]() $\mathcal {C}(H)$
. (If
$\mathcal {C}(H)$
. (If
![]() $\mathcal {C}(H) = \{0\}$
, we define
$\mathcal {C}(H) = \{0\}$
, we define
![]() $\mathrm {hcf}_{\xi }(H) = \infty .$
)
$\mathrm {hcf}_{\xi }(H) = \infty .$
)
By considering the space barrier and the divisibility barrier, we introduce the following parameter measuring both obstacles for the problem. We will show that this is the determining factor for
![]() $\delta _{\mathrm {sub}}(n, H)$
.
$\delta _{\mathrm {sub}}(n, H)$
.
Definition 1.7.
Let
![]() $H$
be a graph. We define
$H$
be a graph. We define
 \begin{align*} \xi ^*(H) \,:\!=\, \begin{cases} \xi (H) &\text {if } \mathrm {hcf}_{\xi }(H) = 1,\\[3pt] \max \left \{\frac {3}{2}, \xi (H)\right \} &\text {if } \mathrm {hcf}_{\xi }(H) = 2,\\[3pt] 2 &\text {otherwise.} \end{cases} \end{align*}
\begin{align*} \xi ^*(H) \,:\!=\, \begin{cases} \xi (H) &\text {if } \mathrm {hcf}_{\xi }(H) = 1,\\[3pt] \max \left \{\frac {3}{2}, \xi (H)\right \} &\text {if } \mathrm {hcf}_{\xi }(H) = 2,\\[3pt] 2 &\text {otherwise.} \end{cases} \end{align*}
We are now ready to state our main theorems. The following theorem gives the asymptotically exact value for
![]() $\delta _{\mathrm {sub}}(n, H)$
except in one case, when
$\delta _{\mathrm {sub}}(n, H)$
except in one case, when
![]() $\mathrm {hcf}_{\xi }(H) = 2$
.
$\mathrm {hcf}_{\xi }(H) = 2$
.
Theorem 1.8.
Let
![]() $H$
be a graph with
$H$
be a graph with
![]() $\mathrm {hcf}_{\xi }(H) \neq 2$
. For every
$\mathrm {hcf}_{\xi }(H) \neq 2$
. For every
![]() $\gamma \gt 0$
, there exists an integer
$\gamma \gt 0$
, there exists an integer
![]() $n_0 = n_0(\gamma , H)$
such that for any
$n_0 = n_0(\gamma , H)$
such that for any
![]() $n \geq n_0$
, the following holds.
$n \geq n_0$
, the following holds.
This theorem asymptotically determines
![]() $\delta _{\mathrm {sub}}(n, H)$
as long as
$\delta _{\mathrm {sub}}(n, H)$
as long as
![]() $\mathrm {hcf}_{\xi }(H) \neq 2$
. If
$\mathrm {hcf}_{\xi }(H) \neq 2$
. If
![]() $\mathrm {hcf}_{\xi }(H) = 2$
, then the parity of
$\mathrm {hcf}_{\xi }(H) = 2$
, then the parity of
![]() $n$
is also important. The following theorem asymptotically determines
$n$
is also important. The following theorem asymptotically determines
![]() $\delta _{\mathrm {sub}}(n, H)$
for this case.
$\delta _{\mathrm {sub}}(n, H)$
for this case.
Theorem 1.9.
Let
![]() $H$
be a graph with
$H$
be a graph with
![]() $\mathrm {hcf}_{\xi }(H) = 2$
. For every
$\mathrm {hcf}_{\xi }(H) = 2$
. For every
![]() $\gamma \gt 0$
, there exists an integer
$\gamma \gt 0$
, there exists an integer
![]() $n_0 = n_0(\gamma , H)$
such that the following holds. For every integer
$n_0 = n_0(\gamma , H)$
such that the following holds. For every integer
![]() $n \geq n_0$
,
$n \geq n_0$
,
 $$\begin{align*} \frac {1}{2}n - 1 &\leq \delta _{\mathrm {sub}}(n, H) \leq \left (\frac {1}{2} + \gamma \right )n &&\textit {if } n \textit { is odd,}\\[3pt] \left (1 - \frac {1}{\xi ^*(H)} \right )n - 1 &\leq \delta _{\mathrm {sub}}(n, H) \leq \left (1 - \frac {1}{\xi ^*(H)} + \gamma \right )n &&\textit {if } n \textit { is even.} \end{align*}$$
$$\begin{align*} \frac {1}{2}n - 1 &\leq \delta _{\mathrm {sub}}(n, H) \leq \left (\frac {1}{2} + \gamma \right )n &&\textit {if } n \textit { is odd,}\\[3pt] \left (1 - \frac {1}{\xi ^*(H)} \right )n - 1 &\leq \delta _{\mathrm {sub}}(n, H) \leq \left (1 - \frac {1}{\xi ^*(H)} + \gamma \right )n &&\textit {if } n \textit { is even.} \end{align*}$$
As a direct consequence of Theorems1.8 and 1.9, we determine the value of
![]() $\delta _{\mathrm {sub}}(n, K_r)$
for each
$\delta _{\mathrm {sub}}(n, K_r)$
for each
![]() $r \geq 2.$
By applying our main theorems directly, we have
$r \geq 2.$
By applying our main theorems directly, we have
![]() $\delta _{\mathrm {sub}}(n, K_2) = \left (\frac {1}{3} + o(1) \right )n$
, and for each
$\delta _{\mathrm {sub}}(n, K_2) = \left (\frac {1}{3} + o(1) \right )n$
, and for each
![]() $r \in \{3, 4, 5\}$
, we have
$r \in \{3, 4, 5\}$
, we have
![]() $\delta _{\mathrm {sub}}(n, K_r) = \left (\frac {2}{r+1} + o(1) \right )n$
. For the case
$\delta _{\mathrm {sub}}(n, K_r) = \left (\frac {2}{r+1} + o(1) \right )n$
. For the case
![]() $r = 7$
, if
$r = 7$
, if
![]() $n$
is even, we have
$n$
is even, we have
![]() $\delta _{\mathrm {sub}}(n, K_7) = \left (\frac {1}{3} + o(1) \right )n$
; otherwise, we have
$\delta _{\mathrm {sub}}(n, K_7) = \left (\frac {1}{3} + o(1) \right )n$
; otherwise, we have
![]() $\delta _{\mathrm {sub}}(n, K_7) = \left (\frac {1}{2} + o(1) \right )n$
. Finally, for every
$\delta _{\mathrm {sub}}(n, K_7) = \left (\frac {1}{2} + o(1) \right )n$
. Finally, for every
![]() $r \geq 8$
and
$r \geq 8$
and
![]() $r = 6$
, we have
$r = 6$
, we have
![]() $\delta _{\mathrm {sub}}(n, K_r) = \left (\frac {1}{2} + o(1) \right )n$
. This is in contrast to the normal
$\delta _{\mathrm {sub}}(n, K_r) = \left (\frac {1}{2} + o(1) \right )n$
. This is in contrast to the normal
![]() $H$
-tiling problem.
$H$
-tiling problem.
This means the determining factors for the minimum degree thresholds of perfect
![]() $H$
-tilings and perfect
$H$
-tilings and perfect
![]() $H$
-subdivision tilings are essentially different. Probably, the most interesting difference between the perfect
$H$
-subdivision tilings are essentially different. Probably, the most interesting difference between the perfect
![]() $H$
-tiling and the perfect
$H$
-tiling and the perfect
![]() $H$
-subdivision tiling is that monotonicity does not hold for subdivision tiling. For a perfect tiling, if
$H$
-subdivision tiling is that monotonicity does not hold for subdivision tiling. For a perfect tiling, if
![]() $H_2$
is a spanning subgraph of
$H_2$
is a spanning subgraph of
![]() $H_1$
, then obviously
$H_1$
, then obviously
![]() $\delta (n, H_2) \leq \delta (n, H_1).$
However, for perfect subdivision tiling, this does not hold in many cases. For example, our results imply
$\delta (n, H_2) \leq \delta (n, H_1).$
However, for perfect subdivision tiling, this does not hold in many cases. For example, our results imply
![]() $\delta _{\mathrm {sub}}(n, K_4) = \frac {2}{5}n + o(n) \lt \delta _{\mathrm {sub}}(n, C_4) = \frac {1}{2}n + o(n).$
$\delta _{\mathrm {sub}}(n, K_4) = \frac {2}{5}n + o(n) \lt \delta _{\mathrm {sub}}(n, C_4) = \frac {1}{2}n + o(n).$
As
![]() $\xi ^*(H)$
is the determining factor for the minimum degree threshold, it is convenient for us to specify the bipartite subdivision achieving the value
$\xi ^*(H)$
is the determining factor for the minimum degree threshold, it is convenient for us to specify the bipartite subdivision achieving the value
![]() $\xi ^*(H).$
We introduce the following definition.
$\xi ^*(H).$
We introduce the following definition.
Definition 1.10.
Let
![]() $H$
be a graph. We denote by
$H$
be a graph. We denote by
![]() $X_H$
the subset of
$X_H$
the subset of
![]() $V(H)$
, where
$V(H)$
, where
![]() $f_H(X_H) = \xi (H).$
We define a graph
$f_H(X_H) = \xi (H).$
We define a graph
![]() $H^*$
obtained from
$H^*$
obtained from
![]() $H$
by replacing all edges in
$H$
by replacing all edges in
![]() $H[X_H]$
and
$H[X_H]$
and
![]() $H[V(H) \setminus X_H]$
with paths of length two.
$H[V(H) \setminus X_H]$
with paths of length two.
There can be multiple choices for
![]() $X_H$
. Then we fix one choice for
$X_H$
. Then we fix one choice for
![]() $X_H$
so that
$X_H$
so that
![]() $X_H$
and
$X_H$
and
![]() $H^*$
are uniquely determined for all
$H^*$
are uniquely determined for all
![]() $H$
. Note that
$H$
. Note that
![]() $H^*$
is a subdivision of
$H^*$
is a subdivision of
![]() $H$
, which is a bipartite graph, and
$H$
, which is a bipartite graph, and
![]() $v(H^*) = v(H) + e(H[X_H]) + e(H[V(H) \setminus X_H])$
. Intuitively,
$v(H^*) = v(H) + e(H[X_H]) + e(H[V(H) \setminus X_H])$
. Intuitively,
![]() $\xi (H)$
seems greater than
$\xi (H)$
seems greater than
![]() $\chi _{cr}(H^*)$
. Indeed, this intuition is correct. However, Theorem1.8 cannot be directly deduced by applying Theorem1.2 for
$\chi _{cr}(H^*)$
. Indeed, this intuition is correct. However, Theorem1.8 cannot be directly deduced by applying Theorem1.2 for
![]() $H^*$
. For example, for a connected graph
$H^*$
. For example, for a connected graph
![]() $H$
, it may satisfy
$H$
, it may satisfy
![]() $\chi ^*(H^*) = 2$
, but
$\chi ^*(H^*) = 2$
, but
![]() $\xi ^*(H) \lt 2$
is possible. Then the minimum degree threshold in Theorem1.8 is smaller than the one in Theorem1.2 when
$\xi ^*(H) \lt 2$
is possible. Then the minimum degree threshold in Theorem1.8 is smaller than the one in Theorem1.2 when
![]() $\mathrm {hcf}_{\xi }(H) = 1$
.
$\mathrm {hcf}_{\xi }(H) = 1$
.
However, as we will see in Observation3.6, for every graph
![]() $H$
with at least one edge, the inequality
$H$
with at least one edge, the inequality
![]() $\xi (H) \geq \chi _{cr}(H^*)$
holds. Hence, if
$\xi (H) \geq \chi _{cr}(H^*)$
holds. Hence, if
![]() $\mathrm {hcf}_{\xi }(H) \leq 2$
, we may instead use Theorem1.1 to find an
$\mathrm {hcf}_{\xi }(H) \leq 2$
, we may instead use Theorem1.1 to find an
![]() $H^*$
-tiling that covers all but at most a constant number of vertices of
$H^*$
-tiling that covers all but at most a constant number of vertices of
![]() $G$
in a graph
$G$
in a graph
![]() $G$
with
$G$
with
![]() $\delta (G) \geq \left (1 - \frac {1}{\xi (H)} + \gamma \right )n$
. To cover the leftover vertices, we use the absorption method. The absorption method was introduced in [Reference Rödl, Ruciński and Szemerédi27], and since then, it has been used to solve various crucial problems in extremal combinatorics. The main difficulty in applying the absorption method in our setting is that, in many cases, the host graph is not sufficiently dense to guarantee that any vertices can be absorbed in the final step. To overcome this difficulty, we use the regularity lemma and an extremal result on the domination number to obtain some control over the vertices that can be absorbed.
$\delta (G) \geq \left (1 - \frac {1}{\xi (H)} + \gamma \right )n$
. To cover the leftover vertices, we use the absorption method. The absorption method was introduced in [Reference Rödl, Ruciński and Szemerédi27], and since then, it has been used to solve various crucial problems in extremal combinatorics. The main difficulty in applying the absorption method in our setting is that, in many cases, the host graph is not sufficiently dense to guarantee that any vertices can be absorbed in the final step. To overcome this difficulty, we use the regularity lemma and an extremal result on the domination number to obtain some control over the vertices that can be absorbed.
2. Preliminaries
We write
![]() $[n] = \{1, \ldots , n\}$
for a positive integer
$[n] = \{1, \ldots , n\}$
for a positive integer
![]() $n$
. If we claim a result holds if
$n$
. If we claim a result holds if
![]() $\beta \ll \alpha _1, \ldots , \alpha _t$
, then it means there exists a function
$\beta \ll \alpha _1, \ldots , \alpha _t$
, then it means there exists a function
![]() $f$
such that
$f$
such that
![]() $\beta \leq f(\alpha _1, \ldots , \alpha _t)$
. We will not explicitly compute these functions. In this paper, we consider
$\beta \leq f(\alpha _1, \ldots , \alpha _t)$
. We will not explicitly compute these functions. In this paper, we consider
![]() $o(1)$
to go to zero as
$o(1)$
to go to zero as
![]() $n$
goes to infinity.
$n$
goes to infinity.
Let
![]() $G$
be a graph. We denote the vertex set and edge set of
$G$
be a graph. We denote the vertex set and edge set of
![]() $G$
by
$G$
by
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
, respectively, and we set
$E(G)$
, respectively, and we set
![]() $v(G) = |V(G)|$
and
$v(G) = |V(G)|$
and
![]() $e(G) = |E(G)|$
. We write
$e(G) = |E(G)|$
. We write
![]() $d_G(v)$
for the degree of
$d_G(v)$
for the degree of
![]() $v \in V(G)$
, and we omit the subscript if the graph
$v \in V(G)$
, and we omit the subscript if the graph
![]() $G$
is clear from the context. We denote by
$G$
is clear from the context. We denote by
![]() $\delta (G)$
and
$\delta (G)$
and
![]() $\Delta (G)$
the minimum degree of
$\Delta (G)$
the minimum degree of
![]() $G$
and the maximum degree of
$G$
and the maximum degree of
![]() $G$
, respectively. For a vertex
$G$
, respectively. For a vertex
![]() $v \in V(G)$
, we denote by
$v \in V(G)$
, we denote by
![]() $N_G(v)$
the set of neighbours of
$N_G(v)$
the set of neighbours of
![]() $v$
in
$v$
in
![]() $G$
which are adjacent to
$G$
which are adjacent to
![]() $v$
. We also omit the subscript if
$v$
. We also omit the subscript if
![]() $G$
is clear from the context.
$G$
is clear from the context.
For a graph
![]() $G$
and a vertex subset
$G$
and a vertex subset
![]() $X \subseteq V(G)$
, we denote by
$X \subseteq V(G)$
, we denote by
![]() $G[X]$
the subgraph of
$G[X]$
the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $X$
. For vertex subsets
$X$
. For vertex subsets
![]() $A$
and
$A$
and
![]() $B$
of
$B$
of
![]() $G$
, we denote by
$G$
, we denote by
![]() $G[A, B]$
the graph where
$G[A, B]$
the graph where
![]() $V(G[A, B]) = A \cup B$
and
$V(G[A, B]) = A \cup B$
and
![]() $E(G[A, B]) = \{uv \in E(G) \,:\, u \in A, v \in B\}$
. Let
$E(G[A, B]) = \{uv \in E(G) \,:\, u \in A, v \in B\}$
. Let
![]() $v$
be a vertex of
$v$
be a vertex of
![]() $G$
and
$G$
and
![]() $X$
be a vertex subset of
$X$
be a vertex subset of
![]() $G$
. We denote by
$G$
. We denote by
![]() $d_G(v;\,X)$
the degree of
$d_G(v;\,X)$
the degree of
![]() $v$
in the induced graph
$v$
in the induced graph
![]() $G[X \cup \{v\}]$
.
$G[X \cup \{v\}]$
.
Let
![]() $G$
be a graph and
$G$
be a graph and
![]() $X \subseteq V(G)$
. We denote by
$X \subseteq V(G)$
. We denote by
![]() $G - X$
the induced graph
$G - X$
the induced graph
![]() $G[V(G) \setminus X]$
. If
$G[V(G) \setminus X]$
. If
![]() $X$
is a single vertex
$X$
is a single vertex
![]() $v$
, we simply denote
$v$
, we simply denote
![]() $G - v$
. Similarly, if a graph
$G - v$
. Similarly, if a graph
![]() $H$
is a subgraph of
$H$
is a subgraph of
![]() $G$
, then we denote by
$G$
, then we denote by
![]() $G - H$
the induced subgraph
$G - H$
the induced subgraph
![]() $G[V(G) \setminus V(H)]$
. Let
$G[V(G) \setminus V(H)]$
. Let
![]() $G^{\prime}$
be a subgraph of
$G^{\prime}$
be a subgraph of
![]() $G$
and
$G$
and
![]() $v \in V(G)$
. We denote by
$v \in V(G)$
. We denote by
![]() $G^{\prime} + v$
a graph such that
$G^{\prime} + v$
a graph such that
![]() $V(G^{\prime} + v) = V(G^{\prime}) \cup \{v\}$
and
$V(G^{\prime} + v) = V(G^{\prime}) \cup \{v\}$
and
![]() $E(G^{\prime} + v) = E(G^{\prime}) \cup E(G[\{v\}, V(G^{\prime})])$
.
$E(G^{\prime} + v) = E(G^{\prime}) \cup E(G[\{v\}, V(G^{\prime})])$
.
We denote by
![]() $K_r$
the complete graph of order
$K_r$
the complete graph of order
![]() $r$
and
$r$
and
![]() $K_{n, m}$
the complete bipartite graph with bipartition of sizes
$K_{n, m}$
the complete bipartite graph with bipartition of sizes
![]() $n$
and
$n$
and
![]() $m$
. We also denote by
$m$
. We also denote by
![]() $C_k$
and
$C_k$
and
![]() $P_k$
the cycle of length
$P_k$
the cycle of length
![]() $k$
and the path of length
$k$
and the path of length
![]() $k$
, respectively. We say
$k$
, respectively. We say
![]() $H^{\prime}$
is a 1-subdivision of
$H^{\prime}$
is a 1-subdivision of
![]() $H$
if
$H$
if
![]() $H^{\prime}$
is obtained from
$H^{\prime}$
is obtained from
![]() $H$
by replacing all edges of
$H$
by replacing all edges of
![]() $H$
with vertex-disjoint paths of length two. We denote by
$H$
with vertex-disjoint paths of length two. We denote by
![]() $H^1$
the 1-subdivision of
$H^1$
the 1-subdivision of
![]() $H$
. We write
$H$
. We write
![]() $\mathrm {Sub}(H)$
for the collection of all subdivisions of
$\mathrm {Sub}(H)$
for the collection of all subdivisions of
![]() $H$
. For a graph
$H$
. For a graph
![]() $F \in \mathrm {Sub}(H)$
, we say a vertex
$F \in \mathrm {Sub}(H)$
, we say a vertex
![]() $v \in V(F) \cap V(H)$
is a branch vertex of
$v \in V(F) \cap V(H)$
is a branch vertex of
![]() $F$
.
$F$
.
In the proofs of the main theorems, we need to count the number of copies of specific bipartite subgraphs where each bipartition is contained in certain vertex subsets. In order to facilitate this counting, we introduce the notion of embedding. Let
![]() $H$
and
$H$
and
![]() $G$
be graphs. An embedding
$G$
be graphs. An embedding
![]() $\phi$
of
$\phi$
of
![]() $H$
into
$H$
into
![]() $G$
is an injective function from
$G$
is an injective function from
![]() $V(H)$
to
$V(H)$
to
![]() $V(G)$
such that for any
$V(G)$
such that for any
![]() $uv \in E(H)$
, its image
$uv \in E(H)$
, its image
![]() $\phi (u) \phi (v)$
is in
$\phi (u) \phi (v)$
is in
![]() $E(G)$
.
$E(G)$
.
The next simple observation will be used in Section 4.
Observation 2.1.
Let
![]() $0 \leq \gamma , \frac {1}{n} \ll \frac {1}{t}, d \lt 1$
. Let
$0 \leq \gamma , \frac {1}{n} \ll \frac {1}{t}, d \lt 1$
. Let
![]() $\mathcal {B}$
be an
$\mathcal {B}$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $t$
-uniform hypergraph with
$t$
-uniform hypergraph with
![]() $|E(\mathcal {B})| \geq dn^t$
. Let
$|E(\mathcal {B})| \geq dn^t$
. Let
![]() $A \subseteq V(\mathcal {B})$
be a vertex subset of size at most
$A \subseteq V(\mathcal {B})$
be a vertex subset of size at most
![]() $\gamma n$
. Then we have
$\gamma n$
. Then we have
![]() $|E(\mathcal {B} - A)| \geq \frac {d}{2}n^t$
.
$|E(\mathcal {B} - A)| \geq \frac {d}{2}n^t$
.
As every vertex is contained in at most
![]() $n^{t - 1}$
edges, by choosing
$n^{t - 1}$
edges, by choosing
![]() $\gamma$
sufficiently small, we can easily verify that Observation2.1 holds. In the following two subsections, we introduce powerful tools in extremal graph theory, so-called supersaturation, and the regularity lemma.
$\gamma$
sufficiently small, we can easily verify that Observation2.1 holds. In the following two subsections, we introduce powerful tools in extremal graph theory, so-called supersaturation, and the regularity lemma.
2.1. The supersaturation
One of the most fundamental problems in extremal graph theory is to determine the maximum number of edges in an
![]() $n$
-vertex graph that does not contain a copy of a specific graph as a subgraph. For a graph
$n$
-vertex graph that does not contain a copy of a specific graph as a subgraph. For a graph
![]() $H$
and a positive integer
$H$
and a positive integer
![]() $n$
, we denote by
$n$
, we denote by
![]() $\mathrm {ex}(n, H)$
the extremal number of
$\mathrm {ex}(n, H)$
the extremal number of
![]() $H$
, defined as the maximum integer
$H$
, defined as the maximum integer
![]() $k$
such that there is an
$k$
such that there is an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $k$
edges not containing
$k$
edges not containing
![]() $H$
as a subgraph.
$H$
as a subgraph.
A classical theorem of Turán determined the exact value of
![]() $\mathrm {ex}(n, K_r)$
. For a graph
$\mathrm {ex}(n, K_r)$
. For a graph
![]() $H$
, we define the Turán density of
$H$
, we define the Turán density of
![]() $H$
as
$H$
as
![]() $\pi (H) \,:\!=\, \lim _{n \to \infty } \frac {\mathrm {ex}(n, H)}{\binom {n}{2}}$
. The existence of Turán density for every graph
$\pi (H) \,:\!=\, \lim _{n \to \infty } \frac {\mathrm {ex}(n, H)}{\binom {n}{2}}$
. The existence of Turán density for every graph
![]() $H$
was proved by Katona, Nemetz, and Simonovits [Reference Katona, Nemetz and Simonovits15]. For every graph
$H$
was proved by Katona, Nemetz, and Simonovits [Reference Katona, Nemetz and Simonovits15]. For every graph
![]() $H$
, the Erdős–Stone–Simonovits [Reference Erdős and Simonovits7, Reference Erdös and Stone9] theorem states that
$H$
, the Erdős–Stone–Simonovits [Reference Erdős and Simonovits7, Reference Erdös and Stone9] theorem states that
![]() $\pi (H) = \left (1 - \frac {1}{\chi (H)-1}\right )$
. We note that if a graph
$\pi (H) = \left (1 - \frac {1}{\chi (H)-1}\right )$
. We note that if a graph
![]() $H$
is bipartite, the Turán density satisfies
$H$
is bipartite, the Turán density satisfies
![]() $\pi (H) = 0$
.
$\pi (H) = 0$
.
Assume that an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
has many more edges than
$G$
has many more edges than
![]() $\mathrm {ex}(n, H)$
. Intuitively, we can expect there to be a lot of copies of
$\mathrm {ex}(n, H)$
. Intuitively, we can expect there to be a lot of copies of
![]() $H$
in
$H$
in
![]() $G$
. Indeed, this is true, and this phenomenon is called supersaturation, proved by Erdős and Simonovits [Reference Erdős and Simonovits8], as follows.
$G$
. Indeed, this is true, and this phenomenon is called supersaturation, proved by Erdős and Simonovits [Reference Erdős and Simonovits8], as follows.
Theorem 2.2 (Supersaturation). Let
![]() $0 \lt \delta \ll \varepsilon , \frac {1}{h} \leq 1$
. For every graph
$0 \lt \delta \ll \varepsilon , \frac {1}{h} \leq 1$
. For every graph
![]() $H$
on
$H$
on
![]() $h$
vertices, the following holds. If
$h$
vertices, the following holds. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $e(G) \geq (\pi (H) + \varepsilon )\binom {n}{2}$
, then
$e(G) \geq (\pi (H) + \varepsilon )\binom {n}{2}$
, then
![]() $G$
contains at least
$G$
contains at least
![]() $\delta n^h$
copies of
$\delta n^h$
copies of
![]() $H$
.
$H$
.
Since the Turán density of a bipartite graph
![]() $H$
is zero, Theorem2.2 leads to the following lemmas.
$H$
is zero, Theorem2.2 leads to the following lemmas.
Lemma 2.3.
Let
![]() $0 \lt \delta \ll \frac {1}{a}, \frac {1}{b}, \varepsilon \leq 1$
and
$0 \lt \delta \ll \frac {1}{a}, \frac {1}{b}, \varepsilon \leq 1$
and
![]() $n$
be a positive integer. For every complete bipartite graph
$n$
be a positive integer. For every complete bipartite graph
![]() $H$
on bipartition
$H$
on bipartition
![]() $A$
and
$A$
and
![]() $B$
with
$B$
with
![]() $|A| = a$
and
$|A| = a$
and
![]() $|B| = b$
, the following holds. Let
$|B| = b$
, the following holds. Let
![]() $G$
be a bipartite graph with bipartition
$G$
be a bipartite graph with bipartition
![]() $X$
and
$X$
and
![]() $Y$
such that
$Y$
such that
![]() $|X|, |Y| \leq n$
. If
$|X|, |Y| \leq n$
. If
![]() $e(G) \geq \varepsilon n^2$
, then the number of embeddings
$e(G) \geq \varepsilon n^2$
, then the number of embeddings
![]() $\phi \,:\, V(H) \to V(G)$
is at least
$\phi \,:\, V(H) \to V(G)$
is at least
![]() $\delta n^{a+b}$
, where
$\delta n^{a+b}$
, where
![]() $\phi (A) \subseteq X$
and
$\phi (A) \subseteq X$
and
![]() $\phi (B) \subseteq Y$
.
$\phi (B) \subseteq Y$
.
Proof. Assume
![]() $a \leq b$
and let
$a \leq b$
and let
![]() $v(G) = n^{\prime}$
. Since
$v(G) = n^{\prime}$
. Since
![]() $e(G) \geq \varepsilon n^2$
, we observe that the inequality
$e(G) \geq \varepsilon n^2$
, we observe that the inequality
![]() $\sqrt {2 \varepsilon } n \leq n^{\prime} = |A| + |B| \leq 2n$
holds. Thus, if we choose
$\sqrt {2 \varepsilon } n \leq n^{\prime} = |A| + |B| \leq 2n$
holds. Thus, if we choose
![]() $n$
sufficiently large, then also
$n$
sufficiently large, then also
![]() $n^{\prime}$
is sufficiently large, and we have
$n^{\prime}$
is sufficiently large, and we have
![]() $e(G) \geq \varepsilon n^{\prime2}$
. By Theorem2.2, the number of copies of
$e(G) \geq \varepsilon n^{\prime2}$
. By Theorem2.2, the number of copies of
![]() $K_{b, b}$
in
$K_{b, b}$
in
![]() $G$
is at least
$G$
is at least
![]() $\delta ^{\prime} n^{\prime2b}$
for some
$\delta ^{\prime} n^{\prime2b}$
for some
![]() $\delta ^{\prime} \gt 0$
. We observe that for each copy of
$\delta ^{\prime} \gt 0$
. We observe that for each copy of
![]() $H$
in
$H$
in
![]() $G$
, where
$G$
, where
![]() $A$
is embedded in
$A$
is embedded in
![]() $X$
, there are at most
$X$
, there are at most
![]() $(n^{\prime})^{b - a}$
copies of
$(n^{\prime})^{b - a}$
copies of
![]() $K_{b, b}$
in
$K_{b, b}$
in
![]() $G$
. Thus, by double counting, the number of embeddings of
$G$
. Thus, by double counting, the number of embeddings of
![]() $H$
in
$H$
in
![]() $G$
, where
$G$
, where
![]() $A$
is embedded in
$A$
is embedded in
![]() $X$
and
$X$
and
![]() $B$
is embedded in
$B$
is embedded in
![]() $Y$
, is at least
$Y$
, is at least
![]() $\delta ^{\prime} (n^{\prime})^{a + b} \geq \delta n^{a + b}$
.
$\delta ^{\prime} (n^{\prime})^{a + b} \geq \delta n^{a + b}$
.
Lemma 2.4.
Let
![]() $0 \lt d \ll \varepsilon , \frac {1}{h} \leq 1$
. For every
$0 \lt d \ll \varepsilon , \frac {1}{h} \leq 1$
. For every
![]() $h$
-vertex bipartite graph
$h$
-vertex bipartite graph
![]() $H$
on bipartition
$H$
on bipartition
![]() $A$
and
$A$
and
![]() $B$
, the following holds. Let
$B$
, the following holds. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree at least
$n$
-vertex graph with minimum degree at least
![]() $\varepsilon n$
. Let
$\varepsilon n$
. Let
![]() $X \subseteq V(G)$
be a set of at least
$X \subseteq V(G)$
be a set of at least
![]() $\varepsilon n$
vertices. Then there are at least
$\varepsilon n$
vertices. Then there are at least
![]() $\delta n^{h}$
distinct embeddings
$\delta n^{h}$
distinct embeddings
![]() $\phi \,:\, V(H) \to V(G)$
, where
$\phi \,:\, V(H) \to V(G)$
, where
![]() $\phi (A) \subseteq X$
.
$\phi (A) \subseteq X$
.
Proof. Let
![]() $X^{\prime} \,:\!=\, V(G) \setminus X$
. If
$X^{\prime} \,:\!=\, V(G) \setminus X$
. If
![]() $e(G[X]) \geq \frac {\varepsilon ^2}{4} n^2$
, by Theorem2.2, the induced graph
$e(G[X]) \geq \frac {\varepsilon ^2}{4} n^2$
, by Theorem2.2, the induced graph
![]() $G[X]$
contains at least
$G[X]$
contains at least
![]() $\delta n^{h}$
distinct copies of
$\delta n^{h}$
distinct copies of
![]() $H$
. Thus, in this case, the lemma is proved. We now assume
$H$
. Thus, in this case, the lemma is proved. We now assume
![]() $e(G[X]) \leq \frac {\varepsilon ^2}{4} n^2$
. Then, by the minimum degree condition of
$e(G[X]) \leq \frac {\varepsilon ^2}{4} n^2$
. Then, by the minimum degree condition of
![]() $G$
, the number of edges in the bipartite subgraph
$G$
, the number of edges in the bipartite subgraph
![]() $G[X, X^{\prime}]$
is at least
$G[X, X^{\prime}]$
is at least
![]() $\frac {\varepsilon ^2}{4}n^2$
. Then, by Lemma2.3, for the bipartite graph
$\frac {\varepsilon ^2}{4}n^2$
. Then, by Lemma2.3, for the bipartite graph
![]() $G[X, X^{\prime}]$
, there are at least
$G[X, X^{\prime}]$
, there are at least
![]() $\delta n^{h}$
distinct desired embeddings. This proves the lemma.
$\delta n^{h}$
distinct desired embeddings. This proves the lemma.
2.2. The regularity lemma
Szemerédi’s regularity lemma [Reference Szemerédi30] is a powerful tool for dealing with large dense graphs. To formulate the regularity lemma, we need to define an
![]() $\varepsilon$
-regular pair. Let
$\varepsilon$
-regular pair. Let
![]() $G$
be a graph and
$G$
be a graph and
![]() $A, B \subseteq G$
. We define the density between
$A, B \subseteq G$
. We define the density between
![]() $A$
and
$A$
and
![]() $B$
as
$B$
as
![]() $d_G(A, B) \,:\!=\, \frac {e(G[A, B])}{|A||B|}$
. The following is the definition of an
$d_G(A, B) \,:\!=\, \frac {e(G[A, B])}{|A||B|}$
. The following is the definition of an
![]() $\varepsilon$
-regular pair.
$\varepsilon$
-regular pair.
Definition 2.5.
Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $d \in [0, 1]$
. A pair
$d \in [0, 1]$
. A pair
![]() $(A, B)$
of disjoint subsets of vertices in a graph
$(A, B)$
of disjoint subsets of vertices in a graph
![]() $G$
is an
$G$
is an
![]() $(\varepsilon , d)$
-regular pair if the following holds. For any subset
$(\varepsilon , d)$
-regular pair if the following holds. For any subset
![]() $A^{\prime} \subseteq A$
,
$A^{\prime} \subseteq A$
,
![]() $B^{\prime} \subseteq B$
with
$B^{\prime} \subseteq B$
with
![]() $|A^{\prime}| \geq \varepsilon |A|$
and
$|A^{\prime}| \geq \varepsilon |A|$
and
![]() $|B^{\prime}| \geq \varepsilon |B|$
,
$|B^{\prime}| \geq \varepsilon |B|$
,
If a pair
![]() $(A, B)$
is
$(A, B)$
is
![]() $(\varepsilon , d)$
-regular for some
$(\varepsilon , d)$
-regular for some
![]() $d \in [0, 1]$
, we say
$d \in [0, 1]$
, we say
![]() $(A, B)$
is an
$(A, B)$
is an
![]() $\varepsilon$
-regular pair. We also say a pair
$\varepsilon$
-regular pair. We also say a pair
![]() $(A, B)$
is
$(A, B)$
is
![]() $(\varepsilon , d{+})$
-regular if
$(\varepsilon , d{+})$
-regular if
![]() $(A, B)$
is
$(A, B)$
is
![]() $(\varepsilon , d^{\prime})$
-regular for some
$(\varepsilon , d^{\prime})$
-regular for some
![]() $d^{\prime} \geq d$
.
$d^{\prime} \geq d$
.
The following is the degree form of the regularity lemma [Reference Komlós and Simonovits21, Theorem 1.10].
Lemma 2.6 (Regularity Lemma-degree form). Let
![]() $0 \lt \frac {1}{T_0} \ll \frac {1}{t_0}, \varepsilon \leq 1$
. For every real number
$0 \lt \frac {1}{T_0} \ll \frac {1}{t_0}, \varepsilon \leq 1$
. For every real number
![]() $d \in [0, 1]$
and every graph
$d \in [0, 1]$
and every graph
![]() $G$
with order at least
$G$
with order at least
![]() $T_0$
, there exists a partition of
$T_0$
, there exists a partition of
![]() $V(G)$
into
$V(G)$
into
![]() $t+1$
clusters
$t+1$
clusters
![]() $V_0, V_1, \ldots , V_t$
and a spanning subgraph
$V_0, V_1, \ldots , V_t$
and a spanning subgraph
![]() $G_0$
of
$G_0$
of
![]() $G$
such that the following holds:
$G$
such that the following holds:
-
•
 $t_0 \leq t \leq T_0$
,
$t_0 \leq t \leq T_0$
, -
•
 $|V_0| \leq \varepsilon v(G)$
,
$|V_0| \leq \varepsilon v(G)$
, -
•
 $|V_1| = \cdots = |V_t|$
,
$|V_1| = \cdots = |V_t|$
, -
•
 $G_0[V_i]$
has no edge for each
$G_0[V_i]$
has no edge for each
 $i \in [t]$
,
$i \in [t]$
, -
•
 $d_{G_0}(v) \geq d_G(v) - (d + \varepsilon )v(G)$
for all
$d_{G_0}(v) \geq d_G(v) - (d + \varepsilon )v(G)$
for all
 $v \in V(G)$
,
$v \in V(G)$
, -
• for all
 $1 \leq i \lt j \leq t$
, either the pair
$1 \leq i \lt j \leq t$
, either the pair
 $(V_i, V_j)$
is an
$(V_i, V_j)$
is an
 $(\varepsilon , d{+})$
-regular pair or the graph
$(\varepsilon , d{+})$
-regular pair or the graph
 $G_0[A, B]$
has no edge.
$G_0[A, B]$
has no edge.
The partition in Lemma2.6 is called an
![]() $(\varepsilon , d)$
-regular partition or simply an
$(\varepsilon , d)$
-regular partition or simply an
![]() $\varepsilon$
-regular partition. We now define an
$\varepsilon$
-regular partition. We now define an
![]() $(\varepsilon , d)$
-reduced graph
$(\varepsilon , d)$
-reduced graph
![]() $R$
on the vertex set
$R$
on the vertex set
![]() $\{V_1, \ldots , V_t\}$
, which is obtained from Lemma2.6, by joining the edges for each
$\{V_1, \ldots , V_t\}$
, which is obtained from Lemma2.6, by joining the edges for each
![]() $V_i, V_j$
if and only if
$V_i, V_j$
if and only if
![]() $(V_i, V_j)$
is an
$(V_i, V_j)$
is an
![]() $(\varepsilon , d{+})$
-regular pair. The following lemma shows that the reduced graph inherits the minimum degree condition [Reference Kühn, Osthus and Taraz24].
$(\varepsilon , d{+})$
-regular pair. The following lemma shows that the reduced graph inherits the minimum degree condition [Reference Kühn, Osthus and Taraz24].
Lemma 2.7 ( [Reference Kühn, Osthus and Taraz24], Proposition 9). For every
![]() $\gamma \gt 0$
, there exist
$\gamma \gt 0$
, there exist
![]() $\varepsilon _0 = \varepsilon _0(\gamma )$
and
$\varepsilon _0 = \varepsilon _0(\gamma )$
and
![]() $d_0 = d_0(\gamma ) \gt 0$
such that for every
$d_0 = d_0(\gamma ) \gt 0$
such that for every
![]() $\varepsilon \leq \varepsilon _0$
,
$\varepsilon \leq \varepsilon _0$
,
![]() $d \leq d_0$
, and
$d \leq d_0$
, and
![]() $\delta \gt 0$
, for every graph
$\delta \gt 0$
, for every graph
![]() $G$
with minimum degree
$G$
with minimum degree
![]() $(\delta + \gamma )n$
, the reduced graph
$(\delta + \gamma )n$
, the reduced graph
![]() $R$
on
$R$
on
![]() $G$
obtained by applying Lemma 2.6
with parameters
$G$
obtained by applying Lemma 2.6
with parameters
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $d$
, the minimum degree of
$d$
, the minimum degree of
![]() $R$
is at least
$R$
is at least
![]() $\left (\delta + \frac {\gamma }{2}\right )|R|$
.
$\left (\delta + \frac {\gamma }{2}\right )|R|$
.
Reduced graphs are useful for analysing the approximate structures of the host graphs, as they inherit many properties of the host graphs, such as the minimum degree.
The main reason that we need the regularity lemma is to get an efficient absorber for the leftover vertices at the final step of the proofs. To achieve this, we need an additional minimum degree condition for the
![]() $\varepsilon$
-regular pair. The following lemma guarantees that we can delete low-degree vertices from
$\varepsilon$
-regular pair. The following lemma guarantees that we can delete low-degree vertices from
![]() $A$
and
$A$
and
![]() $B$
while preserving the
$B$
while preserving the
![]() $\varepsilon$
-regularity.
$\varepsilon$
-regularity.
Lemma 2.8 ( [Reference Böttcher, Schacht and Taraz6], Proposition 12). Let
![]() $(A, B)$
be an
$(A, B)$
be an
![]() $(\varepsilon , d)$
-regular pair in a graph
$(\varepsilon , d)$
-regular pair in a graph
![]() $G.$
Let
$G.$
Let
![]() $B^{\prime} \subseteq B$
with
$B^{\prime} \subseteq B$
with
![]() $|B^{\prime}| \geq \varepsilon |B|.$
Then the size of the set
$|B^{\prime}| \geq \varepsilon |B|.$
Then the size of the set
![]() $\{a \in A \,:\, d_G(a;\,B^{\prime}) \lt (d - \varepsilon )|B^{\prime}|\}$
is at most
$\{a \in A \,:\, d_G(a;\,B^{\prime}) \lt (d - \varepsilon )|B^{\prime}|\}$
is at most
![]() $\varepsilon |A|$
.
$\varepsilon |A|$
.
To get more information on the regularity lemma, see the following papers [Reference Kim, Kühn, Osthus and Tyomkyn16, Reference Komlós, Sárközy and Szemerédi19–Reference Komlós and Simonovits21, Reference Rödl and Schacht28].
3. Extremal examples and properties of
 $\xi (H)$
and
$\xi (H)$
and
 $\chi _{cr}(H^*)$
$\chi _{cr}(H^*)$
We first show that for any
![]() $\gamma \gt 0$
and every graph
$\gamma \gt 0$
and every graph
![]() $H$
, there is
$H$
, there is
![]() $n_0 = n_0(\gamma , H)$
such that for all
$n_0 = n_0(\gamma , H)$
such that for all
![]() $n \geq n_0$
, the inequality
$n \geq n_0$
, the inequality
![]() $\delta _{\mathrm {sub}}(n, H) \leq \left (\frac {1}{2} + \gamma \right )n$
holds. Note that for any graph
$\delta _{\mathrm {sub}}(n, H) \leq \left (\frac {1}{2} + \gamma \right )n$
holds. Note that for any graph
![]() $H$
, we have
$H$
, we have
![]() $\left (1 - \frac {1}{\chi ^*(H^*)} \right ) \leq \frac {1}{2}$
since
$\left (1 - \frac {1}{\chi ^*(H^*)} \right ) \leq \frac {1}{2}$
since
![]() $H^*$
is bipartite. Then Theorem1.2 implies
$H^*$
is bipartite. Then Theorem1.2 implies
![]() $\delta (n, H^*) \leq \left (\frac {1}{2} + \frac {\gamma }{2} \right )n$
if
$\delta (n, H^*) \leq \left (\frac {1}{2} + \frac {\gamma }{2} \right )n$
if
![]() $n$
is sufficiently large and divisible by
$n$
is sufficiently large and divisible by
![]() $v(H^*)$
.
$v(H^*)$
.
Proposition 3.1.
Let
![]() $0 \lt \frac {1}{n} \ll \gamma , \frac {1}{h} \leq 1.$
Then for every
$0 \lt \frac {1}{n} \ll \gamma , \frac {1}{h} \leq 1.$
Then for every
![]() $h$
-vertex graph
$h$
-vertex graph
![]() $H$
, the following holds:
$H$
, the following holds:
Proof. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph and
$n$
-vertex graph and
![]() $\delta (G) \geq \left (\frac {1}{2} + \gamma \right )n.$
By subdividing one edge of
$\delta (G) \geq \left (\frac {1}{2} + \gamma \right )n.$
By subdividing one edge of
![]() $H^*$
at most
$H^*$
at most
![]() $v(H^*)$
more times, we obtain a graph
$v(H^*)$
more times, we obtain a graph
![]() $F$
with a constant number of vertices,
$F$
with a constant number of vertices,
![]() $\chi (F) \leq 3$
, and
$\chi (F) \leq 3$
, and
![]() $v(G) - v(F)$
is divisible by
$v(G) - v(F)$
is divisible by
![]() $v(H^*)$
. By the Erdős–Stone–Simonovits theorem, we can find a copy of
$v(H^*)$
. By the Erdős–Stone–Simonovits theorem, we can find a copy of
![]() $F$
in
$F$
in
![]() $G.$
Since
$G.$
Since
![]() $v(F)$
is bounded, the minimum degree of
$v(F)$
is bounded, the minimum degree of
![]() $G[V(G)\setminus V(F)]$
is greater than
$G[V(G)\setminus V(F)]$
is greater than
![]() $\left (\frac {1}{2} + \frac {\gamma }{2}\right )n$
for
$\left (\frac {1}{2} + \frac {\gamma }{2}\right )n$
for
![]() $n \geq n_0$
, where
$n \geq n_0$
, where
![]() $n_0$
depends only on
$n_0$
depends only on
![]() $H.$
Then by Theorem1.2, there is a perfect
$H.$
Then by Theorem1.2, there is a perfect
![]() $H^*$
-tiling in
$H^*$
-tiling in
![]() $G[V(G)\setminus V(F)]$
which yields a perfect
$G[V(G)\setminus V(F)]$
which yields a perfect
![]() $H$
-subdivision tiling in
$H$
-subdivision tiling in
![]() $G$
together with the copy of
$G$
together with the copy of
![]() $F.$
This completes the proof.
$F.$
This completes the proof.
We now prove lower bounds on
![]() $\delta _{\mathrm {sub}}(n, H)$
by constructing graphs without perfect
$\delta _{\mathrm {sub}}(n, H)$
by constructing graphs without perfect
![]() $H$
-subdivision tilings. The following observation shows that
$H$
-subdivision tilings. The following observation shows that
![]() $H^*$
is a bipartite subdivision with the most unbalanced bipartition. We recall that
$H^*$
is a bipartite subdivision with the most unbalanced bipartition. We recall that
![]() $\xi (H)$
is the minimum value among all possible values of
$\xi (H)$
is the minimum value among all possible values of
![]() $f_H$
where
$f_H$
where
![]() $f_H\,:\, 2^{V(H)}\to \mathbb {R}$
is a function such that for every
$f_H\,:\, 2^{V(H)}\to \mathbb {R}$
is a function such that for every
![]() $X\subseteq V(G)$
,
$X\subseteq V(G)$
,
![]() $f_H(X) = \frac {v(H)+e(H[X])+e(H[Y])}{|X| + e(H[Y])}$
, where
$f_H(X) = \frac {v(H)+e(H[X])+e(H[Y])}{|X| + e(H[Y])}$
, where
![]() $Y = V(G)\setminus X.$
$Y = V(G)\setminus X.$
Observation 3.2.
Let
![]() $H$
be a graph and let
$H$
be a graph and let
![]() $F\in \mathrm {Sub}(H)$
be a bipartite graph with bipartition
$F\in \mathrm {Sub}(H)$
be a bipartite graph with bipartition
![]() $A$
and
$A$
and
![]() $B.$
Then
$B.$
Then
![]() $\frac {|B|}{|A|} \leq \frac {1}{\xi (H) - 1}.$
$\frac {|B|}{|A|} \leq \frac {1}{\xi (H) - 1}.$
Proof. We may assume
![]() $|A| \leq |B|.$
It suffices to show that
$|A| \leq |B|.$
It suffices to show that
![]() $\xi (H) \leq \frac {|A| + |B|}{|B|}.$
Let
$\xi (H) \leq \frac {|A| + |B|}{|B|}.$
Let
![]() $U$
be the branch vertices of
$U$
be the branch vertices of
![]() $F$
and let
$F$
and let
![]() $X = A \cap U$
and
$X = A \cap U$
and
![]() $Y = B \cap U.$
Let
$Y = B \cap U.$
Let
![]() $p = |X| + e(H[Y])$
and
$p = |X| + e(H[Y])$
and
![]() $q = |Y| + e(H[X]).$
Then
$q = |Y| + e(H[X]).$
Then
![]() $f_H(Y) = \frac {p + q}{q}.$
Since
$f_H(Y) = \frac {p + q}{q}.$
Since
![]() $F$
is a bipartite subdivision of
$F$
is a bipartite subdivision of
![]() $H$
with branch set
$H$
with branch set
![]() $X \cup Y$
, every edge in
$X \cup Y$
, every edge in
![]() $H[X, Y]$
is subdivided an even number of times. Thus, there is a non-negative integer
$H[X, Y]$
is subdivided an even number of times. Thus, there is a non-negative integer
![]() $c$
such that
$c$
such that
![]() $\frac {|A| + |B|}{|B|} = \frac {p + q + 2c}{q + c}$
. If
$\frac {|A| + |B|}{|B|} = \frac {p + q + 2c}{q + c}$
. If
![]() $\frac {p + q}{q} \geq 2$
, then
$\frac {p + q}{q} \geq 2$
, then
![]() $\frac {|A| + |B|}{|B|} \geq 2.$
Since
$\frac {|A| + |B|}{|B|} \geq 2.$
Since
![]() $\xi (H) \leq 2$
, in this case, the observation is proved. Otherwise, we may observe that
$\xi (H) \leq 2$
, in this case, the observation is proved. Otherwise, we may observe that
![]() $p \lt q.$
Then
$p \lt q.$
Then
![]() $\frac {|A| + |B|}{|B|} = \frac {p + q + 2c}{q + c} \geq \frac {p + q}{q}$
holds. By the definition of
$\frac {|A| + |B|}{|B|} = \frac {p + q + 2c}{q + c} \geq \frac {p + q}{q}$
holds. By the definition of
![]() $\xi (H)$
, we have
$\xi (H)$
, we have
![]() $\xi (H) \leq H(Y) = \frac {p + q}{q}.$
This completes the proof.
$\xi (H) \leq H(Y) = \frac {p + q}{q}.$
This completes the proof.
By using Observation3.2, we can show the following proposition.
Proposition 3.3.
For every integer
![]() $n \gt 0$
and every graph
$n \gt 0$
and every graph
![]() $H$
, there is an
$H$
, there is an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree at least
$G$
with minimum degree at least
![]() $\left \lfloor \left (1 - \frac {1}{\xi (H)} \right )n\right \rfloor - 1$
such that
$\left \lfloor \left (1 - \frac {1}{\xi (H)} \right )n\right \rfloor - 1$
such that
![]() $G$
does not have a perfect
$G$
does not have a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Proof. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex complete bipartite graph with bipartition
$n$
-vertex complete bipartite graph with bipartition
![]() $X$
and
$X$
and
![]() $Y$
such that
$Y$
such that
![]() $|X| \leq |Y|$
. Note that as
$|X| \leq |Y|$
. Note that as
![]() $G$
is a bipartite graph, every subdivision of
$G$
is a bipartite graph, every subdivision of
![]() $H$
in
$H$
in
![]() $G$
is bipartite. By Observation3.2, if
$G$
is bipartite. By Observation3.2, if
![]() $\frac {|Y|}{|X|} \gt \frac {1}{\xi (H) - 1}$
, then
$\frac {|Y|}{|X|} \gt \frac {1}{\xi (H) - 1}$
, then
![]() $G$
does not have a perfect
$G$
does not have a perfect
![]() $H$
-subdivision tiling. Let
$H$
-subdivision tiling. Let
![]() $|X| = \left \lfloor \left (1 - \frac {1}{\xi (H)} \right )n \right \rfloor - 1$
. Then
$|X| = \left \lfloor \left (1 - \frac {1}{\xi (H)} \right )n \right \rfloor - 1$
. Then
![]() $\delta (G) = \left \lfloor \left (1 - \frac {1}{\xi (H)} \right )n \right \rfloor - 1$
and
$\delta (G) = \left \lfloor \left (1 - \frac {1}{\xi (H)} \right )n \right \rfloor - 1$
and
![]() $\frac {|Y|}{|X|} \gt \frac {1}{\xi (H) - 1}$
. Thus,
$\frac {|Y|}{|X|} \gt \frac {1}{\xi (H) - 1}$
. Thus,
![]() $G$
does not have a perfect
$G$
does not have a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
The next proposition provides a reason for why
![]() $\mathrm {hcf}_{\xi }(H)$
is the determining factor of the value
$\mathrm {hcf}_{\xi }(H)$
is the determining factor of the value
![]() $\xi ^*(H)$
.
$\xi ^*(H)$
.
Proposition 3.4.
Let
![]() $H$
be a graph with
$H$
be a graph with
![]() $\mathrm {hcf}_{\xi }(H) \neq 1$
. Then for every integer
$\mathrm {hcf}_{\xi }(H) \neq 1$
. Then for every integer
![]() $n \gt 0$
, there is an
$n \gt 0$
, there is an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree at least
$G$
with minimum degree at least
![]() $\left \lfloor \frac {n}{2} \right \rfloor - 1$
which does not have a perfect
$\left \lfloor \frac {n}{2} \right \rfloor - 1$
which does not have a perfect
![]() $H$
-subdivision tiling except for
$H$
-subdivision tiling except for
![]() $\mathrm {hcf}_{\xi }(H) = 2$
and
$\mathrm {hcf}_{\xi }(H) = 2$
and
![]() $n$
is even.
$n$
is even.
To prove Proposition3.4, we need the following claim.
Claim 1.
Let
![]() $H$
be a graph with at least one edge and let
$H$
be a graph with at least one edge and let
![]() $H^{\prime}$
be a bipartite subdivision of
$H^{\prime}$
be a bipartite subdivision of
![]() $H$
with bipartition
$H$
with bipartition
![]() $A$
and
$A$
and
![]() $B$
. Then
$B$
. Then
![]() $|B| - |A|$
is divisible by
$|B| - |A|$
is divisible by
![]() $\mathrm {hcf}_{\xi }(H)$
.
$\mathrm {hcf}_{\xi }(H)$
.
Proof of Claim 1. Let
![]() $A^{\prime}$
and
$A^{\prime}$
and
![]() $B^{\prime}$
be the branch vertices of
$B^{\prime}$
be the branch vertices of
![]() $H$
contained in
$H$
contained in
![]() $A$
and
$A$
and
![]() $B$
, respectively. Let
$B$
, respectively. Let
![]() $uv\in E(H)$
be an edge and let
$uv\in E(H)$
be an edge and let
![]() $u z_1, \ldots , z_k, v$
be the subdivided path in
$u z_1, \ldots , z_k, v$
be the subdivided path in
![]() $H^{\prime}$
that corresponds to
$H^{\prime}$
that corresponds to
![]() $uv$
. If
$uv$
. If
![]() $u\in A$
and
$u\in A$
and
![]() $v\in B$
, then
$v\in B$
, then
![]() $k$
is an even number since
$k$
is an even number since
![]() $H^{\prime}$
is a bipartite graph. Thus, we observe that
$H^{\prime}$
is a bipartite graph. Thus, we observe that
![]() $|B\cap \{z_1,\ldots , z_k\}| - |A\cap \{z_1, \ldots , z_k\}| = 0$
. If both
$|B\cap \{z_1,\ldots , z_k\}| - |A\cap \{z_1, \ldots , z_k\}| = 0$
. If both
![]() $u$
and
$u$
and
![]() $v$
are in
$v$
are in
![]() $A$
, the number
$A$
, the number
![]() $k$
is odd and the equality
$k$
is odd and the equality
![]() $|B\cap \{z_1,\ldots , z_k\}| - |A\cap \{z_1, \ldots , z_k\}| = 1$
holds since
$|B\cap \{z_1,\ldots , z_k\}| - |A\cap \{z_1, \ldots , z_k\}| = 1$
holds since
![]() $H^{\prime}$
is a bipartite graph. Similarly, if both
$H^{\prime}$
is a bipartite graph. Similarly, if both
![]() $u$
and
$u$
and
![]() $v$
are in
$v$
are in
![]() $B$
, then we have
$B$
, then we have
![]() $|B\cap \{z_1,\ldots , z_k\}| - |A\cap \{z_1, \ldots , z_k\}| = -1$
. Hence, we have the following.
$|B\cap \{z_1,\ldots , z_k\}| - |A\cap \{z_1, \ldots , z_k\}| = -1$
. Hence, we have the following.
Thus, by the definition of
![]() $\mathrm {hcf}_{\xi }(H)$
, the number
$\mathrm {hcf}_{\xi }(H)$
, the number
![]() $|B| - |A|$
is divisible by
$|B| - |A|$
is divisible by
![]() $\mathrm {hcf}_{\xi }(H)$
. This completes the proof.
$\mathrm {hcf}_{\xi }(H)$
. This completes the proof.
Proof of Proposition 3.4. Let
![]() $F\in \mathrm {Sub}(H)$
be a bipartite graph with bipartition
$F\in \mathrm {Sub}(H)$
be a bipartite graph with bipartition
![]() $A$
and
$A$
and
![]() $B$
. Since
$B$
. Since
![]() $F$
is a bipartite subdivision of
$F$
is a bipartite subdivision of
![]() $H$
, by Claim1, the difference
$H$
, by Claim1, the difference
![]() $|B| - |A|$
is divisible by
$|B| - |A|$
is divisible by
![]() $\mathrm {hcf}_{\xi }(H)$
. If
$\mathrm {hcf}_{\xi }(H)$
. If
![]() $G$
is a bipartite graph, and the difference between the sizes of two bipartitions of
$G$
is a bipartite graph, and the difference between the sizes of two bipartitions of
![]() $G$
is not divisible by
$G$
is not divisible by
![]() $\mathrm {hcf}_{\xi }(H)$
, the graph
$\mathrm {hcf}_{\xi }(H)$
, the graph
![]() $G$
does not have a perfect
$G$
does not have a perfect
![]() $H$
-subdivision tiling since every subdivision of
$H$
-subdivision tiling since every subdivision of
![]() $H$
in
$H$
in
![]() $G$
is bipartite.
$G$
is bipartite.
First, let
![]() $n$
be an even number and
$n$
be an even number and
![]() $\mathrm {hcf}_{\xi }(H) \gt 2$
. Let
$\mathrm {hcf}_{\xi }(H) \gt 2$
. Let
![]() $G = K_{\frac {n}{2} - 1, \frac {n}{2} + 1}$
. Then, the difference between the two bipartitions of
$G = K_{\frac {n}{2} - 1, \frac {n}{2} + 1}$
. Then, the difference between the two bipartitions of
![]() $G$
is two which cannot be divisible by
$G$
is two which cannot be divisible by
![]() $\mathrm {hcf}_{\xi }(H)$
since
$\mathrm {hcf}_{\xi }(H)$
since
![]() $\mathrm {hcf}_{\xi }(H) \gt 2$
.
$\mathrm {hcf}_{\xi }(H) \gt 2$
.
Second, let
![]() $n$
be an odd number and
$n$
be an odd number and
![]() $\mathrm {hcf}_{\xi }(H) \neq 1$
. Let
$\mathrm {hcf}_{\xi }(H) \neq 1$
. Let
![]() $G = K_{\left \lfloor \frac {n}{2} \right \rfloor , \left \lceil \frac {n}{2} \right \rceil }$
. Then, the difference between the sizes of the two bipartitions of
$G = K_{\left \lfloor \frac {n}{2} \right \rfloor , \left \lceil \frac {n}{2} \right \rceil }$
. Then, the difference between the sizes of the two bipartitions of
![]() $G$
is
$G$
is
![]() $1$
, which is not divisible by
$1$
, which is not divisible by
![]() $\mathrm {hcf}_{\xi }(H)$
as
$\mathrm {hcf}_{\xi }(H)$
as
![]() $\mathrm {hcf}_{\xi }(H) \neq 1$
.
$\mathrm {hcf}_{\xi }(H) \neq 1$
.
In the following proposition, we consider the case when
![]() $\mathrm {hcf}_{\xi }(H) = 2$
and the order of the host graph is even.
$\mathrm {hcf}_{\xi }(H) = 2$
and the order of the host graph is even.
Proposition 3.5.
For every graph
![]() $H$
with
$H$
with
![]() $\mathrm {hcf}_{\xi }(H) = 2$
and for every even number
$\mathrm {hcf}_{\xi }(H) = 2$
and for every even number
![]() $n$
, there is an
$n$
, there is an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with minimum degree at least
$G$
with minimum degree at least
![]() $\left \lfloor \frac {1}{3}n \right \rfloor - 1$
such that
$\left \lfloor \frac {1}{3}n \right \rfloor - 1$
such that
![]() $G$
does not contain a perfect
$G$
does not contain a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Proof. Let
![]() $(A, B, C)$
be a partition of
$(A, B, C)$
be a partition of
![]() $[n]$
with sizes
$[n]$
with sizes
![]() $|A| = \left \lfloor \frac {1}{3}n \right \rfloor - 1$
and
$|A| = \left \lfloor \frac {1}{3}n \right \rfloor - 1$
and
![]() $|B| = \left \lfloor \frac {1}{3}n \right \rfloor$
. Let
$|B| = \left \lfloor \frac {1}{3}n \right \rfloor$
. Let
![]() $G$
be a graph on vertex set
$G$
be a graph on vertex set
![]() $[n]$
such that
$[n]$
such that
![]() $G$
is a disjoint union of a clique on
$G$
is a disjoint union of a clique on
![]() $C$
and a complete bipartite graph with bipartition
$C$
and a complete bipartite graph with bipartition
![]() $(A, B)$
. Then, the minimum degree of
$(A, B)$
. Then, the minimum degree of
![]() $G$
is
$G$
is
![]() $\left \lfloor \frac {1}{3}n \right \rfloor - 1$
. Let
$\left \lfloor \frac {1}{3}n \right \rfloor - 1$
. Let
![]() $G_1 = G[A \cup B]$
and
$G_1 = G[A \cup B]$
and
![]() $G_2 = G[C]$
. Since
$G_2 = G[C]$
. Since
![]() $G_1$
and
$G_1$
and
![]() $G_2$
are disjoint, if
$G_2$
are disjoint, if
![]() $G$
contains a perfect
$G$
contains a perfect
![]() $H$
-subdivision tiling, so does
$H$
-subdivision tiling, so does
![]() $G_1$
. However, the difference between the sizes of the bipartitions of
$G_1$
. However, the difference between the sizes of the bipartitions of
![]() $G_1$
is
$G_1$
is
![]() $1$
, which is not divisible by
$1$
, which is not divisible by
![]() $\mathrm {hcf}_{\xi }(H) = 2$
. Thus, by Claim1, the graph
$\mathrm {hcf}_{\xi }(H) = 2$
. Thus, by Claim1, the graph
![]() $G_1$
does not contain a perfect
$G_1$
does not contain a perfect
![]() $H$
-subdivision tiling since
$H$
-subdivision tiling since
![]() $G_1$
is a bipartite graph, so every subdivision of
$G_1$
is a bipartite graph, so every subdivision of
![]() $H$
in
$H$
in
![]() $G$
is also bipartite. Therefore,
$G$
is also bipartite. Therefore,
![]() $G$
does not have a perfect
$G$
does not have a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
The next observation shows the relationship between
![]() $\xi (H)$
and
$\xi (H)$
and
![]() $\chi _{cr}(H^*)$
.
$\chi _{cr}(H^*)$
.
Observation 3.6.
For every graph
![]() $H$
, the inequality
$H$
, the inequality
![]() $\left (1 - \frac {1}{\xi (H)} \right ) \geq \left (1 - \frac {1}{\chi _{cr}(H^*)} \right )$
holds.
$\left (1 - \frac {1}{\xi (H)} \right ) \geq \left (1 - \frac {1}{\chi _{cr}(H^*)} \right )$
holds.
Proof. It suffices to show that
![]() $\chi _{cr}(H^*) \leq \xi (H)$
. We recall that
$\chi _{cr}(H^*) \leq \xi (H)$
. We recall that
![]() $X_H$
is a subset of
$X_H$
is a subset of
![]() $V(H)$
such that
$V(H)$
such that
![]() $f_H(X_H) = \xi (H)$
. Let
$f_H(X_H) = \xi (H)$
. Let
![]() $Y_H \,:\!=\, V(H)\setminus X_H$
. Let
$Y_H \,:\!=\, V(H)\setminus X_H$
. Let
![]() $A = X_H$
and
$A = X_H$
and
![]() $B = Y_H$
. Since
$B = Y_H$
. Since
![]() $H^*$
is obtained by replacing all edges in
$H^*$
is obtained by replacing all edges in
![]() $H[X_H]$
and
$H[X_H]$
and
![]() $H[Y_H]$
with vertex-disjoint paths of length two, we update the set
$H[Y_H]$
with vertex-disjoint paths of length two, we update the set
![]() $B$
by adding vertices that were used to replace the edges in
$B$
by adding vertices that were used to replace the edges in
![]() $H[X_H]$
. Similarly, we update the set
$H[X_H]$
. Similarly, we update the set
![]() $A$
by adding vertices that were used to replace the edges in
$A$
by adding vertices that were used to replace the edges in
![]() $H[Y_H]$
. Then
$H[Y_H]$
. Then
![]() $A$
and
$A$
and
![]() $B$
are independent sets and
$B$
are independent sets and
![]() $|B| = |Y_H| + e(H[X_H])$
. Thus, by the definition of
$|B| = |Y_H| + e(H[X_H])$
. Thus, by the definition of
![]() $\sigma (H^*)$
, the inequality
$\sigma (H^*)$
, the inequality
![]() $\sigma (H^*) \leq |Y_H| + e(H[X_H])$
holds. This implies
$\sigma (H^*) \leq |Y_H| + e(H[X_H])$
holds. This implies
![]() $\chi _{cr}(H^*) \leq \frac {v(H^*)}{v(H^*) - (|Y_H| + e(H[X_H]))} = \frac {v(H)+ e(H[X_H]) + e(H[Y_H])}{|X_H| + e(H[Y_H])} = \xi (H)$
.
$\chi _{cr}(H^*) \leq \frac {v(H^*)}{v(H^*) - (|Y_H| + e(H[X_H]))} = \frac {v(H)+ e(H[X_H]) + e(H[Y_H])}{|X_H| + e(H[Y_H])} = \xi (H)$
.
4.
 $\mathrm {Sub}(H)$
-absorbers
$\mathrm {Sub}(H)$
-absorbers
We use the absorption method to prove Theorems1.8 and 1.9. In order to execute the absorption method, we need some specific structures that we call
![]() $\mathrm {Sub}(H)$
-absorbers.
$\mathrm {Sub}(H)$
-absorbers.
Definition 4.1.
Let
![]() $H$
and
$H$
and
![]() $G$
be graphs and take two subsets
$G$
be graphs and take two subsets
![]() $A\subseteq V(G)$
and
$A\subseteq V(G)$
and
![]() $X\subseteq V(G)\setminus A.$
We say
$X\subseteq V(G)\setminus A.$
We say
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $X$
if both
$X$
if both
![]() $G[A]$
and
$G[A]$
and
![]() $G[A\cup X]$
have perfect
$G[A\cup X]$
have perfect
![]() $H$
-subdivision tilings. If
$H$
-subdivision tilings. If
![]() $X = \{v\}$
, we say
$X = \{v\}$
, we say
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $v.$
$v.$
Our strategy for constructing
![]() $\mathrm {Sub}(H)$
-absorbers is to collect many vertex-disjoint small subgraphs with good properties, which we call absorber units. We define three different types of absorber units, which we call type-
$\mathrm {Sub}(H)$
-absorbers is to collect many vertex-disjoint small subgraphs with good properties, which we call absorber units. We define three different types of absorber units, which we call type-
![]() $1$
, type-
$1$
, type-
![]() $2$
, and type-
$2$
, and type-
![]() $3$
$3$
![]() $\mathrm {Sub}(H)$
-absorbers, respectively. We first introduce the type-
$\mathrm {Sub}(H)$
-absorbers, respectively. We first introduce the type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorber as follows.
$\mathrm {Sub}(H)$
-absorber as follows.
Definition 4.2.
Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $H^1$
be the
$H^1$
be the
![]() $1$
-subdivision of
$1$
-subdivision of
![]() $H.$
Since
$H.$
Since
![]() $H^1$
is bipartite,
$H^1$
is bipartite,
![]() $H^1$
has a bipartition
$H^1$
has a bipartition
![]() $(U, V)$
such that the set
$(U, V)$
such that the set
![]() $U$
consists of all branch vertices. Choose an edge
$U$
consists of all branch vertices. Choose an edge
![]() $xy\in E(H^1)$
, with
$xy\in E(H^1)$
, with
![]() $x\in U$
, and
$x\in U$
, and
![]() $y\in V.$
Now we replace the edge
$y\in V.$
Now we replace the edge
![]() $xy$
with a path of length three, say
$xy$
with a path of length three, say
![]() $x w z y$
and denote by
$x w z y$
and denote by
![]() $T^1_H$
the obtained graph. Let
$T^1_H$
the obtained graph. Let
![]() $u$
and
$u$
and
![]() $v$
be two new vertices and add edges
$v$
be two new vertices and add edges
![]() $uy, uw, vx,$
and
$uy, uw, vx,$
and
![]() $vz$
to
$vz$
to
![]() $T^1_H$
and we denote by
$T^1_H$
and we denote by
![]() $\hat {T}^1_H$
the obtained graph.
$\hat {T}^1_H$
the obtained graph.
Let
![]() $G$
be a graph and let two distinct vertices
$G$
be a graph and let two distinct vertices
![]() $a$
and
$a$
and
![]() $b\in V(G).$
We say a set
$b\in V(G).$
We say a set
![]() $A\subseteq V(G)\setminus \{a, b\}$
is a type-
$A\subseteq V(G)\setminus \{a, b\}$
is a type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $\{a, b\}$
if
$\{a, b\}$
if
![]() $|A| = v(T^1_H)$
and there is an embedding
$|A| = v(T^1_H)$
and there is an embedding
![]() $\phi \,:\, V(\hat {T}^1_H)\to A\cup \{a, b\}$
such that
$\phi \,:\, V(\hat {T}^1_H)\to A\cup \{a, b\}$
such that
![]() $\phi (u) = a$
and
$\phi (u) = a$
and
![]() $\phi (v) = b.$
$\phi (v) = b.$
We assume that the choice of
![]() $xy$
is always the same for all
$xy$
is always the same for all
![]() $H$
, so that
$H$
, so that
![]() $T^1_H$
is uniquely determined for all
$T^1_H$
is uniquely determined for all
![]() $H.$
A graph
$H.$
A graph
![]() $T^1_H$
is a subdivision of
$T^1_H$
is a subdivision of
![]() $H$
since it is obtained from the
$H$
since it is obtained from the
![]() $1$
-subdivision of
$1$
-subdivision of
![]() $H$
by replacing one edge with a vertex-disjoint path of length
$H$
by replacing one edge with a vertex-disjoint path of length
![]() $3.$
By the construction of
$3.$
By the construction of
![]() $\hat {T}^1_H$
, we can replace a path
$\hat {T}^1_H$
, we can replace a path
![]() $xwzy$
with a path
$xwzy$
with a path
![]() $xvzwuy$
, so
$xvzwuy$
, so
![]() $\hat {T}^1_H$
also contains a spanning subdivision of
$\hat {T}^1_H$
also contains a spanning subdivision of
![]() $H.$
Thus, for a graph
$H.$
Thus, for a graph
![]() $G$
and
$G$
and
![]() $a$
and
$a$
and
![]() $b\in V(G)$
, a set
$b\in V(G)$
, a set
![]() $X\subseteq V(G)$
is a type-
$X\subseteq V(G)$
is a type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $\{a, b\}$
, implying both
$\{a, b\}$
, implying both
![]() $G[X]$
and
$G[X]$
and
![]() $G[X\cup \{a, b\}]$
have perfect
$G[X\cup \{a, b\}]$
have perfect
![]() $H$
-subdivision tilings.
$H$
-subdivision tilings.
Type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers are the most efficient bipartite absorber units. If the host graph is bipartite, then we only obtain bipartite absorber units. Note that a bipartite graph cannot absorb a single vertex, so absorbing two vertices is as good as it gets in a bipartite host graph. Moreover, since
$\mathrm {Sub}(H)$
-absorbers are the most efficient bipartite absorber units. If the host graph is bipartite, then we only obtain bipartite absorber units. Note that a bipartite graph cannot absorb a single vertex, so absorbing two vertices is as good as it gets in a bipartite host graph. Moreover, since
![]() $T^1_H$
is bipartite, supersaturation implies that there are many type-
$T^1_H$
is bipartite, supersaturation implies that there are many type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers, allowing us to obtain many efficient
$\mathrm {Sub}(H)$
-absorbers, allowing us to obtain many efficient
![]() $\mathrm {Sub}(H)$
-absorbers.
$\mathrm {Sub}(H)$
-absorbers.
If there are many type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers for every pair of vertices in
$\mathrm {Sub}(H)$
-absorbers for every pair of vertices in
![]() $G$
, it would be ideal to obtain the desired absorbers. However, this is not true in general, so it is useful to define the following auxiliary graph that captures information on vertex pairs that have many type-
$G$
, it would be ideal to obtain the desired absorbers. However, this is not true in general, so it is useful to define the following auxiliary graph that captures information on vertex pairs that have many type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers.
$\mathrm {Sub}(H)$
-absorbers.
Definition 4.3.
Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $d \gt 0$
. For a given
$d \gt 0$
. For a given
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
, we define the
$G$
, we define the
![]() $d$
-absorbing graph
$d$
-absorbing graph
![]() $F$
as the graph on the vertex set
$F$
as the graph on the vertex set
![]() $V(G)$
such that
$V(G)$
such that
![]() $uv\in E(F)$
if and only if the number of type-
$uv\in E(F)$
if and only if the number of type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $\{u, v\}$
is at least
$\{u, v\}$
is at least
![]() $dn^{v(T^1_H)}.$
$dn^{v(T^1_H)}.$
In order to deal with non-bipartite host graphs, we define the following two types of absorber units. Note that these absorbers are able to absorb one vertex.
Definition 4.4.
Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $(U, V)$
be a bipartition of
$(U, V)$
be a bipartition of
![]() $H^1$
such that
$H^1$
such that
![]() $U$
is the set of all branch vertices. Let
$U$
is the set of all branch vertices. Let
![]() $x, y$
be the vertices as in Definition 4.2
. For consistency, we denote by
$x, y$
be the vertices as in Definition 4.2
. For consistency, we denote by
![]() $T^2_H$
the copy of
$T^2_H$
the copy of
![]() $H^1.$
Let
$H^1.$
Let
![]() $u$
be a new vertex and add edges
$u$
be a new vertex and add edges
![]() $ux, uy$
to
$ux, uy$
to
![]() $T^2_H$
and we denote by
$T^2_H$
and we denote by
![]() $\hat {T}^2_H$
the obtained graph.
$\hat {T}^2_H$
the obtained graph.
Let
![]() $G$
be a graph and let
$G$
be a graph and let
![]() $a\in V(G).$
We say a set
$a\in V(G).$
We say a set
![]() $A\subseteq V(G)\setminus \{a\}$
is a type-
$A\subseteq V(G)\setminus \{a\}$
is a type-
![]() $2$
$2$
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $\{a\}$
if
$\{a\}$
if
![]() $|A| = v(T^2_H)$
and there is an embedding
$|A| = v(T^2_H)$
and there is an embedding
![]() $\phi \,:\, V(\hat {T}^2_H)\to A\cup \{a\}$
such that
$\phi \,:\, V(\hat {T}^2_H)\to A\cup \{a\}$
such that
![]() $\phi (u) = a.$
$\phi (u) = a.$
Since
![]() $T^2_H$
is isomorphic to
$T^2_H$
is isomorphic to
![]() $H^1$
, it has a perfect
$H^1$
, it has a perfect
![]() $H$
-subdivision tiling. The graph
$H$
-subdivision tiling. The graph
![]() $\hat {T}^2_H$
contains a spanning subgraph
$\hat {T}^2_H$
contains a spanning subgraph
![]() $F$
which is obtained from
$F$
which is obtained from
![]() $T^2_H$
by replacing the edge
$T^2_H$
by replacing the edge
![]() $xy\in T^2_H$
with the path
$xy\in T^2_H$
with the path
![]() $xuy.$
Thus,
$xuy.$
Thus,
![]() $\hat {T}^2_H$
also has a perfect
$\hat {T}^2_H$
also has a perfect
![]() $H$
-subdivision packing. The next definition is for type-
$H$
-subdivision packing. The next definition is for type-
![]() $3$
$3$
![]() $\mathrm {Sub}(H)$
-absorbers.
$\mathrm {Sub}(H)$
-absorbers.
Definition 4.5.
Let
![]() $H$
be a graph. Let two vertex-disjoint graphs
$H$
be a graph. Let two vertex-disjoint graphs
![]() $H^1$
and
$H^1$
and
![]() $T^1_H$
be given. Let
$T^1_H$
be given. Let
![]() $x, y, z, w$
be the vertices of
$x, y, z, w$
be the vertices of
![]() $T^1_H$
as in Definition 4.2
. Choose an edge
$T^1_H$
as in Definition 4.2
. Choose an edge
![]() $x^{\prime}y^{\prime} \in E(H^1).$
We denote by
$x^{\prime}y^{\prime} \in E(H^1).$
We denote by
![]() $T^3_H$
a graph that is obtained from
$T^3_H$
a graph that is obtained from
![]() $H^1$
and
$H^1$
and
![]() $T^1_H$
by adding two edges
$T^1_H$
by adding two edges
![]() $x^{\prime}z$
and
$x^{\prime}z$
and
![]() $y^{\prime}w.$
Let
$y^{\prime}w.$
Let
![]() $u$
be a new vertex and add edges
$u$
be a new vertex and add edges
![]() $ux, uy$
to
$ux, uy$
to
![]() $T^3_H.$
We denote by
$T^3_H.$
We denote by
![]() $\hat {T}^3_H$
the obtained graph. We write
$\hat {T}^3_H$
the obtained graph. We write
![]() $\tilde {T}^3_H$
to denote a bipartite graph that is
$\tilde {T}^3_H$
to denote a bipartite graph that is
![]() $T^3_H - \{x, y\}.$
$T^3_H - \{x, y\}.$
Let
![]() $G$
be a graph and let
$G$
be a graph and let
![]() $a\in V(G).$
We say a set
$a\in V(G).$
We say a set
![]() $A\subseteq V(G)\setminus \{a\}$
is a type-
$A\subseteq V(G)\setminus \{a\}$
is a type-
![]() $3$
$3$
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $\{a\}$
if
$\{a\}$
if
![]() $|A| = v(T^3_H)$
and there is an embedding
$|A| = v(T^3_H)$
and there is an embedding
![]() $\phi \,:\, V(\hat {T}^3_H)\to A\cup \{a\}$
such that
$\phi \,:\, V(\hat {T}^3_H)\to A\cup \{a\}$
such that
![]() $\phi (u) = a.$
$\phi (u) = a.$
Note that
![]() $T^3_H$
contains vertex-disjoint copies of
$T^3_H$
contains vertex-disjoint copies of
![]() $H^1$
and
$H^1$
and
![]() $T^1_H$
whose union covers all vertices of
$T^1_H$
whose union covers all vertices of
![]() $T^3_H.$
We observe that
$T^3_H.$
We observe that
![]() $\hat {T}^3_H$
contains vertex-disjoint copies of graphs
$\hat {T}^3_H$
contains vertex-disjoint copies of graphs
![]() $F_1$
and
$F_1$
and
![]() $F_2$
such that
$F_2$
such that
![]() $F_1$
is obtained from
$F_1$
is obtained from
![]() $H^1$
by replacing the edge
$H^1$
by replacing the edge
![]() $x^{\prime}y^{\prime}$
of
$x^{\prime}y^{\prime}$
of
![]() $H^1$
with
$H^1$
with
![]() $x^{\prime}wzy^{\prime}$
and
$x^{\prime}wzy^{\prime}$
and
![]() $F_2$
is obtained from
$F_2$
is obtained from
![]() $T^1_H$
by replacing
$T^1_H$
by replacing
![]() $xwzy$
with
$xwzy$
with
![]() $xuy.$
Both
$xuy.$
Both
![]() $F_1$
and
$F_1$
and
![]() $F_2$
are subdivisions of
$F_2$
are subdivisions of
![]() $H.$
Thus, both graphs
$H.$
Thus, both graphs
![]() $T^3_H$
and
$T^3_H$
and
![]() $\hat {T}^3_H$
have perfect
$\hat {T}^3_H$
have perfect
![]() $H$
-subdivision tilings.
$H$
-subdivision tilings.
We note that
![]() $\hat {T}^2_H - u$
and
$\hat {T}^2_H - u$
and
![]() $\hat {T}^3_H - u$
are both bipartite graphs. Moreover,
$\hat {T}^3_H - u$
are both bipartite graphs. Moreover,
![]() $\hat {T}^2_H$
contains one triangle, and
$\hat {T}^2_H$
contains one triangle, and
![]() $\hat {T}^3_H$
contains one
$\hat {T}^3_H$
contains one
![]() $C_5$
, and deleting them leaves a bipartite graph. Hence, in graphs containing many
$C_5$
, and deleting them leaves a bipartite graph. Hence, in graphs containing many
![]() $C_3$
or
$C_3$
or
![]() $C_5$
, we can find many copies of
$C_5$
, we can find many copies of
![]() $\hat {T}^2_H$
and
$\hat {T}^2_H$
and
![]() $\hat {T}^3_H$
, respectively. We will use these properties of
$\hat {T}^3_H$
, respectively. We will use these properties of
![]() $\hat {T}^2_H$
and
$\hat {T}^2_H$
and
![]() $\hat {T}^3_H$
to prove a special case for Theorem1.9.
$\hat {T}^3_H$
to prove a special case for Theorem1.9.
Since all four graphs
![]() $T^2_H$
,
$T^2_H$
,
![]() $\hat {T}^2_H$
,
$\hat {T}^2_H$
,
![]() $T^3_H$
, and
$T^3_H$
, and
![]() $\hat {T}^3_H$
have perfect
$\hat {T}^3_H$
have perfect
![]() $H$
-subdivision tilings, type-
$H$
-subdivision tilings, type-
![]() $2$
and type-
$2$
and type-
![]() $3$
$3$
![]() $\mathrm {Sub}(H)$
-absorbers can be used to absorb a single vertex. Although this is an advantage over the type-
$\mathrm {Sub}(H)$
-absorbers can be used to absorb a single vertex. Although this is an advantage over the type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers, it is not guaranteed that we can always find many type-
$\mathrm {Sub}(H)$
-absorbers, it is not guaranteed that we can always find many type-
![]() $2$
and type-
$2$
and type-
![]() $3$
absorbers in a graph
$3$
absorbers in a graph
![]() $G$
if
$G$
if
![]() $G$
is close to being bipartite. Indeed, we only use type-
$G$
is close to being bipartite. Indeed, we only use type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers to prove Theorem1.8. On the other hand, if
$\mathrm {Sub}(H)$
-absorbers to prove Theorem1.8. On the other hand, if
![]() $\mathrm {hcf}_{\xi }(H)$
is two, type-
$\mathrm {hcf}_{\xi }(H)$
is two, type-
![]() $1$
absorbers are not sufficient to build the desired absorbers. So, the proof of Theorem1.9 uses all three types of absorber units.
$1$
absorbers are not sufficient to build the desired absorbers. So, the proof of Theorem1.9 uses all three types of absorber units.
As we mentioned before, not all vertices may have many absorber units for them. So, it would be useful if we could somehow control what vertices remain uncovered. The following structure allows us to ‘exchange’ the remaining vertices so that we can absorb those vertices better.
Definition 4.6.
Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $(U, V)$
be a bipartition of
$(U, V)$
be a bipartition of
![]() $H^1$
such that
$H^1$
such that
![]() $U$
consists of the branch vertices. Let
$U$
consists of the branch vertices. Let
![]() $x_0y_0 \in E(H)$
be an arbitrary edge. Then there is a unique vertex
$x_0y_0 \in E(H)$
be an arbitrary edge. Then there is a unique vertex
![]() $z\in V$
such that
$z\in V$
such that
![]() $x_0z, y_0z\in E(H^1).$
Let
$x_0z, y_0z\in E(H^1).$
Let
![]() $S_H = H^1 - z.$
We now introduce two new vertices
$S_H = H^1 - z.$
We now introduce two new vertices
![]() $u$
and
$u$
and
![]() $v$
and add edges
$v$
and add edges
![]() $ux_0, uy_0, vx_0, vy_0$
to
$ux_0, uy_0, vx_0, vy_0$
to
![]() $S_H$
and we denote by
$S_H$
and we denote by
![]() $\hat {S}_H$
the obtained graph.
$\hat {S}_H$
the obtained graph.
Let
![]() $G$
be a graph and two distinct vertices
$G$
be a graph and two distinct vertices
![]() $a, b\in V(G).$
We say a set
$a, b\in V(G).$
We say a set
![]() $B\subseteq V(G)\setminus \{a, b\}$
is a
$B\subseteq V(G)\setminus \{a, b\}$
is a
![]() $\mathrm {Sub}(H)$
-exchanger for
$\mathrm {Sub}(H)$
-exchanger for
![]() $\{a, b\}$
if
$\{a, b\}$
if
![]() $|B| = v(S_H)$
and there is an embedding
$|B| = v(S_H)$
and there is an embedding
![]() $\phi : V(\hat {S}_H)\to B\cup \{a, b\}$
such that
$\phi : V(\hat {S}_H)\to B\cup \{a, b\}$
such that
![]() $\phi (u) = a$
and
$\phi (u) = a$
and
![]() $\phi (v) = b.$
$\phi (v) = b.$
We assume that the choice of
![]() $ x_0y_0$
is always the same for all
$ x_0y_0$
is always the same for all
![]() $ H$
, thus
$ H$
, thus
![]() $ S_H$
is uniquely determined for all
$ S_H$
is uniquely determined for all
![]() $ H$
. We note that both
$ H$
. We note that both
![]() $ S_H + a$
and
$ S_H + a$
and
![]() $ S_H + b$
are subdivisions of
$ S_H + b$
are subdivisions of
![]() $ H$
. The following definition is a graph containing information on pairs that have many
$ H$
. The following definition is a graph containing information on pairs that have many
![]() $ \mathrm {Sub}(H)$
-exchangers.
$ \mathrm {Sub}(H)$
-exchangers.
Definition 4.7.
Let
![]() $ H$
be a graph and
$ H$
be a graph and
![]() $ d \gt 0$
. For a given
$ d \gt 0$
. For a given
![]() $ n$
-vertex graph
$ n$
-vertex graph
![]() $ G$
and
$ G$
and
![]() $ B \subseteq V(G)$
, let
$ B \subseteq V(G)$
, let
![]() $ F$
be an auxiliary graph on the vertex set
$ F$
be an auxiliary graph on the vertex set
![]() $ V(G)$
such that
$ V(G)$
such that
![]() $ uv \in E(F)$
if and only if
$ uv \in E(F)$
if and only if
![]() $ u \notin B, v \in B$
and the number of
$ u \notin B, v \in B$
and the number of
![]() $ \mathrm {Sub}(H)$
-exchangers for
$ \mathrm {Sub}(H)$
-exchangers for
![]() $ \{u, v\}$
is at least
$ \{u, v\}$
is at least
![]() $ dn^{v(S_H)}$
. We say such an auxiliary graph
$ dn^{v(S_H)}$
. We say such an auxiliary graph
![]() $ F$
is a
$ F$
is a
![]() $(d, B)$
-exchanging graph.
$(d, B)$
-exchanging graph.
In order to prove the existence of
![]() $ \mathrm {Sub}(H)$
-absorbers, we need to collect several lemmas regarding the following definition.
$ \mathrm {Sub}(H)$
-absorbers, we need to collect several lemmas regarding the following definition.
Definition 4.8.
Let
![]() $ n$
,
$ n$
,
![]() $ t$
be positive integers, and let
$ t$
be positive integers, and let
![]() $ d \in (0, 1)$
. Let
$ d \in (0, 1)$
. Let
![]() $ X$
,
$ X$
,
![]() $ Y$
be sets such that
$ Y$
be sets such that
![]() $ |X| \leq n^2$
and
$ |X| \leq n^2$
and
![]() $ |Y| = n$
. We say a collection of pairs
$ |Y| = n$
. We say a collection of pairs
![]() $ \mathcal {P} \subseteq X \times \binom {Y}{t}$
is an
$ \mathcal {P} \subseteq X \times \binom {Y}{t}$
is an
![]() $(n, t, d)$
-family on
$(n, t, d)$
-family on
![]() $ (X, Y)$
if
$ (X, Y)$
if
![]() $ |\{Z \subseteq Y\,:\, (x, Z) \in \mathcal {P}\}| \geq dn^t$
for all
$ |\{Z \subseteq Y\,:\, (x, Z) \in \mathcal {P}\}| \geq dn^t$
for all
![]() $ x \in X$
.
$ x \in X$
.
The following is the key lemma to obtain
![]() $ \mathrm {Sub}(H)$
-absorbers.
$ \mathrm {Sub}(H)$
-absorbers.
Lemma 4.9.
Let
![]() $ 0 \lt \frac {1}{n} \ll \beta \ll d, \alpha , \frac {1}{t} \leq 1$
. Let
$ 0 \lt \frac {1}{n} \ll \beta \ll d, \alpha , \frac {1}{t} \leq 1$
. Let
![]() $ \mathcal {P}$
be an
$ \mathcal {P}$
be an
![]() $(n, t, d)$
-family on a pair of sets
$(n, t, d)$
-family on a pair of sets
![]() $ (X, Y)$
. Then there is
$ (X, Y)$
. Then there is
![]() $ \mathcal {Y} \subseteq \binom {Y}{t}$
which satisfies the following:
$ \mathcal {Y} \subseteq \binom {Y}{t}$
which satisfies the following:
-
•
 $ \mathcal {Y}$
is a collection of pairwise disjoint sets,
$ \mathcal {Y}$
is a collection of pairwise disjoint sets,
-
•
 $ |\mathcal {Y}| \leq \frac {\alpha }{t} n$
and
$ |\mathcal {Y}| \leq \frac {\alpha }{t} n$
and
 $ |\mathcal {Y}|$
is even,
$ |\mathcal {Y}|$
is even,
-
• for every
 $ x \in X$
, the size of the set
$ x \in X$
, the size of the set
 $ \{Z \in \mathcal {Y}: (x, Z) \in \mathcal {P}\}$
is at least
$ \{Z \in \mathcal {Y}: (x, Z) \in \mathcal {P}\}$
is at least
 $ \beta n$
.
$ \beta n$
.
Proof. Let
![]() $ c = \min \{\frac {\alpha }{2}, \frac {d}{10}\}$
. Consider a random family
$ c = \min \{\frac {\alpha }{2}, \frac {d}{10}\}$
. Consider a random family
![]() $ \mathcal {T}$
of size
$ \mathcal {T}$
of size
![]() $ t$
subsets of
$ t$
subsets of
![]() $ Y$
, such that each set in
$ Y$
, such that each set in
![]() $ \binom {Y}{t}$
is selected independently at random with the probability
$ \binom {Y}{t}$
is selected independently at random with the probability
![]() $ p = \frac {c}{n^{t - 1}}$
. Then
$ p = \frac {c}{n^{t - 1}}$
. Then
![]() $ |\mathcal {T}|$
has a binomial distribution with an expectation less than or equal to
$ |\mathcal {T}|$
has a binomial distribution with an expectation less than or equal to
![]() $ \frac {\alpha }{2 t} n$
. By Chebyshev’s inequality, with probability
$ \frac {\alpha }{2 t} n$
. By Chebyshev’s inequality, with probability
![]() $ 1 - o(1)$
, the following holds.
$ 1 - o(1)$
, the following holds.
For each
![]() $ x \in X$
, let
$ x \in X$
, let
![]() $ \mathcal {Z}_x \,:\!=\, \{Z \subseteq Y\,:\, (x, Z) \in \mathcal {P}\}$
. Then the size
$ \mathcal {Z}_x \,:\!=\, \{Z \subseteq Y\,:\, (x, Z) \in \mathcal {P}\}$
. Then the size
![]() $ |\mathcal {T} \cap \mathcal {Z}_x|$
has a binomial distribution with an expectation
$ |\mathcal {T} \cap \mathcal {Z}_x|$
has a binomial distribution with an expectation
![]() $ |\mathcal {Z}_x| p \geq cd n$
for every
$ |\mathcal {Z}_x| p \geq cd n$
for every
![]() $ x \in X$
. By Chernoff bound, for each
$ x \in X$
. By Chernoff bound, for each
![]() $ x \in X$
, the inequality
$ x \in X$
, the inequality
![]() $ |\mathcal {T} \cap \mathcal {Z}_x| \geq \frac {cd}{2} n$
holds with probability
$ |\mathcal {T} \cap \mathcal {Z}_x| \geq \frac {cd}{2} n$
holds with probability
![]() $ 1 - o(n^{-3})$
. Since
$ 1 - o(n^{-3})$
. Since
![]() $ |X| \leq n^2$
, we have the following with probability
$ |X| \leq n^2$
, we have the following with probability
![]() $ 1 - o(1)$
.
$ 1 - o(1)$
.
We now count the number of intersecting pairs in
![]() $ \mathcal {T}$
. Let
$ \mathcal {T}$
. Let
![]() $ I$
be a random variable which is the number of intersecting pairs of
$ I$
be a random variable which is the number of intersecting pairs of
![]() $ \mathcal {T}$
. Since we have
$ \mathcal {T}$
. Since we have
![]() $ |\{(P, Q)\,:\, P, Q \subseteq [n],\text { } P \cap Q \neq \textit ptyset, \text { and } |P| = |Q| = t\}| \leq n^{2t - 1}$
, and each
$ |\{(P, Q)\,:\, P, Q \subseteq [n],\text { } P \cap Q \neq \textit ptyset, \text { and } |P| = |Q| = t\}| \leq n^{2t - 1}$
, and each
![]() $ P$
,
$ P$
,
![]() $ Q$
are chosen to be in
$ Q$
are chosen to be in
![]() $ \mathcal {T}$
with probability
$ \mathcal {T}$
with probability
![]() $ p = \frac {c}{n^{t-1}}$
, we have
$ p = \frac {c}{n^{t-1}}$
, we have
![]() $ \mathbb {E}(I) \leq c^2 n$
. By Markov’s inequality, with probability at least
$ \mathbb {E}(I) \leq c^2 n$
. By Markov’s inequality, with probability at least
![]() $ \frac {1}{2}$
,
$ \frac {1}{2}$
,
Thus, for all sufficiently large
![]() $ n$
, there is a family
$ n$
, there is a family
![]() $ \mathcal {T}$
that satisfies all Equations (1) to (3). Let
$ \mathcal {T}$
that satisfies all Equations (1) to (3). Let
![]() $ \mathcal {Y}$
be a collection obtained from
$ \mathcal {Y}$
be a collection obtained from
![]() $ \mathcal {T}$
by removing intersecting pairs from
$ \mathcal {T}$
by removing intersecting pairs from
![]() $ \mathcal {T}$
and removing at most one arbitrary element to ensure that
$ \mathcal {T}$
and removing at most one arbitrary element to ensure that
![]() $ |\mathcal {Y}|$
is even.
$ |\mathcal {Y}|$
is even.
Then
![]() $ \mathcal {Y}$
is a collection of pairwise disjoint sets and by (1), we have
$ \mathcal {Y}$
is a collection of pairwise disjoint sets and by (1), we have
![]() $ |\mathcal {Y}| \leq |\mathcal {T}| \leq \frac {\alpha }{t} n$
and
$ |\mathcal {Y}| \leq |\mathcal {T}| \leq \frac {\alpha }{t} n$
and
![]() $ |\mathcal {Y}|$
is even. By (2) and (3), the size of the intersection
$ |\mathcal {Y}|$
is even. By (2) and (3), the size of the intersection
![]() $ |\mathcal {Y} \cap \mathcal {Z}_x| \geq \frac {cd}{2} n - 2c^2 n - 1 \geq \frac {\alpha d^2}{100} n$
for all
$ |\mathcal {Y} \cap \mathcal {Z}_x| \geq \frac {cd}{2} n - 2c^2 n - 1 \geq \frac {\alpha d^2}{100} n$
for all
![]() $ x \in X$
. We now set
$ x \in X$
. We now set
![]() $ \beta = \frac {\alpha d^2}{100}$
. Then
$ \beta = \frac {\alpha d^2}{100}$
. Then
![]() $ \mathcal {Y}$
is the desired collection. This completes the proof.
$ \mathcal {Y}$
is the desired collection. This completes the proof.
We remark that Lemma4.9 is a systematisation of Lemma2.3 from [Reference Rödl, Ruciński and Szemerédi27]. One direct application of Lemma4.9 is the existence of one-side perfect matchings for small sets, which is the following:
Lemma 4.10.
Let
![]() $0 \lt \frac {1}{n} \ll \beta \ll \alpha , \eta \lt 1.$
Let
$0 \lt \frac {1}{n} \ll \beta \ll \alpha , \eta \lt 1.$
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph. Suppose that a vertex subset
$n$
-vertex graph. Suppose that a vertex subset
![]() $B \subseteq V(G)$
has size at least
$B \subseteq V(G)$
has size at least
![]() $\eta n$
and all vertices
$\eta n$
and all vertices
![]() $v \in V(G) \setminus B$
satisfy
$v \in V(G) \setminus B$
satisfy
![]() $d(v, B) \geq \eta n.$
Then there is a set
$d(v, B) \geq \eta n.$
Then there is a set
![]() $B^{\prime} \subseteq B$
such that
$B^{\prime} \subseteq B$
such that
![]() $|B^{\prime}| \leq \alpha n$
and for any
$|B^{\prime}| \leq \alpha n$
and for any
![]() $U \subseteq V(G) \setminus B$
with size at most
$U \subseteq V(G) \setminus B$
with size at most
![]() $\beta n$
, there is a matching on
$\beta n$
, there is a matching on
![]() $G[U, B^{\prime}]$
which covers all vertices in
$G[U, B^{\prime}]$
which covers all vertices in
![]() $U.$
$U.$
Proof. Let
![]() $X = V(G) \setminus B.$
Let
$X = V(G) \setminus B.$
Let
![]() $\mathcal {P} = \{(x, \{y\}) \in X \times \binom {V(G)}{1} \,:\, xy \in E(G[X, B])\}.$
Then
$\mathcal {P} = \{(x, \{y\}) \in X \times \binom {V(G)}{1} \,:\, xy \in E(G[X, B])\}.$
Then
![]() $\mathcal {P}$
is an
$\mathcal {P}$
is an
![]() $(n, 1, \eta )$
-family on
$(n, 1, \eta )$
-family on
![]() $(X, V(G)).$
As
$(X, V(G)).$
As
![]() $\frac {1}{n} \ll \beta \ll \alpha , \eta$
, by applying Lemma4.9 with the parameters
$\frac {1}{n} \ll \beta \ll \alpha , \eta$
, by applying Lemma4.9 with the parameters
![]() $\alpha$
,
$\alpha$
,
![]() $\eta$
,
$\eta$
,
![]() $\beta$
, and
$\beta$
, and
![]() $n$
playing the roles of
$n$
playing the roles of
![]() $\alpha$
,
$\alpha$
,
![]() $d$
,
$d$
,
![]() $\beta$
, and
$\beta$
, and
![]() $n$
, respectively, we obtain
$n$
, respectively, we obtain
![]() $\mathcal {Y} \subseteq \binom {B}{1}$
satisfying the following.
$\mathcal {Y} \subseteq \binom {B}{1}$
satisfying the following.
![]() $|\mathcal {Y}| \leq \alpha n$
and
$|\mathcal {Y}| \leq \alpha n$
and
![]() $|\{(v, \{b\}) \in \mathcal {P} \,:\, \{b\} \in \mathcal {Y}\}| \geq \beta n$
for all
$|\{(v, \{b\}) \in \mathcal {P} \,:\, \{b\} \in \mathcal {Y}\}| \geq \beta n$
for all
![]() $x \in X.$
Let
$x \in X.$
Let
![]() $B^{\prime} = \bigcup _{\{b\} \in \mathcal {Y}} \{b\}.$
Then
$B^{\prime} = \bigcup _{\{b\} \in \mathcal {Y}} \{b\}.$
Then
![]() $|B^{\prime}| \leq \alpha n$
and for any vertex
$|B^{\prime}| \leq \alpha n$
and for any vertex
![]() $v \in V(G) \setminus B$
, the degree
$v \in V(G) \setminus B$
, the degree
![]() $d(v, B^{\prime}) \geq \beta n.$
Thus, for any subset
$d(v, B^{\prime}) \geq \beta n.$
Thus, for any subset
![]() $U \subseteq V(G) \setminus B$
with size at most
$U \subseteq V(G) \setminus B$
with size at most
![]() $\beta n$
, we can find a matching
$\beta n$
, we can find a matching
![]() $M$
greedily in
$M$
greedily in
![]() $G[U, B^{\prime}]$
which covers all vertices of
$G[U, B^{\prime}]$
which covers all vertices of
![]() $U.$
$U.$
Using Lemma4.9, we can obtain the following lemma.
Lemma 4.11.
Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph and
$h$
-vertex graph and
![]() $0 \lt \frac {1}{n}, \beta \ll d, \alpha , \eta , \frac {1}{h} \lt 1.$
Let
$0 \lt \frac {1}{n}, \beta \ll d, \alpha , \eta , \frac {1}{h} \lt 1.$
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph and a vertex subset
$n$
-vertex graph and a vertex subset
![]() $B \subseteq V(G)$
has size at least
$B \subseteq V(G)$
has size at least
![]() $\eta n.$
Let
$\eta n.$
Let
![]() $F$
be the
$F$
be the
![]() $(d, B)$
-exchanging graph of
$(d, B)$
-exchanging graph of
![]() $G.$
Let
$G.$
Let
![]() $U = \{v \in V(G) \setminus B \,:\, d_F(v) \geq \frac {\eta }{3} n\}.$
Then there exists a set
$U = \{v \in V(G) \setminus B \,:\, d_F(v) \geq \frac {\eta }{3} n\}.$
Then there exists a set
![]() $A \subseteq V(G)$
satisfying the following:
$A \subseteq V(G)$
satisfying the following:
-
•
 $G[A]$
has a perfect
$G[A]$
has a perfect
 $H$
-subdivision tiling,
$H$
-subdivision tiling,
-
•
 $|A| \leq \alpha n$
,
$|A| \leq \alpha n$
, -
• for any
 $U^{\prime} \subseteq U \setminus A$
with
$U^{\prime} \subseteq U \setminus A$
with
 $|U^{\prime}| \leq \beta n$
, there exists a subset
$|U^{\prime}| \leq \beta n$
, there exists a subset
 $W \subseteq A \cap B$
such that
$W \subseteq A \cap B$
such that
 $|W| = |U^{\prime}|$
and
$|W| = |U^{\prime}|$
and
 $G[(A \cup U^{\prime}) \setminus W]$
has a perfect
$G[(A \cup U^{\prime}) \setminus W]$
has a perfect
 $H$
-subdivision tiling.
$H$
-subdivision tiling.
Proof. We recall that
![]() $\hat {S}_H$
is a graph defined in Definition4.6 which has two vertices
$\hat {S}_H$
is a graph defined in Definition4.6 which has two vertices
![]() $u$
and
$u$
and
![]() $v$
such that both
$v$
such that both
![]() $S_H - u$
and
$S_H - u$
and
![]() $S_H - v$
contain spanning subdivisions of
$S_H - v$
contain spanning subdivisions of
![]() $H.$
$H.$
Let
For each
![]() $u \in U$
, the number of pairs
$u \in U$
, the number of pairs
![]() $(v, S) \in B \times \binom {V(G)}{v(S_H)}$
such that
$(v, S) \in B \times \binom {V(G)}{v(S_H)}$
such that
![]() $S$
is a
$S$
is a
![]() $\mathrm {Sub}(H)$
-exchanger for
$\mathrm {Sub}(H)$
-exchanger for
![]() $\{u, v\}$
is at least
$\{u, v\}$
is at least
![]() $\frac {\eta d}{3} n^{v(S_H) + 1}.$
Thus,
$\frac {\eta d}{3} n^{v(S_H) + 1}.$
Thus,
![]() $\mathcal {P}$
is an
$\mathcal {P}$
is an
![]() $(n, v(S_H) + 1, \frac {\eta d}{3(v(S_H) + 1)})$
-family on
$(n, v(S_H) + 1, \frac {\eta d}{3(v(S_H) + 1)})$
-family on
![]() $(U, V(G)).$
$(U, V(G)).$
As
![]() $v(S_H) + 1 \leq h^2$
and
$v(S_H) + 1 \leq h^2$
and
![]() $\frac {1}{n}, \beta \ll d, \alpha , \eta , \frac {1}{h}$
, by applying Lemma4.9 with
$\frac {1}{n}, \beta \ll d, \alpha , \eta , \frac {1}{h}$
, by applying Lemma4.9 with
![]() $v(S_H) + 1$
,
$v(S_H) + 1$
,
![]() $\alpha$
,
$\alpha$
,
![]() $\frac {\eta d}{3(v(S_H) + 1)}$
and
$\frac {\eta d}{3(v(S_H) + 1)}$
and
![]() $\beta (v(S_H) + 1)$
playing the roles of
$\beta (v(S_H) + 1)$
playing the roles of
![]() $t$
,
$t$
,
![]() $\alpha$
,
$\alpha$
,
![]() $d$
, and
$d$
, and
![]() $\beta$
, respectively, we obtain a collection of vertex-disjoint subsets
$\beta$
, respectively, we obtain a collection of vertex-disjoint subsets
![]() $\mathcal {Y} \subseteq \binom {V(G)}{v(S_H) + 1}$
satisfying the following.
$\mathcal {Y} \subseteq \binom {V(G)}{v(S_H) + 1}$
satisfying the following.
-
1.
 $|\mathcal {Y}| \leq \frac {\alpha }{v(S_H) + 1} n$
,
$|\mathcal {Y}| \leq \frac {\alpha }{v(S_H) + 1} n$
, -
2.
 $|\{Z \in \mathcal {Y} \,:\, (u, Z) \in \mathcal {P} \}| \geq \beta (v(S_H) + 1) n$
for all
$|\{Z \in \mathcal {Y} \,:\, (u, Z) \in \mathcal {P} \}| \geq \beta (v(S_H) + 1) n$
for all
 $u \in U.$
$u \in U.$
Let
![]() $A \,:\!=\, \bigcup _{Z \in \mathcal {Y}} Z.$
Then
$A \,:\!=\, \bigcup _{Z \in \mathcal {Y}} Z.$
Then
![]() $|A| \leq \alpha n.$
Let
$|A| \leq \alpha n.$
Let
![]() $U^{\prime} \subseteq U \setminus A$
with size at most
$U^{\prime} \subseteq U \setminus A$
with size at most
![]() $\beta n.$
By our choice of
$\beta n.$
By our choice of
![]() $U$
and
$U$
and
![]() $\mathcal {Y}$
, for each vertex
$\mathcal {Y}$
, for each vertex
![]() $x \in U^{\prime}$
, there are at least
$x \in U^{\prime}$
, there are at least
![]() $\frac {\beta (v(S_H) + 1)}{v(S_H) + 1} n = \beta n$
distinct pairs
$\frac {\beta (v(S_H) + 1)}{v(S_H) + 1} n = \beta n$
distinct pairs
![]() $(u, v)$
which use distinct
$(u, v)$
which use distinct
![]() $\mathrm {Sub}(H)$
-exchangers in
$\mathrm {Sub}(H)$
-exchangers in
![]() $\mathcal {Y}$
such that
$\mathcal {Y}$
such that
![]() $v \in A \cap B$
and there is
$v \in A \cap B$
and there is
![]() $Z \in \mathcal {Y}$
, where
$Z \in \mathcal {Y}$
, where
![]() $v \in Z$
and
$v \in Z$
and
![]() $Z - v$
is a
$Z - v$
is a
![]() $\mathrm {Sub}(H)$
-exchanger for
$\mathrm {Sub}(H)$
-exchanger for
![]() $\{u, v\}.$
Thus, we can greedily exchange all vertices in
$\{u, v\}.$
Thus, we can greedily exchange all vertices in
![]() $U^{\prime}$
with a set of distinct vertices
$U^{\prime}$
with a set of distinct vertices
![]() $W$
, by using
$W$
, by using
![]() $\mathrm {Sub}(H)$
-exchangers, where
$\mathrm {Sub}(H)$
-exchangers, where
![]() $W \subseteq A \cap B$
and
$W \subseteq A \cap B$
and
![]() $|W| = |U^{\prime}|.$
$|W| = |U^{\prime}|.$
4.1.
Type-
 $1$
$1$
 $\mathrm {Sub}(H)$
-absorbers
$\mathrm {Sub}(H)$
-absorbers
The following lemma is useful to get
![]() $\mathrm {Sub}(H)$
-absorbers which use type-1
$\mathrm {Sub}(H)$
-absorbers which use type-1
![]() $\mathrm {Sub}(H)$
-absorbers.
$\mathrm {Sub}(H)$
-absorbers.
Lemma 4.12.
Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph and
$h$
-vertex graph and
![]() $0 \lt \frac {1}{n}, \beta \ll d, \alpha , \frac {1}{h} \leq 1.$
Let
$0 \lt \frac {1}{n}, \beta \ll d, \alpha , \frac {1}{h} \leq 1.$
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph and
$n$
-vertex graph and
![]() $F$
be the
$F$
be the
![]() $d$
-absorbing graph of
$d$
-absorbing graph of
![]() $G.$
Then there exists a set
$G.$
Then there exists a set
![]() $A \subseteq V(G)$
satisfying the following.
$A \subseteq V(G)$
satisfying the following.
-
•
 $ |A| \leq \alpha n$
,
$ |A| \leq \alpha n$
, -
•
 $ |A|$
is even,
$ |A|$
is even,
-
• The set
 $A$
is a
$A$
is a
 $\mathrm {Sub}(H)$
-absorber for any vertex set
$\mathrm {Sub}(H)$
-absorber for any vertex set
 $U$
such that
$U$
such that
 $U \subseteq V(G) \setminus A$
,
$U \subseteq V(G) \setminus A$
,
 $ |U| \leq \beta n$
, and
$ |U| \leq \beta n$
, and
 $F[U]$
has a perfect matching.
$F[U]$
has a perfect matching.
Proof. Let
Then
![]() $\mathcal {P}$
is an
$\mathcal {P}$
is an
![]() $(n, v(T^1_H), d)$
-family on
$(n, v(T^1_H), d)$
-family on
![]() $(E(F), V(G))$
. By applying Lemma4.9 with
$(E(F), V(G))$
. By applying Lemma4.9 with
![]() $v(T^1_H)$
,
$v(T^1_H)$
,
![]() $\alpha$
,
$\alpha$
,
![]() $d$
, and
$d$
, and
![]() $\beta$
playing the roles of
$\beta$
playing the roles of
![]() $t$
,
$t$
,
![]() $\alpha$
,
$\alpha$
,
![]() $d$
, and
$d$
, and
![]() $\beta$
, respectively, we obtain a collection of vertex-disjoint subsets
$\beta$
, respectively, we obtain a collection of vertex-disjoint subsets
![]() $\mathcal {Y} \subseteq \binom {V(G)}{v(T^1_H)}$
satisfying the following.
$\mathcal {Y} \subseteq \binom {V(G)}{v(T^1_H)}$
satisfying the following.
-
1.
 $ |\mathcal {Y}| \leq \frac {\alpha }{v(T^1_H)} n$
,
$ |\mathcal {Y}| \leq \frac {\alpha }{v(T^1_H)} n$
, -
2.
 $ |\mathcal {Y}|$
is even,
$ |\mathcal {Y}|$
is even, -
3.
 $ |\{Z \in \mathcal {Y} \,:\, (e, Z) \in \mathcal {P} \}| \geq \beta n$
for all
$ |\{Z \in \mathcal {Y} \,:\, (e, Z) \in \mathcal {P} \}| \geq \beta n$
for all
 $ e \in E(F)$
.
$ e \in E(F)$
.
Let
![]() $A = \bigcup _{Z \in \mathcal {Y}} Z$
. Then
$A = \bigcup _{Z \in \mathcal {Y}} Z$
. Then
![]() $ |A|$
is even and less than or equal to
$ |A|$
is even and less than or equal to
![]() $\alpha n$
. Let
$\alpha n$
. Let
![]() $U$
be a subset of
$U$
be a subset of
![]() $V(G) \setminus A$
with size at most
$V(G) \setminus A$
with size at most
![]() $\beta n$
. Assume
$\beta n$
. Assume
![]() $F[U]$
has a perfect matching
$F[U]$
has a perfect matching
![]() $M$
. Then
$M$
. Then
![]() $ e(M) \leq \frac {\beta }{2} n$
. By our choice of
$ e(M) \leq \frac {\beta }{2} n$
. By our choice of
![]() $\mathcal {Y}$
, for each edge
$\mathcal {Y}$
, for each edge
![]() $e \in E(M)$
, there are at least
$e \in E(M)$
, there are at least
![]() $\beta n$
distinct type-1
$\beta n$
distinct type-1
![]() $\mathrm {Sub}(H)$
-absorbers. Thus,
$\mathrm {Sub}(H)$
-absorbers. Thus,
![]() $A$
can absorb every pair
$A$
can absorb every pair
![]() $e \in E(M)$
greedily. This means
$e \in E(M)$
greedily. This means
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U$
. This proves the lemma.
$U$
. This proves the lemma.
4.2.
Type-
 $2$
and type-
$2$
and type-
 $3$
$3$
 $\mathrm {Sub}(H)$
-absorbers
$\mathrm {Sub}(H)$
-absorbers
In this subsection, we will show how we can obtain
![]() $\mathrm {Sub}(H)$
-absorbers via type-2 and type-3
$\mathrm {Sub}(H)$
-absorbers via type-2 and type-3
![]() $\mathrm {Sub}(H)$
-absorbers, respectively.
$\mathrm {Sub}(H)$
-absorbers, respectively.
Lemma 4.13.
Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph and
$h$
-vertex graph and
![]() $0 \lt \frac {1}{n}, \beta \ll d, \alpha , \eta , \frac {1}{h} \leq 1.$
Let
$0 \lt \frac {1}{n}, \beta \ll d, \alpha , \eta , \frac {1}{h} \leq 1.$
Let
![]() $j \in \{2, 3\}.$
Let
$j \in \{2, 3\}.$
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph and let
$n$
-vertex graph and let
![]() $B \subseteq V(G)$
with size at least
$B \subseteq V(G)$
with size at least
![]() $\eta n$
such that for all
$\eta n$
such that for all
![]() $v \in B$
, there are at least
$v \in B$
, there are at least
![]() $dn^{v(T^j_H)}$
type-
$dn^{v(T^j_H)}$
type-
![]() $j$
$j$
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $v.$
Let
$v.$
Let
![]() $F_1$
and
$F_1$
and
![]() $F_2$
be the
$F_2$
be the
![]() $d$
-absorbing graph and the
$d$
-absorbing graph and the
![]() $(d, B)$
-exchanging graph of
$(d, B)$
-exchanging graph of
![]() $G$
, respectively. Assume that for every
$G$
, respectively. Assume that for every
![]() $v \in V(G) \setminus B$
, at least one of the inequalities
$v \in V(G) \setminus B$
, at least one of the inequalities
![]() $d_{F_1}(v;\,B) \geq \frac {\eta }{3} n$
or
$d_{F_1}(v;\,B) \geq \frac {\eta }{3} n$
or
![]() $d_{F_2}(v;\,B) \geq \frac {\eta }{3} n$
holds. Then, there is a set
$d_{F_2}(v;\,B) \geq \frac {\eta }{3} n$
holds. Then, there is a set
![]() $A \subseteq V(G)$
with size at most
$A \subseteq V(G)$
with size at most
![]() $\alpha n$
such that for all
$\alpha n$
such that for all
![]() $U \subseteq V(G) \setminus A$
with size at most
$U \subseteq V(G) \setminus A$
with size at most
![]() $\beta n$
, the set
$\beta n$
, the set
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U.$
$U.$
Proof. Choose additional constants
![]() $\beta _0, \alpha _0, \alpha _1$
so that the following holds:
$\beta _0, \alpha _0, \alpha _1$
so that the following holds:
We write
![]() $R = V(G) \setminus B$
, and
$R = V(G) \setminus B$
, and
![]() $X = \{v \in R \,:\, d_{F_1}(v;\,B) \geq \frac {\eta }{3} n\}$
. Let
$X = \{v \in R \,:\, d_{F_1}(v;\,B) \geq \frac {\eta }{3} n\}$
. Let
![]() $Y = R \setminus X.$
We note that for all
$Y = R \setminus X.$
We note that for all
![]() $v \in Y$
, we have
$v \in Y$
, we have
![]() $d_{F_2}(v;\,B) \geq \frac {\eta }{3} n.$
We now collect the following two claims.
$d_{F_2}(v;\,B) \geq \frac {\eta }{3} n.$
We now collect the following two claims.
Claim 1.
There exists a set
![]() $A_0 \subseteq V(G)$
satisfying the following. The size of the set
$A_0 \subseteq V(G)$
satisfying the following. The size of the set
![]() $A_0$
is less than or equal to
$A_0$
is less than or equal to
![]() $\alpha _0 n$
, and for any
$\alpha _0 n$
, and for any
![]() $U \subseteq B \setminus A_0$
with size at most
$U \subseteq B \setminus A_0$
with size at most
![]() $\beta _0 n$
, the set
$\beta _0 n$
, the set
![]() $A_0$
is a
$A_0$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U.$
$U.$
Proof of Claim 1. Let
Then
![]() $\mathcal {P}$
is an
$\mathcal {P}$
is an
![]() $(n, v(T^j_H), d)$
-family on
$(n, v(T^j_H), d)$
-family on
![]() $(B, V(G))$
. By applying Lemma4.9 with
$(B, V(G))$
. By applying Lemma4.9 with
![]() $v(T^j_H)$
,
$v(T^j_H)$
,
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $d$
, and
$d$
, and
![]() $\beta _0$
playing the roles of
$\beta _0$
playing the roles of
![]() $t$
,
$t$
,
![]() $\alpha$
,
$\alpha$
,
![]() $d$
, and
$d$
, and
![]() $\beta$
, respectively, we obtain a collection of pairwise disjoint sets
$\beta$
, respectively, we obtain a collection of pairwise disjoint sets
![]() $\mathcal {Y} \subseteq \binom {V(G)}{v(T^j_H)}$
satisfying the following.
$\mathcal {Y} \subseteq \binom {V(G)}{v(T^j_H)}$
satisfying the following.
-
1.
 $ |\mathcal {Y}| \leq \frac {\alpha _0}{v(T^j_H)} n$
,
$ |\mathcal {Y}| \leq \frac {\alpha _0}{v(T^j_H)} n$
, -
2.
 $ |\{Z \in \mathcal {Y} \,:\, (x, Z) \in \mathcal {P} \}| \geq \beta _0 n$
for all
$ |\{Z \in \mathcal {Y} \,:\, (x, Z) \in \mathcal {P} \}| \geq \beta _0 n$
for all
 $x \in B.$
$x \in B.$
Let
![]() $A_0 \,:\!=\, \bigcup _{Z \in \mathcal {Y}} Z.$
Then
$A_0 \,:\!=\, \bigcup _{Z \in \mathcal {Y}} Z.$
Then
![]() $ |A_0| \leq \alpha _0 n.$
Let
$ |A_0| \leq \alpha _0 n.$
Let
![]() $U \subseteq B \setminus A_0$
with size at most
$U \subseteq B \setminus A_0$
with size at most
![]() $\beta _0 n.$
By our choice of
$\beta _0 n.$
By our choice of
![]() $\mathcal {Y}$
, for each vertex
$\mathcal {Y}$
, for each vertex
![]() $x \in U$
, there are at least
$x \in U$
, there are at least
![]() $\beta _0 n$
distinct type-
$\beta _0 n$
distinct type-
![]() $j$
$j$
![]() $\mathrm {Sub}(H)$
-absorbers in
$\mathrm {Sub}(H)$
-absorbers in
![]() $A_0$
. Thus,
$A_0$
. Thus,
![]() $A_0$
can absorb all vertices in
$A_0$
can absorb all vertices in
![]() $U$
greedily. This means
$U$
greedily. This means
![]() $A_0$
is a
$A_0$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U.$
This proves the claim.
$U.$
This proves the claim.
Claim 2.
There exists a set
![]() $ A_1 \subseteq V(G)$
with size at most
$ A_1 \subseteq V(G)$
with size at most
![]() $ \alpha _1 n$
satisfying the following: for any
$ \alpha _1 n$
satisfying the following: for any
![]() $ U \subseteq (B \cup X) \setminus A_1$
with size at most
$ U \subseteq (B \cup X) \setminus A_1$
with size at most
![]() $ \beta n$
, the set
$ \beta n$
, the set
![]() $ A_1$
is a
$ A_1$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $ U$
.
$ U$
.
Proof of Claim 2. We fix additional parameters
![]() $\beta ^{\prime\prime}_0, \alpha ^{\prime\prime}_0, \beta ^{\prime}_0, \alpha ^{\prime}_0$
so that the following holds:
$\beta ^{\prime\prime}_0, \alpha ^{\prime\prime}_0, \beta ^{\prime}_0, \alpha ^{\prime}_0$
so that the following holds:
![]() $\beta \ll \beta ^{\prime\prime}_0 \ll \alpha ^{\prime\prime}_0 \ll \beta _0, \beta ^{\prime}_0 \ll \alpha _0, \alpha ^{\prime}_0 \ll \alpha _1$
. By Claim1, there exists a set
$\beta \ll \beta ^{\prime\prime}_0 \ll \alpha ^{\prime\prime}_0 \ll \beta _0, \beta ^{\prime}_0 \ll \alpha _0, \alpha ^{\prime}_0 \ll \alpha _1$
. By Claim1, there exists a set
![]() $ A_0 \subseteq B$
such that
$ A_0 \subseteq B$
such that
![]() $ |A_0| \leq \alpha _0 n$
and for any
$ |A_0| \leq \alpha _0 n$
and for any
![]() $ U \subseteq B \setminus A_0$
with size at most
$ U \subseteq B \setminus A_0$
with size at most
![]() $ \beta _0 n$
, the set
$ \beta _0 n$
, the set
![]() $ A_0$
is a
$ A_0$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $ U$
. Let
$ U$
. Let
![]() $ G_1 = G - A_0$
,
$ G_1 = G - A_0$
,
![]() $ B_1 = B \setminus A_0$
, and
$ B_1 = B \setminus A_0$
, and
![]() $ X_1 = X \setminus A_0$
. Then
$ X_1 = X \setminus A_0$
. Then
![]() $ v(G_1) \geq (1-\alpha _0)n$
and
$ v(G_1) \geq (1-\alpha _0)n$
and
![]() $ |B_1| \geq \frac {\eta }{2} n$
. By Observation2.1, we know that for every vertex
$ |B_1| \geq \frac {\eta }{2} n$
. By Observation2.1, we know that for every vertex
![]() $ v \in B_1$
, the number of type-
$ v \in B_1$
, the number of type-
![]() $ j$
$ j$
![]() $\mathrm {Sub}(H)$
-absorbers in
$\mathrm {Sub}(H)$
-absorbers in
![]() $ G_1$
is at least
$ G_1$
is at least
![]() $\frac {d}{2}n_1^{v(T^j_H)}$
, and for each pair of vertices
$\frac {d}{2}n_1^{v(T^j_H)}$
, and for each pair of vertices
![]() $ (u, v) \in X_1 \times B_1$
, where
$ (u, v) \in X_1 \times B_1$
, where
![]() $ uv \in E(F_1)$
, the number of type-1
$ uv \in E(F_1)$
, the number of type-1
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $ \{u, v\}$
is at least
$ \{u, v\}$
is at least
![]() $\frac {d}{2}n_1^{v(T^1_H)}$
. Let
$\frac {d}{2}n_1^{v(T^1_H)}$
. Let
![]() $ F^{\prime}_1$
be the
$ F^{\prime}_1$
be the
![]() $\frac {d}{2}$
-absorbing graph of
$\frac {d}{2}$
-absorbing graph of
![]() $ G_1$
. Then for every vertex
$ G_1$
. Then for every vertex
![]() $ v \in X_1$
, the degree
$ v \in X_1$
, the degree
![]() $ d_{F^{\prime}_1}(v,\, B_1) \geq \frac {\eta }{3}n - \alpha _0 n \geq \frac {\eta }{4}n$
.
$ d_{F^{\prime}_1}(v,\, B_1) \geq \frac {\eta }{3}n - \alpha _0 n \geq \frac {\eta }{4}n$
.
By Lemma4.12, there is
![]() $ A^{\prime}_0 \subseteq V(G_1)$
with size at most
$ A^{\prime}_0 \subseteq V(G_1)$
with size at most
![]() $ \alpha ^{\prime}_0 n$
such that for any
$ \alpha ^{\prime}_0 n$
such that for any
![]() $ U \subseteq V(G_1) \setminus A^{\prime}_0$
with size less than
$ U \subseteq V(G_1) \setminus A^{\prime}_0$
with size less than
![]() $ \beta ^{\prime}_0 n$
which has a perfect matching in
$ \beta ^{\prime}_0 n$
which has a perfect matching in
![]() $ F^{\prime}_1$
, the set
$ F^{\prime}_1$
, the set
![]() $ A^{\prime}_0$
is a
$ A^{\prime}_0$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $ U$
.
$ U$
.
Let
![]() $ G_2 = G_1 - A^{\prime}_0$
,
$ G_2 = G_1 - A^{\prime}_0$
,
![]() $ B_2 = B_1 \setminus A^{\prime}_0$
, and
$ B_2 = B_1 \setminus A^{\prime}_0$
, and
![]() $ X_2 = X_1 \setminus A^{\prime}_0$
. Then
$ X_2 = X_1 \setminus A^{\prime}_0$
. Then
![]() $ v(G_2) \geq (1 - \alpha _0 - \alpha ^{\prime}_0)n$
and
$ v(G_2) \geq (1 - \alpha _0 - \alpha ^{\prime}_0)n$
and
![]() $ |B_2| \geq \frac {\eta }{4} n$
. For every
$ |B_2| \geq \frac {\eta }{4} n$
. For every
![]() $ v \in X_2$
, the degree
$ v \in X_2$
, the degree
![]() $ d_{F^{\prime}_1}(v;\,B_2) \geq \frac {\eta }{4} n - \alpha ^{\prime}_0 n \geq \frac {\eta }{10} n$
. Then by Lemma4.10, there is a set
$ d_{F^{\prime}_1}(v;\,B_2) \geq \frac {\eta }{4} n - \alpha ^{\prime}_0 n \geq \frac {\eta }{10} n$
. Then by Lemma4.10, there is a set
![]() $ A^{\prime\prime}_0 \subseteq B_2$
with size at most
$ A^{\prime\prime}_0 \subseteq B_2$
with size at most
![]() $ \alpha ^{\prime\prime}_0 n$
such that for any
$ \alpha ^{\prime\prime}_0 n$
such that for any
![]() $ U \subseteq X_2 \setminus A^{\prime\prime}_0$
with size less than
$ U \subseteq X_2 \setminus A^{\prime\prime}_0$
with size less than
![]() $ \beta ^{\prime\prime}_0 n$
, the graph
$ \beta ^{\prime\prime}_0 n$
, the graph
![]() $ F^{\prime}_1[U, A^{\prime\prime}_0]$
has a matching
$ F^{\prime}_1[U, A^{\prime\prime}_0]$
has a matching
![]() $ M$
which covers all vertices of
$ M$
which covers all vertices of
![]() $ U$
.
$ U$
.
Now, let
![]() $ A_1 = A_0 \cup A^{\prime}_0 \cup A^{\prime\prime}_0$
. Then the size
$ A_1 = A_0 \cup A^{\prime}_0 \cup A^{\prime\prime}_0$
. Then the size
![]() $ |A_1| \leq (\alpha _0 + \alpha ^{\prime}_0 + \alpha ^{\prime\prime}_0)n \leq \alpha _1 n$
. Note that since
$ |A_1| \leq (\alpha _0 + \alpha ^{\prime}_0 + \alpha ^{\prime\prime}_0)n \leq \alpha _1 n$
. Note that since
![]() $ A^{\prime\prime}_0 \subseteq B_1$
and
$ A^{\prime\prime}_0 \subseteq B_1$
and
![]() $ |A^{\prime\prime}_0| \leq \alpha ^{\prime\prime}_0 n \leq \frac {\beta ^{\prime}_0}{2} n$
, the induced graph
$ |A^{\prime\prime}_0| \leq \alpha ^{\prime\prime}_0 n \leq \frac {\beta ^{\prime}_0}{2} n$
, the induced graph
![]() $ G[A_0 \cup A^{\prime\prime}_0]$
has a perfect
$ G[A_0 \cup A^{\prime\prime}_0]$
has a perfect
![]() $ H$
-subdivision tiling. Since
$ H$
-subdivision tiling. Since
![]() $ G[A^{\prime}_0]$
also has a perfect
$ G[A^{\prime}_0]$
also has a perfect
![]() $ H$
-subdivision tiling and
$ H$
-subdivision tiling and
![]() $ A_0$
,
$ A_0$
,
![]() $ A^{\prime}_0$
,
$ A^{\prime}_0$
,
![]() $ A^{\prime\prime}_0$
are vertex-disjoint subsets,
$ A^{\prime\prime}_0$
are vertex-disjoint subsets,
![]() $ G[A_1]$
has a perfect
$ G[A_1]$
has a perfect
![]() $ H$
-subdivision tiling.
$ H$
-subdivision tiling.
We now claim that
![]() $ A_1$
is the desired
$ A_1$
is the desired
![]() $\mathrm {Sub}(H)$
-absorber. Let
$\mathrm {Sub}(H)$
-absorber. Let
![]() $ U \subseteq (B \cup X) \setminus A_1$
with size at most
$ U \subseteq (B \cup X) \setminus A_1$
with size at most
![]() $ \beta n$
. Let
$ \beta n$
. Let
![]() $ U_B = U \cap B$
and
$ U_B = U \cap B$
and
![]() $ U_X = U \cap X$
. Since
$ U_X = U \cap X$
. Since
![]() $ |U_X| \leq \beta n \leq \beta ^{\prime\prime}_0 n$
, by our choice of
$ |U_X| \leq \beta n \leq \beta ^{\prime\prime}_0 n$
, by our choice of
![]() $ A^{\prime\prime}_0$
, there is a set
$ A^{\prime\prime}_0$
, there is a set
![]() $ W \subseteq A^{\prime\prime}_0$
with the same size as
$ W \subseteq A^{\prime\prime}_0$
with the same size as
![]() $ U_X$
such that
$ U_X$
such that
![]() $ F^{\prime}_1[U_X, W]$
has a perfect matching. Since
$ F^{\prime}_1[U_X, W]$
has a perfect matching. Since
![]() $ |U_X \cup W| \leq 2\beta n \leq \beta ^{\prime}_0 n$
, the induced graph
$ |U_X \cup W| \leq 2\beta n \leq \beta ^{\prime}_0 n$
, the induced graph
![]() $ G[(A^{\prime}_0 \cup U_X \cup W)]$
has a perfect
$ G[(A^{\prime}_0 \cup U_X \cup W)]$
has a perfect
![]() $ H$
-subdivision tiling. Let
$ H$
-subdivision tiling. Let
![]() $ W^{\prime} = A^{\prime\prime}_0 \setminus W$
. We note that
$ W^{\prime} = A^{\prime\prime}_0 \setminus W$
. We note that
![]() $ |W^{\prime} \cup U_B| \leq \beta n \leq \beta _0 n$
and
$ |W^{\prime} \cup U_B| \leq \beta n \leq \beta _0 n$
and
![]() $ (W^{\prime} \cup U_B) \subseteq B_1$
, so by our choice of
$ (W^{\prime} \cup U_B) \subseteq B_1$
, so by our choice of
![]() $ A_1$
, the induced graph
$ A_1$
, the induced graph
![]() $ G[(A_0 \cup W^{\prime} \cup U_B)]$
has a perfect
$ G[(A_0 \cup W^{\prime} \cup U_B)]$
has a perfect
![]() $ H$
-subdivision tiling. Thus,
$ H$
-subdivision tiling. Thus,
![]() $ G[A_1 \cup U]$
also has a perfect
$ G[A_1 \cup U]$
also has a perfect
![]() $ H$
-subdivision tiling. Therefore, the set
$ H$
-subdivision tiling. Therefore, the set
![]() $ A_1$
is a
$ A_1$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $ U$
.
$ U$
.
By Claim2, there exists a set
![]() $A_1 \subseteq V(G)$
with size at most
$A_1 \subseteq V(G)$
with size at most
![]() $\alpha _1 n$
such that for any subset
$\alpha _1 n$
such that for any subset
![]() $U$
of
$U$
of
![]() $(B \cup X) \setminus A_1$
with size at most
$(B \cup X) \setminus A_1$
with size at most
![]() $\beta n$
, the set
$\beta n$
, the set
![]() $A_1$
is a
$A_1$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U$
. Let
$U$
. Let
![]() $G_1 = G - A_1$
,
$G_1 = G - A_1$
,
![]() $B_1 = B \setminus A_1$
,
$B_1 = B \setminus A_1$
,
![]() $X_1 = X \setminus A_1$
, and
$X_1 = X \setminus A_1$
, and
![]() $Y_1 = Y \setminus A_1$
. Then
$Y_1 = Y \setminus A_1$
. Then
![]() $v(G_1) \geq (1 - \alpha _1)n$
and
$v(G_1) \geq (1 - \alpha _1)n$
and
![]() $|B_1| \geq \frac {\eta }{2} n$
. By Observation2.1, we know that for each pair of vertices
$|B_1| \geq \frac {\eta }{2} n$
. By Observation2.1, we know that for each pair of vertices
![]() $(u, v) \in Y_1 \times B_1$
, where
$(u, v) \in Y_1 \times B_1$
, where
![]() $uv \in E(F_2)$
, the number of
$uv \in E(F_2)$
, the number of
![]() $\mathrm {Sub}(H)$
-exchangers for
$\mathrm {Sub}(H)$
-exchangers for
![]() $\{u, v\}$
is at least
$\{u, v\}$
is at least
![]() $\frac {d}{2} n_1^{v(S_H)}$
. Let
$\frac {d}{2} n_1^{v(S_H)}$
. Let
![]() $F^{\prime}_2$
be the
$F^{\prime}_2$
be the
![]() $(\frac {d}{2}, B_1)$
-exchanging graph of
$(\frac {d}{2}, B_1)$
-exchanging graph of
![]() $G_1$
. Then for every vertex
$G_1$
. Then for every vertex
![]() $v \in Y_1$
, the degree
$v \in Y_1$
, the degree
![]() $d_{F^{\prime}_2}(v, B_1) \geq \frac {\eta }{3}n - \alpha _1 n \geq \frac {\eta }{4} n$
.
$d_{F^{\prime}_2}(v, B_1) \geq \frac {\eta }{3}n - \alpha _1 n \geq \frac {\eta }{4} n$
.
By Lemma4.11, there is a subset
![]() $A_2$
of
$A_2$
of
![]() $V(G_1)$
with size at most
$V(G_1)$
with size at most
![]() $\alpha _1 n$
such that
$\alpha _1 n$
such that
![]() $G_1[A_2]$
has a perfect
$G_1[A_2]$
has a perfect
![]() $H$
-subdivision tiling and satisfies the following: for any
$H$
-subdivision tiling and satisfies the following: for any
![]() $U \subseteq Y_1 \setminus A_2$
with size at most
$U \subseteq Y_1 \setminus A_2$
with size at most
![]() $\beta n$
, there is a set
$\beta n$
, there is a set
![]() $W \subseteq (A_2 \cap X_1)$
with the same size as
$W \subseteq (A_2 \cap X_1)$
with the same size as
![]() $U$
such that
$U$
such that
![]() $G_1[(A_2 \cup U) \setminus W]$
also has a perfect
$G_1[(A_2 \cup U) \setminus W]$
also has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Now, let
![]() $A = A_1 \cup A_2$
. Then the inequality
$A = A_1 \cup A_2$
. Then the inequality
![]() $|A| \leq 2 \alpha _1 n \leq \alpha n$
holds. Note that both
$|A| \leq 2 \alpha _1 n \leq \alpha n$
holds. Note that both
![]() $G[A_1]$
and
$G[A_1]$
and
![]() $G[A_2]$
have perfect
$G[A_2]$
have perfect
![]() $H$
-subdivision tilings and
$H$
-subdivision tilings and
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are disjoint subsets of
$A_2$
are disjoint subsets of
![]() $V(G)$
. Thus,
$V(G)$
. Thus,
![]() $G[A]$
also has a perfect
$G[A]$
also has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
We now claim that
![]() $A$
is the desired
$A$
is the desired
![]() $\mathrm {Sub}(H)$
-absorber. Let
$\mathrm {Sub}(H)$
-absorber. Let
![]() $U \subseteq V(G) \setminus A$
with size at most
$U \subseteq V(G) \setminus A$
with size at most
![]() $\beta n$
. Let
$\beta n$
. Let
![]() $U_B = U \cap B$
,
$U_B = U \cap B$
,
![]() $U_X = U \cap X$
, and
$U_X = U \cap X$
, and
![]() $U_Y = U \cap Y$
. Since
$U_Y = U \cap Y$
. Since
![]() $|U_Y| \leq \beta n$
, by our choice of
$|U_Y| \leq \beta n$
, by our choice of
![]() $A_2$
, there is a set
$A_2$
, there is a set
![]() $W \subseteq (A_2 \cap X_1)$
with the same size as
$W \subseteq (A_2 \cap X_1)$
with the same size as
![]() $U_Y$
such that
$U_Y$
such that
![]() $G[(A_2 \cup U_Y) \setminus W]$
has a perfect
$G[(A_2 \cup U_Y) \setminus W]$
has a perfect
![]() $H$
-subdivision tiling. Note that
$H$
-subdivision tiling. Note that
![]() $|U_B \cup U_X \cup W| = |U| \leq \beta n$
and
$|U_B \cup U_X \cup W| = |U| \leq \beta n$
and
![]() $(U_B \cup U_X \cup W) \subseteq (B \cup X) \setminus A_1$
. Thus,
$(U_B \cup U_X \cup W) \subseteq (B \cup X) \setminus A_1$
. Thus,
![]() $U_B \cup U_X \cup W$
can be absorbed by
$U_B \cup U_X \cup W$
can be absorbed by
![]() $A_1$
. Thus,
$A_1$
. Thus,
![]() $G[A \cup U]$
has a perfect
$G[A \cup U]$
has a perfect
![]() $H$
-subdivision tiling. Therefore,
$H$
-subdivision tiling. Therefore,
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U$
. This completes the proof.
$U$
. This completes the proof.
5. Proofs
5.1. Proof sketch
In this section, we will prove our main results, Theorems1.8 and 1.9. By Proposition3.1, Proposition3.3, Proposition3.4, and Proposition3.5, it suffices to prove the following two lemmas.
Lemma 5.1.
Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph with
$h$
-vertex graph with
![]() $\mathrm {hcf}_{\xi }(H) = 1$
. Let
$\mathrm {hcf}_{\xi }(H) = 1$
. Let
![]() $0 \lt \frac {1}{n} \ll \gamma , \frac {1}{h} \leq 1$
. Let
$0 \lt \frac {1}{n} \ll \gamma , \frac {1}{h} \leq 1$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph. Then the following holds: If
$n$
-vertex graph. Then the following holds: If
![]() $\delta (G) \geq \left (1 - \frac {1}{\xi (H)} + \gamma \right )n$
, then
$\delta (G) \geq \left (1 - \frac {1}{\xi (H)} + \gamma \right )n$
, then
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Lemma 5.2.
Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph with
$h$
-vertex graph with
![]() $\mathrm {hcf}_{\xi }(H) = 2$
. Let
$\mathrm {hcf}_{\xi }(H) = 2$
. Let
![]() $0 \lt \frac {1}{n} \ll \gamma , \frac {1}{h} \leq 1$
. Let
$0 \lt \frac {1}{n} \ll \gamma , \frac {1}{h} \leq 1$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph, where
$n$
-vertex graph, where
![]() $n$
is even. Then the following holds: If
$n$
is even. Then the following holds: If
![]() $\delta (G) \geq \left (\max \{\frac {1}{3}, 1 - \frac {1}{\xi (H)} \} + \gamma \right )\!n$
, then
$\delta (G) \geq \left (\max \{\frac {1}{3}, 1 - \frac {1}{\xi (H)} \} + \gamma \right )\!n$
, then
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
The proofs of Lemmas5.1 and 5.2 will be provided in Subsections 5.2 and 5.3, respectively. The proofs crucially use the absorption method. Our proof strategy is as follows: Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $G$
be a host graph equipped with a minimum degree condition as in the statements of the above lemmas, in which we want to find a perfect
$G$
be a host graph equipped with a minimum degree condition as in the statements of the above lemmas, in which we want to find a perfect
![]() $H$
-subdivision tiling. Then, together with Observation3.6 and Theorem1.1, we can find an almost perfect
$H$
-subdivision tiling. Then, together with Observation3.6 and Theorem1.1, we can find an almost perfect
![]() $H$
-subdivision tiling in
$H$
-subdivision tiling in
![]() $G$
. Thus, we mainly focus on absorbing the remaining vertices by constructing suitable absorbers for all cases. A detailed proof sketch is provided below.
$G$
. Thus, we mainly focus on absorbing the remaining vertices by constructing suitable absorbers for all cases. A detailed proof sketch is provided below.
-
Step 1: Preprocessing. Apply the regularity lemma with properly chosen parameters on
 $G$
. After that, collect bad vertices and construct absorbing graphs on good vertices.
$G$
. After that, collect bad vertices and construct absorbing graphs on good vertices. -
Step 2: Place the absorber. Place an efficient
 $\mathrm {Sub}(H)$
-absorber by using the abundant properties of
$\mathrm {Sub}(H)$
-absorber by using the abundant properties of
 $\varepsilon$
-regular pairs.
$\varepsilon$
-regular pairs. -
Step 3: Cover almost all vertices. Find a set
 $W \subseteq V(G)$
outside of the
$W \subseteq V(G)$
outside of the
 $\mathrm {Sub}(H)$
-absorber obtained from Step 2 such that
$\mathrm {Sub}(H)$
-absorber obtained from Step 2 such that
 $G[W]$
has a perfect
$G[W]$
has a perfect
 $H$
-subdivision tiling,
$H$
-subdivision tiling,
 $W$
contains all bad vertices, and
$W$
contains all bad vertices, and
 $W$
covers all but at most a constant number of vertices of
$W$
covers all but at most a constant number of vertices of
 $G$
that are not in the
$G$
that are not in the
 $\mathrm {Sub}(H)$
-absorber.
$\mathrm {Sub}(H)$
-absorber. -
Step 4: Absorb the uncovered vertices. Absorb all the vertices that are not covered in Step 3 by using the
 $\mathrm {Sub}(H)$
-absorber obtained from Step 2.
$\mathrm {Sub}(H)$
-absorber obtained from Step 2.
In the above description, we omitted many details. To achieve Step 3, the following lemma would be useful.
Lemma 5.3.
Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph. Let
$h$
-vertex graph. Let
![]() $0 \lt \frac {1}{n} \ll \alpha , \frac {1}{h} \leq 1$
, and
$0 \lt \frac {1}{n} \ll \alpha , \frac {1}{h} \leq 1$
, and
![]() $0 \lt \frac {1}{C} \ll \frac {1}{h} \leq 1$
. Let
$0 \lt \frac {1}{C} \ll \frac {1}{h} \leq 1$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree at least
$n$
-vertex graph with minimum degree at least
![]() $\left (1 - \frac {1}{\xi (H)} + \alpha \right )n$
. Let
$\left (1 - \frac {1}{\xi (H)} + \alpha \right )n$
. Let
![]() $X$
be a subset of
$X$
be a subset of
![]() $V(G)$
with size at most
$V(G)$
with size at most
![]() $\frac {\alpha }{2v(H^*)}n$
. Then there is a set
$\frac {\alpha }{2v(H^*)}n$
. Then there is a set
![]() $W \subseteq V(G)$
with size at least
$W \subseteq V(G)$
with size at least
![]() $n - C$
such that
$n - C$
such that
![]() $X \subseteq W$
and
$X \subseteq W$
and
![]() $G[W]$
have a perfect
$G[W]$
have a perfect
![]() $H$
-subdivision tiling. Moreover, if
$H$
-subdivision tiling. Moreover, if
![]() $\mathrm {hcf}_{\xi }(H) = 2$
, we can get such a set
$\mathrm {hcf}_{\xi }(H) = 2$
, we can get such a set
![]() $W$
whose size is even.
$W$
whose size is even.
Proof. We will first find vertex-disjoint copies of
![]() $ H^*$
covering all vertices of
$ H^*$
covering all vertices of
![]() $ X$
. Let
$ X$
. Let
![]() $ X = \{v_1, \ldots , v_t\}$
where
$ X = \{v_1, \ldots , v_t\}$
where
![]() $ t \leq \frac {\alpha }{2v(H^*)}n$
. Assume for
$ t \leq \frac {\alpha }{2v(H^*)}n$
. Assume for
![]() $ i \lt t$
, we have
$ i \lt t$
, we have
![]() $ \mathcal {F}_i = \{F_1, \ldots , F_i\}$
, where
$ \mathcal {F}_i = \{F_1, \ldots , F_i\}$
, where
![]() $ \mathcal {F}_i$
is a collection of vertex-disjoint copies of
$ \mathcal {F}_i$
is a collection of vertex-disjoint copies of
![]() $ H^*$
and
$ H^*$
and
![]() $ v_j \in V(F_j)$
for each
$ v_j \in V(F_j)$
for each
![]() $ j \in [i]$
, and
$ j \in [i]$
, and
![]() $ G_i = G - \bigcup _{j \in [i]} V(F_i) - X$
.
$ G_i = G - \bigcup _{j \in [i]} V(F_i) - X$
.
We note that
![]() $ \left | \bigcup _{j \in [i]} V(F_i) \cup X \right | \leq \frac {\alpha }{2}n$
holds as
$ \left | \bigcup _{j \in [i]} V(F_i) \cup X \right | \leq \frac {\alpha }{2}n$
holds as
![]() $ i \lt t$
. Thus,
$ i \lt t$
. Thus,
![]() $ \delta (G_i + v_{i+1}) \geq \left ( 1 - \frac {1}{\xi (H^*)} + \frac {\alpha }{2} \right )n$
. Let
$ \delta (G_i + v_{i+1}) \geq \left ( 1 - \frac {1}{\xi (H^*)} + \frac {\alpha }{2} \right )n$
. Let
![]() $ Y$
be the subset of the neighbourhoods of
$ Y$
be the subset of the neighbourhoods of
![]() $ v_{i+1}$
in
$ v_{i+1}$
in
![]() $ G_i + v_{i+1}$
of size
$ G_i + v_{i+1}$
of size
![]() $ \left ( 1 - \frac {1}{\xi (H^*)} + \frac {\alpha }{2} \right )n$
. Let
$ \left ( 1 - \frac {1}{\xi (H^*)} + \frac {\alpha }{2} \right )n$
. Let
![]() $ A$
and
$ A$
and
![]() $ B$
be the bipartition of
$ B$
be the bipartition of
![]() $ H^*$
and
$ H^*$
and
![]() $ u$
be a vertex in
$ u$
be a vertex in
![]() $ A$
. We will embed
$ A$
. We will embed
![]() $ u$
to
$ u$
to
![]() $ v_{i+1}$
first and then embed other vertices of
$ v_{i+1}$
first and then embed other vertices of
![]() $ H^* - u$
while all the vertices of
$ H^* - u$
while all the vertices of
![]() $ B$
are embedded in
$ B$
are embedded in
![]() $ Y$
. By the minimum degree condition on
$ Y$
. By the minimum degree condition on
![]() $ G_{i+1}$
, Lemma2.4 enables us to find such embedding, we obtain a new copy of
$ G_{i+1}$
, Lemma2.4 enables us to find such embedding, we obtain a new copy of
![]() $ H^*$
, say
$ H^*$
, say
![]() $ F_{i+1}$
containing
$ F_{i+1}$
containing
![]() $ v_{i+1}$
. As it is disjoint with
$ v_{i+1}$
. As it is disjoint with
![]() $ \bigcup _{j \leq i} V(F_j) \cup X$
, we may add it to enlarge
$ \bigcup _{j \leq i} V(F_j) \cup X$
, we may add it to enlarge
![]() $ \mathcal {F}_i$
to
$ \mathcal {F}_i$
to
![]() $ \mathcal {F}_{i+1}$
. We iterate this process until we get
$ \mathcal {F}_{i+1}$
. We iterate this process until we get
![]() $ \mathcal {F}_t$
. Let
$ \mathcal {F}_t$
. Let
![]() $ F = \bigcup _{i \in \mathcal {F}_t} V(F_i)$
. Then
$ F = \bigcup _{i \in \mathcal {F}_t} V(F_i)$
. Then
![]() $ X \subseteq F$
and
$ X \subseteq F$
and
![]() $ |F| = v(H^*) t \leq \frac {\alpha }{2}n$
holds.
$ |F| = v(H^*) t \leq \frac {\alpha }{2}n$
holds.
Now, let
![]() $ G^{\prime} = G - F$
. Since
$ G^{\prime} = G - F$
. Since
![]() $ |F| \leq \frac {\alpha }{2}n$
, the minimum degree of
$ |F| \leq \frac {\alpha }{2}n$
, the minimum degree of
![]() $ G^{\prime}$
is at least
$ G^{\prime}$
is at least
![]() $ \left ( 1 - \frac {1}{\xi (H)} + \frac {\alpha }{2} \right )n$
. Thus, by Theorem1.1 and Observation3.6, there is a set
$ \left ( 1 - \frac {1}{\xi (H)} + \frac {\alpha }{2} \right )n$
. Thus, by Theorem1.1 and Observation3.6, there is a set
![]() $ F^{\prime} \subseteq V(G^{\prime})$
such that
$ F^{\prime} \subseteq V(G^{\prime})$
such that
![]() $ G^{\prime}[F^{\prime}]$
has a perfect
$ G^{\prime}[F^{\prime}]$
has a perfect
![]() $ H^*$
-tiling and
$ H^*$
-tiling and
![]() $ v(G^{\prime}) - |F^{\prime}| \leq C$
. Let
$ v(G^{\prime}) - |F^{\prime}| \leq C$
. Let
![]() $ W = F \cup F^{\prime}$
. Then
$ W = F \cup F^{\prime}$
. Then
![]() $ W$
is the desired set.
$ W$
is the desired set.
When
![]() $ \mathrm {hcf}_{\xi }(H) = 2$
, since the order of
$ \mathrm {hcf}_{\xi }(H) = 2$
, since the order of
![]() $ v(H^*)$
is even, the size of
$ v(H^*)$
is even, the size of
![]() $ W$
is also even. This completes the proof.
$ W$
is also even. This completes the proof.
In the proof of Lemma5.1, we will use the concept of dominating sets to obtain an efficient
![]() $\mathrm {Sub}(H)$
-absorber. Let
$\mathrm {Sub}(H)$
-absorber. Let
![]() $G$
be a graph. We say
$G$
be a graph. We say
![]() $D$
is a dominating set of
$D$
is a dominating set of
![]() $G$
if every vertex
$G$
if every vertex
![]() $v \in V(G)$
is either contained in
$v \in V(G)$
is either contained in
![]() $D$
or has a neighbour in
$D$
or has a neighbour in
![]() $D$
. The domination number of
$D$
. The domination number of
![]() $G$
is defined as the minimum size of a dominating set of
$G$
is defined as the minimum size of a dominating set of
![]() $G$
.
$G$
.
The next lemma on domination number, proven by Arnautov [Reference Arnautov4], and independently by Payan [Reference Payan26], will be used in the proof of Lemma5.1.
Lemma 5.4 (Arnautov [Reference Arnautov4], Payan [Reference Payan26]). Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\delta$
. Then the domination number of
$\delta$
. Then the domination number of
![]() $G$
is bounded above by
$G$
is bounded above by
![]() $\frac {1 + \ln (\delta + 1)}{\delta + 1}n$
.
$\frac {1 + \ln (\delta + 1)}{\delta + 1}n$
.
Later, Alon [Reference Alon1] proved that Lemma5.4 is asymptotically best possible.
In order to use type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers, we need to find a perfect matching in a
$\mathrm {Sub}(H)$
-absorbers, we need to find a perfect matching in a
![]() $d$
-absorbing graph for a suitable constant
$d$
-absorbing graph for a suitable constant
![]() $d$
. To achieve this, it would be useful to define a graph as follows.
$d$
. To achieve this, it would be useful to define a graph as follows.
Definition 5.5.
For a given graph
![]() $H$
, consider a family of disjoint unions of bipartite subdivisions of
$H$
, consider a family of disjoint unions of bipartite subdivisions of
![]() $H$
. Among those, choose a graph
$H$
. Among those, choose a graph
![]() $\hat {H}$
with bipartition
$\hat {H}$
with bipartition
![]() $(\hat {A}, \hat {B})$
with the smallest possible
$(\hat {A}, \hat {B})$
with the smallest possible
![]() $v(\hat {H})$
such that
$v(\hat {H})$
such that
![]() $||\hat {A}| - |\hat {B}|| = \mathrm {hcf}_{\xi }(H)$
. If there are multiple choices of
$||\hat {A}| - |\hat {B}|| = \mathrm {hcf}_{\xi }(H)$
. If there are multiple choices of
![]() $\hat {H}$
,
$\hat {H}$
,
![]() $\hat {A}$
, and
$\hat {A}$
, and
![]() $\hat {B}$
, we fix one choice.
$\hat {B}$
, we fix one choice.
We note that for every
![]() $H$
, we can prove that the bipartite graph
$H$
, we can prove that the bipartite graph
![]() $\hat {H}$
exists in the following way. By the definition of
$\hat {H}$
exists in the following way. By the definition of
![]() $\mathrm {hcf}_{\xi }(H)$
, there exist bipartite graphs
$\mathrm {hcf}_{\xi }(H)$
, there exist bipartite graphs
![]() $H_1, \ldots , H_m$
with bipartitions
$H_1, \ldots , H_m$
with bipartitions
![]() $(A_1, B_1), \ldots , (A_m, B_m)$
, respectively, that are bipartite subdivisions of
$(A_1, B_1), \ldots , (A_m, B_m)$
, respectively, that are bipartite subdivisions of
![]() $H$
such that they satisfy the following: there are positive integers
$H$
such that they satisfy the following: there are positive integers
![]() $c_1, \ldots , c_m$
that satisfy the inequality
$c_1, \ldots , c_m$
that satisfy the inequality
![]() $\sum _{i \in [m]} c_i(|A_i| - |B_i|) = \mathrm {hcf}_{\xi }(H)$
. By taking a disjoint union of
$\sum _{i \in [m]} c_i(|A_i| - |B_i|) = \mathrm {hcf}_{\xi }(H)$
. By taking a disjoint union of
![]() $c_i$
copies of
$c_i$
copies of
![]() $H_i$
for each
$H_i$
for each
![]() $i \in [m]$
, we obtain a bipartite graph that is a disjoint union of bipartite subdivisions of
$i \in [m]$
, we obtain a bipartite graph that is a disjoint union of bipartite subdivisions of
![]() $H$
and the difference between the bipartitions is
$H$
and the difference between the bipartitions is
![]() $\mathrm {hcf}_{\xi }(H)$
. Among such bipartite graphs, we can take our desired graph
$\mathrm {hcf}_{\xi }(H)$
. Among such bipartite graphs, we can take our desired graph
![]() $\hat {H}$
.
$\hat {H}$
.
We use
![]() $\hat {H}$
and the bipartition
$\hat {H}$
and the bipartition
![]() $(\hat {A}, \hat {B})$
to find perfect matchings in a
$(\hat {A}, \hat {B})$
to find perfect matchings in a
![]() $d$
-absorbing graph for using type-
$d$
-absorbing graph for using type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers. The following observation shows that complete bipartite graphs with appropriate sizes act like reservoirs for
$\mathrm {Sub}(H)$
-absorbers. The following observation shows that complete bipartite graphs with appropriate sizes act like reservoirs for
![]() $\hat {H}$
.
$\hat {H}$
.
Observation 5.6.
Let
![]() $H$
be a graph with
$H$
be a graph with
![]() $\mathrm {hcf}_{\xi }(H) = t$
and assume
$\mathrm {hcf}_{\xi }(H) = t$
and assume
![]() $\hat {H}$
has a bipartition with sizes
$\hat {H}$
has a bipartition with sizes
![]() $h^{\prime}$
and
$h^{\prime}$
and
![]() $h^{\prime} + t$
. Let
$h^{\prime} + t$
. Let
![]() $b$
be a positive integer. Then for any non-negative integer
$b$
be a positive integer. Then for any non-negative integer
![]() $a \leq b$
, the complete bipartite graph with bipartition sizes
$a \leq b$
, the complete bipartite graph with bipartition sizes
![]() $(2h^{\prime} + t)b - h^{\prime}a$
and
$(2h^{\prime} + t)b - h^{\prime}a$
and
![]() $(2h^{\prime} + t)b - (h^{\prime} + t)a$
has a perfect
$(2h^{\prime} + t)b - (h^{\prime} + t)a$
has a perfect
![]() $\hat {H}$
-tiling.
$\hat {H}$
-tiling.
Proof. Let
![]() $x = (2h^{\prime} + t)b - h^{\prime}a$
and
$x = (2h^{\prime} + t)b - h^{\prime}a$
and
![]() $y = (2h^{\prime} + t)b - (h^{\prime} + t)a$
. Since
$y = (2h^{\prime} + t)b - (h^{\prime} + t)a$
. Since
![]() $x = h^{\prime} (b - a) + (h^{\prime} + t)b$
and
$x = h^{\prime} (b - a) + (h^{\prime} + t)b$
and
![]() $y = (h^{\prime} + t)(b - a) + h^{\prime} b$
, the complete bipartite graph with bipartition sizes
$y = (h^{\prime} + t)(b - a) + h^{\prime} b$
, the complete bipartite graph with bipartition sizes
![]() $x$
and
$x$
and
![]() $y$
has
$y$
has
![]() $2b - a$
vertex-disjoint copies of
$2b - a$
vertex-disjoint copies of
![]() $K_{h^{\prime}, h^{\prime} + t}$
. Thus,
$K_{h^{\prime}, h^{\prime} + t}$
. Thus,
![]() $K_{x, y}$
has a perfect
$K_{x, y}$
has a perfect
![]() $\hat {H}$
-tiling.
$\hat {H}$
-tiling.
5.2. Proof of Theorem1.8
In this subsection, we will prove Lemma5.1, which will complete the proof of Theorem1.8.
Proof of Lemma 5.1. Let
![]() $H$
be an
$H$
be an
![]() $h$
-vertex graph with
$h$
-vertex graph with
![]() $\mathrm {hcf}_{\xi }(H) = 1$
. Let
$\mathrm {hcf}_{\xi }(H) = 1$
. Let
![]() $\hat {H}$
be the bipartite graph as in Definition5.5 with a bipartition
$\hat {H}$
be the bipartite graph as in Definition5.5 with a bipartition
![]() $(\hat {A}, \hat {B})$
with sizes
$(\hat {A}, \hat {B})$
with sizes
![]() $h^{\prime}$
and
$h^{\prime}$
and
![]() $h^{\prime}+1$
. Note that
$h^{\prime}+1$
. Note that
![]() $h^{\prime}$
is bounded above by a constant that depends only on
$h^{\prime}$
is bounded above by a constant that depends only on
![]() $h$
. We fix positive constants as follows:
$h$
. We fix positive constants as follows:
Let
![]() $n \geq n_0$
and
$n \geq n_0$
and
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with minimum degree at least
$n$
-vertex graph with minimum degree at least
![]() $\left (1 - \frac {1}{\xi (H)} + \gamma \right )n$
. We apply the regularity lemma to
$\left (1 - \frac {1}{\xi (H)} + \gamma \right )n$
. We apply the regularity lemma to
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
playing the roles of
$t_0$
playing the roles of
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
, respectively. Let
$t_0$
, respectively. Let
![]() $V_0, V_1, \ldots , V_t$
be an
$V_0, V_1, \ldots , V_t$
be an
![]() $\varepsilon$
-regular partition of
$\varepsilon$
-regular partition of
![]() $G$
and
$G$
and
![]() $G_0$
be a spanning subgraph of
$G_0$
be a spanning subgraph of
![]() $G$
that satisfies the following conditions:
$G$
that satisfies the following conditions:
-
(R1)
 $t_0 \leq t \leq T_0$
,
$t_0 \leq t \leq T_0$
, -
(R2)
 $|V_0| \leq \varepsilon v(G)$
,
$|V_0| \leq \varepsilon v(G)$
, -
(R3)
 $|V_1| = \cdots = |V_t|$
,
$|V_1| = \cdots = |V_t|$
, -
(R4)
 $G_0[V_i]$
has no edges for each
$G_0[V_i]$
has no edges for each
 $i \in [t]$
,
$i \in [t]$
, -
(R5)
 $d_{G_0}(v) \geq d_G(v) - (d + \varepsilon )v(G)$
for all
$d_{G_0}(v) \geq d_G(v) - (d + \varepsilon )v(G)$
for all
 $v \in V(G)$
,
$v \in V(G)$
, -
(R6) for all
 $1 \leq i \lt j \leq t$
, either the pair
$1 \leq i \lt j \leq t$
, either the pair
 $(V_i, V_j)$
is an
$(V_i, V_j)$
is an
 $(\varepsilon , d^{+})$
-regular pair or
$(\varepsilon , d^{+})$
-regular pair or
 $G_0[V_i, V_j]$
has no edges.
$G_0[V_i, V_j]$
has no edges.
By (R5), the minimum degree of
![]() $G_0$
is at least
$G_0$
is at least
![]() $\left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )n$
. Let
$\left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )n$
. Let
![]() $R$
be the
$R$
be the
![]() $(\varepsilon , d)$
-reduced graph on
$(\varepsilon , d)$
-reduced graph on
![]() $\{V_1, \ldots , V_t\}$
. Then, by Lemma2.7,
$\{V_1, \ldots , V_t\}$
. Then, by Lemma2.7,
![]() $\delta (R) \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )t$
. By Lemma5.4, there is a dominating set
$\delta (R) \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )t$
. By Lemma5.4, there is a dominating set
![]() $D \subseteq V(R)$
such that
$D \subseteq V(R)$
such that
 \begin{align*}|D| \leq \frac {1 + \ln \left (\left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )t + 1\right )}{\left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )t + 1}t \leq \frac {\varepsilon }{2}t.\end{align*}
\begin{align*}|D| \leq \frac {1 + \ln \left (\left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )t + 1\right )}{\left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} \right )t + 1}t \leq \frac {\varepsilon }{2}t.\end{align*}
We can pick a set
![]() $D^{\prime} \subseteq V(R) \setminus D$
greedily such that
$D^{\prime} \subseteq V(R) \setminus D$
greedily such that
![]() $R[D, D^{\prime}]$
has a perfect matching
$R[D, D^{\prime}]$
has a perfect matching
![]() $M$
. Let
$M$
. Let
We note that
![]() $v(M) = 2\ell \leq \varepsilon t$
. Since
$v(M) = 2\ell \leq \varepsilon t$
. Since
![]() $D$
is a dominating set of
$D$
is a dominating set of
![]() $R$
, there is a partition
$R$
, there is a partition
![]() $\{\mathcal {V}_1, \ldots , \mathcal {V}_{\ell }\}$
for
$\{\mathcal {V}_1, \ldots , \mathcal {V}_{\ell }\}$
for
![]() $V(R) \setminus (D \cup D^{\prime})$
such that for every
$V(R) \setminus (D \cup D^{\prime})$
such that for every
![]() $V_{i,j} \in \mathcal {V}_i$
, the edge
$V_{i,j} \in \mathcal {V}_i$
, the edge
![]() $X_i V_{i,j} \in E(R)$
. Let
$X_i V_{i,j} \in E(R)$
. Let
![]() $P_i \,:\!=\, \bigcup _{V_{i,j} \in \mathcal {V}_i} V_{i,j} \cup Y_i$
for each
$P_i \,:\!=\, \bigcup _{V_{i,j} \in \mathcal {V}_i} V_{i,j} \cup Y_i$
for each
![]() $i \in [\ell ]$
.
$i \in [\ell ]$
.
For each
![]() $V_{i,j} \in \mathcal {V}_i$
, where
$V_{i,j} \in \mathcal {V}_i$
, where
![]() $i \in [\ell ]$
, let
$i \in [\ell ]$
, let
![]() $U_{i,j} = \{u \in V_{i,j} \,:\, d_{G_0}(u;\, X_i) \lt (d - \varepsilon )|X_i|\}$
. By Lemma2.8, the size of
$U_{i,j} = \{u \in V_{i,j} \,:\, d_{G_0}(u;\, X_i) \lt (d - \varepsilon )|X_i|\}$
. By Lemma2.8, the size of
![]() $U_{i,j}$
is at most
$U_{i,j}$
is at most
![]() $\varepsilon |V_{i,j}| \leq \frac {\varepsilon n}{t}$
. Let
$\varepsilon |V_{i,j}| \leq \frac {\varepsilon n}{t}$
. Let
![]() $V^{\prime}_{i,j} = V_{i,j} \setminus U_{i,j}$
. Similarly, for each
$V^{\prime}_{i,j} = V_{i,j} \setminus U_{i,j}$
. Similarly, for each
![]() $i \in [\ell ]$
, let
$i \in [\ell ]$
, let
![]() $U_{i,D^{\prime}} = \{u \in Y_i \,:\, d_{G_0}(u;\, X_i) \lt (d - \varepsilon )|X_i|\}$
and let
$U_{i,D^{\prime}} = \{u \in Y_i \,:\, d_{G_0}(u;\, X_i) \lt (d - \varepsilon )|X_i|\}$
and let
![]() $Y^{\prime}_i = Y_i \setminus U_{i,D^{\prime}}$
. Then
$Y^{\prime}_i = Y_i \setminus U_{i,D^{\prime}}$
. Then
![]() $|U_{i,D^{\prime}}| \leq \varepsilon |Y_i| \leq \frac {\varepsilon n}{t}$
. Finally, for each
$|U_{i,D^{\prime}}| \leq \varepsilon |Y_i| \leq \frac {\varepsilon n}{t}$
. Finally, for each
![]() $i \in [\ell ]$
, let
$i \in [\ell ]$
, let
![]() $U_{i,D} = \{u \in X_i \,:\, d_{G_0}(u;\, Y_i) \lt (d - \varepsilon )|Y_i|\}$
and let
$U_{i,D} = \{u \in X_i \,:\, d_{G_0}(u;\, Y_i) \lt (d - \varepsilon )|Y_i|\}$
and let
![]() $X^{\prime}_i = X_i \setminus U_{i,D}$
. Then
$X^{\prime}_i = X_i \setminus U_{i,D}$
. Then
![]() $|U_{i,D}| \leq \varepsilon |X_i| \leq \frac {\varepsilon n}{t}$
.
$|U_{i,D}| \leq \varepsilon |X_i| \leq \frac {\varepsilon n}{t}$
.
We collect all the bad vertices, say
![]() $Z = V_0 \cup \bigcup _{i, j} U_{i, j} \cup \bigcup _{i} (U_{i, D} \cup U_{i, D^{\prime}})$
. Then
$Z = V_0 \cup \bigcup _{i, j} U_{i, j} \cup \bigcup _{i} (U_{i, D} \cup U_{i, D^{\prime}})$
. Then
![]() $|Z| \leq \varepsilon n + t \frac {\varepsilon n}{t} \leq 2\varepsilon n$
. We obtain a graph
$|Z| \leq \varepsilon n + t \frac {\varepsilon n}{t} \leq 2\varepsilon n$
. We obtain a graph
![]() $G_1 = G_0 - Z$
. Then
$G_1 = G_0 - Z$
. Then
![]() $v(G_1) \geq (1 - 2\varepsilon )n$
. We get a set
$v(G_1) \geq (1 - 2\varepsilon )n$
. We get a set
![]() $P^{\prime}_i = P_i \setminus Z$
for each
$P^{\prime}_i = P_i \setminus Z$
for each
![]() $i \in [\ell ]$
. Then for each
$i \in [\ell ]$
. Then for each
![]() $i \in [\ell ]$
, for every
$i \in [\ell ]$
, for every
![]() $v \in P^{\prime}_i$
, the degree
$v \in P^{\prime}_i$
, the degree
![]() $d_{G_0}(v;\, X^{\prime}_i) \geq (d - \varepsilon )|X_i| - \varepsilon |X_i| \geq (d - 2\varepsilon )|X_i| \geq d_1 |X_i|$
. For the same reason, for each
$d_{G_0}(v;\, X^{\prime}_i) \geq (d - \varepsilon )|X_i| - \varepsilon |X_i| \geq (d - 2\varepsilon )|X_i| \geq d_1 |X_i|$
. For the same reason, for each
![]() $i \in [\ell ]$
, for every
$i \in [\ell ]$
, for every
![]() $u \in X^{\prime}_i$
, the degree
$u \in X^{\prime}_i$
, the degree
![]() $d_{G_0}(u; Y^{\prime}_i) \geq d_1 |Y_i|$
.
$d_{G_0}(u; Y^{\prime}_i) \geq d_1 |Y_i|$
.
Let
![]() $u \in X^{\prime}_i$
and
$u \in X^{\prime}_i$
and
![]() $v \in P^{\prime}_i$
, where
$v \in P^{\prime}_i$
, where
![]() $i \in [\ell ]$
. We write
$i \in [\ell ]$
. We write
![]() $A_u = N_{G_1}(u) \cap Y^{\prime}_i$
and
$A_u = N_{G_1}(u) \cap Y^{\prime}_i$
and
![]() $B_v = N_{G_1}(v) \cap X^{\prime}_i$
. We observe that the pair
$B_v = N_{G_1}(v) \cap X^{\prime}_i$
. We observe that the pair
![]() $(X_i, Y_i)$
is an
$(X_i, Y_i)$
is an
![]() $\varepsilon$
-regular pair, and the sizes
$\varepsilon$
-regular pair, and the sizes
![]() $|A_u| \geq d_1 |Y_i| \gt \varepsilon |Y_i|$
and
$|A_u| \geq d_1 |Y_i| \gt \varepsilon |Y_i|$
and
![]() $|B_v| \geq d_1 |X_i| \gt \varepsilon |X_i|$
. By the definition of
$|B_v| \geq d_1 |X_i| \gt \varepsilon |X_i|$
. By the definition of
![]() $\varepsilon$
-regular pair, the number of edges
$\varepsilon$
-regular pair, the number of edges
![]() $e_{G_0}(A_u, B_v) \geq (d - \varepsilon )|A_u||B_v| \geq d_1^3 |X_i||Y_i| \geq \frac {d_1^4}{T^2} n^2$
. By Lemma2.3, there are at least
$e_{G_0}(A_u, B_v) \geq (d - \varepsilon )|A_u||B_v| \geq d_1^3 |X_i||Y_i| \geq \frac {d_1^4}{T^2} n^2$
. By Lemma2.3, there are at least
![]() $d_2(v(T^1_H)!) n^{v(T^1_H)}$
copies of
$d_2(v(T^1_H)!) n^{v(T^1_H)}$
copies of
![]() $T^1_H$
in
$T^1_H$
in
![]() $G_1[A_u, B_v]$
. This means there are at least
$G_1[A_u, B_v]$
. This means there are at least
![]() $d_2 n^{v(T^1_H)}$
distinct type-1
$d_2 n^{v(T^1_H)}$
distinct type-1
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $\{u, v\}$
. Let
$\{u, v\}$
. Let
![]() $F$
be a
$F$
be a
![]() $d_2$
-absorbing graph of
$d_2$
-absorbing graph of
![]() $G_1$
. Then the following holds:
$G_1$
. Then the following holds:
By Lemma4.12, there is a set
![]() $A \subseteq V(G_1)$
with size at most
$A \subseteq V(G_1)$
with size at most
![]() $\alpha n$
such that for all subsets
$\alpha n$
such that for all subsets
![]() $U$
of
$U$
of
![]() $V(G_1) \setminus A$
with size at most
$V(G_1) \setminus A$
with size at most
![]() $\beta n$
and
$\beta n$
and
![]() $F[U]$
has a perfect matching, then
$F[U]$
has a perfect matching, then
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U$
. Let us fix such a
$U$
. Let us fix such a
![]() $\mathrm {Sub}(H)$
-absorber
$\mathrm {Sub}(H)$
-absorber
![]() $A$
. For each
$A$
. For each
![]() $i \in [\ell ]$
, let
$i \in [\ell ]$
, let
![]() $X^{\prime\prime}_i = X^{\prime}_i \setminus A$
and
$X^{\prime\prime}_i = X^{\prime}_i \setminus A$
and
![]() $Y^{\prime\prime}_i = Y^{\prime}_i \setminus A$
. Then we have
$Y^{\prime\prime}_i = Y^{\prime}_i \setminus A$
. Then we have
![]() $|X^{\prime\prime}_i| \geq |X^{\prime}_i| - \alpha n \geq (1 - 2\varepsilon ) |X_i|$
and, for the same reason,
$|X^{\prime\prime}_i| \geq |X^{\prime}_i| - \alpha n \geq (1 - 2\varepsilon ) |X_i|$
and, for the same reason,
![]() $|Y^{\prime\prime}_i| \geq (1 - 2\varepsilon ) |Y_i|$
for every
$|Y^{\prime\prime}_i| \geq (1 - 2\varepsilon ) |Y_i|$
for every
![]() $i \in [\ell ]$
.
$i \in [\ell ]$
.
We now claim that for each
![]() $i \in [\ell ]$
, there is a copy
$i \in [\ell ]$
, there is a copy
![]() $Q_i$
of a complete balanced bipartite graph
$Q_i$
of a complete balanced bipartite graph
![]() $K_{(2h^{\prime}+1)C, (2h^{\prime}+1)C}$
. We note that the sizes
$K_{(2h^{\prime}+1)C, (2h^{\prime}+1)C}$
. We note that the sizes
![]() $|X^{\prime\prime}_i| \geq \varepsilon |X_i|$
and
$|X^{\prime\prime}_i| \geq \varepsilon |X_i|$
and
![]() $|Y^{\prime\prime}_i| \geq \varepsilon |Y_i|$
. Since the pair
$|Y^{\prime\prime}_i| \geq \varepsilon |Y_i|$
. Since the pair
![]() $(X_i, Y_i)$
is an
$(X_i, Y_i)$
is an
![]() $\varepsilon$
-regular pair, the number of edges in
$\varepsilon$
-regular pair, the number of edges in
![]() $G_1[X^{\prime\prime}_i, Y^{\prime\prime}_i]$
is at least
$G_1[X^{\prime\prime}_i, Y^{\prime\prime}_i]$
is at least
![]() $(d - \varepsilon ) |X^{\prime\prime}_i||Y^{\prime\prime}_i|$
. Thus, by the Erdős–Stone–Simonovits theorem, there is at least one copy of
$(d - \varepsilon ) |X^{\prime\prime}_i||Y^{\prime\prime}_i|$
. Thus, by the Erdős–Stone–Simonovits theorem, there is at least one copy of
![]() $K_{(2h^{\prime}+1)C, (2h^{\prime}+1)C}$
in
$K_{(2h^{\prime}+1)C, (2h^{\prime}+1)C}$
in
![]() $G_1[X^{\prime\prime}_i, Y^{\prime\prime}_i]$
. Thus, for each
$G_1[X^{\prime\prime}_i, Y^{\prime\prime}_i]$
. Thus, for each
![]() $i \in [\ell ]$
, there exists such a bipartite graph
$i \in [\ell ]$
, there exists such a bipartite graph
![]() $Q_i$
. Let
$Q_i$
. Let
![]() $Q \,:\!=\, \bigcup _{i \in [\ell ]} V(Q_i)$
. We note that by Observation5.6, for each
$Q \,:\!=\, \bigcup _{i \in [\ell ]} V(Q_i)$
. We note that by Observation5.6, for each
![]() $i \in [\ell ]$
, the graph
$i \in [\ell ]$
, the graph
![]() $Q_i$
has a perfect
$Q_i$
has a perfect
![]() $\hat {H}$
-tiling. This implies
$\hat {H}$
-tiling. This implies
![]() $G[Q]$
has a perfect
$G[Q]$
has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Note that
![]() $|Q| = 2(2h^{\prime}+1)C\ell \leq \varepsilon n$
. Let
$|Q| = 2(2h^{\prime}+1)C\ell \leq \varepsilon n$
. Let
![]() $G_2 = G_0 - (A \cup Q)$
. Then we have
$G_2 = G_0 - (A \cup Q)$
. Then we have
![]() $v(G_2) \geq (1 - \alpha - \varepsilon )n$
and
$v(G_2) \geq (1 - \alpha - \varepsilon )n$
and
![]() $\delta (G_2) \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} - (\alpha + \varepsilon )\right )n \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{4}\right )n$
. By Lemma5.3, there is a set
$\delta (G_2) \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{2} - (\alpha + \varepsilon )\right )n \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{4}\right )n$
. By Lemma5.3, there is a set
![]() $W \subseteq V(G_2)$
such that
$W \subseteq V(G_2)$
such that
![]() $G[W]$
has a perfect
$G[W]$
has a perfect
![]() $H$
-subdivision tiling, the set
$H$
-subdivision tiling, the set
![]() $Z$
is contained in
$Z$
is contained in
![]() $W$
, and
$W$
, and
![]() $|V(G_2) \setminus W| \leq C$
. Let
$|V(G_2) \setminus W| \leq C$
. Let
![]() $J = V(G_2) \setminus W$
with size at most
$J = V(G_2) \setminus W$
with size at most
![]() $C$
.
$C$
.
We observe that
![]() $V(G) = A \cup Q \cup W \cup J$
, and
$V(G) = A \cup Q \cup W \cup J$
, and
![]() $J \subseteq \left (\bigcup _{i \in [\ell ]} P^{\prime}_i \cup \bigcup _{i \in [\ell ]} X^{\prime}_i\right ) \setminus (A \cup Q).$
We recall that
$J \subseteq \left (\bigcup _{i \in [\ell ]} P^{\prime}_i \cup \bigcup _{i \in [\ell ]} X^{\prime}_i\right ) \setminus (A \cup Q).$
We recall that
![]() $A$
is the
$A$
is the
![]() $\mathrm {Sub}(H)$
-absorber for a small vertex subset which has a perfect matching in
$\mathrm {Sub}(H)$
-absorber for a small vertex subset which has a perfect matching in
![]() $F.$
For each
$F.$
For each
![]() $i \in [\ell ]$
, let
$i \in [\ell ]$
, let
![]() $J_i^1 = J \cap X^{\prime}_i$
and
$J_i^1 = J \cap X^{\prime}_i$
and
![]() $J_i^2 = J \cap P^{\prime}_i.$
We denote by
$J_i^2 = J \cap P^{\prime}_i.$
We denote by
![]() $J_i$
the union of
$J_i$
the union of
![]() $J_i^1$
and
$J_i^1$
and
![]() $J_i^2.$
Let
$J_i^2.$
Let
![]() $c_i$
be an integer for each
$c_i$
be an integer for each
![]() $i \in [\ell ]$
such that
$i \in [\ell ]$
such that
![]() $c_i = |J_i^1| - |J_i^2|.$
We define
$c_i = |J_i^1| - |J_i^2|.$
We define
![]() $\sigma (c_i) = 1$
if
$\sigma (c_i) = 1$
if
![]() $c_i \gt 0$
; otherwise,
$c_i \gt 0$
; otherwise,
![]() $\sigma (c_i) = 0.$
$\sigma (c_i) = 0.$
For each
![]() $i \in [\ell ]$
, if
$i \in [\ell ]$
, if
![]() $c_i = 0$
, then let
$c_i = 0$
, then let
![]() $S^1_i$
and
$S^1_i$
and
![]() $S^2_i$
be empty sets. Otherwise, let them be sets
$S^2_i$
be empty sets. Otherwise, let them be sets
![]() $S^1_i \subseteq (V(Q_i) \cap X^{\prime}_i)$
with size
$S^1_i \subseteq (V(Q_i) \cap X^{\prime}_i)$
with size
![]() $(h^{\prime} + 1 - \sigma (c_i))c_i$
and
$(h^{\prime} + 1 - \sigma (c_i))c_i$
and
![]() $S^2_i \subseteq (V(Q_i) \cap Y^{\prime}_i)$
with size
$S^2_i \subseteq (V(Q_i) \cap Y^{\prime}_i)$
with size
![]() $(h^{\prime} + \sigma (c_i))c_i.$
By Observation5.6, the induced graph
$(h^{\prime} + \sigma (c_i))c_i.$
By Observation5.6, the induced graph
![]() $G[Q_i \setminus (S^1_i \cup S^2_i)]$
has a perfect
$G[Q_i \setminus (S^1_i \cup S^2_i)]$
has a perfect
![]() $H$
-subdivision tiling for each
$H$
-subdivision tiling for each
![]() $i \in [\ell ].$
For each
$i \in [\ell ].$
For each
![]() $i \in [\ell ]$
, since
$i \in [\ell ]$
, since
![]() $|S^1_i| - |S^2_i| = -c_i$
, the equality
$|S^1_i| - |S^2_i| = -c_i$
, the equality
![]() $|J^1_i \cup S^1_i| = |J^2_i \cup S^2_i|$
holds. We observe that
$|J^1_i \cup S^1_i| = |J^2_i \cup S^2_i|$
holds. We observe that
![]() $(J^1_i \cup S^1_i) \subseteq X^{\prime}_i$
and
$(J^1_i \cup S^1_i) \subseteq X^{\prime}_i$
and
![]() $(J^2_i \cup S^2_i) \subseteq P^{\prime}_i.$
Thus, by (4), the induced graph
$(J^2_i \cup S^2_i) \subseteq P^{\prime}_i.$
Thus, by (4), the induced graph
![]() $F[J_i \cup S^1_i \cup S^2_i]$
has a perfect matching and we have
$F[J_i \cup S^1_i \cup S^2_i]$
has a perfect matching and we have
![]() $|J_i \cup S^1_i \cup S^2_i| = |J_i| + |c_i|(2h^{\prime} + 1).$
Let
$|J_i \cup S^1_i \cup S^2_i| = |J_i| + |c_i|(2h^{\prime} + 1).$
Let
![]() $S = \bigcup _{i \in [\ell ]} S^1_i \cup S^2_i.$
Then,
$S = \bigcup _{i \in [\ell ]} S^1_i \cup S^2_i.$
Then,
![]() $Q \setminus S = \bigcup _{i \in [\ell ]} (V(Q_i) \setminus (S^1_i \cup S^2_i))$
, so
$Q \setminus S = \bigcup _{i \in [\ell ]} (V(Q_i) \setminus (S^1_i \cup S^2_i))$
, so
![]() $G[Q \setminus S]$
has a perfect
$G[Q \setminus S]$
has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Since
![]() $J \cup S = \bigcup _{i \in [\ell ]} (J_i \cup S^1_i \cup S^2_i)$
, the induced graph
$J \cup S = \bigcup _{i \in [\ell ]} (J_i \cup S^1_i \cup S^2_i)$
, the induced graph
![]() $F[J \cup S]$
has a perfect matching. Moreover,
$F[J \cup S]$
has a perfect matching. Moreover,
![]() $|J \cup S| = \sum _{i \in [\ell ]} (J_i \cup S^1_i \cup S^2_i) \leq |J| + (2h^{\prime} + 1) \sum _{i \in [\ell ]} |c_i| \leq (2h^{\prime} + 2)C \leq \beta n$
holds. Thus, the set
$|J \cup S| = \sum _{i \in [\ell ]} (J_i \cup S^1_i \cup S^2_i) \leq |J| + (2h^{\prime} + 1) \sum _{i \in [\ell ]} |c_i| \leq (2h^{\prime} + 2)C \leq \beta n$
holds. Thus, the set
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $J \cup S.$
This means the induced graph
$J \cup S.$
This means the induced graph
![]() $G[A \cup J \cup S]$
has a perfect
$G[A \cup J \cup S]$
has a perfect
![]() $H$
-subdivision tiling. Together with
$H$
-subdivision tiling. Together with
![]() $G[W]$
,
$G[W]$
,
![]() $G[Q \setminus S]$
, and
$G[Q \setminus S]$
, and
![]() $G[A \cup J \cup S]$
, the graph
$G[A \cup J \cup S]$
, the graph
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-subdivision tiling. This completes the proof.
$H$
-subdivision tiling. This completes the proof.
5.3. Proof of Theorem1.9
We now prove Lemma5.2 to complete the proof of Theorem1.9. Our purpose is to find a perfect
![]() $H$
-subdivision tiling in a certain graph, where
$H$
-subdivision tiling in a certain graph, where
![]() $\mathrm {hcf}_{\xi }(H) = 2.$
$\mathrm {hcf}_{\xi }(H) = 2.$
In this case, we cannot apply the same idea as the proof of Theorem1.8. To prove Theorem1.9 with type-
![]() $1$
$1$
![]() $\mathrm {Sub}(H)$
-absorbers, we need to find a perfect matching in an absorbing graph, but since
$\mathrm {Sub}(H)$
-absorbers, we need to find a perfect matching in an absorbing graph, but since
![]() $\mathrm {hcf}_{\xi }(H) = 2$
, parity issues make it difficult to obtain a perfect matching. If the host graph
$\mathrm {hcf}_{\xi }(H) = 2$
, parity issues make it difficult to obtain a perfect matching. If the host graph
![]() $G$
is close to bipartite, we can handle these parity difficulties, but if
$G$
is close to bipartite, we can handle these parity difficulties, but if
![]() $G$
is far from bipartite, then we need to use different types of
$G$
is far from bipartite, then we need to use different types of
![]() $\mathrm {Sub}(H)$
-absorbers. Thus, we divide the cases depending on whether
$\mathrm {Sub}(H)$
-absorbers. Thus, we divide the cases depending on whether
![]() $G$
has many triangles or many
$G$
has many triangles or many
![]() $C_5$
s. If it has many triangles, we will use type-
$C_5$
s. If it has many triangles, we will use type-
![]() $2$
$2$
![]() $\mathrm {Sub}(H)$
-absorbers, and if it has many
$\mathrm {Sub}(H)$
-absorbers, and if it has many
![]() $C_5$
s, then we will use type-
$C_5$
s, then we will use type-
![]() $3$
$3$
![]() $\mathrm {Sub}(H)$
-absorbers.
$\mathrm {Sub}(H)$
-absorbers.
Below is the proof of Lemma5.2, which yields Theorem1.9.
Proof of Lemma 5.2. Let
![]() $H$
be a graph on
$H$
be a graph on
![]() $h$
vertices with
$h$
vertices with
![]() $\mathrm {hcf}_{\xi }(H) = 2$
. Let
$\mathrm {hcf}_{\xi }(H) = 2$
. Let
![]() $\hat {H}$
be the bipartite graph as in Definition5.5 with a bipartition
$\hat {H}$
be the bipartite graph as in Definition5.5 with a bipartition
![]() $(\hat {A}, \hat {B})$
with sizes
$(\hat {A}, \hat {B})$
with sizes
![]() $h^{\prime}$
and
$h^{\prime}$
and
![]() $h^{\prime}+2$
for a positive integer
$h^{\prime}+2$
for a positive integer
![]() $h^{\prime}$
. We note that
$h^{\prime}$
. We note that
![]() $h^{\prime}$
is bounded above by a constant that only depends on
$h^{\prime}$
is bounded above by a constant that only depends on
![]() $h$
. We fix positive constants as follows:
$h$
. We fix positive constants as follows:
Let
![]() $n$
be an even number and let
$n$
be an even number and let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with a minimum degree of at least
$n$
-vertex graph with a minimum degree of at least
![]() $\left (1 - \frac {1}{\xi ^*(H)} + \gamma \right )n$
. We apply the regularity lemma on
$\left (1 - \frac {1}{\xi ^*(H)} + \gamma \right )n$
. We apply the regularity lemma on
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
. Let
$t_0$
. Let
![]() $V_0, V_1, \ldots , V_t$
be an
$V_0, V_1, \ldots , V_t$
be an
![]() $\varepsilon$
-regular partition of
$\varepsilon$
-regular partition of
![]() $G$
and let
$G$
and let
![]() $G_0$
be a spanning subgraph of
$G_0$
be a spanning subgraph of
![]() $G$
which satisfies the following:
$G$
which satisfies the following:
-
(R1)
 $t_0 \leq t \leq T_0,$
$t_0 \leq t \leq T_0,$
-
(R2)
 $|V_0| \leq \varepsilon v(G),$
$|V_0| \leq \varepsilon v(G),$
-
(R3)
 $|V_1| = \cdots = |V_t|,$
$|V_1| = \cdots = |V_t|,$
-
(R4)
 $G_0[V_i]$
has no edges for each
$G_0[V_i]$
has no edges for each
 $i \in [t],$
$i \in [t],$
-
(R5)
 $d_{G_0}(v) \geq d_G(v) - (d + \varepsilon )v(G)$
for all
$d_{G_0}(v) \geq d_G(v) - (d + \varepsilon )v(G)$
for all
 $v \in V(G),$
$v \in V(G),$
-
(R6) for all
 $1 \leq i \lt j \leq t,$
either the pair
$1 \leq i \lt j \leq t,$
either the pair
 $(V_i, V_j)$
is an
$(V_i, V_j)$
is an
 $(\varepsilon , d{+})$
-regular pair or
$(\varepsilon , d{+})$
-regular pair or
 $G_0[A, B]$
has no edges.
$G_0[A, B]$
has no edges.
By (R5), the minimum degree of
![]() $G_0$
is at least
$G_0$
is at least
![]() $\left (1 - \frac {1}{\xi ^*(H)} + \frac {\gamma }{2} \right )n$
. Let
$\left (1 - \frac {1}{\xi ^*(H)} + \frac {\gamma }{2} \right )n$
. Let
![]() $G_1 = G_0 - V_0$
, then the size
$G_1 = G_0 - V_0$
, then the size
![]() $v(G_1) \geq (1-\varepsilon )n$
and
$v(G_1) \geq (1-\varepsilon )n$
and
![]() $\delta (G_1) \geq \delta (G_0) - \varepsilon n \geq \left (\frac {1}{3} + \frac {\gamma }{4} \right )n$
. Let
$\delta (G_1) \geq \delta (G_0) - \varepsilon n \geq \left (\frac {1}{3} + \frac {\gamma }{4} \right )n$
. Let
![]() $R$
be the
$R$
be the
![]() $(\varepsilon , d)$
-reduced graph on
$(\varepsilon , d)$
-reduced graph on
![]() $\{V_1, \ldots , V_t\}$
. Then by Lemma2.7, the minimum degree of
$\{V_1, \ldots , V_t\}$
. Then by Lemma2.7, the minimum degree of
![]() $R$
is at least
$R$
is at least
![]() $\left (1 - \frac {1}{\xi ^*(H)} + \frac {\gamma }{2} \right )t$
. We now divide into two cases depending on the structure of
$\left (1 - \frac {1}{\xi ^*(H)} + \frac {\gamma }{2} \right )t$
. We now divide into two cases depending on the structure of
![]() $R$
.
$R$
.
Case 1:
![]() $R$
contains
$R$
contains
![]() $C_3$
or
$C_3$
or
![]() $C_5$
.
$C_5$
.
Let
![]() $j \in \{2, 3\}$
. We choose
$j \in \{2, 3\}$
. We choose
![]() $j$
as 2 if
$j$
as 2 if
![]() $R$
contains
$R$
contains
![]() $C_3$
. Otherwise, we choose
$C_3$
. Otherwise, we choose
![]() $j$
as 3. We may assume
$j$
as 3. We may assume
![]() $V_1, \ldots , V_{2j-1}$
forms a
$V_1, \ldots , V_{2j-1}$
forms a
![]() $C_{2j-1}$
in
$C_{2j-1}$
in
![]() $R$
, where
$R$
, where
![]() $V_i V_{i+1} \in E(R)$
for each
$V_i V_{i+1} \in E(R)$
for each
![]() $i \in [2j-1]$
. Below, we write
$i \in [2j-1]$
. Below, we write
![]() $V_{2j}$
to denote
$V_{2j}$
to denote
![]() $V_1$
. By Lemma2.8, there exist sets
$V_1$
. By Lemma2.8, there exist sets
![]() $V^{\prime}_1, \ldots , V^{\prime}_{2j-1}$
satisfying the following for each
$V^{\prime}_1, \ldots , V^{\prime}_{2j-1}$
satisfying the following for each
![]() $i \in [2j-1]$
:
$i \in [2j-1]$
:
-
•
 $V^{\prime}_i \subseteq V_i$
,
$V^{\prime}_i \subseteq V_i$
, -
•
 $|V_i \setminus V^{\prime}_i| \leq 2\varepsilon |V_i|$
,
$|V_i \setminus V^{\prime}_i| \leq 2\varepsilon |V_i|$
, -
• for every
 $v \in V^{\prime}_i$
, the degrees
$v \in V^{\prime}_i$
, the degrees
 $d_{G_0}(v;\, V^{\prime}_{i-1}) \geq (d - 3\varepsilon )|V_{i-1}|$
and
$d_{G_0}(v;\, V^{\prime}_{i-1}) \geq (d - 3\varepsilon )|V_{i-1}|$
and
 $d_{G_0}(v;\, V^{\prime}_{i+1}) \geq (d - 3\varepsilon )|V_{i+1}|$
.
$d_{G_0}(v;\, V^{\prime}_{i+1}) \geq (d - 3\varepsilon )|V_{i+1}|$
.
Let
We now claim that
![]() $|B| \geq d_1 n$
.
$|B| \geq d_1 n$
.
Claim 2.
![]() $|B| \geq d_1 n$
.
$|B| \geq d_1 n$
.
Proof of Claim 1. If
![]() $j = 2$
, by the definition of an
$j = 2$
, by the definition of an
![]() $\varepsilon$
-regular pair, the following holds. For each
$\varepsilon$
-regular pair, the following holds. For each
![]() $i \in [3]$
, for every
$i \in [3]$
, for every
![]() $v \in V^{\prime}_i$
, the number of edges between the sets
$v \in V^{\prime}_i$
, the number of edges between the sets
![]() $N_{G_1}(v) \cap V^{\prime}_{i-1}$
and
$N_{G_1}(v) \cap V^{\prime}_{i-1}$
and
![]() $N_{G_1}(v) \cap V^{\prime}_{i+1}$
is at least
$N_{G_1}(v) \cap V^{\prime}_{i+1}$
is at least
![]() $(d - \varepsilon )(d - 3\varepsilon )^2|V_{i-1}||V_{i+1}| \geq \frac {(d - \varepsilon )(d-3\varepsilon )^2(1-\varepsilon )^2}{T^2}n^2 \geq \rho n^2$
. Then by Theorem2.2, there are at least
$(d - \varepsilon )(d - 3\varepsilon )^2|V_{i-1}||V_{i+1}| \geq \frac {(d - \varepsilon )(d-3\varepsilon )^2(1-\varepsilon )^2}{T^2}n^2 \geq \rho n^2$
. Then by Theorem2.2, there are at least
![]() $d_1 (v(T^2_H)!) n^{v(T^2_H)}$
copies of
$d_1 (v(T^2_H)!) n^{v(T^2_H)}$
copies of
![]() $T^2_H$
in
$T^2_H$
in
![]() $G_1[N_{G_1}(v)]$
. This means there are at least
$G_1[N_{G_1}(v)]$
. This means there are at least
![]() $d_1 n^{v(T^2_H)}$
distinct type-2
$d_1 n^{v(T^2_H)}$
distinct type-2
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $v$
. This implies
$v$
. This implies
![]() $\bigcup _{i \in [3]} V^{\prime}_i \subseteq B$
. Since
$\bigcup _{i \in [3]} V^{\prime}_i \subseteq B$
. Since
![]() $|V^{\prime}_1| + |V^{\prime}_2| + |V^{\prime}_3| \geq \frac {3(1-\varepsilon )(1-2\varepsilon )}{T}n \geq d_1 n$
, in this case, the inequality
$|V^{\prime}_1| + |V^{\prime}_2| + |V^{\prime}_3| \geq \frac {3(1-\varepsilon )(1-2\varepsilon )}{T}n \geq d_1 n$
, in this case, the inequality
![]() $|B| \geq d_1 n$
holds.
$|B| \geq d_1 n$
holds.
Now we consider the case
![]() $j = 3$
. We now show that for every
$j = 3$
. We now show that for every
![]() $u \in V^{\prime}_3$
, there are many copies of
$u \in V^{\prime}_3$
, there are many copies of
![]() $T^3_H$
such that each copy forms a
$T^3_H$
such that each copy forms a
![]() $\hat {T}^3_H$
together with
$\hat {T}^3_H$
together with
![]() $u$
. For each vertex
$u$
. For each vertex
![]() $x \in V^{\prime}_2$
and
$x \in V^{\prime}_2$
and
![]() $y \in V^{\prime}_4$
, let
$y \in V^{\prime}_4$
, let
![]() $N_x = N_{G_1}(x) \cap V^{\prime}_1$
and
$N_x = N_{G_1}(x) \cap V^{\prime}_1$
and
![]() $N_y = N_{G_1}(y) \cap V^{\prime}_5$
. By the definition of an
$N_y = N_{G_1}(y) \cap V^{\prime}_5$
. By the definition of an
![]() $\varepsilon$
-regular pair, there are at least
$\varepsilon$
-regular pair, there are at least
![]() $(d-\varepsilon )|N_x||N_y| \geq (d-\varepsilon )(d-3\varepsilon )^2|V_1||V_5| \geq \frac {(d - \varepsilon )(d - 3\varepsilon )^2(1-\varepsilon )^2}{T^2}n^2 \geq \rho n^2$
edges in
$(d-\varepsilon )|N_x||N_y| \geq (d-\varepsilon )(d-3\varepsilon )^2|V_1||V_5| \geq \frac {(d - \varepsilon )(d - 3\varepsilon )^2(1-\varepsilon )^2}{T^2}n^2 \geq \rho n^2$
edges in
![]() $G_1[N_x, N_y]$
. By Lemma2.3, there are at least
$G_1[N_x, N_y]$
. By Lemma2.3, there are at least
![]() $\frac {d_1 T^2}{(d - 3\varepsilon )^2(1-\varepsilon )^2} (v(T^3_H)!)n^{v(\tilde {T}^3_H)}$
distinct copies of
$\frac {d_1 T^2}{(d - 3\varepsilon )^2(1-\varepsilon )^2} (v(T^3_H)!)n^{v(\tilde {T}^3_H)}$
distinct copies of
![]() $\tilde {T}^3_H$
such that together with
$\tilde {T}^3_H$
such that together with
![]() $x$
and
$x$
and
![]() $y$
, each copy forms a
$y$
, each copy forms a
![]() $T^3_H$
. For each
$T^3_H$
. For each
![]() $u \in V^{\prime}_3$
, there are at least
$u \in V^{\prime}_3$
, there are at least
![]() $(d-3\varepsilon )^2 |V_2||V_4| \geq \frac {(d-3\varepsilon )^2(1-\varepsilon )^2}{T^2}n^2$
distinct pairs
$(d-3\varepsilon )^2 |V_2||V_4| \geq \frac {(d-3\varepsilon )^2(1-\varepsilon )^2}{T^2}n^2$
distinct pairs
![]() $(x, y) \in V^{\prime}_2 \times V^{\prime}_4$
such that
$(x, y) \in V^{\prime}_2 \times V^{\prime}_4$
such that
![]() $ux$
,
$ux$
,
![]() $uy \in E(G_1)$
. Thus, there are at least
$uy \in E(G_1)$
. Thus, there are at least
![]() $d_1 (v(T^3_H)!) n^{v(T^3_H)}$
distinct copies of
$d_1 (v(T^3_H)!) n^{v(T^3_H)}$
distinct copies of
![]() $T^3_H$
such that together with
$T^3_H$
such that together with
![]() $u$
, each copy forms a
$u$
, each copy forms a
![]() $\hat {T}^3_H$
. This means, for every
$\hat {T}^3_H$
. This means, for every
![]() $u \in V^{\prime}_3$
, there are at least
$u \in V^{\prime}_3$
, there are at least
![]() $d_1 n^{v(T^3_H)}$
distinct type-3
$d_1 n^{v(T^3_H)}$
distinct type-3
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $u$
. This means
$u$
. This means
![]() $V^{\prime}_3 \subseteq B$
. Since
$V^{\prime}_3 \subseteq B$
. Since
![]() $|V^{\prime}_3| \geq \frac {(1-\varepsilon )(1 - 2\varepsilon )}{T}n \geq d_1 n$
, we have
$|V^{\prime}_3| \geq \frac {(1-\varepsilon )(1 - 2\varepsilon )}{T}n \geq d_1 n$
, we have
![]() $|B| \geq d_1 n$
.
$|B| \geq d_1 n$
.
Let the two graphs
![]() $F_1$
and
$F_1$
and
![]() $F_2$
be the
$F_2$
be the
![]() $d_1$
-absorbing graph and the
$d_1$
-absorbing graph and the
![]() $(d_1, B)$
-exchanging graph of
$(d_1, B)$
-exchanging graph of
![]() $G_1$
, respectively. We denote by
$G_1$
, respectively. We denote by
![]() $X$
the set of vertices of
$X$
the set of vertices of
![]() $G_1$
that are not elements of
$G_1$
that are not elements of
![]() $B$
. Assume for a vertex
$B$
. Assume for a vertex
![]() $u \in X$
, the inequality
$u \in X$
, the inequality
![]() $e(G_1[N_{G_1}(u)]) \gt \rho n^2$
holds. If
$e(G_1[N_{G_1}(u)]) \gt \rho n^2$
holds. If
![]() $j = 2$
, then by Theorem2.2,
$j = 2$
, then by Theorem2.2,
![]() $u$
should be contained in
$u$
should be contained in
![]() $B$
, a contradiction. If
$B$
, a contradiction. If
![]() $j = 3$
, then
$j = 3$
, then
![]() $G_1$
does not have a triangle, so a contradiction. Thus, for every vertex
$G_1$
does not have a triangle, so a contradiction. Thus, for every vertex
![]() $u \in X$
, the inequality
$u \in X$
, the inequality
![]() $e(G_1[N_{G_1}(u)]) \leq \rho n^2$
holds. We now claim the following.
$e(G_1[N_{G_1}(u)]) \leq \rho n^2$
holds. We now claim the following.
Claim 2.
For every
![]() $u \in X$
and
$u \in X$
and
![]() $v \in B$
, the edge
$v \in B$
, the edge
![]() $uv$
is contained in
$uv$
is contained in
![]() $F_1$
or
$F_1$
or
![]() $F_2$
.
$F_2$
.
Proof of Claim 2. Fix a vertex
![]() $v \in B$
and let
$v \in B$
and let
![]() $U = N_{G_1}(v)$
. We partition the set
$U = N_{G_1}(v)$
. We partition the set
![]() $X$
into
$X$
into
![]() $X_1$
and
$X_1$
and
![]() $X_2$
as follows. Let
$X_2$
as follows. Let
![]() $X_1 = \{u \in X \,:\, |N_{G_1}(u) \cap U| \leq \frac {\gamma }{10}n\}$
and
$X_1 = \{u \in X \,:\, |N_{G_1}(u) \cap U| \leq \frac {\gamma }{10}n\}$
and
![]() $X_2 = X \setminus X_1$
.
$X_2 = X \setminus X_1$
.
Let
![]() $u \in X$
. Assume
$u \in X$
. Assume
![]() $u \in X_1$
. Let
$u \in X_1$
. Let
![]() $Z_1 = N_{G_1}(u)$
and let
$Z_1 = N_{G_1}(u)$
and let
![]() $Y = V(G_1) \setminus (Z_1 \cup U)$
. We denote by
$Y = V(G_1) \setminus (Z_1 \cup U)$
. We denote by
![]() $U_1 = U \setminus Z_1$
. Since
$U_1 = U \setminus Z_1$
. Since
![]() $\delta (G_1) \geq \left (\frac {1}{3} + \frac {\gamma }{4}\right )n$
and
$\delta (G_1) \geq \left (\frac {1}{3} + \frac {\gamma }{4}\right )n$
and
![]() $|Z_1 \cap U| \leq \frac {\gamma }{10}n$
, the inequality
$|Z_1 \cap U| \leq \frac {\gamma }{10}n$
, the inequality
![]() $|Y| \leq \left (\frac {1}{3} - \frac {2\gamma }{5} \right )n$
holds. Thus, for every
$|Y| \leq \left (\frac {1}{3} - \frac {2\gamma }{5} \right )n$
holds. Thus, for every
![]() $u^{\prime} \in Z_1$
, the degree
$u^{\prime} \in Z_1$
, the degree
![]() $G_1[u^{\prime};\, Z_1 \cup U]$
is at least
$G_1[u^{\prime};\, Z_1 \cup U]$
is at least
![]() $\frac {\gamma }{2}n$
. Since
$\frac {\gamma }{2}n$
. Since
![]() $u \in X$
, we know that
$u \in X$
, we know that
![]() $e(G_1[Z_1]) \leq \rho n^2$
. These imply that
$e(G_1[Z_1]) \leq \rho n^2$
. These imply that
![]() $e(G_1[Z_1, U_1]) \geq \frac {\gamma }{2}n \left (\frac {1}{3} + \frac {\gamma }{4} \right )n - 2\rho n^2 \geq \frac {\gamma }{10}n^2$
holds. Then by Lemma2.3, there are at least
$e(G_1[Z_1, U_1]) \geq \frac {\gamma }{2}n \left (\frac {1}{3} + \frac {\gamma }{4} \right )n - 2\rho n^2 \geq \frac {\gamma }{10}n^2$
holds. Then by Lemma2.3, there are at least
![]() $d_1(v(T^1_H)!)n^{v(T^1_H)}$
copies of
$d_1(v(T^1_H)!)n^{v(T^1_H)}$
copies of
![]() $T^1_H$
in
$T^1_H$
in
![]() $G_1[Z_1, U_1]$
such that together with
$G_1[Z_1, U_1]$
such that together with
![]() $u$
and
$u$
and
![]() $v$
, each copy of
$v$
, each copy of
![]() $T^1_H$
forms a
$T^1_H$
forms a
![]() $\hat {T}^1_H$
. Thus, there are at least
$\hat {T}^1_H$
. Thus, there are at least
![]() $d_1 n^{v(T^1_H)}$
distinct type-1
$d_1 n^{v(T^1_H)}$
distinct type-1
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $\{u, v\}$
. This means
$\{u, v\}$
. This means
![]() $uv \in E(F_1)$
.
$uv \in E(F_1)$
.
We now assume
![]() $u \in X_2$
. Let
$u \in X_2$
. Let
![]() $Z_2 = N_{G_1}(u)$
. The size
$Z_2 = N_{G_1}(u)$
. The size
![]() $|Z_2 \cap U| \geq \frac {\gamma }{10}n$
causes
$|Z_2 \cap U| \geq \frac {\gamma }{10}n$
causes
![]() $u \in X_2$
. Since
$u \in X_2$
. Since
![]() $\delta (G_1) \geq \left (\frac {1}{3} + \frac {\gamma }{4} \right )n$
, by Lemma2.4, there are at least
$\delta (G_1) \geq \left (\frac {1}{3} + \frac {\gamma }{4} \right )n$
, by Lemma2.4, there are at least
![]() $d_1 (v(S_H)!)n^{v(S_H)}$
copies of
$d_1 (v(S_H)!)n^{v(S_H)}$
copies of
![]() $S_H$
in
$S_H$
in
![]() $G_1 - \{u, v\}$
such that together with
$G_1 - \{u, v\}$
such that together with
![]() $u$
and
$u$
and
![]() $v$
, each copy of
$v$
, each copy of
![]() $S_H$
forms a
$S_H$
forms a
![]() $\hat {S}_H$
. This means there are at least
$\hat {S}_H$
. This means there are at least
![]() $d_1 n^{v(S_H)}$
distinct
$d_1 n^{v(S_H)}$
distinct
![]() $\mathrm {Sub}(H)$
-exchangers for
$\mathrm {Sub}(H)$
-exchangers for
![]() $\{u, v\}$
, so
$\{u, v\}$
, so
![]() $uv \in E(F_2)$
.
$uv \in E(F_2)$
.
Thus, we conclude that for every
![]() $u \in X$
and
$u \in X$
and
![]() $v \in B$
, the edge
$v \in B$
, the edge
![]() $uv$
is contained in
$uv$
is contained in
![]() $F_1$
or
$F_1$
or
![]() $F_2$
.
$F_2$
.
Claim2 implies for all
![]() $u \in X$
, we have
$u \in X$
, we have
![]() $d_{F_1}(u;\, B) \geq \frac {|B|}{2} \geq \frac {d_1}{2}n$
or
$d_{F_1}(u;\, B) \geq \frac {|B|}{2} \geq \frac {d_1}{2}n$
or
![]() $d_{F_2}(u;\, B) \geq \frac {|B|}{2} \geq \frac {d_1}{2}n$
. We are now ready to apply Lemma4.13. By Lemma4.13, there is a set
$d_{F_2}(u;\, B) \geq \frac {|B|}{2} \geq \frac {d_1}{2}n$
. We are now ready to apply Lemma4.13. By Lemma4.13, there is a set
![]() $A \subseteq V(G_1)$
with size at most
$A \subseteq V(G_1)$
with size at most
![]() $\alpha n$
such that for any set
$\alpha n$
such that for any set
![]() $U \subseteq V(G_1) \setminus A$
with size at most
$U \subseteq V(G_1) \setminus A$
with size at most
![]() $\beta n$
, the set
$\beta n$
, the set
![]() $A$
is a
$A$
is a
![]() $\mathrm {Sub}(H)$
-absorber for
$\mathrm {Sub}(H)$
-absorber for
![]() $U$
. Let us fix such a
$U$
. Let us fix such a
![]() $\mathrm {Sub}(H)$
-absorber
$\mathrm {Sub}(H)$
-absorber
![]() $A$
.
$A$
.
Let
![]() $G_2 = G_0 - A$
. Then
$G_2 = G_0 - A$
. Then
![]() $v(G_2) \geq (1 - \alpha )n$
and
$v(G_2) \geq (1 - \alpha )n$
and
![]() $\delta (G_2) \geq \delta (G_0) - \alpha n \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{4}\right )n$
. Then by Lemma5.3, there is a set
$\delta (G_2) \geq \delta (G_0) - \alpha n \geq \left (1 - \frac {1}{\xi (H)} + \frac {\gamma }{4}\right )n$
. Then by Lemma5.3, there is a set
![]() $W \subseteq V(G_2)$
such that
$W \subseteq V(G_2)$
such that
![]() $V_0 \subseteq W$
, the induced graph
$V_0 \subseteq W$
, the induced graph
![]() $G_2[W]$
has a perfect
$G_2[W]$
has a perfect
![]() $H$
-subdivision tiling, and
$H$
-subdivision tiling, and
![]() $|V(G_2) \setminus W| \leq C$
. Let
$|V(G_2) \setminus W| \leq C$
. Let
![]() $J = V(G_2) \setminus W$
. We observe that
$J = V(G_2) \setminus W$
. We observe that
![]() $V(G) = A \cup W \cup J$
and
$V(G) = A \cup W \cup J$
and
![]() $J \subseteq V(G_1) \setminus A$
. Since
$J \subseteq V(G_1) \setminus A$
. Since
![]() $|J| \leq C \leq \beta n$
, by our choice of
$|J| \leq C \leq \beta n$
, by our choice of
![]() $A$
, the induced graph
$A$
, the induced graph
![]() $G_1[A \cup J]$
has a perfect
$G_1[A \cup J]$
has a perfect
![]() $H$
-subdivision tiling. Together with
$H$
-subdivision tiling. Together with
![]() $G[W]$
, the graph
$G[W]$
, the graph
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-subdivision tiling. This completes the proof of Case 1.
$H$
-subdivision tiling. This completes the proof of Case 1.
Case 2:
![]() $R$
is a
$R$
is a
![]() $\{C_3, C_5\}$
-free graph.
$\{C_3, C_5\}$
-free graph.
In this case, we only use the type-1
![]() $\mathrm {Sub}(H)$
-absorbers. The proof is similar to the proof of Theorem1.8, but fortunately, it will be simpler.
$\mathrm {Sub}(H)$
-absorbers. The proof is similar to the proof of Theorem1.8, but fortunately, it will be simpler.
By (R4) and (R6), the graph
![]() $G_1$
is also a
$G_1$
is also a
![]() $\{C_3, C_5\}$
-free graph. A classical result of Andrásfai [Reference Andrásfai3] states that every graph on
$\{C_3, C_5\}$
-free graph. A classical result of Andrásfai [Reference Andrásfai3] states that every graph on
![]() $n$
-vertices with a minimum degree of at least
$n$
-vertices with a minimum degree of at least
![]() $\frac {2}{2k+1} n + 1$
either contains an odd cycle with a length of at most
$\frac {2}{2k+1} n + 1$
either contains an odd cycle with a length of at most
![]() $2k-1$
or is bipartite. Since
$2k-1$
or is bipartite. Since
![]() $\delta (G_1) \geq \left (\frac {1}{3} + \frac {\gamma }{4} \right )n \gt \frac {2}{7}n + 1$
and
$\delta (G_1) \geq \left (\frac {1}{3} + \frac {\gamma }{4} \right )n \gt \frac {2}{7}n + 1$
and
![]() $G_1$
is a
$G_1$
is a
![]() $\{C_3, C_5\}$
-free graph, we can deduce that
$\{C_3, C_5\}$
-free graph, we can deduce that
![]() $G_1$
is a bipartite graph.
$G_1$
is a bipartite graph.
Let
![]() $(X, Y)$
be the bipartition of
$(X, Y)$
be the bipartition of
![]() $G_1$
. Then we have
$G_1$
. Then we have
![]() $\delta (G_1) \leq |X| \leq n - \delta (G_1)$
, implying
$\delta (G_1) \leq |X| \leq n - \delta (G_1)$
, implying
![]() $2\delta (G_1) - |X| \geq \frac {3\gamma }{4}n$
. Let
$2\delta (G_1) - |X| \geq \frac {3\gamma }{4}n$
. Let
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
. We write
$y \in Y$
. We write
![]() $N_x = N_{G_1}(x)$
and
$N_x = N_{G_1}(x)$
and
![]() $N_y = N_{G_1}(y)$
. Since
$N_y = N_{G_1}(y)$
. Since
![]() $G_1$
is bipartite, we have
$G_1$
is bipartite, we have
![]() $N_x \subseteq Y$
and
$N_x \subseteq Y$
and
![]() $N_y \subseteq X$
. Then
$N_y \subseteq X$
. Then
By Lemma2.3, there are at least
![]() $d_1(v(T^1_H)!)n^{v(T^1_H)}$
copies of
$d_1(v(T^1_H)!)n^{v(T^1_H)}$
copies of
![]() $T^1_H$
in
$T^1_H$
in
![]() $G_1[N_x, N_y]$
such that together with
$G_1[N_x, N_y]$
such that together with
![]() $\{x, y\}$
, each copy of
$\{x, y\}$
, each copy of
![]() $T^1_H$
forms a
$T^1_H$
forms a
![]() $\hat {T}^1_H$
. This means for every
$\hat {T}^1_H$
. This means for every
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
, there are at least
$y \in Y$
, there are at least
![]() $d_1n^{v(T^1_H)}$
distinct type-1
$d_1n^{v(T^1_H)}$
distinct type-1
![]() $\mathrm {Sub}(H)$
-absorbers for
$\mathrm {Sub}(H)$
-absorbers for
![]() $\{x, y\}$
.
$\{x, y\}$
.
Let
![]() $F$
be the
$F$
be the
![]() $d_1$
-absorbing graph for
$d_1$
-absorbing graph for
![]() $G_1$
. Then by the previous argument, all pairs
$G_1$
. Then by the previous argument, all pairs
![]() $xy$
with
$xy$
with
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
are edges of
$y \in Y$
are edges of
![]() $F$
. By Lemma4.12, there is a set
$F$
. By Lemma4.12, there is a set
![]() $A \subseteq V(G_1)$
such that
$A \subseteq V(G_1)$
such that
![]() $|A|$
is even,
$|A|$
is even,
![]() $|A|$
is at most
$|A|$
is at most
![]() $\alpha n$
, and it satisfies the following:
$\alpha n$
, and it satisfies the following:
-
The set
 $A$
is a
$A$
is a
 $\mathrm {Sub}(H)$
-absorber for any set
$\mathrm {Sub}(H)$
-absorber for any set
 $U \subseteq V(G_1) \setminus A$
satisfying
$U \subseteq V(G_1) \setminus A$
satisfying
 $|U| \leq \beta n$
and
$|U| \leq \beta n$
and
 $F[U]$
has a perfect matching.
$F[U]$
has a perfect matching.
We now consider a graph
![]() $G_2 = G_1 - A$
. Then
$G_2 = G_1 - A$
. Then
![]() $V(G_2) \geq (1 - \varepsilon - \alpha )n$
and
$V(G_2) \geq (1 - \varepsilon - \alpha )n$
and
![]() $\delta (G_2) \geq \delta (G_1) - \alpha n \geq \left (\frac {1}{3} + \frac {\gamma }{10} \right )n$
. Let
$\delta (G_2) \geq \delta (G_1) - \alpha n \geq \left (\frac {1}{3} + \frac {\gamma }{10} \right )n$
. Let
![]() $X^{\prime} = X \setminus A$
and
$X^{\prime} = X \setminus A$
and
![]() $Y^{\prime} = Y \setminus A$
. Since
$Y^{\prime} = Y \setminus A$
. Since
![]() $e(G_2[X^{\prime}, Y^{\prime}]) \geq \frac {1}{6}n^2$
, by the Erdős–Stone–Simonovits theorem, there is a subgraph
$e(G_2[X^{\prime}, Y^{\prime}]) \geq \frac {1}{6}n^2$
, by the Erdős–Stone–Simonovits theorem, there is a subgraph
![]() $Q$
in
$Q$
in
![]() $G_1$
which is isomorphic to
$G_1$
which is isomorphic to
![]() $K_{(2h^{\prime}+2)C, (2h^{\prime}+2)C}$
. We note that by Observation5.6, the graph
$K_{(2h^{\prime}+2)C, (2h^{\prime}+2)C}$
. We note that by Observation5.6, the graph
![]() $Q$
has a perfect
$Q$
has a perfect
![]() $\hat {H}$
-tiling, so it has a perfect
$\hat {H}$
-tiling, so it has a perfect
![]() $H$
-subdivision tiling.
$H$
-subdivision tiling.
Let
![]() $G_3 = G_0 - (A \cup V(Q))$
. Then
$G_3 = G_0 - (A \cup V(Q))$
. Then
![]() $v(G_3) \geq (1 - \alpha )n - (2h^{\prime} + 2)C$
and
$v(G_3) \geq (1 - \alpha )n - (2h^{\prime} + 2)C$
and
![]() $\delta (G_3) \geq \left (1 - \frac {1}{\xi (H)} \right.$
$\delta (G_3) \geq \left (1 - \frac {1}{\xi (H)} \right.$
![]() $ \left. + \frac {\gamma }{10} \right )n$
. Then by Lemma5.3, there is a set
$ \left. + \frac {\gamma }{10} \right )n$
. Then by Lemma5.3, there is a set
![]() $W \subseteq V(G_3)$
such that
$W \subseteq V(G_3)$
such that
![]() $V_0 \subseteq W$
and
$V_0 \subseteq W$
and
![]() $G[W]$
has a perfect
$G[W]$
has a perfect
![]() $H$
-subdivision tiling,
$H$
-subdivision tiling,
![]() $|V(G_3) \setminus W|$
is at most
$|V(G_3) \setminus W|$
is at most
![]() $C$
, and the size of
$C$
, and the size of
![]() $W$
is even. Let
$W$
is even. Let
![]() $J = V(G_3) \setminus W$
. We observe that
$J = V(G_3) \setminus W$
. We observe that
![]() $V(G) = A \cup V(Q) \cup W \cup J$
. Note that all
$V(G) = A \cup V(Q) \cup W \cup J$
. Note that all
![]() $n$
,
$n$
,
![]() $|A|$
, and
$|A|$
, and
![]() $|W|$
are even, so is
$|W|$
are even, so is
![]() $|J|$
. Moreover,
$|J|$
. Moreover,
![]() $J \subseteq V(G_1) \setminus (A \cup V(Q))$
and
$J \subseteq V(G_1) \setminus (A \cup V(Q))$
and
![]() $|J| \leq C$
.
$|J| \leq C$
.
Let
![]() $J_X = J \cap X$
and
$J_X = J \cap X$
and
![]() $J_Y = J \cap Y$
. We may assume
$J_Y = J \cap Y$
. We may assume
![]() $|J_X| - |J_Y| = 2c$
for some non-negative integer
$|J_X| - |J_Y| = 2c$
for some non-negative integer
![]() $c \leq \frac {C}{2}$
. Let us pick two sets
$c \leq \frac {C}{2}$
. Let us pick two sets
![]() $Q_1 \subseteq V(Q) \cap X$
and
$Q_1 \subseteq V(Q) \cap X$
and
![]() $Q_2 \subseteq V(Q) \cap Y$
such that
$Q_2 \subseteq V(Q) \cap Y$
such that
![]() $|Q_1| = ch^{\prime}$
and
$|Q_1| = ch^{\prime}$
and
![]() $|Q_2| = c(h^{\prime} + 2)$
. Then
$|Q_2| = c(h^{\prime} + 2)$
. Then
![]() $(J_X \cup Q_1) \subseteq X$
and
$(J_X \cup Q_1) \subseteq X$
and
![]() $(J_Y \cup Q_2) \subseteq Y$
. Since
$(J_Y \cup Q_2) \subseteq Y$
. Since
![]() $|Q_1| - |Q_2| = -2c$
, the equality
$|Q_1| - |Q_2| = -2c$
, the equality
![]() $|J_X \cup Q_1| = |J_Y \cup Q_2|$
holds. We showed that
$|J_X \cup Q_1| = |J_Y \cup Q_2|$
holds. We showed that
![]() $F$
contains a complete bipartite graph on the bipartition
$F$
contains a complete bipartite graph on the bipartition
![]() $(X, Y)$
as a subgraph, and the set
$(X, Y)$
as a subgraph, and the set
![]() $J \cup Q_1 \cup Q_2$
has a perfect matching in
$J \cup Q_1 \cup Q_2$
has a perfect matching in
![]() $F$
. Moreover, we have
$F$
. Moreover, we have
![]() $|J \cup Q_1 \cup Q_2| \leq (2h^{\prime} + 2)C \leq \beta n$
. Thus, by our choice of
$|J \cup Q_1 \cup Q_2| \leq (2h^{\prime} + 2)C \leq \beta n$
. Thus, by our choice of
![]() $A$
, the induced graph
$A$
, the induced graph
![]() $G[A \cup J \cup Q_1 \cup Q_2]$
has a perfect
$G[A \cup J \cup Q_1 \cup Q_2]$
has a perfect
![]() $H$
-subdivision tiling. Let
$H$
-subdivision tiling. Let
![]() $Q^{\prime} = Q - (Q_1 \cup Q_2)$
. By Observation5.6, the graph
$Q^{\prime} = Q - (Q_1 \cup Q_2)$
. By Observation5.6, the graph
![]() $Q^{\prime}$
has a perfect
$Q^{\prime}$
has a perfect
![]() $\hat {H}$
-tiling, so it has a perfect
$\hat {H}$
-tiling, so it has a perfect
![]() $H$
-subdivision tiling. Together with
$H$
-subdivision tiling. Together with
![]() $G[W]$
,
$G[W]$
,
![]() $G[A \cup J \cup Q_1 \cup Q_2]$
, and
$G[A \cup J \cup Q_1 \cup Q_2]$
, and
![]() $G[V(Q^{\prime})]$
, the graph
$G[V(Q^{\prime})]$
, the graph
![]() $G$
has a perfect
$G$
has a perfect
![]() $H$
-subdivision tiling. This completes the proof of Lemma5.2.
$H$
-subdivision tiling. This completes the proof of Lemma5.2.
6. Concluding remarks and open problems
In this article, we determined an asymptotically tight minimum degree threshold that ensures the existence of a perfect
![]() $H$
-subdivision tiling for every graph
$H$
-subdivision tiling for every graph
![]() $H$
. In many cases, a minimum degree threshold for perfect
$H$
. In many cases, a minimum degree threshold for perfect
![]() $H$
-subdivision tilings is much smaller than for perfect
$H$
-subdivision tilings is much smaller than for perfect
![]() $H$
-tilings since perfect
$H$
-tilings since perfect
![]() $H$
-subdivision tilings are allowed to use not only
$H$
-subdivision tilings are allowed to use not only
![]() $H$
but also subdivisions of
$H$
but also subdivisions of
![]() $H$
. To prove that the weaker minimum degree suffices, we developed new approaches using the absorption method combined with the regularity lemma and domination numbers.
$H$
. To prove that the weaker minimum degree suffices, we developed new approaches using the absorption method combined with the regularity lemma and domination numbers.
Both Theorems1.8 and 1.9 are tight up to
![]() $o(n)$
terms. We conjecture that our results hold with the minimum degree condition sharp up to additive constants depending only on
$o(n)$
terms. We conjecture that our results hold with the minimum degree condition sharp up to additive constants depending only on
![]() $H$
.
$H$
.
Conjecture 6.1.
Let
![]() $H$
be a graph that is not a disjoint union of isolated vertices. Then there exists a constant
$H$
be a graph that is not a disjoint union of isolated vertices. Then there exists a constant
![]() $C_H$
depending only on
$C_H$
depending only on
![]() $H$
such that the following holds for all
$H$
such that the following holds for all
![]() $n \gt 0.$
$n \gt 0.$
If
![]() $\mathrm {hcf}_{\xi }(H) \neq 2$
,
$\mathrm {hcf}_{\xi }(H) \neq 2$
,
Otherwise,
 \begin{align*} \delta _{\mathrm {sub}}(n, H) &\leq \frac {1}{2}n + C_H &&\text {if } n\ is\ odd,\\[3pt] \delta _{\mathrm {sub}}(n, H) &\leq \left (1 - \frac {1}{\xi ^*(H)}\right )n + C_H &&\text {if } n\ is\ even. \end{align*}
\begin{align*} \delta _{\mathrm {sub}}(n, H) &\leq \frac {1}{2}n + C_H &&\text {if } n\ is\ odd,\\[3pt] \delta _{\mathrm {sub}}(n, H) &\leq \left (1 - \frac {1}{\xi ^*(H)}\right )n + C_H &&\text {if } n\ is\ even. \end{align*}
Our main results, Theorems1.8 and 1.9, imply that perfect
![]() $H$
-subdivision tilings and perfect
$H$
-subdivision tilings and perfect
![]() $H$
-tilings behave differently in many cases. In particular, the numbers
$H$
-tilings behave differently in many cases. In particular, the numbers
![]() $\delta _{\mathrm {sub}}(n, K_r)$
behave irregularly for small values of
$\delta _{\mathrm {sub}}(n, K_r)$
behave irregularly for small values of
![]() $r$
. In contrast to perfect
$r$
. In contrast to perfect
![]() $K_r$
-tilings, the number
$K_r$
-tilings, the number
![]() $\lim _{n\to \infty } \frac {\delta _{\mathrm {sub}}(n, K_r)}{n}$
does not strictly increase as
$\lim _{n\to \infty } \frac {\delta _{\mathrm {sub}}(n, K_r)}{n}$
does not strictly increase as
![]() $r$
increases. For another example, consider a tree
$r$
increases. For another example, consider a tree
![]() $T$
. According to Theorem1.2, we have
$T$
. According to Theorem1.2, we have
![]() $\delta (n, T) = \frac {1}{2}n + O(1)$
. However, for
$\delta (n, T) = \frac {1}{2}n + O(1)$
. However, for
![]() $\delta _{\mathrm {sub}}(n, T)$
, Theorem1.8 implies that there is a positive constant
$\delta _{\mathrm {sub}}(n, T)$
, Theorem1.8 implies that there is a positive constant
![]() $c_T$
such that
$c_T$
such that
![]() $\delta _{\mathrm {sub}}(n, T) \leq \left (\frac {1}{2} - c_T + o(1) \right )n$
since
$\delta _{\mathrm {sub}}(n, T) \leq \left (\frac {1}{2} - c_T + o(1) \right )n$
since
![]() $\mathrm {hcf}_{\xi }(T) = 1$
.
$\mathrm {hcf}_{\xi }(T) = 1$
.
Moreover, as we saw before, monotonicity does not hold for subdivision tilings. For
![]() $H_2 \subseteq H_1$
with
$H_2 \subseteq H_1$
with
![]() $H_2$
being a spanning subgraph,
$H_2$
being a spanning subgraph,
![]() $\delta (n, H_2) \leq \delta (n, H_1)$
is trivial, but
$\delta (n, H_2) \leq \delta (n, H_1)$
is trivial, but
![]() $\delta _{\mathrm {sub}}(n, H_2) \leq \delta _{\mathrm {sub}}(n, H_1)$
is not true as
$\delta _{\mathrm {sub}}(n, H_2) \leq \delta _{\mathrm {sub}}(n, H_1)$
is not true as
![]() $\delta _{\mathrm {sub}}(n, K_4) = \frac {2}{5}n + o(n) \lt \delta _{\mathrm {sub}}(n, C_4) = \frac {1}{2}n + o(n)$
.
$\delta _{\mathrm {sub}}(n, K_4) = \frac {2}{5}n + o(n) \lt \delta _{\mathrm {sub}}(n, C_4) = \frac {1}{2}n + o(n)$
.
A perfect
![]() $H$
-subdivision tiling is a special case of tiling a host graph by several kinds of graphs. Let
$H$
-subdivision tiling is a special case of tiling a host graph by several kinds of graphs. Let
![]() $\mathcal {F}$
be a collection of graphs and let
$\mathcal {F}$
be a collection of graphs and let
![]() $\mathrm {hcf}(\mathcal {F})$
be the highest common factor of the sizes of graphs in
$\mathrm {hcf}(\mathcal {F})$
be the highest common factor of the sizes of graphs in
![]() $\mathcal {F}$
. For each positive integer
$\mathcal {F}$
. For each positive integer
![]() $n$
divisible by
$n$
divisible by
![]() $\mathrm {hcf}(\mathcal {F})$
, we define
$\mathrm {hcf}(\mathcal {F})$
, we define
![]() $\delta (n, \mathcal {F})$
to be the smallest integer
$\delta (n, \mathcal {F})$
to be the smallest integer
![]() $k$
such that any
$k$
such that any
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with a minimum degree of at least
$G$
with a minimum degree of at least
![]() $k$
has a perfect tiling that uses only graphs in
$k$
has a perfect tiling that uses only graphs in
![]() $\mathcal {F}$
. In this notation, we estimated an asymptotically tight value for
$\mathcal {F}$
. In this notation, we estimated an asymptotically tight value for
![]() $\delta (n, \mathrm {Sub}(H))$
for every graph
$\delta (n, \mathrm {Sub}(H))$
for every graph
![]() $H$
. Thus, we suggest the following problem.
$H$
. Thus, we suggest the following problem.
Problem 6.2.
Let
![]() $\mathcal {F}$
be a collection of graphs and
$\mathcal {F}$
be a collection of graphs and
![]() $n$
be a positive integer that is divisible by
$n$
be a positive integer that is divisible by
![]() $\mathrm {hcf}(\mathcal {F})$
. Determine the number
$\mathrm {hcf}(\mathcal {F})$
. Determine the number
![]() $\delta (n, \mathcal {F}).$
$\delta (n, \mathcal {F}).$
Acknowledgement
The author would like to thank his advisor, Jaehoon Kim, for his very helpful comments and advice. He would also like to extend his thanks to anonymous reviewers for very carefully reading this article and providing helpful comments.
Fundind statement
Hyunwoo Lee was supported by the Institute for Basic Science (IBS-R029-C4).