Over two thousand years ago, Archimedes discovered a remarkable result concerning two circles drawn with reference to a configuration of three circles and a straight line. Figure 1 displays this result.
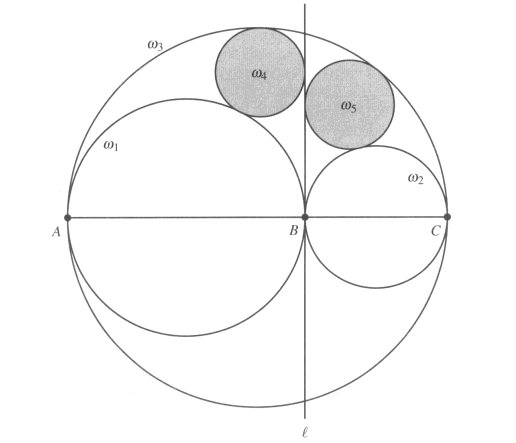
In the figure, A, B, C are three collinear points, with B between A and C; circles ω1, ω2, ω3 are drawn on AB, BC, AC as diameters, respectively; a line l is drawn through B, perpendicular to AC; a circle ω4 is inscribed in the region bounded by {ωl, ω3, l}; and a circle ω5 is inscribed in the region bounded by {ω2, ω3, l}. The Archimedean property is that ω4 and ω5 have equal radii.