Cooling the surface of freshwater bodies, whose temperatures are above the temperature of maximum density, can generate differential cooling between shallow and deep regions. When surface cooling occurs over a long enough period, the thermally induced cross-shore pressure gradient may drive an overturning circulation, a phenomenon called ‘thermal siphon’. However, the conditions under which this process begins are not yet fully characterised. Here, we examine the development of thermal siphons driven by a uniform loss of heat at the air–water interface in sloping, stratified basins. For a two-dimensional framework, we derive theoretical time and velocity scales associated with the transition from Rayleigh–Bénard type convection to a horizontal overturning circulation across the shallower sloping basin. This transition is characterised by a three-way horizontal momentum balance, in which the cross-shore pressure gradient balances the inertial terms before reaching a quasi-steady regime. We performed numerical and field experiments to test and show the robustness of the analytical scaling, describe the convective regimes and quantify the cross-shore transport induced by thermal siphons. Our results are relevant for understanding the nearshore fluid dynamics induced by nighttime or seasonal surface cooling in lakes and reservoirs.

We report on a three-dimensional direct numerical simulation study of flow structure and heat transport in the annular centrifugal Rayleigh–Bénard convection (ACRBC) system, with cold inner and hot outer cylinders corotating axially, for the Rayleigh number range $Ra \in [{10^6},{10^8}]$ and radius ratio range $\eta = {R_i}/{R_o} \in [0.3,0.9]$ ($R_i$ and $R_o$ are the radius of the inner and outer cylinders, respectively). This study focuses on the dependence of flow dynamics, heat transport and asymmetric mean temperature fields on the radius ratio $\eta$. For the inverse Rossby number $Ro^{-1} = 1$, as the Coriolis force balances inertial force, the flow is in the inertial regime. The mechanisms of zonal flow revolving in the prograde direction in this regime are attributed to the asymmetric movements of plumes and the different curvatures of the cylinders. The number of roll pairs is smaller than the circular roll hypothesis as the convection rolls are probably elongated by zonal flow. The physical mechanism of zonal flow is verified by the dependence of the drift frequency of the large-scale circulation (LSC) rolls and the space- and time-averaged azimuthal velocity on $\eta$. The larger $\eta$ is, the weaker the zonal flow becomes. We show that the heat transport efficiency increases with $\eta$. It is also found that the bulk temperature deviates from the arithmetic mean temperature and the deviation increases as $\eta$ decreases. This effect can be explained by a simple model that accounts for the curvature effects and the radially dependent centrifugal force in ACRBC.

Based on an assumption of strongly inhomogeneous potential vorticity mixing in quasi-geostrophic $\beta$-plane turbulence, a relation is obtained between the mean spacing of latitudinally meandering zonal jets and the total kinetic energy of the flow. The relation applies to cases where the Rossby deformation length is much smaller than the Rhines scale, in which kinetic energy is concentrated within the jet cores. The relation can be theoretically achieved in the case of perfect mixing between regularly spaced jets with simple meanders, and of negligible kinetic energy in flow structures other than in jets. Incomplete mixing or unevenly spaced jets will result in jets being more widely separated than the estimate, while significant kinetic energy outside the jets will result in jets closer than the estimate. An additional relation, valid under the same assumptions, is obtained between the total kinetic and potential energies. In flows with large-scale dissipation, the two relations provide a means to predict the jet spacing based only on knowledge of the energy input rate of the forcing and dissipation rate, regardless of whether the latter takes the form of frictional or thermal damping. Comparison with direct numerical integrations of the forced system shows broad support for the relations, but differences between the actual and predicted jet spacings arise both from the complex structure of jet meanders and the non-negligible kinetic energy contained in the turbulent background and in coherent vortices lying between the jets.

Vertical chutes and pipes are a common component of many industrial apparatus used in the transport and processing of powders and grains. Here, a typical arrangement is considered first in which a hopper at the top feeds the chute and a converging outlet at the bottom controls the mass flux. Discrete element method (DEM) simulations reveal that steady uniform flow is only observed for intermediate flow rates, with jamming and unsteady waves dominating slow flows and non-uniform wall detachment in fast flow. Focusing on the steady uniform regimes, a progressive idealisation is carried out by matching with equivalent DEM simulations in periodic cells. These investigations justify a one-dimensional continuum modelling of the problem and provide key test data. Novel exact solutions are derived here for vertical flow using a linear version of the ‘$\mu(I),\varPhi(I)$-rheology’, for which the bulk friction $\mu$ and steady solid volume fraction $\varPhi$ depend on the inertial number I. Despite not capturing the full nonlinear complexities, the solutions match important aspects of the DEM flow fields and reveal simple scaling laws linking many quantities of interest. In particular, this study clearly demonstrates a linear relation between the chute width and the size of the shear zones at the walls. This finding contrasts with previous works on purely quasi-static flow, which instead predict a roughly constant shear zone width, a difference which implies that finite-size effects are minimal for the inertial flows studied here.

This paper investigates the shock-induced instability of the interfaces between gases and dense granular media with finite length via the coarse-grained compressible computational fluid dynamics–discrete parcel method. Despite generating a typical spike-bubble structure reminiscent of the Richtmyer–Meshkov instability (RMI), the shock-driven granular instability (SDGI) is governed by fundamentally different mechanisms. Unlike the RMI arising from baroclinic vorticity deposition on the interface, the SDGI is closely associated with the interfacial and bulk granular dynamics, which evolve with the transient coupling between particles and gases. Consequently, the SDGI follows a growth law distinctly different from that of the RMI, namely a semilinear slow regime followed by an exponentially expedited regime and a quadratic asymptotic regime. We further establish the instability criteria of the SDGI for granular media with infinite and finite lengths, which do not exist in the RMI. A scaling growth law of the SDGI for dense granular media with finite length is derived by normalizing the time with the rarefaction propagation time, which successfully collapses the data from cases with varying shock strength, particle column length and particle volume fraction and ought to hold for granular media with varying particle parameters. The effect of the initial perturbation magnitude can be properly considered in the scaling growth law by incorporating it into the length normalization.

Gravity induced film flow over a rigid smoothly corrugated substrate heated uniformly from below, is explored. This is achieved by reducing the governing equations of motion and energy conservation to a manageable form within the mathematical framework of the well-known long-wave approximation; leading to an asymptotic model of reduced dimensionality. A key feature of the approach and to solving the problem of interest, is proof that the leading approximation of the temperature field inside the film must be nonlinear to accurately resolve the thermodynamics beyond the trivial case of ‘a flat film flowing down a planar uniformly heated incline.’ Superior predictions are obtained compared with earlier work and reinforced via a series of corresponding solutions to the full governing equations using a purpose written finite element analogue, enabling comparisons to be made between free-surface disturbance and temperature predictions, as well as the streamline pattern and temperature contours inside the film. In particular, the free-surface temperature is captured extremely well at moderate Prandtl numbers. The stability characteristics of the problem are examined using Floquet theory, with the interaction between the substrate topography and thermo-capillary instability modes investigated as a set of neutral stability curves. Although there are no relevant experimental data currently available for the heated film problem, recent existing predictions and experimental data concerning the behaviour of corresponding isothermal flow cases are taken as a reference point from which to explore the effect of both heating and cooling.

We investigate the dynamic couplings between particles and fluid in turbulent Rayleigh–Bénard (RB) convection laden with isothermal inertial particles. Direct numerical simulations combined with the Lagrangian point-particle mode were carried out in the range of Rayleigh number $1\times 10^6 \le {Ra}\le 1 \times 10^8$ at Prandtl number ${Pr}=0.678$ for three Stokes numbers ${St_f}=1 \times 10^{-3}$, $8 \times 10^{-3}$ and $2.5 \times 10^{-2}$. It is found that the global heat transfer and the strength of turbulent momentum transfer are altered a small amount for the small Stokes number and large Stokes number as the coupling between the two phases is weak, whereas they are enhanced a large amount for the medium Stokes number due to strong coupling of the two phases. We then derived the exact relation of kinetic energy dissipation in the particle-laden RB convection to study the budget balance of induced and dissipated kinetic energy. The strength of the dynamic coupling can be clearly revealed from the percentage of particle-induced kinetic energy over the total induced kinetic energy. We further derived the power law relation of the averaged particles settling rate versus the Rayleigh number, i.e. $S_p/(d_p/H)^2{\sim} Ra^{1/2}$, which is in remarkable agreement with our simulation. We found that the settling and preferential concentration of particles are strongly correlated with the coupling mechanisms.

The wave-induced resonant flow in a narrow gap between a stationary hull and a vertical wall is studied experimentally and numerically. Vortex shedding from the sharp bilge edge of the hull gives rise to a quadratically damped free surface response in the gap, where the damping coefficient is approximately independent of wave steepness and frequency. Particle image velocimetry and direct numerical simulations were used to characterise the shedding dynamics and explore the influence of discretisation in the measurements and computations. Secondary separation was identified as a particular feature which occurred at the hull bilge in these gap flows. This can result in the generation of a system with multiple vortical regions and asymmetries between the inflow and outflow. The shedding dynamics was found to exhibit a high degree of invariance to the amplitude in the gap and the spanwise position of the barge. The new measurements and the evaluation of numerical models of varying fidelity can assist in informing offshore operations such as the side by side offloading from floating liquefied natural gas facilities.

We study the effects of interfacial kinetics on the electro-hydrodynamics of ion transport near an ion-selective surface using a combination of linear stability analysis and numerical simulation. The finite kinetics of the electrolyte–electrode interface affects the ion transfer and electroconvection in many ways. On a surface of fixed topography, such as a metal surface of slow and stable ion deposition or covered by a polymer membrane, the finite kinetics reduces the current in one-dimensional ion diffusion/migration, increases the critical voltage for the onset of the electroconvective instability, changes the dynamics of the electroconvection and the overlimiting current, and enhances the lateral ion diffusion within the interfacial layer. The first three effects are indirectly caused by the reaction kinetics and can be characterized by an effective voltage difference across the liquid electrolyte. In comparison, the last effect is controlled by a direct interplay between kinetics and nonlinear electroconvection. Scaling laws for ion transport and features of electroconvection are proposed. We also analyse the linear stability of a surface which evolves under ion deposition and find that the finite kinetics decreases the growth rate of both electroconvective and morphological instabilities and therefore modifies the wavenumber of the most unstable mode.

Self-propelled flapping foils with distinct locomotion-enabling kinematic restraints exhibit a remarkably similar Strouhal number ($St$)-Reynolds number ($Re$) dependence. This similarity has been hypothesized to pervade diverse forms of oscillatory self-propulsion and undulatory biolocomotion; however, its genesis and implications on the energetic cost of locomotion remain elusive. Here, using high-resolution simulations of translationally free and restrained foils that self-propel as they are pitched, we demonstrate that a generality in the $St$-$Re$ relationship can emerge despite significant disparities in thrust generation mechanics and locomotory performance. Specifically, owing to a recoil reaction induced passive heave, the fluid's inertial response to the prescribed rotational pitch, the principal source of thrust in unidirectionally free and towed configurations, ceases to produce thrust in a bidirectionally free configuration. Rather, the thrust generated from the leading edge suction mechanics self-propels a bidirectionally free pitching foil. Owing to the foregoing distinction in the thrust generation mechanics, the $St$-$Re$ relationships for the bidirectionally and unidirectionally free/towed foils are dissimilar and pitching amplitude dependent, but specifically for large reduced frequencies, converge to a previously reported unified power law. Importantly, to propel at a given mean forward speed, the bidirectionally free foil must counteract the out-of-phase passive heave through a more intense rotational pitch, resulting in an appreciably higher power consumption over the range $10 \leq Re \leq 10^3$. We highlight the critical role of thrust in introducing an offset in the $St$-$Re$ relation, and through its amplification, being ultimately responsible for the considerable disparity in the locomotory performance of differentially constrained foils.

The effects of chordwise deformation and the half-amplitude asymmetry on the hydrodynamic performance and vortex dynamics of batoid fish have been numerically investigated, in which the two parameters were represented by the wavenumber ($W$) and the ratio of the half-amplitude above the longitudinal axis to that below ($HAR$). Fin kinematics were prescribed based on biological data. Simulations were conducted using the immersed boundary method. It was found that moderate chordwise deformation enhances the thrust, saves the power and increases the efficiency. A large $HAR$ can also increase thrust performance. By using the derivative-moment transformation theory at several subdomains to capture the local vortical structures and a force decomposition, it was shown that, at high Strouhal numbers ($St$), the tip vortex is the main source of thrust, whereas the leading-edge vortex (LEV) and trailing-edge vortex weaken the thrust generation. However, at lower $St$, the LEV would enhance the thrust. The least deformation ($W=0$) leads to the largest effective angle of attack, and thus the strongest vortices. However, moderate deformation ($W=0.4$) has an optimal balance between the performance enhancement and the opposite effect of different local structures. The performance enhancement of $HAR$ was also due to the increase of the vortical contributions. This work provides a new insight into the role of vortices and the force enhancement mechanism in aquatic swimming.

We study energy scale transfer in Rayleigh–Taylor (RT) flows by coarse graining in physical space without Fourier transforms, allowing scale analysis along the vertical direction. Two processes are responsible for kinetic energy flux across scales: baropycnal work $\varLambda$, due to large-scale pressure gradients acting on small scales of density and velocity; and deformation work $\varPi$, due to multiscale velocity. Our coarse-graining analysis shows how these fluxes exhibit self-similar evolution that is quadratic-in-time, similar to the RT mixing layer. We find that $\varLambda$ is a conduit for potential energy, transferring energy non-locally from the largest scales to smaller scales in the inertial range where $\varPi$ takes over. In three dimensions, $\varPi$ continues a persistent cascade to smaller scales, whereas in two dimensions $\varPi$ rechannels the energy back to larger scales despite the lack of vorticity conservation in two-dimensional (2-D) variable density flows. This gives rise to a positive feedback loop in 2-D RT (absent in three dimensions) in which mixing layer growth and the associated potential energy release are enhanced relative to 3-D RT, explaining the oft-observed larger $\alpha$ values in 2-D simulations. Despite higher bulk kinetic energy levels in two dimensions, small inertial scales are weaker than in three dimensions. Moreover, the net upscale cascade in two dimensions tends to isotropize the large-scale flow, in stark contrast to three dimensions. Our findings indicate the absence of net upscale energy transfer in three-dimensional RT as is often claimed; growth of large-scale bubbles and spikes is not due to ‘mergers’ but solely due to baropycnal work $\varLambda$.

Rheotaxis and migration of cells in a flow field have been investigated intensively owing to their importance in biology, physiology and engineering. In this study, first, we report our experiments showing that the microalgae Chlamydomonas can orient against the channel flow and migrate to the channel centre. Second, by performing boundary element simulations, we demonstrate that the mechanism of the observed rheotaxis and migration has a physical origin. Last, using a simple analytical model, we reveal the novel physical mechanisms of rheotaxis and migration, specifically the interplay between cyclic body deformation and cyclic swimming velocity in the channel flow. The discovered mechanism can be as important as phototaxis and gravitaxis, and likely plays a role in the movement of other natural microswimmers and artificial microrobots with non-reciprocal body deformation.

Transport equations for the normalized moments of the longitudinal velocity derivative 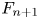${F_{n + 1}}$ (here, 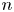$n$ is $1, 2, 3\ldots$) are derived from the Navier–Stokes (N–S) equations for shearless grid turbulence. The effect of the (large-scale) streamwise advection of 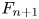${F_{n + 1}}$ by the mean velocity on the normalized moments of the velocity derivatives can be expressed as 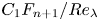$C_1 {F_{n + 1}}/Re_\lambda$, where 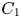$C_1$ is a constant and 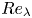$Re_\lambda$ is the Taylor microscale Reynolds number. Transport equations for the normalized odd moments of the transverse velocity derivatives 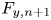${F_{y,n + 1}}$ (here, 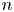$n$ is 2, 4, 6), which should be zero if local isotropy is satisfied, are also derived and discussed in sheared and shearless grid turbulence. The effect of the (large-scale) streamwise advection term on the normalized moments of the velocity derivatives can also be expressed in the form 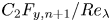$C_2 {F_{y,n + 1}}/Re_\lambda$, where 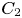$C_2$ is a constant. Finally, the contribution of the mean shear in the transport equation for 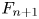${F_{n + 1}}$ can be modelled as 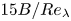$15 B/Re_\lambda$, where 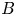$B$ (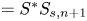$=S^*{S_{s,n + 1}}$) is the product of the non-dimensional shear parameter 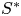$S^*$ and the normalized mixed longitudinal-transverse velocity derivatives 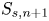${{S_{s,n + 1}}}$; if local isotropy is satisfied, 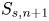$S_{s,n + 1}$ should be zero. These results indicate that if 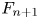${F_{n + 1}}$, 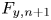${F_{y,n + 1}}$ and $B$ do not increase as rapidly as 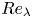$Re_\lambda$, then the effect of the large-scale structures on small-scale turbulence will disappear when 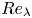$Re_\lambda$ becomes sufficiently large.

Many environmental flows arise due to natural convection at a vertical surface, from flows in buildings to dissolving ice faces at marine-terminating glaciers. We use three-dimensional direct numerical simulations of a vertical channel with differentially heated walls to investigate such convective, turbulent boundary layers. Through the implementation of a multiple-resolution technique, we are able to perform simulations at a wide range of Prandtl numbers ${Pr}$. This allows us to distinguish the parameter dependences of the horizontal heat flux and the boundary layer widths in terms of the Rayleigh number $\mbox {{Ra}}$ and Prandtl number ${Pr}$. For the considered parameter range $1\leq {Pr} \leq 100$, $10^{6} \leq \mbox {{Ra}} \leq 10^{9}$, we find the flow to be consistent with a ‘buoyancy-controlled’ regime where the heat flux is independent of the wall separation. For given ${Pr}$, the heat flux is found to scale linearly with the friction velocity $V_\ast$. Finally, we discuss the implications of our results for the parameterisation of heat and salt fluxes at vertical ice–ocean interfaces.

Bounds are derived for rotating Rayleigh–Bénard convection with free slip boundaries as a function of the Rayleigh, Taylor and Prandtl numbers ${\textit {Ra}}$, ${\textit {Ta}}$ and ${\textit {Pr}}$. At infinite ${\textit {Pr}}$ and ${\textit {Ta}} > 130$, the Nusselt number ${\textit {Nu}}$ obeys ${\textit {Nu}} \leqslant \frac {7}{36} \left ({4}/{{\rm \pi} ^2} \right )^{1/3} {\textit {Ra}} {\textit {Ta}}^{-1/3}$, whereas the kinetic energy density $E_{kin}$ obeys $E_{kin} \leqslant ({7}/{72 {\rm \pi}}) \left ({4}/{{\rm \pi} } \right )^{1/3} {\textit {Ra}}^2 {\textit {Ta}}^{-2/3}$ in the frame of reference in which the total momentum is zero, and $E_{kin} \leqslant ({1}/{2{\rm \pi} ^2})({{\textit {Ra}}^2}/{{\textit {Ta}}})({\textit {Nu}}-1)$. These three bounds are derived from the momentum equation and the maximum principle for temperature and are extended to general ${\textit {Pr}}$. The extension to finite ${\textit {Pr}}$ is based on the fact that the maximal velocity in rotating convection at infinite ${\textit {Pr}}$ is bound by $1.23 {\textit {Ra}} {\textit {Ta}}^{-1/3}$.