In this paper, we establish a number of theorems on the classic Diophantine equation of S. S. Pillai, ${{a}^{x}}-{{b}^{y}}=c$ , where $a,\,b$ and $c$ are given nonzero integers with $a,\,b\,\ge \,2$. In particular, we obtain the sharp result that there are at most two solutions in positive integers $x$ and $y$ and deduce a variety of explicit conditions under which there exists at most a single such solution. These improve or generalize prior work of Le, Leveque, Pillai, Scott and Terai. The main tools used include lower bounds for linear forms in the logarithms of (two) algebraic numbers and various elementary arguments.

Monotone paths on zonotopes and the natural generalization to maximal chains in the poset of topes of an oriented matroid or arrangement of pseudo-hyperplanes are studied with respect to a kind of local move, called polygon move or flip. It is proved that any monotone path on a $d$-dimensional zonotope with $n$ generators admits at least $\left\lceil 2n/\left( n-d+2 \right) \right\rceil -1$ flips for all $n\ge d+2\ge 4$ and that for any fixed value of $n-d$, this lower bound is sharp for infinitely many values of $n$. In particular, monotone paths on zonotopes which admit only three flips are constructed in each dimension $d\ge 3$. Furthermore, the previously known 2-connectivity of the graph of monotone paths on a polytope is extended to the 2-connectivity of the graph of maximal chains of topes of an oriented matroid. An application in the context of Coxeter groups of a result known to be valid for monotone paths on simple zonotopes is included.

Let $\mathcal{G}$ be a finite dimensional simple Lie algebra over the complex numbers $C$. Fernando reduced the classification of infinite dimensional simple $\mathcal{G}$-modules with a finite dimensional weight space to determining the simple torsion free $\mathcal{G}$-modules for $\mathcal{G}$ of type $A$ or $C$. These modules were determined by Mathieu and using his work we provide a more elementary construction realizing each one as a submodule of an easily constructed tensor product module.

In this paper, we study the Mordell-Weil group of an elliptic curve as a Galois module. We consider an elliptic curve 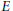$E$ defined over a number field 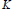$K$ whose Mordell-Weil rank over a Galois extension $F$ is 1, 2 or 3. We show that 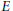$E$ acquires a point (points) of infinite order over a field whose Galois group is one of 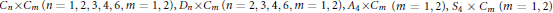${{C}_{n}}\times {{C}_{m}}(n=1,\,2,\,3,\,4,\,6,\,m\,=\,1,\,2),\,{{D}_{n}}\times {{C}_{m}}(n=2,\,3,\,4,\,6,\,m=\,1,\,2),\,{{A}_{4}}\times {{C}_{m}}(m=1,\,2),\,{{S}_{4}}\,\times \,{{C}_{m}}(m=1,\,2)$ . Next, we consider the case where 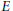$E$ has complex multiplication by the ring of integers 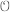$\mathcal{O}$ of an imaginary quadratic field 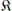$\Re $ contained in 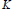$K$. Suppose that the 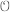$\mathcal{O}$-rank over a Galois extension $F$ is 1 or 2. 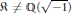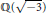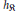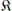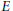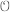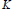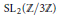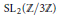If $\Re \ne \mathbb{Q}(\sqrt{-1})$ and $\mathbb{Q}(\sqrt{-3})$ and ${{h}_{\Re }}$ (class number of $\Re $) is odd, we show that $E$ acquires positive $\mathcal{O}$-rank over a cyclic extension of $K$ or over a field whose Galois group is one of $\text{S}{{\text{L}}_{2}}(\mathbb{Z}/3\mathbb{Z})$ , an extension of $\text{S}{{\text{L}}_{2}}(\mathbb{Z}/3\mathbb{Z})$ by 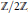$\mathbb{Z}/2\mathbb{Z}$, or a central extension by the dihedral group. Finally, we discuss the relation of the above results to the vanishing of 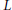$L$-functions.

The Russell-Koras contractible threefolds are the smooth affine threefolds having a hyperbolic ${{\mathbb{C}}^{*}}$-action with quotient isomorphic to the corresponding quotient of the linear action on the tangent space at the unique fixed point. Koras and Russell gave a concrete description of all such threefolds and determined many interesting properties they possess. We use this description and these properties to compute the equivariant Grothendieck groups of these threefolds. In addition, we give certain equivariant invariants of these rings.

The representation parabolically induced from an irreducible supercuspidal representation is considered. Irreducible components of Jacquet modules with respect to induction in stages are given. The results are used for consideration of generalized Steinberg representations.

We classify all 3 letter patterns that are avoidable in the abelian sense. A short list of four letter patterns for which abelian avoidance is undecided is given. Using a generalization of Zimin words we deduce some properties of $\omega$-words avoiding these patterns.

We determine the poles of the standard intertwining operators for a maximal parabolic subgroup of the quasi-split unitary group defined by a quadratic extension $E/F$ of $p$-adic fields of characteristic zero. We study the case where the Levi component $M\simeq \text{G}{{\text{L}}_{n}}\left( E \right)\times {{U}_{m}}\left( F \right)$, with $n\,\equiv \,m\,\left( \bmod \,2 \right)$. This, along with earlier work, determines the poles of the local Rankin-Selberg product $L$-function $L\left( s,\,{\tau }'\,\times \,\tau \right)$, with ${\tau }'$ an irreducible unitary supercuspidal representation of $\text{G}{{\text{L}}_{n}}\left( E \right)$ and $\tau $ a generic irreducible unitary supercuspidal representation of ${{U}_{m}}\left( F \right)$. The results are interpreted using the theory of twisted endoscopy.

Let $\mathbf{H}$ be the Hilbert function of some set of distinct points in ${{\mathbb{P}}^{n}}$ and let $\alpha \,=\,\alpha (\mathbf{H})$ be the least degree of a hypersurface of ${{\mathbb{P}}^{n}}$ containing these points. Write $\alpha ={{d}_{s}}+{{d}_{s-1}}+\cdot \cdot \cdot +{{d}_{1}}$ (where ${{d}_{i}}>0$ ). We canonically decompose $\mathbf{H}$ into $s$ other Hilbert functions $\text{H}\leftrightarrow \text{(}{{\text{H}'}_{s}}\text{,}...\text{,}{{\text{H}'}_{1}}\text{)}$ and show how to find sets of distinct points ${{\mathbb{Y}}_{s}},...,{{\mathbb{Y}}_{1}}$ , lying on reduced hypersurfaces of degrees ${{d}_{s}},...,{{d}_{1}}$ (respectively) such that the Hilbert function of ${{\mathbb{Y}}_{i}}$ is ${{\text{H'}}_{i}}$ and the Hilbert function of $\mathbb{Y}=\bigcup _{i=1}^{s}\,{{\mathbb{Y}}_{i}}$ is $\mathbf{H}$. Some extremal properties of this canonical decomposition are also explored.

A homogeneous real polynomial $p$ is hyperbolic with respect to a given vector $d$ if the univariate polynomial $t\,\mapsto \,p(x\,-\,td)$ has all real roots for all vectors $x$. Motivated by partial differential equations, Gårding proved in 1951 that the largest such root is a convex function of $x$, and showed various ways of constructing new hyperbolic polynomials. We present a powerful new such construction, and use it to generalize Gårding’s result to arbitrary symmetric functions of the roots. Many classical and recent inequalities follow easily. We develop various convex-analytic tools for such symmetric functions, of interest in interior-point methods for optimization problems over related cones.

Soient $F$ un corps commutatif localement compact non archimédien et $\psi$ un caractère additif non trivial de $F$. Soient $n$ et ${n}'$ deux entiers distincts, supérieurs à 1. Soient $\pi$ et ${\pi }'$ des représentations irréductibles supercuspidales de $\text{G}{{\text{L}}_{n}}\left( F \right)$, $\text{G}{{\text{L}}_{{{n}'}}}\left( F \right)$ respectivement. Nous prouvons qu’il existe un élément $c=c\left( \pi ,{\pi }',\psi \right)$ de ${{F}^{\times }}$ tel que pour tout quasicaractère modéré $\mathcal{X}$ de ${{F}^{\times }}$ on ait $\mathcal{E}\left( \chi \pi \times {\pi }',s,\psi \right)=\chi {{\left( c \right)}^{-1}}\mathcal{E}\left( \pi \times {\pi }',s,\psi \right)$. Nous examinons aussi certains cas où $n={n}',{\pi }'={{\pi }^{\text{v}}}$. Les résultats obtenus forment une étape vers une démonstration de la conjecture de Langlands pour $F$, qui ne fasse pas appel à la géométrie des variétés modulaires, de Shimura ou de Drinfeld.

We give explicit formulas for the ${{L}_{4}}$ norm (or equivalently for the merit factors) of various sequences of polynomials related to the polynomials

$$f\left( z \right):=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n}{N} \right){{z}^{n}}.}$$

and

$${{f}_{t}}(z)\,=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n+t}{N} \right){{z}^{n}}.}$$

where $\left( \frac{.}{N} \right)$ is the Jacobi symbol.

Two cases of particular interest are when $N\,=\,pq$ is a product of two primes and $p\,=\,q\,+\,2$ or $p\,=\,q\,+\,4$. This extends work of Høholdt, Jensen and Jensen and of the authors.

This study arises from a number of conjectures of Erdős, Littlewood and others that concern the norms of polynomials with −1, 1 coefficients on the disc. The current best examples are of the above form when $N$ is prime and it is natural to see what happens for composite $N$.

Bivariate polynomials with a fixed leading term ${{x}^{m}}{{y}^{n}}$ , which deviate least from zero in the uniform or ${{L}^{2}}$-norm on the unit disk $D$ (resp. a triangle) are given explicitly. A similar problem in ${{L}^{p}}$ , $1\,\le \,p\,\le \,\infty $ is studied on $D$ in the set of products of linear polynomials.

We present a new approach to singular reduction of Hamiltonian systems with symmetries. The tools we use are the category of differential spaces of Sikorski and the Stefan-Sussmann theorem. The former is applied to analyze the differential structure of the spaces involved and the latter is used to prove that some of these spaces are smooth manifolds.

Our main result is the identification of accessible sets of the generalized distribution spanned by the Hamiltonian vector fields of invariant functions with singular reduced spaces. We are also able to describe the differential structure of a singular reduced space corresponding to a coadjoint orbit which need not be locally closed.

We prove a strong variant of the Borwein-Preiss variational principle, and show that on Asplund spaces, Stegall's variational principle follows from it via a generalized Smulyan test. Applications are discussed.

Let $G$ be a solvable exponential Lie group. We characterize all the continuous topologically irreducible bounded representations $(T,\mathcal{U})$ of $G$ on a Banach space $\mathcal{U}$ by giving a $G$-orbit in ${{n}^{*}}$ ($\mathfrak{n}$ being the nilradical of $\mathfrak{g}$), a topologically irreducible representation of ${{L}^{1}}({{\mathbb{R}}^{n}},\,\,\omega )$ , for a certain weight $\omega $ and a certain $n\,\in \,\mathbb{N}$, and a topologically simple extension norm. If $G$ is not symmetric, i.e., if the weight $\omega $ is exponential, we get a new type of representations which are fundamentally different from the induced representations.

In this paper it is shown that inclusions inside the Segal-Wilson Grassmannian give rise to Darboux transformations between the solutions of the $\text{KP}$ hierarchy corresponding to these planes. We present a closed form of the operators that procure the transformation and express them in the related geometric data. Further the associated transformation on the level of $\tau $-functions is given.

We use some results about stable relations to show that some of the simple, stable, projectionless crossed products of ${{O}_{2}}$ by $\mathbb{R}$ considered by Kishimoto and Kumjian are inductive limits of type I ${{C}^{*}}$-algebras. The type I ${{C}^{*}}$-algebras that arise are pullbacks of finite direct sums of matrix algebras over the continuous functions on the unit interval by finite dimensional ${{C}^{*}}$-algebras.

In this paper, we investigate stratification theory in terms of the defining equations of strata and maps (without tube systems), offering a concrete approach to show that some given family is topologically trivial. In this approach, we consider a weighted version of $\left( w \right)$-regularity condition and Kuo’s ratio test condition.

We provide the reader with a uniform approach for obtaining various useful explicit upper bounds on residues of Dedekind zeta functions of numbers fields and on absolute values of values at $s=1$ of $L$-series associated with primitive characters on ray class groups of number fields. To make it quite clear to the reader how useful such bounds are when dealing with class number problems for CM-fields, we deduce an upper bound for the root discriminants of the normal CM-fields with (relative) class number one.